绝对定向及算例
定类尺度支持的典型数学运算

定类尺度支持的典型数学运算
绝对值尺度支持的典型数学运算包括加法、减法、乘法和除法。
加法:绝对值尺度支持的加法运算是指将两个数的绝对值相加,即$|a|+|b|$,其中$a$和$b$分别为两个数。
例如,$|3|+|-4|=|3+(-4)|=|-1|=1$。
减法:绝对值尺度支持的减法运算是指将两个数的绝对值相减,即$|a|-|b|$,其中$a$和$b$分别为两个数。
例如,$|3|-|-4|=|3-(-4)|=|7|=7$。
乘法:绝对值尺度支持的乘法运算是指将两个数的绝对值相乘,即$|a|\times|b|$,其中$a$和$b$分别为两个数。
例如,
$|3|\times|-4|=|3\times(-4)|=|-12|=12$。
除法:绝对值尺度支持的除法运算是指将两个数的绝对值相除,即$\frac{|a|}{|b|}$,其中$a$和$b$分别为两个数。
例如,
$\frac{|3|}{|-4|}=\frac{|3|}{|4|}=\frac{3}{4}$。
此外,绝对值尺度还支持求幂运算,即$|a|^b$,其中$a$和
$b$分别为两个数。
例如,$|3|^2=|3|\times|3|=9$。
学习测绘技术中的相对定向与绝对定向原理与方法

学习测绘技术中的相对定向与绝对定向原理与方法测绘技术是土地资源管理、城市规划、地形地貌、环境保护等领域中不可或缺的重要工具。
其中,相对定向和绝对定向是测绘技术中两个重要的概念。
本文将深入探讨相对定向与绝对定向的原理与方法。
一、相对定向的原理与方法相对定向是测绘技术中的一个基本概念,其主要目的是确定不同航片之间的相对方位关系。
相对定向的过程包括:图像坐标测量、航带布方、相对定向计算和网片平差。
1. 图像坐标测量图像坐标测量是相对定向的第一步,主要通过肉眼观察或计算机自动提取特征点进行。
常用的特征点有角点、交点等,可以通过这些特征点在航带上进行标注和测量,得到图像坐标。
2. 航带布方航带布方是相对定向的一个重要环节,其目的是实现不同航带之间的精确定位。
布方需要确定具有高精度的起始点、目标点和连接点作为基准,通过测量和计算航带之间的连线长度和角度,确定航带之间的相对位置关系。
3. 相对定向计算相对定向计算是相对定向的核心部分,其主要目的是通过空间后方交会等方法计算不同航带之间的相对方位关系。
常见的相对定向计算方法有解析解法和数值解法。
解析解法适用于简单的相对定向问题,而数值解法适合于复杂的相对定向问题。
4. 网片平差网片平差是相对定向的最后一步,其主要目的是通过调整和优化相对定向计算结果,消除误差。
常见的网片平差方法有最小二乘法和全球最小差法。
最小二乘法通过最小化观测值与估计值的残差平方和来求得最优解,而全球最小差法则通过迭代求解来优化结果。
二、绝对定向的原理与方法绝对定向是在相对定向的基础上,确定航片与地面坐标系之间的外方位元素。
绝对定向包括地面控制点选择、光束法平差、外方位元素计算以及精度评定等步骤。
1. 地面控制点选择地面控制点是绝对定向的基础,其目的是通过标志物或人工测量点将航片与地面实际坐标系联系起来。
选择合适的地面控制点需要兼顾数量、分布、均匀性以及观测条件等因素。
2. 光束法平差光束法平差是绝对定向的核心环节,其目的是根据航测数据和地面控制数据,通过光束法的原理进行计算和调整。
相对定向和绝对定向的解析过程(全面)
三、相对定向元素的计算过程
量测 5 个以上的同名点(定向点) 明显点 1、2点:左、右片的像主点 人工量测:六个标准点位 3、5点:X=0,Y值最大 4、6点:X=b,Y值最大
3
4
X
1
2
5
6
相对定向标准点位
计算框图:以连续像对的相对定向为例
输入像点坐标 (x1,y1),(x2,y2) 确定初始值bu=(x1-x2)1 φ 2=ω 2=κ 2=μ =ν =0 计算右片旋转矩阵R2 计算像点的像空间辅助坐 标(u1 v1 w1)和(u2 v2 w2) 逐点计算误差方程式系数 和常数项 否
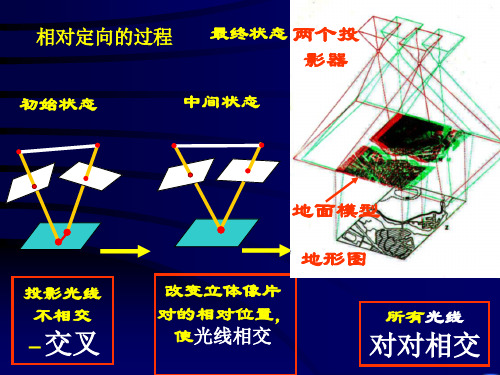
相对定向的过程
初始状态
最终状态 两个投
影器
中间状态
地面模型 地形图
投影光线 不相交
-交叉 改变立体像片 对的相对位置, 使光线相交 所有光线
对对相交
1、连续像对相对定向元素:以左片为基准,右片相对于 左片的相对方位元素 S1 u1v1w1 左片的像空间坐标系 像空间辅助坐标系的选取: S2 u2v2 w2 与 S1 u1v1w1相应坐标轴平行 w2 左、右片相对方位元素 v2 左像片 S2 w1 u2 X S1 0, YS1 0, Z S1 0 y b B w v1 1 0, 1 0, 1 0 bv 右像片 S u
w1 w2
v1
S1 u1
y1
v2 b
S2
X S1 0, YS1 0, Z S1 0
u2
1 , 1 0, 1
右像片
X S 2 bu b, YS 2 bv 0, Z S 2 bw 0
y2
x2
1
1 2
1、1、2、2、2
如何进行相对定向测量与绝对定向测量

如何进行相对定向测量与绝对定向测量相对定向测量与绝对定向测量是测量地球表面和大地构造的常用方法。
它们在测绘、地理信息系统、地质勘探等领域中具有重要的应用价值。
本文将从原理、方法和应用三个方面来介绍相对定向测量与绝对定向测量。
相对定向测量是利用已知位置和方位的控制点,通过测量照片上某个点与控制点之间的方位角和高差,来确定照片上其他点的位置和方位角。
相对定向测量的基本原理是三角形的解算。
首先,通过在控制点上设置捕捉点,使其精确地被相机镜头对应,然后通过测量照片上该点与控制点之间的方位角和倾角,就可以精确地确定照片上其他点的位置和方位角。
在相对定向测量中,常用的方法有后方交会法和前方交会法。
后方交会法是根据从控制点到摄影点的方位角和倾角,以及照片上点到摄影点的方位角和倾角,通过三角形解算,确定照片上点的位置和方位角。
而前方交会法是根据从摄影点到控制点的方位角和倾角,以及照片上点到摄影点的方位角和倾角,通过三角形解算,确定照片上点的位置和方位角。
相对定向测量的应用非常广泛。
在测绘中,它可以用于制作地形图、建筑物平面图等。
在地理信息系统中,它可以用于精确定位和定向照片。
在地质勘探中,它可以用于分析构造和地质现象。
相对定向测量的精度主要受到控制点的精度、照片质量和测量仪器的准确性等因素的影响。
为了提高相对定向测量的精度,需要采用高精度的仪器设备和精确的控制点。
绝对定向测量是通过测量控制点的大地坐标和相机的姿态参数,来确定照片上点的绝对坐标。
绝对定向测量的基本原理是三维解算。
通过在地面上设置控制点,测量其大地坐标,并利用观测数据计算相机的姿态参数,然后再利用相机模型和三维解算方法,确定照片上点的绝对坐标。
在绝对定向测量中,常用的方法有公式解算法和数值解算法。
公式解算法是根据相机模型和观测数据,通过一系列公式来解算照片上点的绝对坐标。
数值解算法是根据相机模型和观测数据,采用数值迭代的方法,通过优化算法来解算照片上点的绝对坐标。
第11讲-绝对定向

XT XT
0
d = - 0, d = - 0, d = - 0, d X0 = X0 - X0 0, d Y0 = Y0 - Y0 0 , d Z0 = Z0 - Z0 0
X T X T X T X T X T dX 0 d d d d X 0
0
( d )( E dM )M X ( X 0 d X 0 )
0 0
0
M X X 0 dM 0 X 0 dMM 0 X ddMM 0 X d X 0
0 0
0
XT
X 0 M 0 X 0 X 0 X 0 X X T dd ' 0 M0 dMMdM dM0 0 X
X T Z tr YT 0 Z T X tr X T Ytr sin YT X tr sin Z tr cos ZT Ytr cos XT 0 YT c3 Z T b3 c3 0 a3 b3 X tr a3 Ytr 0 Z tr
a2 b2 c2
a3 X X 0 b3 Y Y0 c3 Z Z 0
为比例尺因子。
一、绝对定向方程——空间相似变换
XT YT Z T
a1 b1 c 1
三、绝对定向的解算与坐标重心化
• 绝对定向元素的最小二乘解 误差方程式
1 0 0 X 0 1 0 Y 0 0 1 Z 0 Z Y Z 0 X dX 0 dY0 Y dZ0 X Vx X d' Y Vy 0 d Z Vz d d
《摄影测量与遥感》知识点课件-15 相对定向-绝对定向解算地面点坐标

主讲人:孙宝明
课程导入
1、双像解析摄影测量中,该如何处理两张像片的关系呢?
1.相对定向—绝对定向方法
确定一张航摄像片(或摄影光束)在地面坐标系统中的 方位,需要六个外方位元素
影基线b为U轴,左主光轴与摄影基线组成的左主核面为
UW面,V轴垂直于该面构成右手直角坐标系,如图所示。
这一种像空间辅助坐标系也叫做基线坐标系。所以说,
单独像对相对定向系统是以基线坐标系为参考基准的。
W1 V1
W2 V2
S1
y1 1
b U1
o1
1
x1
左主核面
S2 2
U2
y2
2
x2
o2
2 右主核面
2.2单独像对相对定向
左、右像片的相对方位元素为: 左像片:US1=VS1=WS1=0, φ1,ω1=0,κ1 左像片:US2=bu=b,VS2= bv=0,WS2= bw=0,φ2,ω2,
κ2 同样,b只涉及模型比例尺的大小,而不影响模型的建立,
因此,单独像对相对定向元素系统由五个角元素φ1, κ1,φ2,ω2,κ2组成。
左片:Xs1、Ys1、Zs1、φ1、ω1、κ1; 右片:Xs2、Ys2、Zs2、φ2、ω2、κ2。
恢复立体像对中两张像片的12个外方位元素即能恢复其 绝对位置和姿态,重建被摄地面的绝对立体模型。
1.相对定向—绝对定向方法
首先暂不考虑像片的绝对位置和姿态,而只恢复两 张像片之间的相对位置和姿态,这样建立的立体模型称 为相对立体模型,其比例尺和方位均是任意的;然后在 此基础上,将两张像片作为一个整体进行缩放、平移和 旋转,达到绝对位置。这种方法称为相对定向—绝对定 向。
绝对定向和相对定向名词解释

绝对定向和相对定向名词解释
绝对定向和相对定向是两种在移动广告中用于定位和指定广告受众的术语。
绝对定向是指将广告投放到特定的地理位置或者其他特定的受众属性中,例如特定的群体,性别,年龄或兴趣等等。
通常使用 GPS 或其他地理位置技术进行定位。
相对定向是指根据已知的数据,例如用户的浏览历史,搜索行为或应用下载历史来定向广告受众。
这种方式常常用于展示与用户兴趣相关的广告。
两种定向技术都是为了提高广告效果,提高广告投放精度而被广告主广泛使用的。
绝对定向及算例23页PPT

绝对ห้องสมุดไป่ตู้向及算例
11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析绝对定向误差方程
记
X tp X p X0 F Ytp R Yp Y0 Z tp Zp Z0
F F F F F F F X 0 Y0 Z 0 X 0 Y0 Z 0
《摄影测量学》第六章
解析法绝对定向
山东理工大学
建筑工程学院 测量系
上节课内容
核心词:3-6解析法相对定向
1、相对定向原理是:满足同名光线相交条 件,建立与实物相似的几何模型。 2、相对定向相对定向元素和解的数 学模型。
bx F X1 X2
bx bx Y1 Y2 Z1 Z2
Z2
1 bx X 1 Y1 X 2 Y2
常数项
l F F0
0 X X X l X tp p 0 lY Ytp 0 R 0 Yp Y00 0 l Z Z tp Zp Z0
解析绝对定向误差方程 设•Fra bibliotekYtpg
Y
n
n
Z tpg
Z tpi
1
n
解析绝对定向误差方程 设
0 1, 0 0 0 0
Z1 0 Z2
Z1
Y1
bZ bY
X1
Y2
X2
S2
S1
a1
bX
a2
A
Y2 X 2Y2 Y22 Q bx d bx d N2d ( Z 2 ) N2d X 2 N2d Z2 Z2 Z2
X 2Y2 Y22 Y2 VQ d (Z 2 ) N 2 d X 2 N 2 d bx d bx d Q Z2 Z2 Z2
X p X F R Yp Y Zp Z
Y cos cos Z sin F X cos cos Z sin cos X sin Y sin cos
给定绝对定向元素的初值 =1, == = 0, X0, Y0, Z0
计算重心化坐标 计算误差方程式的系数和常数项 解法方程,求绝对定向元素改正数 计算绝对定向元素的新值 判断迭代是否收敛
重心坐标
X pg
重心化坐标
X p X p X pg Yp Yp Ypg Z p Z p Z pg
绝对定向公式
X tp X p X0 Y R Y Y tp p 0 Z tp Zp Z0
Ztp Z0 Ytp X0 Y0
M
Xtp
绝对定向元素: ,X0 , Y0 , Z0 ,, ,
0 1, 0 0 0 0
则
v X 1 0 0 vY 0 1 0 v 0 0 1 Z
X 0 Y0 X Z 0 Y Z 0 l X Y 0 Z X lY Z X Y 0 l Z
F F0
偏导数
1 F 0 X 0 0 0 F 1 Y0 0 0 F 0 Z 0 1
Z F 0 X
Y sin F X sin Z cos Y cos
法方程的建立与求解
量测 2 个平高和 1 个高程以上的控制点可以按 最小二乘平差法求绝对定向元素
V Ax l ,
P
x ( AT PA) 1 ( AT Pl)
V T PV 0 3n 7
Qxx ( AT PA)1
ii mi 0 Qxx
三、绝对定向元素的计算
获取控制点的两套坐标 Xp , Yp , Zp , Xtp , Ytp , Ztp
3、相对定向参数解算步骤
1. 立体坐标量测仪上,两侧选定的6个定向点 的像点坐标 2. 确定参数初始值; 3. 根据初始值,计算右片旋转矩阵R2; 4. 根据输入的像点平面坐标,计算像空间辅助 坐标系; 5. 根据给定的初始值,并根据像空间辅助坐标, 计算个点的投影系数;
6 计算每个定向点的误差方程常数项及系数项, 组成误差方程式。 7 计算法方程系数矩阵及常数项,并求解法方程, 求得未知数的改正数。 8 求未知数新值,即初始值改正数。 9 检查未知数的改正数是否大于限差,若大于限 差,则重复(4)-(9)步的计算,直到所有改 正数都小于限差为止。
目的
• 减少模型点 坐标在计算 过程中的有 效位数,以 保证计算的 精度 使法方程的 系数简化, 个别项数值 变为零,以 提高计算速 度
X
1
n
pi
n
n pi 1
Y pg
Y
n
n
Z pg
Z
1
pi
n
X tpg
X
1
n
tpi
n
n tpi 1
X tp X tp X tpg Ytp Ytp Ytpg Z tp Z tp Z tpg
主要内容
一、绝对定向元素
二、解析绝对定向原理 三、绝对定向元素计算 四、地面坐标计算
一、绝对定向元素
描述立体像对在摄影瞬间的 绝对位置和姿态的参数称~ 通过将相对定向模型进行缩 放、平移和旋转,使其达到 绝对位置
绝对定向元素
Ztp
M
Z0 Ytp X0 Y0
Xtp
绝对定向元素: ,X0 , Y0 , Z0 ,, ,
