2020年甘肃省白银市中考数学试卷

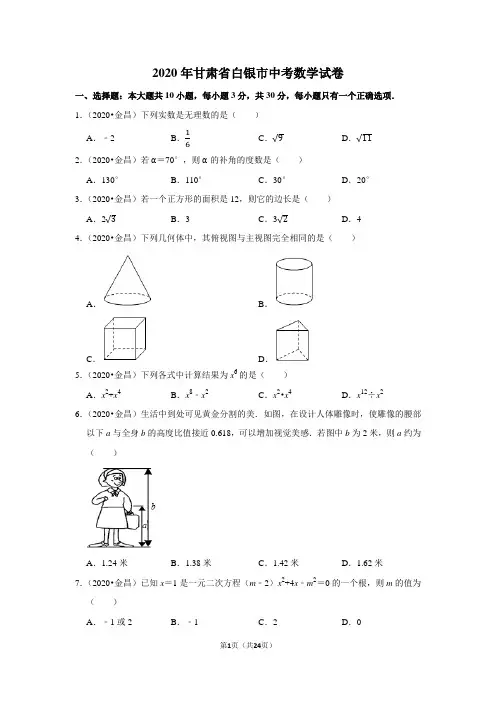
2020年甘肃省白银市中考数学试卷一、选择题：本大题共10小题，每小题3分，共30分，每小题只有一个正确选项．1．（3分）（2020•金昌）下列实数是无理数的是（ ）A ．﹣2B ．16C ．√9D ．√112．（3分）（2020•金昌）若α＝70°，则α的补角的度数是（ ）A ．130°B ．110°C ．30°D ．20°3．（3分）（2020•金昌）若一个正方形的面积是12，则它的边长是（ ）A ．2√3B ．3C ．3√2D ．44．（3分）（2020•金昌）下列几何体中，其俯视图与主视图完全相同的是（ ）A ．B ．C ．D ．5．（3分）（2020•金昌）下列各式中计算结果为x 6的是（ ）A ．x 2+x 4B ．x 8﹣x 2C ．x 2•x 4D ．x 12÷x 26．（3分）（2020•金昌）生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下a 与全身b 的高度比值接近0.618，可以增加视觉美感．若图中b 为2米，则a 约为（ ）A ．1.24米B ．1.38米C ．1.42米D ．1.62米7．（3分）（2020•金昌）已知x ＝1是一元二次方程（m ﹣2）x 2+4x ﹣m 2＝0的一个根，则m的值为（ ）A ．﹣1或2B ．﹣1C ．2D ．08．（3分）（2020•金昌）如图所示的木制活动衣帽架是由三个全等的菱形构成，根据实际需要可以调节AE间的距离．若AE间的距离调节到60cm，菱形的边长AB＝20cm，则∠DAB 的度数是（）A．90°B．100°C．120°D．150°9．（3分）（2020•金昌）如图，A是⊙O上一点，BC是直径，AC＝2，AB＝4，点D在⊙Ô，则DC的长为（）上且平分BCA．2√2B．√5C．2√5D．√1010．（3分）（2020•金昌）如图①，正方形ABCD中，AC，BD相交于点O，E是OD的中点．动点P从点E出发，沿着E→O→B→A的路径以每秒1个单位长度的速度运动到点A，在此过程中线段AP的长度y随着运动时间x的函数关系如图②所示，则AB的长为（）A．4√2B．4C．3√3D．2√2二、填空题：本大题共8小题，每小题3分，共24分．11．（3分）（2020•金昌）如果盈利100元记作+100元，那么亏损50元记作元．12．（3分）（2020•金昌）分解因式：a 2+a ＝ ．13．（3分）（2020•金昌）暑假期间，亮视眼镜店开展学生配镜优惠活动．某款式眼镜的广告如下，请你为广告牌填上原价．原价： 元暑假八折优惠，现价：160元14．（3分）（2020•金昌）要使分式x+2x−1有意义，x 需满足的条件是 ．15．（3分）（2020•金昌）在一个不透明的袋中装有若干个材质、大小完全相同的红球，小明在袋中放入3个黑球（每个黑球除颜色外其余都与红球相同），摇匀后每次随机从袋中摸出一个球，记录颜色后放回袋中，通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，估计袋中红球有 个．16．（3分）（2020•金昌）如图，在平面直角坐标系中，△OAB 的顶点A ，B 的坐标分别为（3，√3），（4，0）．把△OAB 沿x 轴向右平移得到△CDE ，如果点D 的坐标为（6，√3），则点E 的坐标为 ．17．（3分）（2020•金昌）若一个扇形的圆心角为60°，面积为π6cm 2，则这个扇形的弧长为 cm （结果保留π）．18．（3分）（2020•金昌）已知y =√(x −4)2−x +5，当x 分别取1，2，3，…，2020时，所对应y 值的总和是 ．三、解答题（一）：本大题共5小题，共26分．解答应写出必要的文字说明，证明过程或演算步骤．19．（4分）（2020•金昌）计算：（2−√3）（2+√3）+tan60°﹣（π﹣2√3）0．20．（4分）（2020•金昌）解不等式组：{3x −5＜x +12(2x −1)≥3x −4，并把它的解集在数轴上表示出来．21．（6分）（2020•金昌）如图，在△ABC 中，D 是BC 边上一点，且BD ＝BA ．（1）尺规作图（保留作图痕迹，不写作法）：①作∠ABC的角平分线交AD于点E；②作线段DC的垂直平分线交DC于点F．（2）连接EF，直接写出线段EF和AC的数量关系及位置关系．22．（6分）（2020•金昌）图①是甘肃省博物馆的镇馆之宝﹣﹣铜奔马，又称“马踏飞燕”，于1969年10月出土于武威市的雷台汉墓，1983年10月被国家旅游局确定为中国旅游标志．在很多旅游城市的广场上都有“马踏飞燕”雕塑．某学习小组把测量本城市广场的“马踏飞燕”雕塑（图②）最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：课题测量“马踏飞燕“雕塑最高点离地面的高度测量示意图如图，雕塑的最高点B 到地面的高度为BA，在测点C用仪器测得点B 的仰角为α，前进一段距离到达测点E，再用该仪器测得点B 的仰角为β，且点A，B，C，D，E，F均在同一竖直平面内，点A，C，E在同一条直线上．测量数据α的度数β的度数CE的长度仪器CD（EF）的高度31°42°5米1.5米请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度（结果保留一位小数）．（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60，sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）23．（6分）（2020•金昌）2019年甘肃在国际知名旅游指南《孤独星球》亚洲最佳旅游地排名第一．截至2020年1月，甘肃省已有五家国家5A级旅游景区，分别为A：嘉峪关文物景区；B：平凉崆峒山风景名胜区；C：天水麦积山景区；D：敦煌鸣沙山月牙泉景区；E：张掖七彩丹霞景区．张帆同学与父母计划在暑假期间从中选择部分景区游玩．（1）张帆一家选择E：张掖七彩丹霞景区的概率是多少？（2）若张帆一家选择了E：张掖七彩丹霞景区，他们再从A，B，C，D四个景区中任选两个景区去旅游，求选择A，D两个景区的概率（要求画树状图或列表求概率）．四、解答题（二）：本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤．24．（7分）（2020•金昌）习近平总书记于2019年8月在兰州考察时说“黄河之滨也很美”．兰州是古丝绸之路商贸重镇，也是黄河唯一穿城而过的省会城市，被称为“黄河之都”．近年来，在市政府的积极治理下，兰州的空气质量得到极大改善，“兰州蓝”成为兰州市民引以为豪的城市名片．如图是根据兰州市环境保护局公布的2013～2019年各年的全年空气质量优良天数绘制的折线统计图．请结合统计图解答下列问题：（1）2019年比2013年的全年空气质量优良天数增加了天；（2）这七年的全年空气质量优良天数的中位数是天；（3）求这七年的全年空气质量优良天数的平均天数；（4）《兰州市“十三五”质量发展规划》中指出：2020年，确保兰州市全年空气质量优良天数比率达80%以上．试计算2020年（共366天）兰州市空气质量优良天数至少需要多少天才能达标．25．（7分）（2020•金昌）通过课本上对函数的学习，我们积累了一定的经验．下表是一个函数的自变量x与函数值y的部分对应值，请你借鉴以往学习函数的经验，探究下列问题：x…012345…y…632 1.5 1.21…（1）当x＝时，y＝1.5；（2）根据表中数值描点（x，y），并画出函数图象；（3）观察画出的图象，写出这个函数的一条性质：．26．（8分）（2020•金昌）如图，⊙O是△ABC的外接圆，其切线AE与直径BD的延长线相交于点E，且AE＝AB．（1）求∠ACB的度数；（2）若DE＝2，求⊙O的半径．27．（8分）（2020•金昌）如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN ＝45°．把△ADN绕点A顺时针旋转90°得到△ABE．（1）求证：△AEM≌△ANM．（2）若BM＝3，DN＝2，求正方形ABCD的边长．28．（10分）（2020•金昌）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣2交x轴于A，B两点，交y轴于点C，且OA＝2OC＝8OB．点P是第三象限内抛物线上的一动点．（1）求此抛物线的表达式；（2）若PC∥AB，求点P的坐标；（3）连接AC，求△P AC面积的最大值及此时点P的坐标．参考答案一、选择题：本大题共10小题，每小题3分，共30分，每小题只有一个正确选项．1．（3分）（2020•金昌）下列实数是无理数的是（ ）A ．﹣2B ．16C ．√9D ．√11【解答】解：√9=3，则由无理数的定义可知，实数是无理数的是√11．故选：D ．2．（3分）（2020•金昌）若α＝70°，则α的补角的度数是（ ）A ．130°B ．110°C ．30°D ．20°【解答】解：α的补角是：180°﹣∠A ＝180°﹣70°＝110°．故选：B ．3．（3分）（2020•金昌）若一个正方形的面积是12，则它的边长是（ ）A ．2√3B ．3C ．3√2D ．4【解答】解：∵正方形的面积是12，∴它的边长是√12=2√3．故选：A ．4．（3分）（2020•金昌）下列几何体中，其俯视图与主视图完全相同的是（ ）A ．B ．C ．D ．【解答】解：圆锥的主视图是等腰三角形，俯视图是圆，因此A 不符合题意；圆柱的主视图是矩形，俯视图是圆，因此B 不符合题意；正方体的主视图、俯视图都是正方形，因此选项C 符合题意；三棱柱的主视图是矩形，俯视图是三角形，因此D 不符合题意；故选：C ．5．（3分）（2020•金昌）下列各式中计算结果为x 6的是（ ）A ．x 2+x 4B ．x 8﹣x 2C ．x 2•x 4D ．x 12÷x 2【解答】解：x 2与x 4不是同类项，不能合并计算，它是一个多项式，因此A 选项不符合题意；同理选项B 不符合题意；x 2•x 4＝x 2+4＝x 6，因此选项C 符合题意；x 12÷x 2＝x 12﹣2＝x 10，因此选项D 不符合题意； 故选：C ．6．（3分）（2020•金昌）生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下a 与全身b 的高度比值接近0.618，可以增加视觉美感．若图中b 为2米，则a 约为（ ）A ．1.24米B ．1.38米C ．1.42米D ．1.62米【解答】解：∵雕像的腰部以下a 与全身b 的高度比值接近0.618，∴a b ≈0.618， ∵b 为2米，∴a 约为1.24米．故选：A ．7．（3分）（2020•金昌）已知x ＝1是一元二次方程（m ﹣2）x 2+4x ﹣m 2＝0的一个根，则m的值为（ ）A ．﹣1或2B ．﹣1C ．2D ．0【解答】解：把x ＝1代入（m ﹣2）x 2+4x ﹣m 2＝0得：m ﹣2+4﹣m 2＝0，﹣m 2+m +2＝0，解得：m 1＝2，m 2＝﹣1，∵（m ﹣2）x 2+4x ﹣m 2＝0是一元二次方程，∴m ﹣2≠0，∴m≠2，∴m＝﹣1，故选：B．8．（3分）（2020•金昌）如图所示的木制活动衣帽架是由三个全等的菱形构成，根据实际需要可以调节AE间的距离．若AE间的距离调节到60cm，菱形的边长AB＝20cm，则∠DAB 的度数是（）A．90°B．100°C．120°D．150°【解答】解：连结AE，∵AE间的距离调节到60cm，木制活动衣帽架是由三个全等的菱形构成，∴AC＝20cm，∵菱形的边长AB＝20cm，∴AB＝BC＝20cm，∴AC＝AB＝BC，∴△ACB是等边三角形，∴∠B＝60°，∴∠DAB＝120°．故选：C．9．（3分）（2020•金昌）如图，A是⊙O上一点，BC是直径，AC＝2，AB＝4，点D在⊙Ô，则DC的长为（）上且平分BCA．2√2B．√5C．2√5D．√10̂，【解答】解：∵点D在⊙O上且平分BĈ=CD̂，∴BD∵BC是⊙O的直径，∴∠BAC＝∠D＝90°，∵AC＝2，AB＝4，∴BC=√22+42=2√5，Rt△BDC中，DC2+BD2＝BC2，∴2DC2＝20，∴DC=√10，故选：D．10．（3分）（2020•金昌）如图①，正方形ABCD中，AC，BD相交于点O，E是OD的中点．动点P从点E出发，沿着E→O→B→A的路径以每秒1个单位长度的速度运动到点A，在此过程中线段AP的长度y随着运动时间x的函数关系如图②所示，则AB的长为（）A．4√2B．4C．3√3D．2√2【解答】解：如图，连接AE．∵四边形ABCD是正方形，∴AC⊥BD，OA＝OC＝OD＝OB，由题意DE＝OE，设DE＝OE＝x，则OA＝OD＝2x，∵AE＝2√5，∴x2+（2x）2＝（2√5）2，解得x＝2或﹣2（不合题意舍弃），∴OA＝OD＝4，∴AB＝AD＝4√2，故选：A．二、填空题：本大题共8小题，每小题3分，共24分．11．（3分）（2020•金昌）如果盈利100元记作+100元，那么亏损50元记作﹣50元．【解答】解：∵盈利100元记作+100元，∴亏损50元记作﹣50元，故答案为：﹣50．12．（3分）（2020•金昌）分解因式：a2+a＝a（a+1）．【解答】解：a2+a＝a（a+1）．故答案为：a（a+1）．13．（3分）（2020•金昌）暑假期间，亮视眼镜店开展学生配镜优惠活动．某款式眼镜的广告如下，请你为广告牌填上原价．原价：元暑假八折优惠，现价：160元【解答】解：设广告牌上的原价为x元，依题意，得：0.8x＝160，解得：x＝200．故答案为：200．14．（3分）（2020•金昌）要使分式x+2x−1有意义，x 需满足的条件是 x ≠1 ．【解答】解：当x ﹣1≠0时，分式有意义， ∴x ≠1， 故答案为x ≠1．15．（3分）（2020•金昌）在一个不透明的袋中装有若干个材质、大小完全相同的红球，小明在袋中放入3个黑球（每个黑球除颜色外其余都与红球相同），摇匀后每次随机从袋中摸出一个球，记录颜色后放回袋中，通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，估计袋中红球有 17 个．【解答】解：通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，口袋中有3个黑球， ∵假设有x 个红球， ∴x x+3=0.85，解得：x ＝17，经检验x ＝17是分式方程的解， ∴口袋中红球约有17个． 故答案为：17．16．（3分）（2020•金昌）如图，在平面直角坐标系中，△OAB 的顶点A ，B 的坐标分别为（3，√3），（4，0）．把△OAB 沿x 轴向右平移得到△CDE ，如果点D 的坐标为（6，√3），则点E 的坐标为 （7，0） ．【解答】解：∵A （3，√3），D （6，√3）， ∴点A 向右平移3个单位得到D ， ∵B （4，0），∴点B 向右平移3个单位得到E （7，0）， 故答案为（7，0）．17．（3分）（2020•金昌）若一个扇形的圆心角为60°，面积为π6cm 2，则这个扇形的弧长为π3cm （结果保留π）．【解答】解：设扇形的半径为R ，弧长为l ， 根据扇形面积公式得；60π⋅R 2360=π6，解得：R ＝1，∵扇形的面积=12lR =π6， 解得：l =13π． 故答案为：π3．18．（3分）（2020•金昌）已知y =√(x 2−x +5，当x 分别取1，2，3，…，2020时，所对应y 值的总和是 2032 ． 【解答】解：当x ＜4时， 原式＝4﹣x ﹣x +5＝﹣2x +9， 当x ＝1时，原式＝7； 当x ＝2时，原式＝5； 当x ＝3时，原式＝3；当x ≥4时，原式＝x ﹣4﹣x +5＝1，∴当x 分别取1，2，3，…，2020时，所对应y 值的总和是： 7+5+3+1+1+…+1 ＝15+1×2017 ＝2032． 故答案为：2032．三、解答题（一）：本大题共5小题，共26分．解答应写出必要的文字说明，证明过程或演算步骤．19．（4分）（2020•金昌）计算：（2−√3）（2+√3）+tan60°﹣（π﹣2√3）0． 【解答】解：原式＝4﹣3+√3−1 =√3．20．（4分）（2020•金昌）解不等式组：{3x −5＜x +12(2x −1)≥3x −4，并把它的解集在数轴上表示出来．【解答】解：解不等式3x﹣5＜x+1，得：x＜3，解不等式2（2x﹣1）≥3x﹣4，得：x≥﹣2，则不等式组的解集为﹣2≤x＜3，将不等式组的解集表示在数轴上如下：21．（6分）（2020•金昌）如图，在△ABC中，D是BC边上一点，且BD＝BA．（1）尺规作图（保留作图痕迹，不写作法）：①作∠ABC的角平分线交AD于点E；②作线段DC的垂直平分线交DC于点F．（2）连接EF，直接写出线段EF和AC的数量关系及位置关系．【解答】解：（1）如图，①BE即为所求；②如图，线段DC的垂直平分线交DC于点F．（2）∵BD＝BA，BE平分∠ABD，∴点E是AD的中点，∵点F是CD的中点，∴EF是△ADC的中位线，∴线段EF和AC的数量关系为：EF=12AC，位置关系为：EF∥AC．22．（6分）（2020•金昌）图①是甘肃省博物馆的镇馆之宝﹣﹣铜奔马，又称“马踏飞燕”，于1969年10月出土于武威市的雷台汉墓，1983年10月被国家旅游局确定为中国旅游标志．在很多旅游城市的广场上都有“马踏飞燕”雕塑．某学习小组把测量本城市广场的“马踏飞燕”雕塑（图②）最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：课题测量“马踏飞燕“雕塑最高点离地面的高度测量示意图如图，雕塑的最高点B 到地面的高度为BA，在测点C用仪器测得点B 的仰角为α，前进一段距离到达测点E，再用该仪器测得点B 的仰角为β，且点A，B，C，D，E，F均在同一竖直平面内，点A，C，E在同一条直线上．测量数据α的度数β的度数CE的长度仪器CD（EF）的高度31°42°5米1.5米请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度（结果保留一位小数）．（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60，sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）【解答】解：如图，设BG＝x米，在Rt△BFG中，FG=BGtanβ=xtan42°，在Rt△BDG中，DG=BGtanα=xtan31°，由DG﹣FG＝DF得，x tan31°−xtan42°=5，解得，x＝9，∴AB＝AG+BG＝1.5+9＝10.5（米），答：这座“马踏飞燕”雕塑最高点离地面的高度为10.5米．23．（6分）（2020•金昌）2019年甘肃在国际知名旅游指南《孤独星球》亚洲最佳旅游地排名第一．截至2020年1月，甘肃省已有五家国家5A 级旅游景区，分别为A ：嘉峪关文物景区；B ：平凉崆峒山风景名胜区；C ：天水麦积山景区；D ：敦煌鸣沙山月牙泉景区；E ：张掖七彩丹霞景区．张帆同学与父母计划在暑假期间从中选择部分景区游玩． （1）张帆一家选择E ：张掖七彩丹霞景区的概率是多少？（2）若张帆一家选择了E ：张掖七彩丹霞景区，他们再从A ，B ，C ，D 四个景区中任选两个景区去旅游，求选择A ，D 两个景区的概率（要求画树状图或列表求概率）． 【解答】解：（1）共有5种可能选择的结果，因此张帆一家选择“E ：张掖七彩丹霞景区”的概率是15；（2）从A ，B ，C ，D 四个景区中任选两个景区所有可能出现的结果如下：共有12种可能出现的结果，其中选择A 、D 两个景区的有2种， ∴P （选择A 、D ）=212=16． 四、解答题（二）：本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤．24．（7分）（2020•金昌）习近平总书记于2019年8月在兰州考察时说“黄河之滨也很美”．兰州是古丝绸之路商贸重镇，也是黄河唯一穿城而过的省会城市，被称为“黄河之都”．近年来，在市政府的积极治理下，兰州的空气质量得到极大改善，“兰州蓝”成为兰州市民引以为豪的城市名片．如图是根据兰州市环境保护局公布的2013～2019年各年的全年空气质量优良天数绘制的折线统计图．请结合统计图解答下列问题：（1）2019年比2013年的全年空气质量优良天数增加了26天；（2）这七年的全年空气质量优良天数的中位数是254天；（3）求这七年的全年空气质量优良天数的平均天数；（4）《兰州市“十三五”质量发展规划》中指出：2020年，确保兰州市全年空气质量优良天数比率达80%以上．试计算2020年（共366天）兰州市空气质量优良天数至少需要多少天才能达标．【解答】解：（1）∵296﹣270＝26，∴2019年比2013年的全年空气质量优良天数增加了26天；故答案为：26；（2）∵这七年的全年空气质量优良天数分别为：213，233，250，254，270，296，313，∴这七年的全年空气质量优良天数的中位数是254天；故答案为：254；（3）∵x=17（213+233+250+254+270+296+313）≈261（天），则这七年的全年空气质量优良天数的平均天数为261天；（4）∵全年空气质量优良天数比率达80%以上．∴366×80%＝292.8≈293（天），则兰州市空气质量优良天数至少需要293天才能达标．25．（7分）（2020•金昌）通过课本上对函数的学习，我们积累了一定的经验．下表是一个函数的自变量x与函数值y的部分对应值，请你借鉴以往学习函数的经验，探究下列问题：x…012345…y…632 1.5 1.21…（1）当x＝3时，y＝1.5；（2）根据表中数值描点（x，y），并画出函数图象；（3）观察画出的图象，写出这个函数的一条性质：函数y随x的增大而减小．【解答】解：（1）当x＝3时，y＝1.5；故答案为：3；（2）函数图象如图所示：（3）观察画出的图象，这个函数的一条性质：函数y随x的增大而减小．故答案为：函数y随x的增大而减小．26．（8分）（2020•金昌）如图，⊙O是△ABC的外接圆，其切线AE与直径BD的延长线相交于点E，且AE＝AB．（1）求∠ACB的度数；（2）若DE＝2，求⊙O的半径．【解答】解：（1）连接OA，∵AE是⊙O的切线，∴∠OAE＝90°，∵AB＝AE，∴∠ABE＝∠AEB，∵OA＝OB，∴∠ABO＝∠OAB，∴∠OAB＝∠ABE＝∠E，∵∠OAB+∠ABE+∠E+∠OAE＝180°，∴∠OAB＝∠ABE＝∠E＝30°，∴∠AOB＝180°﹣∠OAB﹣∠ABO＝120°，∴∠ACB=12∠AOB＝60°；（2）设⊙O的半径为r，则OA＝OD＝r，OE＝r+2，∵∠OAE＝90°，∠E＝30°，∴2OA＝OE，即2r＝r+2，∴r＝2，故⊙O的半径为2．27．（8分）（2020•金昌）如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN ＝45°．把△ADN绕点A顺时针旋转90°得到△ABE．（1）求证：△AEM≌△ANM．（2）若BM＝3，DN＝2，求正方形ABCD的边长．【解答】（1）证明：∵△ADN≌△ABE，∴∠DAN＝∠BAE，DN＝BE，∵∠DAB＝90°，∠MAN＝45°，∴∠MAE＝∠BAE+∠BAM＝∠DAN+∠BAM＝45°，∴∠MAE＝∠MAN，∵MA＝MA，∴△AEM≌△ANM（SAS）．（2）解：设CD＝BC＝x，则CM＝x﹣3，CN＝x﹣2，∵△AEM≌△ANM，∴EM＝MN，∵BE＝DN，∴MN＝BM+DN＝5，∵∠C＝90°，∴MN2＝CM2+CN2，∴25＝（x﹣2）2+（x﹣3）2，解得，x＝6或﹣1（舍弃），∴正方形ABCD的边长为6．28．（10分）（2020•金昌）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣2交x轴于A，B两点，交y轴于点C，且OA＝2OC＝8OB．点P是第三象限内抛物线上的一动点．（1）求此抛物线的表达式；（2）若PC∥AB，求点P的坐标；（3）连接AC，求△P AC面积的最大值及此时点P的坐标．【解答】解：（1）抛物线y ＝ax 2+bx ﹣2，则c ＝﹣2，故OC ＝2， 而OA ＝2OC ＝8OB ，则OA ＝4，OB =12，故点A 、B 、C 的坐标分别为（﹣4，0）、（12，0）、（0，﹣2）； 则y ＝a （x +4）（x −12）＝a （x 2+72x ﹣2）＝ax 2+bx ﹣2，故a ＝1， 故抛物线的表达式为：y ＝x 2+72x ﹣2；（2）抛物线的对称轴为x =−74，当PC ∥AB 时，点P 、C 的纵坐标相同，根据函数的对称性得点P （−72，﹣2）；（3）过点P 作PH ∥y 轴交AC 于点H ，由点A 、C 的坐标得，直线AC 的表达式为：y =−12x ﹣2，则△P AC 的面积S ＝S △PHA +S △PHC =12PH ×OA =12×4×（−12x ﹣2﹣x 2−72x +2）＝﹣2（x +2）2+8，∵﹣2＜0，∴S 有最大值，当x ＝﹣2时，S 的最大值为8，此时点P （﹣2，﹣5）．。