外接球专项训练(带详细答案)
外接球训练(2)——老师专用

外接球专训——老师专用一、选择题1.已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为( )A.3172 B .210 C.132D .310【答案】C【解析】如图所示,由球心作平面ABC 的垂线,则垂足为BC 的中点M .又AM =12BC =52,OM =12AA 1=6,所以球O 的半径R =OA =522+62=132. 2.【2018南阳第一中学】已知三棱锥P ABC -的四个顶点均在某球面上, PC 为该球的直径, ABC ∆是边长为4的等边三角形,三棱锥P ABC -的体积为163,则该三棱锥的外接球的表面积为( ) A.163π B. 403π C. 643π D. 803π 【答案】D3.已知三棱锥A BCD -中,,,且各顶点均在同一个球面上,则该球的体积为( ) A .323π B . 4π C . 2π D . 43π【答案】D【解析】补体为底面边长为1,外接球的球心为长方体体对角线中点,所以球的半径1r =,球的体积,故选D .4.在四边形ABCD 中,, BC =, CD =, AB AD ⊥,现将ABD ∆沿BD 折起,得三棱锥A BCD -,若三棱锥A BCD -的四个顶点都在球O 的球面上,则球O 的体积为( )A .B .C .D . 【答案】D【解析】BD =,所以,所以球心在BD 的中点处,,所以,故选D.5.已知三棱锥S ABC -, ABC ∆是直角三角形,其斜边平面,则三棱锥的外接球的表面积为( )A . 64πB . 68πC . 72πD . 100π 【答案】D6.【2019四川乐山四校联考*模型法】如图,在等腰梯形ABCD 中,, E 为AB 中点.将ADE ∆与BEC ∆分别沿ED 、EC 折起,使A 、B 重合于点P ,则三棱锥P DCE -的外接球的体积为( )A.27 B. 2 C. 8 D. 246.C 【解析】由题意可知,折叠所得的几何体是一个棱长为1的正四棱锥,将其放入正方体如图所示,由题意可得,该三棱锥的外接球直径为:,外接球的体积:.7.【2018四川省联考*外接球的性质】设点,,A B C 是半径为2的球O 的球面上的三个不同的点,且OA BC ⊥, 3BC =,,则三棱锥O ABC -的体积为( )A.4 B. 2 C. 4D. 【答案】A【解析】作△ABC 的外接圆圆1O ,球心为1O ,由题意可得: 1OO ⊥平面ABC ,设△ABC 外接圆半径为r ,由正弦定理有,取BC 中点E ,由OB OC =可得: OE BC ⊥, 结合OA BC ⊥可知直线BC ⊥平面OAE ,则BC AE ⊥, 结合BE CE =可得: AB AC =,等腰三角形ABC 中,,则,,由勾股定理可得:,由三棱锥体积公式可得:.8.【2018河南漯河中学二模】四面体的四个顶点都在球的表面上,,,,平面,则球的表面积为( )A.B.C.D.8.D 【解析】如图,∵BC=CD=1,∠BCD=60°∴底面△BCD为等边三角形,取CD中点为E,连接BE,∴△BCD的外心G在BE上,设为G,取BC中点F,连接GF,在Rt△BCE中,由,,得,又在Rt△BFG中,得BG=,过G作AB的平行线与AB的中垂线HO交于O,则O为四面体ABCD 的外接球的球心,即R=OB,∵AB⊥平面BCD,∴OG⊥BG,在Rt△BGO中,求得OB=,∴球O的表面积为4π9.如图,在菱形ABCD中,∠BAD=60°,,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P﹣BCD的外接球的表面积为()A.28πB.32πC.16πD.12π【答案】A10.已知四棱锥P ABCD -的顶点都在球O 上,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,PAD ∆为正三角形,,则球O 的表面积为A.323π B.32π C.64π D.643π【答案】D【解析】如图2,将四棱锥P ABCD -补为一个三棱柱,因为PAD ∆为正三角形,2AD =,所以PAD ∆的外接圆的半径为3,所以球O 的半径为,所以球O 的表面积为11.已知三棱锥S-ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S-ABC 的体积为9,则球O 的表面积为________. 【答案】36π【解析】取SC 的中点O ,连接,OA OB ,因为所以因为平面SAC ⊥平面SBC 所以OA ⊥平面SBC 设OA r =所以,所以球的表面积为2436r ππ=12.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑中平面,,则该鳖臑的外接球与内切球的表面积之和为__________.【答案】【解析】设的中点为,如图,由,且为直角三角形,得.由两两垂直,可知为和的斜边,故点到点的距离相等,故点为鳖臑的外接球的球心,设高鳖臑的外接球的半径与内切球的半径分别为,则由.得,解得.由等体积法,知.即,解得.13.【2017陕西汉中二模】如图中的三个直角三角形是一个体积为320cm 的几何体的三视图,则该几何体外接球的面积(单位 2cm )等于 ( ).A . 55πB . 75πC . 77πD . 65π 【答案】C 【解析】14.【2017福建4月质检】已知三棱锥P ABC -的三条侧棱两两互相垂直,且2AB BC AC ===,则此三棱锥的外接球的体积为( )A .83π B . C . 163π D . 323π 【答案】B【解析】由题意可知 可将三棱锥放入长方体中考虑,则长方体的外接球即三棱锥的外接球,故球的半径为长方体体对角线的一半,设PA x =,则2222275471PB PC BC x x x +==⇒-+-=⇒=,故1,2,PA PB PC R ===⇒== 343R π=15.【2017四川宜宾二诊】三棱锥A BCD -内接于半径为2的球O , BC 过球心O ,当三棱锥A BCD -体积取得最大值时,三棱锥A BCD -的表面积为A . 6+B . 8+C . 4+D . 8+【答案】D16.【2017安徽马鞍山三模】已知△ABC 的顶点都在半径为R 的球O 的球面上,球心O 到平面ABC 的R , AB BC AC ===,则球O 的体积是( ) A .163π B . 16π C . 323π D . 32π 【答案】C【解析】ABC ∆是等边三角形,所以球心O 在底面的射影是ABC ∆的中心'O ,点'OO A 是直角三角形,满足2221R R ⎫=+⎪⎪⎭,解得 24R =, 2R =,所以343233V R ππ==,故选C . 【点睛】本题考查了球与几何体的组合体问题,考查了空间想象能力以及计算能力,球心与截面圆的圆心连线垂直于截面,所以很多求球心问题,可先找底面多边形的外接圆的圆心,过圆心垂直于多边形的直线必过球心,然后再利用球心到所有顶点的距离相等的性质和构造直角三角形求球的半径.17.【2017黑龙江哈师大附中三模】已知三棱锥—P ABC 的四个顶点均在同一个球面上,底面ABC ∆满足BA BC ==, π2ABC ∠=,若该三棱锥体积的最大值为3,则其外接球的体积为( ) A . 8π B . 16π C . 16π3 D . 32π3【答案】D 【解析】18.【2017辽宁考前模拟】正四面体ABCD 的棱长为4, E 为棱AB 的中点,过E 作此正四面体的外接球的截面,则截面面积的最小值是( ) A . 4π B . 8π C . 12π D . 16π 【答案】A【解析】 将四面体ABCD 放置在正方体中,如图所示,可得正方体的外接球就是四面体ABCD 的外接球,因为正四面体ABCD 的棱长为4,所以正方体的棱长为,可得外接球的半径满足2R ==R =,又E 为BC 的中点,过E 作其外接球的截面,当截面到球心O 的距离最大时,此时截面圆的面积最小,此时球心O 到截面的距离等于正方体棱长的一半,可得截面圆的半径为2r ==,得到截面圆的面积的最小值为24S r ππ==,故选A .二、单选题19.若一个正三棱柱存在外接球与内切球,则它的外接球与内切球表面积之比为A . 3 1B . 4 1C . 5 1D . 6 1 【答案】选C20.在正四棱锥S -ABCD 中,侧面与底面所成的角为3π,则它的外接球半径R 与内切球半径r 之比为( ) A . 5 B . 32 C . 10 D . 52【答案】D【解析】由于侧面与底面所成角为,可知底面对边中心线与两个对面斜高构成正三角形,设底面边长为a ,则斜高也为a ,进而可得侧棱长为 ,高为四棱锥的内切球半径就是上述正三角形的内切圆半径为,其外接球球心必在顶点与底面中心连线上,如图 半径为R ,球心为O ,顶点为P ,底面中心为O 1,底面一个顶点为B ,则OB =OP ,于是就有 ( ﹣R )2+()2=R 2解得R =.所以两者的比为 .故选D三、填空题21.【2017安徽阜阳二模】已知,,,A B C D 是球面上不共面的四点,AB AC BD CD BC =====,平面ABC ⊥平面BCD ,则此球的体积为_________.22.【2017河北唐山三模】直角ABC 的三个顶点都在球O 的球面上, 2AB AC ==,若球O 的表面积为12π,则球心O 到平面ABC 的距离等于__________.【答案】1【解析】直角ABC 的斜边CB 为ABC 所在截面小圆的直径,则该截面小圆的半径为r =,由球的表面积为12π可得球的半径R =O 到平面ABC 的距离1d ==.23.在三棱锥中,侧棱两两垂直,的面积分别为,则三棱锥的外接球的体积为_______.【答案】考点球与几何体【方法点睛】球与几何体的问题,属于中档题型,当条件为三棱锥有同一顶点的三条棱两两垂直时,可联想到长方体,这样的三棱锥就是长方体的一部分,如图所示,此时三棱锥的外接球就是长方体的外接球,而长方体的外接球的直径就是长方体的对角线,.24.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑中平面,,则该鳖臑的外接球与内切球的表面积之和为__________.【答案】【解析】设的中点为,如图,由,且为直角三角形,得.由两两垂直,可知为和的斜边,故点到点的距离相等,故点为鳖臑的外接球的球心,设高鳖臑的外接球的半径与内切球的半径分别为,则由.得,解得.由等体积法,知.即,解得.故该鳖臑的外接球与内切球的表面积之和为.25.已知边长为ABCD 中,∠BAD =60°,沿对角线BD 折成二面角A BD C 的大小为120°的四面体,则四面体的外接球的表面积为________. 【答案】28π 【解析】26.在四棱锥P ABCD -中, PC ⊥底面ABCD ,底面为正方形, //QA PC , PBC AQB ∠=∠= 60,记四棱锥P ABCD -的外接球与三棱锥B ACQ -的外接球的表面积分别为12,S S ,则21S S =___. 【答案】157点睛 球的半径的计算,关键在球心位置的确定,三棱锥B AQC -中,QAC QBC ∆∆均为直角三角形,因此外接球的球心就是QC 的中点,因为它到四个顶点的距离是相等的.同理四棱锥P ABCD -外接球的球心就是AP 的中点.27.已知直三棱柱中,,侧面的面积为,则直三棱柱外接球表面积的最小值为 . 【答案】考点 1、几何体的外接球;2、基本不等式;3、球的体积和表面积. 【方法点睛】设,则有,利用直三棱柱中,,从而直三棱柱外接球的半径为,所以其比表面积的最小值为.根据直三棱柱中,,侧面的面积为,设,,利用均值不等式,确定直三棱柱外接球的半径的最小值是关键.28.如图所示,三棱锥P ABC -中,ABC 是边长为3的等边三角形, D 是线段AB 的中点,DE PB E ⋂=,且DE AB ⊥,若120EDC ∠=︒, 32PA =, PB =,则三棱锥P ABC -的外接球的表面积为__________.【答案】13π【解析】三棱锥P ABC -中,ABC 是边长为3的等边三角形,设ABC ∆的外心为1O ,外接圆的半径1032sin60O A ==PAB ∆中, 3,32PA PB AB ===,满足222PA PB AB +=, PAB ∆为直角三角形, PAB ∆的外接圆的圆心为D ,由于,CD AB ED AB ⊥⊥, 0120EDC ∠=为二面角P AB C --的平面角,分别过两个三角形的外心1,O D 作两个半平面的垂线交于点O ,则O 为三棱锥P ABC -的外接球的球心,在1Rt OO D ∆中, 01130,ODO DO ∠==,则01cos301O D OD OD ===,连接OA ,设OA R =,则22222313124R AD OD ⎛⎫=+=+=⎪⎝⎭, 21344=134S R πππ==⨯球. 【点睛】求多面体的外接球的面积和体积问题常用方法有(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心,本题就是第三种方法.。
(完整版)外接球专项训练(带详细答案)

外接球专项训练参考答案一.选择题1、已知球的半径为2,圆和圆是球的互相垂直的两个截面,圆和圆的面积分别为和,则( )A .1 B.2 D【答案】D【解析】因由球心距与截面圆的半径之间的关系得,故D 。
考点:球的几何性质及运算。
2、在三棱锥中,,中点为,,则此三棱锥的外接球的表面积为( ) A .B .C .D .【答案】C如图,易由余弦定理可因,故;同理,故,所以是棱长为应选C 。
考点:球与几何体的外接和表面积的计算公式。
3、球的球面上有四点,其中四点共面,是边长为2的正三角形,面面,则棱锥的体积的最大值为( )A.4 【答案】AO M N M N 2ππ||MN =538212221222221=-=+⇒⎪⎩⎪⎨⎧=+=+d d R d R d 222PA AB PB =+BA PB ⊥222PC CB PB =+BC PB ⊥C B A P ,,,O ,,,S A B C ,,,O A B C ABC ∆SAB ⊥ABC S ABC -【解析】设球心和的外心为,延长交于点,则由球的对称性可知,继而由面面可得所在的平面,所以是三棱锥的高;再由四点共面可知是A 。
考点:几何体的外接球等有关知识的运用。
【易错点晴】球与几何体的外接和内切问题一直是高中数学中题的重要题型,也高考和各级各类考试的难点内容。
本题将三棱锥与球外接整合在一起考查三棱锥的体积的最大值无疑是加大了试题的难度。
解答本题时要充分利用题设中提供的有关信息,先确定球心的位置是三角形的外心,定当4、已知在三棱锥中,面,,若三棱锥的外接球的半径是3,,则的最大值是( )A .36B .28C .26D .18 【答案】D【解析】因为面,所以,,又因为,所以平面,所以,所以有,则由基本不等式可得,当且仅当时等号成立,所以的最大值是,故选D.考点:1.线面垂直的判定与性质;2.长方体外接球的性质;3.基本不等式.【名师点睛】本题考查线面垂直的判定与性质、长方体外接球的性质、基本不等式,中档题;立体几何的最值问题通常有三种思考方向:(1)根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;(2)将几何体平面化,如利用展开图,在平面几何图中直观求解;(3)建立函数,通过求函数的最值或利用基本不等式来求解.5、如图所示是一个几何体的三视图, 则这个几何体外接球的表面积为( )ABC ∆O CO AB P AB PD ⊥SAB ⊥ABC ⊥PD ABC ∆PD ,,,O A B C O ABC ∆O ABC PD P ABC -PA ⊥ABC PC AB ⊥P ABC -ABC ABP ACP S S S S ∆∆∆=++S PA ⊥ABC PA AB ⊥PA AC ⊥PC AB ⊥AB ⊥PAC AB AC⊥2222(23)36AB AC AP ++=⨯=AB AC AP ==S 36A .B .C .D . 【答案】C【解析】几何体为一个四棱锥,外接球球心为底面正方形(边长为4C.考点:三视图,外接球【方法点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解. 6、如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体 外接球的表面积为( )A . C . D 【答案】D【解析】由三视图可知,这个几何体是三棱锥.如图所示,为球心,为等边三角形的外心,由图可8π16π32π64π8π9πO F BCD考点:三视图. 【思路点晴】设几何体底面外接圆半径为,常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.若长方体长宽高分别为则其体对角线长为长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心. 7、如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的外接球半径为( )A【答案】C【解析】从三视图可以看出这是一个正方体上的一个四面体,如图,其中正其外接圆的同样正的外接圆的半径是由球的对称性可知球心必在正方体的对角线上,,该球经过六个点,设球心到平面的距离为;球心到平面的距离为,而两个平面和之间的距离为则由球心距、垂面圆半径之间的关系可得,所以,即,将其代入可得由应选C. x ,,a b c MNP ∆111P N M ∆O AC 111,,,,,P N M P N M O 111P N M ∆1d O MNP ∆2d MNP 111P N M 2222221212,r d R r d R +=+=822212122=-=-r r d d 82122=-d d 82122=-d d考点:三视图的识读和理解及几何体体积的计算. 【易错点晴】本题以网格纸上的几何图形为背景,提供了一个三棱锥的几何体的三视图,要求求其外接球的半径,是一道较为困难的难题.难就难在无法搞清其几何形状,只知道是一个三棱锥(四面体)是没有任何用的.通过仔细观察不难看出这是一个正方体上的一个四面体,如图,正的边长为,其外接圆的半径,同样正的外接圆的半径是,由球的对称性可知球心必在对角线上,且经过六个点,设球心到平面的距离为;球心到平面的距离为,而两个平面和之间的距离为,则由球心距垂面圆半径之间的关系可得,所以,即,又,将其代入可得,由此可得,所以,所以外接球的半径,其中计算时可用等积法进行.8、一直三棱柱的每条棱长都是,且每个顶点都在球的表面上,则球的半径为( ) A .B .C .D . 【答案】A【解析】球的半径满足考点:外接球【方法点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解. 9、若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和侧视图如图所示,则此几何体的表面积是 A .24π B .24π+8πOO 2O 1P 1N 1M 1C APNMMNP ∆243241=r 111P N M ∆3222=r O 111,,,,,P N M P N M O 111P N M ∆1d O MNP ∆2d MNP 111P N M 2121334)(34d d h h d +==+-=2222221212,r d R r d R +=+=822212122=-=-r r d d 82122=-d d 33421=+d d 82122=-d d 3212=-d d 3352=d 113333832522222==+=+=r d R 11=R 21,h h 3O O 212673O 2223321()(3)232R R =+⋅⇒=C .24π+4πD .32π答案:C10、已知三棱锥的底面是以为斜边的等腰直角三角形,则三棱锥的外接球的球心到平面的距离是( ) (A(B )1 (C(D【答案】A【解析】因为三棱锥的底面是以为斜边的等腰直角三角形,,在面内的射影为中点,平面,上任意一点到的距离相等.,,在面内作的垂直平分线,则为的外接球球心.,,,即为到平面的距离,故选A .考点:球内接多面体;点到面的距离的计算.【名师点睛】(1)一般要过球心及多面体中的特殊点或过线作截面将空间问题转化为平面问题,从而寻找几何体各元素之间的关系.(2)若球面上四点P ,A ,B ,C 中PA ,PB ,PC两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接问题.(3)一般三棱锥的外接球的球心可通过其中一个面的外心作此平面的垂线,则球心必在此垂线上.11、已知三棱锥的底面是以为斜边的等腰直角三角形,则三棱锥的外接球的球心到平面的距离是( )(A (B)1 (C (D 【答案】A12、某四棱锥的三视图如图所示,则该四棱锥外接球的表面积是( )A . C【答案】B【解析】几何体为一个四棱锥,其顶点为长方体四个顶点,长方体的长宽高为4,3,3,因此四棱锥外接球直径S ABC -AB 2,2,AB SA SB SC ====ABC S ABC -AB 2SA SB SC ===S ∴ABC AB H SH ∴⊥ABC SH ∴,,A B C 1CH =SHC SC MO O S ABC -2SC =Q 1SM ∴=30OSM ∠=︒O ABC S ABC -AB 2,2,AB SA SB SC ====ABC 34π,表面积是选B.考点:三视图【方法点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解. 13、已知三棱锥S-ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC=2,则此棱锥的体积为( )A .B .C .D .【答案】A【解析】连接,则由已知得,可知三棱锥是棱长为的正四面体,其高为,则三棱锥的高为,所以三棱锥的体积为考点:三棱锥外接球.14、半径为1的三个球平放在平面上,且两两相切,其上放置一半径为2的球,由四个球心构成一个新四面体,则该四面体外接球的表面积为()A. D【答案】A【解析】由已知条件可知,该四面体是底面边长为的等边三角形,且侧棱长为.该四面体外接球半径计算公式为,其中为底面外接圆半径,为高.本题中,故考点:球的内接几何体.15、在正三棱锥中,是的中点,且,则正三棱锥的外接球的表面积为( )A .B .C .D . 【答案】【解析】根据三棱锥为正三棱锥,可证明出AC ⊥SB ,结合SB ⊥AM ,得到SB ⊥平面SAC ,因此可得SA 、SB 、SC 三条侧棱两两互相垂直.最后利用公式求出外接圆的直径,结合球的表面积公式,可得正三棱锥S-ABC 的外接2434.R ππ=OC OB OA ,,1======AC BC AB OC OB OA ABC O -1ABC S -ABC S -,,A B C αD ,,,A B C D O 9π23x h S ABC -M SC AM SB ⊥S ABC -6π12π32π36π球的表面积.取AC 中点,连接BN 、SN ,∵N 为AC 中点,SA=SC ,∴AC ⊥SN , 同理AC ⊥BN ,∵SN ∩BN=N ,∴AC ⊥平面SBN ,∵SB 平面SBN ,∴AC ⊥SB,∵SB ⊥AM 且AC ∩AM=A , ∴SB ⊥平面SAC ?SB⊥SA 且SB ⊥AC , ∵三棱锥S-ABC 是正三棱锥,∴SA 、SB 、SC 三条侧棱两两互相垂直. SA=2,∴正三棱锥S-ABC ∴正三棱锥S-ABC 的外接球的表面积是,故选:B .考点:空间线面垂直的判定与性质;球内接多面体16、已知三棱锥,在底面中则此三棱锥的外接球的表面积为( )A. 【答案】D【解析】底面三角形内,根据正弦定理,可得,,满足勾股定理,,底面,所以,那么平面,所以,那么直角三角形有公共斜边,所以三棱锥的外接球的球心就是的中点,是其外接球的直径,,所以外接球的表面积,故选D.⊂2412S R ππ==P ABC -ABC ∆16π2=AC 222AC BC AB =+090=∠ABC ⊥PA ABC BC PA ⊥⊥BC PAB PB BC ⊥PBC PAC ,PC PC O PC 4=PC ππ1642==R S考点:球与几何体17、已知直三棱柱的个顶点都在球的球面上,若,,,,则球的表面积为为( )A .B .C .D . 【答案】C【解析】由题意,三棱柱为直三棱柱,底面为直角三角形,把直三棱柱补成四棱柱,则四棱柱的体对角线是其外接球的直径,则三棱柱1外接球的表面积是故选C .考点:几何体的外接球18、如图,是边长为1的正方体,是高为1的正四棱锥,若点,在同一个球面上,则该球的表面积为( )111C C AB -A B 6O 3AB =C 4A =C AB ⊥A 112AA =O 153π160π169π360π111C C AB -A B C AB 111C C AB -A B 111C C AB -A B 224169R cm ππ=.1111ABCD A B C D -S ABCD -S 1111,,,A B C DA【答案】D【解析】按如图所示作辅助线,为球心,设,则,则在中,,D .考点:1、球内接多面体的性质;2、球的表面积公式.19、在平行四边形中,,,将此平行四边形沿折成直二面角,则三棱锥外接球的表面积为( )A . C . D . 【答案】A【解析】因为平行四边形中,,沿折成直二面角,所以三棱锥的外接球的直径为,所以三棱锥的外接球的半径,所以三棱锥A . O 1OG x =12OB SO x ==-11Rt OB G ∆2221111OB G B OG =+ABCD AB BD ⊥22421AB BD +=BD A BCD -π2π4πABCD BD AB ⊥BDC BD A --BCD A -AC BCD A -BCD A -考点:1.平面图形的折叠问题;2.多面体与球的组合.20、如图, 在菱形中为对角线的中点, 将沿折起到的位置,若 ,则三棱锥的外接球的表面积为( )A .B .C .D .【答案】A【解析】设分别是等边三角形的外心,则画出图象如下图所示,由图象可知,,外接球面积为.考点:球的内接几何体. 21、已知从点出发的三条射线,,两两成角,且分别与球相切于,,三点.若球的体积为,则,两点间的距离为( )(A (B (C )3 (D ) 【答案】B【解析】连接交平面于,由题意可得:和为正三角形,所以.因为ABCD BD ABD ∆BD PBD ∆120PEC ∠=o P BCD -28π32π16π12π,M N ,PBD CBD 11,2O N NC ==11120,60MO N OO N ∠=∠=o o 244728R πππ=⋅=P PA PB PC 60︒O A B C O 36πO P 6OP ABC 'O ABC ∆PAB ∆'AO PO OA PA ⊥⊥,为球的体积为,所以半径,所以考点:点、线、面间的距离计算. 【思路点睛】连接交平面于,由可得,根据球的体积可得半径,进而求出答案. 22、在半径为1的球面上有不共面的四个点A ,B ,C ,D 且,,,则等于( )A .16B .8C .4D .2【答案】B 【解析】如图,构造长方体,设长方体的长、宽、高分别为,则,根据题意,得,则;故选B .考点:多面体与球的组合23、“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图所示,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是( )【答案】B【解析】因为相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖),且正视图和侧视图是一个圆,所以从上向下看,相对的两个曲面在同一个圆柱的侧面上,即俯视图是有两条对角线且为实线的正方形;故选B .36π3OA =OP ABC 'O 'AO PO OA PA ⊥⊥,3OA =AB CD x ==BC DA y ==CA BD z ==222x y z ++c b a ,,422222==++c b a 222222222,,z c a y c b x b a =+=+=+8)(2222222=++=++c b a z y x考点:三视图.24、某一简单几何体的三视图如图所示,该几何体的外接球的表面积是( ) A . B . C . D .【答案】C【解析】从三视图可以看出该几何体是底面对角线长为正方形高为正四棱柱,故其对角线长为故该几何体的外接球的面积为,选C.考点:三视图与几何体的外接球.25、如图,边长为2的正方形ABCD 中,点E ,F 分别是边AB ,BC 的中点△AED ,△EBF ,△FCD 分别沿DE ,EF ,FD 折起,使A ,B ,C 三点重合于点A ′,若四面体A ′EFD 的四个顶点在同一个球面上,则该球的半径为( )C【答案】D 【解析】因为折起后三点重合,所以两两垂直,三棱锥的外接球,就是棱长为的长方体的外接球,球半径满足 D. 考点:几何体外接球的性质.26、已知三棱锥S ﹣ABC ,满足SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SCQ 是外接球上一动点,则点Q 到平面ABC 的距离的最大值为( )A .3B .2C 【答案】D【解析】因为三棱锥中,,且,所以三棱锥的外接球即为以43ππ2542==R S ,,A B C ',','A E A F A D 1,1,2R S ABC -,,SA SB SB SC SC SA ⊥⊥⊥SA SB SC ==,,SA SB SC所以球心到平面的距离所以点到平面的距离的最大值为D.考点:球的性质及组合体的应用.27、一个直棱柱的三视图如图所示,其中俯视图是一个顶角为的等腰三角形,则该直三棱柱外接球的表面积为()A.20 B. D【答案】A,两腰为的等腰三角形,高为,底面三角形的外接半径为,设该三棱柱的外接球的半径为,则,所以该三棱柱的外接球的表面积为,故选A.考点:1.三视图;2.球的切接问题;3.球的表面积.【名师点睛】本题主要考查三视图、球的切接问题、表面积公式及空间想象能力、运算能力,中档题;识图是数学的基本功,空间想象能力是数学与实际生活必备的能力,本题将这些能力结合在一起,体现了数学的实用价值,同时也考查了学生对球的性质与表面积公式的掌握与应用、计算能力.28、某四面体的三视图如图,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的体积为()A. B. C. D.【答案】BABC Q ABCο120π25π222R221215R=+=2420S Rππ==【解析】由题意此四面体是棱长为的正四面体,其外接球半径为,所以B . 考点:三视图,外接球,球体积.【名师点睛】正四面体的内切球与外接球:(1) 正四面体的内切球,如图. 位置关系:正四面体的四个面都与一个球相切,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有(可以利用体积桥证明)(2) 正四面体的外接球,如图5. 位置关系:正四面体的四个顶点都在一个球面上,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有(可用正四面体高减去内切球的半径得到)29、如图所示,在直三棱柱中,,,,点是线段的中点,则三棱锥的外接球的体积是( )a h R a h R h C C '''AB -A B C C A ⊥B C 2'B =BB =C 4A =M 'AB C M -ABA . B【答案】A 【解析】由题意可取的中点,连接,在直角中,所以点在平面内的射影是的外心,即为的中点,设三棱锥的外接球的球心为,由球的截面性质可得,即,解得,故选A.考点:棱锥与球的组合体及球的体积.【方法点睛】本题主要考查了棱锥与球的组合体,球的截面性质及球的体积,考查了考生的空间想象能力属于中档题.本题解答的关键是根据已知条件求得,从而判断点在平面内的射影位置,而又是直角三角形,其外心位于斜边的中点上,据此可知三棱锥外接球的球心在上,根据球的截面性质得到球的半径,求得其体积.30、已知球面上有四个点,球心为点,在上,若三棱锥则该球的表面积为( ) A . B .C【答案】B 【解析】设球的半径,首先因为在上,所以为球的直径,为直角三角形,,若使三角形的面积最大,则点到边的距离最大即可,因为三点共面.所以最大距离为半径,三角形;当点距离平面最大时为,则三棱锥的体积的,,所以该球的表面积为,选B . 考点:1.球的表面积;2.棱锥的体积.31、一个几何体的顶点都在球面上,它们的正视图、侧视图、俯视图都是下图.图中圆内有一个以 圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是( )36πAB D ,MD CD MCD ∆M ABC ABC ∆AB C M -AB O ()222MD r CD r -+=()2215r r -+=3r =MA MB MC ==M ABC ABC ∆C M -AB MD ,,,A B C D O O CD A BCD -O 4π16πr O CD CD O BCD ∆2CD r =B CD ,,B C D r BCD A BCD r A BCD -2r =4416ππ⋅=A .2π B.3π C .4π D.5π【答案】B【解析】由三视图可知:该四面体是正方体的一个内接正四面体,此四面体的外接球的半径为正方体的对角线B .二、填空题(注释)32、在四棱锥中,底面,底面是边长为2的正方形.若直线与平面所成的角为30°,则四棱锥的外接球的表面积为_______.【答案】【解析】连结交于,则可证得平面,连接,则就是直线与平面所成的角,即,四棱锥的外接球的半,则所求外接球的表面积为,故应填.考点:四棱锥的外接球的面积及求法.33、已知矩形的顶点都在半径为的球的球面上,且棱锥的体积为,则= ________.【答案】【解析】由题可得四棱锥的侧棱为,则P ABCD -PB ⊥ABCD ABCD PC PDB P ABCD -12πAC BD H AC ⊥PDB PH CPH ∠PC PDB 30CPH ∠=°∴P ABCD -12π12πABCD R O O ABCD -R 4R考点:多面体与外接球.。
高考数学 外接球30题-含答案

Hale Waihona Puke 一、单选题 1.在三棱锥 A BCD 中, BAC 120, BDC 60 ,二面角 A BC D 为直二面角,
当三棱锥 A BCD 的体积的最大值为 1 时,其外接球的表面积为( ) 3
A.
10π 3
B.10π
C. 20π 3
D. 20π
试卷第 1页,共 30页
2.已知三棱锥 P ABC 满足 PA PB PC BC 2 3, BAC 60 .则其外接球 O 的
S
ABC
的外接球体积分别为V1
, V2
,V,则
V1
V2 V
的取值范围是(
)
A.
2 2
,1
B. 1, 2
C. 2, 2
D. 3, 2
试卷第 10页,共 30页
11.如图, ABCD 为直角梯形, AB ∥CD, AD DC, AD 3,CD 3, AB 2 3 .连 AC , 将△ADC 沿 AC 翻折成三棱锥 D ABC ,当三棱锥 D ABC 外接球表面积的最小值时, 二面角 D AC B 的余弦值为( )
A. 80 3 π 3
B.
70 3
π
C. 20π
D. 80 π 3
试卷第 3页,共 30页
4.在四面体
ABCD
中,
AB
BC
,
AB
AD
,向量
BC
与
AD
的夹角为
2π 3
,若
AB
6
,
BC AD 3 ,则该四面体外接球的表面积为( )
A.18π
B. 36π
C. 54π
D. 72π
试卷第 4页,共 30页
高中外接球试题及答案大全

高中外接球试题及答案大全1. 已知正方体ABCD-A1B1C1D1的棱长为a,求正方体的外接球的半径。
答案:设正方体的外接球的半径为R,则有R=\(\frac{\sqrt{3}}{2}a\)。
2. 已知三棱锥P-ABC的四个顶点都在同一个球面上,且PA=PB=PC=a,AB=BC=CA=b,求球的半径。
答案:设球的半径为R,则有R=\(\frac{a}{\sqrt{3}}\)。
3. 已知长方体ABCD-A1B1C1D1的长、宽、高分别为a、b、c,求长方体的外接球的半径。
答案:设长方体的外接球的半径为R,则有R=\(\frac{\sqrt{a^2+b^2+c^2}}{2}\)。
4. 已知四面体ABCD的四个顶点都在同一个球面上,且AB=BC=CD=DA=a,求球的半径。
答案:设球的半径为R,则有R=\(\frac{\sqrt{3}}{2}a\)。
5. 已知圆锥的底面半径为r,母线长为l,求圆锥的外接球的半径。
答案:设圆锥的外接球的半径为R,则有R=\(\frac{\sqrt{l^2+4r^2}}{2}\)。
6. 已知正四面体ABCD的棱长为a,求正四面体的外接球的半径。
答案:设正四面体的外接球的半径为R,则有R=\(\frac{\sqrt{2}}{2}a\)。
7. 已知球的半径为R,球内接于一个长方体,长方体的长、宽、高分别为a、b、c,求长方体的体积。
答案:设长方体的体积为V,则有V=\(\frac{4}{3}\pi R^3\)。
8. 已知球的半径为R,球内接于一个正三棱柱中,正三棱柱的底面边长为a,求正三棱柱的高。
答案:设正三棱柱的高为h,则有h=\(\frac{3\sqrt{3}}{4}R\)。
9. 已知球的半径为R,球内接于一个正四棱锥中,正四棱锥的底面边长为a,求正四棱锥的高。
答案:设正四棱锥的高为h,则有h=\(\frac{\sqrt{2}}{2}R\)。
10. 已知球的半径为R,球内接于一个正六棱柱中,正六棱柱的底面边长为a,求正六棱柱的高。
高中数学空间几何体的外接球专题(附经典例题与解析)
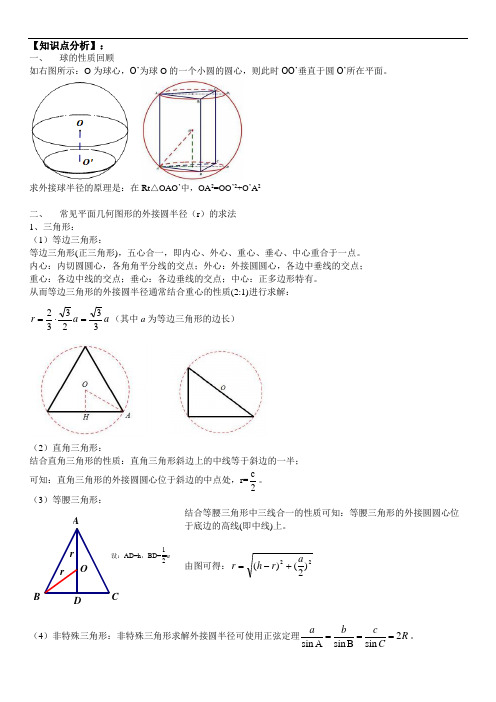
【知识点分析】: 一、 球的性质回顾如右图所示:O 为球心,O’为球O 的一个小圆的圆心,则此时OO’垂直于圆O’所在平面。
求外接球半径的原理是:在Rt △OAO ’中,OA 2=OO ’2+O ’A 2二、 常见平面几何图形的外接圆半径(r )的求法1、三角形:(1)等边三角形:等边三角形(正三角形),五心合一,即内心、外心、重心、垂心、中心重合于一点。
内心:内切圆圆心,各角角平分线的交点;外心:外接圆圆心,各边中垂线的交点;重心:各边中线的交点;垂心:各边垂线的交点;中心:正多边形特有。
从而等边三角形的外接圆半径通常结合重心的性质(2:1)进行求解:a a r 332332=⋅=(其中a 为等边三角形的边长)(2)直角三角形:结合直角三角形的性质:直角三角形斜边上的中线等于斜边的一半;可知:直角三角形的外接圆圆心位于斜边的中点处,r=2c 。
(3)等腰三角形: 结合等腰三角形中三线合一的性质可知:等腰三角形的外接圆圆心位于底边的高线(即中线)上。
由图可得:22)2()(a r h r +-=(4)非特殊三角形:非特殊三角形求解外接圆半径可使用正弦定理2sin sin sin a b c R C===A B 。
rrAD=h ,BD=12a B CO2、四边形常见具有外接圆的四边形有:正方形、矩形、等腰梯形,其中正方形与长方形半径求解方法转化为直角三角形,等腰梯形的外接圆圆心不在中学考察范围内。
外接圆圆心是在圆心到各个顶点距离相同的点;外接球球心则是球心到几何体各个顶点距离相同的点。
结论:几何体的外接球球心与底面外心的连线垂直于底面,(也即球心落在过底面外心的垂线上,)简单称之为:球心落在底面外心的正上方。
【相似题练习】2.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【知识点分析】:类型一:直(正)棱柱:上下两底面三角形的外心连线与侧棱平行与底面垂直,从而球心O 必位于上下两底面外心连线的中点处,即121'AA OO =,从而R 可求.【相似题练习】1.三棱柱ABC ﹣A 1B 1C 1中,底面ABC 是边长为2的正三角形,侧棱AA 1垂直于底面ABC ,且AA 1=4,则此三棱柱外接球的表面积为( )A .B .C .D .【知识点分析】:类型二:侧棱垂直底面的三棱锥,法一:补形法:该几何体可由正三棱柱沿平面PBC 切割得来,故可转化为原三棱柱的外接球;法二:先确定底面三角形ABC 的外心O’,从而球心位于O’的正上方,即OO’ ⊥平面ABC ,同时:OP=OA ,故,过O 作OM ⊥PA 于M ,此时M 必为PA 中点,从而四边形OMAO’为矩形,所以PA AM OO 21'==,在直角三角形OO’A 中有:222'OO r R +=.【相似题练习】2.已知在三棱锥P ﹣ABC 中,△ABC 是边长为2的正三角形,若PA ⊥底面ABC 且PA =2,则该三棱锥的外接球的表面积为( )A .32πB .28πC .24πD .20π3.在三棱锥P ﹣ABC 中,PA ⊥平面ABC ,PA =2,AB =4,AC =3,∠BAC =,则三棱锥P ﹣ABC 的外接球的半径R =( )A .B .C .D .【知识点分析】:类型三:正三棱锥:由底面正三角形边长可得r ,在直角三角形OO’A 中,222'OO r R +=,故只需确定OO’的长度即可,结合图形,OO’=PO’-OP=H-R ,代入222)(R H r R -+=即可求解.【相似题练习】3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 .2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )【知识点分析】:类型四:侧面垂直于底面的三棱锥:设△ABC和△PAB的外心分别为O’,O’’,则PM⊥AB,球心设为O,则OO’ ⊥平面ABC,OO’’⊥平面PAB,从而四边形OO’MO’’是矩形,可得:OO’=O’’M,在Rt△OO’C中用勾股定理求解.【讲透例题】1.在四面体A﹣BCD中,AB=5,BC=CD=3,DB=2,AC=4,∠ACD=60°,则该四面体的外接球的表面积为.解析:如图:取AB的中点O,在△ACD中,由余弦定理得:AD2=AC2+CD2﹣2×AC×CD cos60°=13,在△ABD中,∵AB2=BD2+AD2,∴∠ADB=90°,∴OA=OB=OD,在△ABC中,∵AB2=BC2+AC2,∴∠ACB=90°,∴OA=OB=OC,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心,其半径R=AB=,∴S球=4πR2=4π()2=25π.故答案为:25π.【相似题练习】4.在三棱锥P-ABC中,面PAB⊥面ABC,三角形ABC和三角形PAB均为等边三角形,且AB=3,求该几何体外接球半径.2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为.5、如图,在四棱锥P﹣ABCD中,底面ABCD为长方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.7、如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π课后作业:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.参考答案与解析12.(5分)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π【解答】解:由题意可知图形如图:⊙O1的面积为4π,可得O1A=2,则AO1=AB sin60°,,∴AB=BC=AC=OO1=2,外接球的半径为:R==4,球O的表面积:4×π×42=64π.故选:A.1.1.一个几何的三视图如图所示,它们都是腰长为1的等腰直角三角形,则该几何体的外接球的体积等于()A.B.C.πD.2π解析:由三视图可知:该几何体是一个如图所示的三棱锥,其中底面是一个两直角边都为1的直角三角形,PC⊥底面ABC,且PC=1.将此三棱锥恢复为棱长为1的正方体,可知该正方体的外接球的直径即为正方体的对角线,∴V外接球==.故选:B.1.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【解答】解:三棱锥P﹣ABC中,PA=PB=PC=2,AB=AC=BC,如图,过点p作PM⊥平面ABC的垂足为M,则球O的内接三棱锥P﹣ABC的球心O在PM所在直线上,∵球O的半径为2,∴OB=OP=2,∴由余弦定理得cos∠BPM==∴∠BPM=30°,∴在Rt△PMB中,∠PBM=60°,∴PM=PB sin∠PBM=3.故选:D.1.三棱柱ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1垂直于底面ABC,且AA1=4,则此三棱柱外接球的表面积为()A.B.C.D.【解答】解:∵正三棱柱ABC﹣A1B1C1的中,底面边长为2,高为4,由题意可得:三棱柱上下底面中心连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,∴正三棱柱ABC﹣A1B1C1的外接球的球心为O,外接球的半径为r,表面积为:4πr2.球心到底面的距离为2,底面中心到底面三角形的顶点的距离为:=,所以球的半径为r==.外接球的表面积为:4πr2=π故选:D.2.已知在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,若PA⊥底面ABC且PA=2,则该三棱锥的外接球的表面积为()A.32πB.28πC.24πD.20π【解答】解:由正弦定理可知,正△ABC的外接圆的直径为,∵PA⊥平面ABC,所以,该三棱锥的外接球的直径为,则.因此,该三棱锥的外接球的表面积为4πR2=20π.故选:D.3.在三棱锥P﹣ABC中,PA⊥平面ABC,PA=2,AB=4,AC=3,∠BAC=,则三棱锥P﹣ABC的外接球的半径R=()A.B.C.D.【解答】解:∵AC=3,AB=4,∠BAC=,∴由余弦定理可得BC=,∴△ABC外接圆的半径r=,设球心到平面ABC的距离为d,则d=PA=1.由勾股定理可得R =,故选:D .3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 1 . 【解答】解:过点P 作PH ⊥平面ABC 于H ,则∵AH 是PA 在平面ABC 内的射影 ∴∠PAH 是直线PA 与底面ABC 所成的角,得∠PAH =60°, ∴Rt △PAH 中,AH =PA cos60°=,PH =PA sin60°=设三棱锥外接球的球心为O ,∵PA =PB =PC ,∴P 在平面ABC 内的射影H 是△ABC 的外心由此可得,外接球心O 必定在PH 上,连接OA 、OB 、OC ∵△POA 中,OP =OA , ∴∠OAP =∠OPA =30°,可得PA =OA =,∴三棱锥外接球的半径R =OA =1故答案为:1.2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )A .16πB .12πC .9πD .8π【解答】解:根据几何体的三视图转换为直观图为:该几何体为底面为等腰直角三角形,高为2的三棱锥体. 如图所示:所以该三棱锥体的外接球的球心为O ,外接球的半径为OA =r ,则:,解得.故S =.故选:C .4.在三棱锥P-ABC 中,面PAB ⊥面ABC ,三角形ABC 和三角形PAB 均为等边三角形,且AB=3,求该几何体外接球半径.由题可得:333,2331'''=====AB r PM M O OO ,所以215'22=+=OO r R2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.【解答】解:∵在边长为2的菱形ABCD中,;如图,由已知可得,△ABC与△ACD均为等边三角形,取AC中点G,连接BG,DG,则BG⊥AC,∴DG=⇒cos∠GDA=⇒∠GDA=⇒∠ADC=;∵二面角B﹣AC﹣D为直二面角,则BG⊥平面ACD,分别取△BCD与△ABD的外心E,F,过E,F分别作两面的垂线,相交于O,则O为三棱锥A﹣BCD的外接球的球心,由△BCA与△ACD均为等边三角形且边长为2,可得OE=OF=DG=.∴DE=DG﹣GE=.∴OD===.∴三棱锥A﹣BCD的外接球的表面积为4π×R2=4π×()2=.故选:C.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为10π.【解答】解:因为O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,根据球的性质,球心一定在垂线l,∵球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,在△PBC中,由余弦定理得cos B=,⇒sin B=,由正弦定理得:,解得R=,∴三棱锥P﹣ABC外接球的表面积为s=4πR2=10π,故答案为:10π.1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD 中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.【解答】证明:(1)∵PA⊥底面ABCD,AB⊂底面ABCD,∴PA⊥AB,又∵底面ABCD为矩形,∴AB⊥AD,PA∩AD,又PA⊂平面PAD,AD⊂平面PAD,∴AB⊥平面PAD,又PD⊂平面PAD,∴AB⊥PD,AD=AP,E为PD中点,∴AE⊥PD,AE∩AB=A,AE⊂平面ABE,AB⊂平面ABE,∴PD⊥平面ABE.解:(II)四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O,由已知BD===4,设C为BD中点,∴AM=2,OM=AP=1,∴OA===3,∴四棱锥P﹣ABCD外接球的体积是=36π.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.【解答】(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.又因为AB⊄平面PDE,DE⊂平面PDE,所以AB∥平面PDE.因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,所以AB∥FG.(2)解:连接AD,EM,相交于O′,易得AO′=,PO′=.由正四棱锥P﹣AMDE的对称性,得正四棱锥P﹣AMDE得外接球球心在线段PO′上,不妨设为O点.设OA=OP=R,则OO′=﹣R,∵AO2=AO′2+OO′2,∴R2=2+(﹣R)2,∴R=∴S=4πR2=,∴正四棱锥P﹣AMDE的外接球的表面积为.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.【解答】解:(I)∵四边形ABCD是矩形,∴AD⊥CD,又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,∴CD⊥平面PAD,∵CD⊂平面PCD,∴平面PAD⊥平面PCD.(II)过P作PE⊥AD,垂足为E,∵△PAD是等腰直角三角形,∠APD=90°,∴PE==1.∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PE⊂平面PAD,PE⊥AD,∴PE⊥平面ABCD,∴V棱锥P﹣ABD=S△ABD•PE=••2•4•1=.(III)取BD中点M,过M作MN⊥平面ABCD,则球心O在直线MN上,连接AM,则AM==.∵PE⊥平面ABCD,∴MN∥PE.∵四棱锥P﹣ABCD内接于球,,∴OA==.∴S⊙O=4πOA2=20π.∴E为外心,∴OM=1.如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π【解答】解:几何体的直观图如图:是长方体的一部分,上底面PCD的外接圆的半径:O1D==,几何体的外接球的半径为:OD==,该四棱锥的外接球的表面积是:4=π.故选:A.课后作业答案:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π【解答】解:设正三棱柱的外接球的半径为R,则∵俯视图是边长为的正三角形∴底面三角形外接圆的半径为=1,∵正三棱柱的高为2∴正三棱柱的外接球的半径为=∴正三棱柱的外接球的表面积等于4π×=8π故选:C.2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π【解答】解:由三视图可知:该四面体是正方体的一个内接正四面体.∴此四面体的外接球的直径为正方体的对角线长=.∴此四面体的外接球的表面积为表面积==3π.故选:B.3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π【解答】解:由题意可知,几何体的直观图如图:是四棱锥D1﹣ABCD,是棱长为1的正方体的一部分,外接球奇数正方体的外接球,取得直径是体对角线,r=,外接球的表面积为:4=3π.故选:A.4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.【解答】证明:(1)设AD的中点为E,则∵PA=PD,∴PE⊥AD,∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PE⊥平面ABCD,∵PA在平面ABCD内的射影为AE,AE⊥CD,∴PA⊥CD,∵PA⊥PD,CD∩PD=D,∴PA⊥平面PCD∴PA⊥PC;解:(2)连接AC交BD于F,球心O在底面的射影必为点F,取截面PEF,PE=,EF=1.假设OF=x,则由OA2=x2+4=1+得x=0,∴球的半径为2,∴四棱锥P﹣ABCD的外接球的体积为=.。
外接球专题集训(含答案)

外接球专题(含答案)类型一:正方体、长方体、直棱锥(有三条线两两互相垂直于同一点)1.在长方体ABCD﹣A1B1C1D1中,AB=AD=,AA1=2,则该长方体的外接球的表面积为()A.4πB.8πC.16πD.32π2.在三棱锥P﹣ABC中,三条侧棱P A,PB,PC两两互相垂直,且△P AB,△P AC,△PBC 的面积依次为1,1,2,则三棱锥P﹣ABC的外接球的半径为()A.B.3C.4D.2类型二:柱体、侧棱垂直底面的棱锥3.已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,AA1=2,BC=2,∠BAC=,则三棱柱ABC﹣A1B1C1外接球的体积为()A.4B.6C.8D.124.三棱锥S﹣ABC中,SA⊥平面ABC,AB⊥BC,SA=2,AB=BC=1,则三棱锥S﹣ABC 的外接球的表面积为()A.6πB.12πC.16πD.24π类型三:侧棱相等的椎体5.在三棱锥P﹣ABC中,P A=PB=PC=2,AB=AC=1,BC=,则该三棱锥的外接球的表面积为()A.8πB.C.D.6.已知正四面体A﹣BCD的外接球的体积为8π,则这个四面体的表面积为()A.18B.16C.14D.12类型四:侧面垂直底面的椎体7.已知在三棱锥P﹣ABC中,P A=PB=BC=1,AB=,AB⊥BC,平面P AB⊥平面ABC,若三棱锥的顶点在同一球面上,则该球的表面积为()A.B.3πC.D.2π类型五:若椎体顶点可构成共斜边的直角三角形,则公共斜边的中点就是外接球的球心8.如图,已知矩形ABCD中,,现沿AC折起,使得平面ABC⊥平面ADC,连接BD,得到三棱锥B﹣ACD,则其外接球的体积为()A.B.C.D.9.在三棱锥S﹣ABC中,SB⊥BC,SA⊥AC,SB=BC,SA=AC,AB=SC,且三棱锥S ﹣ABC的体积为,则该三棱锥的外接球的半径为()A.1B.2C.3D.4答案详解1.在长方体ABCD﹣A1B1C1D1中,AB=AD=,AA1=2,则该长方体的外接球的表面积为()A.4πB.8πC.16πD.32π【解答】解:由题意可知,长方体的对角线长为,则该长方体的外接球的半径为r=,因此,该长方体的外接球的表面积为4πr2=8π.故选:B.11.在三棱锥P﹣ABC中,三条侧棱P A,PB,PC两两互相垂直,且△P AB,△P AC,△PBC 的面积依次为1,1,2,则三棱锥P﹣ABC的外接球的半径为()A.B.3C.4D.2【解答】解:由题意得,,解得,,由P A,PB,PC两两垂直可知该三棱锥是球内接长方体的一角,球的直径即为长方体的体对角线长,体对角线长为=3,∴外接球半径为:,故选:A.4.已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,AA1=2,BC=2,∠BAC=,则三棱柱ABC﹣A1B1C1外接球的体积为()A.4B.6C.8D.12【解答】解:由正弦定理可知,△ABC的外接圆直径为,由于三棱柱ABC﹣A1B1C1的侧棱与底面垂直,该三棱柱为直三棱柱,所以,该三棱柱的外接球直径为,则.因此,三棱柱ABC﹣A1B1C1外接球的体积为.故选:A.19.三棱锥S﹣ABC中,SA⊥平面ABC,AB⊥BC,SA=2,AB=BC=1,则三棱锥S﹣ABC 的外接球的表面积为()A.6πB.12πC.16πD.24π【解答】解:取SC的中点为O,则∵SA⊥平面ABC,BC⊂平面ABC,AC⊂平面ABC∴SA⊥BC,SA⊥AC∵AB⊥BC,SA∩AB=A∴BC⊥平面SAB∵SB⊂平面SAB∴BC⊥SB∵SC的中点为O∴OS=OA=OB=OC∴O为三棱锥S﹣ABC的外接球的球心∵SA=2,AB=BC=1∴SC=∴三棱锥S﹣ABC的外接球的表面积为=6π故选:A.21.在三棱锥P﹣ABC中,P A=PB=PC=2,AB=AC=1,BC=,则该三棱锥的外接球的表面积为()A.8πB.C.D.【解答】解:如图,由P A=PB=PC=2,过P作PG⊥平面ABC,垂足为G,则G为三角形ABC的外心,在△ABC中,由AB=AC=1,BC=,可得∠BAC=120°,则由正弦定理可得:=2AG,即AG=1.∴PG==.取P A中点H,作HO⊥P A交PG于O,则O为该三棱锥外接球的球心.由△PHO∽△PGA,可得,则PO==.即该棱锥外接球半径为.∴该三棱锥外接球的表面积为,故选:B.5.已知正四面体A﹣BCD的外接球的体积为8π,则这个四面体的表面积为()A.18B.16C.14D.12【解答】解:∵V,得R=,即OA=OB=,在正四面体A﹣BCD中,=,∴OO′=,∴O′B=,∴BC=4,S=4×=16,故选:B.8.已知在三棱锥P﹣ABC中,P A=PB=BC=1,AB=,AB⊥BC,平面P AB⊥平面ABC,若三棱锥的顶点在同一球面上,则该球的表面积为()A.B.3πC.D.2π【解答】解:由题意,AC为截面圆的直径,AC==,设球心到平面ABC的距离为d,球的半径为R,∵P A=PB=1,AB=,∴P A⊥PB,∵平面P AB⊥平面ABC,∴P到平面ABC的距离为.由勾股定理可得R2=()2+d2=()2+(﹣d)2,∴d=0,R2=,∴球的表面积为4πR2=3π.故选:B.31.如图,已知矩形ABCD中,,现沿AC折起,使得平面ABC⊥平面ADC,连接BD,得到三棱锥B﹣ACD,则其外接球的体积为()A.B.C.D.【解答】解:设矩形对角线的交点为0,则由矩形对角线互相平分,可知OA=OC=OD =OB.∴点O到四面体的四个顶点A,B,C,D的距离相等,即点O为四面体的外接球的球心,如图所示.∴外接球的半径5.外接球的体积V==.故选:D.15.在三棱锥S﹣ABC中,SB⊥BC,SA⊥AC,SB=BC,SA=AC,AB=SC,且三棱锥S ﹣ABC的体积为,则该三棱锥的外接球的半径为()A.1B.2C.3D.4【解答】解:如图,取SC的中点O,连接OB,OA,∵SB⊥BC,SA⊥AC,SB=BC,SA=AC,∴OB⊥SC,OA⊥SC,OB=SC,OA=SC,∴SC⊥平面OAB,O为三棱锥的外接球的球心,SC为球O的直径,设球O得半径为R,则AB=SC=R,∴△AOB为正三角形,则∠BOA=60°,∴V S﹣ABC=V S﹣OAB+V C﹣OAB=,解得R=3.故选:C.。
外接球难题训练2024.6.6解析

外接球难题训练2024.6.6解析一、单选题1.(2023·浙江·模拟预测)在三棱锥D ABC -中,2AB BC ==,90ADC ∠= ,二面角D AC B --的平面角为30 ,则三棱锥D ABC -外接球表面积的最小值为()A.()161πB.()163π-C.()161πD.()163π令2cos (0,1)t θ=∈,则2213(21)412122481283t R t t t t -=+=+-≥-=-所以2416(233)S R ππ=≥-,当且仅当33t =时取等,故选:B【点睛】关键点点睛:本题主要考查了三棱锥外接球的求法、三角函数的最值问题,据题意找出外接球的球心位置,考察学生的空间想象能力和逻辑思维能力,运算能力,属于难题.2.(2023·浙江·模拟预测)如图1,直角梯形ABCD 中,1,90,22AB DC DCB DC BC AB ∠==== ∥,取AB 中点E ,将BCE 沿EC 翻折(如图2),记四面体B ECD -的外接球为球O (O 为球心).P 是球O 上一动点,当直线AO 与直线AP 所成角最大时,四面体P AEC -体积的最大值为()A .455B .4515C .4105D .15【答案】D【分析】首先得到球心O 在EC 的中点,然后当AP 与球O 相切时直线AO 与直线AP 所成角的最大,过P 作PH AO ⊥垂足为H ,当PH ⊥平面ADE 时四面体P AEC -体积取得最大值,即可求出答案.3.(2023·河南·模拟预测)已知直四棱柱1111ABCD A B C D -的底面为正方形,12,1AA AB ==,P 为1CC 的中点,过,,A B P 三点作平面α,则该四棱柱的外接球被平面α截得的截面圆的周长为()A .6πB .5πC .2πD .2【答案】D 【分析】先根据题意得到该四棱柱的外接球球心ABPE ,再利用线面平行的性质与线面垂直的判定定理求得球心而得解.【详解】由题意知直四棱柱111ABCD A B C D -如图,取1DD 的中点E ,连接,,AE PE BP ,易知四边形ABPE ,由四棱柱的对称性可知,其外接球的球心连接1O O ,则11//,O O EP O O ⊄平面面APE 的距离与1O 到平面过点1O 作1O H AE ⊥,垂足为易知AB ⊥面11AA D D ,又AB ⋂,,AE A AB AE =又1O H =1sin 45O E ︒=由球的性质知,截面圆的半径所以截面圆的周长为2π故选:D.【点睛】关键点睛:本题的关键是求得球心可得解.4.(21-22高三下·四川成都·开学考试)在四棱锥P ABCD -中,底面ABCD 为等腰梯形,PB ⊥底面ABCD .若1PB AB CD AD ====, 2BC =,则这个四棱锥的外接球表面积为()A .3πB .4πC .5πD .6π【答案】C【分析】先求得四棱锥的外接球的半径,再去求外接球表面积即可解决.【详解】取BC 中点E ,连接EA 、ED ,取PC 中点H ,连接EH 、BH ,△PBC 中,,PH CH BE =又PB ⊥底面ABCD ,则又22HA HE EA HE =+==HP HB HC HA HD ===5.(2023·浙江金华·模拟预测)三棱锥-P ABC 中,,2,,AB AC AB BC PC AC PB ⊥==⊥=-P ABC 的外接球表面积的最小值为()A .16πB .18πC .20πD .21π【答案】C【分析】先将三棱锥-P ABC 画在长方体方体中,并建立空间直角坐标系O xyz -,由题目条件分析出点P 的轨迹方程,再有三棱锥-P ABC 的外接球的球心O 满足||||OA OP =,找到球心O 满足的条件,再求出其最值,从而找到半径的最小值,解决问题.【详解】如图,将三棱锥-P ABC 画在长方体方体中,并建立空间直角坐标系PC ,由AC ⊥面11DD C C ,可知P 25,BD ⊥面11DD C C ,所以△4,即P 点轨迹为以D 为圆心,半径为),0,p P z ,则2216P p x z +=—①,ABC 为等腰直角三角形,所以三棱锥)1,1,O z ,由||||OA OP =,得202z +=联立①②得:16282P P o p px x z z z --==,)8,0和点(),p p x z 的直线斜率为k ,则由直线与圆相切,可得33,33k ⎡⎤∈-⎢⎥⎣⎦,3=,所以min 5r =,所以4πS =二、多选题6.(23-24高三上·湖北武汉·期末)如图,已知二面角l αβ--的棱l 上有A ,B 两点,C α∈,AC l ⊥,D β∈,BD l ⊥,且AC AB BD ==,则()A .当αβ⊥时,直线CD 与平面βB .当二面角l αβ--的大小为60︒时,直线AB 与CD 所成角为45︒C .若22CD AB ==,则三棱锥A BCD -的外接球体积的为6D .若2CD AB =,则二面角C BD A --的余弦值为7则四边形ABDE 为正方形,所以成角,因为BD l ⊥,四边形ABDE 又因为AC l ⊥,所以CAE ∠由2CD =,在Rt DEC 中,易得在ACE △中,由余弦定理得cos 过C 点作CO AE ⊥交线段EA 的延长线于点过O 点作OH BD ⊥,交线段DB 则CHO ∠为二面角C BD A --的平面角,易得32CO =,1HO =,CH =所以27cos 7OH CHO CH ∠==,故对C 选项:同选项D 可知CAE ∠如图,分别取线段AD ,AE 的中点则球心O '必在该垂线上,设球的半径为又ACE △的外接圆半径12r =⨯7.(23-24高三上·山东济南·期末)如图,ABC 中,4AB BC ==,AB BC ⊥,M 是AB 中点,N 是AC 边上靠近A 的四等分点,将AMN 沿着MN 翻折,使点A 到点P 处,得到四棱锥P BCNM -,则()A .记平面PBC 与平面PMN 的交线为l ,则//l 平面BCNMB .记直线PM 和BC 与平面PNC 所成的角分别为α,β,则αβ=C .存在某个点P ,满足平面PBC ⊥平面PNMD .四棱锥P BCNM -外接球表面积的最小值为20π【答案】BCD【分析】对A :找到过点P 且与平面BCNM 平行的线,由l 过点P 且不为该支线,即可得l 不平行于平面BCNM ;对B :结合线面角定义,找到PM 与BC 在平面PNC 上的投影即可得;对C :当PC PN ^时,可得结论,即证存在点P ,能使PC PN ^,结合折叠时的角度范围即可得;对D :找出底面BCNM 的外接圆圆心,易得该点为四棱锥P BCNM -外接球球心时有最小半径,即可得最小的外接球表面积.【详解】对A :连接点B 与AC 中点D ,连接PD ,由题意可得N 为AD 中点,M 是AB 中点,故//MN BD ,又MN ⊂平面PMN 、BD ⊄平面PMN ,故//BD 平面PMN ,设直线l '=平面PMN 平面PBD ,由BD ⊂平面PBD ,则//D l B ',【点睛】关键点睛:本题D 选项关键在于如何找到球心,找棱锥外接球球心时,可先找底面外接圆圆心,则外接球球心必在过该点且垂直底面的直线上8.(2024·新疆乌鲁木齐·一模)某广场设置了一些石凳供大家休息,这些石凳是由棱长为40cm 的正方体截去八个一样的四面体得到的,则()A .该几何体的顶点数为12B .该几何体的棱数为24C .该几何体的表面积为2(4800800+D .该几何体外接球的表面积是原正方体内切球、外接球表面积的等差中项【答案】ABD【分析】对于A ,该几何体的顶点是正方体各棱的中点,由正方体有于B ,由该几何体有6个面为正方形即可判断;根据正三角形及正方形的面积公式求解即可判断;原正方体外接球的半径为2240402++对于C ,该几何体的棱长为三角形,所以该几何体的表面积为对于D ,原正方体内切球的半径为原正方体外接球的半径为()224π2034800S =⨯=由题意得该几何体外接球的球心为原正方体的中心,故外接球半径为所以该几何体外接球的表面积为因为26400π1600πS ==所以该几何体外接球的表面积是原正方体内切球、外接球表面积的等差中项,故故选:ABD.9.(2023·河北唐山·模拟预测)如图,在三棱台111ABC A B C -中,V 表示体积,下列说法正确的是()A .1111B AAC A BB C V V --=B .111111,,A A B C A BB C C ABC V V V ---成等比数列C .若该三棱台存在内切球,则111AA BB CC ==D .若该三棱台存在外接球,则111AA BB CC ==对于D ,如图3,若该三棱台的外接球为为球M ,球M 在上下底面的投影点为12,O O ,则12,O O 分别为111,A A C C B B 的外心,所以111111O A O B O C ==,222O A O B O C ==,12O O ⊥平面ABC ,12O O ⊥平面111A B C ,因为11O A ⊂平面111A B C ,所以1211O O O A ^,同理可证122O O O A ^,所以四边形112O A AO 是一个直角梯形,同理可得四边形112O C CO ,112O B BO 也是直角梯形,所以三个直角梯形全等,则111AA BB CC ==,故D 正确.故选:ABD.【点睛】关键点睛:多面体的外接球球心在组成多面体各面的投影点为该多边形的外心,由外心作该面的垂线,两条垂线的交点即为球心.10.(22-23高二下·湖南长沙·期末)如图,正四棱柱1111ABCD A B C D -中,122AA AB ==,动点P 满足1AP aAC bAA =+,且(),0,1a b ∈.则下列说法正确的是()A .当12a =时,直线AC ⊥平面1BPB B .当1a b +=时,1PB PB +C .若直线BP 与BD 所成角为π4,则动点P 的轨迹长度为πD .当21a b +=时,三棱锥-P ABC 外接球半径的取值范围是⎣⎭当12a =时,则12AP AC = 在正四棱柱1ABCD A B -且O 为AC 中点,所以四边形11AAC C 为平行四边形,则所以1AP AO bAA AO =+= 即1OP bOO =,()0,1b ∈所以点P 在线段1OO 上(不含端点)在正四棱柱1ABCD A B -所以1OO ⊥平面ABCD ,所以1PB PB PB +=则1PB PB +最小值为因为AP aAC bAA =+由题意知,BA 、BC 易知1π4OBP ∠=,则动点P 的轨迹是以则动点P 的轨迹长为22易知三棱锥-P ABC 外接球的球心在直线设球心为2O ,2OO h =,作易知1AE =,2AC =,则设三棱锥-P ABC 外接球的半径为则222222R h ⎛⎫=+= ⎪ ⎪⎝⎭所以2232122x R -=+=易知当23x =时,2R 取得最小值则三棱锥-P ABC 外接球的半径的取值范围为故选:ABD.【点睛】关键点睛:本题关键是结合各选项准确的画出图形,共线,将动点转化到定直线上11.(22-23高一下·湖北十堰·期末)上海世博会中国国家馆以城市发展中的中华智慧为主题,表现出了“东方之冠,鼎盛中华,天下粮仓,富庶百姓”的中国文化精神与气质.如图,现有一个与中国国家馆结构类似的六面体1111ABCD A B C D -,设矩形ABCD 和1111D C B A 的中心分别为1O 和2O ,若12O O ⊥平面ABCD ,126O O =,10AB =,AD =118A B =,114A D =,11//AB A B ,11//BC B C ,11//AD A D ,11//CD C D ,则()A .这个六面体是棱台B .该六面体的外接球体积是288πC .直线AC 与11A C 异面D .二面角1A BC C --【详解】11A D AD≠,所以四条侧棱的延长线不能交于一点,所以这个六面体不是棱台,所以A 错误.由题意可知,这个六面体的外接球球心O 在直线()222212116OO O A OO R =+-=,12.(2023·河北沧州·模拟预测)如图所示,该几何体由一个直三棱柱111ABC A B C -和一个四棱锥11D ACC A -组成,12AB BC AC AA ====,则下列说法正确的是()A .若AD AC ⊥,则1AD A C⊥B .若平面11AC D 与平面ACD 的交线为l ,则AC //l C .三棱柱111ABC A B C -的外接球的表面积为143πD .当该几何体有外接球时,点D 到平面11ACC A 的最大距离为3【答案】BD【分析】根据空间线面关系,结合题中空间几何体,逐项分析判断即可得解.【详解】对于选项A ,若AD AC ⊥,又因为1AA ⊥平面ABC ,但是D 不一定在平面ABC 上,所以A 不正确;13.(22-23高二下·安徽安庆·开学考试)如图,在正方体1111ABCD A B C D -中,E 、F 分别是11A D 、11C D 的中点,G 为线段BC 上的动点(含端点),则下列结论中正确的是()A .存在点G 使得直线BD ⊥平面EFGB .存在点G 使得直线AB 与EG 所成角为45°C .G 为BC 的中点时和G 、C 重合时的三棱锥1G EFD -的外接球体积相等D .当G 与B 重合时三棱锥1G EFD -的外接球体积最大【答案】BCD【分析】AB 选项,建立空间直角坐标系,写出点的坐标,表达出()2,22,0BG BC G λλλ=⇒--uuu r uuu r,[]0,1λ∈,利用空间向量验证是否存在点G 使得线面垂直和异面直线夹角;CD 选项,找到球心的位置,设出球心的坐标()0,1,O m -,利用半径相等,则()2,0,0A ,()0,2,0B ,(2,0,0C -()0,4,0BD =-uuu r ,BG BC G λ=⇒uuu r uuu r(21,32,22)EG λλ=----,EF A 选项;显然,(04,,0B EF D ⋅-=u u ruu r uu 若BD ⊥平面EFG ,EG 在面EFG 而()4320BD EG λλ⋅=-⨯-=⇒uuu r uuu r B 选项;当G 为BC 中点时,EG uuu 故(2,2,0cos ,AB EG AB EG AB EG-⋅==⋅故直线AB 与EG 所成角为45°,结论成立,对于C 、D 选项;球心O 必在过设()0,1,O m -,G 在BC 上运动时,()()(1,1,220,1,1,0,OE m =---=故2228129OG m λλ=-++,OE14.(2023·辽宁沈阳·模拟预测)如图,在三棱柱111ABC A B C -中,1AA ⊥底面1,4,2ABC AA AC BC ===,90,ACB D ∠= 为线段11B C 上的动点,,E F 分别为线段111,A C AA 中点,则下列命题中正确的是()A .三棱锥D ABC -的外接球体积的最大值为B .直线CD 与AB 所成角的余弦值的取值范围是⎡⎢⎣⎦C .当D 为11B C 中点时,三棱锥E FBD -的体积为13D .存在点D ,使得1CD BA ⊥故选:AC.【点睛】知识点点睛:本题考查线面平行的判定定理,锥体体积公式,利用向量研究异面直线的夹角,利用向量研究空间位置关系和多面体与球的切接关系,属于综合题15.(22-23高三上·广东佛山·期末)数学中有许多形状优美,寓意独特的几何体,如图1所示的礼品包装盒就是其中之一.该礼品包装盒可以看成是一个十面体,其中上、下底面为全等的正方形,所有的侧面是全等的等腰三角形.将长方体1111ABCD A B C D -的上底面1111D C B A绕着其中心旋转45°得到如图2所示的十面体ABCD EFGH -.已知2,AB AD AE ===,则()A .十面体ABCD EFGH -1B .十面体ABCD EFGH -的表面积是8C .十面体ABCD EFGH -外接球球心到平面ABE 的距离是12D .十面体ABCD EFGH -外接球的表面积是(11π+连接11A C 交HE 于点M 得22211A E A M ME =+=又因为长方体ABCD -所以11AA A E ⊥,所以AE 解得21322AA =+,即16.(22-23高三上·湖北·期末)如图,棱长为2的正方体1111ABCD A B C D -中,动点P 满足111(R,[0,1])B P B D λλλ=∈∈.则以下结论正确的为()A .[0,1]λ∃∈,使直线1AP ⊥面1P B B B .直线1AA 与面1A BDC .[0,1]λ∀∈,三棱锥1P A BD -体积为定值43D .当12λ=时,三棱锥1P A BD -的外接球表面积为11π则1(0,0,0),(2,0,0),(2,2,0),(2,0,2),D A B A 设平面1A BD 的法向量为(,n x y =三、填空题17.(23-24高三上·江苏南通·期末)在平面四边形ABCD中,AB=AD=,BC=CD=3,BC⊥CD,将△ABD沿BD折起,使点A到达A′,且A C'=A′BCD的外接球O的体积为;若点E在线段BD上,且BD=4BE,过点E作球O的截面,则所得截面圆中面积最小的圆半径为.第二空,根据题意可知,将四面体过点E作球O的截面,若要所得的截面圆中面积最小,只需截面圆半径最小,设球面的距离d,只需球心到截面的距离故答案为:①2732π,②18.(2024·浙江嘉兴·二模)在四面体ABCD 中,2,90BC ABC BCD ∠∠=== ,且AB 与CD所成的角为60 .若四面体ABCD 的体积为,则它的外接球半径的最小值为.【答案】3【分析】根据题意,将四面体43ABCD V =求得24xy =,在222DF x y xy =+-,结合基本不等式求解【详解】依题意,可将四面体所成的角为60 ,所以60DCF ∠=o 或120 ,设外接球的球心如图点O .易知//AF 平面BCDE ,所以点13A BCD F BCD V V BC S --∴==⋅⋅在2Rt OCO 中,22R OC =在CDF 中,由余弦定理得【点睛】关键点点睛:本题关键是将求四面体求直三棱柱外接球半径的最小值19.(2024·山东烟台·一模)在三棱锥-P ABC 中,2PB PC ===,且,,APB BPC CPA E F ∠∠∠==分别是,PC AC 的中点,90BEF ∠= ,则三棱锥-P ABC 外接球的表面积为,该三棱锥外接球与内切球的半径之比为.【答案】10π【分析】第一空作出辅助线,证明三三垂直,将三棱锥放入长方体中求解外接球半径即可,第二空利用体积相等求出内切球半径,再求比值即可【详解】如图,AP B ∠可得PAB PAC ≅△△,则则,AD BC PD BC ⊥⊥,又则该长方体外接球即为所求三棱锥其中点O 为所求外接球的球心,设其半径为可得222(2)R =2+2+设该三棱锥内切球半径为则1P ABC O ABC V V V --=+可得13PBC PA S ⨯⨯= 故PBC ABC PA S S =(⨯ 而222(2)AB =+易知1O 是CB 的中点,由而由勾股定理得AO 故可将PBC PA S =(⨯ 122222=(⨯⨯2⨯解得2221r =+,而半径比为故答案为:10π;10【点睛】关键点点睛:本题考查内切球和外接球的半径问题,解题关键是构造出长方体,将三棱锥放入其中,然后求出外接球半径,得到面积,进而由体积关系转化得到所要求的内切球半径,再求比值即可.20.(22-23高三下·河北石家庄·阶段练习)已知球O 是正四面体-P ABC 的外接球,E 为棱PA 的中点,F 是棱PB 上的一点,且2FC EF =,则球O 与四面体P EFC -的体积比为.【点睛】关键点点睛:解题的关键点是利用勾股定理求出三棱锥的高和外接球的半径,了学生的空间想象能力、运算能力。
高中数学立体几何外接球专题练习(含解析)

高中数学立体几何外接球专题练习(含解析)1.已知菱形ABCD满足|AB|=2,∠ABC=120°,将菱形ABCD沿对角线AC折成一个直二面角B-AC-D,则三棱锥B-ACD外接球的表面积为()。
A。
πB。
8πC。
7πD。
4π2.如图,四面体ABCD中,面ABD和面BCD都是等腰直角三角形,AB=BD=BC=1,∠CBD=60°,且二面角A-BD-C的大小为120°,∠BAD=45°,若四面体ABCD的顶点都在球O上,则球O的表面积为()。
A。
12πB。
20πC。
24πD。
36π3.如图,网格纸上小正方形的边长为2,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为()。
A。
28πB。
32πC。
41πD。
31π4.已知一个几何体是由半径为2的球挖去一个三棱锥得到(三棱锥的顶点均在球面上).若该几何体的三视图如图所示(侧视图中的四边形为菱形),则该三棱锥的体积为()。
A。
4/3B。
2/3C。
8/3D。
16/35.已知一个几何体的三视图如图所示,则该几何体的表面积是()。
A。
2+2+2B。
4+4+2C。
2+4+4D。
4+4+46.某三棱锥的三视图如图所示,则它的外接球表面积为()。
A。
25πB。
20πC。
16πD。
40π7.如图是某几何体的三视图,则该几何体的表面积是()。
A。
18+2B。
15+2C。
12+2D。
18+48.在四面体ABCD中,AD⊥底面ABC,DE⊥AC,E为棱BC的中点,DG⊥BE,点G在AE上且满足AG=2GE,若四面体ABCD的外接球的表面积为S,则tan∠AGD=S/12.A。
1/2B。
1C。
2D。
49.在三棱锥S-ABC中,∠ASB=90°,SA=SB=SC=2,且三棱锥S-ABC的体积为8/3,则该三棱锥的外接球的表面积为()。
A。
4πB。
16πC。
36πD。
72π10.如图所示,正方形ABCD的边长为2,切去阴影部分围成一个正四棱锥,则当正四棱锥体积最大时,该正四棱锥外接球的表面积为()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
外接球专项训练参考答案一.选择题1、已知球O 的半径为2,圆M 和圆N 是球的互相垂直的两个截面,圆M 和圆N 的面积分别为2π和π,则||MN =( )A .1 BC .2 D【答案】D【解析】因由球心距与截面圆的半径之间的关系得538212221222221=-=+⇒⎪⎩⎪⎨⎧=+=+d d R d R d ,故52221=+=d d MN ,应选D 。
考点:球的几何性质及运算。
2、在三棱锥P ABC -中,,2AB BC AB BC PA PC ⊥====,AC 中点为M,cos PMB ∠锥的外接球的表面积为( )A .32π B .2π C .6π D【答案】C【解析】CA如图,易知312,1212=-===PM AC BM ,由余弦定理可得2333231=⨯⨯-+=PB ,因222PA AB PB =+,故BA PB ⊥;同理222PC CB PB =+,故BC PB ⊥,所以C B A P ,,,是棱长为2的正方体的四个顶点,其外接球就是正方体的外接球,半径为223⋅=R ,所以外接球的面积为ππ6464=⨯=S ,应选C 。
考点:球与几何体的外接和表面积的计算公式。
3、球O 的球面上有四点,,,S A B C ,其中,,,O A B C 四点共面,ABC ∆是边长为2的正三角形,面SAB ⊥面ABC ,则棱锥S ABC -的体积的最大值为( )A.3B ..4 【答案】A【解析】设球心和ABC ∆的外心为O ,延长CO 交AB 于点P ,则由球的对称性可知AB PD ⊥,继而由面SAB ⊥面ABC 可得⊥PD ABC ∆所在的平面,所以PD 是三棱锥的高;再由,,,O A B C 四点共面可知O 是ABC ∆的中心,故332,33==R OP ,当三棱锥的体积最大时,其高为1)33()332(22=-=PD ,故三棱锥的体积的最大值为331243312=⨯⨯⨯,应选A 。
考点:几何体的外接球等有关知识的运用。
【易错点晴】球与几何体的外接和内切问题一直是高中数学中题的重要题型,也高考和各级各类考试的难点内容。
本题将三棱锥与球外接整合在一起考查三棱锥的体积的最大值无疑是加大了试题的难度。
解答本题时要充分利用题设中提供的有关信息,先确定球心O 的位置是三角形ABC 的外心,再求外接球的半径332=R 并确定当PD为三棱锥的高时,该三棱锥的体积最大并算出其最大值为3。
4、已知在三棱锥P ABC -中,PA ⊥面ABC ,PC AB ⊥,若三棱锥P ABC -的外接球的半径是3,ABC ABP ACP S S S S ∆∆∆=++,则S 的最大值是( )A .36B .28C .26D .18 【答案】D【解析】因为PA ⊥面ABC ,所以PA AB ⊥,PA AC ⊥,又因为PC AB ⊥,所以AB ⊥平面PAC ,所以AB AC ⊥,所以有2222(23)36AB AC AP ++=⨯=,则由基本不等式可得22211()()1822ABC ABP ACP S S S S AB AC AB AP AP AC AB AC AP ∆∆∆=++=⋅+⋅+⋅≤++=,当且仅当AB AC AP ==时等号成立,所以S 的最大值是36,故选D.AC考点:1.线面垂直的判定与性质;2.长方体外接球的性质;3.基本不等式.【名师点睛】本题考查线面垂直的判定与性质、长方体外接球的性质、基本不等式,中档题;立体几何的最值问题通常有三种思考方向:(1)根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;(2)将几何体平面化,如利用展开图,在平面几何图中直观求解;(3)建立函数,通过求函数的最值或利用基本不等式来求解.5、如图所示是一个几何体的三视图, 则这个几何体外接球的表面积为( )A .8πB .16πC .32πD .64π 【答案】C【解析】几何体为一个四棱锥,外接球球心为底面正方形(边长为4)中心,所以半径为22,表面积为24(22)32ππ=,选C.考点:三视图,外接球【方法点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解. 6、如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体 外接球的表面积为( )A .203π B .8π C .9π D .193π【答案】D【解析】由三视图可知,这个几何体是三棱锥.如图所示,O 为球心,F 为等边三角形BCD 的外心,由图可知2222213192212R OF CF ⎫⎛⎫=+=+=⎪ ⎪⎪⎝⎭⎝⎭,故外接球面积为193π. EDOF考点:三视图. 【思路点晴】设几何体底面外接圆半径为x ,常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.若长方体长宽高分别为,,a b c 则其体对角线长为222a b c ++;长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心.7、如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的外接球半径为( )A .272C 11D .23【答案】C【解析】从三视图可以看出这是一个正方体上的一个四面体,如图,其中正MNP ∆的边长为24,其外接圆的半径3241=r ,同样正111P N M ∆的外接圆的半径是3222=r ,由球的对称性可知球心O 必在正方体的对角线AC 上,且934,9382211====h CO h AO ,该球经过六个点111,,,,,P N M P N M ,设球心O 到平面111P N M ∆的距离为1d ;球心O 到平面MNP ∆的距离为2d ,而两个平面MNP 和111P N M 之间的距离为2121334)(34d d h h d +==+-=,则由球心距、垂面圆半径之间的关系可得2222221212,r d R r d R +=+=,所以822212122=-=-r r d d ,即82122=-d d ,又33421=+d d ,将其代入82122=-d d 可得3212=-d d ,由此可得3352=d ,所以113333832522222==+=+=r d R ,所以外接球的半径11=R ,应选C.OO 2O 1P 1N 1M 1C APNM考点:三视图的识读和理解及几何体体积的计算. 【易错点晴】本题以网格纸上的几何图形为背景,提供了一个三棱锥的几何体的三视图,要求求其外接球的半径,是一道较为困难的难题.难就难在无法搞清其几何形状,只知道是一个三棱锥(四面体)是没有任何用的.通过仔细观察不难看出这是一个正方体上的一个四面体,如图,正MNP ∆的边长为24,其外接圆的半径3241=r ,同样正111P N M ∆的外接圆的半径是3222=r ,由球的对称性可知球心O 必在对角线上,且经过六个点111,,,,,P N M P N M ,设球心O 到平面111P N M ∆的距离为1d ;球心O 到平面MNP ∆的距离为2d ,而两个平面MNP 和111P N M 之间的距离为2121334)(34d d h h d +==+-=,则由球心距垂面圆半径之间的关系可得2222221212,r d R r d R +=+=,所以822212122=-=-r r d d ,即82122=-d d ,又33421=+d d ,将其代入82122=-d d 可得3212=-d d ,由此可得3352=d ,所以113333832522222==+=+=r d R ,所以外接球的半径11=R ,其中计算21,h h 时可用等积法进行.8、一直三棱柱的每条棱长都是3,且每个顶点都在球O 的表面上,则球O 的半径为( ) A .21B .6C .7D .3 【答案】A【解析】球O 的半径满足2223321()(3)232R R =+⋅⇒=考点:外接球【方法点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解. 9、若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和侧视图如图所示,则此几何体的表面积是 A .24π B .24π+8πC .24π+4πD .32π答案:C10、已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2,2,AB SA SB SC ====则三棱锥的外接球的球心到平面ABC 的距离是( ) (A )3 (B )1 (C)3 (D )332【答案】A【解析】因为三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2SA SB SC ===,S ∴在面ABC 内的射影为AB 中点H ,SH ∴⊥平面ABC ,SH ∴上任意一点到,,A B C 的距离相等. 3SH =Q ,1CH =,在面SHC 内作SC 的垂直平分线MO ,则O 为S ABC -的外接球球心.2SC =Q ,1SM ∴=,30OSM ∠=︒,233,SO OH ∴==,即为O 到平面ABC 的距离,故选A .考点:球内接多面体;点到面的距离的计算.【名师点睛】(1)一般要过球心及多面体中的特殊点或过线作截面将空间问题转化为平面问题,从而寻找几何体各元素之间的关系.(2)若球面上四点P ,A ,B ,C 中PA ,PB ,PC 两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接问题.(3)一般三棱锥的外接球的球心可通过其中一个面的外心作此平面的垂线,则球心必在此垂线上.11、已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2,2,AB SA SB SC ====则三棱锥的外接球的球心到平面ABC 的距离是( ) (A )3 (B )1 (C )3 (D )332【答案】A12、某四棱锥的三视图如图所示,则该四棱锥外接球的表面积是( )A .172π B .34π C.3 D. 【答案】B【解析】几何体为一个四棱锥,其顶点为长方体四个顶点,长方体的长宽高为4,3,3,因此四棱锥外接球直径为长方体对角线,即2R 2434.R ππ=选B.考点:三视图【方法点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解. 13、已知三棱锥S-ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC=2,则此棱锥的体积为( )ABCD【答案】A【解析】连接OC OB OA ,,,则由已知得1======AC BC AB OC OB OA ,可知三棱锥ABC O -是棱长为1的正四面体,其高为36,则三棱锥ABC S -的高为362,所以三棱锥ABC S -的体积为623624331=⨯⨯. 考点:三棱锥外接球.14、半径为1的三个球,,A B C 平放在平面α上,且两两相切,其上放置一半径为2的球D ,由四个球心,,,A B C D 构成一个新四面体,则该四面体外接球O 的表面积为( )A .24323π B .24392π C .9π D【答案】A【解析】由已知条件可知,该四面体是底面边长为2的等边三角形,且侧棱长为3.该四面体外接球半径计算公式为222x h R h+=,其中x 为底面外接圆半径,h 为高.本题中x h ==,故24238169243,44464232323R S R πππ+⋅====⋅=⋅⋅.考点:球的内接几何体.15、在正三棱锥S ABC -中,M 是SC 的中点,且AM SB ⊥,底面边长22AB =,则正三棱锥S ABC -的外接球的表面积为( )A .6πB .12πC .32πD .36π 【答案】【解析】根据三棱锥为正三棱锥,可证明出AC ⊥SB ,结合SB ⊥AM ,得到SB ⊥平面SAC ,因此可得SA 、SB 、SC 三条侧棱两两互相垂直.最后利用公式求出外接圆的直径,结合球的表面积公式,可得正三棱锥S-ABC 的外接球的表面积.取AC 中点,连接BN 、SN ,∵N 为AC 中点,SA=SC ,∴AC ⊥SN , 同理AC ⊥BN ,∵SN ∩BN=N ,∴AC ⊥平面SBN ,∵SB ⊂平面SBN ,∴AC ⊥SB ,∵SB ⊥AM 且AC ∩AM=A , ∴SB ⊥平面SAC ?SB ⊥SA 且SB ⊥AC , ∵三棱锥S-ABC 是正三棱锥,∴SA 、SB 、SC 三条侧棱两两互相垂直. ∵底面边长22AB =,∴侧棱SA=2,∴正三棱锥S-ABC 的外接球的直径为:2233R R =∴=,, ∴正三棱锥S-ABC 的外接球的表面积是2412S R ππ==,故选:B .考点:空间线面垂直的判定与性质;球内接多面体16、已知三棱锥P ABC -,在底面ABC ∆中,1=AB 60,3,A BC PA ∠==⊥o 面,23ABC PA =,则此三棱锥的外接球的表面积为( ) A .163π B .43π C .323πD .16π 【答案】D【解析】底面三角形内,根据正弦定理,可得2=AC ,222AC BC AB =+,满足勾股定理,090=∠ABC ,⊥PA 底面ABC ,所以BC PA ⊥,那么⊥BC 平面PAB ,所以PB BC ⊥,那么直角三角形PBC PAC ,有公共斜边PC ,所以三棱锥的外接球的球心就是PC 的中点O ,PC 是其外接球的直径,4=PC ,所以外接球的表面积ππ1642==R S ,故选D.考点:球与几何体17、已知直三棱柱111C C AB -A B 的6个顶点都在球O 的球面上,若3AB =,C 4A =,C AB ⊥A ,112AA =,则球O 的表面积为为( )A .153πB .160πC .169πD .360π 【答案】C【解析】由题意,三棱柱111C C AB -A B 为直三棱柱,底面C AB 为直角三角形,把直三棱柱111C C AB -A B 补成四棱柱,则四棱柱的体对角线是其外接球的直径,22213412132++= 则三棱柱111C C AB -A B 1外接球的表面积是224169R cm ππ=.故选C . 考点:几何体的外接球18、如图,1111ABCD A B C D -是边长为1的正方体,S ABCD -是高为1的正四棱锥,若点S ,1111,,,A B C D 在同一个球面上,则该球的表面积为( )A .916π B .2516π C .4916π D .8116π 【答案】D【解析】按如图所示作辅助线,O 为球心,设1OG x =,则12OB SO x ==-,同时由正方体的性质知112B G =,则在11Rt OB G ∆中,2221111OB G B OG =+,即()222222x x ⎛⎫-=+ ⎪ ⎪⎝⎭,解得78x =,所以球的半径198R OB ==,所以球的表面积为281416S R ππ==,故选D .考点:1、球内接多面体的性质;2、球的表面积公式.19、在平行四边形ABCD 中,AB BD ⊥,22421AB BD +=,将此平行四边形沿BD 折成直二面角,则三棱锥A BCD -外接球的表面积为( ) A .2πB .πC .2πD .4π 【答案】A【解析】因为平行四边形ABCD 中,BD AB ⊥,沿BD 折成直二面角C BD A --,所以三棱锥BCD A -的外接球的直径为AC ,且212222222=+=++=BD AB CD BD AB AC ,所以三棱锥BCD A -的外接球的半径为42,所以三棱锥BCD A -的外接球的表面积为21624ππ=⨯;故选A .考点:1.平面图形的折叠问题;2.多面体与球的组合.20、如图, 在菱形ABCD 中,60,23,BAD AB E ∠==o 为对角线BD 的中点, 将ABD ∆沿BD 折起到PBD ∆的位置,若 120PEC ∠=o ,则三棱锥P BCD -的外接球的表面积为( )A .28πB .32πC .16πD .12π 【答案】A【解析】设,M N 分别是等边三角形,PBD CBD 的外心,则11,2O N NC ==画出图象如下图所示,由图象可知,11120,60MO N OO N ∠=∠=o o ,故1tan 603ON =⋅=o ,2234R OC ON NC ==+=+7=,外接球面积为244728R πππ=⋅=.考点:球的内接几何体.21、已知从点P 出发的三条射线PA ,PB ,PC 两两成60︒角,且分别与球O 相切于A ,B ,C 三点.若球O 的体积为36π,则O ,P 两点间的距离为( )(A )32(B )33(C )3 (D )6 【答案】B【解析】连接OP 交平面ABC 于'O ,由题意可得:ABC ∆和PAB ∆为正三角形,所以33'3AB APO A ==.因为'AO PO OA PA ⊥⊥,,所以OP AP OA AO =',所以3APOP OA OA AO =⋅='.又因为球的体积为36π,所以半径3OA =,所以33OP =.考点:点、线、面间的距离计算.【思路点睛】连接OP 交平面ABC 于'O ,由题意可得:33'33AB APO A ==.由'AO PO OA PA ⊥⊥,可得OP APOA AO =',根据球的体积可得半径3OA =,进而求出答案. 22、在半径为1的球面上有不共面的四个点A ,B ,C ,D 且AB CD x ==,BC DA y ==,CA BD z ==,则222x y z ++等于( )A .16B .8C .4D .2 【答案】B【解析】如图,构造长方体,设长方体的长、宽、高分别为c b a ,,,则422222==++c b a ,根据题意,得222222222,,z c a y c b x b a =+=+=+,则8)(2222222=++=++c b a z y x ;故选B .考点:多面体与球的组合 23、“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图所示,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是( )【答案】B【解析】因为相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖),且正视图和侧视图是一个圆,所以从上向下看,相对的两个曲面在同一个圆柱的侧面上,即俯视图是有两条对角线且为实线的正方形;故选B . 考点:三视图.24、某一简单几何体的三视图如图所示,该几何体的外接球的表面积是( )A .π13B .π16C .π25D .π27 【答案】C【解析】从三视图可以看出该几何体是底面对角线长为4正方形高为3正四棱柱,故其对角线长为R l 254322==+=,故该几何体的外接球的面积为ππ2542==R S ,选C.考点:三视图与几何体的外接球.25、如图,边长为2的正方形ABCD 中,点E ,F 分别是边AB ,BC 的中点△AED ,△EBF ,△FCD 分别沿DE ,EF ,FD 折起,使A ,B ,C 三点重合于点A ′,若四面体A ′EFD 的四个顶点在同一个球面上,则该球的半径为( )ABCDEFEFDA2 B .52 C 11.62【答案】D【解析】因为折起后,,A B C 三点重合,所以',','A E A F A D 两两垂直,三棱锥的外接球,就是棱长为1,1,2的长方体的外接球,球半径R 满足222241126,R R =++==6D. 考点:几何体外接球的性质.26、已知三棱锥S ﹣ABC ,满足SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SC 3Q 是外接球上一动点,则点Q 到平面ABC 的距离的最大值为( )A .3B .2C .3D .43【答案】D【解析】因为三棱锥S ABC -中,,,SA SB SB SC SC SA ⊥⊥⊥,且SA SB SC ==,所以三棱锥的外接球即为以,,SA SB SC 为长宽高的正方体的外接球,因为该三棱柱外接球的半径为3,所以正方体的对角线长为23,所以球心到平面ABC 的距离为1233233⨯=,所以点Q 到平面ABC 的距离的最大值为343333+=,故选D .考点:球的性质及组合体的应用.27、一个直棱柱的三视图如图所示,其中俯视图是一个顶角为ο120的等腰三角形,则该直三棱柱外接球的表面积为( )A .20πB .205π C .25π D .255π 【答案】A【解析】由三视图可知,该三棱柱为底面为顶角为23π,两腰为2的等腰三角形,高为2,底面三角形的外接圆直径为234sin3π=,半径为2,设该三棱柱的外接球的半径为R ,则221215R =+=,所以该三棱柱的外接球的表面积为2420S R ππ==,故选A .考点:1.三视图;2.球的切接问题;3.球的表面积.【名师点睛】本题主要考查三视图、球的切接问题、表面积公式及空间想象能力、运算能力,中档题;识图是数学的基本功,空间想象能力是数学与实际生活必备的能力,本题将这些能力结合在一起,体现了数学的实用价值,同时也考查了学生对球的性质与表面积公式的掌握与应用、计算能力.28、某四面体的三视图如图,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的体积为( )A .B .C .D .【答案】B【解析】由题意此四面体是棱长为2的正四面体,其外接球半径为63242⨯=,所以3433()322V ππ=⨯=.故选B .考点:三视图,外接球,球体积.【名师点睛】正四面体的内切球与外接球: (1) 正四面体的内切球,如图. 位置关系:正四面体的四个面都与一个球相切,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为a ,高为h ;球的半径为R ,这时有643R h a ==;(可以利用体积桥证明)(2) 正四面体的外接球,如图5. 位置关系:正四面体的四个顶点都在一个球面上,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为a ,高为h ;球的半径为R ,这时有436R h a ==;(可用正四面体高h 减去内切球的半径得到)29、如图所示,在直三棱柱C C '''AB -A B 中,C C A ⊥B ,C 2'B =BB =,C 4A =,点M 是线段'AB 的中点,则三棱锥C M -AB 的外接球的体积是( )A .36πB .205πC .6πD .43π 【答案】A【解析】由题意可知162MA MB AB '===,取AB 的中点D ,连接,MD CD ,在直角MCD ∆中,226MC MD CD =+=,所以点M 在平面ABC 内的射影是ABC ∆的外心,即为AB 的中点,设三棱锥C M -AB 的外接球的球心为O ,由球的截面性质可得()222MD r CD r -+=,即()2215r r -+=,解得3r =,所以其外接球的体积为34363V R ππ==,故选A.考点:棱锥与球的组合体及球的体积.【方法点睛】本题主要考查了棱锥与球的组合体,球的截面性质及球的体积,考查了考生的空间想象能力属于中档题.本题解答的关键是根据已知条件求得MA MB MC ==,从而判断点M 在平面ABC 内的射影位置,而ABC ∆又是直角三角形,其外心位于斜边的中点上,据此可知三棱锥C M -AB 外接球的球心在MD 上,根据球的截面性质得到球的半径,求得其体积.30、已知球面上有四个点,,,A B C D ,球心为点O ,O 在CD 上,若三棱锥A BCD -的体积的最大值为83,则该球O 的表面积为( )A .4πB .16πC .163π D .323π【答案】B【解析】设球的半径r ,首先因为O 在CD 上,所以CD 为球O 的直径,BCD ∆为直角三角形,2CD r =,若使三角形的面积最大,则点B 到边CD 的距离最大即可,因为,,B C D 三点共面.所以最大距离为半径r ,三角形BCD 面积的最大值为2122r r r ⋅⋅=;当点A 距离平面BCD 最大时为r ,则三棱锥A BCD -的体积的最大值为23118333r r r ⋅==,2r =,所以该球的表面积为4416ππ⋅=,选B . 考点:1.球的表面积;2.棱锥的体积.31、一个几何体的顶点都在球面上,它们的正视图、侧视图、俯视图都是下图.图中圆内有一个以 圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是( )A .2π B.3π C.4π D.5π 【答案】B【解析】由三视图可知:该四面体是正方体的一个内接正四面体,此四面体的外接球的半径为正方体的对角线长为3,利用球的表面积公式得234()32s ππ==,故选B .考点:球的结合体.评卷人 得分二、填空题(注释)32、在四棱锥P ABCD -中,PB ⊥底面ABCD ,底面ABCD 是边长为2的正方形.若直线PC 与平面PDB 所成的角为30°,则四棱锥P ABCD -的外接球的表面积为_______. 【答案】12π【解析】连结AC 交BD 于H ,则可证得AC ⊥平面PDB ,连接PH ,则CPH ∠就是直线PC 与平面PDB 所成的角,即30CPH ∠=°,2CH =Q 22PC ∴=23PD ∴=∴四棱锥P ABCD -的外接球的半径312π,故应填12π. 考点:四棱锥的外接球的面积及求法.33、已知矩形ABCD 的顶点都在半径为R 的球O 的球面上,且6,23AB BC ==,棱锥O ABCD -的体积为3R = ________.【答案】4【解析】由题可得四棱锥的侧棱为R ,则162383,23V h h =⨯⨯==,再由;4 R==.考点:多面体与外接球.。
