On the Causality and Stability of the Relativistic Diffusion Equation
时间回溯作文模板

时间回溯作文模板英文回答:Time regression is a captivating concept that has captivated the imagination of philosophers, scientists, and storytellers alike. It is the hypothetical ability to go back in time, alter past events, and return to the present. However, such a phenomenon remains a theoreticalpossibility and is currently beyond the realm of scientific capability.The implications of time regression are bothtantalizing and potentially paradoxical. On the one hand, it offers the allure of correcting past mistakes, reliving cherished moments, and preventing tragedies. On the other hand, it raises profound questions about causality, the nature of free will, and the stability of the present.If time regression were possible, it would necessitate a radical shift in our understanding of time itself. Timewould no longer be a linear progression but rather a malleable construct that could be manipulated and altered. This would challenge our most fundamental assumptions about the universe and our place within it.The practical applications of time regression are equally fascinating. It could potentially revolutionize fields such as medicine, history, and criminal justice. By going back in time, doctors could diagnose and treat diseases at their earliest stages, historians could witness firsthand key events, and investigators could potentially solve crimes before they occur.However, it is crucial to recognize the ethical and philosophical dilemmas that time regression wouldinevitably entail. Altering the past could have unpredictable consequences for the present and the future. Moreover, it raises questions about the value of human agency and the potential for abuse of power.Ultimately, time regression remains an enigmatic and tantalizing concept that continues to inspire bothscientific inquiry and philosophical contemplation. Whileit may not be within our grasp today, it serves as a reminder of the vast mysteries that still lie ahead.中文回答:时间倒流是一个引人入胜的概念,它吸引了哲学家、科学家和故事讲述者的想象力。
商务英语阅读(第二版)-王关富-Unit-6-Goodbye--Free-Trade-课后答案

Unit 6Goodbye, Free Trade?Exercises1.Answer the questions on the text.1) What was the result when the House of Representatives passed theHawley-Smoot Tariff Act in 1930?The economic recession in the United States became even worse.2) According to the author, what happens when a currency appreciates?It diminishes the export advantage of the country and makes it difficult to increase exports or even maintain the status quo.3) How did American politicians take advantage of the public’s stronganti-free-trade sentiment in the United States?They created a talking point in charges of unfair trade so that they thought they could benefit in the mid-term elections.4) What did American politicians and economists agree and disagree over theHawley-Smoot Tariff Act?Almost all of them agreed that it was a bad law, but they disagreed whether it triggered the Great Depression in the 1930s.5) What did Milton Friedman think were the more important reasons for theGreat Depression?The malfunctioning gold standard system and inept monetary policy of the Federal Reserve.6) What was the foreign reaction unexpected by the American lawmakers afterthe Hawley-Smoot Tariff Act was enacted?The trading partners were angered and imposed discriminatory tariffs on American goods. Canada in particular, as the largest export market for the US, reacted fiercely and handed its market over to the British competitors.7) Why is it unlikely for the US to adopt another Smoot-Hawley today in the eyeof the author?(1)The US is much more integrated into the world economy today than it was inthe 1930s.(2)Import restrictions seldom achieve their intended goals, instead, often end uphurting American industries and consumers.(3)The Americans have learned to consider the possible strong foreignretaliation against US exporters.8) What were the respective results for those countries withdrawing from thegold standard and those clinging to it during the 1930s according to the author?Those countries going off the gold standard allowed their currencies to depreciate, avoided protectionist trade policies and, instead, used monetary policy to end price deflation and stimulate economic growth.Those countries choosing to stay on pursued protectionist trade policies by imposing high tariffs, import quotas and exchange controls, which did little in boosting their economic growth. Thus they suffered a longer economic depression.9) How does the author justify his support for the policy of "quantitativeeasing"?(1) Historically, the most important tool for resisting protectionist sentiment in the1930s was a monetary policy that would promote economic growth.Today the US is in a similar situation. Taking right monetary policy can alleviate the pressure on Washington to adopt protectionist trade policy and can help to raise output before it leads to a high inflation.(2) He also quotes what Charles Evens said: Additional measures taken by the Fedto stimulate growth should condoned, not condemned.(3) What Mr. Friedman wrote 1997 about Japan: The surest road to a healthyeconomic recovery is to increase the rate of monetary growth, to shift from tight money to easier money.10) What does the author imply about the US Congress?In comparison with the Fed, the US Congress is following a trade protectionist policy in blaming other countries for its unemployment and may cause serious trade retaliations from trading partners.2. Fill in each blank of the following sentences with one of the phrases in the list given below. Make changes when necessary.1)As the financial scandal involves so many people, the probe in to it could dragon for another year.2)In the age of globalization more individuals are forced to integrate intomultinational work teams.3)Many in Europe are now very much worried that it may sink into a Japan-styleeconomic recession.4)But the business leaders yesterday warned against interest rate rises, arguing thatinflation was being driven not by consumer spending, but by rising commodity prices.5)After the call scandal, the American automakers and some politicians there wereso eager to keep their rival Toyota at bay in the auto market.6)Under the current labor law, two categories of employees are exempt fromminimum wage and overtime requirements.7)Though the local partner made a revised offer, the foreigner investor refused andreverted back to the original agreement conditions.8)Last Friday the two parties met for more than five hours only to end up walkingaway from the table once again, reaching no agreement at all.9)When the government supervises banks, it should take into account their payand bonus structures which may often be the source of corruption.10)The customers severely affected in the incident demanded that the company putin place effective measures to avoid occurrence of such things in the future. 11)It’s critical to take hold of any opportunity coming your way because it willnever come back again once lost.12)At times of economic depression, people are more inclined to unethical means intheir business.3. Match the terms in column A with the definitions in column B:A__________________________ B____________________________________ 1)unfair trade A) Restrictions that governments put in placeon the purchase or sale of a foreign or localcurrency, particularly by those in shortageof hard currencies. 62) real estate B) Escalation of protectionism between two ormore countries that impose punitive tariffsand barriers in retaliation for each other. 83) business cycle C) A general decline in prices often caused bya reduction in the money supply or a decreasein spending. 54) trade protectionism D) Unjustifiable and discriminatory policiesand supports by a government to its ownfirms, ranging from export subsidies to anti-competitive practices. 15) price deflation E) Land, buildings, homes or anything fixed,immovable, or permanently attached that canbe traded in the market. 26) exchange control F) The policy of imposing duties or quotas onimports in order to protect home jobs,markets or industries from overseascompetition. 97) competitive currency devaluation G) A company or country with whom you havean ongoing business relationship and engagein importing or exporting activities. 108) trade war H) A predictable long-term pattern ofeconomic activity that an economyexperiences four stages including decline,recession, recovery and boom. 39) import barriers I) The currency devaluation by a governmentto make its goods more competitive in theinternational markets. 710) trading partner L) The economic policy of restrainingbusiness between states through a variety ofgovernment actions to discourage importsand prevent foreign take-over of domesticmarkets and companies. 44. Translate the following passage into Chinese.按官方的说法,中美间过去三天日益严重的贸易纠纷涉及轮胎、鸡肉和汽车,但实际上远远超出此范围。
格兰杰因果关系检验平稳性分析ADF检验ARMA模型G解读

格兰杰因果关系检验论文:国内房地产发展趋势研究及销售价格指数基于ARMA模型的预测分析【中文摘要】本文以国内房地产业为背景,对房地产业近几十年的发展趋势进行了初步研究,并在此基础上对国内房地产销售价格指数建立了ARMA模型进行预测分析。
在文章的第三部分,我们分别对国内城镇常住人口变化情况、房地产业的投资开发情况以及国内房地产业的发展情况进行了分析和探讨。
本文运用了格兰杰因果关系检验、平稳性分析、ADF检验等方法,得到了1992年-2007年间房地产行业的增加值、增长率及占GDP的比重都是非平稳序列,GDP的贡献率是平稳序列的结论。
随后,我们又对这四个序列分别进行了回归拟合,得到的回归方程为:xf1=896193.2-449.4383 t+1.105133Xt-11+0.155901 xt-21+0.335704Xt-31-0.088315 Xt-41-0.097913Xt-51+0.912867Xt-61.xt2=-3315.636+1.663423 t-0.548474 xt-12-0.013403 xt-22+0.137781 xt-32+0.340514 xt-42.xt3=0.893319+0.824929 xt-13-0.125995 xt-23-0.030363 xt-33+0.500...【英文摘要】This paper made some research on the developmenttrend of real estate on the background of domestic real estate industry in recent decades.and on this bases, we made some forecast analysis of sales price index on ARMA model.In the third part of this paper, we analysised and discussed the change of domestic town resident population,the investment and development of real estate,the development of demestic real estate industry respectively.We used Granger causality test, stability analysis,ADF test and so ...【关键词】格兰杰因果关系检验平稳性分析 ADF检验 ARMA模型GA-LS算法 RLS-LS算法 Eviews6.O MATLAB【英文关键词】Granger causality test Stability analysis ADF test ARMA model GA-LS arithmetic RLS-LS arithmeticEviews6.0 MATLAB【索购全文】联系Q1:138113721 Q2:139938848【目录】国内房地产发展趋势研究及销售价格指数基于ARMA模型的预测分析摘要5-7Abstract7-81. 问题背景和研究现状11-122. 模型假设12-133. 国内房地产业发展趋势初步研究13-263.1 中国城镇常住人口变化情况13-153.2 国内房地产业的投资开发情况15-173.2.1 总体情况分析15-163.2.2 格兰杰因果关系检验16-173.3 国内房地产业发展情况分析17-263.3.1 平稳性分析18-203.3.2 ADF检验20-213.3.3 预测分析21-264. 国内房地产销售价格指数基于ARMA 模型的预测分析26-484.1 ARMA模型建立26-284.1.1 AR模型26-274.1.2 MA模型274.1.3 ARMA模型27-284.2 模型求解28-444.2.1 平稳性检验28-304.2.2 相关性检验304.2.3 参数(p,q的确定304.2.4 用RLS-LS算法估计模型参数及预测分析30-384.2.5 用GA-LS算法估计模型参数及预测分析38-444.3 RLS-LS算法和GA-LS算法的结果对比分析44-454.4 GA-LS算法和RLS-LS算法的优缺点45-464.5 ARMA模型及GA-LS算法的评价和改进46-485. 结语48-49参考文献49-50附录50-63致谢63。
The Pros and Cons of Globalization

The Pros and Cons of Globalization Globalization has been a hotly debated topic for decades, with proponents and opponents passionately arguing their respective positions. The concept of globalization refers to the interconnectedness and interdependence of countriesand their economies, facilitated by the rapid advancements in technology, communication, and transportation. While globalization has undeniably broughtabout numerous benefits, it has also sparked intense criticism and raised concerns about its potential drawbacks. In this essay, we will explore the pros and cons of globalization from various perspectives. One of the most significant advantagesof globalization is the unprecedented economic growth and development it has facilitated. By opening up markets and encouraging free trade, globalization has allowed countries to specialize in the production of goods and services in which they have a comparative advantage. This has led to increased efficiency, lower prices for consumers, and higher profits for businesses. Moreover, globalization has enabled the flow of foreign direct investment (FDI) and the transfer of technology, which has contributed to the economic development of many developing countries. In addition to economic benefits, globalization has also played a pivotal role in promoting cultural exchange and understanding. The interconnectedness of the world has allowed for the dissemination of ideas, values, and traditions across borders. This has led to a more diverse and interconnected global society, where individuals have the opportunity to learn from andappreciate different cultures. Furthermore, globalization has facilitated the spread of information and knowledge, leading to advancements in education, science, and technology on a global scale. On the other hand, globalization has been met with staunch criticism and opposition, particularly in relation to its impact on labor and employment. Critics argue that globalization has led to the outsourcing of jobs to countries with lower labor costs, resulting in job displacement and wage stagnation in developed countries. Moreover, the race to the bottom phenomenon, where multinational corporations seek the lowest production costs, has led to exploitation of workers in developing countries and the violation of labor rights. Another contentious issue surrounding globalization is its environmental impact. The increased interconnectedness of economies has led to a surge in globalproduction and consumption, resulting in heightened environmental degradation and the depletion of natural resources. The reliance on fossil fuels fortransportation and the production of goods has contributed to climate change and pollution, posing significant threats to the planet and future generations. Furthermore, globalization has been criticized for exacerbating income inequality within and between countries. While some regions and social groups have reaped the benefits of globalization, others have been left behind, facing economic marginalization and social exclusion. This has given rise to social unrest and political instability in various parts of the world, as marginalized communities feel disenfranchised and neglected by the forces of globalization. In conclusion, the debate surrounding the pros and cons of globalization is complex and multifaceted. While globalization has undoubtedly fostered economic growth, cultural exchange, and technological advancements, it has also raised significant concerns regarding labor rights, environmental sustainability, and income inequality. As the world continues to grapple with the implications of globalization, it is crucial to strike a balance between reaping its benefits and mitigating its adverse effects. Only through thoughtful and collaborative efforts can we harness the potential of globalization while addressing its challenges in a sustainable and equitable manner.。
时光机英语作文

时光机英语作文英文回答:Traveling through time has been a captivating concept that has fascinated humans for centuries. From fictional stories to scientific theories, the idea of traversing the timelines has sparked imaginations and ignited countless debates. While the possibility of time travel remains a matter of scientific speculation, exploring the implications, paradoxes, and potential consequences of such a phenomenon offers intriguing insights into the nature of time and our place within its enigmatic tapestry.Philosophical Implications:The advent of time travel would undoubtedly challenge our fundamental understanding of time and causality. The notion of visiting past events would raise questions about the malleability of history and the possibility of altering the course of events. Could we correct past mistakes, averttragedies, or prevent future conflicts? Or would such interventions create an intricate web of unintended consequences, unraveling the delicate fabric of time?Moreover, time travel would necessitate a re-examination of our concept of free will. If we could alter the past, would our actions in the present still be predetermined, or would we gain a degree of autonomy over our destiny? These philosophical dilemmas would undoubtedly provoke profound contemplations on the nature of choice, responsibility, and the intricate interplay between our actions and their potential ramifications.Scientific Challenges:From a scientific perspective, time travel presents formidable challenges that defy our current understanding of physics. The fundamental laws of thermodynamics, particularly the second law, seem to prohibit thepossibility of traveling back in time. Entropy, the measure of disorder in a system, tends to increase over time, making it improbable to reverse the flow of events.Additionally, the theory of relativity suggests that time dilation can occur when an object approaches the speed of light. However, the immense energy requirements and the potentially harmful effects of such relativistic speeds pose significant obstacles to practical time travel.Paradoxes and Temporal Anomalies:The concept of time travel also introduces a host of paradoxes that strain our logical reasoning. The grandfather paradox, for instance, poses the question of what would happen if a time traveler were to go back and prevent the birth of their own grandfather. Such paradoxes challenge our intuitive understanding of causality and raise questions about the stability and coherence of the time-space continuum.Temporal anomalies, such as time loops and alternative timelines, further complicate the complexities of time travel. If we could visit the past, would we createparallel realities or alter the timeline of our own? Theimplications for our understanding of history, causality, and the interconnectedness of events would be profound.中文回答:时间旅行的哲学意义:时间旅行的出现无疑会挑战我们对时间和因果关系的基本理解。
电化学交流阻抗

电感:
L=
Z=jωL
LR(RC)
R(Q(R[(RL)(RQ)]))
R(Q(R[RL]))
500 250
0 -250 -500 -750100
FRA test LR(RC) 2.5
2.0
1000
1.5
750
1.0 500
0.5 250
0
0 -0.5
-250
350
600
850
1100
1350
-1.04.5
R(Q(R[(RL)(RQ)]))
100ppbcu(illumination) 29/7-1
5.0
5.5
6.0
6.5
7.0
7.5
8.0
0
250
500
750
1000
1250
1500
Z' / ohm
Z' / ohm
Z' / ohm
-Z'' / ohm -Z'' / ohm -Z'' / ohm
“前”电感
LRQ
“前”电感来自于: 电解池电缆, 接触, 参比电极反应缓慢, 恒电位仪不理想.
log(Z)(o) -Z'' / ohm
Electrode
+
+
+
+
e-
+
+
+
+
Potential
Double layer capacitance: Cdl
IHP OHP Diffusion layer
Solution
பைடு நூலகம்
2020智慧树知道网课《英语学术论文写作》课后章节测试满分答案
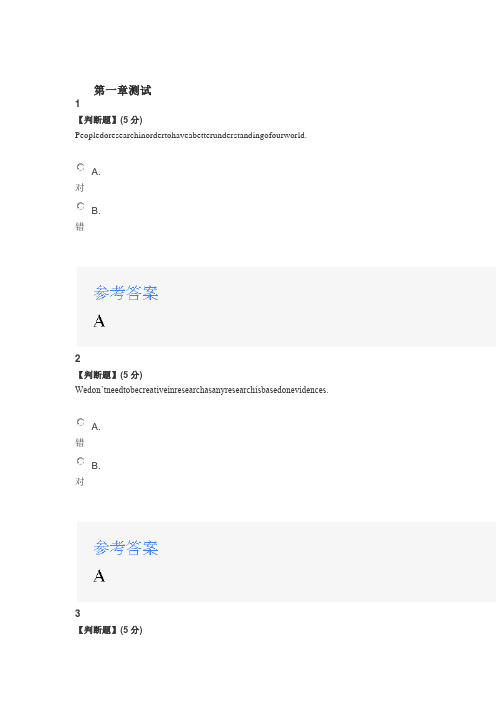
第一章测试1【判断题】(5分) Peopledoresearchinordertohaveabetterunderstandingofourworld.A.对B.错2【判断题】(5分)Wedon’tneedtobecreativeinresearchasanyresearchisbasedonevidences.A.错B.对3【判断题】(5分)Goodresearchquestionsareimportantinresearch.A.错B.对4【判断题】(5分) Literaturereviewisneededinsomeresearchpapers.A.对B.错5【判断题】(5分) Agoodresearchpaperneedscarefulrevisingandproofreading.A.错B.对6【判断题】(5分) Unintentionalplagiarismcanbeexcusedasitisnotcommitteddeliberately.A.对B.错7【判断题】(5分) Academicfalsificationisonecommontypeofacademicdishonesty.A.对B.错8【多选题】(5分) Whatroledoesaliteraturereviewplayinaresearchpaper?A.Itenhancesthecredibilityofyourpaper.B.Itprovestheexistenceofaresearchgap.C.Itsynthesizestheexistingstudiesinyourarea.D.Itprovidesevidencesforyourargument.9【单选题】(5分) WhichofthefollowingisNOTanessentialstepinaresearchpaperwriting?A.ChoosingatopicB.ConsultinginstructorsC.LocatingsourcesD.OutliningthePaper10【多选题】(5分) Whichofthefollowingmayleadtoacademicdishonesty?A.AcademicplagiarismB.AcademicpromotionC.AcademicinterestD.Academicfabrication第二章测试1【多选题】(5分)Inchoosingaresearchtopic,whichofthefollowingdoweneedtoconsider?A.PublicationpossibilitiesB.AcademicimportanceC.OurresearchinterestD.Ourmanageability2【判断题】(5分)Tocheckthevalidityofaresearchtopic,weneedtobecriticalenough.A.对B.错3【判断题】(5分) Itisanactofplagiarismifonesimplyparaphrasesabookforaresearchpaper.A.对B.错4【判断题】(5分) StudentsshouldbebraveenoughtotrychallengingissuesfortheirBAtheses.A.对B.错5【判断题】(5分) Carefulreadingofliterarytextisimportantinliterarystudies.A.对B.错6【判断题】(5分) Literarytheoriestakepriorityoverliterarytextsinliteraryanalysis.A.错B.对7【判断题】(5分) ICstudycanbechallengingbutinterestingandpracticalinlife.A.错B.对8【判断题】(5分) Expertssharesimilarunderstandingsoverthestandardsoftranslation.A.错B.对9【判断题】(5分) Translationstrategiesandtranslationtechniquesaredifferentconceptsintranslation.A.对B.错10【判断题】(5分) Sociolinguisticsisoneofthebranchesofappliedlinguistics.A.对B.错第三章测试1【判断题】(5分) Aworkingbibliographyincludesthesourceswehavesofarcollectedforaresearchproject.A.对B.错2【判断题】(5分) Knowingwhatsourcesyouneedisofvitalimportanceinevaluatingyoursources.A.错B.对3【判断题】(5分) Sourcesfromleadingscholarscanbeveryusefultoyourresearch.A.错B.对4【判断题】(5分)Inreadingsources,weneedtobecriticalandformourpersonalresponses.A.对B.错5【判断题】(5分) Theplanforanempiricalresearchshouldcoveritspurpose,method,subjects,andprocedure.A.错B.对6【判断题】(5分) Itiswisefortheobservernottotakepartintheactivityobservedatalltime.A.错B.对7【多选题】(5分)InBooleanLogic,ifonewantstosearchonlyforsourcesrelevantwithcomputervirus,thesearchformul ashouldbe_______.A.computernotvirusB.computernearvirusC.computerorvirusD.computerandvirus8【多选题】(5分) Theannotationofasourceinanannotatedbibliographymayhaveyour____:A.reflectionofthesourceB.adaptationofthesourceC.summaryofthesourceD.assessmentofthesource9【单选题】(5分)Inaquestionnaireentitled“ASurveyontheThirdYearEnglishMajors’EnglishVocabularyinXXUniv ersity”,the“thethirdyearEnglishmajors”shouldbe:A.ThetimeofthesurveyB.ThesubjectofthesurveyC.ThecontentofthesurveyD.Themodeofthesurvey10【单选题】(5分)Inanexperimententitled“AStudyontheEffectsofWriting-after-ReadingActivityonEnglishMajors EnglishVocabulary”,students’languageproficiencyshouldbe:A.IrrelevantvariableB.dependentvariableC.Independentvariable第四章测试1【判断题】(5分)Aresearchproposalshouldbepersuasiveinnature.A.错B.对2【判断题】(5分) Wecanaskforsuggestionsfromtheexpertsforourresearchinourproposal.A.错B.对3【判断题】(5分) Weneedtoputforwardourresearchquestionsinourresearchproposals.A.错B.对4【判断题】(5分) Aresearchproposaldemonstratesthesignificanceofourproposedresearch.A.错B.对5【判断题】(5分) Theliteraturereviewsectioninaproposalprovestheexistenceofaresearchgap.A.对B.错6【判断题】(5分)The“ApplicationoftheResearch”tellshowyourresearchwillbenefitinpractice.A.对B.错7【判断题】(5分)A“PreliminaryBibliography”isalistofthesourcesyouhavecitedinyourproposal.A.错B.对8【判断题】(5分) Thesignificanceofyourresearchemphasizespossibleresearchcontributions.A.对B.错9【判断题】(5分)Simpleasitis,aBAthesisproposalincludesalltheelementsinagrantresearchproposal.A.错B.对10【多选题】(5分)WhichofthefollowingisNOTincludedinthree-moveschemeoftheproposalsummary?A.researchneedB.potentialcontributionsC.possiblelimitationsD.researchmethod第五章测试1【判断题】(5分) Theuseofsignalphrasesincitationcanenhancethefluencyofwriting.A.对B.错2【判断题】(5分) Theintegrationofthesourcesmustfitourwritinginstructureandgrammar.A.错B.对3【判断题】(5分) Researchlimitationisacompulsoryelementinallresearchpapers.A.错B.对4【判断题】(5分) CARSModelisapatternforintroductionwritinginresearchpapers.A.对B.错5【判断题】(5分)Inrevising,weneedtofocusontheerrorslikegrammarandspelling.A.错B.对6【判断题】(5分) Aliteraturereviewmainlypresentsasummaryofeachsourceinchronologicalorder.A.错B.对7【单选题】(5分) Characteristicsofacademicwritingincludesallthefollowingexcept________.A.thefirst-personviewB.aformaltoneC.aclearfocusD.precisewordchoice8【单选题】(5分) Itisessentialtoalwaysacknowledgethesourceofborrowedideasinyourpaper.Todootherwiseisconsi dered_________.A.IgnoranceB.CarelessnessC.Plagiarism9【单选题】(5分)Whichofthefollowingarefeaturesofagoodtitle?A.ClearB.AlloftheaboveC.Attractive.D.Direct10【单选题】(5分)Abstractscanbedividedintotwotypes accordingto their_________.A.functionsB.length第六章测试1【判断题】(5分)MLAin-textcitationrequiresthattheauthorinformationshouldbeputeitherinthetextofthepaperorint heparentheticalcitation.A.错B.对2【判断题】(5分)InMLAdocumentation,parentheticalcitationinthetextofthepapermustalwaysincludetheauthor’sn ameandthework’stitle.A.错B.对3【判断题】(5分)MLAworkscitedlistisorganizedalphabeticallybytheauthor’slastnames(orbytitleforaworkwithnoa uthor).A.错B.对4【判断题】(5分)Whenawork’sauthorisunknown,theworkislistedunder“Anonymous”inthelistofMLAworkscited.A.错B.对5【单选题】(5分)Lee(2007)stated,“Theabilitytothinkcriticallyisneededinthisrevolutionaryageoftechnologicalcha nge”(p.82).Thein-textcitationusedhereis__________.A.integratedB.non-integrated6【多选题】(5分)WhatarethefunctionsofAPAdocumentation?A.Tociteothers’ideasandinformationusedwithinyourpaperB.TodemonstratethetypeofresearchconductedC.ToindicatethesourcesintheReferenceslist7【单选题】(5分)Writethelistofworkscited,usingtheAPAformat.Aparaphraseofanideafrompage121ofWritingSpace:TheComputer;Hypertext,andtheHistoryofWr iting,byJayDavidBolter.This1991bookwaspublishedbyLawrenceErlbaumAssociatesofHillsdale, NewJersey.Whichofthefollowingiscorrectfortheauthor’sname?A.Bolter,J.DB.J.D.BolterC.Jay,D.BolterD.Bolter,JayDavid【单选题】(5分)Writethelistofworkscited,usingtheAPAformat.Aquotationfrompage78ofanarticlebyBartKoskoandSatornIsakafromtheJuly1993issueofScientifi cAmerican,amonthlypublication.Thearticleisentitled"FuzzyLogic"andappearsonpages76to81in volume239,ofthejournal. Whichofthefollowingisthecorrectformatforthevolumeandpagernumber?A.ScientificAmerican,239,78B.ScientificAmerican,239,76-81C.ScientificAmerican,239:76-81D.ScientificAmerican,239,76-81.9【多选题】(5分)Bohren,M.A.,G.J.Hofmeyr,C.Sakala,R.K.Fukuzawa,andA.Cuthbert.(2017).Continuoussupportf orwomenduringchildbirth.CochraneDatabaseofSystematicReviews,2017(7).https:///10.1 002/14651858.CD003766.pub6Errorsmadeinthisentryinclude_________.A.authors’namesB.issuenumberC.theword“and”D.doinumber10【单选题】(5分)Perrey,S.(2017).Doweperformbetterwhenweincreaseredbloodcells?TheLancetHaematology,17, 2352-3026.https:///10.1016/S2352-3026(17)30123-0.RetrievedAugust23,2018.Whatinfo rmationisNOTneededinthisentry?A.ThedateofretrievalB.ThepagerangeC.Thedoinumber。
信号与系统目录(Signal and system directory)

信号与系统目录(Signal and system directory)Chapter 1 signals and systems1.1 INTRODUCTION1.2 signalContinuous signals and discrete signalsTwo. Periodic signals and aperiodic signalsThree, real signal and complex signalFour. Energy signal and power signalThe basic operation of 1.3 signalAddition and multiplicationTwo, inversion and TranslationThree, scale transformation (abscissa expansion)1.4 step function and impulse functionFirst, step function and impulse functionTwo. Definition of generalized function of impulse functionThree. The derivative and integral of the impulse functionFour. Properties of the impulse functionDescription of 1.5 systemFirst, the mathematical model of the systemTwo. The block diagram of the systemCharacteristics and analysis methods of 1.6 systemLinearTwo, time invarianceThree, causalityFour, stabilityOverview of five and LTI system analysis methodsExercise 1.32The second chapter is the time domain analysis of continuous systemsThe response of 2.1LTI continuous systemFirst, the classical solution of differential equationTwo, about 0- and 0+ valuesThree, zero input responseFour, zero state responseFive, full response2.2 impulse response and step responseImpulse responseTwo, step response2.3 convolution integralConvolution integralTwo. The convolution diagramThe properties of 2.4 convolution integralAlgebraic operations of convolutionTwo. Convolution of function and impulse function Three. Differential and integral of convolutionFour. Correlation functionExercise 2.34The third chapter is the time domain analysis of discretesystemsThe response of 3.1LTI discrete systemsDifference and difference equationsTwo. Classical solutions of difference equationsThree, zero input responseFour, zero state response3.2 unit sequence and unit sequence responseUnit sequence and unit step sequenceTwo, unit sequence response and step response3.3 convolution sumConvolution sumTwo. The diagram of convolution sumThree. The nature of convolution sum3.4 deconvolutionExercise 3.27The fourth chapter is Fourier transform and frequency domainanalysis of the systemThe 4.1 signal is decomposed into orthogonal functions Orthogonal function setTwo. The signal is decomposed into orthogonal functions 4.2 Fourier seriesDecomposition of periodic signalsTwo, Fourier series of odd even functionThree. Exponential form of Fu Liye seriesThe spectrum of 4.3 period signalFrequency spectrum of periodic signalTwo, the spectrum of periodic matrix pulseThree. The power of periodic signal4.4 the spectrum of aperiodic signalsFirst, Fu Liye transformTwo. Fourier transform of singular functionsProperties of 4.5 Fourier transformLinearTwo, parityThree, symmetryFour, scale transformationFive, time shift characteristicsSix, frequency shift characteristicsSeven. Convolution theoremEight, time domain differential and integral Nine, frequency domain differential and integral Ten. Correlation theorem4.6 energy spectrum and power spectrumEnergy spectrumTwo. Power spectrumFourier transform of 4.7 periodic signals Fourier transform of sine and cosine functionsTwo. Fourier transform of general periodic functionsThree 、 Fu Liye coefficient and Fu Liye transformFrequency domain analysis of 4.8 LTI systemFrequency responseTwo. Distortionless transmissionThree. The response of ideal low-pass filter4.9 sampling theoremSampling of signalsTwo. Time domain sampling theoremThree. Sampling theorem in frequency domainFourier analysis of 4.10 sequencesDiscrete Fourier series DFS of periodic sequencesTwo. Discrete time Fourier transform of non periodic sequences DTFT4.11 discrete Fu Liye and its propertiesDiscrete Fourier transform (DFT)Two. The properties of discrete Fourier transformExercise 4.60The fifth chapter is the S domain analysis of continuous systems 5.1 Laplasse transformFirst, from Fu Liye transform to Laplasse transformTwo. Convergence domainThree, (Dan Bian) Laplasse transformThe properties of 5.2 Laplasse transformLinearTwo, scale transformationThree, time shift characteristicsFour, complex translation characteristicsFive, time domain differential characteristicsSix, time domain integral characteristicsSeven. Convolution theoremEight, s domain differential and integralNine, initial value theorem and terminal value theorem5.3 Laplasse inverse transformationFirst, look-up table methodTwo, partial fraction expansion method5.4 complex frequency domain analysisFirst, the transformation solution of differential equation Two. System functionThree. The s block diagram of the systemFour 、 s domain model of circuitFive, Laplasse transform and Fu Liye transform5.5 bilateral Laplasse transformExercise 5.50The sixth chapter is the Z domain analysis of discrete systems 6.1 Z transformFirst, transform from Laplasse transform to Z transformTwo, z transformThree. Convergence domainProperties of 6.2 Z transformLinearTwo. Displacement characteristicsThree, Z domain scale transformFour. Convolution theoremFive, Z domain differentiationSix, Z domain integralSeven, K domain inversionEight, part sumNine, initial value theorem and terminal value theorem 6.3 inverse Z transformFirst, power series expansion methodTwo, partial fraction expansion method6.4 Z domain analysisThe Z domain solution of difference equationTwo. System functionThree. The Z block diagram of the systemFour 、 the relation between s domain and Z domainFive. Seeking the frequency response of discrete system by means of DTFTExercise 6.50The seventh chapter system function7.1 system functions and system characteristicsFirst, zeros and poles of the system functionTwo. System function and time domain responseThree. System function and frequency domain responseCausality and stability of 7.2 systemsFirst, the causality of the systemTwo, the stability of the system7.3 information flow graphSignal flow graphTwo, Mason formulaStructure of 7.4 systemFirst, direct implementationTwo. Implementation of cascade and parallel connectionExercise 7.39The eighth chapter is the analysis of the state variables of the system8.1 state variables and state equationsConcepts of state and state variablesTwo. State equation and output equationEstablishment of state equation for 8.2 continuous systemFirst, the equation is directly established by the circuit diagramTwo. The equation of state is established by the input-output equationEstablishment and Simulation of state equations for 8.3discrete systemsFirst, the equation of state is established by the input-output equationTwo. The system simulation is made by the state equationSolution of state equation of 8.4 continuous systemFirst, the Laplasse transform method is used to solve the equation of stateTwo, the system function matrix H (z) and the stability of the systemThree. Solving state equation by time domain methodSolution of state equation for 8.5 discrete systemsFirst, the time domain method is used to solve the state equations of discrete systemsTwo. Solving the state equation of discrete system by Z transformThree, the system function matrix H (z) and the stability of the systemControllability and observability of 8.6 systemsFirst, the linear transformation of state vectorTwo, the controllability and observability of the systemExercise 8.32Appendix a convolution integral tableAppendix two convolution and tableAppendix three Fourier coefficients table of commonly used periodic signalsAppendix four Fourier transform tables of commonly used signalsAppendix five Laplasse inverse exchange tableAppendix six sequence of the Z transform table。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :c o n d -m a t /0010276v 1 [c o n d -m a t .s t a t -m e c h ] 19 O c t 2000On the Causality and Stability of the Relativistic Diffusion EquationPeter Kost¨a dt and Mario Liu ∗Institut f¨u r Theoretische Physik,Universit¨a t Hannover,30167Hannover,Germany (Phys.Rev.D 62,023003(2000))This paper examines the mathematical properties of the relativistic diffusion equation.The peculiar solution which Hiscock and Lindblom identified as an instability is shown to emerge from an ill-posed initial value problem.These do not meet the mathematical conditions required for realistic physical problems and can not serve as an argument against the relativistic hydrodynamics of Landau and Lifshitz.47.75.+f,02.30.Jr,03.30.+p,05.70.LnI.INTRODUCTIONThe relativistic generalization of the hydrodynamic theory,as developed by Landau and Lifshitz [1],leads to differential equations of the parabolic type.Consider for instance the diffusion equation for the viscous shear flow.In a frame in which the background equilibrium state is at rest (“comoving frame”),it is[c −2(e +p )∂t −η∂2x ]δu i (x,t )=0,(1)where δu i with i =y,z is the perturbation in thetransverse velocity.Equation (1)is the archetype of a parabolic equation.In non-relativistic physics,it pro-vides an excellent description of a wide range of phys-ical phenomena,as countless experiments have shown.Within the relativistic framework,however,it seems to fail,as two deficiencies become evident:The first,acausality,refers to the fact that Eq.(1)allows for prop-agation of signals with arbitrarily large velocities.(This should be,and indeed has already been,a worry in the Galilean hydrodynamics,since one has very definite ideas of the velocities of the constituent microscopic particles,which represent an upper limit of the signal velocity in a dilute system of hard-core interaction.)The second de-fect is an instability found by Hiscock and Lindblom [2],who showed that Eq.(1)develops a solution that grows exponentially with time in any non-comoving Lorentz frames.It is noteworthy that the growth time scale was found to be microscopically short.To overcome these deficiencies,extended fluid theories were put forward which start from the hydrodynamic the-ory but include additional dynamic variables;see e.g.[3].The resultant larger set of phenomenological coefficients can be chosen such that all the equations are hyperbolic,ensuring causality and stability.The price for this is twofold:A rather more complicated theory and the dif-ficulty of finding a universally accepted set of additionalvariables (except perhaps in dilute systems).In fact,re-cently it has been shown by Geroch [4]and Lindblom [5]that the complicated dynamical structure which ensures causality is unobservable.The evolution of any physi-cal fluid state according to any causal theory results in energy-momentum tensors and particle currents that are experimentally indistinguishable from the respective hy-drodynamic expressions.In this paper,we take a step back and again fo-cus on the simpler and more universal parabolic equa-tion (1).While acausality is an expected feature of parabolic differential equations,already discussed in the non-relativistic context [6–8],instability is not.Being absent in a comoving frame,one is astonished at its ap-pearance in non-comoving frames.Our main purpose thus is to examine the origin and physical relevance of the instability.The paper is organized as follows:In Sec.II some gen-eral mathematical aspects of partial differential equations are reviewed.We especially recall the intuitive meaning of the characteristics.Section III is devoted to the one-dimensional diffusion equation in a comoving frame.We discuss the problem of causality and examine the two types of Cauchy problems that can be formulated with respect to a parabolic equation.In Sec.IV the discus-sion is generalized to non-comoving Lorentz frames.We especially scrutinize the solution that Hiscock and Lind-blom have identified as an instability,and show that it is a result of an ill-posed initial value problem.In Sec.V we briefly examine the general case,in which the spatial dimension of the diffusion equation is greater than one.II.PRELIMINARIESLet us first review some general aspects of partial dif-ferential equations that can be found in standard text-books on mathematical physics (eg.[9]).Consider a lin-ear partial differential equation of second order for the unknown function ϑ(x,t ).It can be written,most gen-erally,in the formA ∂2x +2B ∂x ∂t +C ∂2tϑ+F (x,t,ϑ,∂x ϑ,∂t ϑ)=0,(2)where A ,B and C are given functions of the two inde-pendent variables x and t .Depending on the value ofD ≡B 2−AC at a given point,Eq.(2)is referred to be of the elliptic (D <0),parabolic (D =0),or hyperbolic1(D>0)type in this point.In the following we shall restrict ourselves to the cases in which A,B and C are constants.The type of Eq.(2)then remains unchanged throughout the entire region.The equationA(∂xϕ)2+2B(∂xϕ)(∂tϕ)+C(∂tϕ)2=0(3)is called the equation of characteristics of the partial dif-ferential equation(2).Correspondingly,the family of curves,ϕ(x,t)=const,(4)withϕ(x,t)satisfying Eq.(3),is called the family of characteristics.We collect the following facts:(i)An equation of the hyperbolic type has two dis-tinct families of real characteristics,an equation of the parabolic type has only one;an elliptic equation does not have real characteristics.(ii)The equation of characteristics is invariant with respect to arbitrary transformations of the independent variables,˜x=˜x(x,t),˜t=˜t(x,t).This implies that,if ϕ(x,t)is a solution of Eq.(3),and ifϕ(x,t)transforms into˜ϕ(˜x,˜t),then˜ϕ(˜x,˜t)is a solution of the equation of characteristics accompanying the transformed differential equation.(iii)The outer real characteristics that pass through a given point(x0,t0)bound the domain of influenceΩ0of this point.If we consider the variable t as the time and think of the solutionϑ(x,t)as a quantity that varies in x-space with time t,then this means that for t>t0the solution in the region outsideΩ0is not influenced by the initial data given at(x0,t0).As an example,consider the telegraph equation∂tϑ−α ∂2x−1∂n S=Θ1(x,t).(7)It is important to note that the domain in which the un-known solution has to be determined is not specified be-forehand.So generally,the initial manifold S lies within the domain of definition of the solution.A problem is said to be well-posed if it has the follow-ing properties:The solution(i)exists,(ii)is uniquely de-termined,and(iii)depends continuously on the assigned data.The last requirement is imposed in connection with the fact that the initial data of physical problems are de-termined experimentally and so small errors occur.It is thus necessary to be sure that the solution does not depend essentially on the measurement errors of these data.III.THE DIFFUSION EQUATION IN ACOMOVING FRAMEA well-known example of Eq.(2)is given by the parabolic diffusion equation∂tϑ−α∂2xϑ=0,(8)whereα>0.With A=−αand B=C=0its equation of characteristics(3)takes the form(∂xϕ)2=0.Hence, the characteristics are given by the one-parameter family of linesϕ(x,t)=t=const.(9)It is obvious from this that the diffusion equation allows for the propagation of disturbances with infinite velocity. Indeed,the initial value ofϑat the point(x0,t0)has influence on the solutionϑ(x,t)in the whole semi-infinite region t≥t0.This fact,however,does not in practice cause any com-plications:The superluminal propagation speeds are as-sociated only with variations on microscopically small time and length scales(and with amplitudes of the or-der of thermodynamicfluctuations).On these scales a macroscopic description loses validity,and the diffusion equation and its solutions break down accordingly.The acausal consequences are therefore precluded by restrict-ing the solutions of Eq.(8)to the hydrodynamic range of validity,∂xϑξ, ∂tϑτ,(10) withϑ0denoting the constant part ofϑ;andξ,τthe characteristic distance and time between collisions of par-ticles,or elementary excitations.For gases this has been first demonstrated by Weymann[6].As an example,consider the solution of Eq.(8)that satisfies the initial conditionϑ|t=0=ϑ0+(A/d)e−x2/2d2. It isϑ(x,t)=ϑ0+(A/which represents a Gaussian distribution with width √ω/2α,(17) which represents a superposition of two modesϑ1,2(x,t)=δϑ1,2(ω)e i(±x√ω/2α,(18) with the amplitudesδϑ1,2(ω)being determined by the two Cauchy conditions(15).One hasδϑ1,2(ω)=14B(i−1)ω/2α)for any x>0.Consequently,the non-characteristic Cauchy problem(15)is not well-posed.Recalling the intuitive concept of the characteristics (cf.Sec.II),the reason for this becomes obvious.The initial data given at some point(0,t0)affect the value of the solution exactly in those points which lie in the domain of influenceΩ0={(x,t)|x∈I R,t≥t0}.Solving Eqs.(8),(15)thus yields the solution for x>0as well as for x<0.Confer the two modes of Eq.(18).They describe damped waves which carry the initial data given at x=0to the left and to the right.Physical intuition suggests,however,thatϑ1andϑ2do exist only for x<0 and x>0,respectively.A superposition in the form of Eq.(16)does not make any physical sense.Now,the sideways problem will not be well-posed un-less the behavior at infinity is prescribed.In fact,the physically realistic assumption thatϑbe bounded as x→∞[1]leads to a solution that exists,is unique,and depends continuously on the initial data given at x=0. The correct formulation of the sideways problem thus is the following:Find the bounded solution of Eq.(8)in the region x>0(−∞<t<∞),satisfyingϑ|x=0=A e iωt,ω∈I R.(20) Note that the boundedness condition”replaces”the sec-ond Cauchy condition.Equation(15)is an example of a non-characteristic Cauchy problem with the initial data given on a line that is timelike.For the following,it is important to consider also the case where the Cauchy data are given on a space-like line.As we shall see,this problem is not well-posed either.In the half-space{(x,t)|x∈I R,ct−βx>0}we seek the solutions of Eq.(8)satisfying periodic initial data on the non-characteristic spacelike line ct−βx=0(β∈I R,0<β<1).Here c is the speed of light.With γ≡(1−β2)−1/2,xµ=(x,ct),ηµν=diag(1,−1),and nµ=−γ(β,1),eµ=γ(1,β)respectively denoting the timelike and spacelike unit vector normal and parallel to the initial line ct−βx=nµxµ=0,the general Ansatz ϑ(x,t)∼e ikeµxµ+Γnµxµ/c,k∈I R,Γ∈withϑ|ct−βx=0∼exp(ikγ−1x).Inserting Eq.(22)into the diffusion equation(8)yieldsγαβ2ck Γ−γαk2+iβck=0.(23)For k=0the two rootsΓ1,2(k)are complex.The real parts are given byΓR1,R2=1114C3γ−3αk2,(24)where C≡(γαβ2/c2)−1.From this onefinds the in-equalitiesΓR1+ΓR2=C>0,(25)ΓR1ΓR2=114C3γ−3αk2≤0,(26)which imply that exactly one mode grows exponentiallywith time.Now,as k→∞,the general solution divergeslike exp(γ k)for any t>βx/c,while the initial values are bounded on t−βx/c=0.Hencesmall changes in the initial data would cause considerable changes in the solution,indicating that the problem is not well-posed.IV.THE DIFFUSION EQUATION IN AGENERAL LORENTZ FRAMENext we turn our attention to the diffusion equation in an inertial frame˜K,in which the medium moves with constant velocity v in the negative x-direction.Employ-ing the Lorentz transformation rules∂t=γ∂˜t−γv∂˜x and ∂x=γ∂˜x−γ(v/c2)∂˜t,we get from Eq.(8)the boosted diffusion equationγ(∂˜t−v∂˜x)ϑ−αγ2 ∂2˜x−2v c4∂2˜t ϑ=0.(27)It is straightforward to verify that this equation still be-longs to the parabolic type.In a covariant language,it is rewritten asuµ∂µϑ−α∆µν∂µ∂νϑ=0,(28) where∆µν=ηµν+c−2uµuν,uµ=γ(−v,c),∂µ= (∂˜x,∂c˜t),andηµν=diag(1,−1).According to Eq.(3), the equation of characteristics becomesγ2 ∂˜x˜ϕ−vc2˜x=t=const,(31)with t being the proper time measured in a comoving frame K.Recalling Eq.(9),we explicitly see that the characteristics are invariant under Lorentz boosts;cf.Sec.II.With Eq.(31),the relativistic equivalent to the char-acteristic Cauchy problem(13)is the following:Find a solution to Eq.(27)which satisfies prescribed values at the initial manifold˜t+(v/c2)˜x=0.Clearly,this prob-lem is well-posed only for˜t+(v/c2)˜x>0.Its exponential solution can easily be found from Eq.(14)by making use of the Lorentz transformation,t=γ˜t+γ(v/c2)˜x and x=γ˜x+γv˜t.Now,the solutions of Eq.(27)that Hiscock and Lind-blom[2]examine satisfy periodic initial data∼e i˜k˜x (˜k∈I R)on the non-characteristic line˜t=0.Takingϑ(˜x,˜t)∼e i˜k˜x+˜Γ˜t,(32) theyfind the dispersion relationγαv2c2˜k ˜Γ−γα˜k2+iv˜k=0,(33)see Eq.(67)of Ref.[2].For˜k=0the two roots˜Γ1,2(˜k) are complex.The real parts satisfy the conditions˜ΓR1+˜ΓR2=c4v 2≤0,(35)which imply that one of the two modes diverges as ˜t→∞.¿From this the authors of Ref.[2]conclude that the Landau-Lifshitz theory of relativistic hydrodynam-ics is unstable(in the sense that small spatially bounded departures from equilibrium will diverge with time)and hence must be abandoned as a physically realistic theory.We disagree with this conclusion.The reason is that the above non-characteristic Cauchy problem is not well-posed,in complete analogy to its non-relativistic equiva-lent,Eqs.(8),(22).[Note that Eq.(23)equals Eq.(33) ifβ=v/c.]Its solution does not depend continuously on the initial data and therefore does not meet one of the three mathematical requirements to be posed with regard to realistic physical problems(cf.Sec.II).So it is the type of the initial-value problem here which is physically unacceptable,and not the instability of the resulting solution.Nevertheless,it is illuminating to interpret the Hiscock-Lindblom solution in terms of wave propagation (while ignoring the fact that the domain of definition of4the above Cauchy problem is restricted to the half space{(˜x ,˜t )|˜x ∈I R ,˜t≥0}).The general solution consists of two damped waves traveling to the regions ˜t>0and ˜t<0,respectively.Referring again to the discussion of the sideways problem,Sec.III,this is a consequence to be expected.Since the initial manifold crosses the charac-teristics (31),the information (given at ˜t =0)propagates (along the characteristic lines ˜t +[v/c 2]˜x =const )in bothdirections.One thus gets two modes,each transporting the effects of the initial data in the respective region.It is important to note that the appearance of a mode running backwards in time in non-comoving frames is directly related to the infinite signal speeds accompany-ing the parabolic equation.In fact,it is well-known [11]that “superluminal acausality”in a Lorentz frame K causes “chronological acausality”in any other Lorentzframes ˜K.For example,consider a process in a frame K whereby an event P 1=(x,t )causes another event P 2=(x +∆x,t +∆t )at superluminal velocity U >c .Let the time difference be ∆t >0so that ∆x =U ∆t >0.Then,in a frame ˜K,moving with velocity v relative to K ,we have ∆˜t=γ∆t −γ(v 2/c )∆x =γ∆t (1−v U/c 2).If c 2/U <v <c ,this yields ∆˜t<0.This means that in ˜Kthe signal goes backward in time,or equivalently,that the response P 2precedes the stimulus P 1.Now,as we have seen in Sec.III,the superluminal acausality in K does not lead to any physical conse-quences;it is automatically precluded by a restriction to the hydrodynamic range of validity.Accordingly,we see from Eqs.(34)and (35)that the damping rate of the mode which propagates in the past is bounded below by ˜ΓR+≥c 4/γαv 2.With τdenoting the characteristic mi-croscopic time in K (referred to as the collision time indilute systems),and ˜τ=γτthe respective time in ˜K,we thus have˜ΓR+˜τ=c 4τuµdxµ=0,(37) which assigns to each point xµan infinitesimal character-istic3-flat normal to the direction of the time-like velocity uµat that point.The crucial point now is that generally these infinitesimal3-flats do not integrate to3-surfaces ϕ(xµ)=const.To see this,let us suppose that a general integral ϕ(xµ)=const exists.Then,we havedϕ=(∂µϕ)dxµ=0,(38) and hence∂µϕ=λuµ,(39) with someλ=λ(xµ).Since∂µ∂νϕ=∂ν∂µϕ,this yields ∂µuν−∂νuµ=λ−1(uµ∂νλ−uν∂µλ),(40) from whichεµναβuν∂αuβ=0oruα(∂νuµ−∂µuν)+uµ(∂αuν−∂νuα)+uν(∂µuα−∂αuµ)=0(41) results.Equation(41)is a necessary condition for inte-grability.It can be proved(see eg.[12])that it is also suf-ficient,ie.,if it is satisfied,a general integral exists.[Note that Eq.(41)is identically satisfied forα,µ,ν=1,2. Thus,in the case of one spatial dimension,characteris-tics can always be found.]Multiplying the condition of integrability with uα,one finds∆µα∆νβ(∂αuβ−∂βuα)=0.(42) So,characteristic hypersurfaces exist only if the back-ground equilibrium state is non-rotating.This fact has led various authors to believe that generally the parabolic diffusion equation lacks an initial-value formulation,and hence turns out not to be viable.This,however,would be true only if the non-characteristic Cauchy problem is ill-posed,just like it is in the case of one spatial di-mension.Unfortunately,very little seems to be known about the non-characteristic Cauchy problem in space-times with more than one spatial dimension.Further work should give clarity here.。
