5.2复数的四则运算课件
合集下载
复数的四则运算公开课完整ppt课件

z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i
2、复数的乘法: 设z1=a+bi,z2=c+di(a,b,c,d∈R)是
任意两个复数,则它们积为
z1•z2=(a+bi)•(c+di)=(ac-bd)+(bc+ad)i 3、(复a数b的i) 除(法c:di)abi (abi)(cdi)
显然,实数集R是复数集C的真子集,即R C.
问题:复数集是实数集的扩展,如何规定 复数的运算?
1.复数加减法的运算法则: (1)运算法则:设复数z1=a+bi,z2=c+di,
那么:z1+z2=(a+c)+(b+d)i; z1-z2=(a-c)+(b-d)i.
即: 两个复数相加(减)就是实部与实部, 虚部与虚部分别相加(减).
一复习引入
4. 两个复数相等
设z1=a+bi,z2=c+di(a、b、c、dR),则 z1=z2
a
b
ห้องสมุดไป่ตู้
c,
d
即实部等于实部,虚部等于虚部.
特别地,a+bi=0 a=b=0 .
注意:一般地,两个复数只能说相等或不相等,而不能比较大小.
思考:对于任意的两个复数到底能否比较大小?
答案:当且仅当两个复数都是实数时,才能比较大小.
x2 x24,
x2 3x220.
解得
x 3或x 2 x 3或x 6
所以 x3.
复数的除法应怎样进行呢? 注意到,实数的除法运算是乘法的逆运算,类
比思考,我们可定义复数的除法:
定义: 把满足(c+di)(x+yi) =a+bi (c+di≠0) 的 复 数 x+yi 叫做复数 a+bi 除以复数 c+di 的商, 其中a,b,c,d,x,y都是实数,
2、复数的乘法: 设z1=a+bi,z2=c+di(a,b,c,d∈R)是
任意两个复数,则它们积为
z1•z2=(a+bi)•(c+di)=(ac-bd)+(bc+ad)i 3、(复a数b的i) 除(法c:di)abi (abi)(cdi)
显然,实数集R是复数集C的真子集,即R C.
问题:复数集是实数集的扩展,如何规定 复数的运算?
1.复数加减法的运算法则: (1)运算法则:设复数z1=a+bi,z2=c+di,
那么:z1+z2=(a+c)+(b+d)i; z1-z2=(a-c)+(b-d)i.
即: 两个复数相加(减)就是实部与实部, 虚部与虚部分别相加(减).
一复习引入
4. 两个复数相等
设z1=a+bi,z2=c+di(a、b、c、dR),则 z1=z2
a
b
ห้องสมุดไป่ตู้
c,
d
即实部等于实部,虚部等于虚部.
特别地,a+bi=0 a=b=0 .
注意:一般地,两个复数只能说相等或不相等,而不能比较大小.
思考:对于任意的两个复数到底能否比较大小?
答案:当且仅当两个复数都是实数时,才能比较大小.
x2 x24,
x2 3x220.
解得
x 3或x 2 x 3或x 6
所以 x3.
复数的除法应怎样进行呢? 注意到,实数的除法运算是乘法的逆运算,类
比思考,我们可定义复数的除法:
定义: 把满足(c+di)(x+yi) =a+bi (c+di≠0) 的 复 数 x+yi 叫做复数 a+bi 除以复数 c+di 的商, 其中a,b,c,d,x,y都是实数,
复数的四则运算(2个课时)(课件)高一数学(人教A版2019必修第二册)

i2021 i45051 (i4 )505 i i
2i 5 5
55
3.实系数一元二次方程在复数集内的解
x2 2x 1 0在复数集内的解: 析 : (2)2 4 1 (1) 8 0, 配方得(x 1)2 2 ( 2 )2
x 1 2, x 1 2.
求根公式: x 2 8 1 2
②若 b2 4ac 0, 方程系数化为1得x2 b x c 0,
aa
配方得(x
b )2 2a
b2 4ac 4a2
[(b2 4ac)] 4a2
[(b2 4ac)]i2 4a2
x b 2a
(b2 4ac) i, x
b
2a
2a
b2 4ac i b 2a
b2 4ac i 2a
(1)z 1; (2)z i; (3)z (2 i) 复数加减法→对应向量加减法
(1)记OZ1 (1,0),则z 1对应的向量是OZ OZ1 OA1.
(2)记OZ2 (0,1),则z i对应的向量是OZ OZ2 Z2Z.
(3)记OZ3 (2,1),则z (2 i)对应的向量是OZ OZ3 OA2.
y
y
A2
y
Z A1
Z
Z
Z2
Z3
Z1
x
x
x
[例6]复数z满足 | z i | 2,求复数z对应的点Z在复平面内的轨迹. 析 : 设i对应的点Z1(0,1).
| z 1|| OZ OZ1 | | Z1Z | 2
即Z与Z1(0,1)的距离为2. 点Z的轨迹是以(0,1)为圆心,以2为半径的圆.
[变1]复数z满足| z i | 1 3i,求复数z对应的点Z 在复平面内的轨迹. 析 : 即 | z i | 2. (同上)
复数的四则运算公开课课件

应用:信号分析
复数和傅里叶变换有重要关系。通过将信号化简为一系列复数,就可以方便地进行处理,找到其 中的周期性和规律。
应用:频域滤波
傅里叶变换后,一个信号就可以变成频域上的一条曲线。可以通过对这条曲线进行复数运算,如 旋转或拉伸等,来实现对信号的改变和优化。
应用:图像处理
图像可以看成由一个个像素点构成的矩阵。通过将颜色信息表示成复数的形式,就可以对图像进 行各种复数运算,并在频域上进行过滤和优化。
应用:量子力学中的波函数
波函数用来描述粒子的运动状态。可以将某个物理量关联到一个复函数,然 后通过对这个函数进行一系列复数运算,来求出这个粒子的各种物理性质和 概率分布。
复数的模
复数的模长的平方为实部的平方加上虚部的平方。
复数的幂
复数的幂满足和实数的幂的规则完全一样。可以把复数映射成一个向量,然 后旋转向量并拉伸长度。
球面坐标系下的复数
可以通过将复平面旋转,将复平面变成球面上的一个维度,从而建立球面坐标系下的复数,并且 可以通过这种方式增加复数属性。
极坐标系下的复数
复数相除等于在复 平面上旋转和缩小
相当于把一个向量在复 平面上旋转一个角度, 同时将其长度缩小了。
复数的倒数
一个非零复数的倒数为其共轭复数除以模长的平方。
实部和虚部
复数z= a+bi,a为实数部分,b为虚数部分。实数可以看作虚数部分为0的复数。
共轭复数
复数z= a+bi的共轭复数为a-bi。共轭复数实部相等,虚部相反,通过把这个复 数映射成平面上的一个向量,共轭复数就相当于把这个向量垂直反转了。
无理数加减法规则
有理数
有理数是可以表示成两个整 数的比值的数,如3/4 、12/5 等。
高中数学-5.2复数的四则运算

特征:两个复数的积仍然是一个复数。运算与多项式运算 类似
2、复数的乘法满足交换律、结合律及乘法对加法的 分配律。 (1)z1z2=z2z1 (交换律) (2)(z1z2)z3=z1(z2z3) (结合律) (3)z1(z2+z3)=z1z2+z1z3 (分配律)
3、复数中正整数指数幂的运算律(其中m,n为正整数)
5.2 复数的四则运算
知识回顾
我们一起来回顾一下上一节课所学知识: i2 1
数
复数代数式 Z a bi(a,b R)
系 的
数
复数分类条件 b 0和b 0
扩 充
复数相等条件
与 复
实部 实部且虚部 虚部
数 的
形
复数的模长(绝对值)的计算
引
入
Z a bi a2 b2
两个复数能比较大小,则一定均为实数
新课讲解
三、复数的除法
把满足(c+di)(x+yi) =a+bi (c+di≠0) 的复数 x+yi 叫做复数
a+bi 除以复数c+di的商,
记做(a bi) (c
di
)或
a
bi
.
c di
(a bi) (c di) a bi (a bi)(c di) c di (c di)(c di)
4 i2 2
25
i 2i2
i 1i
2 2
31 2i
2 3i 1 2i 2 3i
2 3i 2 3i
1
2i2
4 9i2
3i
2 7i 6i2 13
4 7i 4 7 i
13
13 13
试一试
(1)
2、复数的乘法满足交换律、结合律及乘法对加法的 分配律。 (1)z1z2=z2z1 (交换律) (2)(z1z2)z3=z1(z2z3) (结合律) (3)z1(z2+z3)=z1z2+z1z3 (分配律)
3、复数中正整数指数幂的运算律(其中m,n为正整数)
5.2 复数的四则运算
知识回顾
我们一起来回顾一下上一节课所学知识: i2 1
数
复数代数式 Z a bi(a,b R)
系 的
数
复数分类条件 b 0和b 0
扩 充
复数相等条件
与 复
实部 实部且虚部 虚部
数 的
形
复数的模长(绝对值)的计算
引
入
Z a bi a2 b2
两个复数能比较大小,则一定均为实数
新课讲解
三、复数的除法
把满足(c+di)(x+yi) =a+bi (c+di≠0) 的复数 x+yi 叫做复数
a+bi 除以复数c+di的商,
记做(a bi) (c
di
)或
a
bi
.
c di
(a bi) (c di) a bi (a bi)(c di) c di (c di)(c di)
4 i2 2
25
i 2i2
i 1i
2 2
31 2i
2 3i 1 2i 2 3i
2 3i 2 3i
1
2i2
4 9i2
3i
2 7i 6i2 13
4 7i 4 7 i
13
13 13
试一试
(1)
复数的四则运算课件
共轭复数
1.设Z =a+bi (a,b∈R )
Z + Z = 2a
Z- Z = 2bi
2.共轭复数的性质
(1) z1 z2 z1 z2
(2) z1 z2 z1 z2
(3) z1 z2 z1 z2
(4)
z1 z2
z1 z2
(5)zz R, z z R; (6)z z; (7)zn (z)n (n 2).
c di
a c
bi di
(a (c
bi)(c di) di)(c di)
ac
bd (bc c2 d2
ad )i
ac c2
bd d2
bc c2
ad d2
i
例题选讲
1 i i
1.计算: ①
1 1
i i
①
i
②
1 1
i i
②
-
i
③ (1+2i)÷(3-4i);
③ (- 1+2i)/5
对于任意复数z=a+bi ,有 (a+bi)(a-bi)=a2+b2
其中Z =a + bi 与a – bi 叫共轭复数.
如果两个复数的实部相等,虚部互为相反数 时,这两个复数叫做互为共轭复数。(当虚部 不等于0时也叫做互为共轭虚数) 思考:复数Z 为实数的充要条件是 Z = Z
即 实数的共轭复数仍是其本身.
证明: Z 1+Z2 = Z1+Z2 ,Z1-Z=2 Z-1 Z2
证明:设Z=1 a1+b1i, Z2= a2+b2i (a1 , a2 , b1 , b2) ∈R ,则
Z1+Z2 = (a1+b1i )+ (a2+b2i ) = (a1+a2) + (b1+b2 )i = (a1+a2)-( b1+b2 )i = (a1-b1i)+( a2-b2 i) =Z1+ Z2
复数四则运算【公开课教学PPT课件】

=-47+79i
(4)(3 + 2i)^2
=5+12i
(5)试求,i1,i2,i3,i4,i5,i6,i7,i8的值; i,-1,-i,1,i,-1,-i,1
(6)由(1)推测in(n∈N+)的值有什么规律,
并求 i 2016的值.
①i4n+1=i,i4n+2=-1,i4n+3=-i, i4n=1(n∈N+);
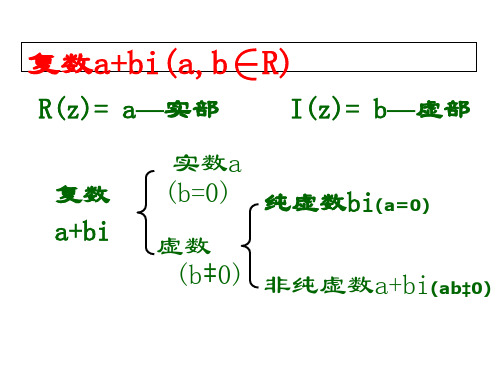
1.复数的定义: 形如a+bi(a,b∈R)的数叫做复数.
z=a+b i ,a ∈R,b∈R
2.复数的分类. 实部 虚部
实数b 0
复数a+bi
虚数b
纯虚数a 0,b 0 0非纯虚数a 0,b
0
3.复数相等.
若a,b,c,d ∈R,
a+bi=c+d i
1:1+ i 2 = 0
[例2] 计算:
(1)(1 + 4i) (7 - 2i)
1 7 (2)i 4 7i 8i2 7 + 26i + 8 15+ 26i
练习:
(1)(-2-i)(3+i)
(2)(-2-3i)(-1+3i)
=-5-5i
=11-3i
(3)(3 - 2i) ( - 4 + 3i)(5 + i)
i 2016 =1
观察下列三组复数
(1)z1=2+i;z2=2-i;
5
(2)z1=3+4i;z2=3-4i; 25
(3)z1=4i;z2=-4i.
16
实部相等,虚部互为相反数.
并且z1与z2的积等于z1的实部与虚部的平方和.
共轭复数
当两个复数的 实部 相等, 虚部 互为相反数时,这样的
《复数——复数的四则运算》数学教学PPT课件(4篇)

=(1-i)(1+i)-12+
3
2
i
=(1-i2)-12+
3
2
i
=2-12+ 23i=-1+ 3i.
第七章 复 数
栏目 导引
第七章 复 数
(2)选 D.因为 a-i 与 2+bi 互为共轭复数, 所以 a=2,b=1,所以(a+bi)2=(2+i)2=3+4i. (3)设 z=a+bi(a,b∈R),则-z =a-bi, 由已知得,(1+2i)(a-bi)=(a+2b)+(2a-b)i=4+3i,由复数相等 的条件知,a2+a-2bb==43,,解得 a=2,b=1, 所以 z=2+i.
复数 z=14+ -ii的虚部为________. 解析:z=41- +ii=( (41- +ii) )( (11- -ii) )=3-2 5i=32-52i. 答案:-52
栏目 导引
第七章 复 数
复数的乘法运算
(1)(1-i)-12+ 23i(1+i)=(
)
A.1+ 3i
B.-1+ 3i
C. 3+i
(2)
1+i 1-i
2
019
=
(1+i)(1+i) (1-i)(1+i)
2
9
=
2i
2
2
019
=
i2
019 =
(i4)504·i3=1504·(-i)=-i.
【答案】 (1)B (2)-i
栏目 导引
第七章 复 数
(1)i 的周期性要记熟,即 in+in+1+in+2+in+3=0(n∈N*). (2)记住以下结果,可提高运算速度. ①(1+i)2=2i,(1-i)2=-2i. ②11- +ii=-i,11+ -ii=i. ③1i =-i.
复数的四则运算PPT优秀课件

特别地,a+bi=0 a=b=0 .
问题:
a=0是z=a+bi(a、bR)为 纯虚数的 必要不充分条件
注意:一般地,两个复数只能说相等 或不相等,而不能比较大小.
思考:对于任意的两个复数到底能否 比较大小? 答案:当且仅当两个复数都是实数 时,才能比较大小.
1.复数加减法的运算法则:
(1)运算法则:设复数z1=a+bi,z2=c+di,
例1.计算 (5 6 i) ( 2 i) (3 4 i)
解: (56i)(2i)(34i) (523)(614)i 11i
2.复数的乘法与除法
(1)复数乘法的法则 复数的乘法与多项式的乘法是类似
的,但必须在所得的结果中把i2换成-1, 并且把实部合并.即:
(2) 那么:z1+z2=(a+c)+(b+d)i;
(3)
z1-z2=(a-c)+(b-d)i.
即:两个复数相加(减)就是实部与
实部,虚部与虚部分 别相加(减).
(2)复数的加法满足交换律、结合律,
即对任何z1,z2,z3∈C,有
z1+z2=z2+z1, (z1+z2)+z3=z1+(z2+z3).
例2:计算( 1) (ab)ia (b)i
a 2 a bai bb 2 ii2
a2 b2
( 2 ) (ab)2ia22 a bb2 i2
a22abbi2
( 3 ) (1 2 i)3 ( 4 i) ( 2 i)
(12i)(34i)(2i) (11 2i)(2i) 2015i
97.有三个人是我的朋友爱我的人.恨我的人.以及对我冷漠的人。 爱我的人教我温柔;恨我的人教我谨慎;对我冷漠的人教我自立。――[J·E·丁格] 98.过去的事已经一去不复返。聪明的人是考虑现在和未来,根本无暇去想过去的事。――[英国哲学家培根] 99.真正的发现之旅不只是为了寻找全新的景色,也为了拥有全新的眼光。――[马塞尔·普劳斯特] 100.这个世界总是充满美好的事物,然而能看到这些美好事物的人,事实上是少之又少。――[罗丹] 101.称赞不但对人的感情,而且对人的理智也发生巨大的作用,在这种令人愉快的影响之下,我觉得更加聪明了,各种想法,以异常的速度接连涌入我的脑际。――[托尔斯泰] 102.人生过程的景观一直在变化,向前跨进,就看到与初始不同的景观,再上前去,又是另一番新的气候――。[叔本华] 103.为何我们如此汲汲于名利,如果一个人和他的同伴保持不一样的速度,或许他耳中听到的是不同的旋律,让他随他所听到的旋律走,无论快慢或远近。――[梭罗] 104.我们最容易不吝惜的是时间,而我们应该最担心的也是时间;因为没有时间的话,我们在世界上什么也不能做。――[威廉·彭] 105.人类的悲剧,就是想延长自己的寿命。我们往往只憧憬地平线那端的神奇【违禁词,被屏蔽】,而忘了去欣赏今天窗外正在盛开的玫瑰花。――[戴尔·卡内基] 106.休息并非无所事事,夏日炎炎时躺在树底下的草地,听着潺潺的水声,看着飘过的白云,亦非浪费时间。――[约翰·罗伯克] 107.没有人会只因年龄而衰老,我们是因放弃我们的理想而衰老。年龄会使皮肤老化,而放弃热情却会使灵魂老化。――[撒母耳·厄尔曼] 108.快乐和智能的区别在于:自认最快乐的人实际上就是最快乐的,但自认为最明智的人一般而言却是最愚蠢的。――[卡雷贝·C·科尔顿] 109.每个人皆有连自己都不清楚的潜在能力。无论是谁,在千钧一发之际,往往能轻易解决从前认为极不可能解决的事。――[戴尔·卡内基] 110.每天安静地坐十五分钟·倾听你的气息,感觉它,感觉你自己,并且试着什么都不想。――[艾瑞克·佛洛姆] 111.你知道何谓沮丧---就是你用一辈子工夫,在公司或任何领域里往上攀爬,却在抵达最高处的同时,发现自己爬错了墙头。--[坎伯] 112.「伟大」这个名词未必非出现在规模很大的事情不可;生活中微小之处,照样可以伟大。――[布鲁克斯] 113.人生的目的有二:先是获得你想要的;然后是享受你所获得的。只有最明智的人类做到第二点。――[罗根·皮沙尔·史密斯] 114.要经常听.时常想.时时学习,才是真正的生活方式。对任何事既不抱希望,也不肯学习的人,没有生存的资格。
