一种点目标三维重构的新算法
三维重构
三维重构三维重构(一)(2007-08-29 11:00:26)标签:知识/探索(一)空间的三维重构问题按照不同的实际情况来看算法的种类非常多,但核心的思想还是利用三角形来覆盖待重构区域的表面。
传统的算法将“覆盖”的思想体现的并不是非常形象,通常只是将待重构区域利用各种方法撒一些点,然后利用三角形来连接这些节点。
如:假如已知某物体的空间的三个剖面,那么如何重建这个物体呢?第一步:将每个剖面的轮廓线提取出来。
第二步:从每条轮廓线中取出拐点和端点。
第三步:利用这些点和三角形来实现物体的重构。
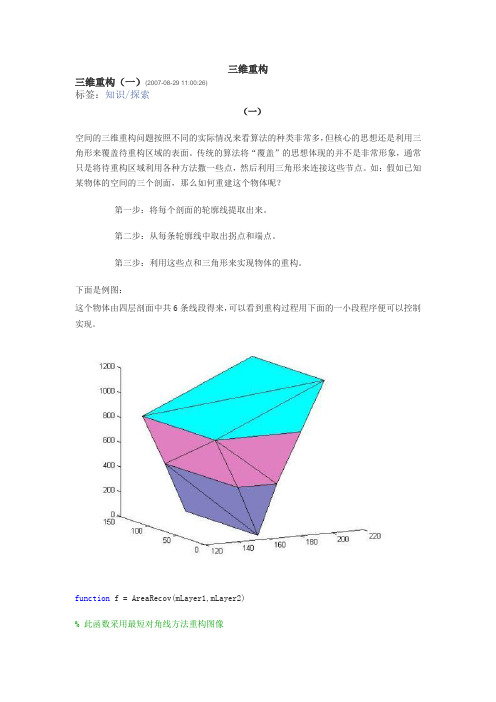
下面是例图:这个物体由四层剖面中共6条线段得来,可以看到重构过程用下面的一小段程序便可以控制实现。
function f = AreaRecov(mLayer1,mLayer2)% 此函数采用最短对角线方法重构图像% 输入:% mLayer1 第一层的点坐标集 n*3% mLayer2 第二层的点坐标集 m*3% 输出:% f 输出的三角形顶点集 max(n,m)*3*3 max(n,m)*三个顶点*三维坐标% 注: 原对角线的重构方法只适用于两层点数相同的情况,% 现在的算法对原算法进行了一些改动。
[Len1,vTemp2,vTemp3] = size(mLayer1) ;[Len2,vTemp2,vTemp3] = size(mLayer2) ;mMaxNum = max([Len1,Len2]) ;f = zeros(mMaxNum,3,3) ;if mMaxNum == Len1vLayer1 = mLayer1 ;vLayer2 = mLayer2 ;elsevLayer1 = mLayer2 ;vLayer2 = mLayer1 ;Len2 = Len1 ; % 用Len2存储小长度endfor counter = 1:mMaxNum-1f(counter,1,:) = vLayer1(counter,:) ;[f(counter,2,:),mIndexTemp] = NearPoint(vLayer1(counter,:),vLayer2) ;% 寻找三角形的第三个顶点if mIndexTemp<=Len2-1 %如果点少的一层还有剩余点vTemp2 = DistanJudg( vLayer1(counter,1:2),vLayer1(counter+1,1:2),...vLayer2(mIndexTemp,1:2),vLayer2(mIndexTemp+1,1:2) ) ;f(counter,3,:) = vLayer2(mIndexTemp+1,:) ;if vTemp2 == -1f(counter,3,:) = vLayer1(counter+1,:) ;endelse% 如果点少的一层没有剩余点,则直接取临点作为第三个顶点f(counter,3,:) = vLayer1(counter+1,:) ;endend对于这个简单的例子来说实现的很完美,但实际中的问题有如下几点:1,寻找物体表层的点时会有很复杂的判断问题,即选择哪几个点作为小三角形的定点来连接。
基于双目立体视觉的三维重构研究

基于双目立体视觉的三维重构研究一、本文概述随着科技的不断发展,三维重构技术在许多领域,如机器人导航、自动驾驶、虚拟现实、增强现实、医疗诊断以及工业检测等,都发挥着越来越重要的作用。
在众多三维重构技术中,基于双目立体视觉的三维重构方法因其设备简单、成本低廉、实时性强等特点而备受关注。
本文旨在探讨基于双目立体视觉的三维重构技术的研究现状、基本原理、关键技术和应用前景,以期对这一领域的研究者和实践者提供有益的参考和启示。
本文将首先介绍双目立体视觉三维重构的基本原理,包括双目视觉的成像模型、立体匹配算法以及三维坐标计算等。
接着,将详细分析当前双目立体视觉三维重构技术中的关键问题,如视差计算、图像预处理、遮挡和纹理映射等,并探讨相应的解决方法和技术。
本文还将对双目立体视觉三维重构技术在不同领域的应用案例进行介绍,分析其优势和局限性,并展望未来的发展趋势和应用前景。
通过本文的研究,我们希望能够为基于双目立体视觉的三维重构技术的发展提供新的思路和方法,推动这一领域的技术进步和应用发展。
我们也希望本文能够为相关领域的学者和工程师提供有益的参考和借鉴,共同推动三维重构技术的发展和应用。
二、双目立体视觉原理双目立体视觉是人类和许多动物天生具备的一种空间感知能力,通过两只眼睛从稍微不同的角度观察物体,然后大脑综合这两个不同的视觉信号,形成立体视觉。
这种视觉原理为三维重构提供了重要的理论基础。
在双目立体视觉系统中,两个相机(模拟双眼)从不同的位置观察同一物体,得到两幅具有视差的图像。
视差是指同一物体在左右两幅图像中的像素坐标之差。
视差的大小取决于相机的基线距离(两个相机光心之间的距离)和物体到相机的距离。
物体距离相机越近,视差越大;物体距离相机越远,视差越小。
为了从这两幅图像中恢复物体的三维形状,我们需要利用三角测量的方法。
在三角测量中,我们知道相机的内外参数(包括相机的内参矩阵、畸变系数、旋转矩阵和平移向量等),通过匹配两幅图像中的同名点(即同一物体在两个图像中的像素坐标),可以计算出这些点在世界坐标系中的三维坐标。
点云处理与三维建模技术的原理和应用

点云处理与三维建模技术的原理和应用1引言随着图形应用技术的飞速发展,二维数据已经无法满足现代信息技术领域应用的需求,三维信息能更加直观地描述真实世界,因此如何快速获取并利用三维信息成为了新的研究目标。
图1-1从二维图像到三维模型经过不断探索,学者们相继提出通过立体视觉、结构光等多种方法提取三维信息,而激光雷达的出现更是为快速、主动、大量、实时、直接地获得被测目标在三维空间中的立体信息提供了重要的技术支持。
激光雷达是二十世纪六十年代发展起来的一种新兴的探测设备,集成了激光测距技术、计算机技术、三维数字化技术等多项高新技术。
激光雷达通过测量角度、距离等位置信息以直接获得目标物体的三维坐标,从而达到提取三维信息并实现三维重构的目的,是一种新型高效的三维空间信息获取设备。
激光雷达除了在速度和精度上有很大优势,同时采用非接触的方式采集目标对象的表面属性点信息,不会导致物体表面发生形变或损坏,因而它在三维激光扫描领域取得了广泛应用。
激光雷达适用于扫描各种复杂的空间场景,它能完整地采集到真实场景中结构复杂、表面不规则的物体的三维数据,并通过计算机设备对数据进行展示、精简、拼接、重构等处理。
通过激光雷达扫描采集到的离散空间点集呈点状分布,因此被称为点云数据。
虽然点云数据的结构十分简单,但是它却可以精确描述出具有复杂的几何结构和细节的三维模型,而且每一个离散点都存储了丰富的几何信息和物体表面属性,如空间位置坐标、大小、法向量、纹理、透明度等。
近年来,激光雷达在扫描效率、精度、速度及可操作性等方面得到极大的发展,在三维数据的采集速度和精度不断提高的同时,但是采集到的原始点云数据仍存在着各种各样的缺陷,譬如:在实际测量中,环境、振动、人为因素、扫描设备本身存在测量误差致使点云数据常常含有噪声;真实场景的点云数据量庞大,后续处理起来十分困难,需要对点云数据进行压缩简化;由于光的线性传播特性,三维激光扫描设备在同一视角下对于形状复杂的物体通常存在视觉盲区,需要在不同视角下多次测量才能完整采集到模型的三维数据。
医学影像图像的三维重建技术

医学影像图像的三维重建技术医学影像是临床医学中一个极其重要的领域。
医学影像可以为医生提供非常直观且准确的生物信息,从而帮助医生更好地进行疾病诊断和治疗。
在医学影像中,图像重建技术是一个非常重要的领域,其中三维图像重构技术就是一个非常重要的技术。
三维重建技术是指从一组二维影像数据中,通过计算机算法将其重建为三维的图像。
因为三维图像包含了更多的信息,相比二维图像,它能够更好地还原真实的形态,减小医生在诊断上的误差,并且同时降低了人的主观判断的影响。
针对这个问题,三维重建技术得到了广泛的应用,特别是在疾病的早期诊断和治疗上,同时也可以在手术操作中提高安全性和准确性,为医生工作提供了更多的便利和准确性。
在医学影像中,CT和MRI成像技术是最常用的影像技术。
这些技术生成的图像都是二维图像。
然而,对于一些局部较小的器官、动脉、淋巴结等等,二维图像的显示很难准确地表达出体内的情况。
对于这些情况,三维重建技术提供了一种可行的解决方案。
通过三维重建技术,可以将这些较小的器官、动脉、淋巴结等等按照真实比例还原,从而给予医生更加深入的视觉和准确的生物信息。
三维图像重建技术有很多方法和算法,目前主要有以下几种:1. 预处理法:预处理法主要是通过对图像数据进行处理,提取出一些关键的信息,以此来重建三维图像模型。
例如,通过对图像数据进行阈值处理、边缘检测等操作,提取出某些区域的信息,然后把这些信息组合在一起,生成三维模型。
但是,预处理法对图像质量要求比较高。
2. 直接体绘制法:直接体绘制法主要是通过对边界数据进行处理,生成三维图像。
边缘数据由计算机算法进行处理,将重点区域的边缘数据和其它区域的边缘数据整合到一起,利用计算机技术进行加工处理,最终生成三维模型。
3. 点云法:点云法主要是利用激光扫描技术,将整个目标扫描成一个点云,然后再通过一定的算法进行处理,最终生成三维模型。
点云法在医学影像处理中广泛应用于骨科和牙科领域中。
一种基于正等轴测草图的三维重构算法

计
算
机
科
学
Co mp u t e r S c i e n c e
Vo 1 . 4 0 No . 9 S e p 2 0 1 3
种 基 于正 等 轴 测 草 图 的 三维 重构 算 法
伍晓 亮 田怀 文
( 西南交通大学机械工程学院 成都 6 1 0 0 3 1 )
据此以手绘二维轴测草图为研究对象以重建草图三维线框模型为目标提出重构算法实现策略研究如何进行草图信息组织和草图美化以及求解平面立体表面积的相关技术探索平面立体表面积与可行解之间的关系较好地解决了轴测草图的识别重构问题为基于草图的三维重构研究进行了有益的探索
第4 O卷 第 9 期 2 0 1 3年 9月
r e s o l v e s t h e f a t h e r - f a c a o f a x o n o me t r i c s k e t c h i n g b y p r o j e c t i o n i n v e r s e t r a n s f o r ma t i o n . L a s t , i t r o t a t e s t h e c h i l d - f a c e s a —
摘 要 为便 于实现 平面立体的三维重构 , 提 出一种基于正等 轴测草 图的重构 算法。首先按 面片组织轴测 草 图轮廓
信息 , 通过 交互指定父面 , 并建立各个面片之 间的关 系。其 次对轴测 草图的父面进 行投 影逆 变换求解 。然后将子 面绕 与父 面连接 的公共 棱边旋转 , 并进行 分类计 算 , 当立体 的表 面积 最大时 , 生成相应 的 目标 形体。给 出了用 Ma t l a b实现
r o u n d t h e e d g e l i n k e d t o t h e f a t h e -f r a c e , a n d c a l c u l a t e s t h e m c a t e g o r i c a l l y wh e n t h e a r e a o f t h e t r i d i me n s i o n a l r e a c h e s
三维重构中一种快速全局最优算法

数的误差函数获得空间点的初始坐标 , 这个解有可 能是 局部 最优 的 , 后 判 断误 差 函数 在给 定 的 凸区 然 域 的 凹凸性 。如 果 目标 函数 为 凸 , 么获 得 的局部 那 最优 就是全 局最 优 , 则 就调 用 全 局 最优 算法 进行 否 计算 。该策略可 以在保证计算精度的情况下 , 明显 提高 了基于大规模 图像 的空间点重构速度。
这 个性 质 , 用 分 支 限界 策 略 结 合 二 次 锥 面优 化 利 ( O P 方 法进行 求解 。该 类 方 法 可 以在 理 论 上确 SC ) 保 获得 的结果是 全局 最 优 的 , 缺 点 是计 算 速 度很 但
慢 而且对外 点很 敏感 。
dX ( )=∑ li P( l — X )
f0 1 0I ( 7 )
L
一
对 应 的
Ⅳ
2 / 0 3 / J z x2 z
d )=∑ Ii P( )I≤ ( l —i X l
i =1
() 3
通过计算知 , 该矩阵的特征值 中有 2个正值和
1 负值 , 个 故该 矩阵非 正定 , 而对 应 的代 价 函数非 从
周果清 , 王 庆
7 07 ) 10 2
( 西北工业大学 计算机学院 , 陕西 西安
摘
要: 在机 器视 觉 中, 维重构是一 个重要 问题 。基于无 穷范数表 示的误 差 函数 已经证 明可以获得 三
全局 最优 , 但是计 算速度很慢 。基 于二 范数 的最 一二 乘 法速 度 虽然很 快 , 因为误 差 函数 是非 凸的 , J 、 但 所 以无法在理论上 证 明获得 的结果是全局 最优 的 , 即使是 通过二分迭代 等方 法 , 往也 只能获得 一个 往
一种新的增强现实三维注册算法

个 坐标 都为正确定唯一的准仿射重构 。 无穷远平面在准仿射 空间中被 日 映射到无穷远。 根据 3 . 2 . 1
3 . 2 . 2 由无 穷远 平 面 求解 仿 射 重构
节构造方法 的准仿射重构, 由无穷远平面 =( , v , , 1 ) 是
日 的符 号为正 的特 征值所对应 求得 的特征 向量 。仿射 空间 中, 无穷远平面 的标准坐标是 =( O , 0 , 0 , 1 ) , 那么求得无穷远 平 面的在准仿射 空 间的坐 标就可 以得 到仿射重构 。 由性质 : 如 果无 穷远平 面位 于特 征点及 摄像机 中心 的 凸包 之外 ,则
的无缝交互 ;
E = [ t L R = S R = U d i a g ( 1 , 1 , o ) v。
确 定双 目摄像机的平移 向量 :
( 2 ) ( 3 )
t = u ( 0 , 0 , 1 ) = U 3( 相差一个长度因子)
U 有正负两个方 向,由于两个 摄像 机的位姿不受符号影
机 的增 强现 实头 戴设 备 。新 型增 强现 实显 示头 戴 由双 目摄
像机, 双 目显 示器集成 , 实现 虚 、 实双重场 景 的三 维拼接融合
效果。
3 摄像 机 双 目标定 算 法
摄像机标定技术是增强现实技术中三维重建的关键技术 “ ,
{ f > 0 ; > 0 c 是摄像 机中心, 是 准仿射重构空间点 ) 成立。 c
对 图像坐标归一化 , 采用 五点法得 到本 质矩 阵, 对本质矩
阵 奇异 值 ( S V D) 分解 :
接, 增 强互动能力 。增强现实技 术, 可实现第一视角在 舞台实 景中展示数字舞美 设计 作品 , 实现虚 实互动的快速变换 , 是灯
基于KinectV2_的猪体三维点云重构与体尺测量

第 23卷第 1期2024年 1月Vol.23 No.1Jan.2024软件导刊Software Guide基于KinectV2的猪体三维点云重构与体尺测量李哲,林文祉,翁智,郑志强(内蒙古大学电子信息工程学院,内蒙古呼和浩特 024005)摘要:体尺参数是评价育肥猪生长状况的重要指标,针对单目CCD相机在猪体体尺测量中受角度、光源等因素影响导致的测量参数单一、测量结果误差较大等问题。
首先利用深度相机KinectV2从正上方和左右两侧视角同步获取猪体局部点云数据;然后进行点云去噪、精简分割等处理,运用改进后的ICP点云配准技术处理点云信息;最后采用精确估算技术精简点云数据。
在不同角度比较实验测量与人工测量的结果发现,猪体数据中体长平均相对误差为2.65%、体高平均相对误差为1.87%、体宽平均相对误差为1.75%、臀高平均相对误差为2.07%、臀宽平均相对误差为1.96%,整体上误差较小,证明了所提方法的有效性,以期为猪体尺寸测量提供新的解决方法。
关键词:育肥猪;图像处理;KinectV2;三维点云;体尺测量DOI:10.11907/rjdk.232094开放科学(资源服务)标识码(OSID):中图分类号:TP391 文献标识码:A文章编号:1672-7800(2024)001-0161-06KinectV2-based 3D Point Cloud Reconstruction and Body SizeMeasurement of Pig BodyLI Zhe, LIN Wenzhi, WENG Zhi, ZHENG Zhiqiang(School of Electronic and Information Engineering, Inner Mongolia University, Hohhot 024005, China)Abstract:Body size parameter is an important indicator for evaluating the growth status of fattening pigs. It addresses the problems of single measurement parameters and large measurement errors caused by factors such as angle and light source in pig body size measurement using a monocular CCD camera. Firstly, use the depth camera KinectV2 to synchronously obtain local point cloud data of the pig body from the top and left and right perspectives; Then, point cloud denoising, simplification and segmentation are carried out, and the improved ICP point cloud registration technology is used to process point cloud information; Finally, precise estimation techniques are used to streamline point cloud da⁃ta. Comparing the results of experimental and manual measurements from different angles, it was found that the average relative error of body length was 2.65%, the average relative error of body height was 1.87%, the average relative error of body width was 1.75%, the average rela⁃tive error of hip height was 2.07%, and the average relative error of hip width was 1.96% in pig body data. Overall, the error was relatively small, proving the effectiveness of the proposed method and providing a new solution for pig body size measurement.Key Words:growing and fattening pigs; image processing; KinectV2; 3D point cloud; body size measurement0 引言育肥猪养殖生产过程中连续监测猪体尺参数,能有效掌握猪的生长状态,是反映猪体健康与否的有效手段,是保证动物福利的有力工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 0 Si eh E gg 08 c .T c . nn .
一
种 点 目标 三 维 重构 的 新 算 法
付 强 王春 平
( 军械工程 学院 , 石家庄 00 0 ) 50 0
摘
要
双 目立体视觉研 究利 用二维投影 图像恢复 三维 景物 世界 的 问题 , 中三维 重构是 立体视 觉测量 过程 的主要 组成部 其
1 算法原理
设 两个 C D摄像 机 的外部 参 数 ( C 即两个 摄像 机 的坐 标 系相对 于 世界 坐 标 系 ( , , z )的旋转 矩 阵 和平移 矩 阵 ) 别 为 R 、 , t、, 其 中 分 R 、 t ,
R =l z 6 , , 1 " l 2 5 R =l " 6 ; z zl 4 r 5 4 1
精度。
关键 词
双 目立体视 觉
三维重构
异面直线
中图法 分类 号 T 91 N 1;
文献 标志码
A
双目 立体视觉测量 系统
中, 三维重构原理
/ -乘 法 没 有 考 虑 所 建 立 的超 定 方 程 组所 代 表 的 b- 几何 意义 , 算 出的 物 点 坐 标精 度 不 高 。本 文 采 用 计 求解 三 维 空 间 中两 条 射 线 相 交 的方 法 来 确 定 物 点 坐标 。 由于 图像 平 面 坐 标 的 测量 误 差 、 噪声 以及 摄 像机 畸 变 等 因 素 的 影 响 , 条 射 线 可 能 不 会 相 两 交 J所 以交 汇定 位 问题 就 是 求 异 面直 线公 垂 线 段 , 中点 的坐标 。实 验 表 明 , 算 法 较传 统 的 最小 二 乘 该 法具 有更 高 的测 量精 度 。
如图 1 所示 , 对于每个摄像机而言, 如果光心和像点
已知 , 可 以 确 定 光 心 和像 点 组 成 的 唯 一 射 线 , 就 在 针 孔成 像模 型下 , 物点 必 然 在 此 射 线 上 。有 几 台摄 像 机进 行交 汇就有 几 条 这 样 的射 线 , 所 有 的射 线 且 都 应经 过物 点 , 即应 用 各 射 线应 在 物 点相 交 的原 理 就 可 以对 空 间物点 进行 交 汇定 位 。
火力控制、 图像处理研究 。Em i f i yu cm c 。 - a :u a o .o .n l q @e
维普资讯
科
学
技
术
与
工
程
8卷
化简得 :
=
ll +tz l ; zl t l R l y Y
=l + ,l, l£ l t y y
() 1
f R £ 一( £ = ( ) £ )
£
【 R 一 R = ( R ) (L )
根据 克莱姆 法则 可得 :
R
() 6
两 射线 方程 还可表 示 为 :
=
B R 一( LR ) £ R T £ B R 一( LR ) R R T R R T £ 一( LR ) RR R T £
维普资讯
第8 卷
第 3期
20 0 8年 2月
科
学
技
术
与
工
程
⑥
Vo . N . 18 o3
Fb 0 8 e .2 0
17 —8 9 20 ) -6 30 6 11 1 ( 0 8 3 04 —5
S in eT c n lg n n ie r g c e c e h oo y a d E gn e n i
出这两点的位置平均值 , 就得到 目标物点 的三维坐
标 P( Y 即 , ,),
=
[ :一:3 [ [兰, c 兰 i;[ ] ] ] 一i +[ ] ]
) P (, , , 、 , 别 为两 摄 像 机焦 和 , , , )( YF F分
距) 。则 P 、 , 』 P 与两 摄像 机 坐标 系原 点所 组 成 的射 线方 程 可表示 为 :
第一作 者简介 : 付
强 (9 1 ) 男 , 1 8 一 , 河北保定 人 , 硕士 , 究方 向 : 研
分之一 , 是从 二维 图像 恢复三维景物 的关键环 节。针对 空间点 目标 的三维重构 , 统 的方法是 采用 最小 二乘法进行 的, 传 但是 由于最小二乘法没有考虑所建 立的超定 方程组所代表 的几何 意义 , 以计算 出的点坐标精 度不 高。对 此 , 几何 学的角度 出 所 从
发 , 出 了一种异 面直 线公 垂线段 中心法来提 高点 目标 的重构精度 。实验表 明 , 方法 比传 统 的最小二乘 法具 有更 高 的测量 提 该
图 1
r r 8 9 t t ( , , ) ,t t t t , ( , t t 。 t, ”, )
rf ,2 ]
r 23] , rr
摄 像机 交汇 定位 问题 , 统 的做 法 是 利用 最 小 传
二乘法求解联立的超定方程组得到最优解 , 将最优
解 近似地 看作 空 间 物 点 的 三 维坐 标 。但 是 , 由于 最
20 0 7年 1 O月 2 日收 到 9
设在 世 界 坐 标 系 中 有 一 物 点 P( ,,), 点 xyz 该 在 两 个摄 像 机 图 像 平 面 上 的投 影 点 在 摄 像 机 坐 标
系 0 , , 0 , Z 和 中 的坐 标 分 别 为 P ( , Y,
・
/ l
]
R T R 一( LR ) RR R T R
=£ l r, l, + l l Y
・
(I t  ̄ r
IR £ BR 1 RT R £ Leabharlann / l () 2
=
㈩
lR R 一RTR l RT R (£ ) R
将 和 的代 入 ( ) , 2 式 则得 到射线 中垂 线段 对 应 两 点 的坐 标 (p , )和 (p,p )。求 f , r,, ,,
