_学年高中数学4.2圆周率同步精练北师大版选修3_1
北师大版高中数学选修3-1圆周率练习.docx

圆周率练习1.关于圆周率的最早记录出自( )A.《周髀算经》B.《九章算术》C.莱茵德草卷D.《几何原本》2.世界上第一个把π计算到3.141 592 6<π<3.141 592 7的数学家是( ) A.刘徽B.阿基米德C.祖冲之D.卡瓦列利3.最早用穷竭法研究圆周率的数学家是( )A.阿基米德B.安提丰C.刘徽D.布里松4.证明π是无理数的数学家是( )A.高斯B.阿基米德C.兰伯特D.林德曼5.圆周率的计算是我国古代数学史上的伟大的成就之一,很久以前我们的祖先就发现圆的周长和直径之比是一个定数,这个定数被命名为圆周率.那么圆周率在不断地精确过程中有哪些突出的成就呢?6.查找资料,了解阿基米德与穷竭法.7. 如图所示,已知直线y=2x+3与抛物线y=x2交于A,B两点,试用阿基米德穷竭法求抛物弓形AOB的面积.参考答案1.答案:C2.答案:C3.答案:B4.答案:C5.答:①《周髀算经》,采用的圆周率是“周三径一”,即π=3;②魏晋时期刘徽创立割圆术,为计算圆周率建立了严密理论和算法,求出π≈3.141 6,采用了极限思维,是近代微积分思想的萌芽;③祖冲之求出的圆周率,在3.141 592 6和3.141 592 7之间,并且确立两个分数形式的近似值:约率和密率,祖冲之的成果在世界上一直领先了1 000年.6.答:在古希腊,利用穷竭法作出重要贡献的是阿基米德,阿基米德(Archime d es ,公元前287—前212)出生于意大利西西里岛的叙拉古,是古希腊最杰出的数学家、力学家,他的几何著作成为古希腊数学的顶峰,他的数学著作主要有《圆的度量》《论球与圆柱》《抛物线求积法》《论螺线》等.在这些著作中,阿基米德巧妙地将穷竭法与原子论观点结合起来,通过严密的计算,获得了许多重要的结果,例如他在《抛物线求积法》一书中,使用穷竭法求出了抛物线弓形的面积,他的方法简述如下:作三角形ABC ,设其面积为S 1,其中l 1∥AC ,B 是切点,再作抛物线的切线l 2和l 3使之分别平行于AB 和BC ,切点分别是D 和E ,再作三角形ADB 和三角形BEC (如图),设两个三角形面积之和为S 2,用A 1表示S 1,A 2表示S 1+S 2,那么用完全同样的方法可以得到A n =S 1+S 2+…+S n .很明显,只要取n 足够大,弓形面积S 与A n 的差S -A n 就可以任意小.由抛物线的性质可知S 1=4S 2,∴A n =S 1+1111121141444334n n S S S S S --++⋅⋅⋅+=-⋅. 最后,阿基米德用反证法证明了S =143S . 特别要提到的是,阿基米德在计算以他的名字命名的曲线——阿基米德螺线第一周围成的区域的面积时,使用了类似于现代积分学中的大和、小和的概念.他的用法,用今天的符号表示就是:将2π n 等分,在每一部分上作出顶角2nπ的内接圆扇形和外接圆扇形(如下图),它们的面积之和,分别用A n 与S n 表示,显然所求之面积S 满足不等式A n <S <S n ,经过计算A n =324111132a n n π⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭, S n =324111132a n n π⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭,于是,对任意的n ,有A n <3243a π<S n .阿基米德经过猜测,并使用反证法进行了证明,得出螺线第一周所围成的面积S =3243a π. 阿基米德突破了传统的有限运算,大胆地采用了无限逼近的思想,从而将穷竭法发展到了高峰,但是由于当时没有极限概念,不承认无限,因此,穷竭法仍是有限的形式,并且局限在几何直观上,运算也很烦琐,所以自阿基米德之后,很长时间没有被人重视.尽管这种方法有很大的缺点,但是,他的求积方法已具有了定积分思想的萌芽.7. 分析:可以求出弦AB 的中点C ,过C 作y 轴的平行线交抛物线与点D ,这样抛物弓形AOB 的面积是△ABD 面积的43,因此我们只要求△ABD 的面积即可.解:设A ,B 两点的坐标为A(x 1,y 1),B(x 2,y 2), 则有2,23,y x y x ⎧=⎨=+⎩解得12121,3,1,9.x x y y =-=⎧⎧⎨⎨==⎩⎩ ∴A (-1,1),B (3,9),中点C (1,5).过中点C(1,5)作y 轴的平行线交抛物线于D(1,1),再求△ABD 的面积. |AB|=[]223(1)(91)4 5.--+-=点D 到直线AB 的距离为d =21134455415⨯-+==+. ∴S △ABD =12|AB |·d =1454525⨯⨯=8. ∴抛物弓形AOB 的面积为S =43S △ABD =432833⨯=.。
高二数学(北师大版)选修3-1同步精练:第六章 2 哥尼斯堡七桥问题 Word版含答案

哥尼斯堡七桥问题练习1.欧拉出生于( )A.瑞士B.俄国C.德国D.英国2.欧拉把哥尼斯堡七桥问题抽象成图进行讨论,影响深远,推动了两门新生数学分支的诞生,这两门数学分支是( )A.群论和图论B.运筹学和图论C.图论和拓扑学D.控制论和拓扑学3.被人们形容为“橡皮泥的几何学”的数学分支是( )A.立体几何B.解析几何C.拓扑学D.图论4.1727年,推荐欧拉到圣彼得堡科学院工作的数学家是 ( )A.约翰·贝努利B.丹尼尔·伯努利C.高斯D.莱布尼茨5.用f(x)表示函数的首创数学家是( )A.欧拉B.莱布尼茨C.牛顿D.高斯6.欧拉的三本书____________、________和________称为微积分发展史上里程碑式的著作.7.欧拉在《无穷分析引论》中给出了著名的极限________,其中e为自然对数的底.8.在下图的七个圆圈内各填一个数,要求每一条直线上的三个数中,当中的数是两边两个数的平均数.现在已经填好两个数,那么X=________.9.你能笔尖不离纸,一笔画出下图所示的每个图形吗?10.下图是用小华制的“四巧板”拼成的“船”.如果画在一张纸上你能否用剪刀一次连续剪下“船”中的每个图形?11.上网查找欧拉的事迹并整理.参考答案1.答案:A2.答案:C3.答案:C4.答案:B5.答案:A6.答案:《无穷分析引论》《微分学》《积分学》7.答案:1lim1xx x→∞⎛⎫+⎪⎝⎭=e8.解析:为了说明的方便,余下的四个圆圈分别用A,B,C,D四个字母来表示(如下图)由每一条直线上三个数的关系知A=(13+17)÷2=15C=(15+B)÷2=(17+D)÷2①D=(13+B)÷2②从①式中知,B比D大2,那么②式可写成D=(13+D+2)÷2D=15所以C=(17+15)÷2=16(13+X)÷2=16所以X=19.答案:199.答:图(a)有两个奇数顶点,可从任一“奇数顶点”出发,以另一“奇数顶点”为终点一笔画出.A→B→C→A→D;图(b)、图(c)都是“偶数顶点”的连通图,可从任一点出发,一笔画出.如图(b)A→G→C→B→F→H→B→A,图(c)A→B→E→B→C→I→J→F→E→D→F→J→H→I→C→A.10.答:能一次连续剪下图中的四个图形,要求剪刀必须连续剪过图中所有的线,即问题的实质是这个图能否一笔画.显然,图中只有两个“奇数点”A,D,因此,可以很快判断能办到,剪刀所走的路线可以是:A→B→C→A→D→C→G→H→I→J→G→F→E→D.11.答:欧拉 (Euler,Léonh a r d,1707—1783),瑞士数学家.1707年4月15日生于瑞士巴塞尔,1783年9月18日卒于俄国圣彼得堡.他生于牧师家庭.15岁在巴塞尔大学获学士学位,翌年得硕士学位.1727年,欧拉应圣彼得堡科学院的邀请到俄国.1733年接替丹尼尔伯努利成为圣彼得堡科学院数学教授.他以旺盛的精力投入研究,在俄国的14年中,他在分析学、数论和力学方面作了大量出色的工作.1741年受普鲁士腓特烈大帝的邀请到柏林科学院工作,达25年之久.在柏林期间他的研究内容更加广泛,涉及行星运动、刚体运动、热力学、弹道学、人口学,这些工作和他的数学研究相互推动.欧拉这个时期在微分方程、曲面微分几何以及其他数学领域的研究都是开创性的.1766年他又回到了圣彼得堡.欧拉是18世纪数学界最杰出的人物之一.他不但在数学上作出伟大贡献,而且把数学用到了几乎整个物理领域.他又是一个多产作者.他写了大量的力学、分析学、几何学、变分法的课本,《无穷分析引论》《微分学》《积分学》都成为数学中的经典著作.除了教科书外,他的全集有74卷.18世纪中叶,欧拉和其他数学家在解决物理问题过程中,创立了微分方程这门学科.值得提出的是,偏微分方程的纯数学研究的第一篇论文是欧拉写的《方程的积分法研究》.欧拉还研究了函数用三角级数表示的方法和解微分方程的级数法等等.欧拉引入了空间曲线的参数方程,给出了空间曲线曲率半径的解析表达式.1766年他出版了《关于曲面上曲线的研究》,建立了曲面理论.这篇著作是欧拉对微分几何最重要的贡献,是微分几何发展史上的一个里程碑.欧拉在分析学上的贡献不胜枚举.如他引入了Г函数和B函数,证明了椭圆积分的加法定理,最早引入了二重积分,等等.数论作为数学中一个独立分支的基础是由欧拉的一系列成果所奠定的.他还解决了著名的组合问题:哥尼斯堡七桥问题.在数学的许多分支中都常常见到以他的名字命名的重要常数、公式和定理.欧拉是历史上最多产的一位数学家.他生前发表的著作与论文有560 余篇,并遗留下大量手稿,甚至在他去世80 年后,圣彼得堡科学院院报上还在刊登欧拉的遗作.1911 年瑞士自然科学协会开始出版欧拉全集,现已出版70 多卷,计划出齐84 卷,都是大四开本.欧拉的研究涉足众多领域.他扩展了微积分领域,为无穷级数、微分方程、微分几何学等分支和学科的产生与发展奠定了基础;开创了现代三角学和现代数论;还由解决哥尼斯堡七桥问题而引发图论分支的研究等等.除创建纯粹数学理论外,他还应用这些数学工具去解决天文学、物理学、力学等方面的实际问题,取得巨大成果.此外,欧拉扶植后学,关心教育.在欧拉48 岁时,年仅19 岁的法国青年学者拉格朗日与欧拉通信,讨论“等周问题”,欧拉也在研究这个问题.后来拉格朗日获得成果,欧拉就压下自己的论文,让拉格朗日首先发表,使他一举成名.欧拉出色的工作和高尚的品德赢得后人的广泛尊敬,著名数学家拉普拉斯曾说过:“读读欧拉,读读欧拉,他是我们大家的老师.”。
北师大版九年级数学下册第三章《圆》3

北师大版九年级数学下册第三章《圆》3.1同步练习题(含答案)一、选择题1、已知⊙O 与点P 在同一平面内,若⊙O 的半径为5,线段OP 的长为4,则点P( ) A .在⊙O 上 B .在⊙O 内C .在⊙O 外D .在⊙O 上或在⊙O 内 2、下列说法错误的是( ) A .圆有无数条直径B .连接圆上任意两点之间的线段叫弦C .过圆心的线段是直径D .能够重合的圆叫做等圆 3、下列说法正确的是( ) A .相等的圆心角所对的弧相等B .在同圆中,等弧所对的圆心角相等C .在同圆中,相等的弦所对的弧相等D .相等的弦所对的圆心角相等4、如图,AB ,CD 是⊙O 的直径,AE ︵=BD ︵.若∠AOE =32°,则∠COE 的度数是( ) A .32°B .60°C .68°D .64°5、如图,在⊙O 中,AC ︵=2AB ︵,则以下数量关系正确的是( ) A .AB =ACB .AC =2ABC .AC <2ABD .AC >2AB6、如图,已知AD ︵=BC ︵,则AB 与CD 的关系为( ) A .AB =CDB .AB>CDC .AB<CD D .不能确定7、如图,在矩形ABCD 中,AB =8,BC =35,点P 在边AB 上,且BP =3AP.如果⊙P 是以点P 为圆心、PD 为半径的圆,那么下列判断正确的是( )A .点B ,C 均在⊙P 外B .点B 在⊙P 外,点C 在⊙P 内C .点B 在⊙P 内,点C 在⊙P 外D .点B ,C 均在⊙P 内二、填空题8、如图,在矩形ABCD 中,AB =4,AD =3,以顶点D 为圆心作半径为r 的圆.若要求另外三个顶点A ,B ,C 中至少有一个点在圆内,且至少有一个点在圆外,则r 的取值范围是____;9、已知点C 在线段AB 上,且0<AC <12AB.如果⊙C 经过点A ,那么点B 与⊙C 的位置关系是____.10、如图,AB 和DE 是⊙O 的直径,弦AC ∥DE.若弦BE =3,则弦CE =____.11、如图,已知BD 是⊙O 的直径,点A ,C 在⊙O 上,AB ︵=BC ︵,∠AOB =60°,则∠COD 的度数是____12、如图,CD 是⊙O 的直径,∠EOD =84°,AE 交⊙O 于点B ,且AB =OC ,则∠A 的度数是____13、如图,AB 为⊙O 的直径,△PAB 的边PA ,PB 与⊙O 的交点分别为C ,D.若AC ︵=CD ︵=DB ︵,则∠P 的大小为____三、解答题14、如图,Rt △ABC 的两条直角边BC =3 cm ,AC =4 cm ,斜边AB 上的高为CD.若以点C 为圆心,分别以r 1=2 cm ,r 2=2.4 cm ,r 3=3 cm 为半径作圆,试判断点D 与这三个圆的位置关系.15、如图,小虎牵着小狗上街,小虎的手臂与绳共2.5 m(手臂与拉直的绳子在一条直线上),手臂肩部距地面 1.5 m .当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.16、如图,以▱ABCD 的顶点A 为圆心,AB 为半径作⊙A ,交AD ,BC 于点E ,F ,延长BA 交⊙A 于点G.求证:GE ︵=EF ︵.17、如图,台风中心位于点P ,并沿东北方向PQ 移动,已知台风移动的速度为15千米/时,受影响区域的半径为100千米,B 市位于点P 的北偏东75°方向上,距离点P160千米处.(1)说明本次台风会影响B 市; (2)求这次台风影响B 市的时间.18、如图,已知AB 是⊙O 的直径,M ,N 分别是AO ,BO 的中点,CM ⊥AB ,DN ⊥AB.求证:AC ︵=BD ︵.19、如图,在⊙O 中,AC ︵=CB ︵,CD ⊥OA 于点D ,CE ⊥OB 于点E ,求证:AD =BE.参考答案一、选择题1、已知⊙O 与点P 在同一平面内,若⊙O 的半径为5,线段OP 的长为4,则点P(B) A .在⊙O 上 B .在⊙O 内C .在⊙O 外D .在⊙O 上或在⊙O 内 2、下列说法错误的是(C)A .圆有无数条直径B .连接圆上任意两点之间的线段叫弦C .过圆心的线段是直径D .能够重合的圆叫做等圆 3、下列说法正确的是(B)A .相等的圆心角所对的弧相等B .在同圆中,等弧所对的圆心角相等C .在同圆中,相等的弦所对的弧相等D .相等的弦所对的圆心角相等4、如图,AB ,CD 是⊙O 的直径,AE ︵=BD ︵.若∠AOE =32°,则∠COE 的度数是(D) A .32°B .60°C .68°D .64°5、如图,在⊙O 中,AC ︵=2AB ︵,则以下数量关系正确的是(C) A .AB =ACB .AC =2ABC .AC <2ABD .AC >2AB6、如图,已知AD ︵=BC ︵,则AB 与CD 的关系为(A) A .AB =CDB .AB>CDC .AB<CD D .不能确定7、如图,在矩形ABCD 中,AB =8,BC =35,点P 在边AB 上,且BP =3AP.如果⊙P 是以点P 为圆心、PD 为半径的圆,那么下列判断正确的是(C)A .点B ,C 均在⊙P 外B .点B 在⊙P 外,点C 在⊙P 内 C .点B 在⊙P 内,点C 在⊙P 外D .点B ,C 均在⊙P 内二、填空题8、如图,在矩形ABCD 中,AB =4,AD =3,以顶点D 为圆心作半径为r 的圆.若要求另外三个顶点A ,B ,C 中至少有一个点在圆内,且至少有一个点在圆外,则r 的取值范围是3<r <5;9、已知点C 在线段AB 上,且0<AC <12AB.如果⊙C 经过点A ,那么点B 与⊙C 的位置关系是点B 在⊙C 外.10、如图,AB 和DE 是⊙O 的直径,弦AC ∥DE.若弦BE =3,则弦CE =3.11、如图,已知BD 是⊙O 的直径,点A ,C 在⊙O 上,AB ︵=BC ︵,∠AOB =60°,则∠COD 的度数是120°.12、如图,CD 是⊙O 的直径,∠EOD =84°,AE 交⊙O 于点B ,且AB =OC ,则∠A 的度数是28°.13、如图,AB 为⊙O 的直径,△PAB 的边PA ,PB 与⊙O 的交点分别为C ,D.若AC ︵=CD ︵=DB ︵,则∠P 的大小为60°.三、解答题14、如图,Rt △ABC 的两条直角边BC =3 cm ,AC =4 cm ,斜边AB 上的高为CD.若以点C 为圆心,分别以r 1=2 cm ,r 2=2.4 cm ,r 3=3 cm 为半径作圆,试判断点D 与这三个圆的位置关系.解:在Rt △ABC 中,根据勾股定理,得AB =5 cm ,则CD =AC ·BCAB=2.4 cm.①当r 1=2 cm 时,2.4>2,点D 在圆外; ②当r 2=2.4 cm 时,点D 在圆上; ③当r 3=3 cm 时,2.4<3,点D 在圆内15、如图,小虎牵着小狗上街,小虎的手臂与绳共2.5 m(手臂与拉直的绳子在一条直线上),手臂肩部距地面 1.5 m .当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.解:小狗在地面上环绕的圆的半径为r = 2.52-1.52=2.0(m),S =πr 2=4π(m 2).故小狗在平整的地面上活动的最大区域是以2.0 m 为半径的圆,其面积为4π m 2.如图:16、如图,以▱ABCD 的顶点A 为圆心,AB 为半径作⊙A ,交AD ,BC 于点E ,F ,延长BA交⊙A 于点G.求证:GE ︵=EF ︵.证明:连接AF. ∵AB =AF ,∴∠ABF =∠AFB.∵四边形ABCD 是平行四边形, ∴AD ∥BC.∴∠DAF =∠AFB ,∠GAE =∠ABF. ∴∠GAE =∠EAF.∴GE ︵=EF ︵.17、如图,台风中心位于点P ,并沿东北方向PQ 移动,已知台风移动的速度为15千米/时,受影响区域的半径为100千米,B 市位于点P 的北偏东75°方向上,距离点P160千米处.(1)说明本次台风会影响B 市; (2)求这次台风影响B 市的时间.解:(1)作BH ⊥PQ 于点H , 在Rt △BHP 中,由条件知,PB =160千米,∠BPQ =75°-45°=30°, ∴BH =160sin30°=80千米<100千米. ∴本次台风会影响B 市. (2)若台风中心移动到P 1时,台风开始影响B 市,台风中心移动到P 2时,台风影响结束, 由(1)得BH =80千米,由条件得BP 1=BP 2=100千米, ∴P 1P 2=21002-802=120(千米).∴台风影响B 市的时间t =12015=8(小时).答:台风影响B 市的时间为8小时.18、如图,已知AB 是⊙O 的直径,M ,N 分别是AO ,BO 的中点,CM ⊥AB ,DN ⊥AB.求证:AC ︵=BD ︵.证明:连接OC ,OD ,∵AB 是⊙O 的直径,M ,N 分别是AO ,BO 的中点,∴OM =ON. ∵CM ⊥AB ,DN ⊥AB , ∴∠OMC =∠OND =90°.在Rt △OMC 和Rt △OND 中,⎩⎪⎨⎪⎧OM =ON ,OC =OD ,∴Rt △OMC ≌Rt △OND(HL). ∴∠COM =∠DON.∴AC ︵=BD ︵.19、如图,在⊙O 中,AC ︵=CB ︵,CD ⊥OA 于点D ,CE ⊥OB 于点E ,求证:AD =BE.证明:连接OC. ∵AC ︵=CB ︵,∴∠AOC =∠BOC. ∵CD ⊥OA ,CE ⊥OB , ∴∠CDO =∠CEO =90°.在△COD 和△COE 中,⎩⎪⎨⎪⎧∠DOC =∠EOC ,∠CDO =∠CEO ,CO =CO ,∴△COD ≌△COE(AAS).∴OD =OE.∵AO =BO ,∴AD =BE.。
北师大数学选修同步作业:第3章 变化率与导数 作业 含解析

课时作业(十八)1.函数y =x·lnx 的导数是( ) A .x B.1x C .lnx +1 D .lnx +x答案 C解析 y ′=x ′·lnx +x·(lnx)′=lnx +x·1x =lnx +1.2.下列求导数运算正确的是( ) A.⎝⎛⎭⎫x +1x ′=1+1x 2 B .(log 2x)′=1xln2C .(3x )′=3x log 3eD .(x 2cosx)′=-2xsinx 答案 B3.函数y =x cosx 的导数是( )A.1+x cosxB.cosx -xsinx cos 2xC.cosx +x cos 2xD.cosx +xsinx cos 2x答案 D解析 y ′=x ′cosx -x (cosx )′cos 2x =cosx +xsinxcos 2x .4.已知f ⎝⎛⎭⎫1x =x1+x ,则f ′(x)=( ) A.11+x B .-11+xC.1(1+x )2 D .-1(1+x )2答案 D解析 ∵f ⎝⎛⎭⎫1x =x 1+x =11x +1, ∴f(x)=1x +1. ∴f ′(x)=-1(1+x )2.5.已知f(x)=ax 3+3x 2+2,若f ′(-1)=4,则a 的值是( ) A.193B.163C.133D.103答案 D解析 f ′(x)=3ax 2+6x ,f ′(-1)=3a -6=4,a =103.6.设点P 是曲线y =x 3-3x +23上的任意一点,点P 处切线倾斜角为α,则角α的取值范围是( ) A.⎣⎡⎭⎫23π,π B.⎝⎛⎦⎤π2,56π C.⎣⎡⎭⎫0,π2∪⎝⎛⎭⎫56π,π D.⎣⎡⎭⎫0,π2∪⎣⎡⎭⎫23π,π 答案 D解析 由y ′=3x 2-3易知y ′≥-3,即tan α≥- 3. ∴0≤α<π2或23π≤α<π.7.设函数f(x)=g(x)+x 2,曲线y =g(x)在点(1,g(1))处的切线方程为y =2x +1,则曲线y =f(x)在点(1,f(1))处的切线的斜率为( ) A .4 B .-14C .2D .-12答案 A解析 依题意得f ′(x)=g ′(x)+2x ,f ′(1)=g ′(1)+2=4,选A.8.(高考真题·天津卷)已知函数f(x)=axlnx ,x ∈(0,+∞),其中a 为实数,f ′(x)为f(x)的导函数,若f ′(1)=3,则a 的值为________. 答案 3解析 因为f ′(x)=a(1+lnx),所以f ′(1)=a =3.9.直线y =kx +1与曲线y =x 3+ax +b 相切于点A(1,3),则b 的值为________. 答案 3解析 由已知点A 为切点,∴3=k +1,∴k =2, 即切线方程为y =2x +1.且当x =1时y ′=3+a =2.又∵3=13+a +b ,∴⎩⎪⎨⎪⎧a =-1,b =3.10.已知f(x)=alnx +bx 2+x ,且x =1与x =2是方程f ′(x)=0的两个实数根,则a =________,b =________. 答案 -23 -1611.(2018·课标全国Ⅲ,理)曲线y =(ax +1)e x 在点(0,1)处的切线的斜率为-2,则a =________. 答案 -3解析 y ′=a·e x +(ax +1)·e x =e x ·(ax +a +1),据题意e 0·(a·0+a +1)=-2,∴a =-3. 12.求下列函数的导数: (1)f(x)=x 2sinx +2cosx ;(2)f(x)=e x +1e x -1.解析 (1)f ′(x)=2xsinx +x 2cosx -2sinx. (2)f ′(x)=e x (e x -1)-(e x +1)e x(e x -1)2=e 2x -e x -e 2x -e x (e x -1)2=-2e x (e x -1)2. 13.已知函数f(x)=x ,g(x)=alnx ,a ∈R .若曲线y =f(x)与曲线y =g(x)相交,且在交点处有相同的切线,求a 的值及该切线的方程. 解析 f ′(x)=12x ,g ′(x)=ax (x>0),由已知得⎩⎪⎨⎪⎧x =alnx ,12x =a x.解得a =12e ,x =e 2. ∴两条曲线交点的坐标为(e 2,e),切线的斜率为k =f ′(e 2)=12e ,所以切线的方程为y -e =12e (x-e 2),即x -2ey +e 2=0.14.在曲线y =x 3-x 上有两个点O(0,0)、A(2,6),求弧OA 上点P 的坐标,使△AOP 的面积最大.解析 由题意知,使△AOP 面积最大,则点P 在与OA 平行且与曲线相切的直线的切点处. 因为k OA =3,所以过弧OA 上点P 且与OA 平行的直线的斜率k ′=k OA =3.所以k ′=y ′=3x 2-1=3.所以3x2=4.所以x=233或x=-233(舍去).所以x=233,y=239,即P⎝⎛⎭⎫233,239.15.已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12,和直线l:y=kx+9,又f′(-1)=0.(1)求a的值;(2)是否存在k的值,使直线l既是曲线y=f(x)的切线,又是曲线y=g(x)的切线?如果存在,求出k的值;如果不存在,请说明理由.解析(1)f′(x)=3ax2+6x-6a,f′(-1)=0,即3a-6-6a=0,∴a=-2.(2)∵直线l恒过定点(0,9),先求直线l是曲线y=g(x)的切线,设切点为(x0,3x02+6x0+12),∵g′(x0)=6x0+6,∴切线方程为y-(3x02+6x0+12)=(6x0+6)(x-x0),将点(0,9)代入,得x0=±1.当x0=-1时,切线方程为y=9;当x0=1时,切线方程为y=12x+9.由f′(x)=0得-6x2+6x+12=0,即有x=-1或x=2,当x=-1时,y=f(x)的切线方程为y=-18;当x=2时,y=f(x)的切线方程为y=9.∴公切线是y=9.又由f′(x)=12,得-6x2+6x+12=12.∴x=0或x=1.当x=0时,y=f(x)的切线方程为y=12x-11;当x=1时,y=f(x)的切线方程为y=12x-10.∴公切线不是y=12x+9.综上所述公切线是y=9,此时存在k=0.。
北师大版-数学-六年级上册-《圆的周长》同步精练

圆的周长一、选择填空1、车轮滚动一周,前进的距离是求车轮的()A.半径B.直径C.周长2、2、圆的周长是直径的()倍。
A. 3.14B. πC. 33、3、大圆的周长除以直径的商()小圆的周长除以直径的商。
A. 大于B. 小于C.等于4、圆周率π()3.14。
A.大于B.等于C.小于5、一个圆的周长是62.8M,它的半径是()。
A.3.14MB.10MC.20M6、一个圆的半径扩大为原来的4倍,它的周长就扩大为原来的()倍。
A.4B.6C.87、小圆的直径和大圆的半径都是6厘米,小圆的周长是大圆周长的()。
A.1/2B.1/4C.1/68、两根一样长的铁丝分别围成一个正方形和一个圆,这两个图形的周长相比,()。
A.圆的周长长B.正方形的周长长C.一样长9、一个圆的半径扩大2倍,那么它的周长扩大()。
A、2倍B、4倍C、6倍D、8倍10、下面各图形中,对称轴最多的是()。
A、正方形B、圆C、等腰三角形 D.梯形11、绕半径是2米的圆形花坛一周是所走的路程是()A.25.12米B. 12.56米C. 25.1米D.6.28米12、甲乙两只蚂蚁以同样的速度,同时从A点出发,甲蚂蚁沿着正方形走,乙蚂蚁沿着圆形走()先到起点。
A. 甲B. 乙C. 同时D.无法确定13、甲乙两人从A地到B地,分别选择⑴、⑵两条路线,所走过的路程是()A. ⑴条长B. ⑵条长C. ⑴⑵同样长D.由于它们半径长度不知道,无法比较 14、在长5厘米,宽3厘米的圆中,画两个最大的等圆,这两个圆的周长之和是( )厘米。
A.9.42B.18.84C. 7.85D. 15.715、把一个圆沿着直径剪成两半后,得到的半圆的周长( )。
A.是整圆周长的一半B.比圆周长多一个半径C. 比圆周长的21多两个半径 D.用c=2πr ,求出来的结果,就是半圆的周长 16、圆的周长是这个圆半径( ) 倍A.6B.2πC.3.14D.6.28 17、圆的半径增加2厘米,它的周长就增加了( )厘米。
高二数学(北师大版)选修3-1同步精练:第二章 3 数学符号 Word版含答案

数学符号练习1.下列符号中哪些不是欧拉发明的( )①函数符号y=f(x) ②自然对数的底e ③积分符号∫④根号⑤求和符号∑A.①② B.①②⑤ C.③④ D.④⑤2.请用文字叙述公式S球=4πR2.3.举例说明莱布尼茨在数学符号史上的贡献.4.试把我们常用的数学符号⊥、∧、∩、≠、≡、≤、≈、∶、√、÷、∪、∑、∈、∥、∝、×、π(圆周率)、∠、~、±、∫、≥、≌、∨、△、⊙、⌒按几何符号、代数符号、运算符号、集合符号、特殊符号进行分类.5.查找资料,了解三角函数符号的使用历史.参考答案1.答案:C2.答:先计算R的平方,然后与π的4倍相乘,所得结果即为球的表面积.3.答:莱布尼茨是数学史上最伟大的符号大师之一,他曾经说过:“要发明,就要挑选恰当的符号,用含义简明的少量符号来表达和比较忠实地描绘事物的内在本质,从而最大限度地减少人的思维劳动.”他用拉丁文Summa(求和)的第一个字母S的拉长——∫表示积分和用dy,dx表示微分,这些符号沿用至今,对微积分的发展起了很大的促进作用.莱布尼茨借助解析几何发现,“∫意味着和,d意味着差.”他用和与差的关系说明∫与d的互逆关系.这样,莱布尼茨明确地指出了积分和微分是互逆过程,这成为他具有微积分思想的标志.4.答:常用数学符号的分类如下:(1)几何符号:⊥、∥、∠、⌒、⊙、≡、≌、△(2)代数符号:∝、∧、∨、~、∫、≠、≤、≥、≈、∶(3)运算符号:×、÷、√、±(4)集合符号:∪、∩、∈(5)特殊符号:∑、π(圆周率)5.答:三角函数中有许多符号,其中sin,cos,tan,cot,sec,csc是最重要的符号,但是在这些符号使用以前,人们都是用文字来进行叙述的,这样使用起来非常麻烦.在实际应用中,人们渐渐地用符号来代替它们.正弦的符号开始记为sine,这一词是由阿拉伯人创造的,但是最早把它应用于三角函数上的是德国数学家雷基奥蒙坦,他是15世纪西欧数学界的领导人物,在他1464年著的《论一般三角形》一书中,首先使用了符号“sine”.这本书是专门讲三角学的,它脱离了天文学,成为一门独立的数学分支.余弦开始记为cosine,它是由英国人根日尔在1620年出版的《炮兵测量学》一书中首先创造并使用的.后来,人们在使用中发现这些符号比较长,而且写起来容易出错.1623年,阿贝尔特把“sine”“tangent”“secant”,简写为“sin”“tan”“sec”.到了1675年,英国人奥斯特又把“cosine”“cotangent”“cosecant”简写为“cos” “cot”“csc”,但是这些符号并没有通行开来,直到1748年,经过数学家欧拉的提倡,才得以普及.新中国成立后,我国的数学教材受到了苏联数学的影响,把“cot”改为“ctg”,“tan”改为“tg”,其余四个符号没有改动,这六个符号一直在三角函数中广泛应用,在现行的教材中,又把“ctg”改为原来的“cot”,“tg”改为原来的“tan”,使现用的三角函数符号与国际接轨,即为sin,cos,tan,cot,sec,csc.。
北师大版高中数学选修选修3-3同步全解

第一章球面的基本性质通过丰富的实际问题(如测量、航空、卫星定位),体会引入球面几何知识的必要性。
通过球面图形与平面图形的比较,感受球面几何与欧氏平面几何的异同。
例如,球面上的大圆相当于平面上的直线,球面上两点之间的最短距离是大圆弧的劣弧部分,球幂定理。
通过对实例的分析,体会球面具有类似平面的对称性质。
了解球面上的一些基本图形:大圆、小圆、球面角、球面二角形(月形)、极与赤道、球面三角形、球面三角形的极对称三角形(简称球极三角形)。
1 直线,平面与球面的位置关系1.我们生活在地球上,地球表面十分接近于一个球面。
因此,在实际生活中,球面上的几何(简称球面几何)知识有着广泛的实际应用。
例如,大地(天体)测量、航空、卫星定位等方面均需利用球面几何的知识。
在理论上,球面几何是一个与欧氏平面几何不同的几何模型,是一个重要非欧几何的数学模型,球面几何在几何学的理论研究方面,具有特殊的作用。
2.球面所围成的几何体叫做球体,简称球。
半圆的圆心叫做球心。
连结球心和球面上任意一点的线段叫做球的半径。
连结球面上两点并且经过球心的线段叫做球的直径。
用一个平面去截一个球,截面是圆面。
球的截面有以下性质:(1)球心和截面圆心的连线垂直于截面。
(2)球心到截面的距离d与球的半径R及截面的半径r有下面的关系:r^2=R ^2-d^2球面被经过球心的平面截得的圆叫做大圆,被不经过球心的截面截得的圆叫做小圆。
在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离。
半径是R的球的体积计算公式是:V=(4/3)πR^3(三分之四乘以π乘以R的三次方)。
半径是R的球的表面积计算公式是:S=4πR^2(4倍的π乘以R的二次方)3.球面空间中与一定点的距离为定值的动点的轨迹。
定点称为球心,定距离称为半径。
球面也可以看成是由半圆绕着它的直径旋转一周所形成的曲面。
球面所包围的立体称为球体,简称球。
高二数学北师大版选修1-1同步精练3.3计算导数 Word版含答案
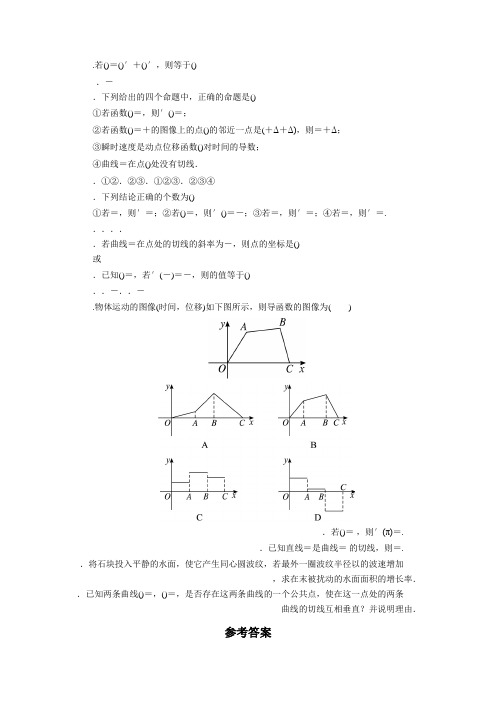
.若()=()′+()′,则等于().-.下列给出的四个命题中,正确的命题是()①若函数()=,则′()=;②若函数()=+的图像上的点()的邻近一点是(+Δ+Δ),则=+Δ;③瞬时速度是动点位移函数()对时间的导数;④曲线=在点()处没有切线..①②.②③.①②③.②③④.下列结论正确的个数为()①若=,则′=;②若()=,则′()=-;③若=,则′=;④若=,则′=......若曲线=在点处的切线的斜率为-,则点的坐标是()或.已知()=,若′(-)=-,则的值等于()..-..-.物体运动的图像(时间,位移)如下图所示,则导函数的图像为( ).若()=,则′(π)=..已知直线=是曲线=的切线,则=..将石块投入平静的水面,使它产生同心圆波纹,若最外一圈波纹半径以的波速增加,求在末被扰动的水面面积的增长率..已知两条曲线()=,()=,是否存在这两条曲线的一个公共点,使在这一点处的两条曲线的切线互相垂直?并说明理由.参考答案.解析:∵()=()′+()′=-,∴=-=-=-.答案:.解析:①中′()=()′=,当=时无意义;④中′=()′=,′()=,有切线.答案:.解析:在①中,()′=,②③④都对.答案:.答案:.解析:由()=,可得′()=-,∴′(-)=(-)-=-,∴=.答案:.答案:.解析:∵()=,∴′()= .∴′(π)=π=.答案:.解析:′=( )′=,则=.∴=.∴=×=.∴曲线=过点,即= .∴=.答案:.解:设被扰动水面面积为,时间为(≥),∴=π=π()=π,∴′=(π)′=π,∴当=时,水面面积的增长率为π..解:假设存在公共点(,).所以两条曲线在(,)处的斜率分别为=′()=,=′()=-.因为两条曲线的切线互相垂直,所以·=-,即-·=-.所以=.因为∈[-],所以假设不成立.故不存在这两条曲线的一个公共点,使在这一点处的两条曲线的切线互相垂直.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆周率练习
1.关于圆周率的最早记录出自( )
A.《周髀算经》B.《九章算术》
C.莱茵德草卷D.《几何原本》
2.世界上第一个把π计算到3.141 592 6<π<3.141 592 7的数学家是( ) A.刘徽B.阿基米德
C.祖冲之D.卡瓦列利
3.最早用穷竭法研究圆周率的数学家是( )
A.阿基米德B.安提丰
C.刘徽D.布里松
4.证明π是无理数的数学家是( )
A.高斯B.阿基米德
C.兰伯特D.林德曼
5.圆周率的计算是我国古代数学史上的伟大的成就之一,很久以前我们的祖先就发现圆的周长和直径之比是一个定数,这个定数被命名为圆周率.那么圆周率在不断地精确过程中有哪些突出的成就呢?
6.查找资料,了解阿基米德与穷竭法.
7. 如图所示,已知直线y=2x+3与抛物线y=x2交于A,B两点,试用阿基米德穷竭法求抛物弓形AOB的面积.
参考答案
1.答案:C
2.答案:C
3.答案:B
4.答案:C
5.答:①《周髀算经》,采用的圆周率是“周三径一”,即π=3;②魏晋时期刘徽创立割圆术,为计算圆周率建立了严密理论和算法,求出π≈3.141 6,采用了极限思维,是近代微积分思想的萌芽;③祖冲之求出的圆周率,在3.141 592 6和3.141 592 7之间,并且确立两个分数形式的近似值:约率和密率,祖冲之的成果在世界上一直领先了1 000年.
6.答:在古希腊,利用穷竭法作出重要贡献的是阿基米德,阿基米德(Archime d es ,公元前287—前212)出生于意大利西西里岛的叙拉古,是古希腊最杰出的数学家、力学家,他的几何著作成为古希腊数学的顶峰,他的数学著作主要有《圆的度量》《论球与圆柱》《抛物线求积法》《论螺线》等.在这些著作中,阿基米德巧妙地将穷竭法与原子论观点结合起来,通过严密的计算,获得了许多重要的结果,例如他在《抛物线求积法》一书中,使用穷竭法求出了抛物线弓形的面积,他的方法简述如下:作三角形ABC ,设其面积为S 1,其中l 1∥AC ,B 是切点,再作抛物线的切线l 2和l 3使之分别平行于AB 和BC ,切点分别是D 和E ,再作三角形ADB 和三角形BEC (如图),设两个三角形面积之和为S 2,用A 1表示S 1,A 2表示S 1+S 2,那么用完全同样的方法可以得到A n =S 1+S 2+…+S n .
很明显,只要取n 足够大,弓形面积S 与A n 的差S -A n 就可以任意小.
由抛物线的性质可知S 1=4S 2,
∴A n =S 1+
1111121141444334
n n S S S S S --++⋅⋅⋅+=-⋅. 最后,阿基米德用反证法证明了S =143S . 特别要提到的是,阿基米德在计算以他的名字命名的曲线——阿基米德螺线第一周围成的区域的面积时,使用了类似于现代积分学中的大和、小和的概念.他的用法,用今天的符号表示就是:将2π n 等分,在每一部分上作出顶角2n
π的内接圆扇形和外接圆扇形(如下图),它们的面积之和,分别用A n 与S n 表示,显然所求之面积S 满足不等式A n <S <S n ,
经过计算A n =324111132a n n π⎛⎫⎛⎫-- ⎪⎪⎝
⎭⎝⎭
, S n =324111132a n n π⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭,
于是,对任意的n ,有A n <3243a π<S n .
阿基米德经过猜测,并使用反证法进行了证明,得出螺线第一周所围成的面积S =3243
a π. 阿基米德突破了传统的有限运算,大胆地采用了无限逼近的思想,从而将穷竭法发展到了高峰,但是由于当时没有极限概念,不承认无限,因此,穷竭法仍是有限的形式,并且局限在几何直观上,运算也很烦琐,所以自阿基米德之后,很长时间没有被人重视.尽管这种方法有很大的缺点,但是,他的求积方法已具有了定积分思想的萌芽.
7. 分析:可以求出弦AB 的中点C ,过C 作y 轴的平行线交抛物线与点D ,这样抛物弓形AOB 的面积是△ABD 面积的43
,因此我们只要求△ABD 的面积即可.
解:设A ,B 两点的坐标为A(x 1,y 1),B(x 2,y 2), 则有2,23,
y x y x ⎧=⎨=+⎩
解得1212
1,3,1,9.x x y y =-=⎧⎧⎨⎨==⎩⎩ ∴A (-1,1),B (3,9),中点C (1,5).
过中点C(1,5)作y 轴的平行线交抛物线于D(1,1),再求△ABD 的面积.
=
点D 到直线AB 的距离为d
==. ∴S △ABD =12
|AB |·
d
=125⨯=8. ∴抛物弓形AOB 的面积为S =43S △ABD =432833
⨯=.。
