习题答案1-7

合集下载

电子测量技术基础课后习题答案上1,2,5,6,7,8

习题一1.1 解释名词：①测量；②电子测量。

答：测量是为确定被测对象的量值而进行的实验过程。

在这个过程中，人们借助专门的设备，把被测量与标准的同类单位量进行比较，从而确定被测量与单位量之间的数值关系，最后用数值和单位共同表示测量结果。

从广义上说，凡是利用电子技术进行的测量都可以说是电子测量；从狭义上说，电子测量是指在电子学中测量有关电的量值的测量。

1.2 叙述直接测量、间接测量、组合测量的特点，并各举一两个测量实例。

答：直接测量：它是指直接从测量仪表的读数获取被测量量值的方法。

如：用电压表测量电阻两端的电压，用电流表测量电阻中的电流。

间接测量：利用直接测量的量与被测量之间的函数关系，间接得到被测量量值的测量方法。

如：用伏安法测量电阻消耗的直流功率P，可以通过直接测量电压U，电流I，而后根据函数关系P＝UI，经过计算，间接获得电阻消耗的功耗P；用伏安法测量电阻。

组合测量：当某项测量结果需用多个参数表达时，可通过改变测试条件进行多次测量，根据测量量与参数间的函数关系列出方程组并求解，进而得到未知量，这种测量方法称为组合测量。

例如，电阻器电阻温度系数的测量。

1.3 解释偏差式、零位式和微差式测量法的含义，并列举测量实例。

答：偏差式测量法：在测量过程中，用仪器仪表指针的位移(偏差)表示被测量大小的测量方法，称为偏差式测量法。

例如使用万用表测量电压、电流等。

零位式测量法：测量时用被测量与标准量相比较，用零示器指示被测量与标准量相等(平衡)，从而获得被测量从而获得被测量。

如利用惠斯登电桥测量电阻。

微差式测量法：通过测量待测量与基准量之差来得到待测量量值。

如用微差法测量直流稳压源的稳定度。

1.4 叙述电子测量的主要内容。

答：电子测量内容包括：（1）电能量的测量如：电压，电流电功率等；（2）电信号的特性的测量如：信号的波形和失真度，频率，相位，调制度等；（3）元件和电路参数的测量如：电阻，电容，电感，阻抗，品质因数，电子器件的参数等：（4）电子电路性能的测量如：放大倍数，衰减量，灵敏度，噪声指数，幅频特性，相频特性曲线等。

高等数学-习题答案 -第一章

习题 1-11．求下列函数的自然定义域：（1）211y x =+- 解：依题意有21020x x ⎧-≠⎨+≥⎩，则函数定义域{}()|2x 1D x x x =≥-≠±且．（2）21arccosx y -= 解：依题意有2211360x x x ⎧-≤⎪⎨⎪-->⎩，则函数定义域()D x =∅．（3）2ln(32)y x x =-+-；解：依题意有2320x x -+->，则函数定义域{}()|12D x x x =<<．（4）312x xy -=；解：依题意有30x x -≠，则函数定义域{}()|x 0,1D x x x =-∞<<+∞≠±且．（5）1sin1,121;x y x x ⎧≠⎪=-⎨⎪=⎩, ，解：依题意有定义域{}()|D x x x =-∞<<+∞．（6）1arctan y x =+解：依题意有030x x ≠⎧⎨-≥⎩，则函数定义域{}()|3x 0D x x x =≤≠且．2．已知()f x 定义域为[0,1]，求2(), (sin ), (), ()()f x f x f x a f x a f x a +++-(0a >)的定义域．解：因为()f x 定义域为[0,1]，所以当201x ≤≤时，得函数2()f x 的定义域为[1,1]-；当0sin 1x ≤≤时，得函数(sin )f x 定义域为[2π,(21)π]k k +；当01x a ≤+≤时，得函数()f x a +定义域为[,1]a a --+；当0101x a x a ≤+≤⎧⎨≤-≤⎩时，得函数()()f x a f x a ++-定义域为：（1）若12a <，[],1x a a ∈-；（2）若12a =，12x =；（3）若12a >，x ∈∅．3．设21()1,f x x ⎛⎫= ⎝其中0,a >求函数值(2),(1)f a f ．解：因为21()1f x x ⎛⎫= ⎝，则 2211(2)142a f a a a a -⎛⎫=-= ⎪⎝⎭，20 ,>1,11(1)1 2 ,0<<111a a f a a ⎛⎫⎧-=-= ⎪⎨ ⎪-⎩⎝⎭．4．设1||1,()0||1,()21|| 1.x x f x x g x x <⎧⎪===⎨⎪->⎩，求(())f g x 与(())g f x ，并做出函数图形．解：121(())0211 21x x xf g x ⎧<⎪==⎨⎪->⎩，即10(())001 0x f g x x x <⎧⎪==⎨⎪->⎩，1012||1(())2||12||1x g f x x x -⎧<⎪==⎨⎪>⎩，即2||1(())1||11 ||12x g f x x x ⎧⎪<⎪==⎨⎪⎪>⎩，函数图形略．5．设1,0,()1,0,x x f x x +<⎧=⎨≥⎩试证：2,1,[()]1, 1.x x f f x x +<-⎧=⎨≥-⎩证明：1(),()0[()]1,()0f x f x f f x f x +<⎧=⎨≥⎩，即2,1,[()]1,1x x f f x x +<-⎧=⎨≥-⎩，得证． 6．下列各组函数中，()f x 与()g x 是否是同一函数？为什么？（1）))()ln,()ln3f x x g x ==- ；不是，因为定义域和对应法则都不相同．（2）()()f x g x ==；是．（3）22()2,()sec tan f x g x x x ==-；不是，因为对应法则不同．（4）2()2lg ,()lg f x x g x x ==；不是，因为定义域不同．7．确定下列函数在给定区间内的单调性：（1）3ln y x x =+，(0,)x ∈+∞；解：当(0,)x ∈+∞时，函数13y x =单调递增，2ln y x =也是单调递增，则12y y y =+在(0,)+∞内也是递增的．（2）1xy x-=-，(,1)x ∈-∞．解：(1)111111x x y x x x ---===+---，当(,1)x ∈-∞时，函数11y x =-单调递增，则21111y y x ==-是单调递减的，故原函数1xy x-=-是单调递减的． 8. 判定下列函数的奇偶性．（1）lg(y x =+；解：因为1()lg(lg(lg(()f x x x x f x --=-+==-+=-，所以lg(y x =+是奇函数．（2）0y =；解：因为()0()f x f x -==，所以0y =是偶函数．（3）22cos sin 1y x x x =++-；解：因为2()2cos sin 1f x x x x -=+--，()()()()f x f x f x f x -≠-≠-且，所以22cos sin 1y x x x =++-既非奇函数，又非偶函数．（4）2x xa a y -+=.解：因为()()2x x a a f x f x -+==，所以函数2x xa a y -+=是偶函数． 9．设()f x 是定义在[,]l l -上的任意函数，证明：（1）()()f x f x +-是偶函数，()()f x f x --是奇函数；（2）()f x 可表示成偶函数与奇函数之和的形式. 证明：（1）令()()(),()()()g x f x f x h x f x f x =+-=--，则()()()(),()()()()g x f x f x g x h x f x f x h x -=-+=-=--=-，所以()()f x f x +-是偶函数，()()f x f x --是奇函数．（2）任意函数()()()()()22f x f x f x f x f x +---=+，由（1）可知()()2f x f x +-是偶函数，()()2f x f x --是奇函数，所以命题得证． 10．证明：函数在区间I 上有界的充分与必要条件是：函数在I 上既有上界又有下界.证明：（必要性）若函数()f x 在区间I 上有界，则存在正数M ，使得x I ∈，都有()f x M ≤成立，显然()M f x M -≤≤，即证得函数()f x 在区间I 上既有上界又有下界（充分性）设函数()f x 在区间I 上既有上界2M ，又有下界1M ，即有12()()f x M f x M ≥≤且，取12max{,}M M M =，则有()f x M ≤，即函数()f x 在区间I 上有界．11．下列函数是否是周期函数？对于周期函数指出其周期：（1）|sin |y x =；周期函数，周期为π．（2）1sin πy x =+；周期函数，周期为2．（3）tan y x x =；不是周期函数．（4）2cos y x =.周期函数，周期为π．12．求下列函数的反函数：（1）331xx y =-；解：依题意，31x y y =-，则3log 1yx y =-，所以反函数为13()log ,(,0)(1,)1xf x x x -=∈-∞⋃+∞-．（2）()ax by ad bc cx d+=≠+；解：依题意，b dy x cy a -=-，则反函数1()()b dxf x ad bc cx a--=≠-．（3）(lg y x =+；解：依题意，1(1010)2y y x -=+，所以反函数11()(1010),2x x f x x R --=+∈．（4）ππ3cos 2,44y x x ⎛⎫=-≤≤ ⎪⎝⎭．解：依题意，arccos 32y x =，所以反函数1arccos3(),[0,3]2x f x x -=∈． 13．在下列各题中，求由所给函数构成的复合函数，并求这函数分别对应于给定自变量值1x 和2x 的函数值：（1）212e ,1,0,2u y u x x x ====＋；（2）2121,e 1,1,1,1v y u u v x x x =+=-=+==-．解：（1）215()e ,(0),(2)x y f x f e f e +====（2）12()(e 1)1x y f x +==-+，42(0)22f e e =-+，(1)1f -=．14．在一圆柱形容器内倒进某种溶液，该容器的底半径为r ，高为H ．当倒进溶液后液面的高度为h 时，溶液的体积为V ．试把h 表示为V 的函数，并指出其定义区间．解：依题意有2πV r h =，则22,[0,π]πV h V r H r =∈．解：依题意有0.64,0 4.5() 4.50.64( 4.5) 3.2, 4.5x x f x x x ≤≤⎧=⎨⨯+-⨯>⎩，所以(3.5) 2.24(4.5) 2.88(5.5) 6.08f f f ===元，元，元．习题 1-21．设21(1,2,3,)31n n a n n +==+，（1）求110100222||,||,||333a a a ---的值；（2）求N ，使当n N >时，不等式42||103n a --<成立；（3）求N ，使当n N >时，不等式2||3n a ε-<成立．解：(1) 12321||||,34312a -=-= 1022121||||,331393a -=-=100220121||||33013903a -=-=．（2）要使 42||10,3n a --< 即 4113310<（n+1），则只要9997,9n > 取N＝99971110,9⎡⎤=⎢⎥⎣⎦故当n>1110时，不等式42||103n a --<成立．（3）要使2||3n a ε-<成立，13,9n εε-> 取139N εε-⎡⎤=⎢⎥⎣⎦，那么当n N >时， 2||3n a ε-<成立.2．根据数列极限的定义证明：（1）1lim 0!n n →∞=；（2）1n →∞=．解：（1）0ε∀>，要使111|0|!!n n n ε-<<＝，只要取1N ε⎡⎤=⎢⎥⎣⎦，所以，对任意0ε>，存在1N ε⎡⎤=⎢⎥⎣⎦，当n N >时，总有1|0|!n ε-<，则1lim 0!n n →∞=.(2) 0ε∀>,要使221|2n ε-=<<, 即n >,只要取N =,所以,对任意的ε>0,存在N =, 当n N >, 总有1|ε-<,则1n →∞=. 3．若lim n n x a →∞=，证明lim ||||n n x a →∞=．并举例说明：如果数列}{||n x 有极限，但数列}{n x 未必有极限．证明: 因为lim n n x a →∞=, 所以0ε∀>, 1N ∃, 当1n N >时, 有||n x a ε-<.不妨假设a>0, 由收敛数列的保号性可知:2N ∃, 当2n N >时, 有0n x >, 取{}12max ,N N N =, 则对0ε∀>, N ∃, 当n N >时, 有||||||||n n x a x a ε-=-<.故lim ||||n n x a →∞=. 同理可证0a <时, lim ||||n n x a →∞=成立.反之,如果数列{}||n x 有极限, 但数列{}||n x 未必有极限.如：数列()1nn x =-,||1n x =，显然lim ||1n n x →∞=, 但lim n n x →∞不存在．4．设数列{}n x 有界，又lim 0n n y →∞=．证明：lim 0n n n x y →∞=．证明: 依题意,存在M>0, 对一切n 都有||n x M ≤，又lim 0n n y →∞=, 对0ε∀>,存在N ,当n N >时, |0|n y ε-<, 因为对上述N , 当n N >时, |0|||||n n n n n x y x y M y M ε-=≤<,由ε的任意性, 则lim 0n n n x y →∞=．5．设数列{}n x 的一般项(3)π2n n x +=，求lim n n x →∞．解: 因为0x =, (3)π|cos |12n +≤, 所以 (3)π02x n +=. 6．对于数列{}n x ，若21()k x A k -→→∞，2()k x A k →→∞，证明：()n x A n →→∞．证明: 由于21lim k k x A -→∞=, 所以, 0ε∀>, 10N ∃>, 当1>k N 时，有21||k x A ε--<,同理, 0ε∀>,20N ∃>, 当2k N >时, 有2||k x A ε-<．取N =max {}12,N N , 0ε∀>, 当n N >时, ||n x A ε-<成立, 故()n x A n →→∞．习题 1-31．当1x →时，234y x =+→．问δ等于多少，使当|1|x δ-<时，|4|0.01y -<？解：令 1|1|2x -<，则35|1|22x <+<，要使225|4||34||1||1||1||1|0.012y x x x x x -=+-=-=-+<-<，只要|1|0.004x -<，所以取0.004δ=，使当 |1|x δ-< 时，|4|0.01y -<成立．2．当x →∞时，222123x y x +=→-．问X 等于多少，使当||x X >时，|2|0.001y -<？解：要使222217|2||2|3|3|x y x x +-=-=--2|3|7000x ->, 即237000x ->. 因此,只要||x >,所以取X ≥3．根据函数极限的定义证明：（1）3lim(21)5x x →-=；（2）35lim31x x x →∞+=-；（3）224lim 42x x x →--=-+；（4）lim0x =. 证明:(1) 由于|(21)5|2|3|x x --=-, 任给0ε>,要使|(21)5|x ε--<,只要|3|2x ε-<．因此取2εδ=,则当0|3|x δ<-<时, 总有|(21)5|x ε--<,故3lim(21)5x x →-=．(2) 由于358|3|1|1|x x x +-=--,任给0ε>, 要使35|3|1x x ε+-<-,只要8|1|x ε<-,即81x ε>+或81x ε<-, 因为0ε>,所以88|1||1|εε+>-, 取8|1|M ε=+，则当||x M >时,对0ε∀>,总有35|3|1x x ε+-<-,故有35lim 31x x x →∞+=-．(3)由于24|(4)||2|2x x x ---=++,任给0ε>,,要使24|(4)|2x x ε---<+,只要|2|x ε+<,因此取δε=,则当0|(2)|x δ<--<时,总有24|(4)|2x x ε---<+,故224lim 42x x x →--=-+. (4) 由于0|-<,任给0ε>,要使|0|ε<,ε<,即21x ε>,因此取21M ε=,则当x>M 时,总有0|ε-<,故lim 0x =. 4．用X ε-或εδ-语言，写出下列各函数极限的定义：（1）lim ()1x f x →-∞=；（2）lim ()x f x a →∞=；（3）lim ()x a f x b +→=；（4）3lim ()8x f x -→=-．解: (1) 0,ε∀> 0M ∃>, 当x<-M 时, 总有|()1|f x ε-<;(2) 0,ε∀> 0M ∃>, 当||x M >, 总有|()|f x a ε-<;(3) 0,ε∀> 0δ∃>, 当a x a δ<<+时, 总有|()|f x b ε-<; (4) 0,ε∀> 0δ∃> 当33x δ-<<时, 总有|()8|f x ε+<． 5．证明:0lim ||0x x →=.证明: 由于00lim ||lim 0x x x x ++→→==, 00lim ||lim()0x x x x --→→=-=,所以0lim ||0x x →=.6．证明：若x →+∞及x →-∞时，函数()f x 的极限都存在且都等于A ，则lim ()x f x A →∞=．证明: 由于lim ()x f x A →+∞=,则对0ε∀>,10M ∃>,当1x M >时,有|()|f x A ε-<．又lim ()x f x A →-∞=,则20M ∃>,当2x M <-,有|()|f x A ε-<.取{}12max ,M M M =那么对0ε∀>,当||x M >时,总有|()|f x A ε-<,故有lim ()x f x A →∞=.习题 1-41．根据定义证明：（1）211x y x -=+为当1x →时的无穷小；（2）1sin y x x =为当x →∞时的无穷小；（3）13xy x+=为当0x →时的无穷大．证明:(1) 0ε∀>,因为21|0||1|1x x x --=-+,取δε=,则当0|1|x δ<-<时, 总有0x ≠,故211lim 01x x x →-=+． (2) 0ε∀>,因为111|sin 0||sin |||||x x x x x -=≤,取1M ε=, 则当||x M >时, 总有1|sin |1|sin 0|||||x x x x x ε-=≤<, 故1lim sin 0x x x →∞=.(3) 0M ∀>, 13M δ∃=+,当0||x δ<<时,总有1311|||3|3||x M x x x +=+>->,所以013lim x x x→+=∞. 2．函数sin y x x =在(0,)+∞内是否有界？该函数是否为x →+∞时的无穷大？解答: 取2πn x n =,则0n y =,因此当2πn x n =()n →∞时, ()0n n y x →→+∞故函数sin y x x = 当x →+∞时,不是无穷大量．下证该函数在()0,+∞内是无界的. 0M ∀>,π2π2n x n ∃=+ 且()n x n →+∞→∞,πππ2πsin 2π2π222n y n n n ⎛⎫⎛⎫=++=+ ⎪ ⎪⎝⎭⎝⎭，取[]01N M =+, 00π2π(0,)2x N ∃=+∈+∞,有0π2π2n y N M =+≥，所以sin y x x =是无界的.3．证明：函数11cos y x x=在区间(0,1]上无界，但这函数不是0x +→时的无穷大．证明: 令1t x=,类似第2题可得．习题 1-51．求下列极限：（1）23231lim 41n n n n n →∞+++-；（2）111lim 1223(1)n n n →∞⎡⎤+++⎢⎥⋅⋅+⎣⎦；（3）22212lim n n n n n →∞⎛⎫+++ ⎪⎝⎭；（4）1132lim 32n nn n n ++→∞+-；（5）2211lim 54x x x x →--+；（6）3221lim 53x x x x →+-+；（7）limx →+∞；（8）2221lim 53x x x x →∞+++；（9）330()lim h x h x h→+-；（10）22131lim 41x x x x →+-+；（11）3131lim 11x x x →⎛⎫- ⎪--⎝⎭；（12）23lim 531x x xx x →∞+-+；（13）x →（14）3lim 21x x x →∞+；（15）3lim(236)x x x →∞-+；（16）323327lim 3x x x x x →+++-．解:(1) 23231lim 41n n n n n →∞+++- = 233311lim 0411n n n n n n→∞++=+-． (2) 111lim 1223(1)n n n →∞⎡⎤+++⎢⎥⋅⋅+⎣⎦= 111111lim ()()()12231n n n →∞⎡⎤-+-++-⎢⎥+⎣⎦= 1lim(1)11n n →∞-=+． (3) 22212lim n n n n n →∞⎛⎫+++ ⎪⎝⎭=21(1)12lim 2n n n n →∞+=． (4) 1132lim 32n nn n n ++→∞+-=21()13lim 2332()3n n n →∞+=-⋅．(5) 2211lim 54x x x x →--+=1(1)(1)lim (1)(4)x x x x x →-+--=112lim 43x x x →+=--． (6) 3221lim 53xx x x →+-+=322132523+=--⨯+．(7) limx →+∞=limx=limx =111lim 2x -=． (8) 2221lim53x x x x →∞+++=2212lim 2531x x x x→∞+=++． (9) 330()lim h x h x h →+-=322330(33)lim h x x h xh h x h→+++-=3220lim(33)3h x xh h x →++=．(10) 3131lim 11x x x →⎛⎫- ⎪--⎝⎭=2313(1)lim 1x x x x →⎛⎫-++ ⎪-⎝⎭=21(1)(2)lim (1)(1)x x x x x x →-+-++ =212lim11x xx x →+=++．(11) 23lim 531x x x x x →∞+-+=22311lim 0315x x x x x→∞+=-+．(12) x →=x →=x →(13) 3lim 21x x x →∞+=2lim12x x x→∞=+∞+． (14) 3lim(236)x x x →∞-+=32336lim (2)x x x x→∞-+=∞．(15) 323327lim 3x x x x x →+++-=32331lim(327)lim 3x x x x x x →→+++⨯=∞-．2．设,0,()2,0.x e x f x x a x ⎧<=⎨+≥⎩问当a 为何值时，极限0lim ()x f x →存在．解：因为0000lim ()lim 1,lim ()lim(2)x x x x x f x e f x x a a --++→→→→===+=，所以，当00lim ()lim ()x x f x f x -+→→=，即1a =时，0lim ()x f x →存在． 3．求当x 1→时，函数12111x x e x ---的极限．解：因为11211111lim lim(1)0,1x x x x x e x e x ----→→-=+=-所以12111lim 1x x x e x -→--不存在。

管理会计学课后习题与答案7

管理会计学课后习题与答案7一、单选题1、在日常实施成本全面控制的同时，应有选择地分配人力、物力和财力，抓住那些重要的、不正常的、不符合常规的关键'性成本差异作为控制重点，该项成本控制原则是指（）A.例外管理原则B.全面控制原则C.讲求效益原则D.责权利相结合原则正确答案：A2、在下列各项中，属于标准成本控制系统前提和关键的是（）A. 成本差异的计算B.标准成本的制定C.成本差异的账务处理D.成本差异的分析正确答案：B3、下列关于制定正常标准成本的表述中，正确的是（）A.直接人工标准工时包括直接加工操作必不可少的时间，不包括各种原因引起的停工工时B.直接人工的价格标准是指标准工资率，它可以是预定的工资率，也可以是正常的工资率C.直接材料的价格标准不包括购进材料发生的检验成本D.固定制造费用和变动制造费用的用量标准可以相同，也可以不同。

例如，以直接人工工时作为变动制造费用的用量标准，同时以机器工时作为固定制造费用的用量标准正确答案：B4、以资源无浪费、设备无故障、产出无废品、工时都有效的假设前提为依据而制定的标准成本是（）A.正常标准成本B.现行标准成本C.理想标准成本D.基本标准成本正确答案：C5、与预算成本不同，标准成本是一种（）A.历史成本B.单位成本的概念C.实际成本D.总额的概念正确答案：B6、下列情况中，需要对基本标准成本进行修订的是（）A.重要的原材料价格发生重大变化B.工作方法改变引起的效率变化C.生产经营能力利用程度的变化D.市场供求变化导致的售价变化正确答案：A7、下列各项中，属于“直接人工标准工时”组成内容的是（）A.由于外部供电系统故障产生的停工工时B.由于设备意外故障产生的停工工时C.由于生产作业计划安排不当产生的停工工时D.由于更换产品产生的设备调整工时正确答案：D8、基本标准成本，在发生（）变化时，就需要进行调整A.由于工作方法改变而引起的效率变化B.产品的物理结构变化C.市场供求变化导致的售价变化D.市场供求变化导致的生产经营能力利用程度正确答案：B9、在标准成本控制系统中，成本差异是指在一定时期内生产一定数量的产品所发生的（）A.预算成本与实际成本之差B.预算成本与标准成本之差C.实际成本与计划成本之差D.实际成本与标准成本之差正确答案：D10、实际固定性制造费用脱离预算而形成的差异称为（）A.效率差异B.生产能力利用差异C.能量差异D.预算差异正确答案：D11、通常应对不利的材料价格差异负责的部门是( )A.质量控制部门B.采购部门C.生产部门D.工程设计部门正确答案：B12、期末标准成本差异的下列处理中，错误的是（）A.本期差异按比例分配给已销产品成本和存货成本B.结转成本差异的时间可以是月末，也可以是年末C.本期差异按比例分配给期末产成品成本和期末在产品成本D.本期差异全部按本期损益负担正确答案：C13、计算价格差异的公式是（）A.实际数量×（实际价格—标准价格）B.标准数量×（实际价格—标准价格）C.标准价格×（实际数量—标准数量）D.实际价格×（实际数量—标准数量）正确答案：A14、固定制造费用的能量差异，可以进一步分解成（）A.以上任何两种差异B.闲置能量差异和效率差异C.闲置能量差异和耗费差异D.耗费差异和效率差异正确答案：B15、本月生产甲产品1 000件，实际耗费A材料2 000千克，其实际价格为每千克20元。

物理学简明教程马文蔚第1至7章课后习题答案详细讲解

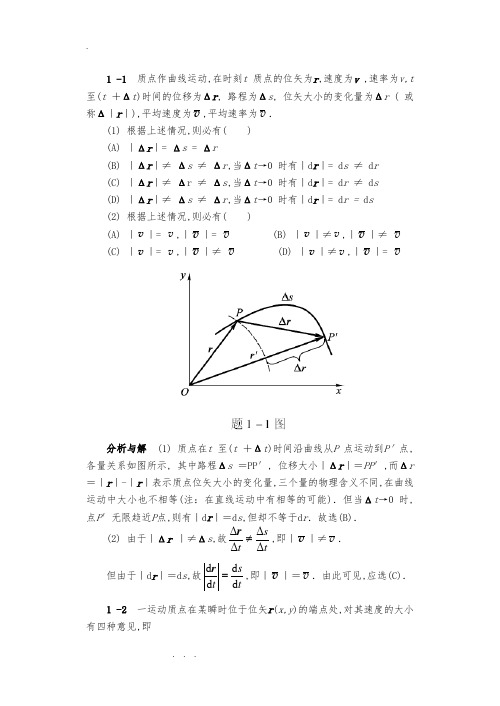
1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v,t 至(t ＋Δt )时间的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ｜r ｜),平均速度为v ,平均速率为v ． (1) 根据上述情况,则必有( )(A) ｜Δr ｜= Δs = Δr(B) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d s ≠ d r(C) ｜Δr ｜≠ Δr ≠ Δs ,当Δt →0 时有｜d r ｜= d r ≠ d s(D) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d r = d s (2) 根据上述情况,则必有( )(A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠v ,｜v ｜≠ v(C) ｜v ｜= v ,｜v ｜≠ v (D) ｜v ｜≠v ,｜v ｜= v分析与解 (1) 质点在t 至(t ＋Δt )时间沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs ＝PP′, 位移大小｜Δr ｜＝PP ′,而Δr ＝｜r ｜-｜r ｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt →0 时,点P ′无限趋近P 点,则有｜d r ｜＝d s ,但却不等于d r ．故选(B)．(2) 由于｜Δr ｜≠Δs ,故ts t ΔΔΔΔ≠r ,即｜v ｜≠v ．但由于｜d r ｜＝d s ,故ts t d d d d =r ,即｜v ｜＝v ．由此可见,应选(C)． 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ； (2)t d d r ； (3)t s d d ； (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x ．下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；td d r 表示速度矢量；在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解．故选(D)． 1 -3 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解加速度的切向分量a ｔ起改变速度大小的作用,而法向分量a n 起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于a ｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时, a ｔ恒为零；质点作匀变速率圆周运动时, a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．1 -4 质点的运动方程为23010t t x +-=和22015t t y -=，式中x ,y 的单位为m,t 的单位为ｓ。

有机化学汪小兰 1-7习题难点讲解

417溴苯氯代后分离得到两个分子式为cclbr的异构体a和b将a溴代得到几种分子式为c的产物而b经溴代得到两种分子式为c的产物c和da溴代后所得产物之一与c相同但没有任何一个与d相同
有机化学1-7章习题难点及易错讲解
1.1 扼要归纳典型的以离子键形成的化合物与以共价键形成的化合物的物理性质。
答案：
正庚烷
Br2 / CCl4
1,4－庚二烯
褪色无反应
1,4－庚二烯正庚烷
b. 2－甲基戊烷
灰白色 1－己炔
2－己炔
Ag(NH3)2+
褪色
2－己炔
1－己炔
无反应
2－甲基戊烷 Br2 / CCl4
2－己炔
无反应
2－甲基戊烷
3.21. 完成下列反应式
Cl
a.
HCl (过量) CH3CH2CH2C CH
C2H5
b. CH2=C(Cl)CH3
c. C2H5CH=CHCH2I
d. CH3CH=CHCH(CH3)2
e. CH3CH=CHCH=CH2 f. CH3CH=CHCH=CHC 2H5
答案： c , d , e ,f 有顺反异构
c. C2H5
C
H
CH2I
C H
H
CH2I d.
CC
C2H5
H
( Z )－1－碘－2－戊烯 ( E )－1－碘－2－戊烯
CH3 + C CH
CH3
CH3
CH3
>+ H3C C CH2 CH2 CH3
3.15. 写出下列反应的转化过程：
H3C
CH3
C=CHCH2CH2CH2CH=C
H+

电路与电子技术基础第1章习题参考答案

《电路与电子技术基础》习题一参考解答
第4页
U3+U9=11(V) 根据后 3 个方程无法求出其余的 3 个电压，并且在后 3 个方程中有两个方程是相同的，因此只有两个独立方程，用两个方程解出 3 个未知量有无穷解。 1-11 电路如题图 1-3 所示，采用关联得参考方向，且已知下列各支路电流：I1=2A， I4=5A，I7=–5A 以及 I10=–3A。其他各支路电流是否都能确定？试尽可能多地确定各未知电流。解：各支路电流采用关联参考方向，因此不在图中标出电流方向。除已知电流之外，还需求解 6 个未知电流。在图中标出节点 a、b、c、d、e、f。对 f 节点 –I9–I10–I4=0 代入数据得 I9=-2(A) 对 a 节点 I1+I5+I7=0 代入数据得 I5=3(A) 对其余的 4 个节点列出节点方程，必然有一个方程不独立，即 3 个独立方程要解出 4 个未知量，其有无穷多解。 1-12 220V、40W 的灯泡显然比 2.5V、0.3A 的小电珠亮的多。求 40W 灯泡额定电流和小电珠的额定功率。我们能不 + 电能说瓦数大的灯泡，所以它的额定电流也大？流 0.5Ω 10V 表答：40W 的灯泡的额定电流为
P 1000 = = 4.55A U 220 1-4 某电流表的量程为 10mA．当某电阻两端的电压为 8V 时，通过的电流为 2mA．如果给这个电阻两端加上 50V 的电压，能否用这个电流表测量通过这个电阻的电流？解：根据电阻两端压降和流过电阻中的电流，由欧姆定理可以确定电阻的值为： U 8 R= = = 4 (kΩ) I 2 × 10 −3 如果给电阻上加 50V 的电压，流过电阻的电流为： U 50 I= = = 12.5 (mA) R 4 × 10 3 电流表的量程为 10mA，也就是允许通过的最大电流为 10mA，显然不能使用该电流表测量通过流过该电阻的电流。 1-5 在电路中已经定义了电流、电压的实际方向，为什么还要引入参考方向？参考方向与实际方向有何区别和联系？答：在求解电路参数时，对于稍微复杂的电路，必须列方程求解，列出方程又必须知道电流、电压的方向，为此，引入电流、电压参考方向，根据参考方向列出电路方程，利用方程求出电路参数，若结果为负，表明实际的方向与参考方向相反，若结果为正，表明参考方向就是实际方向。 1-6 如何计算元件的吸收功率？如何从计算结果判断该元件为有源元件或无源元件？答：在关联参考方向下： P = UI ；在非关联参考方向下： P = −UI 。在此前提下，当 P>0 时为吸收功率。若 P<0 为有源元件，否则为无源元件。 1-7 标有 10kΩ（称为标称值）、1/4W（额定功率）的金属膜电阻，若使用在直流电路中，试问其工作电流和电压不能超过多大数值？ I=

工程力学教程篇(第二版)习题第7章答案

第7章刚体的平面运动习题7-1 直杆AB 长为l ，两端分别沿着水平和铅直方向运动，已知点A 的速度A υ为常矢量，试求当 60=θ时，点B 的速度和杆AB 的角速度。

（a ）（b ）解法一（如图a ）1.运动分析：杆AB 作平面运动。

2.速度分析：A B A B v v v +=，作速度矢量合成图 IA AB υυυ360tan == A A BA υυυ260cos /==A BAlAB υυω2==解法二（如图b ）1.运动分析：杆AB 作平面运动。

2.速度分析：杆AB 的速度瞬心是点I 。

ωυ⨯=AP A A All υυω260cos ==A AB ll BP υυωυ3260sin =⨯⨯=⨯=s rad /6=ω，试求图示位置时，滑块B 的速度以及连杆AB 的角速度。

解：1.运动分析：杆AB 均作一般平面运动，滑块作直线运动，杆OA 作定轴转动。

2.速度分析：对杆AB ，s m OA A /12=⨯=ωυA B A B v v v +=或AB B AB A v v ][][=30cos B A υυ=s m B /38=υs m A BA /3430tan =⨯=υυ s rad ABBAAB /2==υω7-3 图示机构，滑块B 以s m /12的速度沿滑道斜向上运动，试求图示瞬时杆OA 与杆AB 的角速度。

解：AB 杆运动的瞬心为I 点。

AB B BP ωυ⨯= s r a d BAB /325.043=⨯=υωs m AP AB A /2.7323.043=⨯⨯=⨯=ωυ 4.0⨯=OA A ωυ s rad OA /184.02.7==ω 或利s /m .B A 2753==υυOA=2m ，，圆轮半径为2m ，s rad /60=ω，试求图示位置时，轮心的速度，圆轮的角速度及连杆AB 的角速度。

解：1.运动分析：圆轮和杆AB 均作一般平面运动。

杆OA 作定轴转动。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

E FN1 FN3 FN2 β (c)

2-1 试绘出下列各杆的轴力图。 2-2求下列结构中指定杆内的应力。已知(a)图中杆的横截面面积A1=A2=1150mm2；解：（1）分析整体，作示力图

0)(iBFM：

041088AF 40kNAF （2）取部分分析，示力图见（b） 0)(iCFM：

02442.22qFFAN

2(404402)36.36kN2.2NF 3262236.361031.62MPa115010N

A







杆

（3）分析铰E，示力图见（c） 0ixF：

0sin12NNFF 22122140.65kN2NNFF

3161137.961035.3MPa115010N

A







杆

F 2F FN 2F FN

A E

D B

FA FB

C FA

FCy FCx

FN2 (b) 2-3求下列各杆内的最大正应力。（3）图(c)为变截面拉杆，上段AB的横截面积为40mm2，下段BC的横截面积为30mm2，杆材料的ρg=78kN/m3。解：1.作轴力图，BC段最大轴力在B处

6N120.530107812.0kNBF

AB段最大轴力在A处 6N1212(0.5300.540)107812.0kNAF

3N2612.010400MPa30mm3010BBF





3N2612.010300MPa40mm4010AAF





杆件最大正应力为400MPa，发生在B截面。

2-4一直径为15mm，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm，直径缩小了0.022mm，确定材料的弹性模量E、泊松比ν。解：加载至58.4kN时，杆件横截面中心正应力为

2458.410330.48MPa1.5104FA

＝

线应变：333Δ0.9104.51020010ll 弹性模量：33330.48MPa73.410MPa4.510E 侧向线应变：310467.115022.0＝， 泊松比：,0.326

2-6图示短柱，上段为钢制，长200mm，截面尺寸为100×100mm2；下段为铝制，长300mm，截面尺寸为200×200mm2。当柱顶受F力作用时，柱子总长度减少了0.4mm，试求F值。已知E钢=200GPa，E铝=70GPa。解：柱中的轴力都为F，总的变形（缩短）为：

120.20.3ΔglFFlEAEA

A B C

12.0 12.0 FN (kN) 12399Δ0.20.30.4100.20.3200100.10.170100.20.21931.0kNgllFEAEA











2-7图示等直杆AC，材料的容重为ρg，弹性模量为E，横截面积为A。求直杆B截面的位移ΔB。

解： AB段内轴力 N1FFgAx

BC段内轴力 N22FFgAx B点位移为杆BC的伸长量： 22(2)d21.5l

FgAxxFlgAlEAEA

2-8图示结构中，AB可视为刚性杆，AD为钢杆，面积A1=500mm2，弹性模量E1=200GPa；CG为铜杆，面积A2=1500mm2，弹性模量E2=100GPa；BE为木杆，面积A3=3000mm2，弹性模量E3=10GPa。当G点处作用有F=60kN时，求该点的竖直位移ΔG。解：（1）求①、②杆轴力由平衡方程可以求出:

N1N3N2

240kN320kN360kNFFFFFF

 （2）求杆的变形 34N11961140101Δ410m2001050010ADFllEA





（压缩）

34N22962260100.5Δ210m10010150010CGFllEA





（拉伸）

36N33963320101Δ6.6710m1010300010BEFllEA





（压缩）

（3）由几何关系：421321ΔΔΔ6.8910m33Glll-＝（下降） 2-11图示一挡水墙示意图，其中AB杆支承着挡水墙，各部分尺寸均已示于图中。若AB杆为圆截面，材料为松木，其容许应力［σ］=11MPa，试求AB杆所需的直径。解：（1）求水压力的合力： 21

240kNPhb

（2）作示力图（a）由平衡方程求轴力

2N3

()0:0.60.4011.11kNOiMFFPF



（3）由强度条件，设计截面尺寸： N3632[]411.1110/(1110)1.28610m3.58cmFAdd



2-12图示结构中的CD杆为刚性杆，AB杆为钢杆，直径d=30mm，容许应力［σ］=160MPa，弹性模量E=2.0×105MPa。试求结构的容许荷载F。解：（1）求AB杆的轴力FN

0)(iCFM：

sin3022.502.5FFFF



（2）由强度条件求F 

N

462.591016010445.2kN2.5FFAAF



3-1 试作下列各杆的扭矩图。

FN P 3m

4m 2m 3-2一直径d=60mm的圆杆，其两端受外力偶矩T=2kN·m的作用而发生扭转。试求横截面

上1，2，3点处的切应力和最大切应变，并在此三点处画出切应力的方向。(G=80GPa)。解：横截面上切应力大小沿半径线性分布，方向垂直半径

213

200047.2MPa3.140.06/160.02/331.4MPaTW 4max3/5.910radG

3-3 从直径为300mm的实心轴中镗出一个直径为150mm的通孔而成为空心轴，问最大切应力增大了百分之几?

解：实心轴max13P116xxMMWd

空心轴max234P216(10.5)xxMMWd 最大切应力增大了4343

max2max14max13

16160.5(10.5)100%101610.5xxxMMddMd



3-4一端固定、一端自由的钢圆轴，其几何尺寸及受力情况如图所示（空心处有两段，内径10mm，外径30mm）,试求： (1)轴的最大切应力。 (2)两端截面的相对扭转角(G=80GPa)。解：（1）作扭矩图， AB段中最大切应力

max36P6035.56MPa31016xMW





31

60л30л 40л

A B C D

2 1 Mx

(kN·m)

5 3 CD段中最大切应力 

max

946P644031101616401024MPa2713xMW









所以轴中，MPa56.35max （2）相对扭转角分四段计算

P1P1P2P2400.2300.1300.1600.15ΔΔΔΔΔDCCEEBBAGIGIGIGI

P1P2P1P211121112GIGIGII





94844811120.011426rad118010310133103232







3-5一圆轴AC如图所示。AB段为实心，直径为50mm；BC段为空心，外径为50mm，内径为35mm。要使杆的总扭转角为0.12°，试确定BC段的长度a。设G=80GPa。解：（1）作扭矩图 100NmxM

（2）杆件A、C截面相对扭转角分两段计算

4PP

ΔΔΔ0.91ACBCBAxxMaMaGIGI

P4P948Δ350.9,0.7501Δ0.315960.980100.12510180320.91000.315960.405mACxACx

GIa

aMGIaMaa其中＝＝

3-8传动轴的转速为n=500转/分，主动轮输入功率P1=500kW，从动轮2、3分别输出功率P2=200kW，P3=300kW。已知［τ］=70MPa，［θ］=1°/m，G=8×104MPa。 (1)确定AB段的直径d1和BC段的直径d2。 (2)若AB和BC两段选用同一直径，试确定直径d。解：（1）由输入和输出功率求等效力偶，作扭矩图

⊕100N·m Mx A C