高数16个基本初等函数
基本初等函数公式总结推荐文档

基本初等函数公式总结推荐文档在数学中,基本初等函数是指由已知的基本函数通过基本运算(如加、减、乘、除和函数复合)而产生的函数。
基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数等。
1.常数函数:常数函数是指函数的取值在一个集合上恒为常数。
常见的常数函数有零函数和单位函数。
零函数的公式为f(x)=0,单位函数的公式为f(x)=12.幂函数:幂函数是指以一个固定的实数为底,以自变量的不同次幂为指数的函数。
常见的幂函数包括平方函数和立方函数等。
平方函数的公式为f(x)=x^2,立方函数的公式为f(x)=x^33.指数函数:指数函数是以指数为自变量的函数,其中底数为常数且大于0且不等于1、常见的指数函数包括以e为底的自然指数函数和以10为底的常用对数函数。
自然指数函数的公式为 f(x)=e^x,常用对数函数的公式为 f(x)=log(x)。
4.对数函数:对数函数是指以对数为自变量的函数,其中底数为常数且大于0且不等于1、常见的对数函数包括自然对数函数和常用对数函数。
自然对数函数的公式为 f(x)=ln(x),常用对数函数的公式为f(x)=log(x)。
5.三角函数:三角函数是以角度或弧度为自变量的函数,其中常见的三角函数包括正弦函数、余弦函数和正切函数等。
正弦函数的公式为f(x)=sin(x),余弦函数的公式为 f(x)=cos(x),正切函数的公式为f(x)=tan(x)。
6.反三角函数:反三角函数是三角函数的反函数,其中常见的反三角函数包括反正弦函数、反余弦函数和反正切函数等。
反正弦函数的公式为f(x)=asin(x),反余弦函数的公式为 f(x)=acos(x),反正切函数的公式为 f(x)=atan(x)。
总结起来,基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数等。
掌握这些基本函数的公式和性质,能够帮助我们解决很多数学问题。
推荐的文档是《初等函数与普通函数》一书,该书详细介绍了基本初等函数的公式和性质,同时还包括了基本初等函数的图像和应用等内容。
最全高数基本初等函数概念图像及性质完整版

基本初等函数. 幂函数(a 为实数 )要记住最常见的几个幂函数的定义域及图形..指数函数定义域:,值域:,图形过( 0, 1)点, a>1 时,单调增加; a 时,单调减少。
今后用的较多。
.对数函数定义域:,值域:,与指数函数互为反函数,图形过(1, 0)点, a>1 时,单调增加;a<1 时,单调减少。
.三角函数,奇函数、有界函数、周期函数;,偶函数、有界函数、周期函数;,的一切实数,奇函数、周期函数,的一切实数,奇函数、周期函数;,.反三角函数;;;。
以上是五种基本初等函数,关于它们的常用运算公式都应掌握注:( 1)指数式与对数式的性质由此可知,今后常用关系式,如:( 2)常用三角公式积化和差sina*cosb=(sin(a+b)+sin(a-b))/2 cosa*sinb=(sin(a+b)-sin(a-b))/2cosa*cosb=(cos(a+b)+cos(a-b))/2 sina*sinb=-(cos(a+b)-cos(a-b))/2和差化积sinx+siny=2sin((x+y)/2)*cos((x-y)/2) sinx-siny=2cos((x+y)/2)*sin((x-y)/2) cosx+cosy=2cos((x+y)/2)*cos((x-y)/2) cosx-cosy=-2sin((x+y)/2)*sin((x-y)/2)赠送以下资料《二次函数的应用》中考题集锦10 题已知抛物线y x2mx 2m 2 (m 0).( 1)求证:该抛物线与x 轴有两个不同的交点;( 2)过点P(0,n)作y 轴的垂线交该抛物线于点 A 和点 B (点 A 在点 P 的左边),是否存在实数 m,n ,使得 AP2PB ?若存在,则求出m,n 满足的条件;若不存在,请说明理由.答案:解:( 1)证法 1:29 m2,y x2mx 2m2x m24当 m0 时,抛物线顶点的纵坐标为9 m20 ,4顶点总在 x 轴的下方.而该抛物线的开口向上,该抛物线与x 轴有两个不同的交点.(或者,当 m 0 时,抛物线与y 轴的交点(0,2m2)在x轴下方,而该抛物线的开口向上,该抛物线与 x 轴有两个不同的交点.)证法 2:m2 4 1 ( 2m2 ) 9m2,当 m0时, 9m20 ,该抛物线与 x 轴有两个不同的交点.( 2)存在实数m,n,使得AP2PB .设点 B 的坐标为(t,n),由 AP2PB 知,y①当点 B 在点 P 的右边时, t0,点 A 的坐标为(2t, n) ,A PBx 且 t, 2t是关于 x 的方程 x2mx2m2n 的两个实数根.O m24( 2m2n) 9m24n 0 ,即 n9 m2.4且 t ( 2t )m (I), t ( 2)t2(II)m n由( I)得,t m,即m 0.将 t m代入(II)得, n0 .y 当 m0且 n0 时,有 AP2PB .②当点 B 在点 P 的左边时, t0,点 A 的坐标为(2 t,n),且 t,2t 是关于x的方程 x 2mx2m2n 的两个实数根.xOm24( 2m2n) 9m24n 0 ,即 n9 m2.4AB P且 t 2t m (I),t 2t2m2n (II)由( I)得,t m0 .3,即m将 t m代入( II )得,n20 m2且满足 n9 m2.32094当 m0 且n m2时,有AP2PB9第 11 题一人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离S (米)与时间t (秒)间的关系式为S 10t t 2,若滑到坡底的时间为 2 秒,则此人下滑的高度为()A.24米B.12米C. 12 3 米D.6米答案:B第 12 题我市英山县某茶厂种植“春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月 25日起的 180 天内,绿茶市场销售单价y (元)与上市时间t (天)的关系可以近似地用如图( 1)中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z (元)与上市时间t (天)的关系可以近似地用如图(2)的抛物线表示.y (天)z(元 )16060140( 180, 92)5012040100858036020401020140160100120O20 40 6080 100 120150 180t(天)O204060 80110140160 180t(天 )( 1)直接写出图(1)中表示的市场销售单价y (元)与上市时间t (天)(t0)的函数关图 (1)图 (2)系式;( 2)求出图( 2)中表示的种植成本单价z(元)与上市时间t (天)(t 0)的函数关系式;( 3 )认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?(说明: 市场销售单价和种植成本单价的单位:元/500 克.)答案:解:( 1)依题意,可建立的函数关系式为:2 t 160 (0t,3 120)y 80 (120 ≤ t,150)2 20 (150 ≤t ≤ .5( 2)由题目已知条件可设za(t 110) 220 .85图象过点 (60, ) ,385 a(60 110) 2 20. a1 . 3300z1(t 110) 2 20 (t 0 ). 300( 3)设纯收益单价为W 元,则 W =销售单价 成本单价.2 1601110) 220 (0 t,t(t120)3300故W 801 (t 220(120 ≤t,300 110)150)2 201 220 (150 ≤ t≤.5300化简得1 2100(0,300W1(t 110)2 60 (120≤ t 150), 30012 56 (150 ≤ t ≤.300①当 W1 (t 10)2 100(0 t 120) 时,有 t 10时, W 最大,最大值为 100;300②当 W1 (t 110)2 60(120 ≤ t 150) 时,由图象知,有 t 120 时, W 最大,最大300值为 59 2 ;3③当 W1 (t 170)2 56(150 ≤ t ≤ 180) 时,有 t 170 时, W 最大,最大值为 56.300综上所述,在 t 10 时,纯收益单价有最大值,最大值为100 元.第 13 题如图,足球场上守门员在O 处开出一高球,球从离地面1 米的 A 处飞出( A 在 y 轴上),运动员乙在距O 点6 米的B 处发现球在自己头的正上方达到最高点M,距地面约 4 米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.( 1)求足球开始飞出到第一次落地时,该抛物线的表达式.( 2)足球第一次落地点 C 距守门员多少米?(取 43 7)( 3)运动员乙要抢到第二个落点D ,他应再向前跑多少米?(取26 5)y4 M2 1 AOBCDx答案:解:( 1)( 3 分)如图,设第一次落地时,抛物线的表达式为ya(x6) 2 4.y由已知:当 x 0 时 y 1.即 1 36a 4, a1 . 4M12E FN表达式为 y124. 2 ( x 6)1 A1 x2 12OBCDx(或 yx 1 )12 1( 2)(3 分)令 y0, ( x6)2 4 0.12(x6)2 48. x 4 3 6 ≈ 13,x4 3 6 0 (舍去).12足球第一次落地距守门员约 13 米.( 3)(4 分)解法一:如图,第二次足球弹出后的距离为CD根据题意: CDEF (即相当于将抛物线 AEMFC 向下平移了 2 个单位)21( x 6) 24解得 x6 2 6,x2 6 26.121CD x 1 x 2 4 6 ≈10.BD 13 6 1017 (米).解法二: 令1( x 6) 2 4 0.12解得x 1 6 4 3 (舍), x 26 4 3 ≈13.点 C 坐标为( 13, 0).设抛物线 CND 为 y1( x k) 2 2.12将 C 点坐标代入得:1(13 k) 2 2 0.12解得:k 1 13 2 613 (舍去),k 2 6 4 3 2 6 ≈ 6 7 5 18.y1( x 18)2 212 令 y0, 01( x 18)2 2.12x 118 2 6 (舍去), x 2 18 2 6≈23.BD 23 6 17 (米).解法三:由解法二知, k 18,所以 CD 2(18 13) 10, 所以 BD(136) 10 17.答:他应再向前跑17 米.第 14 题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知:平均修建每公顷大棚要用支架、农膜等材料费 2.7 万元;购置滴灌 设备,这项费用(万元)与大棚面积(公顷)的平方成正比,比例系数为 0.9 ;另外每公顷种植蔬菜需种子、化肥、农药等开支 0.3 万元.每公顷蔬菜年均可卖7.5 万元.y (万元),( 1)基地的菜农共修建大棚 x (公顷),当年收益(扣除修建和种植成本后)为写出 y 关于 x 的函数关系式.( 2)若某菜农期望通过种植大棚蔬菜当年获得 5 万元收益,工作组应建议他修建多少公项大棚.(用分数表示即可)( 3)除种子、化肥、农药投资只能当年受益外, 其它设施 3 年内不需增加投资仍可继续使用. 如果按 3 年计算,是否修建大棚面积越大收益越大?修建面积为多少时可以得到最大收益?请帮工作组为基地修建大棚提一项合理化建议.答案:( 1) y 7.5x2.7x 0.9x 20.3x0.9x 2 4.5x .( 2)当 0.9x 24.5x5 时,即 9x 245x 50 0 , x 15 , x 2 1033从投入、占地与当年收益三方面权衡,应建议修建5公顷大棚.(3)设3Z (万元)3年内每年的平均收益为Z 7.5x0.9x 0.3x20.3x0.3x2 6.3x20.3 x 10.5 33.075(10分)不是面积越大收益越大.当大棚面积为10.5 公顷时可以得到最大收益.建议:①在大棚面积不超过10.5公顷时,可以扩大修建面积,这样会增加收益.②大棚面积超过10.5公顷时,扩大面积会使收益下降.修建面积不宜盲目扩大.③当 0.3x2 6.3x0时, x10 , x2 21.大棚面积超过21公顷时,不但不能收益,反而会亏本.(说其中一条即可)第 15 题一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18 元,按定价 40元出售,每月可销售 20 万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价 1元,月销售量可增加 2 万件.(1)求出月销售量y(万件)与销售单价x(元)之间的函数关系式(不必写x的取值范围);(2)求出月销售利润z(万元)(利润=售价-成本价)与销售单价x(元)之间的函数关系式(不必写 x 的取值范围);(3)请你通过( 2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于 480 万元.答案:略.第 16 题一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为 2m ,隧道最高点P 位于 AB 的中央且距地面6m ,建立如图所示的坐标系(1)求抛物线的解析式;(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?yPA BO Cx答案:( 1)由题意可知抛物线经过点A0,2 ,P 4,6 ,B 8,2设抛物线的方程为y ax2bx c将 A,P,D 三点的坐标代入抛物线方程.解得抛物线方程为y1x22x 24( 2)令 y4 ,则有 1 x 2 2x2 44解得x 14 2 2, x 2 4 2 2x 2 x 14 2 2货车可以通过.( 3)由( 2)可知1x 2 x 1 2 2 22 货车可以通过.第 17 题如图,在矩形ABCD 中, AB 2 AD ,线段 EF 10 .在 EF 上取一点 M ,分别以EM , MF 为一边作矩形 EMNH 、矩形 MFGN ,使矩形 MFGN ∽ 矩形 ABCD .令 MN x ,当 x 为何值时,矩形 EMNH 的面积 S 有最大值?最大 D C值是多少?ABHN GEMF答案:解:矩形 MFGN ∽ 矩形 ABCD ,MN MF .AD ABAB2 AD , MN x ,MF 2x .EMEFMF 10 2x .Sx(10 2x) 2 x 2 10x22 52 x52.2当 x5时, S 有最大值为25.22第 18 题某企业信息部进行市场调研发现:信息一:如果单独投资A 种产品,则所获利润 y A (万元)与投资金额 x (万元)之间存在正比例函数关系: y A kx ,并且当投资 5 万元时,可获利润 2 万元.信息二:如果单独投资B 种产品,则所获利润y B (万元)与投资金额 x (万元)之间存在二次函数关系:y B ax 2 bx ,并且当投资2 万元时,可获利润 2.4 万元;当投资4 万元时,可获利润 3.2 万元.(1)请分别求出上述的正比例函数表达式与二次函数表达式;(2)如果企业同时对A,B两种产品共投资 10 万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?答案:解:(1)当x 5 时,y1,,0.4 ,2 25k ky A0.4x ,当x 2 时,y B 2.4 ;当x 4 时,y B 3.2.2.44a2b3.216a4ba0.2解得1.6by B0.2x2 1.6 x .( 2)设投资B种商品x万元,则投资 A 种商品(10x) 万元,获得利润W万元,根据题意可得W0.2x2 1.6 x0.4(10 x)0.2 x2 1.2x4W0.2( x3)2 5.8当投资 B 种商品 3 万元时,可以获得最大利润 5.8 万元,所以投资A种商品7万元, B种商品 3 万元,这样投资可以获得最大利润 5.8 万元.第 19 题如图所示,图(1)是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m ,支柱 A3 B3 50m , 5 根支柱 A1 B1, A2 B2, A3 B3, A4 B4,A5 B5之间的距离均为15m ,B1B5∥ A1 A5,将抛物线放在图( 2)所示的直角坐标系中.(1)直接写出图( 2)中点 B1, B3, B5的坐标;(2)求图( 2)中抛物线的函数表达式;( 3)求图( 1)中支柱 A2 B2, A4 B4的长度.B3yB2B430m B3B1B5B1B5A1A2 A3 A4 A5O l图 (1)图(2)答案:B1 ( 30, 0) , B3 (0,30) , B5 (30,0) ;(1)( 2)设抛物线的表达式为y a(x 30)( x30) ,把 B3 (0,30) 代入得 y a(030)(030)30 .∴ a 1.301( x∵ 所求抛物线的表达式为:y30)( x30) .30( 3)∵B4点的横坐标为15,∴ B4的纵坐标 y41(1530)(1530)45.302∵ A3B350 ,拱高为30,∴立柱 A4B4 204585(m) .2285(m) 。
初等函数包括哪些

初等函数elementary function ,数学术语,包括代数函数和超越函数。
在研究函数的一般理论中起着很重要的作用。
最常用的一类函数,包括常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数,以及由这些函数经过有限次四则运算或函数的复合而得的所有函数。
①常数函数。
对定义域中的一切x对应的函数值都取某个固定常数的函数。
②幂函数。
形如y=xa的函数,式中a为不等于零的常数。
③指数函数。
形如y =ax的函数,式中a为不等于1的正常数。
④对数函数。
指数函数的反函数,记作y=log a x,式中a为不等于1的正常数。
指数函数与对数函数之间成立关系式,loga ax=x。
⑤三角函数。
即正弦函数y=sinx ,余弦函数y=cosx ,正切函数y=tgx,余切函数y=ctgx ,正割函数y=secx,余割函数y=cscx(见三角学)。
⑥反三角函数。
三角函数的反函数——反正弦函数y =arc sinx ,反余弦函数y=arc cosx (-1≤x≤1,0≤y≤π),反正切函数y=arc tgx ,反余切函数y =arc ctgx(-∞<x<+∞,θ<y<π)等。
以上这些函数常统称为基本初等函数。
一个初等函数,除了可以用初等解析式表示以外,往往还有其他表示形式,例如,三角函数y=sinx 可以用无穷级数表为初等函数可以按照解析表达式分类为:初等函数是最先被研究的一类函数,它与人类的生产和生活密切相关,并且应用广泛。
为了方便,人们编制了各种函数表,如平方表、开方表、对数表、三角函数表等。
(完整版)高数知识点总结

高数重点知识总结1、基本初等函数:反函数(y=arctanx),对数函数(y=lnx),幂函数(y=x),指数函数(x a y =),三角函数(y=sinx),常数函数(y=c)2、分段函数不是初等函数。
3、无穷小:高阶+低阶=低阶 例如:1lim lim020==+→→x xxx x x x 4、两个重要极限:()e x ex xxxx xx x =⎪⎭⎫⎝⎛+=+=∞→→→11lim 1lim )2(1sin lim )1(10 经验公式:当∞→→→)(,0)(,0x g x f x x ,[])()(lim )(0)(1lim x g x f x g x x x x ex f →=+→例如:()33lim 10031lim -⎪⎭⎫ ⎝⎛-→==-→e ex x x xx x5、可导必定连续,连续未必可导。
例如:||x y =连续但不可导。
6、导数的定义:()0000')()(lim)(')()(limx f x x x f x f x f xx f x x f x x x =--=∆-∆+→→∆7、复合函数求导:[][])(')(')(x g x g f dxx g df •= 例如:xx x x x x x y x x y ++=++=+=24122211', 8、隐函数求导:(1)直接求导法;(2)方程两边同时微分,再求出dy/dx例如:yxdx dy ydy xdx y xy yy x y x -=⇒+-=⇒=+=+22,),2('0'22,),1(122左右两边同时微分法左右两边同时求导解:法 9、由参数方程所确定的函数求导:若⎩⎨⎧==)()(t h x t g y ,则)(')('//t h t g dt dx dt dy dx dy ==,其二阶导数:()[])(')('/)('/)/(/22t h dt t h t g d dt dx dt dx dy d dx dx dy d dx y d === 10、微分的近似计算:)(')()(000x f x x f x x f •∆=-∆+ 例如:计算 ︒31sin11、函数间断点的类型:(1)第一类:可去间断点和跳跃间断点;例如:xxy sin =(x=0是函数可去间断点),)sgn(x y =(x=0是函数的跳跃间断点)(2)第二类:振荡间断点和无穷间断点;例如:⎪⎭⎫ ⎝⎛=x x f 1sin )((x=0是函数的振荡间断点),xy 1=(x=0是函数的无穷间断点) 12、渐近线:水平渐近线:c x f y x ==∞→)(lim铅直渐近线:.)(lim 是铅直渐近线,则若,a x x f ax =∞=→斜渐近线:[]ax x f b xx f a b ax y x x -==+=∞→∞→)(lim ,)(lim,即求设斜渐近线为例如:求函数11223-+++=x x x x y 的渐近线13、驻点:令函数y=f(x),若f'(x0)=0,称x0是驻点。
基本初等函数知识总结

基本初等函数知识总结含义:常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数1.常数函数(y=C)(1)定义域: D(f)=(-∞,+∞)(2)值域: Z(f)=C(3) 性质: 它的图像是一条平行于x轴并通过点(0,C)在y轴上截距为C的直线(4 )图像:(5)周期性:常值函数是一个周期函数. 因对于任何x∈(-∞,+∞)和实数T,f(x+T)=f(x)=T,但并无最小正周期【注】常值函数不含自变量且不存在反函数2.幂函数(1)定义:形如y=x^a(a为常数)的函数,即以底数为自变量,幂为因变量,指数为常量的函数称为幂函数.(2)性质:在(0,+∞)内总有意义①当α>0时函数图像过点(0,0)和(1,1),在(0,+∞)内单调增加且无界②当α<0时函数图像过点(1,1),在(0,+∞)内单调减少且无界(3)图像:3.指数函数y=a^x(a>0且a≠1)(1)定义域:x∈R(2)值域:(0,+∞)(3)性质:①单调性:1.当0<a<1时,在(-∞,+∞)内单调减少 2.当a >1时,在(-∞,+∞)内单调增加②奇偶性:非奇非偶函数③周期性:非周期函数④有界性:无界函数(4)图像:①由指数函数y=a^x与直线x=1相交于点(1,a)可知:在y轴右侧,图像从下到上相应的底数由小变大。
②由指数函数y=a^x与直线x=-1相交于点(-1,1/a)可知:在y轴左侧,图像从下到上相应的底数由大变小。
③指数函数的底数与图像间的关系可概括的记忆为:在y轴右边“底大图高”;在y轴左边“底大图低” 如图:(5)运算法则:①②③④4.对数函数y=logax(a>0 且a≠1)(1)定义:如果a^x=N(a>0,且a ≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数一般地,函数y=logax(a>0,且a ≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数(2)定义域:(0,+∞),即x>0(3)值域:R(4)性质:①单调性:1.当0<a<1时,在(0,+∞)内单调减少 2.当a >1时,在(0,+∞)内单调增加②奇偶性:非奇非偶函数③周期性:非周期函数④有界性:无界函数(5)图像:【注】①负数和零没有对数②1的对数是零③底数的对数等于1(6)常用法则/公式:5.三角函数⑴正弦函数y=sin x(1)定义:对边与斜边的比(2)定义域:R(3)值域:【-1,1】(4)最值:1.当X=2Kπ(K∈Z)时,Y 取最大值1 2.当X=2Kπ+3π/2(K∈Z时,Y取最小值-1(5)性质:①周期性:最小正周期都是2πT=2π②奇偶性:奇函数③对称性:对称中心是(Kπ,0),K ∈Z;对称轴是直线x=Kπ+π/2,K ∈Z④单调性:在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增;在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减⑤有界性:有界函数(6)图像:(2)余弦函数y=cos x(1)定义:邻边与斜边之比(2)定义域:R(3)值域:【-1,1】(4)最值:1.当X=2Kπ +π /2(K∈Z)时,Y取最大值1 2.当X=2Kπ +π (K∈Z)时,Y取最小值-1(5)性质:①周期性:最小正周期都是2πT=2π②奇偶性:偶函数③对称性:对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z④单调性:在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增⑤有界性:有界函数(6)图像:(3)正切函数y=tan x(1)定义:对边与邻边之比(2)定义域:{x∣x≠Kπ+π/2,K∈Z}(3)值域:R(4)最值:无最大值和最小值(5)性质:①周期性:最小正周期都是πT=π②奇偶性:奇函数③对称性:对称中心是(Kπ/2,0),K∈Z④单调性:在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增⑤有界性:无界函数(6)图像:(4)余切函数y=cot x(1)定义:在直角三角形中,某锐角的相邻直角边和相对直角边的比,叫做该锐角的余切。
高数总结:基本初等函数图像及其性质
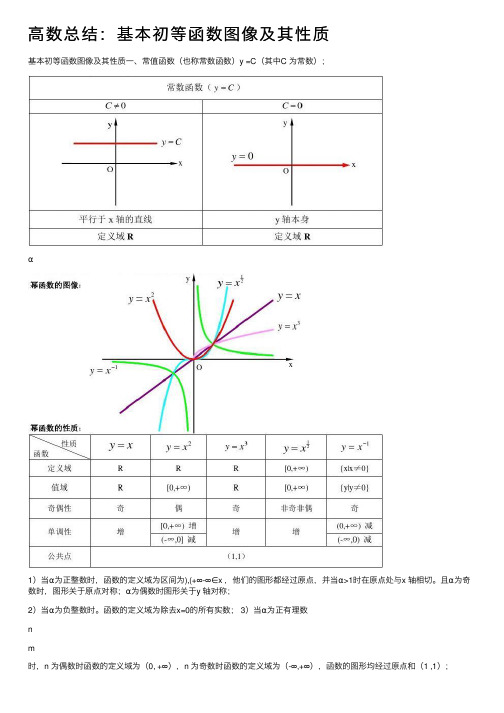
⾼数总结:基本初等函数图像及其性质基本初等函数图像及其性质⼀、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数n4)如果m>n 图形于x 轴相切,如果m5)当α为负有理数时,n 为偶数时,函数的定义域为⼤于零的⼀切实数;n 为奇数时,定义域为去除x=0以外的⼀切实数。
三、指数函数xa y =(x 是⾃变量,a 是常数且0>a ,1≠a ),定义域是R ;[⽆界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上⽅; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的⼤⼩⽐较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ?=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越⼤,xa y =的图像越靠近y 轴;b.2.当10<的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=?m n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m n m(2))1,,,0(11*>∈>==-n Z n m a a amnm nm yxf x xxx g ?=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [⽆界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式⼦N a log 叫做对数式。
大一高数之函数
……
……
t 年后人口为p=9.6259×(1+12‰) t
即
p 9.6259 1.012t
到2005年底,即27年后, 我国人口为 p 9.6259 1.012 .
27
两边取常用对数, lg p lg 9.6259 27 lg1.012 4.9835 27 0.0051 5.1212, 查反对数表, p 13.22(亿).
即根据1978年的数据,可推算出2005年底 我国人口为13.22亿.
人口模型 : 设某地某年人口为p0,人口自然 增长率为r,那么t 年后的人口p为 p p0 (1 r ) .
t
马尔萨斯(malthus,英,1776 — 1834) 根据上述模型提出了他的人口理论,这一模 型只适用于生物种群的生存环境较为优雅宽 松的情况.当生物种群数量增长到一定值时, 恶化的生态环境将抑制种群数量的增长,进 而出现负增长,此时马尔萨斯人口模型就不 适用了.
A1 A(1 r )t ;
r 若每期结算m次,则每次利率为 , m t期内共结算mt次,t期后的本利和为
r mt Am A(1 ) . m 如果,即按照每个瞬间“即存即算” 来计算本利和,则归结为求极限
r mt lim A(1 ) m m
这个求极限问题将在第二章的应用中 介绍.
y cos x
正切函数
y tan x
π π 定义域 : ( kπ , kπ ), k Z; 值域( , ), 2 2 π π 以π 为周期, 在每个开区间( kπ , kπ )上 2 2 递增.
余切函数
y cot x
定义域 : kπ ,( k 1)π ), k Z;值域( , ), ( 以π 为周期, 在每个开区间( π ,( k 1)π ) k 上 递减.
高数第一章初等函数

2)反余弦函数 余弦函数
反余弦函数
y cos x
y
1
0
2
x [0, ]
y arccos x x [1,1]
y
y [1,1]
y [0, ]
x
1
1
0
x 1
余弦函数 y cos x 在 [0, ] 上的反函数,称为
反余弦函数,记为 y arccos x x [1,1] y [0, ]
10
例2 判断函数 f ( x) ln ( x 2 1 x) 的奇偶性. 解
f x f x
ln [ x 2 1 x] [ x 2 1 x]
ln1 0
则此函数为奇函数
11
(4)三角函数 1)正弦函数的性质
y sin x
x ,
解:
x e ln x , x 0
ln x 1 0 e 1 f ln x ln x ln x e e 1
ye
y
x
1 f x x e
0 e 1
x
e 1
x
0,1
x
1 x 0 f x x e 0 x
22
反余弦函数的性质
y arccos x
x [1,1]
y
y [0, ]
(1)在[ -1, 1 ]是有界函数;
0 arccos x
(2)是非奇非偶函数;
1
0
x 1
(3)在 [1, 1] 上是单调减函数。
23
3)反正切函数 正切函数 y tan x 在 (
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高数是一门重要的数学课程,其中最基础的内容就是16个基本初等函数。
这些函数在数
学和实际应用中都有着广泛的应用,下面我们将逐一介绍这16个函数。
一、常数函数
常数函数是指函数f(x)=c,其中c为常数。
这个函数的图像是一条平行于x轴的直线,它的斜率为0。
常数函数在实际应用中常用于表示一些固定的量,如重力加速度g=9.8m/s²。
二、幂函数
幂函数是指函数f(x)=x^a,其中a为常数。
幂函数的图像随着a的不同而变化,当a>1时,函数的图像呈现出上升的趋势,当0<a<1时,函数的图像呈现出下降的趋势。
幂函数在实
际应用中常用于描述一些具有指数增长或衰减的现象,如人口增长、放射性衰变等。
三、指数函数
指数函数是指函数f(x)=a^x,其中a为常数。
指数函数的图像随着a的不同而变化,当
a>1时,函数的图像呈现出上升的趋势,当0<a<1时,函数的图像呈现出下降的趋势。
指
数函数在实际应用中常用于描述一些具有指数增长或衰减的现象,如利息的复利计算、细
胞的增长等。
四、对数函数
对数函数是指函数f(x)=loga(x),其中a为常数。
对数函数的图像是一条上升的曲线,它的斜率在x=1处为1。
对数函数在实际应用中常用于描述一些量的倍数关系,如声音的强度、地震的震级等。
五、三角函数
三角函数是指正弦函数、余弦函数和正切函数。
正弦函数和余弦函数的图像都是周期性波
动的曲线,它们的周期为2π。
正切函数的图像则是一条无限延伸的曲线。
三角函数在实
际应用中常用于描述周期性变化的现象,如天体运动、电流的交流等。
六、反三角函数
反三角函数是指正弦函数的反函数、余弦函数的反函数和正切函数的反函数。
反三角函数
的图像是一条上升或下降的曲线,它们的定义域和值域与对应的三角函数相反。
反三角函
数在实际应用中常用于求解三角函数的反函数值,如角度的计算、电路的分析等。
七、双曲函数
双曲函数是指双曲正弦函数、双曲余弦函数和双曲正切函数。
双曲函数的图像都是一条无
限延伸的曲线,它们的定义域和值域与对应的三角函数不同。
双曲函数在实际应用中常用
于描述一些具有双曲形变的现象,如弹性变形、电场的分布等。
八、反双曲函数
反双曲函数是指双曲正弦函数的反函数、双曲余弦函数的反函数和双曲正切函数的反函数。
反双曲函数的图像是一条上升或下降的曲线,它们的定义域和值域与对应的双曲函数相反。
反双曲函数在实际应用中常用于求解双曲函数的反函数值,如材料的弹性模量、电容的计
算等。
九、指数型函数
指数型函数是指函数f(x)=a^x+b,其中a和b为常数。
指数型函数的图像是一条上升的曲线,它们的斜率随着x的增大而增大。
指数型函数在实际应用中常用于描述一些具有指数
增长的现象,如病毒的传播、物种的扩散等。
十、对数型函数
对数型函数是指函数f(x)=loga(x)+b,其中a和b为常数。
对数型函数的图像是一条上升的曲线,它们的斜率随着x的增大而减小。
对数型函数在实际应用中常用于描述一些具有
对数增长的现象,如城市的规模、科技的进步等。
十一、多项式函数
多项式函数是指函数f(x)=anxn+an-1xn-1+...+a1x+a0,其中an、an-1、...、a1、a0都
是常数。
多项式函数的图像是一条平滑的曲线,它们的斜率和曲率随着x的变化而变化。
多项式函数在实际应用中常用于描述一些复杂的现象,如经济的发展、物理的运动等。
十二、有理函数
有理函数是指函数f(x)=p(x)/q(x),其中p(x)和q(x)都是多项式函数。
有理函数的图像
是一条平滑的曲线,它们的斜率和曲率随着x的变化而变化。
有理函数在实际应用中常用
于描述一些复杂的现象,如电路的分析、化学反应的速率等。
十三、指数分布函数
指数分布函数是指函数f(x)=λe^(-λx),其中λ为常数。
指数分布函数的图像是一条下降的曲线,它们的斜率随着x的增大而减小。
指数分布函数在实际应用中常用于描述一些
具有指数衰减的现象,如放射性物质的衰变、设备的寿命等。
十四、正态分布函数
正态分布函数是指函数f(x)=1/(σ√(2π))e^(-(x-μ)²/(2σ²)),其中μ和σ为常数。
正态分布函数的图像是一条钟形曲线,它们的最高点在x=μ处。
正态分布函数在实际应
用中常用于描述一些具有随机性的现象,如人口的身高、温度的变化等。
十五、逻辑函数
逻辑函数是指函数f(x)=1/(1+e^(-x)),它的图像是一条S形曲线。
逻辑函数在实际应用
中常用于描述一些具有二元关系的现象,如人口的性别、电子的状态等。
十六、分段函数
分段函数是指函数f(x)在不同的定义域内采用不同的函数表达式。
分段函数的图像是由多条曲线组成的,它们的形状和特点随着定义域的不同而不同。
分段函数在实际应用中常用
于描述一些具有不同特征的现象,如经济的发展、物理的运动等。
总之,这16个基本初等函数在数学和实际应用中都有着广泛的应用。
掌握这些函数的特
点和用法,可以帮助我们更好地理解和应用数学知识。
