2013年中考数学模拟试题卷
2013年中考数学第一次模拟考试题(含答案邯郸市)

2013年中考数学第一次模拟考试题(含答案邯郸市)锛掞紣锛??涓€銆?閫夋嫨棰?1銆佸湪-3锛?1锛?锛??锛?A 銆?3 B銆?1 C銆? D銆? 2涓哄渾鐨勬槸锛?锛?3锛?A銆佸繀鐒朵簨浠?B銆侀殢鏈轰簨浠?C銆佺‘瀹氫簨浠?D4锛?A 銆?B銆?x+2y=6xy C銆?D銆?5BC缁忚繃鍙樻崲寰楀埌鈻矰EF锛?A銆佹妸鈻矨BC缁曠偣C閫嗘椂閽堟柟鍚戞棆杞?0o 锛屽啀鍚戜笅骞崇Щ2鏍?B 銆佹妸鈻矨BC缁曠偣C椤烘椂閽堟柟鍚戞棆杞?0o锛屽啀鍚戜笅骞崇Щ5鏍?C 銆佹妸鈻矨BC鍚戜笅骞崇Щ4鏍硷紝鍐嶇粫鐐笴閫嗘椂閽堟柟鍚戞棆杞?80o D 銆佹妸鈻矨BC鍚戜笅骞崇Щ5鏍硷紝鍐嶇粫鐐笴椤烘椂閽堟柟鍚戞棆杞?80o6銆佷笉绛夊紡缁?鐨勮В闆嗕负锛?锛?A銆?<X<2 B銆亁>1 C銆亁<2 D銆亁<1鎴杧>2 7?脳4鐨勭煩褰㈢綉鏍间腑锛屾瘡鏍煎皬姝f柟褰㈢殑杈归暱閮芥槸1锛岃嫢鈻矨BC屽垯tan鈭燗BC鐨勫€间负A銆?B銆?C銆?D銆? 8AB OD B,鍨傝冻涓篗锛屼笅鍒楃粨璁轰笉鎴愮珛鐨勬槸锛?锛?A锛嶤M=DM B銆佸姬CB= B C銆佲垹ACD=鈭燗DC D銆丱M=MB9銆佽嫢,鍒?鐨勫€兼槸锛?锛?A銆? B銆?6 C銆? D銆? 10銆侀偗閮稿競瀵瑰煄у5绫虫牻1妫碉紝鍒欐爲鑻楃己21妫碉紝濡傛灉姣忛殧6绫虫牻1妫碉紝鍒欐爲x锛?A銆?锛坸+21-1锛?6锛坸-1锛?B銆?锛坸+21锛?6锛坸-1锛?C銆?锛坸+21-1锛?6x D銆?锛坸+21锛?6x 11D涓衡柍ABC鍐呬竴鐐癸紝CD骞冲垎鈭燗CB锛孊E D,鍨傝冻涓篋锛屼氦AC浜庣偣E锛屸垹A=鈭燗BE,C=5,BC=3,鍒橞D鐨勯暱涓猴紙锛?A銆?.5 B銆?.5 C銆? D銆?12ABC暱涓?鐨勫皬姝f柟褰㈢粍鎴愮殑锛屽弽姣斾緥鍑芥暟OABC鐨勪腑蹇僂锛屽弽姣斾緥鍑芥暟杩嘇B BC浜庣偣N?鈶犲弻鏇茬嚎鐨勮В鏋愬紡涓?鈶′C=2NC鈶e弽姣斾緥鍑芥暟嬪嚱鏁?鐨勫?鍏朵腑姝g‘鐨勭粨璁烘槸锛?A銆佲憼鈶?B銆佲憼鈶?C銆佲憽鈶?D銆佲憿鈶?13銆?= 14鏈夋剰涔夛紝鍒檟鐨勫彇鍊艰寖鍥存槸銆?15銆佹瘝绾块暱涓?锛屽簳闈㈠渾鐨勭洿寰勪负2鐨勫渾閿ョ殑渚ч銆?16涓庣洿绾?鐩镐氦浜庣偣P锛?锛?锛夛紝鍒欏叧浜巟鐨勪笉绛夊紡鐨勮В闆嗕负銆?172cm锛?cm锛?cm锛?cm鐨勫洓鏍规湪鏉★紝灏忓己鎷垮嚭浜嗕竴鏍?cm闀跨殑鏈銆?18鎰忛潪闆跺疄鏁皒锛寉瀹氫箟鐨勬柊杩愮畻鈥?鈥? ,鍑忔硶鐨勮繍绠楋紝宸茬煡锛?锛屽垯= 銆?涓夈€佽В19銆佸厛鍖栫畝锛屽湪姹傚€硷細锛屽叾涓?20銆佹煇鏍′负浜嗚В锛?锛夛紙2娊鍙栫殑浜斾釜绛夌骇鎵€鍗犳瘮渚嬪拰浜烘暟鍒嗗竷鎯呭喌锛岀粯鍒跺嚭涔濆勾绾э紙1?锛夌彮鐨勭粺璁¤〃銆?锛?т汉鏁?锛?锛変節锛?锛夌彮銆佷節锛?锛屼腑浣嶆暟鍒嗗埆涓?锛??21銆佹煇瀛︽牎璁″垝鍒╃敤鏆戝亣浜嬩欢锛堝叡60澶繘琛岀矇鍒凤紝鐜版湁鐢蹭箼涓や釜宸ョ▼闃熸潵鎵垮寘锛岃皟鏌ュ彂鐜帮細涔欓槦鍗曠嫭瀹屾垚宸ョ▼鐨勬椂闂存槸鐢查槦鐨?.5鍊嶏紱鐢层€佷箼涓ら槦鍚堜綔瀹屾垚宸ョ▼闇€瑕?0澶╋紱鐢查槦姣忓ぉ鐨勫伐浣滆垂鐢ㄤ负1000鍏冿紝涔欓槦姣忓ぉ鐨勫伐浣滆垂鐢ㄤ负600锛?锛夌敳銆佷箼涓ら槦鍗曠嫭瀹屾垚杩欓」宸ョ▼鍚勯渶澶氬皯澶╋紵锛?锛夆憼鈶′粠璧22BCD E锛孎涓鸿竟BC銆丆D涓婄殑鐐癸紝涓擟E=CF E锛孉F锛屸垹ABC E浜庣偣G锛岃繛G銆?(1)姹傝瘉锛欰G=CG 锛?锛夋眰璇侊細CG F (3)G=CG锛屽垯鈻矨BE涓庘柍BGE?23銆佽幏鎮夆€滆帿瑷€鑾峰緱浜?012?00鍏冮挶鍒颁功搴楄喘涔拌帿瑷€浣滃搧渚?閮ㄥ垎涔︾睄鍜?涔﹀悕鍘熶环锛堝厓锛?銆婅洐銆?37.5 銆婄敓姝荤柌鍔炽€?15 銆婄孩楂樼脖瀹舵棌銆?21 鑻ユ潕20細锛?锛夎喘涔般€婄孩楂樼脖瀹舵棌銆嬬殑鎬讳环涓?鍏冿紙鐢ㄥ惈x锛寉鐨勪唬鏁板紡琛ㄧず锛?锛?伴噺鐨?鍊嶏紝璇峰啓鍑簑鍏充簬x鐨勫嚱鏁板叧绯诲紡锛屽苟姹傚嚭銆婅洐銆(3)鑻ユ潕鑰佸笀鍦ㄤ功鍩庤喘涔颁簡浠ヤ笂?50?24BCD AD C锛屸垹BCD=90o,宸茬煡AB=5锛孊C=6,cosB= 銆傜偣O鐢辩偣B鍚戠偣C浠ユ瘡绉?C t OB涓哄崐寰勭殑鈯橭涓嶢B杈逛氦浜庣偣P銆?锛?锛夋眰AD鐨勯暱锛?锛夊綋t=AD鏃讹紝濡傚浘锛?锛夛紝姹侭P鐨勯暱锛?锛夌偣O杩愬姩鐨勮繃绋嬩腑锛岃繃鐐笵鐨勭洿绾緿Q涓庘姍O鐩稿垏浜庣偣Q锛屼氦BC浜庣偣E3锛夛紝褰揇Q B鏃讹紝姹倀鐨勫€笺€?25BCA锛?锛?锛夈€佺偣B(1.0),鎶涚墿绾?缁忚繃鐐笴銆?锛?锛夋眰鐐笴鐨勫潗鏍囧拰鎶涚墿绾跨殑瑙f瀽寮?锛?锛夎嫢鎶涚墿绾跨殑瀵圭О杞翠簬AB鐨勪氦鐐逛负M锛屾眰鈻矨CM鐨勯潰绉?锛?锛夎嫢灏嗏柍ABC娌緼B缈绘姌锛岀偣C囩▼锛?鑻ュ皢鈻矨BC娌緽C缈绘姌锛岀偣A嚎涓婏紵鐩存帴鍐欏嚭缁撴灉锛?26銆佸皾璇曟帰绌讹細灏忓紶鍦ㄦ暟瀛﹀疄璺垫椿鍔ㄤ腑锛岀敾浜嗕竴涓猂t鈻矨BC锛屼娇鈭燗CB=90o锛孊C=1锛孉C=2BC涓哄崐寰勭敾寮т氦AB浜庣偣D锛岀劧鍚庝互A 涓哄渾蹇冧互AD C浜庣偣E E= 锛E2 =AC C,,璇峰悓瀛︿滑楠岃瘉灏忓紶鐨勫彂鐜版槸?鎷撳睍寤朵几锛?AC鍙婄偣E 锛屾帴鐫€鏋勯€燗E=EF=CF F锛屽緱鍒颁笅鍥撅紝璇曞畬鎴愪互涓嬮棶棰橈細鈶犳眰璇佲柍ACF鈭解柍FCE 鈶℃眰鈭燗鐨勫害鏁帮紱鈶㈡眰cos鈭燗搴旂敤杩佺Щ锛?鍒╃敤涓婇潰鐨勭粨璁猴紝鐩存帴鍐欏嚭锛?鈶犲崐寰勪负2鐨勫渾鍐呮帴姝e崄杈瑰舰鐨勮竟闀夸负鈶¤竟闀夸负2锛掞紣锛??垎鏍囧噯涓€銆侀€夋嫨棰橈細1銆丄銆€銆€2銆丆3銆丅銆€銆€4銆丆5銆丅銆€銆€6銆丄7銆丄銆€銆€8銆丏9銆丅銆€銆€10銆丄11銆丏銆€銆€12銆丅?鍒嗭紝鍏?8鍒嗭級13. 1 銆€銆€14. x鈮?1 15. 3蟺銆€銆€16. x鈮? 17. 銆€銆€18. 4锛?涓夈€佽В绛?2鍒嗭級19.瑙o細= 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?3鍒?= 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?5鍒?褰揳=-1,b= 鏃讹紝鍘熷紡=4+ 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?20.锛?锛?锛?锛塁銆丅锛汣銆丆鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?6鍒?锛?锛夊洜涓轰腑浣嶆暟鐩稿悓锛屼絾锛?锛夌殑浼楁暟灏忎簬锛?锛夌殑浼楁暟锛屾墍浠ユ垜璁や负锛?锛夋洿鍠︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?紭鍔f寜A銆丅銆丆銆丏銆丒鐢遍珮鍒颁綆銆傝嫢瀛︾敓浠嶢绛夌骇缁煎悎鑰冭檻璁や负锛?锛夊ソ涔熷彲缁欐弧鍒嗐€?21.瑙o細锛?鎴愰渶x澶╋紝鍒欎箼鍗曠嫭瀹屾垚闇€1.5x鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?3鍒?瑙e緱x=50锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?4鍒?=50В锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?5鍒?鍒?.5x=75锛?鎵€浠ョ敳銆佷箼涓ら槦鍗曠嫭瀹屾垚杩欓」宸ョ▼鍚勯渶50銆?5澶┿€?鈥︹€︹€︹€︹€︹€?6鍒?锛?锛夆憼鍥犱负瀛︽牎鍋囨湡涓?0澶╋紝鐢茬殑瀹屾垚鏃堕棿涓?0澶╋紝灏忎簬60澶╋紱涔欑殑瀹屾垚鏃堕棿涓?5澶╋紝澶т簬60澶╋紝鎵€浠ヤ粠鏃堕棿涓婅€冭檻搴旈€夋嫨鐢查槦锛涒€︹€︹€︹€︹€︹€?7鍒?鈶$敳鎵€闇€鐨勮祫閲戯細50脳1000=50000鍏冿紱涔欐墍闇€璧勯噾锛?5脳600=45000鍏冿紱45000锛?0000 鎵€浠ヤ粠璧勯噾瑙掑害鑰冭檻搴旈€夋嫨涔欓槦銆傗€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?21. 璇佹槑锛?锛?BCD?鈭碅B=BC 鍙堚埖鈭燗BG=鈭燙BG锛孊G=BG 鈭粹柍AGB鈮屸柍CGB锛圫AS锛?鈭碅G=CG 鈥︹€︹€︹€︹€︹€︹€?2鍒?锛?锛夎繛缁揂C 鈥︹€︹€︹€︹€︹€︹€?3鍒?鈭靛洓杈瑰舰ABCD?鈭粹垹DCA=鈭燘CA 鍙堚埖CF=CE锛孋A=CA 鈭粹柍AFC鈮屸柍AEC锛圫AS锛?鈭粹垹FAC=鈭燛AC 鈭礎G=CG 鈭粹垹EAC=鈭燝CA 鈭粹垹FAC=鈭燝CA 鈭碈G F 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?5鍒?锛?锛夆埖BG=CG 鈭粹垹GBC=鈭燝CB 鈭碘柍AGB鈮屸柍CGB 锛堝凡璇侊級鈭粹垹GAB=鈭燝CB 鈭粹垹GAB=鈭燝BC 鍙堚埖鈭燗EB=鈭燗EB 鈭粹柍ABE鈭解柍BGE 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?23.锛?锛?20-21x-21y 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?1鍒?锛?锛墄=2锛?0-x-y锛夛紝y=20-1.5x锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?2鍒?w=37.5x+15y+21锛?0-x-y锛?25.5x+300锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?3鍒?瑙e緱锛?鍥犱负x,鎵€浠ヨ兘涔?︹€︹€︹€︹€︹€︹€︹€?6鍒?锛?锛? 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?24.1锛夎繃鐐笰浣淎E C浜庣偣E锛?鈭礎B=5锛宑osB= 鈭碆E=AB osB=3 鈭碋C=BC-BE=3 鈥︹€︹€︹€︹€︹€︹€︹€︹€?2鍒?鈭礎D C锛屸垹BCD=90掳鈭粹垹C=鈭燚=鈭燗EC=90掳鈭村洓杈瑰舰AECD?鈭碅D=3 鈥︹€︹€︹€︹€︹€︹€︹€︹€?3鍒?锛?锛夆埖AD=3 鈭村綋t =AD鏃讹紝OB=3 杩囩偣O浣淥F P浜庣偣F 鈭碆F= BP 鈭礳osB= 鈭碆F=BO osB= 鈭碆P= 鈥︹€︹€︹€︹€︹€︹€︹€︹€?6鍒?锛?Q 鈭礑Q B锛孉D C 鈭村洓杈瑰舰ABED鈭碆E=AD=3锛孌E=AB=5 鈭碈D= =4 鈭礏O=t 鈭碠E=3-t 鈭电洿绾緿Q涓庘姍O鐩稿垏浜庣偣Q 鈭粹垹OQE=鈭燙=90掳鈭碘垹OEQ=鈭燚EC锛?鈭粹柍OQE鈭解柍DCE 鈭?鈭?鈭磘= 鈥︹€︹€︹€︹€︹€︹€︹€︹€?9鍒?25. 瑙o細锛?锛夎繃C鐐逛綔CE鈭碘柍ABC 涓虹瓑鑵扮洿瑙掍笁瑙掑舰鈭碅B=AC 鈭?ABC=900 鍦≧t鈻矨OB涓?鈭燨AB+鈭燗BO=900 鈭碘垹ABO+鈭?CBE=900 鈭粹垹OAB=鈭燙BE 鈭碘垹CEB=鈭燗OB=900 鈭粹柍AOB鈮屸柍BEC 鈥︹€︹€︹€︹€︹€︹€?1鍒?鈭碆E=AO CE=OB 鈭礎(0,2)B(1,0) 鈭碅O=2 BO=1 鈭碆E=2 CE=1 鈭碠E=3 鈭?C(3,1) 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?2鍒?甯﹀叆y=ax2-ax-2鍥惧儚涓?鈭碼= 鈭磞= x2- x-2 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?3鍒?锛?=- =- = 鈥︹€︹€︹€︹€︹€?4鍒?AB浜庣偣F 鈭寸偣M鐨勫潗鏍囦负锛?锛?锛?鈭寸偣M鏄疧B鐨勪腑鐐?鈭礛F?鈭碏鏄疉B鐨勪腑鐐?鈭靛湪Rt鈻矨OB AB= = 鈭碨鈻矨CM= S鈻矨BC = 脳脳脳= 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?7鍒?锛?BC 娌緼B缈绘姌鍚庡緱鍒扳柍ABD锛?杩囩偣D浣淒M锛?锛夛紝鈭礏D=BC锛屸垹MBD=鈭燛BC锛屸垹DMB=鈭燙EB=90掳锛?鈭粹柍DBM 鈮屸柍CBE锛?鈭碆M=BE=2锛孌M=CE=1锛?鈭碊锛?1锛?1偣D鍦?鎶涚墿绾縴= x2- x-2涓婏紱鈥︹€︹€︹€︹€︹€︹€?鍒?灏嗏柍ABC娌緽C缈绘姌锛岀偣A涓嶅湪璇ユ姏鐗╃嚎涓娿€傗€︹€︹€︹€︹€︹€︹€?0鍒?26.锛?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?1鍒?AE2=6-2 ,AC C=6-2 ,鈭寸?鈥︹€︹€︹€︹€︹€︹€?2鍒?鈶犫埖AE2=AC C锛?鈭?鈭礎E=FC 鈭?鍙堚埖鈭燘=鈭燘鈭粹柍ACF鈭解柍FEC 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?5鍒?鈶♀埖鈻矨CF鈭解柍FEC锛屼笖EF=FC 鈭碅C=AF 鈭礎E=EF 鈭粹垹A=鈭燗FE 鈭粹垹FEC=2鈭燗鈭礒F=FC 鈭粹垹C=2鈭燗鈭粹垹AFC=鈭燙=2鈭燗鈭碘垹AFC+鈭燙+鈭燗=180掳鈭粹垹A=36掳鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?鈶㈣繃鐐笷浣淔MB B浜庣偣M 鐢憋紙1E= 锛孍B= 鈭礒F=FB 鈭碝E= 鈭碅M= 鈭碿os鈭燗= = 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?10鍒?锛?锛夆憼鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?11鍒?鈶?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?12鍒?。
南安实验中学2013年中考数学模拟试题(一)

南安实验中学2013年中考数学模拟试题(一)(满分:150分;考试时间:120分钟)班级: 姓名: 座号: 成绩: 一、选择题:(每小题3分,共21分) 1. -3的绝对值是( )A .13B . - 13 C .3 D .-32. 下列运算正确的是( )A .632)(x x = B .22)(xy xy = C .22x x x =⋅ D .422x x x =+ 3.下列图形中,一定是中心对称图形的是( ).A .等腰三角形B .直角三角形C .梯形D .平行四边形 4.不等式组⎩⎨⎧<>-4201x x 的解集是( ).A .x >1B .x <2C .1<x <2D .无解 5.下列正多边形中,能够铺满地面的是( ).A .正五边形B .正六边形C .正七边形D .正八边形6.已知⊙O 1和⊙O 2的半径分别为5和2,O 1O 2=7,则⊙O 1和⊙O 2的位置关系是( ). A .外离 ; B .外切 ; C. 相交 ; D .内含 .7. 已知A 、B 、C 、D 、E 是反比例函数16y x=(x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是( ).A .2613-πB .3216-πC .2814-πD .2412-πP 二、填空题:(每小题4分,共40分) 8.-2的相反数是 .9.宝岛台湾的面积约为36 000平方公里,用科学记数法表示约为________平方公里. 10.分解因式:x x 22- = .11.“明天会下雨”是 事件.(填“必然”或“不可能”或“可能” ). 12.二元一次方程组2,x y x y +=⎧⎨-=⎩的解是 .13.如图,AB ∥CD ,AC ⊥BC ,∠BAC =65°,则∠BCD =________度. 14.已知正比例函数)0(≠=k kx y 的图像过点A (2,1),则k =________. 15.如图,正方形ABCD 是⊙O 的内接正方形,点P 是⌒CD 上不同于点C 的任意一点,则∠BPC 的度数是_____________度.16.圆锥的母线长为5cm ,底面半径为3cm ,那么它的侧面展开图的圆心角等于 .17.如图5,已知∠ABC =90°,AB =πr ,BC =πr2,半径为r 的⊙O 从点A 出发,沿A →B →C 方向滚动到点C 时停止.请你根据 题意,在图5上画出圆心..O 运动路径的示意图; 圆心O 运动的路程是 . 三、解答题:(共89分)18.(9分)计算:218212013420⨯-⎪⎭⎫ ⎝⎛-+--AFBECD19.(9分)先化简,再求值:()()()2212-+--a a a ,其中252+-=a .20.(9分)某校课题研究小组对本校九年级全体同学体育测试情况进行调查,他们随机抽查部分同学体育测试成绩(由高到低分A 、B 、C 、D 四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.请根据以上不完整的统计图 提供的信息,解答下列问题: (1)该课题研究小组共抽查了 _________名同学的体育测试成绩,扇形统计图中B 级所占的百分比 B=___________;(2)补全条形统计图;(3)若该校九年级共有400名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C 级)约有___________名.21.(9分)已知:如图点C E B F ,,,在同一直线上,AC DF ∥,AC DF =,BF CE =. 求证:DEF ABC ∆≅∆。
2013年福建省永安中学中考模拟试题数学试卷及答案

通江县永安中学2013级中考模拟考试数 学 试 题本试卷分为第Ⅰ卷(选择性试题)和第Ⅱ卷(非选择性试题)。
全卷共10页。
全卷总分为150分,考试时间为120分钟。
第Ⅰ卷(选择题,共30分)一、选择题:将你认为正确的答案填入题后的答题卡内。
(每小题3分,共30分) 1.2-的倒数是( )A .12B .12-C .2D .2-2.下列运算正确的是( )A 、4222a a a =+ B 、552233=+C 、()112-=- D 、()42242a a =-3.下面的图形中既是轴对称图形又是中心对称图形的是( )4、下列说法不正确的是( )A 数据6、3、5、4、1、-2的中位数是3.5;B 方差反映了一组数据的波动大小,方差越大,波动越大;C 某种彩票的中奖率是1%,因此买100张该种彩票一定会中奖;D 在选举中,人们通常最关心是数据的众数.5.如图,已知四边形ABCD 是平行四边形,下列结论中正确的是( ) A.当AC ⊥BD 时,它是矩形 B.当AB=BC 时,它是菱形C.当∠ABC=90°时,它是菱形DBAD.当AC=BD 时,它是正方形6.如图CD 是Rt △ABC 斜边上的高,AC=4,BC=3,则cos ∠BCD 的值是( ).A .35B .34C .43D .457、ΔABC 内接于⊙O ,∠A =400,则∠BCO 的度数为( ) A . 400 B. 500 C. 600 D 800 8. 针对代数式x 2一6x+10的值的说法,其中叙述错误的是( )A.找不到实数x ,使得x 2一6x+10的值为0;B.只有当x=3时,x 2一6x+10的值为1;C.x 2一6x+10的值随x 的变化而变化,x 可取一切实数,所以该代数式没有最小值;D.当x 取大于3的实数时,x 2一6x+10的值随x 的增大而增大,所以该式没有最大值。
9.如图,在等边ΔABC 中,点O 在AC 边上,AC=9,AO=3,点P 是AB 边上一动点,连结OP ,将线段OP 绕点O 逆时针旋转600得到线段OD .要使点D 恰好落在上BC ,则AP 的长是( )A .4B .5C .6D .810、二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列结论错误的是( ) A a 、b 异号 B 当y =5时,x 的取值可能为0 C 4a +b =0 D 当x =-1和x =4时,函数值相等CODPBA17.如图,在ABC∆中,点D、E分别在AB、E,15AB=,则AD=。
2013年中考数学模拟试题及答案
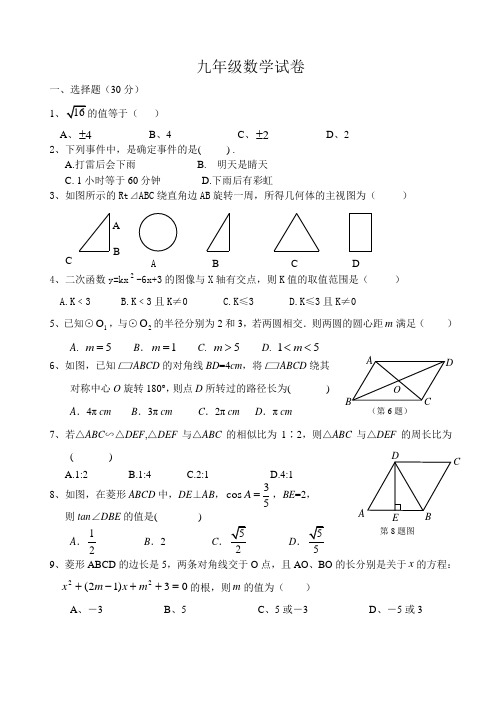
九年级数学试卷一、选择题(30分) 1)A 、4±B 、4C 、2±D 、2 2、下列事件中,是确定事件的是( ) .A.打雷后会下雨B. 明天是睛天C. 1小时等于60分钟D.下雨后有彩虹3、如图所示的Rt ⊿ABC 绕直角边AB 旋转一周,所得几何体的主视图为( )4、二次函数y=kx 2) A.K ﹤3 B.K ﹤3且K ≠0 C.K ≤3 D.K ≤3且K ≠05、已知⊙1O ,与⊙2O 的半径分别为2和3,若两圆相交.则两圆的圆心距m 满足( ) A . 5m = B .1m = C . 5m > D . 15m <<6、如图,已知□ABCD 的对角线BD =4cm ,将□ABCD 绕其对称中心O 旋转180°,则点D 所转过的路径长为( ) A .4π cmB .3π cmC .2π cmD .π cm7、若△ABC ∽△DEF ,△DEF 与△ABC 的相似比为1∶2,则△ABC 与△DEF 的周长比为( )A.1:2B.1:4C.2:1D.4:1 8、如图,在菱形ABCD 中,DE ⊥AB ,3cos 5A =,BE =2, 则tan ∠DBE 的值是( )A .12 B .2 C .2 D .59、菱形ABCD 的边长是5,两条对角线交于O 点,且AO 、BO 的长分别是关于x 的方程:03)12(22=++-+m x m x 的根,则m 的值为( )A 、-3B 、5C 、5或-3D 、-5或3CC第8题图(第6题)ABCDO10、已知二次函数2(0)y ax bx c a =++≠的图象如右图所示, 下列结论: ①0abc > ②b a c <+③20a b += ④()(1a b m am b m +>+≠的实数), 其中正确的结论有( )A 1个B .2个C . 3个D .4个二、填空题(18分) 11、在函数y =x 的取值范围是 . 12、已知三角形两边长是方程2560x x -+=的两个根,则三角形的第三边c 的取值范围是13、从1,2,3,…,19,20这二十个整数中任意取一个数,这个数是3的倍数的概率是 . 14、在半径为1的⊙O 中,弦AB 、AC 的长分别为2和3,则∠BAC 的度数为 。
浙江省湖州市2013年中考数学模拟试题10

第4题图E D OCBA1A 2A 3A 4A 5A 6A7A 8A 9A 12A O2013年湖州市中考数学模拟卷10(考试时间120分钟,满分120分) 姓名 一、选择题1.61-的相反数是A .6 B .6- C . 61 D .61-2.下列运算正确的是A .23a a a += B .22(3)6a a = C .623a a a ÷= D .34aa a =· 3. 3月11日,日本发生地震和海啸,3月12日,中国红十字会向日本红十字会提供100万元人民币的紧急援助,同时发出慰问电,向日本受灾群众表示诚挚的慰问,对地震遇难者表示深切的哀悼,并表示将根据灾区需求继续提供及时的人道援助. 100万这个数用科学记数法表示为 A. 410.01⨯ B. 610.01⨯ C. 510.01⨯ D. 6101.0⨯4.如图,四边形ABCD 的对角线互相平分,要使它成为矩形, 那么需要添加的条件是A.CD AB =B.BC AD =C.BC AB =D.BD AC = 5.某射击队要从四名运动员中选拔一名运动员参加比赛,选拔赛中每名队员的平均成绩x 与方差2S 如下表所示.如果要选择一个成绩高 且发挥稳定的人参赛,则这个人应是 A .甲 B .乙 C .丙 D .丁6.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若 该水库的蓄水量V (万米3)与降雨的时间t (天)的关系如图 所示,则下列说法正确的是A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米37.如图,AB 是⊙O 的直径,CD 为弦,AB CD ⊥于E ,则下列结论中不.成立的是 A.∠A ﹦∠D B.CE ﹦DE C.∠ACB ﹦90°D .CE ﹦BD8.已知抛物线2y ax bx c =++(a <0)过)0,2(-A 、)0,0(O 、),3(1y B -、),3(2y C 四点,则1y 与2y 的大小关系是A .1y >2yB .1y 2y =C .1y <2yD .不能确定 9.如图,已知121=A A , 9021=∠A OA ,3021=∠OA A ,以斜边2OA 为直角边作直角三角形,使得3032=∠OA A ,依次以前一个直角三角形的斜边为直角边一直作含o30角的直角三角形,则甲 乙 丙 丁89 9 8 111.21.3t/天V/万米350403020165432100x 2S第13题图AB OA D C BO 1 2 1 2 yx20112010OA A Rt ∆的最小边长为A .20092B .20102C .2009)32(D .2010)32(10.如图是一个空心圆柱形纸筒,高为3,底面圆周长为4,若将这个纸筒沿圆筒侧面线路B M A →→剪开铺平,所得图形可能为 A .边长为3和4的矩形 B .边长为5和4的矩形C .边长为5和3的平行四边形D .边长为5和4的平行四边形二、填空题11.因式分解m m 43- = .12.在一个不透明的布袋中,黄色、白色的乒乓球共10个,这些球除颜色外其他都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中白色球的个数很可能是 个.13.某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO =8米, 母线AB =10米,则该圆锥的侧面积是 平方米(结果保留π).14.如图,有一种动画程序,屏幕上正方形ABCD 是黑色区域(含正方形边界),其中A (1,1)、B (2,1)、C (2,2)、D (1,2),用信号枪沿直线b x y +=2发射信号,当信号遇到黑色区域时,区域便由黑变白,则能使黑色区域变白的b 的取值范围为 .15.如图,已知直线1l ∥2l ∥3l ∥4l ∥5l ,相邻两条平行直线间的距离都相等,如果直角梯形ABCD 的三个顶点在平行直线上,90=∠ABC 且AB=3AD ,则αtan = .16.有两个等腰三角形甲和乙,甲的底角等于乙的顶角,甲的底长等于乙的腰长,甲的腰长等于乙的底长,则甲的底角是 度.三、解答题17.计算: |2-|o 2o 12sin30(3)(tan45)-+--+18.化简求值:)11(x -÷11222-+-x x x 其中2=x .19.如图,利用尺规求作所有点P ,使点P 同时满足下列两个条件:○1αABCD2l 1l3l 4l 5l BA1l2lO点P 到B A ,两点的距离相等;②点P 到直线21,l l 的距离相等.(要求保留作图痕迹, 不必写出作法)20. 甲、乙两校参加县教体局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现 学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.(1)在图1中,“7分”所在扇形的圆心角等于 度;甲校成绩统计表中得分为9分的人数是 .求出乙校的参赛人数,并将图2的统计图补充完整.(2)如果该教体局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?21.图①是一个小朋友玩“滚铁环”的游戏,将这个游戏抽象为数学问题如图②,已知铁环的半径为25cm ,设铁环中心为O ,铁环与地面接触点为F ,铁环钩与铁环的接触点为A ,铁环钩与手的接触点是B ,铁环钩AB 长75cm, BG 表示点B 距离地面的高度.(1)当铁环钩AB 与铁环相切时(如图③),切点A 离地面的高度AM 为5cm ,求水平距离FG的长;(2)当点A 与点O 同一水平高度时(如图④),铁环容易向前滚动,现将如图③铁环钩的一端从A 点提升到与O 点同一水平高度的C 点,铁环钩的另一端点从点B 上升到点D ,且水平距离FG 保持不变,求BD 的长(精确到1cm ).22. 某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日平均销售的关系如下:销售单价6 6.57 7.58 8.5 9分数 7 分 8 分 9 分 10分 人数118乙校成绩扇形统计图10分9分 8分72° 54°7分乙校成绩条形统计图8 6 48分 9分 分数人数 2 10分 708 45 甲校成绩统计表② ① ③CI H MOA DFBGPI H MO A FBGH O FG AB④(元) 日平均销售量(瓶)480 460440420400380360(1)若记销售单价比每瓶进价多x 元,则销售量为 (用含x 的代数式表示);求日均毛利润(毛利润=售价-进价-固定成本)y 与x 之间的函数关系式. (2)若要使日均毛利润达到1400元,则销售单价应定为多少元?(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元? 23. 将正方形ABCD 绕中心O 顺时针旋转角α得到正方形1111D C B A ,如图1所示.(1)当α=45o时(如图2),若线段OA 与边11D A 的交点为E ,线段1OA 与AB 的交点为F ,可得下列结论成立 ①FOP EOP ∆≅∆;②1PA PA =,试选择一个证明.(2)当oo900<<α时,第(1)小题中的结论1PA PA =还成立吗?如果成立,请证明;如果不成立,请说明理由.(3)在旋转过程中,记正方形1111D C B A 与AB 边相交于P ,Q 两点,探究POQ ∠的度数是否发生变化?如果变化,请描述它与α之间的关系;如果不变,请直接写出POQ ∠的度数.24.如图,二次函数452+-=x x y 的图象与x 轴交于A ,B 两点(点A 在点B 左侧),顶点为C ,有一个动点E 从点B 出发以每秒一个单位向点A 运动,过E 作y 轴的平行线,交ABC ∆的边BC 或AC 于点F ,以EF 为边在EF 右侧作正方形EFGH ,设正方形EFGH 与ABC ∆重叠部分面积为S ,E 点运动时间为t 秒.(1)求顶点C 的坐标和直线AC 的解析式;(2)求当点F 在AC 边上,G 在BC 边上时t 的值;(3)求动点E 从点B 向点A 运动过程中,S 关于t 的函数关系.APBQ1B C1C D1D O图1yyyDC1B B PFEOA1C1D图21A1AI H MOA FBG九年级数学参考答案 一.选择题CDBDB BDACD二.填空题11.)2)(2(-+m m m 12.4 13.60π 14.03≤≤-b 15.43 16.o36或60(答对一个得3分)三.解答题解:(1) 原式=1312+-+ =1(2)原式=2)1()1)(1(1--+⋅-x x x x x =x x 1+ 当2=x 时,上式=2318. (1) 144. 1每空 1分,共2分乙校的参赛总人数为人20415=÷ 2分作图如图所示. 1分(2)选择甲校,因为甲校满分的人数就是8人,而乙校满分的人数只有5人,也就是说甲校前八名的平均水平高于乙校前八名的平均水平,所以选择甲校. 3分.19.本题满分8分 作图略,即作AB 的垂直平分线和∠AOB 及其补角的角平分线,它们的交点即为21,P P , 每条线作出得3分,定出每点1分,共8分.21.本题满分10分解:(1)如图四边形HFGI ,HFMA 是矩形,20525=-=-=-=AM OF HF OF OHOHA Rt ∆中,1522=-=OH OA HA 2分 方法一 ∵AB 是圆的切线,∴090=∠OAB∴090=∠+∠=∠+∠AOH OAH BAI OAH ,得AOH BAI ∠=∠,又90=∠=∠AIB OHA , ∴备用图1 备用图23 乙校成绩条形统计图8 6 4 8分 9分 分数人数2 10分 图27分 0 845OHA ∆∽△AIB ,得AIABOH OA = 即AI752025=得60=AI 2分 756015=+=+==AI HA HI FG (cm) 1分(2)如图3,四边形OFGP 是矩形,502575=-=-=-=OC FG OC OP CP 1分 CPD Rt ∆中90.5552550752222≈=-=-=CP CD DP ; AIB Rt ∆中,455375sin =⨯=∠⋅=BAI AB IB 2分 50545=+=+=AM BI BG ,90.802590.55=+=+=OF DP DG 90.305090.80=-=-=BG DG BD 31≈(cm ) 2分22.本题满分12分解:(1)x 40520- 2分日均毛利润20052040200)40520(2-+-=--=x x x x y (130<<x )(2)1400=y 时,即1400200520402=-+-x x得8,521==x x 满足0﹤x ﹤13 2分此时销售单价为10元或13元,日均毛利润达到1400元. 2分 (3) 1490)213(402005204022+--=-+-=x x x y 2分 ∵132130<<,∴当213=x 时,即销售单价定为11.5元, 日均毛利润达到最大值1490元. 2分23本题满分12分.(1)若证明①FOP EOP ∆≅∆当α=45o 时,即o451=∠AOA ,又o 45=∠PAO ∴o 90=∠PFO ,同理o90=∠PEO ∴2ABFO EO == 2分 在Rt EOP ∆和Rt FOP ∆中,有⎩⎨⎧==OP OP OFOE∴FOP EOP ∆≅∆ 2分 若证明②1PA PA =DC1B B 1A P F EOA 1C1D1AB1BC1C D1DOEFP Q A 法一证明:连结1AA ,则∵O 是两个正方形的中心,∴1OA OA =451=∠=∠PAO O PA∴AO A O AA 11∠=∠ 2分 ∴PAO AO A O PA O AA ∠-∠=∠-∠111 即AP A P AA 11∠=∠∴1PA PA = 2分(2)成立 1分证明如下:法一证明:连结1AA ,则∵O 是两个正方形的中心,∴1OA OA =451=∠=∠PAO O PA∴AO A O AA 11∠=∠ 2分 ∴PAO AO A O PA O AA ∠-∠=∠-∠111 即AP A P AA 11∠=∠∴1PA PA = 2分(3)在旋转过程中,POQ ∠的度数不发生变化, 1分45=∠POQ 2分24.本题满分14分 (1)452+-=x x y =49)25(2--x ,顶点C 的坐标为(49,25-) 2分 452+-=x x y =)4)(1(--x x ,故点A (1,0)B (4,0) 设AC 直线为b kx y +=,得⎪⎩⎪⎨⎧+=-+=b k b k 25490,解得2323+-=x y 3分(2)可求得BC 直线为623-=x y ,当F 在AC 边上,G 在BC 边上时yE HHG FCB A E 点E 坐标为(0,4t -),点F 坐标为(2923,4--t t ) 得EF =t 2329-, 而EF =FG , 2分方法一:因为抛物线的对称轴和等腰三角形的对称轴重合所以FG =32)]4(25[2-=--t t t 2329-=32-t 解得715=t 3分方法二:抽取如图三角形,设正方形边长为x , 从FCG ∆∽ACB ∆得49493xx -=,得79=x , 2分即792329=-=t EF ,得715=t 1分(3)点E 坐标为(0,4t -)随着正方形的移动,重叠部分的形状不同,可分以下几种情况:① 点F 在BC 上时,如图1重叠部分是BEF ∆,此时230≤<t 时,点F 坐标为(t t 23,4--) BE EF S ⋅=212432321t t t =⋅⋅= 1分②点F 在AC 上时,点F 坐标为(2923,4--t t )又可分三种情况:Ⅰ.如图2,EH EB ≤时重叠部分是直角梯形EFKB ,此时5923≤<t427949)2329()32(212-+-=-⋅-+=t t t t t S 1分Ⅱ.如图3,EH EB >,点G 在BC 下方时,重叠部分是五边形EFKMH.此时71559<<t ,t EF 2329-=,点H 坐标为(0,25217t -),点M 坐标为(t t 415427,25217--) 427415-=t HM ,t GM 421445-=,t KG 27215-= KMG EFGH S S ∆=S -=(2923-t )2)421445)(27215(21t t ---OA CE FHGB yx图1H x yK GF CB AE 图2H xyMKGF CB A E=163518207161112-+-t t (如果不化成一般式不扣分)1分 Ⅲ.如图4, 点G 在BC 上或BC 上方时, 重叠部分是正方形EFGH,此时359<≤t2)2923(-=t S 1分直接分类给出表达式不扣分.H xyGFCBA E 图4。
2013年中考数学全新模拟试题(三)

2013年中考数学全新模拟试题(三)(120分钟)一、选择题(本题共8个小题,每小题4分,共32分) 在下列各题的四个备选答案中,只有一个是正确的. 1.-3的相反数是 A .3B .-3C .3±D .31-2.温家宝总理在2010年3月5日的十一届全国人大第三次会议的政府工作报告中指出,2010年,再解决60 000 000农村人口的安全饮水问题。
将60 000 000用科学记数法表示应为A .6106⨯B .7106⨯C .8106⨯D .61060⨯3.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32o, 那么∠2的度数是A.32oB.58oC.68oD.60o4.一个几何体的三视图如右图所示,这个几何体是 A .圆锥B .圆柱C .三棱锥D .三棱柱5.小明要给刚结识的朋友小林打电话,他只记住了电话号码的前5位的顺序,后3位是3,6,8三个数字的某一种排列顺序,但具体顺序忘记了,那么小明第一次就拨通电话的概率是A .121 B .61C .41D .31 俯视图左 视 图主视图第4题图6.2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是A.32,31B.31,32C.31,31D.32,357.若反比例函数ky x=的图象经过点(3)m m ,,其中0m ≠,则此反比例函数的图象在 A .第一、三象限B .第一、二象限C .第二、四象限8.如图,已知⊙O 是以数轴的原点O 为圆心,半径为1的圆,45AOB ∠=︒,点P 在数轴上运动,若过点P 且与OA 平行的直线与⊙O 有公共点, 设x OP =,则x 的取值范围是A .-1≤x ≤1B .x ≤2C .0≤x ≤2D .x >2 二、填空题(本题共16分,每小题4分) 9.在函数23-=x y 中,自变量x 的取值范围是 . 10.如图,CD AB ⊥于E ,若60B ∠=,则A ∠= 度.11.分解因式:=+-a 8a 8a 223 .12.如图,45AOB ∠=,过OA 上到点O 的距离分别为1357911 ,,,,,,的点作OA 的垂线与OB 相交,得到并标出一组黑色梯形,它们的面积分别为1234S S S S ,,,,. 则第一个黑色梯形的面积=1S ;观察图中的规律, 第n(n 为正整数)个黑色梯形的面积=n S .三、解答题(本题共25分,每小题5分) 13.计算:︒+⎪⎭⎫⎝⎛--+--30tan 3312010231.第8题第12题14. 解分式方程:22125=---xx15. 已知:如图,点E 、F 分别为□ABCD 的BC 、AD 边上的点,且∠1=∠2. 求证:AE=FC.16.已知0342=+-x x ,求)x 1(21x 2+--)(的值.17.如图,直线1l :1y x =+与直线2l :y mx n =+相交于点), 1(b P . (1)求b 的值;(2)不解关于y x ,的方程组 请你直接写出它的解; (3)直线3l :y nx m =+是否也经过点P ?请说明理由.OxyP第17题1l2l四、解答题(本题共10分,每小题 5分)18.如图,有一块半圆形钢板,直径AB =20cm ,计划将此钢板切割成下底为AB 的等腰梯形,上底CD 的端点在圆周上,且CD =10cm .求图中阴影部分的面积.19. 已知,如图,直线MN 交⊙O 于A,B 两点,AC 是直径,AD 平分∠CAM 交⊙O 于D ,过D 作DE⊥MN 于E .(1)求证:DE 是⊙O 的切线;(2)若6DE =cm ,3AE =cm ,求⊙O 的半径.第18题五、解答题(本题共6分)20.初中生对待学习的态度一直是教育工作者关注的问题之一.为此,某区教委对该区部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:(1)此次抽样调查中,共调查了名学生;(2)将图①补充完整;(3)求出图②中C级所占的圆心角的度数;(4)根据抽样调查结果,请你估计该区近20000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?六、解答题(本题共9分,21小题 5分,22小题4分)21.解应用题:某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.(1)这两种台灯各购进多少盏?(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?22.如图(1),凸四边形ABCD,如果点P满足∠=∠=,APD APBα∠=∠=,且BPC CPDβ则称点P为四边形ABCD的一个半等角点.(1)在图(2)正方形ABCD内画一个半等角点P,且满足αβ≠;(2)在图(3)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法).七、解答题(共22分,其中23题7分、24题8分,25题7分)23.已知:关于x 的一元二次方程01)2()1(2=--+-x m x m (m 为实数) (1)若方程有两个不相等的实数根,求m 的取值范围;(2)在(1)的条件下,求证:无论m 取何值,抛物线1)2()1(2--+-=x m x m y 总过x 轴上的一个固定点;(3)若m 是整数,且关于x 的一元二次方程01)2()1(2=--+-x m x m 有两个不相等的整数根,把抛物线1)2()1(2--+-=x m x m y 向右平移3个单位长度,求平移后的解析式.24.如图,已知抛物线C 1:5)2(2--=x a y 的顶点为P ,与x 轴相交于A 、B 两点(点A 在点B 的左边),点A 的横坐标是1-. (1)求p 点坐标及a 的值;(2)如图(1),抛物线C 2与抛物线C 1关于x 轴对称,将抛物线C 2向左平移,平移后的抛物线记为C 3,C 3的顶点为M ,当点P 、M 关于点A 成中心对称时,求C 3的解析式k h x a y +-=2)(;(3)如图(2),点Q 是x 轴负半轴上一动点,将抛物线C 1绕点Q 旋转180°后得到抛物线C 4.抛物线C 4的顶点为N ,与x 轴相交于E 、F 两点(点E 在点F 的左边),当以点P 、N 、E为顶点的三角形是直角三角形时,求顶点N 的坐标.25.已知,正方形ABCD中,∠MAN=45°, ∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由.如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)答案一、选择题(本题共8个小题,每小题4分,共32分)⎪⎩⎪⎨⎧∠=∠=∠=∠D B CD AB 21 ∴△ABE≌△CDF.……………………………………………………………………………4分 ∴AE=CF .………………………………………………………………………………………5分16.已知0342=+-x x ,求)x 1(21x 2+--)(的值.解: )x 1(21x 2+--)(x 221x 2x 2--+-= …………………………………………………………2分 1x 4x 2--= ………………………………………………………………3分由,03x 4x 2=+-得3x 4x 2-=-……………………………………………………4分所以,原式413-=--= …………………………………………………………5分 17.解:(1)∵),1(b 在直线1+=x y 上, ∴当1=x 时,211=+=b .…1分Ox y OP1l(2)解是⎩⎨⎧==.2,1y x…………………3分(3)直线m nx y +=也经过点P∵点P )2,1(在直线n mx y +=上, ∴2=+n m .……………………4分 把,1x =代入m nx y +=,得2m =+n .∴直线m nx y +=也经过点P .…………………………………………………5分四、解答题(本题共10分,每小题 5分)18.解:连结OC ,OD ,过点O 作OE⊥CD 于点E.……………………………………1分 ∵OE⊥CD,∴CE=DE=5,=53, ……………………………………………………2分 ∵∠OED=90°,DE=OD 21,∴∠DOE=30°, ∠DOC=60°. ∴3503601060S 2∏=⨯∏=扇形(cm 2) …………3分S △OCD =12·OE·CD = 25 3 (cm 2) ……………………………………………………4分∴S 阴影= S 扇形-S △OCD = (503π-253) cm 2∴阴影部分的面积为(503π-253) cm 2. ……………………………………………………5分说明:不答不扣分. 19.(1)证明:连接OD . ∵OA=OD ,OAD ODA ∴∠=∠. ∵AD 平分∠CAM ,OAD DAE ∠=∠ , ODA DAE ∴∠=∠. ∴DO∥MN. DE MN ⊥ ,∴DE⊥OD.………………………………………………………………………………1分A∵D 在⊙O 上,DC ∴是⊙O 的切线.……………………………………………………………………2分 (2)解:90AED ∠= ,6DE =,3AE =,AD ∴=3分连接CD .AC 是⊙O 的直径,90ADC AED ∴∠=∠= .CAD DAE ∠=∠ ,ACD ADE ∴△∽△.………………………………………………………………………4分 AD AC AE AD∴=.=∴15AC =(cm ).∴⊙O 的半径是7.5cm . ……………………………………………………………………5分(说明:用三角函数求AC 长时,得出tan ∠DAC =2时,可给4分.) 五、解答题(本题共6分)20.(1)200;…………………………………………………………………………………1分(2)2001205030--=(人).画图正确. ································ 3分(3)C 所占圆心角度数360(125%60%)54=⨯--=°°. ············ 4分 (4)20000(25%60%)17000⨯+=(名) ·················· 5分 ∴估计该区初中生中大约有17000名学生学习态度达标. ············ 6分六、解答题(本题共9分,21小题 5分,22小题4分)21.解:(1)设A 型台灯购进x 盏,B 型台灯购进y 盏.…………………….……1分 根据题意,得5040652500x y x y +=⎧⎨+=⎩ ···················· 2分解得:3020x y =⎧⎨=⎩···························· 3分(2)设购进B 种台灯m 盏.根据题意,得 1400)m 50(20m 35≥-+ 解得, 380m ≥···························· 4分 答:A 型台灯购进30盏,B 型台灯购进20盏;要使销售这批台灯的总利润不少于 1400元,至少需购进B 种台灯27盏 .……………………………………………………5分 22.解 :(1)所画的点P 在AC 上且不是AC 的中点和AC 的端点.(如图(2))……………2分 (2)画点B 关于AC 的对称点B ',延长DB '交AC 于点P ,点P 为所求(不写文字说明不扣分).………………………………………………………………………………………….4分(说明:画出的点P 大约是四边形ABCD 的半等角点,而无对称的画图痕迹,给1分)图(2)AC七、解答题(共22分,其中23题7分、24题8分,25题7分) 23.解:(1)△=22)1(4)2(m m m =-+- ∵方程有两个不相等的实数根,∴0≠m .………………………………………………………………………………………1分 ∵01≠-m ,∴m 的取值范围是1,0≠≠m m 且.…………………………………………………………2分 (2)证明:令0=y 得,01)2()1(2=--+-x m x m .∴)1(2)2()1(2)2(2-±--=-±--=m m m m m m x . ∴1)1(221-=--+-=m m m x ,11)1(222-=-++-=m m m m x . …………………………………4分∴抛物线与x 轴的交点坐标为(0,1-),(0,11-m ),∴无论m 取何值,抛物线1)2()1(2--+-=x m x m y 总过定点(0,1-).…………5分 (3)∵1-=x 是整数 ∴只需11-m 是整数. ∵m 是整数,且1,0≠≠m m ,∴2=m .……………………………………………………………………………………6分 当2=m 时,抛物线为12-=x y .把它的图象向右平移3个单位长度,得到的抛物线解析式为861)3(22+-=--=x x x y .……………………………………………………………7分24.解:(1)由抛物线C 1:5)2(2--=x a y 得顶点P 的坐标为(2,5)………….1分 ∵点A (-1,0)在抛物线C 1上∴95a =.………………2分(2)连接PM ,作PH⊥x 轴于H ,作MG⊥x 轴于G.. ∵点P 、M 关于点A 成中心对称, ∴PM 过点A ,且PA =MA.. ∴△P A H≌△M AG..∴MG=PH =5,AG =AH =3.∴顶点M 的坐标为(4-,5).………………………3分 ∵抛物线C 2与C 1关于x 轴对称,抛物线C 3由C 2平移得到 ∴抛物线C 3的表达式5)4(952++-=x y . …………4分 (3)∵抛物线C 4由C 1绕x 轴上的点Q 旋转180°得到 ∴顶点N 、P 关于点Q 成中心对称. 由(2)得点N 的纵坐标为5.设点N 坐标为(m ,5),作PH⊥x 轴于H ,作NG⊥x 轴于G ,作PR ⊥NG 于R. ∵旋转中心Q 在x 轴上, ∴EF=AB =2AH =6.∴EG =3,点E 坐标为(3m -,0),H 坐标为(2,0),R 坐标为(m ,-5). 根据勾股定理,得,104m 4m PR NR PN 2222+-=+= 50m 10m HE PH PE 2222+-=+=3435NE 222=+=①当∠PN E =90º时,PN 2+ NE 2=PE 2,解得m =344-,∴N 点坐标为(344-,5)②当∠P EN =90º时,PE 2+ NE 2=PN 2, 解得m =310-,∴N 点坐标为(310-,5). ③∵PN>NR =10>NE ,∴∠NP E ≠90º ………7分 综上所得,当N 点坐标为(344-,5)或(310-,5)时,以点P 、N 、E 为顶点的三角形是直角三角形.…………………………………………………………………………………8分 说明:点N 的坐标都求正确给8分,不讨论③不扣分.25.解:(1)如图①AH=AB………………………..1分 (2)数量关系成立.如图②,延长CB 至E ,使BE=DN ∵ABCD 是正方形∴AB=AD,∠D=∠ABE=90°∴Rt△AEB≌Rt△AND………………………………3分∴AE=AN,∠EAB=∠NAD∴∠EAM=∠NAM=45°∵AM=AM∴△AEM≌△ANM………………………………….4分∵AB、AH是△AEM和△ANM对应边上的高,∴AB=AH…………………………………………….. .5。
2013年佛山市中考模拟试题数学科试卷(三模)
2013年佛山市高中阶段招生考试模拟试题(三模)数学科试卷说 明:本试卷分为第Ι卷(选择题)和第Ⅱ卷(非选择题)两部分,满分120分,考试时间100分钟. 注意事项:1.试卷的选择题和非选择题都在答题卡上作答,不能答在试卷上.2.要作图(含辅助线)或画表,先用铅笔进行画线、绘图,再用黑色字迹的钢笔或签字笔描黑.3.其余注意事项,见答题卡.第Ⅰ卷(选择题 共30 分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.答案选项填涂在答题卡上) 1、5的相反数是( )A 、 5B 、5-C 、51 D 、51- 2、下列运算中正确的是 ( )A 、532a a a =+ B 、842a a a =⋅ C 、632)(a a = D 、326a a a =÷ 33、一个正方体的每个面都有一个汉字,其平面展开图如图所示,那么在该正方体中和“毒”字相对的字是( )A .卫B .防C .讲D .生4、.下列图形中,不是..轴对称图形的是( )A.B.C. D5、去年参加我市初中毕业生学业考试的考生总数为45730人,这个数据用科学记数法表示为( )A .0.4573×105B .4.573×104C .-4.573×104D .45.73×104(第3题图)讲 卫 生防 病 毒6、在半径为3的圆中,弦AB=3,则AB 的长度为( ) A 、π91B 、π32 C 、π D 、π317、 如图,在菱形ABCD 中,对角线AC=4,∠BAD=120°,则菱形ABCD 的周长为( )A .15B .16C .18D .20 8、下列事件是必然事件的是( ) A .明天一定会下雨.B .打开电视机,任选一个频道,屏幕上正在播放篮球比赛节目.C .某种彩票的中奖率为1%,买100张彩票一定中奖.D .13名学生中一定有两个人在同一个月过生日. 9、数轴上点P 表示的数可能是( ) B. C. 3.2-D.10、如图,在ΔABC 中,D 、E 分别为AB 、AC 的中点,连接DE ,S △ADE =1,则S △ABC =( ) A 、2 B 、3 C 、4 D 、6第Ⅱ卷(非选择题 共90分)二、填空题(本大题共5小题,每小题3分,共1511、不等式()2392+≥+x x 解集为 . 12、分解因式=-2732x ___ ___;13、连续抛一枚硬币三次,三次都是正面朝上的概率是 . 14、如图,⊙A 和⊙B 都与x 轴和y 轴相切,圆心A 和圆心B 都在反比例函数1y x=的图象上,则图中阴影部分的面积等于 。
2013年徐州市中考模拟考试数学试题
2013年徐州市中考模拟考试数学试题一、选择题:(本大题共8个小题.每小题3分;共24分) 1.3-的倒数是( )A .13-B .13C .3-D .32.下列运算正确的是( ) A.632a a a =⋅ B.()236aa =C.55a a a ÷= D.224x x x +=3.估算219+的值是在( )A. 5和6之间B. 6和7之间C. 7和8之间D. 8和9之间4.如图,AD BC ∥,点E 在BD 的延长线上,若155ADE ∠=,则DBC ∠的度数为( ) A.35B.50C.45D.255.在()()222y xy x 的括号( )中,分别填上“+”或“-”,在所得的代数式中,能构成完全平方式的概率是( )A.41B. 21C. 43D. 16.与如图所示的三视图对应的几何体是( )7.小明在九年级进行的六次数学测验成绩如下(单位:分):76、82、91、85、84、85,则这次数学测验成绩的众数和中位数分别为( )A .91,88B .85,88C .85,85D .85,84.58.如图,AB 是半圆ACB 的直径,半径OC ⊥AB 于点O ,AD 平分∠CAB 交弧BC 于点D ,连接CD 、OD ,给出以下四个结论:(1)AC ∥OD (2)CE=OE (3)△ODE ∽△ADO (4)2CD 2=CE ×AB 其中正确的个数是( )A. 1B. 2C. 3D. 4ADECA B C D二、填空题:(本大题共10个小题.每小题3分,共30分)9.函数11+=xy自变量x的取值范围是______________.10.分解因式:29xy x-=____________11.2012年江苏省财政收入为5860亿元,用科学记数法表示“5860亿”的结果是:12.若关于x的方程220xx m--=有两个不相等的实数根,则m的取值范围是.13.代数式238a b-++的值为18,那么代数式962b a-+14.如图,已知△ABC中,∠A=50°,剪去∠A15.如图,平行四边形ABCD中,AB3=,5BC=,AC的垂直平分线交AD于E,则CDE△的周长是__________.16.点P在双曲线(0)ky kx=≠上,点(12)P',与点P关于y轴对称,则此双曲线的解析式为.17.如图,如果将半径为9cm的圆形纸片剪去一个13圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为18.一次函数1y kx b=+与2y x a=+的图像如图,则下列结论①0k<;②0a>;③当3x<时,12y y<中,正确的序号是三、解答题:(本大题共10个小题,计86分.解答应写出文字说明、演算步骤.)19. (本小题满分10分)(1021)(1);+-(2)化简:23111a a aa a a-⎛⎫-⎪-+⎝⎭·第18題C20. (本小题满分10分)(1)解方程1x -3+1=2-x x -3. (2) 解不等式组205121123x x x ->⎧⎪+-⎨+⎪⎩,≥,21.(本小题满分8分)某小区从不同住宅楼中随机选取了200名居民,调查小区居民双休日的学习状况,并将得到的资料制成扇形统计图和频数分布直方图.(1)在这个调查中,200名居民双休日在家学习的有____________人;(2)在这个调查中,在图书馆等场所学习的居民学习时间的平均数和众数分别是多少? (3)估计该小区2 000名居民双休日学习时间不少于4小时的人数.22.(本题7分)北京时间2013年4月20日8:02,在四川雅安发生7.0级强震,政府迅速派出救援队前往救援。
2013年初三数学中考模拟试题
1-x<4方正中学2013届中考模拟数学试题(120分完卷,满分120分)考生注意:①请考生将学校、班级、姓名、准考证号准确写在规定的位置;②不允许使用科学一、选择题:(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是正确的,请将正确答案的字母填入题后的括号内.)1.0.2的倒数是()A.-0.2B.51C. 5D.-52.下列正确的是()A.zyxyxzxy45222)(3=-∙-B.525±=C.222332yyxx+-是三次三项式D.21-是整式3.下列图形中,是中心对称图形的是()4.下列调查中,适宜采用抽样方式的是()A 调查我市中学生每天体育锻炼的时间B 调查某班学生对“五个重庆”的知晓率C 调查一架“歼20”隐形战机各零部件的质量D 调查广州亚运会100米参赛运动员兴奋剂的使用情况5.如图所示几何体的主视图是()A.B.C.D.6.下列正确的是( )A因式分解:=-aam8222)2(2-ma B.若02=+aa,则a取值范围是0〈a aC.两直线被第三条直线所截,内错角相等。
D.关于x的方程02=+-qpxx的两个根是0和-3,则q-p=37.如图水库大坝横断面为梯形ABCD,坝顶7米,坝高CE,DE=8米,CD=10米,下底AD=27米,被水坡AB的坡度为( )A.1:3 B 1:2 C.1:2.5 D .1:1.58.下列中有两个不相等的实数根的方程是()A.012=+-xx B.)1(8)12(2+-=+xxC.622=-xx D.0442=+-yy9.右图⊙I是△ABC的内切圆与AB、BC、CA分别相切于点D、E、F,G在上,直线MN交AB、AC分别于P、H,∠BPN=600,∠AHM=1400,则∠DGF=()A.5000D.80010)A. B. C. D.11.如图,在等腰梯形ABCD中,AD∥BC,连结AC,且AC⊥AB于点A,∠CAD=30°AB=2,则梯形ABCD的中位线长是()A.52B.23C. 6D. 312.如图,二次函数)0,,(2≠++=acbacbxaxy是常数,图象的对称轴是直线1=x,其图象的一部分,对于下列说法正确的个数是()①0〈abc②03〈+ca③0〈+-cba④31〈〈-x时,y>0;A.1B.2C.3D.4第Ⅱ卷(非选择题,共88分)二、填空题:(本大题共4个小题,每小题3分,共12分)13.函数113-++=xxy中自变量x的取值范围是.14.一个不透明的口袋中有红、白、黄三种颜色的乒乓球(除颜色外其它都相同),其中有红球2个,白球1个,若从中任意摸出一个球,这个球是红球的概率为0.5.则口袋中黄球有_______个.15.已知圆锥底面半径为5cm,侧面积为65πcm2,设母线与高的夹角为θ,则cosθ的值为。
2013年中考模拟考试数学学业水平测试试题
第2题图 2013年学业水平考试模拟考试数 学 试 题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分120分.第Ⅰ卷1至2页,第Ⅱ卷3至8页.考试时间120分钟.2.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用2B 铅笔涂写在答题卡上,并同时将考点、姓名、准考证号、座号填写在试卷规定的地方.3.选择题选出答案后,用2B 铅笔把答题卡上对应题目的正确答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,答案写在试卷上无效.4.数学考试不允许使用计算器,考试结束后,应将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.如果+10%表示“增加10%”,那么“减少8%”可以记作 A .-18% B .-8% C .+2% D .+8% 2.如图,右面几何体的俯视图是3.在2008年北京奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为84.610⨯帕的钢材,那么84.610⨯的原数为 A .4 600 000 B .46 000 000 C .460 000 000 D .4 600 000 000 4.下列说法或运算正确的是A .1.0×102有3个有效数字B .222()a b a b -=-C .235a a a +=D .a 10÷a 4= a 6 5.已知反比例函数y =2x ,则下列点中在这个反比例函数图象的上的是 A .(-2,1) B .(1,-2) C .(-2,-2) D .(1,2)6.下列说法错误的是A的平方根是±2 B.2是分数 CD7.在10到99这些连续正整数中任意选一个数,其中每个数被选出的机会相等,求选出的数其十位数字与个位数字的和为9的概率A .908B .909C .898D .899A .B .C .D .第9题图B第8题图 A 1 B 1 C 12A 3B 2B 3C 2 C 3 第14题图第15题图OB第12题图D A 8.如图,在△ABC 中,∠C =90°.若BD ∥AE ,∠DBC =20°,则∠CAE 的度数是A .40°B .60°C .70°D .80° 9.已知两圆的半径分别为R 和r (R >r ),圆心距为d .如图所示, 若数轴上的点A 表示R -r ,点B 表示R +r ,当两圆外离时,表 示圆心距d 的点D 所在的位置是 A .在点B 右侧 B .与点B 重合C .在点A 和点B 之间D .在点A 左侧 10.已知21x y =⎧⎨=⎩是二元一次方程组81mx ny nx my +=⎧⎨-=⎩的解,则2m n -的算术平方根为A .4B .2C . 2D .±211.如果关于x 的一元二次方程x 2+px +q =0的两根分别为x 1=2,x 2=1,那么p ,q 的值分别是A .-3,2B .-3,-2C .3,2D .3,-212.如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD 于点O ,AE ⊥BC ,DF ⊥BC ,垂足分别为E 、F ,AD =4,BC =8,则AE +EF 等于A .9B .10C .11D .1213.已知抛物线2y ax bx c =++(a <0)过A (2-,0)、O (0,0)、B (3-,1y )、C (3,2y )四点,则1y 与2y 的大小关系是 A .1y >2yB .1y 2y =C .1y <2yD .不能确定14.如图,小红作出了边长为1的第1个正△A 1B 1C 1,算出了正△A 1B 1C 1的面积,然后分别取△A 1B 1C 1三边的中点A 2,B 2,C 2, 作出了第2个正△A 2B 2C 2,算出了正△A 2B 2C 2的面积,用同样的 方法,作出了第3个正△A 3B 3C 3,算出了正△A 3B 3C 3的面积……,由此可得,第8个正△A 8B 8C 8的面积是A 71()2B 81()2C 71()4D 81()415.在一次自行车越野赛中,甲乙两名选手行驶的路程y (千米)随时间x (分)变化的图象(全程)如图所示,根据图象判定下列结论不正确...的是 A .甲先到达终点 B .前30分钟,甲在乙的前面 C .第48分钟时,两人第一次相遇 D .这次比赛的全程是28千米第18题图第20题图第21题图AP DCB 第Ⅱ卷(非选择题 共75分)题中横线上.16.分解因式:229121m n -=____________________________.17.小颖妈妈经营的玩具店某次进了一箱黑白两种颜色的塑料球3000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球的个数约是_______.18.如图所示,一个宽为2 cm 的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数 恰好是“2”和“10”(单位:cm ),那么该光盘的直径是cm.. 19.如图,1∠的正切值等于. 20.已知函数y 1=x 2与函数y 2=-12x +3的图象大致如图,若y 1<y 2,则自变量x 的取值范围是21.已知:如图,在正方形ABCD 外取一点E ,连接AE ,BE ,DE .过点A 作AE 的垂线交ED 于点P .若1AE AP ==, PB =APD ≌△AEB ;②点B 到直线AE 的距离为;③EB ED ⊥;④1APD APB S S +=+V V ;⑤4ABCD S =+正方形其中正确的结论是__________.(将正确结论的序号填在横线上.)第22题图 AB CD FE 三、解答题:本大题共7个小题.共57分.解答应写出文字说明、证明过程或演算步骤.22.(本小题满分7分)⑴解不等式组122 3x x x +⎧⎪-⎨+⎪⎩>0 ≤⑵如图,将直角边长为6的等腰Rt △AOC 放在如图所示的平面直角坐标系中,点O为坐标原点,点C 、A 分别在x 、y 轴的正半轴上,一条抛物线经过点A 、C 及点B (–3,0).求该抛物线的解析式.23.(本小题满分7分)⑴解方程:33122x x x-+=--⑵如图,分别过点C 、B 作△ABC 的BC 边上的中线AD 及其延长线的垂线,垂足分别为E 、F .求证:BF =CE .第25题图 24.(本小题满分8分)为了增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:⑴在这次调查中共调查了多少名学生?⑵求户外活动时间为1.5小时的人数,并补充频数分布直方图; ⑶求表示户外活动时间 1小时的扇形圆心角的度数;⑷本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数是多少.25. (本小题满分8分)某商场为缓解“停车难”问题,拟建造地下停车库,如图所示是该地下停车库坡道入口的设计示意图,其中, AB ⊥BD ,∠BAD =18°,C 在BD 上,BC =0.5m .根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD 的长就是所限制的高度,而小亮认为应该以CE 的长作为限制的高度.小明和小亮谁说的对?请你判断并计算出正确的结果.(结果精确到0.1m )参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32,sin72°≈0.95,cos72°≈0.31.26.(本小题满分9分)为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80%销售.现购买太阳能路灯x个,如果全部在甲商家购买,则所需金额为y1元;如果全部在乙商家购买,则所需金额为y2元.⑴分别求出y1、y2与x之间的函数关系式;⑵若市政府投资140万元,最多能购买多少个太阳能路灯?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
数学试题卷
满分:120分 时间:90分钟
一、选择题(每题4分,共40分)
1、把26个英文字母依照轴对称性和中心对称性分成5组,现在还有5个字母D 、M 、Q 、X 、Z 请你按原规律补上,其顺序依次为 -------------------------------------------------------------------( )
①FRPJLG ②HIO ③NS ④BCKE ⑤VATYWU (A )QXZMD (B )DMQZX (C )ZXMDQ (D )QXZDM
2、若12
1
≤≤-
x ,则式子1449612222++++-++-x x x x x x 等于------( ) (A )-4x +3
(B )5
(C )2x +3
(D )4x +3
3、若不论k 取什么实数,关于x 的方程
16
32=--+bk
x a kx (a 、b 是常数)的根总是x =1,则a+b =---------------------------------------------------------------------------------------------------------( )
(A )
2
1
(B )
23 (C )21-
(D )2
3- 4、若m m m =-+-20082007,则=-2
2007m ---------------------------------------( ) (A )2007 (B )2008 (C )20082 (D )-20082
5、方程07946=--+y x xy 的整数解的个数为 -------------------------------------------( ) (A )1 (B )2 (C )3 (D )4
6、在平面直角坐标系中有两点A (–2,2),B (3,2),C 是坐标轴上的一点,若△ABC 是直角三角形,则满足条件的点C 有----------------------------------------------------------------------------( )
(A )1个 (B )2个 (C )4个 (D )6个
7、一个各面分别标有数字1、2、3、4、5、6的骰子,连续投掷二次,分别出现数字m 、n ,得到一个点P (m ,n ),则点P 既在直线6+-=x y 上,又在双曲线x
y 8
=
上的概率为------ ( ) (A )
61 (B )91 (C )181 (D )36
1
8、二次函数y=ax 2+bx+c 的图像如图所示,下列结论:①0>b ,
②0<c ,③042
>-ac b ,④0>++c b a ,⑤024>++c b a .
其中正确的有---------------------------------------------------------------( )
(A )2个 (B )3个 (C )4个 (D )5个 第8题图
9、如图,若将左边正方形剪成四块,恰能拼成右边的矩形,设a =1,则这个正方形的面积为------------------------------------------------------------------------------------------------------------------ ( )
(A ) 2)21(+ (B)
2
5
1+ (C )
2
53+ (D ) 25
37+
10.二次函数267y x x =-+-,当x 取值为2t x t ≤≤+时有最大值2
(3)2y t =--+,则t 的取值范
围为( )
(A )t ≤0 (B )0≤t ≤3 (C )t ≥3 (D )以上都不对.
第9题图
x
y o
1
=x
2
F
E
D
C
B A M
B
C D
A
二、填空题(每题 6分,共30分)
11、已知关于x 的不等式mx -2≤0的负整数解只有-1,-2,则m 的取值范围是 _____ . 12、用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正 多边形的边数为x 、y 、z ,则
z
y x 1
11++的值为_______________. 13、如图,△OAP 、△ABQ 是等腰直角三角形,点P 、Q 在双曲线)0(4
>=x x
y 上,直角顶点A 、B 均在x 轴上,则点Q 的坐标为_______________.
第11题图 第13题图 14、若关于x 、y 的方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解为⎩⎨⎧==6
5
y x ,则方程组⎩⎨⎧=+=+222111435435c y b x a c y b x a 的
解为____________.
15、如图,墙角处有若干大小相同的小正方体堆成如图所示的立体图形,如果你搬走其中部分小正方体,但希望搬完后从正面、从上面、从右面用平行光线照射时,在墙面及地面上的影子不变,那么你最多可以搬走 __ ____ 个小正方体.
三、解答题(共50分)
16、(本题满分6分)
如图,ABCD 是矩形纸片,E 是AB 上一点,且BE :EA =5:3,
EC =155,把△BCE 沿折痕EC 向上翻折,若点B 恰好落在AD 边上,设
这个点为F ,求AB 、BC 的长.
17、(本题满分8分)
如图,已知四边形ABCD 内接于一圆,AB =BD ,BM ⊥AC 于M ,求证:AM =DC +CM
3
(图1)
(图2)
O
M N Q P
H
K F
E
D
C
B
A
A
B
C
D
P
E F
G
o
y
x
18、(本题满分13分)
某种电缆在空中架设时,两端挂起的电缆下垂都近似成抛物线2
100
1x y =
的形状,现按操作要求,电缆最低点离水平地面不得小于6米.
⑴ 如图1,若水平距离间隔80米建造一个电缆塔柱,求此电缆塔柱用于固定电缆的位置离地面至少应有多少米的高度?
⑵ 如图2,若在一个坡度为1:5的斜坡上,按水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱。
①求这种情况下在竖直方向上,下垂的电缆与坡面的最近距离为多少米? ②这种情况下,直接写出下垂的电缆与坡面的最近距离为多少米?
19、(本题满分13分)
如图,直线AD 对应的函数关系式为1--=x y ,与抛物线交于点A (在x 轴上)、点D ,抛物线与 x 轴另一交点为B (3,0), 抛物线与y 轴交点C (0,-3),; (1)求抛物线的解析式;
(2)P 是线段AD 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)若点F 是抛物线的顶点,点G 是直线AD 与抛物线对称轴的交点,在线段AD 上是否存在一点P ,使得四边形GFEP 为平行四边形;
(4)点H 抛物线上的动点,在x 轴上是否存在点Q ,使A 、D 、H 、Q 这四个点为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的Q 点坐标;如果不存在,请说明理由.
20、(本题满分10分)
一幢33层的大楼里有一部电梯停在第一层,•它一次最多能容纳32人,而且只能在第2层至第33层中某一层停一次.对于每个人来说,他往下走一层楼梯感到1分不满意,往上走一层楼梯感到3分不满意.现在有32•人在第一层,并且他们分别住在第2层至第33层的每一层.问:电梯停在哪一层,•可以使得这32个人满意的总分达到最小?最小值是多少?(•有些人可以不乘电梯而直接从梯梯上楼).
4。
