《流体力学》徐正坦主编课后答案第三章..
流体力学课后习题详解(第三、四章)

第三章 流体运动学3-1解:质点的运动速度1031014,1024,1011034=-=-==-=w v u 质点的轨迹方程1031,52,103000twt z z t vt y y t ut x x +=+=+=+=+=+=3-2 解:2/12/12/3222/12/12/3220375.0232501.02501.00375.0232501.02501.00t t t dt d dt y d a t t t dt d dt x d a a y x z =⨯⨯=⎪⎭⎫⎝⎛⨯===⨯⨯=⎪⎭⎫⎝⎛⨯===由501.01t x +=和10=Ax ,得19.1501.011001.015252=⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=A x t故206.00146.0146.00,146.0,014619.150375.0222222/1=++=++=====⨯=zyxz x y x a a a a a a a a3-3解:当t=1s 时,点A (1,2)处的流速()()sm s m yt xt v s m s m y xt u /1/1211/5/2211222-=⨯-⨯=-==⨯+⨯=+=流速偏导数112221121,1,/12,1,/1-----=-=∂∂==∂∂==∂∂=∂∂==∂∂==∂∂s t yvs t x v s m t t v s yu s t x u s m x t u点A(1,2)处的加速度分量()[]()()[]222/11151/3/21151s m y v v x v u t v Dt Dv a s m s m yuv x u u t u Dt Du a y x -⨯-+⨯+=∂∂+∂∂+∂∂===⨯-+⨯+=∂∂+∂∂+∂∂==3-4解:(1)迹线微分方程为dt udy dt u dx ==, 将u,t 代入,得()tdtdy dt y dx =-=1利用初始条件y(t=0)=0,积分该式,得221t y =将该式代入到式(a ),得dx=(1-t 2/2)dt.利用初始条件x(t=0)=0,积分得361t t x -=联立(c )和(d )两式消去t,得过(0,0)点的迹线方程023492223=-+-x y y y (2)流线微分方程为=.将u,v 代入,得()tdx dy y tdyy dx =-=-11或将t 视为参数,积分得C xt y y +=-221 据条件x(t=1)=0和y(t=1)=0,得C=0.故流线方程为xt y y =-221 3-5 答:()(),满足满足002,0001=+-=∂∂+∂∂+∂∂++=∂∂+∂∂+∂∂k k zw y v x u zw y v x u()()()(),满足,满足000040223222222=++=∂∂+∂∂+∂∂=+-++=∂∂+∂∂+∂∂zw yv xu yxxyyxxyzw yv xu()()()()()()处满足,其他处不满足仅在,不满足,满足,满足满足,满足0,41049000018001760000522==∂∂+∂∂=∂∂+∂∂=++=∂∂++∂∂=++-=∂∂++∂∂=++=∂∂+∂∂+∂∂y y yv x u yv x u u r r u r u rk r k u r r u r u zw yv xu r r r rθθθθ3-6 解:max 02042020max 20320max 20200max 2020214222111000u r r r r u dr r r r r u rdrdr r u r udA r V r rAr =⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-==⎰⎰⎰⎰⎰πππππ3-7 证:设微元体abcd 中心的速度为u r ,u θ。
流体力学课后题题解(第3章)
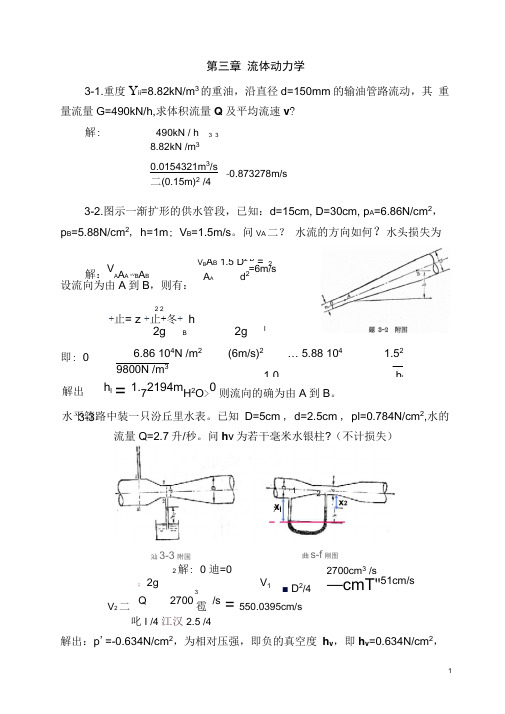
第三章 流体动力学3-1.重度Y ii =8.82kN/m 3的重油,沿直径d=150mm 的输油管路流动,其 重量流量G=490kN/h,求体积流量Q 及平均流速v ?3 3解:490kN / h8.82kN /m 30.0154321m 3/s二(0.15m)2/4-0.873278m/s3-2.图示一渐扩形的供水管段,已知:d=15cm, D=30cm, p A =6.86N/cm 2, p B =5.88N/cm 2, h=1m ; V B =1.5m/s 。
问V A 二? 水流的方向如何?水头损失为V B A B 1.5 D 2 B = 2=6m/sA A d 2设流向为由A 到B ,则有:解:VA A A =VB A B 2 2+止= z +止+冬+ h2g B2gl即: 0 6.86 104N /m 2 (6m/s)2… 5.88 104 1.52― 1.0h l9800N /m 3解出h l=1.72194mH 2O >0则流向的确为由A 到B 。
3-3汕3-3附国2解: 0 迪=0; 2g3V 2 二Q 2700雹/s= 550.0395cm/s叱I /4 江汉2.5 /4V 1■ D 2/42700cm 3 /s—cmT"51cm/s解出:p '=-0.634N/cm 2,为相对压强,即负的真空度 h v ,即h v =0.634N/cm 2,x i曲s-f 刚图水平管路中装一只汾丘里水表。
已知 D=5cm , d=2.5cm , pl=0.784N/cm 2,水的流量Q=2.7升/秒。
问h v 为若干毫米水银柱?(不计损失)二55.556m3/h 二0.0154321m3/ s而1N/cm2=75.061mmHg,故h v=47.588 mmHg。
3-4水银压差计连接在水平放置的汾丘里流量计上。
今测得其中水银面高差h=80mm。
已知D=10cm, d=5cm,汾丘里流量计的流量系数卩=0.98 问水通过流量计的实际流量为若干?解:0 . P . v! = 0 . p .遵P1- P2 _ v2 _ V:w 2g _w 2g w 「2g而p i w(X i D/2) = p2 M h wX d/2)即P i w(h X2 d/2) = p2 M h w(X2 d /2)贝U P i - P2 = h( M -w) —---- -- - h(— - 1) = 100.8mw w2 2 2二v2 -v1 = 2g 汉100.8cm = 197568(cm/s)V1A1 = V2 A?故v2 = 197568(:m/S)二210739.2 ; V2 二459.06cm/ s-(D)4贝U Q =J v2A^ 0.98 459.06cm/s 二52/^ 8833.415cm3/ s= 8.83 升/s3-5某选矿厂的一台碎矿机,每小时可以处理矿石352.8kN。
流体力学第三章课后习题答案

流体力学第三章课后习题答案流体力学第三章课后习题答案流体力学是研究流体运动和流体力学性质的学科。
在学习流体力学的过程中,课后习题是巩固知识和提高理解能力的重要环节。
本文将为大家提供流体力学第三章的课后习题答案,帮助读者更好地掌握流体力学的相关知识。
1. 一个液体的密度为1000 kg/m³,重力加速度为9.8 m/s²,求其比重。
解答:比重定义为物体的密度与水的密度之比。
水的密度为1000 kg/m³,所以比重为1。
因此,该液体的比重也为1。
2. 一个物体在液体中的浮力与物体的重力相等,求物体在液体中的浸没深度。
解答:根据阿基米德原理,物体在液体中的浮力等于物体所排除液体的重量。
浮力的大小等于液体的密度乘以物体的体积乘以重力加速度。
物体的重力等于物体的质量乘以重力加速度。
根据题目条件,浮力等于重力,所以液体的密度乘以物体的体积等于物体的质量。
浸没深度可以通过浸没体积与物体的底面积之比来计算。
3. 一个圆柱形容器中盛有液体,容器的高度为10 cm,直径为5 cm,液体的密度为800 kg/m³,求液体的压强。
解答:液体的压强等于液体的密度乘以重力加速度乘以液体的深度。
容器的高度为10 cm,所以液体的深度为10 cm。
重力加速度为9.8 m/s²,所以液体的压强为800 kg/m³乘以9.8 m/s²乘以0.1 m,即784 Pa。
4. 一个水龙头的出水口半径为2 cm,水流速度为10 m/s,求水龙头出水口附近的压强。
解答:根据质量守恒定律,水流速度越大,压强越小。
根据伯努利定律,水流速度越大,压强越小。
因此,水龙头出水口附近的压强较小。
5. 在一个垂直于水平面的圆柱形容器中,盛有密度为900 kg/m³的液体。
容器的半径为10 cm,液体的高度为20 cm。
求液体对容器底部的压力。
解答:液体对容器底部的压力等于液体的密度乘以重力加速度乘以液体的高度。
流体力学课后答案.
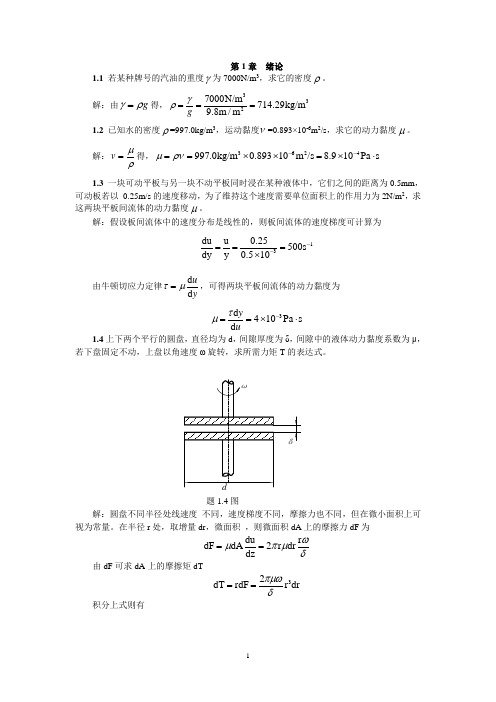
第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3,求它的密度ρ。
解:由g γρ=得,3327000N/m 714.29kg/m9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3,运动黏度ν=0.893×10-6m 2/s ,求它的动力黏度μ。
解:ρμ=v 得,3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中,它们之间的距离为0.5mm ,可动板若以 0.25m/s 的速度移动,为了维持这个速度需要单位面积上的作用力为2N/m 2,求这两块平板间流体的动力黏度μ。
解:假设板间流体中的速度分布是线性的,则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=,可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘,直径均为d ,间隙厚度为δ,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以角速度ω旋转,求所需力矩T 的表达式。
题1.4图解:圆盘不同半径处线速度 不同,速度梯度不同,摩擦力也不同,但在微小面积上可视为常量。
在半径r 处,取增量dr ,微面积 ,则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示,水流在平板上运动,靠近板壁附近的流速呈抛物线形分布,E 点为抛物线端点,E 点处0d d =y u ,水的运动黏度ν=1.0×10-6m 2/s ,试求y =0,2,4cm 处的切应力。
(提示:先设流速分布C By Ay u ++=2,利用给定的条件确定待定常数A 、B 、C )题1.5图解:以D 点为原点建立坐标系,设流速分布C By Ay u ++=2,由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dyτμ=得du(1250y 50)dy τμρν==-+ y=0cm 时,221510N/m τ-=⨯;y=2cm 时,222 2.510N/m τ-=⨯;y=4cm 时,30τ= 1.6 某流体在圆筒形容器中。
流体力学习题及答案-第三章

第三章 流体运动学3-1粘性流体平面定常流动中是否存在流函数? 答:对于粘性流体定常平面流动,连续方程为:()()0=∂∂+∂∂yv x u ρρ; 存在函数:v t y x P ρ-=),,(和()u t y x Q ρ=,,,并且满足条件:()()yP x Q ∂∂=∂∂。
因此,存在流函数,且为:()()()dy u dx v Qdy Pdx t y x ρρψ+-=+=⎰⎰,,。
3-2轴对称流动中流函数是否满足拉普拉斯方程?答:如果流体为不可压缩流体,流动为无旋流动,那么流函数为调和函数,满足拉普拉斯方程。
3-3 就下面两种平面不可压缩流场的速度分布分别求加速度。
(1)22222 ,2yx ym v y x x m u +⋅=+⋅=ππ (2)()()()222222222 ,yxKtxyv yxx y Kt u +-=+-=,其中m ,K 为常数。
答:(1)流场的加速度表达式为:yv v x v u t v a y u v x u u t u a x ∂∂+∂∂+∂∂=∂∂+∂∂+∂∂=y ,。
由速度分布,可以计算得到:0 ,0=∂∂=∂∂tvt u ,因此: ()222222y x x y m x u +-⋅=∂∂π,()22222y x xy m y u +-⋅=∂∂π;()22222y x xy m x v +-⋅=∂∂π,()222222y x y x m y v +-⋅=∂∂π。
代入到加速度表达式中:()()()22222222222222222222220y x x m y x xym y x y m y x x y m y x x m a x +⋅⎪⎭⎫⎝⎛-=+-⋅⋅+⋅++-⋅⋅+⋅+=πππππ()()()22222222222222222222220y x y m y x y x m y x y m y x xym y x x m a y +⋅⎪⎭⎫⎝⎛-=+-⋅⋅+⋅++-⋅⋅+⋅+=πππππ(2)由速度分布函数可以得到:()()()322222222 ,y x Kxyt v y x x y K t u +-=∂∂+-=∂∂ ()()3222232y x y x Ktx x u +-⋅=∂∂,()()3222232y x y x Kty y u +-⋅=∂∂; ()()3222232y x x y Kty x v +-⋅-=∂∂,()()3222232yx y x Ktx y v +-⋅-=∂∂。
工程流体力学课后答案 第三章 流体动力学基础

第3章 流体动力学基础3.1 解: zuu y u u x u u t u a x z x y x x x x ∂∂+∂∂+∂∂+∂∂=()()342246222222222=++++=+-++++=++=z y x t z y t y x t u u y xzu u yu u xu u tu a y zy yy xy y ∂∂+∂∂+∂∂+∂∂=()()32111=-++=-+++--=+-=z y x z x t z y t u u x yzu u y u u x u u t u a z z z y z x z z ∂∂+∂∂+∂∂+∂∂=()()112122211=++++=-+-+++=-+=z y x t z y t y x t u u z x222286.35s m a a a a z y x =++=3.2 解:(1)3235623=-=+=xy xy u xy y u a y x x222527310.3333231s m a a a y u y a y x y y =+===-=(2)二元流动(3)恒定流 (4)非均匀流 3.3 解:bh u y h u bdy h y u udA Q h hA m ax 07871m ax 071m ax 8787==⎪⎭⎫ ⎝⎛==⎰⎰ m ax 87u A Q v ==3.4 解:s m dd v v 02.011.02221221=⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛= 3.5 解:Hd v d 1v 1q 1q 2223d 3v Dv 1dv 2(1)s m v d Q 332330785.04==πs m q Q Q 32321.0=+= s m Q q Q 321115.0=+=(2)s m d Q v 12.242111==πs m d Q v 18.342222==π 3.6 解:渠中:s m m m s m bh v Q 311612/3=⨯⨯==管中:2231242.1d v s m Q Q Q ⨯⨯==-=πm v Q d 0186.1422==π 3.7 解: s m d d v v ABB A62.04.05.1442222=⨯=⋅=ππ以过A 点的水平面为等压面,则OmH g v g p h H OmH g v g p H B B B A A A 2222226964.58.925.18.9405.128980.48.9268.9302=⨯++=++==⨯+=+=ρρ可以看出:A B H H >,水将从B 点流向A 点。
流体力学课后作业答案

流 体 力 学
yD 2
(1.8 / sin 60 ) 1 (2 / sin 60 )
2.292m
由力矩平衡
yD F1 yD1 F2 ( yD 2 (1 0.8) / sin 60 ) F
油 h1 F1 F yD2 θ
yD1 yD
2.35m
F2 水 h2
46
解: 阀关时,由静力学方程
z1 p1
流 体 力 学
g
z2
p2
g
5mH 2O
阀开时,由伯努利方程
1 1 2 2
z1
p1
g
v1
2
2g
z2
p2
g
v
2
v2
2
2g
hl
5 0 0.1
1
2g
v 8.74m/s
50
3.28 管末端喷嘴d =10cm,D =40cm,Q=0.4m3/s,12 个螺栓固定法兰,不计质量,求每个螺栓的受力。 解:v1
l
hf
13.6 0.92
2
h 1.24m
又 h l v f
0.92
0.2
d 2g 设为层流 Re 64 320 2000 成立
h
vd Re
1 0.025 320
7.8 10 m /s
2
5
若反向流动,Q不变,Re不变,λ不变,hf不变, 所以h不变,只是反向高差为9cm。
第一章习题解答
1-3 水的密度ρ=1000kg/m3,μ=0.599×10-3Pa· s,求运动粘 度ν。 解: / 0.599 103 /1000 5.99 106 m2 /s 1-7 20º C的空气在直径为2.5cm的管中流动,距管壁上1mm 处的空气速度为3cm/s。求作用于单位长度管壁上的粘性切 力为多少? 解:T=20º C时, μ=0.0183×10-3Pa· s 空气层厚度很小(1mm),速度可认为是线性分布
流体力学课后习题及答案-第3章

3-1 用欧拉法表示流体质点的加速度 a等于:u u tu d u u c t u b t r a)()( ;))(( ;)( ;d d )(22∇⋅+∂∂∇⋅∂∂3-5 无旋流动限于:(a) 流线是直线的流动; (b) 迹线是直线的流动; (c) 微团无旋转的流动; (d) 恒定流动。
3-8 已知流速场 31 32xy u y u xy u z y x =-==,,试求: (1)点(1,2,3)的加速度; (2)是几元流动; (3)是恒定流还是非恒定流。
解: (1) 先求加速度各分量43223102310xy xy y y xy z u u y u u x u u t u a x z x y x x x x =+⋅-⋅+=∂∂+∂∂+∂∂+∂∂=523310))(31(00y y y z u u yu u xu u tu a yzy yy xy y =+--++=∂∂+∂∂+∂∂+∂∂=332320310xy x y y xy z u u y u u x u u t u a z z z y z x z z =+⋅-⋅+=∂∂+∂∂+∂∂+∂∂=将x =1,y =2, z =3代入以上各式得2m/s 33.5=x a 2m/s 67.10=y a 2m/s 33.5=z a2222m/s 06.13=++=z y x a a a a (2)是三元流动; (3)是恒定流。
3-14 已知不可压缩流体平面流动,在 y 方向的速度分量为y x y u y 222+-=。
试求速度在x 方向的分量 u x 。
解: 由不可压缩流体平面流动的连续性微分方程得22--=∂∂-=∂∂y yu x u y x )(22 y f x xy u x +--=⇒3-15 如图在送风道的璧上有一面积为0.4m 2的风口,试求风口出流的平均速度解: 风口出流流量为/s m 5.15.243=-=Q风口过流断面面积为2m 2.030sin 4.0== A风口出流的平均速度为m/s 5.7==AQv 3-18 已知流动速度场为 32 32 32y x u x z u z y u z y x +=+=+=,,试求旋转角速度和角变形速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章习题简答3-1 已知流体流动的速度分布为22y x u x -= ,xy u y 2-=,求通过1,1==y x 的一条流线。
解:由流线微分方程yx u dyu dx =得dy u dx u x y =则有 dy y x xydx )(222-=-两边积分可得C y y x yx +-=-3322即0623=+-C y x y将x=1,y=1代入上式,可得C=5,则 流线方程为05623=+-y x y3-3 已知流体的速度分布为⎭⎬⎫==-=-=tx x u ty y u y x 00εωεω(ω>0,0ε>0)试求流线方程,并画流线图。
解:由流线微分方程yx u dyu dx =得dy u dx u x y =则有 tydy txdx 00εε-=两边积分可得C y x +-=22流线方程为C y x =+223-5 以平均速度s m v /5.1=流入直径为D=2cm 的排孔管中的液体,全部经8个直径d=1mm 的排孔流出,假定每孔出流速度依次降低2%,试求第一孔与第八孔的出流速度各为多少?题3-5图解:由题意得:v 2=v 1(1-2%),v 3=v 1(1-2%)2,…,v 8=v 1(1-2%)7 根据质量守恒定律可得282322212832144444dv d v d v d v D v Q Q Q Q Q πππππ⋅+⋅⋅⋅+⋅+⋅+⋅=⋅+⋅⋅⋅+++=sm d vD v v d v v v v d D v /4.80)98.01(001.002.002.05.1)98.01()98.01(98.01)98.01(4)(448228221812832122=-⨯⨯⨯=--⋅=∴--⋅=+⋅⋅⋅+++⋅=⋅πππ则 v 8=v 1(1-2%)7=80.4×(1-2%)7=69.8m/s3-6 油从铅直圆管向下流出。
管直径cm d 101=,管口处的速度为s m v /4.11=,试求管口处下方H=1.5m 处的速度和油柱直径。
题3-6图解:取1-1和2-2断面,并以2-2断面为基准面 列1-1、2-2断面的伯努利方程2221221222211/6.54.15.18.922202s m v gH v p p gv g p g v g p H =+⨯⨯=+==++=++ ρρ由连续方程22221144d v d v ππ⋅=⋅得cm d v v d 5106.54.121212=⨯==3-8 利用毕托管原理测量输水管的流量如图示。
已知输水管直径d=200mm ,测得水银差压计读书p h =60mm ,若此时断面平均流速max 84.0u v =,这里max u 为毕托管前管轴上未受扰动水流的流速。
问输水管中的流量Q 为多大?题3-8图解:由题意可得sm d v Q s m u v s m h g u Hg /102.02.04234.34/234.385.384.084.0/85.3110001360006.08.9212322max max =⨯⨯=⋅==⨯==∴=⎪⎭⎫ ⎝⎛-⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛-∆=ππρρ3-9 水管直径50mm ,末端阀门关闭时,压力表读值为212/m kN 。
阀门打开后读值降至5.52/m kN ,如不计水头损失,求通过的流量。
题3-9图解:根据能量守恒定理可得()()sL s m d v Q sm p p v g v g p g p /9.10/0109.005.0456.54/56.5100055002100022232221221==⨯⨯=⋅==-⨯=-=+=ππρρρ3-10 水箱中的水从一扩散短管流到大气中,直径mm d 1001=,该处绝对压强5.01=p 大气压,直径mm d 1502=,求水头H ,水头损失忽略不计。
题3-10图解:以0-0截面为基准面,列2-2、3-3截面的伯努利方程gH v H gv2002002222=++=++得——————————①列1-1、2-2截面的连续方程gH d d v d d v d v d v 244414222414221222211⋅==⋅=⋅得ππ——————②列1-1、2-2截面的伯努利方程gv g p g v g p 2020222211++=++ρρ将p 1=0.5p a ,p 2=p a 及①式和②式代入上式中,得mH H H H H Hg pH d d g p a a 23.11006.559800980001.015.09800980005.005.00444142=⇒+=++=+⨯++=++ρρ 3-11 同一水箱上、下两孔口出流,求证:在射流交点处,2211y h y h =。
题3-11图解:列容器自由液面0至小孔1及2流动的伯努利方程,可得到小孔处出流速度v =Toricelli ),它在形式上与初始速度为零的自由落体运动一样,这是不考虑流体粘性的结果。
由212y gt =公式,分别算出流体下落y 距离所需的时间,其中12t t ==经过1t 及2t 时间后,两孔射流在某处相交,它们的水平距离相等,即 1122v t v t =,其中1v =,2v =,因此= 即 1122h y h y =3-12 水自下而上流动,已知: cm d 301=、cm d 152=,U 型管中装有水银,a =80cm 、b =10cm ,试求流量。
题3-12图解:取等压面3-3gbb h g p p gb ga p h b a g p Hg Hg ρρρρρ+-=-∴++=-++)()(2121列1-1、2-2截面的伯努利方程,并以1-1为基准面h gp p d d g Q g d Q g p h g d Q g p d Q v d Q v g v g p h g v g p --=-++=++==++=++ρππρπρππρρ214241221422222412211222211222211)11(88804,4,220代入得而将gb b h g p p H g ρρ+-=-)(21及各数据代入上式1.010001.013360)15.013.01(8.98)11(8442214241221-⨯=-⨯-+-=-πρρπQ hb b h d d g Q Hgs m Q /091.03=解得3-13 离心式通风机用集流器A 从大气中吸入空气,直径mm d 200=处接一根细玻璃管,已知管中的水上升mm H 150=,求进气流量(空气的密度3/29.1m kg =ρ)。
题3-13图解:取等压面3-3gH p gH p 水水ρρ-=⇒+=220列1-1、2-2截面的伯努利方程gvg p 20000222++=++ρs m d gH d v Q gHgH p v /5.12.0429.115.0980024242)(223222222=⨯⨯⨯⨯=⋅=⋅=∴=--=-=ππρρπρρρρρ水水水则3-14 由喷嘴射出速度s m v /7=的自由射流,欲达到H=2m ,试问喷嘴轴线的倾斜角θ是多少?题3-14图解:由能量守恒定理可得()︒==∴=⨯⨯===38.63894.0arcsin 894.0728.922sin 2sin 2θθθv gH gv H 3-15 倾斜水管上的文丘里流量计cm d 301=,cm d 152=,倒U 形差压计中装有比重为6.0的轻质不混于水的液体,其读数为cm h 30=,收缩管中的水头损失为1d 管中速度水头的%20,试求喉部速度2v 与管中流量Q 。
题3-15图解:列1-1、2-2截面的伯努利方程gv g v g p z g v g p z 22.0222122222111+++=++ρρ连续方程22122122221144v d dv d v d v =⇒⋅=⋅ππ代入伯努利方程可得()()g v d d gv g p z g p z gvg p z g v d d g p z 28.02228.02241222221122222241211-=⎪⎪⎭⎫ ⎝⎛+-+++=++ρρρρ而 h ggh h g gh h g p z g p z 4.06.0')(2211=-=-=+-+ρρρρρρ 则 ()h gv d d g v4.028.022241222=-()sm d v Q sm d d ghv /0278.015.04927.14/574.13.015.08.013.08.98.08.018.03222244122=⨯⨯=⋅=∴=⎪⎭⎫⎝⎛⨯-⨯⨯=-=ππ3-16 高层楼房煤气立管B 、C 两个供煤气点各供应s m Q /02.03=的煤气量。
假设煤气的密度为3/6.0m kg ,管径50mm ,压强损失AB 段用2321vρ计算,BC 段用2422vρ,假定C 点要求保持余压为2/300m N ,求A 点酒精(3/806m kg =酒ρ)液面应有的高差(空气密度为3/2.1m kg )。
题3-16图解:由题意可求得s m d Q v sm d Q v /18.1005.0402.04/37.2005.04202.0422222211=⨯===⨯⨯==ππππ取断面1-1、2-2,列出伯努利方程m m m g p h Paz z g p v v p p p v p z z g v p a l l a 6.440446.08.980635232608.9)6.02.1(218.106.04237.206.03)37.2018.10(26.0300)()()(22)()(21222212212122212122212211==⨯===⨯⨯--⨯⨯+⨯⨯+-+=---+-+=++=--++--ρρρρρρρρ 3-17锅炉省煤器的进口处测得烟气负压O mmH h 215.10=,出口负压O mmH h 2220=。
如炉外空气3/2.1m kg =ρ,烟气的平均3/6.0m kg ='ρ,两测压断面高差H=5m ,试求烟气通过省煤器的压强损失。
题3-17图解:本题要应用气流以相对压强表示的伯努利方程。
由进口断面1-1至出口断面2-2列伯努利方程p v p z z g v p a ∆++=--++2')()(2'22212211ρρρρ式中10.0 1059 807102.97Pa p =-⨯=- 20.029 807196.14Pa p =-⨯=-v 1=v 2故 102.979.81(1.20.6)(05)196.14p -+⨯-⨯-=-+∆ 得Δ63.74Pa p =3-18 图为矿井竖井和横向坑道相连,竖井高为200m ,坑道长为300m ,坑道和竖洞内气温保持恒定C t ︒=15,密度3/18.1m kg =ρ,坑外气温在清晨为C ︒5,30/29.1m kg =ρ,中午为C ︒20,30/16.1m kg =ρ,问早午空气的气流流向及气流速v 的大小。
