人教版数学八年级下册 18.2 特殊的平行四边形正方形同步测试
2020-2021学年人教版数学八年级下册 18.2 特殊的平行四边形 同步测试题

18.2 特殊的平行四边形同步测试题(满分120分;时间:90分钟)一、选择题(本题共计8 小题,每题3 分,共计24分,)1. 在▱ABCD中,增加下列条件中的一个,就能断定它是矩形的是()A.∠A+∠C=180∘B.AB=BCC.AC⊥BDD.AC=2AB2. 矩形ABCD的对角线AC、BD相交于点O,∠AOD=120∘,AC=8,则△ABO的周长为()A.16B.12C.24D.203. 矩形具有而菱形不一定具有的性质是()A.对角线相等B.四边相等C.对角线互相垂直D.对角线互相平分4. 如图,在梯形ABCD中,AD // BC,∠B+∠C=90∘,E、F分别是AD、BC的中点,若AD=5cm,BC=13cm,那么EF=()A.4cmB.5cmC.6.5cmD.9cm5. 下列各组条件中,能判定四边形ABCD是矩形的一组是()A.AB//CD,AC=BDB.AB//CD,∠A=∠C=90∘C.AB//CD,∠B=∠C=90∘D.AB//CD,∠A=∠D=90∘6. 已知,在四边形ABCD中,∠A=∠B=90∘,要使四边形ABCD为矩形,那么需要添加的一个条件是()A.AB=BCB.AD=BCC.AD=ABD.BC=CD7. 菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,则点O到边AB的距离为()A.2B.94C.73D.1258. 如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30∘,则下列结论:(1)DC=3OG;(2)OG=12BC;(3)四边形AECF为菱形;(4)S△AOE=16S四边形ABCD.其中正确的个数为()A.1个B.2个C.3个D.4个二、填空题(本题共计7 小题,每题3 分,共计21分,)9. 菱形的面积为24cm2,一条对角线长为6cm,则另一条对角线长为________.10. 两张宽2cm矩形纸片重叠在一起,然后将其中的一张任意旋转一个角度,则重叠部分(图中的阴影部分)的四边形ABCD的形状为________,其面积的最小值为________cm2.FC,则四边11. 如图,矩形ABCD中,AB=8cm,BC=3cm,E是DC的中点,BF=12形DBFE的面积为________cm2.12. 在矩形ABCD中,再增加条件________(只需填一个)可使矩形ABCD成为正方形.13. 如图,△ABC中,∠ABC=90∘,O为AC的中点,连接BO并延长到D,连接AD,CD.添加一个条件,使四边形ABCD是矩形(填一个即可).________14. 如图,已知菱形ABCD的边长为5,对角线AC,BD相交于点O,BD=6,则菱形ABCD的面积为________.15. 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,a n,则a7=________.三、解答题(本题共计7 小题,共计75分,)16. 已知,如图,在△ABC中,D是AB边上的一点,且BD=BC,BE⊥CD于点E,交AC于点F,请再添加一个条件,使四边形DMCF是菱形,并加以证明.17. 如图,在△ABC中,∠ABC=90∘,点D为AC的中点,过点C作CE⊥BD于点E,过点A 作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)证明:四边形BDFG是菱形;(2)若AC=10,CF=6,求线段AG的长度.18. 附加题:已知正方形ABCD的面积35平方厘米,E、F分别为边AB、BC上的点,AF 和CE相交于点G,并且△ABF的面积为5平方厘米,△BCE的面积为14平方厘米,求四边形BEGF的面积.19. 如图,∠ADC=90∘,E是AC的中点,BE=DE.求证:AB⊥BC.20. 如图所示,在等边三角形中,BC=8cm,射线AG // BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;(2)填空:①当t为________s时,四边形AFCE是菱形;②当t为________s时,△ACE的面积是△ACF的面积的2倍.21. 如图,将一长方形纸片ABCD沿着EF折叠,已知AF // BE,DF // CE,CE交AF于点G,过点G作GH // EF,交线段BE于点H.(1)判断∠CGH与∠DFE是否相等,并说明理由;(2)①判断GH是否平分∠AGE,并说明理由;②若∠DFA=52∘,求∠HGE的度数.22. 如图,在四边形ABCD中,AD//BC,∠B=90∘,AD=24cm,AB=8cm,BC= 26cm,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,动点P,Q分别从点A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒.(1)当t为何值时,四边形ABQP为矩形?(2)当t为何值时,四边形PQCD为平行四边形?。
八年级数学人教版下册18.2《特殊的平行四边形》测试卷、练习卷(带答案解析)

18.2《特殊的平行四边形》测试卷、练习卷(带答案解析)一、选择题(本大题共10小题,共30.0分)1.如果一个四边形的对角线相等,那么顺次连接这个四边形各边中点所得四边形是()A. 平行四边形B. 正方形C. 矩形D. 菱形2.矩形具有而一般平行四边形不具有的性质是()A. 对角相等B. 对边相等C. 对角线相等D. 对角线互相平分3.平行四边形两邻边之比为3:4,两条对角线长都是10,则这个平行四边形的周长是().A. 14B. 20C. 28D. 无法确定4.如图,P为矩形ABCD外一点,S△PCD=5,S△PBC=8,则△PAC的面积是().A. 3B. 4C. 1.5D. 2.55.顺次连结矩形各边的中点,所得四边形是().A. 筝形B. 矩形C. 菱形D. 正方形6.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为()A. (√3,1)B. (2,1)C. (1,√3)D. (2,√3)7.如图,正方形ABCD的边长为4,点A的坐标为(−1,1),AB平行于x轴,则点C的坐标为()A. (3,1)B. (−1,1)C. (3,5)D. (−1,5)8.如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是()A. BE=AFB. ∠DAF=∠BECC. ∠AFB+∠BEC=90∘D. AG⊥BE9.如图,在边长为2的菱形ABCD中,∠B=45∘,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD交于点F,则B′F的长度为()A. 1B. √2C. 2−√2D. 2√2−210.如图,在正方形ABCD中,E、F是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,EF=2,设AE=x.当△PEF是等腰三角形时,下列关于P点个数的说法中,一定正确的是()①当x=0(即E、A两点重合)时,P点有6个②当0<x<4√2−2时,P点最多有9个③当P点有8个时,x=2√2−2④当△PEF是等边三角形时,P点有4个A. ①③B. ①④C. ②④D. ②③二、填空题(本大题共4小题,共12.0分)11.如图,在菱形ABCD中,∠B=50∘,点E在CD上,若AE=AC,则∠BAE=°.12.如下图,将矩形ABCD折叠,折痕为EF,BC的对应边B′C′与CD交于点M,若∠B′MD=50∘,则∠BEF的度数为.13.如下图,矩形ABCD的面积为20cm2,对角线交于点O,以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,⋯⋯,依次类推,则平行四边形AO2019C2020B的面积为.14.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.三、解答题(本大题共7小题,共58.0分)15.已知:四边形ABCD中,AB=CD,∠A+∠D=180°,AC、BD相交于点O,△AOB是等边三角形。
人教版八年级下册:18.2特殊的平行四边形同步练习卷 含答案解析

人教版八年级下册:18.2特殊的平行四边形同步练习卷一.选择题(共10小题)1.下列性质中,矩形不一定具有的是()A.对角线相等B.对角线互相平分C.4个内角相等D.一条对角线平分一组对角2.如图,菱形ABCD中,∠D=130°,则∠1=()A.30°B.25°C.20°D.15°3.如图,已知△ABC中,AD是BC边上的中线,则下列结论不一定正确的是()A.B.BD=CD C.D.4.如图所示,在平行四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定平行四边形ABCD为矩形的是()A.∠ABC=90°B.AC=BD C.AD=AB D.∠BAD=∠ADC 5.如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.若要使四边形ABCD为菱形,则可以添加的条件是()A.AC=BD B.AB⊥BC C.∠AOB=60°D.AC⊥BD6.如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD =8,∠ABD=∠CDB,则四边形ABCD的面积为()A.40B.24C.20D.157.如图,已知四边形ABCD是正方形,E是AB延长线上一点,且BE=BD,则∠BDE的度数是()A.22.5°B.30°C.45°D.67.5°8.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是()A.3B.C.D.49.已知四边形ABCD是平行四边形,再从四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是()①AB=BC,②∠ABC=90˚,③AC=BD,④AC⊥BDA.选①②B.选①③C.选②③D.选②④10.如图,在正方形ABCD内,以BC为边作等边三角形BCM,连接AM并延长交CD于N,则下列结论不正确的是()A.∠DAN=15°B.∠CMN=45°C.AM=MN D.MN=NC二.填空题(共8小题)11.工人师傅在测量一个门框是否是矩形时,只需要用到一个直角尺,则他用到的判定方法是.12.如图,两张等宽的长方形纸条交叉重叠在一起,重叠的部分ABCD是.13.矩形ABCD中,要使矩形ABCD成为正方形还需满足的条件是(横线只需填一个你认为合适的条件即可)14.如图,已知菱形ABCD的面积为6cm2,BD的长为4cm,则AC的长为cm.15.如图,在矩形ABCD中,AC,BD交于点O,M、N分别为BC、OC的中点.若BD=8,则MN的长为.16.如图,Rt△ABC中,∠ACB=90°,∠A=28°,D是AB的中点,则∠DCB=度.17.在坐标平面内,A,B两点的坐标分别是(1,5),(4,1),点C在y轴上,点D在坐标平面内,以A,B为顶点的四边形是矩形,则点D的坐标为.18.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN,若AB=9,BE=6,则MN 的长为.三.解答题(共8小题)19.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.20.如图,正方形ABCD的对角线AC与BD交于点O,过点C作CE∥BD,过点D作DE ∥AC,CE与DE交于点E.求证:四边形OCED是正方形.21.如图.在平行四边形ABCD中,E、F分别为AB、CD的中点,连结DE、DB、BF.(1)求证:DE=BF;(2)若∠ADB=90°,证明:四边形BFDE是菱形.22.已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.(1)求证:△AOD≌△EOC;(2)连接AC、DE,当∠B=∠AEB=45°时,求证四边形ACED是正方形.23.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)求证:四边形ADCF是菱形;(2)若AC=12,AB=16,求菱形ADCF的面积.24.如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.(1)求证:四边形CEDF为平行四边形;(2)若AB=6cm,BC=10cm,∠B=60°,①当AE=cm时,四边形CEDF是矩形;②当AE=cm时,四边形CEDF是菱形.25.如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF ∥AE交AD延长线于点F.(1)求证:四边形AECF是矩形;(2)连接OE,若AE=4,AD=5,求OE的长.26.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.(1)求证:四边形ABCD是正方形.(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.参考答案一.选择题(共10小题)1.【解答】解:∵矩形的对角线互相平分且相等,故选项A、B不合题意;∵矩形的四个角都是直角,故选项C不合题意;∵矩形的一条对角线不一定平分一组对角;故D符合题意;故选:D.2.【解答】解:∵四边形ABCD是菱形,∴DC∥AB,∠DAC=∠1,∵∠D=130°,∴∠DAB=180°﹣130°=50°,∴∠1=∠DAB=25°.故选:B.3.【解答】解:如图,在△ABC中,AD是BC边上的中线,则BD=CD=BC,故选项A、B、D不符合题意.若∠BAC=90°时,AD=BC才成立,否则不成立.故选项C符合题意.故选:C.4.【解答】解:A.根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意;B.根据对角线相等的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意;C.不能判定平行四边形ABCD为矩形,故此选项符合题意;D.平行四边形ABCD中,AB∥CD,∴∠BAD+∠ADC=180°,又∵∠BAD=∠ADC,∴∠BAD=∠ADC=90°,根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意.故选:C.5.【解答】解:∵OA=OC,OB=OD,∴四边形ABCD为平行四边形,A、∵AC=BD,∴四边形ABCD是矩形,故选项A不符合题意;B、∵AB⊥BC,∴四边形ABCD是矩形,故选项B不符合题意;C、∵∠AOB=60°,不能得出四边形ABCD是菱形;选项C不符合题意;D、∵AC⊥BD,∴四边形ABCD是菱形,故选项D符合题意;故选:D.6.【解答】解:∵AB=AD,点O是BD的中点,∴AC⊥BD,∠BAO=∠DAO,∵∠ABD=∠CDB,∴AB∥CD,∴∠BAC=∠ACD,∴∠DAC=∠ACD,∴AD=CD,∴AB=CD,∴四边形ABCD是菱形,∵AB=5,BO=BD=4,∴AO=3,∴AC=2AO=6,∴四边形ABCD的面积=×6×8=24,故选:B.7.【解答】解:∵BE=DB,∴∠BDE=∠E,∵∠DBA=∠BDE+∠BED=45°∴∠BDE=×45°=22.5°.故选:A.8.【解答】解:∵四边形COED是矩形,∴CE=OD,∵点D的坐标是(1,3),∴OD==,∴CE=,故选:C.9.【解答】解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;B、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;C、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意.D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;故选:C.10.【解答】解:作MG⊥BC于G.∵四边形ABCD是正方形,∴BA=BC,∠ABC=∠DAB=°∠DCB=90°∵△MBC是等边三角形,∴MB=MC=BC,∠MBC=∠BMC=60°,∵MG⊥BC,∴BG=GC,∵AB∥MG∥CD,∴AM=MN,∴∠ABM=30°,∵BA=BM,∴∠MAB=∠BMA=75°,∴∠DAN=90°﹣75°=15°,∠CMN=180°﹣75°﹣60°=45°,故A,B,C正确,故选:D.二.填空题(共8小题)11.【解答】解:用直角尺测量门框的三个角是否都是直角,如果都是直角,则四边形是矩形.故答案为:三个角是直角的四边形为矩形12.【解答】解:过点A作AE⊥BC于E,AF⊥CD于F,如图,∵两条纸条宽度相同,∴AE=AF.∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形.∵S▱ABCD=BC•AE=CD•AF.又∵AE=AF.∴BC=CD,∴四边形ABCD是菱形;故答案为:菱形.13.【解答】解:添加的条件可以是AB=BC.理由如下:∵四边形ABCD是矩形,AB=BC,∴四边形ABCD是正方形.故答案为:AB=BC(答案不唯一).14.【解答】解:∵菱形ABCD的面积为6cm2,BD的长为4cm,∴×4×AC=6,解得:AC=3,故答案为:3.15.【解答】解:如图,∵四边形ABCD是矩形,AC,BD交于点O,BD=8∴BD=2BO,即2BO=8.∴BO=4.又∵M、N分别为BC、OC的中点,∴MN是△CBO的中位线,∴MN=BO=2.故答案是:2.16.【解答】解:∵∠ACB=90°,D是AB的中点,∴CD=AB=AD,∴∠ACD=∠A=28°,∴∠DCB=90°﹣28°=62°,故答案为:62.17.【解答】解:如图,当AB为对角线时,观察图象可知D(5,3).当AB为矩形的边时,观察图象可知D2(﹣3,2),∴直线AD2的解析式为y=x+,∴C1(0,),∵AC1=BD1,∴D1(3,),综上所述,满足条件的点D的坐标为(5,3)或(﹣3,2)或(3,).故答案为(5,3)或(﹣3,2)或(3,).18.【解答】解:连接CF,∵正方形ABCD和正方形BEFG中,AB=9,BE=6,∴GF=GB=6,BC=9,∴GC=GB+BC=6+9=15,∴CF===3.∵M、N分别是DC、DF的中点,∴MN==.故答案为:.三.解答题(共8小题)19.【解答】证明;∵四边形ABCD中,AB=CD,AD=BC,∴四边形ABCD是平行四边形,∴AC=2AO,BD=2OD,∵OA=OD,∴AC=BD,∴四边形ABCD是矩形.20.【解答】证明:∵CE∥BD,DE∥AC,∴四边形CODE是平行四边形,∵正方形ABCD的对角线AC与BD交于点O,∴OD=OC,∠DOC=90°,∴四边形CODE是正方形.21.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,DC=AB,∵E,F分别为边AB、CD的中点,∴DF=CF=DC,AE=BE=AB,∴DF=BE,∴四边形DEFB是平行四边形,∴DE=BF;(2)证明:由(1)得,四边形DEBF是平行四边形,∴DC=AB,CD∥AB,∴DF∥EB,∵E,F分别为边AB、CD的中点,∴DF=CF=DC,AE=BE=AB,∴DF=EB,∴四边形DEBF是平行四边形,∵∠ADB=90°,∴DE=AB,∴DE=EB,∴四边形DEBF是菱形.22.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC.∴∠D=∠OCE,∠DAO=∠E.∵O是CD的中点,∴OC=OD,在△AOD和△EOC中,,∴△AOD≌△EOC(AAS);(2)∵△AOD≌△EOC,∴OA=OE.又∵OC=OD,∴四边形ACED是平行四边形.∵∠B=∠AEB=45°,∴AB=AE,∠BAE=90°∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠COE=∠BAE=90°.∴▱ACED是菱形.∵AB=AE,AB=CD,∴AE=CD.∴菱形ACED是正方形.23.【解答】(1)证明:∵E是AD的中点,∴AE=DE,∵AF∥BC,∴∠AFE=∠DBE,在△AEF和△DEB中,∵,∴△AEF≌△DEB(AAS),∴AF=DB,∴四边形ADCF是平行四边形,∵∠BAC=90°,D是BC的中点,∴AD=CD=BC,∴四边形ADCF是菱形;(2)解:设AF到CD的距离为h,∵AF∥BC,AF=BD=CD,∠BAC=90°,∴S菱形ADCF=CD•h=BC•h=S△ABC=AB•AC=×12×16=96.24.【解答】(1)证明:∵四边形ABCD是平行四边形,∴CF∥ED,∴∠FCD=∠GCD,∵G是CD的中点,∴CG=DG,在△FCG和△EDG中,∴△CFG≌△EDG(ASA),∴FG=EG,∴四边形CEDF是平行四边形;(2)①解:当AE=7时,平行四边形CEDF是矩形,理由是:过A作AM⊥BC于M,∵∠B=60°,AB=6,∴BM=3,∵四边形ABCD是平行四边形,∴∠CDA=∠B=60°,DC=AB=6,BC=AD=10,∵AE=7,∴DE=3=BM,在△MBA和△EDC中,,∴△MBA≌△EDC(SAS),∴∠CED=∠AMB=90°,∵四边形CEDF是平行四边形,∴四边形CEDF是矩形,故答案为:7;②当AE=4时,四边形CEDF是菱形,理由是:∵AD=10,AE=4,∴DE=6,∵CD=6,∠CDE=60°,∴△CDE是等边三角形,∴CE=DE,∵四边形CEDF是平行四边形,∴四边形CEDF是菱形,故答案为:4.25.【解答】(1)证明:∵菱形ABCD,∴AD∥BC.∵CF∥AE,∴四边形AECF是平行四边形.∵AE⊥BC,∴平行四边形AECF是矩形;(2)解:∵AE=4,AD=5,∴AB=5,BE=3.∵AB=BC=5,∴CE=8.∴AC=4,∵对角线AC,BD交于点O,∴AO=CO=2.∴OE=2.26.【解答】(1)证明:∵四边形ABCD是菱形,∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,∴∠BAD+∠ABC=180°,∵∠CAD=∠DBC,∴∠BAD=∠ABC,∴2∠BAD=180°,∴∠BAD=90°,∴四边形ABCD是正方形;(2)证明:∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,CO=AC,DO=BO,∴∠COB=∠DOC=90°,CO=DO,∵DH⊥CE,垂足为H,∴∠DHE=90°,∠EDH+∠DEH=90°,∵∠ECO+∠DEH=90°,∴∠ECO=∠EDH,在△ECO和△FDO中,,∴△ECO≌△FDO(ASA),∴OE=OF.。
人教版数学八年级下册 18.2 特殊的平行四边形 同步测试

18.2 特殊的平行四边形一、选择题1.如图,在矩形ABCD中,对角线AC,BD相交于点O,以下说法错误的是(D)A.∠ABC=90°B.AC=BDC.OA=OBD.OA=AD2.下列说法中正确的是(D)A.一个角是直角,两条对角线相等的四边形是矩形B.一组对边平行且有一个角是直角的四边形是矩形C.对角线互相垂直的平行四边形是矩形D.一个角是直角且对角线互相平分的四边形是矩形3.(2018·十堰)菱形不具备的性质是(B)A.四条边都相等B.对角线一定相等C.是轴对称图形D.是中心对称图形4.如图,若要使▱ABCD成为菱形,则可添加的条件是(C)A.AB=CDB.AD=BCC.AB=BCD.AC=BD5.平行四边形、矩形、菱形、正方形都具有的性质是(A)A.对角线互相平分B.对角线互相垂直C.对角线相等D.对角线互相垂直平分且相等6.如图,在Rt△ABC中,CD是斜边AB上的中线.若∠A=20°,则∠BDC=(B)A.30°B.40°C.45°D.60°7.(2018·孝感)如图,菱形ABCD的对角线AC,BD相交于点O,AC=10,BD=24,则菱形ABCD的周长为(A)A.52 B.48 C.40 D.208.顺次连接对角线相等的四边形各边中点,所得四边形是(C)A.矩形B.平行四边形C.菱形D.任意四边形9.下列说法不正确的是(D)A.一组邻边相等的矩形是正方形B.对角线相等的菱形是正方形C.对角线互相垂直的矩形是正方形D.有一个角是直角的平行四边形是正方形10.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E.若∠DAE∶∠BAE=3∶1,则∠EAC的度数是(C)A.18°B.36° C.45°D.72°二、填空题11.如果矩形的一边长为6,一条对角线的长为10,那么这个矩形的另一边长是8.12.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是答案不唯一,如:AD=BC或AB∥CD等.(写出一种情况即可)13.如图是根据四边形的不稳定性制作的边长为15 cm的可活动菱形衣架.若墙上钉子间的距离AB=BC=15 cm,则∠1=120__°.14.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是45__°.15.(2018·福建)如图,在Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,则CD=3.16.四边形ABCD 是菱形,∠BAD =60°,AB =6,对角线AC 与BD 相交于点O ,点E 在AC 上.若OE =3,则CE 的长为三、解答题17.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE =CF ,连接OE ,OF.求证:OE =OF.证明:∵四边形ABCD 为矩形,∴∠ADC =∠BCD =90 °,AC =BD ,OD =12BD ,OC =12AC ,即OD =OC. ∴∠ODC =∠OCD.∴∠ADC -∠ODC =∠BCD -∠OCD ,即∠EDO =∠FCO.又∵DE =CF ,∴△ODE ≌△OCF(SAS).∴OE =OF.18.如图所示,矩形ABCD 的对角线相交于点O ,E ,F ,G ,H 分别是AO ,BO ,CO ,DO 的中点,请问四边形EFGH 是矩形吗?请说明理由.解:四边形EFGH 是矩形.理由如下:∵四边形ABCD 是矩形,∴AC =BD ,AO =BO =CO =DO.∵E ,F ,G ,H 分别是AO ,BO ,CO ,DO 的中点,∴EO =FO =GO =HO.∴四边形EFGH 是平行四边形.∵EO +GO =FO +HO ,即EG =FH ,∴四边形EFGH 是矩形.19.如图,在▱ABCD 中,BC =2AB =4,点E ,F 分别是BC ,AD 的中点.(1)求证:△ABE ≌△CDF ;(2)当四边形AECF 为菱形时,求出该菱形的面积.解:(1)证明:∵四边形ABCD 为平行四边形,∴AB =CD ,BC =AD ,∠ABC =∠CDA.又∵BE =EC =12BC ,AF =DF =12AD , ∴BE =DF.∴△ABE ≌△CDF(SAS).(2)∵四边形AECF 为菱形,∴AE =EC.又∵点E 是边BC 的中点,∴BE =EC ,即BE =AE.又∵BC =2AB =4,∴AB =12BC =BE =2. ∴AB =BE =AE ,即△ABE 为等边三角形.过点A 作AH ⊥BC 于点H ,则在Rt △ABH 中,∠BAH =30 °,∴BH =12AB =1. ∴AH =AB 2-BH 2=22-12= 3.∴S 菱形AECF =EC ·AH =2 3.20.如图,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF.(1)求证:AF =DC ;(2)若AB ⊥AC ,试判断四边形ADCF 的形状,并证明你的结论.解:(1)证明:∵E 是AD 的中点,∴AE =ED.∵AF ∥BC ,∴∠AFE =∠DBE ,∠FAE =∠BDE.∴△AFE ≌△DBE(AAS).∴AF =DB.∵AD 是BC 边上的中线,∴DB =DC.∴AF =DC.(2)四边形ADCF 是菱形.证明:由(1)知,AF =DC ,∵AF ∥DC ,∴四边形ADCF 是平行四边形.又∵AB ⊥AC ,∴△ABC 是直角三角形.∵AD 是BC 边上的中线,∴AD =12BC =DC. ∴四边形ADCF 是菱形.21.如图,在Rt △ABC 中,∠ACB =90°,过点C 的直线MN ∥AB ,D 为AB 边上一点,过点D 作DE ⊥BC ,交直线MN 于点E ,垂足为F ,连接CD ,BE.(1)求证:CE =AD ;(2)当D 在AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由;(3)若D 为AB 中点,则当∠A 的大小满足什么条件时,四边形BECD 是正方形?请说明你的理由.解:(1)证明:∵DE ⊥BC ,∴∠DFB =90 °.∵∠ACB =90 °,∴∠ACB =∠DFB.∴AC ∥DE.又∵MN ∥AB ,即CE ∥AD ,∴四边形ADEC 是平行四边形.∴CE =AD.(2)四边形BECD 是菱形.理由:∵D 为AB 中点,∴AD =BD.又由(1)得CE =AD ,∴BD =CE.又∵BD ∥CE ,∴四边形BECD 是平行四边形. ∵∠ACB =90 °,D 为AB 中点,∴CD =12AB =BD. ∴四边形BECD 是菱形.(3)当∠A =45 °时,四边形BECD 是正方形.理由: ∵∠ACB =90 °,∠A =45 °,∴∠ABC =∠A =45 °.∴AC =BC.∵D 为AB 中点,∴CD ⊥AB.∴∠CDB =90 °. ∵四边形BECD 是菱形,∴四边形BECD 是正方形.。
人教版八年级数学下第18章平行四边形《正方形》同步练习题(精品测试卷)

(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的 ;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.
第二套《一次函数》测试题
姓名:_____________
8.延长正方形ABCD的BC边至点E,使CE=AC,连结AE,交CD于F,那么∠AFC的度数为______,若BC=4cm,则△ACE的面积等于______.
9.在正方形ABCD中,E为BC上一点,EF⊥AC,EG⊥BD,垂足分别为F、G,如果 cm,那么EF+EG 长为______.
10.已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,∠ANM的度数______.
(1) 当0≤x≤60时,y与x的函数关系式是。
②当60<x≤100时,y与x的函数关系式是。
③当x>100时,y与x的函数关系式是.为了不亏本,请你求出这时x所能取得的最大值。
(2) 当0≤x≤60时,李萌该月获得的最大利润y是元。
②当60<x≤100时,李萌该月获得的最大利润y是元。
③当x>100时,李萌该月获得的最大利润y是元。
(1)m为何值时,图象过原点.
(2)已知y随x增大而增大,求m的取值范围.
(3)函数图象与y轴交点在x轴上方,求m取值范围.
(4)图象过二、一、四象限,求m的取值范围.
20.(8分)已知,直线y=2x+3与直线y=-2x-1.
(1)求两直线与y轴交点A,B的坐标;
(2)求两直线交点C的坐标;
2020-2021学年人教版 八年级数学 下册18.2 特殊平行四边形 同步测试题

18.2特殊平行四边形同步测试题(总分值120分;时间:90分钟)一、选择题(此题共计10 小题,每题3 分,共计30分, )1. 矩形、菱形、正方形都具有的性质是()A.对角线相等B.对角线互相平分C.对角线互相垂直D.对角线平分对角2. 如图,在Rt△ABC中,∠ACB=90∘,D是AB的中点,假设AB=16,那么CD的长是( )A.6B.8C.10D.123. 如图,在梯形ABCD中,AD // BC,∠B+∠C=90∘,E、F分别是AD、BC的中点,假设AD=5cm,BC=13cm,那么EF=()A.4cmB.5cmC.6.5cmD.9cm4. 在△ABC中,点D是边BC上的点(与B,C两点不重合) ,过点D作DE // AC,DF // AB,分别交AB,AC于E,F两点,那么以下说法正确的选项是( )A.假设AD垂直平分BC,那么四边形AEDF是菱形B.假设BD=CD,那么四边形AEDF是菱形C.假设AD平分∠BAC,那么四边形AEDF是矩形D.假设AD⊥BC,那么四边形AEDF是矩形5. 菱形的两条对角线长分别为6和8,那么该菱形的对称中|心到任意一边的距离为( )A.10B.5C.2.5D.2.46. 菱形的边长为5,一内角为60∘,那么较长对角线长为( )A.5 2B.5√32C.5D.5√37. 对角线互相垂直且相等的四边形是( )A.菱形B.矩形C.正方形D.以上结论都不对8. 如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们较小的交角为60∘,那么它们重叠局部的面积为()A.1B.2C.√3D.2√339. 菱形不具备的性质是( )A.四条边都相等B.对角线一定相等C.是轴对称图形D.是中|心对称图形10. 如图,矩形ABCD中,AB=10,AD=4,点E从D向C以每秒1个单位的速度运动,以AE 为一边在AE的左上方作正方形AEFG.同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当点F落在直线MN上,设运动的时间为t,那么t的值为( )A.143B.103C.4D.1二、填空题(此题共计9小题,每题3 分,共计27分, )11. 如图,在平行四边形ABCD中,添加一个条件________使平行四边形ABCD是菱形.12. 如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=________时,四边形MENF是正方形.13. 如图,矩形ABCD的对角线AC,BD相交于点O,CE // BD,DE // AC.假设AC=4,那么四边形CODE的周长是________.14如图,正方形ABCD的对角线AC=4,那么它的边长AB=________.15. 如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F,且AE=DE,那么∠A的度数是60∘,∠EBF=________.16. 如下列图是一个矩形ABCD,在AD上取一点P,过P作PF⊥AC于F,PE⊥BD于E,其中AD=12,AB=5,求PE+PF=________.17. 如图,菱形ABCD的对角线AC=24,BD=10,那么菱形的周长L=________.18. 如图,正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.假设PQ=AE,那么AP=________cm.19矩形ABCD中,要使矩形ABCD成为正方形还需满足的条件是________ (横线只需填一个你认为适宜的条件即可)三、解答题(此题共计6 小题,共计63分, )20. 如图,矩形ABCD中,点O为AC的中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO,假设∠COB=60∘,FO=FC.求证:(1 )四边形EBFD是菱形;(2 )BM:OE=3:2.21如图,O为矩形ABCD对角线的交点,过点D作DE // AC,过点C作CE // BD,且DE,CE相交于E点.试判断四边形OCED的形状,并说明理由.22. (1 )如图1,△ABC中,AD平分∠BAC交BC于点D,在AB上截取AE=AC,过点E作EF // BC交AD于点F.求证:四边形CDEF是菱形;(2 )如图2,△ABC中,AD平分△ABC的外角∠EAC交BC的延长线于点D,在BA的延长线上截取AE=AC,过点E作EF // BC交DA的延长线于点F.四边形CDEF还是菱形吗?如果是,请证明;如果不是,请说明理由.23如图,在△ABC中,∠ACB=90∘,∠CAB=30∘,以线段AB为边向外作等边△ABD,点E 是线段AB的中点,连接CE并延长交线段AD于点F.(1 )求证:四边形BCFD为平行四边形;(2 )假设AB=6,求平行四边形BCFD的面积.24求证:对角线相等的菱形是正方形.:四边形ABCD是菱形,且AC=BD (又:AC,BD互相平分)求证:四边形ABCD是正方形.25如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….(1 )记正方形ABCD的面积为S1=1,按上述方法所作的正方形的面积依次为S2,S3,S4,… ,S n,请求出S2,S3,S4的值.(2 )根据以上规律写出S n的表达式.。
人教版八年级下数学 18.2 特殊的平行四边形 同步测试
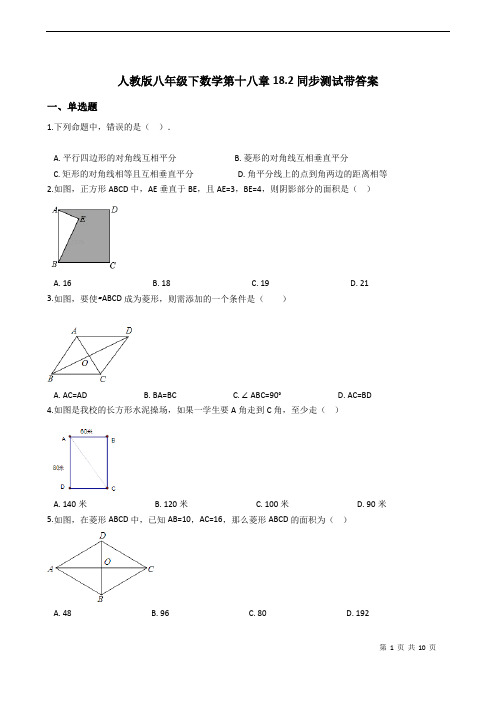
人教版八年级下数学第十八章18.2同步测试带答案一、单选题1.下列命题中,错误的是().A. 平行四边形的对角线互相平分B. 菱形的对角线互相垂直平分C. 矩形的对角线相等且互相垂直平分D. 角平分线上的点到角两边的距离相等2.如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是()A. 16B. 18C. 19D. 213.如图,要使▱ABCD成为菱形,则需添加的一个条件是()A. AC=ADB. BA=BCC. ∠ABC=90°D. AC=BD4.如图是我校的长方形水泥操场,如果一学生要A角走到C角,至少走()A. 140米B. 120米C. 100米D. 90米5.如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为()A. 48B. 96C. 80D. 1926.如图,菱形ABCD的周长为24cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE 的长等于()A. 3cmB. 4cmC. 2.5cmD. 2cm7.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )A. 30B. 34C. 36D. 408.如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为()A. cmB. 4cmC. cmD. 2 cm9.如图,正方形的面积为9 . 是等边三角形,点在正方形内,在对角线上有一点,使的和最小,则这个最小值为( ).A. 3B.C.D.10.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是()A. S1>S2B. S1=S2C. S1<S2D. 3S1=2S211.如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是()A. 四边形ACEF是平行四边形,它的周长是4B. 四边形ACEF是矩形,它的周长是2+2C. 四边形ACEF是平行四边形,它的周长是4D. 四边形ACEF是矩形,它的周长是4+412.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG﹥60⁰,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )A. 4个B. 3个C. 2个D. 1个13.在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是()A. ②③B. ③④C. ①②④D. ②③④14.如图,正方形ABCD的边长为4,M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为().A. 3B. 4C. 5D.15.在直线l上依次摆放着七个正方形(如图所示)。
八年级数学下册 第十八章 平行四边形 18.2正方形同步练习(含解析)(新版)新人教版

18.2正方形测试题一.选择题(每题3分,共30分)1.在四边形ABCD中,AC、BD相交于O点,下列条件能判断四边形ABCD是正方形的是()A。
OA=OC,OB=OCB。
OA=OB=OC=ODC.OA=OC,OB=OD,AC=BDD。
OA=OB=OC=OD,AC⊥BD2.已知四边形ABCD中,∠A=∠B=∠C=90°.如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是()A.∠D=90°B.AB=CDC。
AD=BCD。
BC=CD3.如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED,延长BE交AD于点F,若∠DEB=140°,则∠AFE的度数为()A.65°B。
70°C。
60°D.80°4.菱形、矩形、正方形都具有的性质是()A.对角线相等且互相平分B.对角线相等且互相垂直平分C。
对角线互相平分D.四条边相等,四个角相等5。
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()A。
5 B。
2 C.7 D。
296.点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()A.5B.23C.7D.297。
如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有()A.4个B。
6个C。
8个D.10个8.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E、F两点,下列说法正确的是( )A.若AD⊥BC,则四边形AEDF是矩形B。
若AD垂直平分BC,则四边形AEDF是矩形C。
若BD=CD,则四边形AEDF是菱形D。
若AD平分∠BAC,则四边形AEDF是菱形9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《正方形》基础练习1.下列命题中的真命题是( ).A .有一组邻边相等的四边形是菱形B .对角线相等的四边形是矩形C .有一组对边平行的四边形是梯形D .对角线相等的菱形是正方形2.下列四边形中,对角线相等且互相垂直平分的是( ).A .平行四边形B .正方形C .等腰梯形D .矩形3.正方形的面积为4,则它的对角线长为 .4.如图,四边形ABCD 是正方形,延长AB 到E ,使AE =AC ,则∠BCE 的度数是 度.5.如图,正方形ABCD 的周长为16cm ,顺次连接正方形ABCD 各边的中点,得到四边形EFGH ,则四边形EFGH 的周长等于 cm ,四边形EFGH 的面积等于 cm 2.参考答案1. D 解析:根据菱形.矩形.梯形.正方形的判定作出判断:A .假命题,有一组邻边相等的平行四边形才是菱形;B .假命题,例如等腰梯形,对角线也相等;C .假命题,例如平行四边形的一组对边也平行;D .真命题,符合矩形的判定定理.2. B 解析:平行四边形的对角线互相平分;等腰梯形的对角线相等;矩形的对角线相等且互相平分;正方形的对角线相等且互相垂直平分.故选B .3. 解析:正方形的面积为4,可得其边长为2,由勾股定理易得其对角线长为4. 22.5 解析:由AC 是正方形ABCD 的对角线,可得∠CAE =∠ACB =45°,又AE =AC ,得()11804567.52ACE ∠=︒-︒=︒, 故67.54522.5BCE ACE ACB ∠=∠-∠=︒-︒=︒.5.;8 解析:正方形ABCD 的周长为16cm ,则它的边长为4 cm ,对角线是.顺次连接正方形ABCD 各边的中点,得到四边形EFGH ,所以利用中位线性质可得四边形EFGH 的边长为cm .∴四边形EFGH 的周长等于cm .由正方形的定义可知四边形EFGH 是正方形,所以面积等于8 cm 2.《正方形》拓展练习1.点P 是正方形ABCD 边AB 上一点(不与A 、B 重合),连接PD 并将线段PD 绕点P 顺时针旋转90°,得线段PE ,连接BE ,则∠CBE 等于( ).A .75°B .60°C .45°D .30°2.如图,点P 是正方形ABCD 的对角线BD 上一点,PE ⊥BC 于点E ,PF ⊥CD 于点F , 连接EF .给出下列五个结论:①AP =EF ;②AP ⊥EF ;③△APD 一定是等腰三角形; ④∠PFE =∠BAP ;⑤PD = 2EC .其中正确结论的序号是 .3. 以四边形ABCD 的边AB 、BC 、CD 、DA 为斜边分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH .(1)如图1,当四边形ABCD 为正方形时,我们发现四边形EFGH 是正方形;如图2,当四边形ABCD 为矩形时,请判断:四边形EFGH 的形状(不要求证明);(2)如图3,当四边形ABCD 为一般平行四边形时,设∠ADC =α(0°<α<90°),① 试用含α的代数式表示∠HAE ;② 求证:HE =HG ;③ 四边形EFGH 是什么四边形?并说明理由.4.如图,正方形ABCD 的四个顶点分别在四条平行线1l 、2l 、3l 、4l 上,这四条直线中相邻两条之间的距离依次为1h 、2h 、3h (1h >0,2h >0,3h >0).(1)求证:1h =3h ;(2)设正方形ABCD 的面积为S ,求证:S =21221)(h h h ++;(3)若12321=+h h ,当1h 变化时,说明正方形ABCD 的面积S 随1h 的变化情况.参考答案1.C解析:过点E 作EF ⊥AF ,交AB 的延长线于点F ,则∠F =90°,∵四边形ABCD 为正方形,∴AD =AB ,∠A =∠ABC =90°.∴∠ADP +∠APD =90°. 由旋转可得:PD =PE ,∠DPE =90°,∴∠APD +∠EPF =90°.∴∠ADP =∠EPF . 在△APD 和△FEP 中,∵∠ADP =∠EPF ,∠A =∠F ,PD =PE ,∴△APD ≌△FEP (AAS ).∴AP =EF ,AD =PF .又∵AD =AB ,∴PF =AB ,即AP +PB =PB +BF .∴AP =BF .∴BF =EF又∵∠F =90°,∴△BEF 为等腰直角三角形.∴∠EBF =45°.又∵∠CBF =90°,∴∠CBE =45°.故选C .2.①、②、④、⑤.解析:作PM ⊥AB 于点M ,易证∴△APM ≌△FEP ,∴AP =EF , ∠PFE =∠BAP .故①、④正确.延长AP 交EF 于点N .∵∠BAP +∠APM =90°,∠APM =∠FPN ,∴∠PFE +∠FPN =90°.∴∠PNF =90°.即AP ⊥EF .故②正确.由PE ⊥BC ,PF ⊥CD ,正方形ABCD ,易得四边形ECFP 是矩形, △DFP 为等腰直角三角形.∴PF =EC , PD = 2PF .∴PD = 2EC .故⑤正确.l l l l∵点P是正方形ABCD的对角线BD上一点,∴AD AP AD≤≤,0DP<.∴不能保证△APD一定是等腰三角形.故③不正确.3.解:(1)四边形EFGH是正方形.(2) ①∠HAE=90°+a.在□ABCD中,AB∥CD,∴∠BAD=180°-∠ADC=180°-a.∵△HAD和△EAB都是等腰直角三角形,∴∠HAD=∠EAB=45°.∴∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-a)=90°+a.②∵△AEB和△DGC都是等腰直角三角形,∴AEAB,DGCD.在□ABCD中,AB=CD,∴AE=DG.∵△HAD和△GDC都是等腰直角三角形,∴∠DHA=∠CDG= 45°.∴∠HDG=∠HAD+∠ADC+∠CDG=90°+a=∠HAE.∵△HAD是等腰直角三角形,∴HA=HD.∴△HAE≌△HDG.∴HE=HG.③四边形EFGH是正方形.由②同理可得:GH=GF,FG=FE,∵HE=HG(已证),∴GH=GF=FG=FE.∴四边形EFGH是菱形.∵△HAE≌△HDG(已证),∴∠DHG=∠AHE.又∵∠AHD=∠AHG+∠DHG=90°,∴∠EHG=∠AHG+∠AHE=90°.∴四边形EFGH是正方形.4.解:(1)过A点作AF⊥l3分别交l2、l3于点E、F,过C点作CG⊥l3交l3于点G,∵四边形ABCD为正方形,∴AD=AB=CD,∠BAD=∠ADC=90°.∵l2∥l3,∴∠2 =∠3.∵∠1+∠2=90°,∠4+∠3=90°,∴∠1=∠4.又∵∠BEA=∠DGC=90°, BA=DC,∴△BEA≌△DGC.∴AE=CG,即1h=3h.llll(2)∵∠F AD +∠3=90°,∠4+∠3=90°,∴∠F AD =∠4.又∵∠AFD =∠DGC =90°, AD =DC ,∴△AFD ≌△DGC .∴DF =CG =3h =1h . ∵AD 2=AF 2+FD 2,∴S =21221)(h h h ++.(3)由题意,得12321h h -=, 所以 5452451452312112121211+⎪⎭⎫ ⎝⎛-=+-=+⎪⎭⎫ ⎝⎛-+=h h h h h h S 又⎪⎩⎪⎨⎧〉-〉0231011h h ,解得0<h 1<32. ∴当0<h 1<52时,S 随h 1的增大而减小; 当h 1=52时,S 取得最小值54; 当52<h 1<32时,S 随h 1的增大而增大. 《正方形》拔高练习1.下列说法不正确...的是( ). A .一组邻边相等的矩形是正方形B .对角线相等的菱形是正方形C .对角线互相垂直的矩形是正方形D .有一个角是直角的平行四边形是正方形2.如图,从边长为(a +1)cm 的正方形纸片中剪去一个边长为(a ﹣1)cm 的正方形 (a >1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( ).A .2 cm 2B .2a cm 2C .4a cm 2D .(a 2﹣1)cm 23. 正方形ABCD 的边长为a ,点E 、F 分别是对角线BD 上的两点,过点E 、F 分别作AD 、AB 的平行线,如图所示,则图中阴影部分的面积之和等于 .4. 如图,已知正方形ABCD 的边长为3,E 为CD 边上一点, 1DE =.以点A 为中心,把△ADE 顺时针旋转90︒,得△ABE ',连接EE ',则EE '的长等于 .5.如图,四边形ABCD 是正方形,点E 是边BC 的中点,∠AEF =90°,EF 交正方形外角平分线CF 于点F ,取边AB 的中点G ,连接EG .(1)求证:EG =CF ;(2)将△ECF 绕点E 逆时针旋转90°,请在图中直接画出旋转后的图形,并指出旋转后CF 与EG 的位置关系.参考答案1. D 解析:有一个角是直角的平行四边形是矩形,故D 不正确,选D .2. C 解析:根据题意得出矩形的面积是()()22114a a a +--=(cm 2).故选C . 3.212a 解析:正方形ABCD 是轴对称图形,得阴影部分的面积之和等于正方形ABCD 面积的一半,即212a .4. 解析:∵△ADE 顺时针旋转90︒得△ABE ',∴1BE DE '==.∵正方形ABCD 的边长为3,∴314CE BC BE ''=+=+=,312CE CD DE =-=-=,90C ∠=︒.∴EE'==5.解:(1)证明:∵正方形ABCD,点G,E为边AB、BC中点,∴AG=BG=EC=EB,∠B=90°.∴△BEG为等腰直角三角形.∴∠AGE=180°﹣45°=135°.又∵CF为正方形外角平分线,∴∠ECF=90°+45°=135°.∴∠AGE=∠ECF.∵∠AEF=90°,∴∠GAE=90°-∠AEB=∠CEF.∴△AGE≌△ECF(ASA).∴EG=CF.(2)画图如图所示:旋转后CF与EG平行.。
