Add Maths 2000 Paper 2
外研版四年级上学期英语句型转换考点知识练习

外研版四年级上学期英语句型转换考点知识练习班级:_____________ 姓名:_____________【句型转换】1. 按要求完成下列各题。
1. It will be rainy in Beijing. (变成一般疑问句)_______ _______ be rainy in Beijing?2. They will play basketball. (就句子主题意思提问)_______ _______ they _______?3. Will you do your homework? (作肯定回答)_______, _______ _______.4. fly, kite, my, will, I (.) (连词成句)5. housework, they, the, will, do (?) (连词成句)2. 按要求完成下列各题。
[1]The floor is green.(就句子主题意思提问)[2]Her name is Amy.(就句子主题意思提问)[3]a, I have, new friend(.)(连词成句)[4]what’s, the classroom, in(?)(连词成句)[5]is, who, the boy(?)(连词成句)3. 按要求完成下列各题。
[1]much, are, those, shoes, how, nice(?)(连词成句)[2]The skirt is very pretty. (对句子主题意思提问)[3]Are the sunglasses cheap? (作否定回答)[4]The red scarf is expensive. (改为否定句)[5]How much is your schoolbag? (根据实际情况回答)4. 按要求改写句子。
[1]I can see some boats on the lake.(对句子主题意思提问) ______ ______ you ______ on the lake?[2]I can make a cake.(对句子主题意思提问)______ ______ you ______?[3]She can see some flowers over there.(改为一般疑问句) ______ she ______ ______ flowers over there?[4]My brother likes drawing in the park.(改为否定句)My brother ______ ______ drawing in the park.[5]We can see five trees.(对句子主题意思提问)______ ______ ______ can you see?5. 句子加工厂。
2021-2022学年上海市罗星中学八年级(上)期末英语试卷

2021-2022学年上海市罗星中学八年级(上)期末英语试卷试题数:34,总分:1051.(单选题,1分)Grandma Wang told ____ amusing story to her grandson just now.()A.aB.anC.theD./2.(单选题,1分)At last Captain King and his crew escaped ____ Gork and kangaroos successfully.()A.fromB.inC.toD.above3.(单选题,1分)My friend Amy always does ____ a favour when I meet trouble in my maths.()A.IB.myC.meD.mine4.(单选题,1分)My mum ____ shops on WeChat because she thinks it is not safe.()A.alwaysB.neveruallyD.sometimes5.(单选题,1分)Our life is becoming ____ than before because of the new inventions.()A.convenientB.most convenientC.the most convenientD.more convenient6.(单选题,1分)Is there ____ between the blackboard and the noticeboard,Mary?()A.somethingC.nothingD.everything7.(单选题,1分)The home-made yogurt in this bakery tastes____.Would you like some?()A.niceB.nicelyC.badlyD.softly8.(单选题,1分)We'd better ____ talking.The class will start in a minute.()A.stopB.to stopC.stoppingD.stops9.(单选题,1分)Nancy ____ lots of trees in our town in her free time since last year.()A.has plantedB.plantedC.plantsD.is planting10.(单选题,1分)Tera is interested in Chinese culture.She ____ to study in Shanghai University two years ago.()A.beginB.beginsC.beganD.will begin11.(单选题,1分)Students ____ be careful when they do experiments in the lab.()A.canB.mustC.shouldD.need12.(单选题,1分)--______will the architect finish the plan of the bridge?--In two weeks.()A.How longB.How farC.How often13.(单选题,1分)Jane was late for an important meeting ____ her alarm clock didn't work.()A.beforeB.whyC.becauseD.when14.(单选题,1分)The ten-year-old boy saved his neighbours in a fire.____brave boy he was!()A.HowB.WhatC.What anD.What a15.(单选题,1分)--- I have nothing to do.Let's go and see a film.--- ____ .()A.I'm afraid notB.I agree with youC.Never mindD.Sounds great16.(问答题,4分)pletely B.with C.but D.making E.withoutWendy Martin is a university student who used to love chatting with friends online.She often spent much of her free time(1)___ new friends online.Then something awful happened.It(2)___ changed Wendy's feelings about the Internet.Visiting the chat rooms on music websites was Wendy's favourite thing to do online.Then Wendy first met Anne.The two women liked each other immediately.Soon they exchanged e-mail addresses and were chatting online every day.They both liked the same music,the same clothes and the same films,(3)___ they also had the same worries about studying and the future.Anne had e-mailed her a photo of herself- she even looked like Wendy.So,when Anne asked Wendy for her address and phone number,Wendy gave them(4)___ thinking.17.(问答题,4分)A.Always B.different C.In fact D.Never E.bankWhen Wendy got a letter from the bank,she realized something was wrong.Anne was not who she said she was.(1)___ ,"Anne" was a 45-year-old man called Tim Histanon.He had used Wendy's personal information to spend all the money in her(2)___ .Fortunately,Tim Histanon was finally caught by the police and Wendy got most of her money back.Everyone can learn from the mistakes that Wendy made.(3)___ give out personal information while chatting online and always make sure your user name is(4)___ from your real name.18.(问答题,1分)Peter has got ___ different birthday presents from his friends.(fifth)19.(问答题,1分)I moved to a new flat last month.There are thirty ___ in my block.(storey)20.(问答题,1分)Susan enjoyed the ___ of the school holidays with her cousin last month.(free)21.(问答题,1分)The little boy was really ___ to see so many mice for the first time.(frighten)22.(问答题,1分)It took him much time to ___ the magic character in the new film.(creative)23.(问答题,1分)Computers can add,subtract,multiply and divide ___ nowadays.(accurate)24.(问答题,1分)There will be a big ___ park called Legoland in Fengjing Town soon. (amuse)25.(填空题,2分)They'll take a plane to go on business to Dalian next week. (改为否定句)They ___ ___ a plane to go on business to Dalian next week.26.(填空题,2分)The story about Captain King took place on an unexplored planet.(改为反意疑问句)The story about Captain King took place on an unexplored planet, ___ ___ ?27.(填空题,2分)John likes the Monkey King best because he is clever and brave. (对划线部分提问)___ ___ John like the Monkey King best?28.(填空题,2分)The old lady is too weak to open the door of the car by herself. (保持原句意思不变)The old lady is ___ weak ___ she can't open the door of the car by herself.29.(问答题,2分)an architect,my ambition,I,is,leave school,when,to be (连词成句)___30.(填空题,6分)The Beijing 2022 Winter Olympic Games will begin on February 4,2022.It will end on February 20,2022.The Winter Paralympics (残奥会) will begin a month later.Do you know the two lovely mascots?On September 17 of the year 2021,the two lovely mascots first showed on TV.Let's meet the mascots!Look at the panda!It looks like an astronaut.It wears an ice shell,which helps the panda toskate,snowboard and ski and it looks fat,so we call it "Bing Dwen Dwen" (冰墩墩) .The design for Bing Dwen Dwen was chosen from over 5,800 pieces of designs from China and 35 countries around the world.White is the colour of ice and snow. "Bing Dwen Dwen" likes ice sports very much and is good at them.That's why it is the mascot of 2022 Beijing Winter Olympic Games.Do you think the red mascot looks like a lantern?The lantern 's name is "Shuey Rhon Rhon"(雪容融) .When the Chinese New Year comes,people always make or buy red lanterns.Red is the colour of hope and good luck,so people think their dreams will come true in the new year."Shuey Rhon Rhon" can give players hope and help them do well in the 2022 Beijing Winter Paralympic Games.Many people in different countries like the two mascots very much,and they show their love for them on the Internet.(1)The Beijing 2022 Winter Olympic Games will last for ___ .A.more than a monthB.more than twenty-four daysC.more than half a monthD.more than two months(2)___ is the mascot of 2022 Beijing Winter Olympic Games.A.An astronautB.Shuey Rhon RhonC.A red lanternD.Bing Dwen Dwen(3)The underlined word "mascot" in the first paragraph means ___ .A.a song of the Olympic GamesB.a sport of the Olympic GamesC.a symbol of the Olympic GamesD.a colour of the Olympic Games(4)Why do people make or buy red lanterns when the Chinese New Year comes? ___A.Because people think red lanterns can bring good luck.B.Because"Shuey Rhon Rhon" is a mascot.C.Because people think red lanterns are very lovely.D.Because it is easy to make red lanterns.(5)Which of the following statements is TRUE according to the passage? ___A.The design for Bing Dwen Dwen was only chosen from China.B."Shuey Rhon Rhon" likes ice sports and is good at them.C.Everybody likes the two mascots and shows his love on the Internet.D.The two lovely mascots first showed on TV on September 16.(6)What's the best title of the passage? ___A.The sports in Olympic GamesB.Two Olympic mascots come to lifeC.2022 Beijing Winter Olympic GamesD.2022 Beijing Winter Paralympic Games31.(填空题,6分)One day I walked along the sea for about an hour then I felt hungry.It was seven.I went to my favourite restaurant,where I often went to eat two or three times a week.I knew the owner well.I went into the crowded restaurant and ordered my meal.While I was(1)___ ,I saw a man sitting at a corner table near the door keeping looking in my direction,as if he knew me.The man had a newspaper open in front of him.But I could see that he was keeping an eye on me.When the waiter brought my soup,the man was(2)___ puzzled by the waiter and me.We talked with each other warmly like family members.He found that I was well known in the restaurant.(3)___ he got up and went into the kitchen.After a few minutes he came out,paid for his meal and left.When I finished the dinner,I asked the owner(4)___ the man had wanted.The owner told me he was a detective."Really?" I was surprised. "He was certainly interested in me.But why?" I asked." He followed you here because he thought you were a man he was looking for,"the owner said."When he came into the kitchen,he showed me a(5)___ of the wanted man.He certainly looked like you!Of course I told him that he had made a mistake."How(6)___ I was!I came to a restaurant where I was known well,or I might have been in trouble!(1)A.eating B.singing C.waiting D.sleeping(2)A.quickly B.clearly C.slowly D.badly(3)A.At first B.At last C.At most D.At least(4)A.which B.why C.when D.what(5)A.photo B.book C.magazine D.paper(6)A.strange B.bad C.lucky D.amazing32.(问答题,7分)In Spelling Bee competitions,children try to spell difficult words correctly.And by spelling the word""murraya"(a type of tree)14-year-old Zaila Avant-garde w (1)___ the first prize in the 2021 U.S.National Spelling Bee.To get to this point,Avant- garde practiced for seven hours a day.She tried to remember the spelling of about 13,000 words per day.But the girl says spelling is her side hobby.Her"r(2)___ hobby" is basketball.Avant- garde started practicing dribbling(运球)w(3)___ she was five years old.For her eighth birthday,her parents gave her a Guinness(吉尼斯)World Records book.After r(4)___ it,the girl wanted to get a record for herself.Now,Avant-garde has three Guinness World Records for her basketball skills.Her favorite record is the most basketballs(six)dribbled at the same time by one person.She practiced it for two years before creating the record for her 13th birthday.Avant-garde a(5)___ has more than 12,000 followers on the Internet.And videos of her dribbling basketballs attracted some famous players."I'm not just playing basketball.I'm trying to go somewhere with it," the girl says. "Spelling is like the d(6)___ basketball is like the main dish."Avant-garde says she is trying to get as many achievements as she can.She hopes to help the girls around the world.She wants t(7)___ to know that they can do any that they put their minds to.33.(问答题,7分)Shenzhou-13 crew members Zhai Zhigang,Wang Yaping and Ye Guangfu gave the first live class from China's space station to students on the earth on Thursday afternoon,9 December,2021.The class began at 3:40 p.m. (Beijing Time),with a total of 1,420 students attending the lecture from five classrooms across China.The primary classroom is located in the China Science and Technology Museum in Beijing.Classrooms have also been set up in Nanning in south China's Guangxi Zhuang Autonomous Region,Wenchuan County in Sichuan Province,Hong Kong and Macao.Wang Yaping,helped by the two other crew members,gave the students a tour of the living and working areas of the space station.She showed them the microwave,water dispenser(自动取物装置)and refrigerator in the space kitchen.She opened the mini-fridge and took out a fresh apple.In response to a student's questions,Wang described what she could see in space."The stars we see are much brighter,but they do not twinkle.The sky we see isn't blue,but deep black.And every day,we can see the sun rise 16 times because we circle the Earth every 90 minutes," she said.Zhai Zhigang introduced the special uniform Ye Guangfu was wearing during theclass.According to Zhai,it is called a"penguin jumpsuit" and it has multiple elastic bands(多弹性带)inside it to help the astronauts maintain their muscle strength.The three astronauts answered the questions carefully and ended the class with their best wishes."The secrets of space and science are boundless(无止境的),and the future is yours,"said Zhai Zhigang.(1)When did the students on the earth have the first live class from China's space station?___(2)How did Wang Yaping give the students a tour of the living and working areas of the space station? ___(3)The three astronauts can't have fresh fruit in the space station,can they? ___(4)How many times do the three astronauts circle the Earth every day? ___(5)What is the use of multiple elastic bands inside a"penguin jumpsut"? ___(6)What do you think of the live class from China's space station ?Why? ___ ___34.(问答题,9分)Write at least 60 words on the topic"A letter to ____ "(寒假即将来临,你已制定好你的寒假计划,并想分享给你的笔友Simon,请以"给 ____ 的一封信"为题,写一篇正文不少于60词的书信,标点符号不占格。
初中核心2000单词(自然拼读法分类)
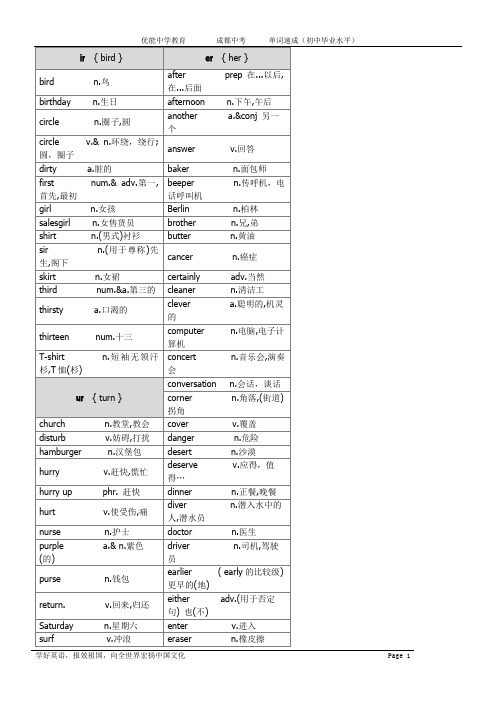
description n.描述,描写
English a.英国(人)的n.英语
dictionary n.字典;词典
finish v.完成,结束
education n.教育,培养
car n.汽,小汽车
bring v.带来,拿来
card n.纸牌,卡片
crossing n.十字路口,交叉点
chart n.图表
dumpling n.饺子
dark a.深(浓)色的,黑暗的
during prep在...的期间
far a.& adv.远
evening n.傍晚;晚上
farm n.农场
mother n.母亲
supermarket n.超级市场
Mr=mister n.先生(用于姓名前)
supper n.晚餐
neither a.& pron.(两者)都不
surfer n.冲浪者
nervous a.紧张不安的
sweater n.毛衣,厚运动衫
never adv.从来,决不
teacher n.教师
ar{ car }
ing
arm n.手臂;胳膊
amazing a.令人惊奇的
art n.艺术,艺术品
anything pron.任何事(物)
Artist n.画家,艺术家
beginning n.开始,开端
Barn n.谷仓,堆物房;马房,牛舍
boating n.划船
bookmark n.书签
boring a.令人厌烦的
Thursday n.星期四
explorer n.探测者,探险者
turkey n.火鸡
17Module1模块小结(练习)2

Module 1 Feelings and impressions模块小结要点1 感叹句(高频考题,重点训练)What a delicious smell? 多香的气味啊!由what 引导的感叹句 What + a/an +形容词+可数名词单数+主语+谓语!What +形容词+可数名词复数+主语+谓语!What +形容词+不可数名词+主语+谓语!由 how 引导的感叹句 How +形容词 / 副词+主语+谓语!How +形容词+ a/an +可数名词单数+主语+谓语!How +主语+谓语!由 what 引导的感叹句与由 how 引导的感叹句有时可以转换,但句中部分单词的顺序要有所变【典例分析】1. __________ special classes we had! We have learned a lot about paper cutting.A. WhatB. What aC. How aD. How【点拨】A 句意为“我们上了多么特殊的课啊!我们已经学会了很多有关剪纸的知识。
”分析句子结构可知,感叹句的中心词为名词classes ,因此应用what 来修饰,故选A 。
2. ________special classes we had! We have learned a lot about paper cutting. (2020,山东青岛卷)A. WhatB. What aC. How aD. How 思维导图 知识要点一、重点单词,短语及句。
【点拨】A句意:我们上的课多么不寻常啊!我们学到了很多剪纸的知识。
感叹句的基本结构:How+形容词/副词+主语+谓语+其他! What+(a/an)+(形容词)+名词+主语+谓语+其他!题干中的中心词classess 是可数名词复数,符合“What+形容词+可数名词复数+(主语+谓语+其他)!”,故答案选A。
注意:判断感叹句是由what还是how引导的方法:首先,断句。
Mathematics(ProjectMaths)

Pre-Leaving Certificate ExaminationMathematics (Project Maths)Paper 2Ordinary Level (with solutions)February 2010 2½ hours300 marksFor examinerQuestion Mark1 23 4 5 6 7 8 9 TotalInstructionsThere are three sections in this examination paper:question Section 0 Area & Volume (old syllabus) 50marks 1 Section A Concepts and Skills 125 marks 5 questionsSection B Contexts and Applications 125 marks 3 questionsAnswer all nine questions, as follows:In Section 0, answer question 1In Section A, answer questions 2, 3, 4, 5 and 6In Section B, answer:7questionquestion8either question 9A or question 9B.Write your answers in the spaces provided in this booklet. There is space for extra work at the backof the booklet. Extra paper may be used if needed. Label any extra work clearly with the question number and part.The booklet Formulae and Tables may be used.Marks will be lost if all necessary work is not clearly shown.Answers should include the appropriate units of measurement, where relevant.Answers should be given in simplest form, where relevant.Section 0 Area and Volume (old syllabus) 50 marks Answer Question 1 from this section.Question 1 (50 marks)(a)(b)page running10 marks (att 3) old syllabusB11 m 12 m11 m 16 m 84 m(c)Section A Concepts and Skills 125 marks Answer all five questions from this section.Question 2 (25 marks) Sarah is on a TV game show called Take the Money and Run.She has won €10 000 so far. She now has four options:Option 1: Leave the show with €10,000 – that is, Take the Money and Run.Option 2: Play on and take a 50% chance of winning €50 000Option 3: Play on and take a 30% chance of winning €75 000Option 4: Play on and take a 20% chance of winning €100 000If she plays on and does not win the higher amount, she loses the €10 000.(a)(b)page runningThe ray method was used to enlarge a design for a Valentine card. The original is labelled A and the image is labelled B.B(a)Find the centre of enlargement. Answer: Construction lines (as shown, or suitablealternatives) to get point C on the diagram.10 B(b)Find the scale factor of the enlargement. Show your work. 5 BTwo spinners, each with four equal segments numbered 1 to 4, are spun.(a)Using a list, table, tree diagram, or otherwise, show all the possible outcomes. 10 Cpage running(a)Two points A(–3, 2) and B(4, –1) are shown on the diagram below. Plot two suitable pointsC andD so that ABCD is a parallelogram. Label the points and write down their co-ordinates.5 B(b) By performing suitable calculations, show that the figure you have drawn is indeed aparallelogram. 10 C(c)Other valid methods accepted. Example: calculation of diagonal lengths and half lengths.Question 6 (25 marks)(a)On the diagram below, show the triangle ABC, where A is (–4, 1), B is (–2, 5) and C(6,1). 5 Bis(b) Find D, the midpoint of [AC], and label this point on the diagram. 5 Bpage runningSection B Contexts and Applications 125 marksin this section, answer Question 7 and Question 8, and either Question 9A or Question 9B.Question 7 Probability and Statistics (40 marks) (a) A teacher asked the students in her class to estimatethe height of the church opposite the school in metres.The stem-and-leaf diagram shows all the results:3 5 94 0 2 6 8 85 3 3 5 7 7 96 0 5 5 57 48 8 2 7Key: 3 5 represents 35 m(b) Alex and Bobby are running in the final of a 100 metre race and a 200 metre race. The probabilities of each of them winning each race are given in the table below. The probability that neither of them wins the 100 metre race is also given.(i) Complete the table above, by inserting the probability that someone other than Alex orBobby wins the 200 metre race. 5 A(ii) Using the tree diagram, or otherwise, complete the list of outcomes below. For example, the outcome that Alex wins the first race and the second race is recordedas (A, A), as shown. 10 CWrite the probability of each outcome in the space beside it.(c) What is the probability that Alex and Bobby win a race each?161 + 161 = 815 Bpage runningQuestion 8Geometry and Trigonometry (40 marks)The students mentioned in Question 7(a) above went to measure the height of the church.(a) Peter explained his group’s method:“We made a clinometer from a protractor, a pentube, some thread and a weight. We measured the distance from here to the church and it was 92 metres.We made sure the ground was flat. Then we used the clinometer to look up at the top of the spire of the church. The weight had moved from 90° to 65°, so we knew the angle up was 25°. We worked out the height from that. But we had to remember to add on my height of 1·8 metres at the end” (i)On the diagram below, show the measurements that Peter’s group made.5 B(ii) Show how Peter’s group used these measurements to find the height of the church.tan 25 =92hso h = 92 tan 25 = 42.910 C*Add Peter’s height (1.8) Height of church is 44.7 m(b)Hannah was in a different group from Peter. She explained her group’s method for findingthe height of the church: 15 C*“It was really sunny and we used the shadows cast by the sun.Amy stood with her back to the sun and we used a tape measure to measure Amy’s shadowalong the ground from the tips of her toes to top of her shadow’s head. We also measuredAmy’s height and recorded the results in the table.Then we recorded the length of the shadow cast by the church. We measured along theground from the base of the church out to the end of its shadow and recorded thismeasurement.”Amy’s shadow 2 mAmy’s height 1·7 mChurch’s shadow 69·4 mShow how Hannah’s group used their results to calculate the height of the church.(c)page runningQuestion 9A Probability and Statistics (45 marks) Oxygen levels in a polluted river were measured at randomly selected locations before and after a clean-up. These results are given in the table.Before (mg/l) After (mg/l)20 23 2 11 2523102010119115261131310 10 915 11 118 11 4(a)(b)(c)(d) Oxygen levels were measured at 400 different sites on different rivers.The measurements are summarised in the table below.10 COxygen level (mg/l) <5 <10 <15 <20 <25 Number of sites 200285365385400Draw a cumulative frequency diagram to represent this data, using the scale indicated. 400 350 300 250 200150 100550N u m b e r o f s i t e s (c u m u l a t i v e )10152025••• •• Oxygen level, in mg/l(e) Use your cumulative frequency curve to estimate:5 A(i)the number of sites with oxygen levels below 23 mg/l395± 10 (ii) the interquartile range11 - 2.48.65 B(f)An oxygen level of between 2 and 8 mg/l indicates that the site is moderately polluted . If a site is chosen at random from the 400 sites in part (d), what is the probability that it is moderately polluted? 5 B No. sites moderately polluted = 250 – 80 = 170Probability of selecting one of these from the 400 sites = 170 ÷ 400 = 0.425page runningmarks) Question 9B Geometry and Trigonometry (45Noel and Anne were taking part in a mathematics competition with other students from the ProjectMaths schools. They were finding the area of the face of the triangular sculpture shown below.Noel said: “We should measure the height and the base of the triangle. Then use the formula thatsays the area is half the base by the height.”Sarah said: “Ok, but how do we know which side is the base?”Noel said: “It doesn’t matter, because of the theorem we did.”(a)State the theorem that Noel is talking about. 5 BIn a triangle, base times height does not depend on the choice of base. [Theorem 16]Could be stated as: In any triangle, the base multiplied by the altitude does not depend on thechoice of base [is the same for all bases; is constant].(b)Noel and Sarah trace the triangle from the photograph onto a page to find its area. Theirdrawing is shown here. By making suitable measurements on the drawing, verify the theorem you stated in part (a).(c)page runningpage runningNote to readers of this document:This pre-Leaving Certificate paper is intended to help teachers and candidates in the 24 Project Maths initial schools prepare for the June 2010 examination. The content and structure of the paper do not necessarily reflect the 2011 or subsequent examinations in the initial schools or in all other schools.Mathematics (Project Maths) – Paper 2Pre-Leaving Certificate Paper – Ordinary LevelFebruary 2010。
IB Maths HL 2014 Nov Paper 1 Questionpaper

14 pagesN14/5/MATHL/HP1/ENG/TZ0/XXWednesday 12 November 2014 (afternoon)MATHEMATICS HIGHER LEVEL PAPER 1INSTRUCTIONS TO CANDIDATES Write your session number in the boxes above.Do not open this examination paper until instructed to do so. You are not permitted access to any calculator for this paper. Section A: answer all questions in the boxes provided.Section B: answer all questions in the answer booklet provided. Fill in your session numberon the front of the answer booklet, and attach it to this examination paper and your cover sheet using the tag provided.Unless otherwise stated in the question, all numerical answers should be given exactly or correct to three signi fi cant fi gures.A clean copy of the Mathematics HL and Further Mathematics HL formula booklet is required for this paper.The maximum mark for this examination paper is [120 marks].Examination code 8814–721Candidate session number2 hours© International Baccalaureate Organization 2014881472011.– 3 –Turn overN14/5/MATHL/HP1/ENG/TZ0/XX2. [Maximum mark: 6]The quadratic equation 28102x x −+= has roots α and β. (a) Without solving the equation, find the value of (i)αβ+;(ii) αβ.[2]Another quadratic equation x px q 20++=, p q ,∈ has roots 2α and 2β.(b) Find the value of p and the value of q .[4]...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ............................................................................................................................................Turn overEvents A and B are such that P ().A =02 and P ().B =05. (a) Determine the value of P ()A B ∪ when (i)A andB are mutually exclusive;(ii) A and B are independent.[4](b) Determine the range of possible values of P (|)A B .[3]...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ...................................................................... ............................................................................................................................................SECTION BAnswer all questions in the answer booklet provided. Please start each question on a new page.11. [Maximum mark: 23] The function f is defined as f x x ()=+e 31, x ∈ . (a) (i)Find f x −1().(ii) State the domain of f −1.[4]The function g is defined as g x x ()ln =, x ∈+ .The graph of y g x =() and the graph of y f x =−1() intersect at the point P. (b) Find the coordinates of P.[5]The graph of y g x =() intersects the x -axis at the point Q.(c)Show that the equation of the tangent T to the graph of y g x =() at the point Qis y x =−1.[3]A region R is bounded by the graphs of y g x =(), the tangent T and the line x =e . (d) Find the area of the region R .[5](e) (i)Show that g x x ()≤−1, x ∈+ .(ii) By replacing x with1xin part (e)(i), show that x x g x −≤1(), x ∈+ .[6]Turn over12. [Maximum mark: 14]The position vectors of the points A, B and C are a , b and c respectively, relative to anorigin O. The following diagram shows the triangle ABC and points M, R, S and T.CBdiagram not to scaleM is the midpoint of [AC].R is a point on [AB] such that AR AB →→=13.S is a point on [AC] such that AS AC →→=23.T is a point on [RS] such that RT RS →→=2.(a) (i) Express AM →in terms of a and c .(ii) Hence show that BM →=−+1212a b c .[4](b) (i) Express RA →in terms of a and b .(ii) Show that RT →=−−+292949a b c .[5](c)Prove that T lies on [BM].[5]Please do not write on this page. Answers written on this pagewill not be marked.Please do not write on this page. Answers written on this pagewill not be marked.。
2-6年级谐音记忆

二年级(上)“读音谐音记忆法”记忆的单词1、jigsaw (拼图)处理:谐音—几个锁联想:几个锁正在玩拼图比赛2、party (聚会)处理:谐音—怕踢联想:怕踢就不要去参加聚会3、we (我们)处理:谐音—为联想:为了好成绩我们要努力学习4、have (有)处理:谐音—海屋联想:海屋里有很多动物5、Maths (数学)处理:谐音—麦斯联想:麦斯发明了数学6、Music (音乐)处理:谐音—缪热可联想:缪热可是一种新流行的音乐7、please (请)处理:谐音—普利日联想:普利日请你滚出去8、half (半小时)处理:谐音—哈佛联想:去哈佛走半小时就到了9、listen (听)处理:谐音—李生联想:李生用鼻子在听10、ship (船)处理:谐音—犀浦联想:到犀浦要坐船才能去11、sweater (毛线衫)处理:谐音—斯威特联想:斯威特每天都穿毛线衫12、warm (暖和)处理:谐音—我们联想:我们掉进水里感觉好暖和13、Christmas (圣诞节)处理:谐音—克瑞斯麦斯联想:克瑞斯麦斯拉来了圣诞节14、with (和…...一起)处理:谐音—尾日联想:尾日我才能和你在一起15、OK (好)处理:谐音—呕咳联想:我呕咳一下就好了16、PE (体育课)处理:谐音—皮衣联想:穿着皮衣才能上体育课17、time(时间)处理:谐音—太猛联想:太猛了时间就跑了18、hungry(饥饿的)处理:谐音—航格瑞联想:航格瑞饥饿的时候吃垃圾三年级(上)“读音谐音记忆法”记忆的单词1、people人们处理:谐音—皮破联想:皮破了人们就认为那不吉祥。
.2、knife刀处理:谐音—来虎联想:来虎的时候我们要用刀去抵挡.3、naughty淘气的处理:谐音—裸体联想:看那个裸体的小男孩真淘气.4、mouse老鼠处理:谐音—猫死联想:猫死了以后,老鼠变的猖狂起来.5、cough咳嗽处理:谐音—克服联想:感冒了一定要克服咳嗽.6、stone石头处理:谐音—石头硬联想:石头硬不一定说明石头好.11、jump跳处理:谐音—酱铺联想:酱铺里有一个跳着走路的伙计.12、biscuit饼干处理:谐音—鼻屎扣得联想:鼻屎扣得到处都是还沾在了饼干上面.13、animal动物处理:谐音—爱你摸联想:动物都爱你摸它。
_2_精品文档

英语参考答案第一部分听力1~5:BCBAA 6~10:CCABC11~15:ACBAB 16~20:ABBCA第二部分阅读第一节A【语篇导读】这是一篇应用文。
文章介绍了《时代》杂志选出的25个最佳发明中最有趣的三项.21.A【解析】细节理解题。
根据Tasty One Top部分it'll tell you when to turn your steak or when to add certain ingredients可知,Tasty One Top通过教人们如何烹饪来帮助人们。
22.C【解析】细节理解题。
根据Jibo部分Said to be “the world's first social robot for the home”以及It can also set alarms, remind you of important things, tell you the weather and read news or messages from your friends and family.可知,Jibo可能是家庭助手.23.B【解析】推理判断题。
根据文章开头的信息并结合文章中介绍的三项发明可推知,这篇文章旨在介绍一些新发明。
B【语篇导读】这是一篇新闻报道。
文章介绍了被评为“2022年最美教师”之一的天津职业大学教师李建国,他为培养学生职业技能和国家技术专家做出了贡献。
24.B【解析】推理判断题.根据第二段Li has stood out by taking the lead in the training of students in vocational skills, gaining a number of honors including being named as a national role model teacher. He has mentored. seven national-level technique experts and a team of 14 technique masters.可推知,作者在第二段提到郭金鹏是为了展示李建国的成就。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.
y A(1, 2)
P
O Figure 2
B(2, 0)
x
In Figure 2, the coordinates of points A and B are (1, 2) and (2, 0) respectively. Point P divides AB internally in the ratio 1 : r. (a) (b) (c) Find the coordinates of P in terms of r . Show that the slope of OP is 2r . 2+r (6 marks)
(c)
C1
C2 O
C3 x Figure 5
Figure 5 shows the circles C1 and C2 in (b). L is a common tangent to C1 and C2. C3 is a circle touching C2 , L and the x-axis but it is not in F. (See Figure 5.) Find the equation of C3. (Hint : The centres of the three circles are collinear.) (5 marks)
π intersect at the point ( , − 1) . Find the area of the shaded region 4 π bounded by C1 , C 2 and the line x = . 3 (5 marks)
2000-CE-A MATH 2–6 –5–
保留版權 All Rights Reserved 2000
–8–
Go on to the next page
保留版權 All Rights Reserved 2000
11.
(a)
y
O –h x2 + y2 = r2
x
9.
Given a family of circles
F : x 2 + y 2 + (4 k + 4) x + (3k + 1) y − (8k + 8) = 0 ,
where k is real. C1 is the circle x 2 + y 2 − 2 y = 0 . (a) Show that (i) (ii) (b) C1 is a circle in F, C1 touches the x-axis. (4 marks)
sin A + sin B = 2 sin
sin A − sin B = 2 cos
cos A + cos B = 2 cos
cos A − cos B = −2 sin
2 sin A cos B = sin ( A + B) + sin ( A − B) 2 cos A cos B = cos ( A + B) + cos ( A − B) 2 sin A sin B = cos ( A − B) − cos ( A + B)
2000-CE A MATH
PAPER 2
HONG KONG EXAMINATIONS AUTHORITY HONG KONG CERTIFICATE OF EDUCATION EXAMINATION 2000
ADDITIONAL MATHEMATICS PAPER 2
11.15 am – 1.15 pm (2 hours) This paper must be answered in English
two distinct points on P, where t1 < 0 < t 2 . L1 and L2 are tangents to P at A and C respectively and they intersect at point B. Let M be the midpoint of AC. (a) Show that (i) (ii) (iii) the equation of L1 is x − t1 y + t12 = 0 , the coordinates of B are (t1t 2 , t1 + t 2 ) , BM is parallel to the x-axis. (7 marks)
1. 2. 3. 4.
Answer ALL questions in Section A and any THREE questions in Section B. All working must be clearly shown. Unless otherwise specified, numerical answers must be exact. The diagrams in the paper are not necessarily drawn to scale.
3.
y
Q(4 cos θ , 3 sin θ )
P(–4, 0) O R E
x
Figure 1 y2 x2 P(−4, 0) and + = 1. 16 9 π Q (4 cos θ , 3 sin θ ) are points on E, where 0 < θ < . R is a point such 2 that the mid-point of QR is the origin O. Figure 1 shows the ellipse E : (a) (b) Write down the coordinates of R in terms of θ . If the area of ∆ PQR is 6 square units, find the coordinates of Q . (6 marks)
∫ cos 3x cos x d x .
sin 5 x − sin x = 4 cos 3 x cos x . sin x
(3 marks)
(b)
Show that
Hence, or otherwise, find
∫
sin 5 x dx . sin x
(4 marks)
(c)
Using a suitable substitution, show that
7.
(a)
By expressing cos x − 3 sin x in the form r cos ( x + θ ) , or otherwise, find the general solution of the equation cos x − 3 sin x = 2 .
(b)
Find the number of points of intersection of the curves y = cos x and y = 2 + 3 sin x for 0 < x < 9π . (8 marks)
香港考試局 保留版權
Hong Kong Examinations Authority All Rights Reserved 2000
2000-CE-A MATH 2–1
FORMULAS FOR REFERENCE
sin ( A ± B ) = sin A cos B ± cos A sin B cos ( A ± B) = cos A cos B # sin A sin B tan ( A ± B) = tan A ± tan B 1 # tan A tan B A+ B A− B cos 2 2 A+ B A− B sin 2 2 A+ B A− B cos 2 2 A+ B A− B sin 2 2
If ∠ AOP = 45° , find the value of r .
2000-CE-A MATH 2–4
–3–
保留版權 All Rights Reserved 2000
6.
y
C
A
O Figure 3
x y = –x + 1
dy = 2 x + 3 . The dx line y = − x + 1 is a tangent to the curve at point A. (See Figure 3.) Find The slope at any point ( x, y ) of a curve C is given by (a) (b) the coordinates of A, the equation of C. (7 marks)
∫
(d) y
π 4 π 6
sin 5 x dx = sin x
∫
π 3 π 4
cos 5 x dx . cos x
(π 3
x
(
π , − 1) 4
Figure 4 sin 5 x cos 5 x and C 2 : y = sin x cos x
In Figure 4, the curves C1 : y =
2000-CE-A MATH 2–2
–1–
保留版權 All Rights Reserved 2000
Section A (42 marks) Answer ALL questions in this section.
1.
Find
∫
2x +1 d x . (4 marks)
2.
Expand (1 + 2 x) 7 (2 − x) 2 in ascending powers of x up to the term x 2 . (5 marks)
2000-CE-A MATH 2–8
–7–
