辽宁省大连金石滩实验学校2019-2020学年七年级下学期5月网络授课摸底考试数学试题
大连中学2019-2020学年度七年级(下)数学用卷周测(1)

大连中学2019-2020学年度七(下)网课周末实战演练《实数》单元检测卷(2020年3月14日星期六)满分:100分 考试时间:晚18:00--19:00 成绩评定:一、选择题(每小题3分,共30分)1.9的平方根是( )A .113B .-3C .±3D .32在实数范围内有意义,则x 的取值范围是( )A .x ≥2B .x >2C .x >-2D .x ≥-23.估计5 )A .1和2之间B .2和3之间C .3和4之间D .4和5之间4的算术平方根是( )A .3B .9C .±3D .±9 5.一个正数的两个不同的平方根是a -1与a +3,则a 的值是( )A .0B .1C .-1D .26.自然数m 的算术平方根是a ,则自然数m +1的算术平方根是( )A .(a +1)B .±(a +1)C D .7.已知(a -27)2+|b +3|=0=( ) A .0B .1C .-1D .±18.先观察下列三个等式,再回答下列问题:①1+11-12112=1+12-13116=;1+13-141112=,… ) A .211110 B .11110 C .1121 D .11109.已知a +1的算本平方根是2,2a +b -3的平方根是±3,求a +b 的值是( )A .3B .5C .7D .910=x ,则满足条件的实数x =1;②若4x 2-16=0,则x 的值为±2;③±3是27的立方根;=-(a 3-64)2,则a -b 的算术平方根是2.其中正确的有( )个. A .1 B .2 C .3D .4二、填空题(每小题3分,共18分)11.比较大小:12(填“<”,“=”,“>”)12.225的平方根是_____________________.13.我们把半径为1的圆从数轴上表示-1的点A 开始沿数轴向右滚动一周(如图所示),圆上的点A 到达点A ´,则14.用“@”表示一种新运算:对于任意正实数a ,b ,都有a @b1,如8@91,则m @25的结果是_________. 15.如图所示是小华同学设计的一个计算机程序,请你看懂后再做题:若输出的结果是0且没有返回运算,输入的数x 是__________.第13题图第14题图16.如图,在数轴上-1的对应点分别为A ,C ,A 是线段BC 的中点,则点B 所表示的数是___________.三、解答题(共6题,共52分)17.(本题8分)计算:(1(2)|1|+ 18.(本题8分)求下列各式中x 的值(1)(x +2)2=9 (2)12(2x -1)3=-4.19.(本题8分)实数a ,b在数轴上的位置如图所示.化简:a b -a0b20.(本题8分)a+1的平方根是±4,3b+1的立方根是-2,求2a+b的立方根.21.(本题8+7的小数部分是a,7的小数部分是b,求a+b的值.22.(本题10分)填空:(1__________=__________=_________.(2=____________________=__________.观察上述(1),(2)的规律,并解答(3a=__________.28912.89,则x=______(4)若将一个正方形的面积扩大为原来的100倍,则它的边长为原来的多少倍?面积扩大原来的10000倍呢?n倍呢?。
辽宁省2019-2020年七年级下学期模拟预测数学试卷

P 的坐标即可.
6.下列调查中,适合作全面调查的是(
)
A .了 解海尔牌电冰箱的市场占有率
B . 了 解奇瑞牌汽车每百里的耗油量
3
21.如图, AD ∥ BC, AD 平分∠ EAC ,你能确定∠ B 与∠ C 的数量关系吗?请说明理由.
22.某中学现有学生 2870 人,学校为了进一步丰富学生课余生活,拟调整兴趣活动小组, 为此进行了一次抽样调查,根据采集到的数据绘制的统计图(不完整)如下:
请你根据图中提供的信息,完成下列问题:
.
16.已知直线 a∥ b,点 M 到直线 a 的距离是 5cm,到直线 b 的距离是 3cm,那么直线 a 和
直线 b 之间的距离为
.
2
17.经调查,某校学生上学所用的交通方式中,选择
“自行车 ”、“公交车 ”、 “其他 ”的比例为
7: 3: 2,若该校学生有 3000 人,则选择 “公交车 ”的学生人数是
5.如果 P( m+3, 2m+4)在 y 轴上,那么点 P 的坐标是(
A .( ﹣ 2, 0)
B .( 0,﹣ 2)
C. ( 1, 0)
) D. ( 0, 1)
考点 :点 的坐标. 分析:根 据点在 y 轴上,可知 P 的横坐标为 0,即可得 m 的值,再确定点 解答:解 :∵ P( m+3, 2m+4 )在 y 轴上,
)
C. 3
D.4
3.方程 2x ﹣ 3y=5,x+ =6 ,3x﹣ y+2z=0 ,2x+4y ,5x ﹣ y>0 中是二元一次方程的有(
辽宁省大连市2019-2020学年中考物理五模考试卷

辽宁省大连市2019-2020学年中考物理五模考试卷一、单项选择题1.有经验的渔民都知道.只有瞄准鱼的下方才能把鱼叉到,如图所示.下列四幅光路图,能够正确说明叉到鱼的道理的是( )A. B. C. D.2.如图所示,将苹果和梨子放入水中后,苹果漂浮,梨子沉底。
若苹果的质量、体积及受到的浮力为m1、V1和F1,梨子的质量、体积及受到的浮力为m2、V2和F2,现有以下判断,正确的是(1)若m1>m2,则F1一定小于F2(2)若m1=m2,则F1一定大于F2(3)若V1=V2,则F1一定小于F2(4)若V1>V2,则F1一定大于F2。
A.(1)(3)B.(1)(4)C.(2)(3)D.(2)(4)3.单板滑雪项目的重头戏之一是U型池场地比赛,图甲是U型池场地。
在2018年平昌冬奥会单板滑雪女子U型池场地决赛中,中国选手刘佳宇获得中国代表团的首枚奖牌。
图乙是她在决赛中完成某个动作的一瞬间,下列说法中正确的是A.她从离开池沿腾空至最高点的过程中,动能减少,势能增加B.她腾空到最高点时,合力为零C.她在下落过程中,惯性逐渐增大D.她沿内壁下滑过程中,只受重力4.如图所示,两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置。
已知连续两次曝光的时间间隔是相等的。
两木块运动情况在v-t图像中描述正确的是()A.B.C.D.5.深秋的大巴山常常出现“缥缈的雾,晶莹的露,轻柔的雪,凝重的霜”这种现象,你对所描述的物理现象理解正确的是()A.“缥缈的雾”是升华现象B.“晶莹的露”是熔化现象C.“轻柔的雪”是凝固现象D.“凝重的霜”是凝华现象6.如图,将两个底面平整、干净的铅柱紧压后,两个铅柱就会结合在一起,即使在下面吊一个较重的物体也不会将它们拉开。
下列现象所包含的道理与之相同的是A.磁铁吸引铁块B.带电体吸引不带电的物体C.往水杯中倒水,可以倒到稍稍高出杯沿,而水不会满溢出来D.封闭在容器内的液体很难被压缩7.关于如图所示的各种情景,下列说法中正确的是A.甲图中:特技演员驾车冲向空中,在空中减速上升时,演员和车的惯性小于重力B.乙图中:跳水运动员在空中下落的过程中,运动员的动能逐渐减小C.丙图中:足球在空中竖直上升的过程中,足球受力的方向竖直向下D.丁图中:人躺在“死海”水面上看报,海水给人的浮力大于重力二、多项选择题8.兴趣小组想通过实验测量某品牌牛奶的密度,实验室提供以下四种实验器材的组合方案,可测出牛奶密度的是A.一个烧杯、足量的牛奶、弹簧测力计、大小合适的鹅卵石、细线B.一个烧杯、足量的牛奶、天平和砝码、量筒C.两个烧杯、足量的牛奶、足量水、天平和砝码、记号笔D.一个烧杯、足量的牛奶、标有等间距小格的杠杆、钩码、塑料小桶、细线9.入春以来气候干燥,龙东地区多处发生火灾。
大连中学2019-2020学年度七年级(下)数学用卷网课检测复习学案

大连中学2019-2020学年度七年级(下)网课检测复习学案1、49的平方根表示为________,值为_________,2、5的算术平方根表示为_______,3、-8的立方根是_____.4、38表示__________,值为__________.5、下列语句中正确的是 ( )A.49的算术平方根是7B.49的平方根是-7C.-49的平方根是7D.49的算术平方根是 6、下列说法正确的是( )A .-1是1的算术平方根B .1是-1的算术平方根C .1的平方根是±1D .0的平方根是0 7、16的算术平方根是( ) A .4B . 4C .2D . 28、(-8)2的算术平方根是 ;(-13)2的算术平方根是 .9、下列对的大小估计正确的是( ).A .在4~5之间B .在5~6之间C .在6~7之间D .在7~8之间 10、下列选项中的整数,与17最接近的是( ) A .3B .4C .5D .611、与50最接近的整数是 . 12、下列各数中是无理数的是( ) A. 3.14 B. 722-C. 38D.5 13、在五个数32-,⋅7.0,34,π,16中,无理数的个数是( )A. 1B. 2C. 3D. 414、.如图2,将直径为1个单位长度的圆从数轴上原点开始向左滚动一周,恰好到达数轴上的另一点A ’处,则A ’对应的数是___________.15、如图1,在数轴上以表示数1的点为圆心,2长为半径画弧,交数轴于点A ,则点A 表示的数是( )A . -2B . 1-2C . -1+2D . -1-216、2(3)-+13--(31)+7±60A 'A0–1–2–3–41-101图1-1 0 1 2235-27--43)(+---ππ17、点(0,3)在___轴上;点(-4,0)在___轴上.18、已知点A 在第二象限,试写出一个符合条件的点A 的坐标为_______19、点(3,-2)在第__象限,到x 轴的距离是______,到y 轴的距离是_________. 20、若x 轴上的点P 到y 轴的距离为3,则点P 的坐标为( )。
大连市名校2019-2020学年初一下学期期末数学学业水平测试试题

解:A、根据不等式的性质1,可得x-5>y-5,x+4>y+4,故A,B选项正确;
C,根据不等式的性质2可得 ,故选项C正确.
D,根据不等式的性质3可得﹣6x<﹣6y,所以选项D错误.
所以答案选D.
【点睛】
本题考查了不等式的性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
根据矩形的性质,AC、BD的中点为矩形的中心,
所以, = ,
= ,
解得x=8,y=13,
所以,点C的坐标为(8,13).
故答案为:(8,13).
【点睛】
本题考查了坐标与图形性质,主要利用了矩形的对角线互相平分且相等的性质,以及中点公式.
17.x<﹣1
【解析】
【分析】
第一象限的点的横坐标大于0,纵坐标大于0,得到1−m>0,则m−1<0,解这个不等式就是不等式左右两边同时除以m−1,不等号的方向改变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
9.D
【解析】
【分析】
根据整式乘法求出p+q,pq的值,即可进行求解.
【详解】
∵
∴p+q=2,pq=-8,
故 =(-8)2=64.
【点睛】
此题主要考查整式乘法公式,解题的关键是熟知整式乘法的运算法则.
A.25000名考生是总体B.每名考生的成绩是个体
C.1000名考生是总体的一个样本D.样本容量是25000
8.若x>y,则下列式子中错误的是()
A.x﹣5>y﹣5B.x+4>y+4C. D.﹣6x>﹣6y
大连市七年级下学期数学5月月考试卷

大连市七年级下学期数学5月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)在同一平面内,两条直线可能的位置关系是()A . 平行B . 相交C . 相交或平行D . 垂直2. (2分)(2019·邵阳模拟) 在平面直角坐标系中,若点P(m-2,m+1)在第二象限,则m的取值范围是()A . m<-1B . m>2C . -1<m<2D . m>-13. (2分) (2017七下·潮南期末) 下列实数是无理数的是()A .B .C . ﹣D . 04. (2分) (2017七下·杭州期中) 如图,直线b、c被直线a所截,则∠1与∠2是()A . 同位角B . 内错角C . 同旁内角D . 对顶角5. (2分)下列语句错误的是()A . 连接两点的线段的长度叫做两点间的距离B . 两条直线平行,同旁内角互补C . 若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角D . 平移变换中,各组对应点连成两线段平行且相等6. (2分) (2019七下·河池期中) 在平面直角坐标中,点与点的横坐标相同,纵坐标不同,则直线与轴的位置关系为()A . 平行B . 垂直C . 相交D . 以上均不对7. (2分)在同一平面上,正方形ABCD的四个顶点到直线l的距离只取四个值,其中一个值是另一个值的3倍,这样的直线l可以有()A . 4条B . 8条C . 12条D . 16条8. (2分)如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE 的度数为()A . 50°B . 100°C . 45°D . 30°9. (2分) 2008年5月12日,在四川省汶川县发生8.0级特大地震,能够准确表示汶川这个地点的位置的是()A . 北纬31°B . 东经103.5°C . 浙江省金华市的西北方向上D . 北纬31° ,东经103.5°10. (2分)数轴上A、B两点表示的数分别是1和,点A关于点B的对称点是点C,则点C所表示的数是A .B .C .D .二、填空题 (共13题;共22分)11. (1分) (2016七下·黄冈期中) 如图所示,一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,测量的根据是________.12. (1分) (2019七上·鸡西期末) =________.13. (1分) (2018八下·北海期末) 已知直线y=2x﹣5经过点A(a,1﹣a),则A点落在第________象限.14. (1分)比较大小:2 ________5.15. (1分) (2020七下·北京月考) 如图,有一块长为、宽为的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是________ .16. (1分)已知直线y=2x+1和y=3x+b的交点在第二象限,则b的取值范围是________.17. (1分) (2019七下·江苏月考) 如图,A、B为观测站,C为岛屿,现在A处测得C在A北偏东30°方向,在B处测得C在B北偏西60°方向,则AC与BC的位置关系为________18. (1分) (2016七上·港南期中) 若|a﹣3|+(2b﹣4)2=0,则3(a﹣b)﹣2(2a﹣3b)的值是________.19. (1分)(2017·恩施) 16的平方根是________.20. (1分) (2017八上·永定期末) 如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为________(用n表示).21. (7分) (2016九上·路南期中) 如图为一段圆弧形弯道,弯道长12π米,圆弧所对的圆心角是81°.(1)用直尺和圆规作出圆弧所在的圆心O;(不写作法,保留作图痕迹)(2)求这段圆弧的半径R.22. (3分) (2015八下·成华期中) 如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.(1)求点B的坐标;(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.(3)连接OQ,当OQ∥AB时,求P点的坐标.23. (2分) (2019七下·锡山月考) 如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.(1)求证:CE∥GF;(2)试判断∠AED与∠D之间的数量关系,并说明理由;(3)若∠EHF=70°,∠D=30°,求∠AEM的度数.三、解答题 (共4题;共31分)24. (5分)(2018·枣阳模拟) 如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.(1)求证:DP∥AB;(2)若AC=6,BC=8,求线段PD的长.25. (10分)(2013·嘉兴) 计算下列各题(1)计算:|﹣4|﹣ +(﹣2)0;(2)化简:a(b+1)﹣ab﹣1.26. (10分) (2020八上·相山期末) △ABC在平面直角坐标系中的位置如图所示。
2019-2020学年度辽宁省大连市七年级下册期中数学模拟试卷解析版
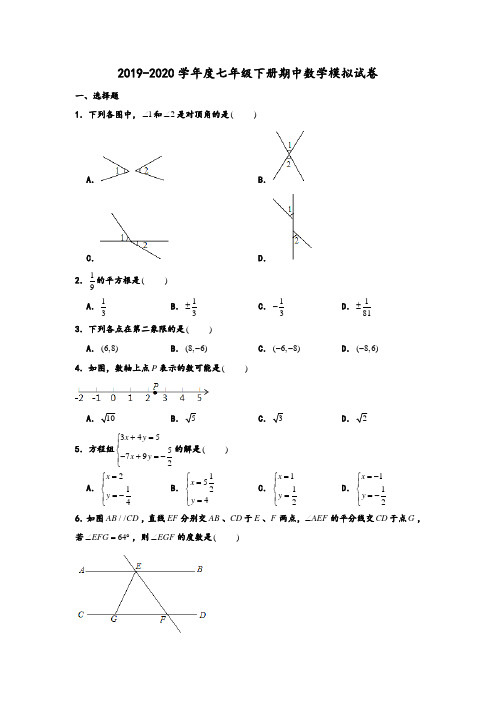
2019-2020学年度七年级下册期中数学模拟试卷一、选择题1.下列各图中,1∠和2∠是对顶角的是()A .B .C .D .2.19的平方根是() A.13B.13±C.13-D.181±3.下列各点在第二象限的是()A.(6,8)B.(8,6)-C.(6,8)--D.(8,6)-4.如图,数轴上点P表示的数可能是()A.10B.5C.3D.25.方程组3455792x yx y+=⎧⎪⎨-+=-⎪⎩的解是()A.214xy=⎧⎪⎨=-⎪⎩B.1524xy⎧=⎪⎨⎪=⎩C.112xy=⎧⎪⎨=⎪⎩D.112xy=-⎧⎪⎨=-⎪⎩6.如图//AB CD,直线EF分别交AB、CD于E、F两点,AEF∠的平分线交CD于点G,若64EFG∠=︒,则EGF∠的度数是()A .32︒B .58︒C .64︒D .128︒7.如图,下列条件中能判定//AE CD 的是( )A .A C ∠=∠B .180A ABC ∠+∠=︒ C .C CBE ∠=∠D .A CBE ∠=∠8.篮球联赛中每场比赛都要分出胜负,每队胜1场得2分,负1场得1分,某队在10场比赛中得到16分,那么这个队负的场数是( ) A .4场 B .5场 C .6场 D .7场二.填空题9.10π-的绝对值是 . 10.计算:13(3)3-= .11.命题“如果两条平行线被第三条直线所截,那么同位角相等”的结论是 . 12.如图,在ABC ∆中,90C ∠=︒,则点B 到直线AC 的距离是线段 .13.若点(53,24)P m m --在x 轴上,则点P 的坐标为 . 14.如图//AD BE ,//AB CD ,若114A ∠=︒,则DCE ∠= .15.已知4x =,2y =-与2x =-,5y =-都是方程y kx b =+的解,则k b +的值为 . 16.一个长方形的长减少5cm ,宽增加2cm ,就成为一个正方形,并且这两个图形的面积相等.若设这个长方形的长为xcm ,宽为ycm ,求这个长方形的长和宽分别是 . 三.解答题(本题共3小题,每小题6分,共18分) 172330.64()0.1252+--18.解方程组:2317 34121623x yx y⎧+=⎪⎪⎨⎪-=-⎪⎩.19.如图,三角形ABC中,D是AB上一点,E是AC上一点,140BDE∠=︒,40B∠=︒,60AED∠=︒.(1)判断DE和BC的位置关系,并说明理由;(2)求C∠的度数.四.解答题(本题共3小题,每小题8分,共24分)20.如图小方格的边长为1个单位.(1)画出坐标系,使A、B的坐标分别为(1,1)、(2,0)-,并写出点C的坐标;(2)若将ABC∆向右平移4个单位,再向上平移3个单位,得到△A B C''',在图中画出△A B C''';(3)写出ABC∆的面积.21.如图点E在线段AB上,F在线段CD上,线段BC分别交线段AF、DE于点G、H,已知A D∠=∠,AGC DHB∠=∠,试判断B∠与C∠的数量关系,并说明理由.22.有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛是古代的一种容量位),1个大桶加上5个小桶可以盛酒2斛. (1)1个大桶、1个小桶分别可以盛酒多少斛?(2)盛酒16斛,需要大桶、小桶各多少?(写出两种方案即可) 五.解答题(本题共3小题,每小题10分,共30分)23.如图//AB CD ,点P 是平面内直线AB 、CD 外一点连接PA 、PC . (1)写出所给的四个图形中APC ∠、PAB ∠、PCD ∠之间的数量关系; (2)证明图(1)和图(3)的结论.24.某公司有甲型、乙型、丙型三种型号的电脑,其中甲型每台6000元乙型每台4000元、丙型每台2500元.某中学现有资金100500元,计划全部用从这家电脑公司购进36台两种型号的电脑,请你设计几种不同的购买方案供这个学校选择,并说明理由. 25.如图,在平面直角坐标系中,ABC ∆的顶点坐标分别为(2,1)A --、(2,0)B 、(0,3)C ,AC 交x 轴于点D ,AB 交y 轴于点E . (1)ABC ∆的面积为 ; (2)点E 的坐标为 ; (3)若点P 的坐标为(0,):m①线段EP 的长为 (用含m 的式子表示); ②当2PAB ABC S S ∆∆=时,求点P 的坐标.参考答案一.选择题(本题共8小题)1.下列各图中,1∠和2∠是对顶角的是()A.B.C.D.【分析】根据对顶角的定义求解即可.解:一个角的两边是另一个角两边的反向延长线,故B符合题意;故选:B.2.19的平方根是()A.13B.13±C.13-D.181±【分析】根据一个正数有两个平方根,它们互为相反数进行解答即可.解:11 93=±.故选:B.3.下列各点在第二象限的是()A.(6,8)B.(8,6)-C.(6,8)--D.(8,6)-【分析】点在第二象限的条件是:横坐标是负数,纵坐标是正数,直接得出答案即可.解:Q点在第二象限,∴点的横坐标是负数,纵坐标是正数,∴只有D符合要求.故选:D.4.如图,数轴上点P表示的数可能是()A 10B 5C 3D 2【分析】先根据数轴估算出P 点所表示的数,再根据选项中的数值进行选择即可. 解:A 、91016<<Q ,32104<<,故本选项错误; B 、459<<Q ,253∴<<,故本选项正确; C 、134<<Q ,132∴<<,故本选项错误;D 、124<<Q ,122∴<<,故本选项错误.故选:B .5.方程组3455792x y x y +=⎧⎪⎨-+=-⎪⎩的解是( )A .214x y =⎧⎪⎨=-⎪⎩B .1524x y ⎧=⎪⎨⎪=⎩C .112x y =⎧⎪⎨=⎪⎩D .112x y =-⎧⎪⎨=-⎪⎩【分析】解二元一次方程组有两种解法,即加减消元法和代入消元法,解此题时应注意题中方程的形式,观察适合哪种方法,由于此题中系数都比较复杂,因此用加减消元法. 解:3455792x y x y +=⎧⎪⎨-+=-⎪⎩①②,①9⨯,得273645x y +=③, ②4⨯,得283610x y -+=-④, ③-④,得5555x =, 解,得1x =.把1x =代入①,得345y +=, 所以12y =. 因此原方程组的解为112x y =⎧⎪⎨=⎪⎩.故选:C .6.如图//AB CD ,直线EF 分别交AB 、CD 于E 、F 两点,AEF ∠的平分线交CD 于点G ,若64EFG ∠=︒,则EGF ∠的度数是( )A .32︒B .58︒C .64︒D .128︒【分析】利用平行线的性质以及角平分线的定义即可解决问题. 解://AB CD Q , 64BEF EFG ∴∠=∠=︒, 18064116AEF ∴∠=︒-︒=︒, EG Q 平分AEF ∠,1116582AEG ∴∠=⨯︒=︒, //AB CD Q ,58EGF AEG ∴∠=∠=︒,故选:B .7.如图,下列条件中能判定//AE CD 的是( )A .A C ∠=∠B .180A ABC ∠+∠=︒ C .C CBE ∠=∠D .A CBE ∠=∠【分析】根据平行线的判定方法一一判断即可. 解:C CBE ∠=∠Q , //CD AE ∴,故选:C .8.篮球联赛中每场比赛都要分出胜负,每队胜1场得2分,负1场得1分,某队在10场比赛中得到16分,那么这个队负的场数是( ) A .4场B .5场C .6场D .7场【分析】设这个队胜x 场,负y 场,根据在10场比赛中得到16分,列方程组求解即可.解:设这个队胜x场,负y场,根据题意,得10 216x yx y+=⎧⎨+=⎩,解得:64 xy=⎧⎨=⎩所以负了4场,故选:A.二.填空题(本题共8小题,每小题3分共24分)9.ππ.【分析】先判断出π的符号,再根据绝对值的定义进行计算即可.解:Q0π-<,∴ππ,π.10= 2 .【分析】先利用乘法的分配律得到原式=,然后利用二次根式的性质化简后进行减法运算.解:原式=31=-2=.故答案为2.11.命题“如果两条平行线被第三条直线所截,那么同位角相等”的结论是同位角相等.【分析】根据命题的定义求解即可.解:命题“如果两条平行线被第三条直线所截,那么同位角相等”的结论是同位角相等,故答案为:同位角相等.12.如图,在ABC∆中,90C∠=︒,则点B到直线AC的距离是线段BC.【分析】直接利用点到直线的距离定义得出答案.解:如图,三角形ABC 中,90C ∠=︒,则点B 到直线AC 的距离是:线段BC . 故答案是:BC .13.若点(53,24)P m m --在x 轴上,则点P 的坐标为 (7,0) . 【分析】直接利用x 轴上纵坐标为零进而得出m 的值. 解:Q 点(53,24)P m m --在x 轴上, 240m ∴-=,解得:2m =, 537m ∴-=,故点P 的坐标为:(7,0). 故答案为:(7,0).14.如图//AD BE ,//AB CD ,若114A ∠=︒,则DCE ∠= 66︒ .【分析】利用平行线的性质求出B ∠即可解决问题. 解://AD BE Q , 180A B ∴∠+∠=︒,114A ∠=︒Q , 66B ∴∠=︒, //AB CD Q , 66DCE B ∴∠=∠=︒,故答案为66︒.15.已知4x =,2y =-与2x =-,5y =-都是方程y kx b =+的解,则k b +的值为 3.5- .【分析】把x 与y 的两对值代入方程计算求出k 与b 的值,求出k b +即可.解:把4x =,2y =-与2x =-,5y =-代入方程得:4225k b k b +=-⎧⎨-+=-⎩①②, ①+②得:227k b +=-,则 3.5k b +=-,故答案为: 3.5-16.一个长方形的长减少5cm ,宽增加2cm ,就成为一个正方形,并且这两个图形的面积相等.若设这个长方形的长为xcm ,宽为ycm ,求这个长方形的长和宽分别是3,43cm . 【分析】设这个长方形的长为xcm ,宽为ycm ,根据长方形的长减少5cm ,宽增加2cm ,组成正方形,且面积相等,列方程组求解.解:设这个长方形的长为xcm ,宽为ycm ,由题意得,52(5)(2)x y xy x y -=+⎧⎨=-+⎩, 解得:25343x y ⎧=⎪⎪⎨⎪=⎪⎩. 故答案为:253cm ,43cm . 三.解答题(本题共3小题,每小题6分,共18分)17+ 【分析】直接利用立方根的性质以及二次根式的性质分别化简得出答案.解:原式30.80.52=++ 2.8=. 18.解方程组:231734121623x y x y ⎧+=⎪⎪⎨⎪-=-⎪⎩. 【分析】方程组整理后,利用加减消元法求出解即可.解:方程组整理得:891732x yx y+=⎧⎨-=-⎩①②,①+②3⨯得:1111x=,即1x=,将1x=代入②得:1y=,则方程组的解为11xy=⎧⎨=⎩.19.如图,三角形ABC中,D是AB上一点,E是AC上一点,140BDE∠=︒,40B∠=︒,60AED∠=︒.(1)判断DE和BC的位置关系,并说明理由;(2)求C∠的度数.【分析】(1)求出180B BDE∠+∠=︒,根据平行线的判定得出即可;(2)根据平行线的性质得出C AED∠=∠,代入求出即可.解:(1)//DE BC,理由是:140BDE∠=︒Q,40B∠=︒,180B BDE∴∠+∠=︒,//DE BC∴;(2)//DE BCQ,C AED∴∠=∠,60AED∠=︒Q,60C∴∠=︒.四.解答题(本题共3小题,每小题8分,共24分)20.如图小方格的边长为1个单位.(1)画出坐标系,使A、B的坐标分别为(1,1)、(2,0)-,并写出点C的坐标;(2)若将ABC∆向右平移4个单位,再向上平移3个单位,得到△A B C''',在图中画出△A B C''';(3)写出ABC ∆的面积.【分析】(1)利用点A 、B 的坐标画出直角坐标系,然后写出C 点坐标;(2)利用点平移的坐标变换规律写出A '、B '、C '的坐标,然后描点即可得到△A B C ''';(3)用1个矩形的面积分别减去三个直角三角形的面积可计算出ABC ∆的面积. 解:(1)如图,点C 的坐标为(1,5)-;(2)如图,△A B C '''为所作;(3)ABC ∆的面积111353142517222=⨯-⨯⨯-⨯⨯-⨯⨯=. 21.如图点E 在线段AB 上,F 在线段CD 上,线段BC 分别交线段AF 、DE 于点G 、H ,已知A D ∠=∠,AGC DHB ∠=∠,试判断B ∠与C ∠的数量关系,并说明理由.【分析】求出AGC EHC∠=∠,根据平行线的判定得出//AF DE,根据平行线的性质得出D AFC∠=∠,求出A AFC∠=∠,根据平行线的判定得出//AB DC即可.解:B C∠=∠,理由是:BHD EHC∠=∠Q,AGC DHB∠=∠,AGC EHC∴∠=∠,//AF DE∴,D AFC∴∠=∠,A D∠=∠Q,A AFC∴∠=∠,//AB DC∴,B C∴∠=∠.22.有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛是古代的一种容量位),1个大桶加上5个小桶可以盛酒2斛.(1)1个大桶、1个小桶分别可以盛酒多少斛?(2)盛酒16斛,需要大桶、小桶各多少?(写出两种方案即可)【分析】(1)设1个大桶可以盛酒x斛,1个小桶可以盛酒y斛,根据“5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设需要大桶m个,小桶n个,根据盛酒的总量1=个大桶的盛酒量⨯使用大桶的数量1+个小桶的盛酒量⨯使用小桶的数量,即可得出关于m,n的二元一次方程,结合m,n均为非负整数,即可求出结论.解:(1)设1个大桶可以盛酒x斛,1个小桶可以盛酒y斛,依题意,得:5352x yx y+=⎧⎨+=⎩,解得:1324724 xy⎧=⎪⎪⎨⎪=⎪⎩.答:1个大桶可以盛酒1324斛,1个小桶可以盛酒724斛.(2)设需要大桶m个,小桶n个,依题意,得:137162424m n+=,384137mn-∴=.mQ,n均为非负整数,∴153mn=⎧⎨=⎩,840mn=⎧⎨=⎩,1527mn=⎧⎨=⎩,2214mn=⎧⎨=⎩,291mn=⎧⎨=⎩,∴共有5种方案,方案1:使用1个大桶,53个小桶;方案2:使用8个大桶,40个小桶;方案3:使用15个大桶,27个小桶;方案4:使用22个大桶,14个小桶;方案5:使用29个大桶,1个小桶(任选2个方案即可).五.解答题(本题共3小题,每小题10分,共30分)23.如图//AB CD,点P是平面内直线AB、CD外一点连接PA、PC.(1)写出所给的四个图形中APC∠、PAB∠、PCD∠之间的数量关系;(2)证明图(1)和图(3)的结论.【分析】(1)依据图形可得APC∠、PAB∠、PCD∠之间的数量关系;(2)过P作//PE AB,即可得到//PE CD,再根据平行线的性质以及角的和差关系,即可得出360APC PAB PCD∠+∠+∠=︒,APC PCD PAB∠=∠-∠.解:(1)如图1,360APC PAB PCD∠+∠+∠=︒,如图2,APC PAB PCD∠=∠+∠,如图3,APC PCD PAB∠=∠-∠,如图4,APC PAB PCD∠=∠-∠.(2)如图1,过P作//PE AB,//AB CDQ,//PE CD∴,180A APE∴∠+∠=︒,180C CPE∠+∠=︒,360A APE C CPE∴∠+∠+∠+∠=︒,即360APC PAB PCD∠+∠+∠=︒;如图3,过P作//PE AB,//AB CDQ,//PE CD∴,PCD CPE∴∠=∠,PAB APE∠=∠,APC CPE APE C A∴∠=∠-∠=∠-∠.24.某公司有甲型、乙型、丙型三种型号的电脑,其中甲型每台6000元乙型每台4000元、丙型每台2500元.某中学现有资金100500元,计划全部用从这家电脑公司购进36台两种型号的电脑,请你设计几种不同的购买方案供这个学校选择,并说明理由.【分析】分三种情况:一是购买甲+乙36=,甲的单价⨯数量+乙的单价⨯数量100500=;二是购买甲+丙36=,甲的单价⨯数量+丙的单价⨯数量100500=;三是购买乙+丙36=,乙的单价⨯数量+丙的单价⨯数量100500=.解:设从该电脑公司购进甲型电脑x台,购进乙型电脑y台,购进丙型电脑z台,则可分以下三种情况考虑:(1)只购进甲型电脑和乙型电脑,依题意可列方程组:6000400010050036x yx y+=⎧⎨+=⎩,解得21.7557.75x y =-⎧⎨=⎩, 不合题意,应该舍去.(2)只购进甲型电脑和丙型电脑,依题意可列方程组:6000250010050036x z x z +=⎧⎨+=⎩, 解得:333x z =⎧⎨=⎩,(3)只购进乙型电脑和丙型电脑,依题意可列方程组:4000250010050036y z y z +=⎧⎨+=⎩, 解得:729y z =⎧⎨=⎩, 答:有两种方案供该校选择,第一种方案是购进甲型电脑3台和丙型电脑33台; 第二种方案是购进乙型电脑7台和丙型电脑29台.25.如图,在平面直角坐标系中,ABC ∆的顶点坐标分别为(2,1)A --、(2,0)B 、(0,3)C ,AC 交x 轴于点D ,AB 交y 轴于点E .(1)ABC ∆的面积为 7 ;(2)点E 的坐标为 ;(3)若点P 的坐标为(0,):m①线段EP 的长为 (用含m 的式子表示);②当2PAB ABC S S ∆∆=时,求点P 的坐标.【分析】(1)根据已知条件得到直线AC 的解析式为23y x =+,即可得到3(2D -,0),根据三角形的面积公式即可得到结论;(2)根据已知条件得到直线AB 的解析式为1142y x =-,于是得到结论; (3)①根据点的坐标求得线段EP 的长11||||22m m --=+; ②根据三角形的面积公式列方程即可得到结论. 解:(1)(2,1)A --Q 、(0,3)C ,∴直线AC 的解析式为23y x =+,∴当0y =时,32x =-, 3(2D ∴-,0), ABC ∴∆的面积13(2)(31)722=⨯+⨯+=; (2)(2,1)A --Q 、(2,0)B ,∴设直线AB 的解析式为:y kx b =+, ∴1202k b k b -=-+⎧⎨=+⎩, ∴1412k b ⎧=⎪⎪⎨⎪=-⎪⎩, 1142y x ∴=-, 1(0,)2E ∴-; (3)①Q 点P 的坐标为(0,)m ,∴线段EP 的长11||||22m m --=+;②2PAB ABC S S ∆∆=Q , ∴11||(22)2722m ⨯+⨯+=⨯, 6.5m ∴=或7.5m =-.故答案为:7,1(0,)2-,1||2m +.。
2019-2020学年辽宁省大连市中考数学模拟试题(有标准答案)(word版)

大连市初中毕业升学考试数学一、选择题(本题共8小题,每小题3分,共24分,在每小题给出的四个选项中,只有一个选项正确) 1.-3的相反数是( ) A.31 B.31- C.3 D.-3 2.在平面直角坐标系中,点(1,5)所在的象限是( )A.第一象限B. 第二象限C. 第三象限D. 第四象限 3.方程2x+3=7的解A. x=5B. x=4C. x=3.5D. x=2 4.如图,直线AB ∥CD ,AE 平分∠CAB ,AE 与CD 相交于点E , ∠ACD=40°则∠BAE 的度数是( )A. 40°B. 70°C. 80°D. 140° 5.不等式组⎩⎨⎧++2322x x xx <>的解集是( )A. x >-2B. x <1C. -1<x <2D.-2<x <16.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,、2、3、4,随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球的标号的积小于4的概率是( ) A.61 B. 125 C. 31 D. 21 7.某文具店三月份销售铅笔100支,四、五两个月销售量连续增长,若月平均增长率为x ,则该文具店五月份销售铅笔的支数( )A. 100(1+x )B. 100(1+x )2C. 100(1+x 2) D. 100(1+2x ) 8. 如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm ) A. 40πcm 2B. 65πcm 2C. 80πcm 2D. 105πcm 2二、填空题(本题共8小题,每小题3分,共24分) 9.因式分解:x 2-3x=______________________ 10.若反比例函数xky =的图象经过点(1,-6),则k 的值为_________________ 11.如图,将△ABC 绕A 顺时针旋转得到△ADE ,点C 和点E 是对应点, 若∠CAE=90°,AB=1,则BD=_________ 12.下表是某校女子排球队队员的年龄分布13.如图,在菱形ABCD 中,AB=5,AC=8,则菱形的面积是_________________(第8题)(第11题)14.若关于x 的方程2x 2+x-a=0有两个不相等的实数根,则实数a 的取值范围是_____________15.如图,一艘渔船位于灯塔P 的北偏东30°方向距离灯塔18海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东55°方向上的B 处,此时渔船与灯塔P 的距离约为___________海里(结果取整数)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辽宁省大连金石滩实验学校2019-2020学年七年级下学期5月网络授课摸底考试数学试题
学校_________ 班级__________ 姓名__________ 学号__________
一、单选题
1. 在平面直角坐标系中,点(2,﹣4)在()
A.第一象限B.第二象限C.第三象限D.第四象限
2. 若解集在数轴上的表示如图所示,则这个不等式组可以是()
A.B.
C.D.
3. 正十边形的外角的度数是( )
A.18°B.36°C.45°D.60°
4. 在实数﹣,0.,,π,中,无理数的个数是()
A.1 B.2 C.3 D.4
5. 若实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.B.C.D.
6. 若三角形两条边的长分别是 3,5,第三条边的长是整数,则第三条边的长的最大值是()
A.2 B.3 C.7 D.8
7. 不等式x - 3≤0 的正整数解的个数是()A.1 B.2 C.3 D.4 8. 下列命题正确的是()
A.三角形的三条中线必交于三角形内一点B.三角形的三条高
均在三角形内部
C.三角形的外角可
能等于与它不相邻
的内角
D.四边形具有稳定
性
9. 若多边形的内角和大于900°,则该多边形的边数最小为()
A.9 B.8 C.7 D.6
10. 点 P(x, y) 为平面直角坐标系 xOy 内一点,xy>0 ,且点 P 到x轴,y 轴的距离分别为 2,5,则点 P 的坐标为()
A.(2, 5) 或(-2,-5) B.(5, 2) 或(-5,-2)
C.(5, 2) 或(-2,-5) D.(2, 5) 或(-5,-2)
二、填空题
11. 的算术平方根是________
12. 如图,△ABC 的外角平分线 AM 与边 BC 平行,则∠B_____∠C(填
“>”,“=”,或“<”).
13. 请写出一个比1大比2小的无理数:________________.
14. 如图,在长方形 ABCD 内,两个小正方形的面积分别为 1,2,则图中阴影部分的面积等于_____.
15. 如图,已知等边△AB
A.若以 BC 为一条边在其上方作等腰直角△BCD,则∠ABD 的度数为_____.
16. 篮球比赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,艾美所在的球队在8场比赛中得14分.若设艾美所在的球队胜场,负场,则可列出方程组为__.
三、解答题
17. (1)计算:+﹣()2
(2)求x的值 3x2﹣12=0
18. 解下列方程组
(1);
(2)用代入法解.
19. 解不等式组,并把解集表示在数轴
上.
20. 如图,点B,E分别在AC,DF上,BD,CE均与AF相交,∠A=∠F,∠C=∠D,
求证:∠l=∠2.
21. 已知关于的方程组的解满足不等式,求实数的取值范围.
22. 如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E.求∠AEC的度数.
23. 方程组与有相同的解,求a,b及方程组的解.
24. 在平面直角坐标系 xOy 中,点A,B的坐标分别为(-2,0),(1,0).同时将点A ,B先向左平移1个单位长度,再向上平移2个单位长度,得到点A,B的对应点依次为C,D,连接CD,AC, B
A.
(1)写出点C , D 的坐标;
(2)在 y 轴上是否存在点E,连接EA ,EB,使S
△EAB =S
四边形ABDC
?若存在,求出
点E的坐标;若不存在,说明理由;
(3)点 P 是线段 AC 上的一个动点,连接 BP , DP ,当点 P 在线段 AC 上移动时(不与 A , C 重合),直接写出ÐCDP 、ÐABP 与ÐBPD 之间的等量关系.
25. 已知:△ABC,点M 是平面上一点,射线BM 与直线AC 交于点D ,射线CM 与直线AB 交于点
A .过点A 作
AF∥CE,AF 与BC 所在的直线交于点 B .
(1)如图1,当BD⊥AC,CE⊥AB 时,写出∠BAD 的一个余角,并证明∠ABD=∠CAF; (2)若∠BAC=80°,∠BMC=120°.
①如图2,当点M 在△ABC 内部时,用等式表示∠ABD 与∠CAF 之间的数量关系,并加以证明;
②如图3,当点M 在△ABC 外部时,依题意补全图形,并直接写出用等式表示的∠ABD 与∠CAF 之间的数量关系.。
