最新精编 人教版数学八年级上册(新)13.3《等腰三角形》同步测试含答案
人教版八年级上册数学《等腰三角形》同步训练含答案
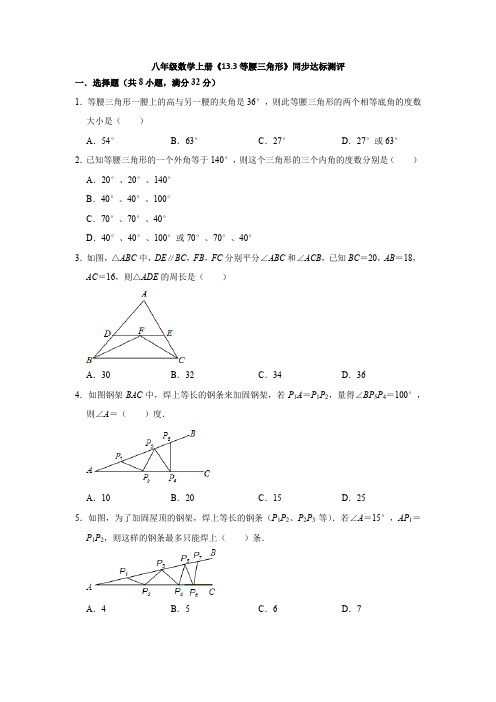
八年级数学上册《13.3等腰三角形》同步达标测评一.选择题(共8小题,满分32分)1.等腰三角形一腰上的高与另一腰的夹角是36°,则此等腰三角形的两个相等底角的度数大小是()A.54°B.63°C.27°D.27°或63°2.已知等腰三角形的一个外角等于140°,则这个三角形的三个内角的度数分别是()A.20°、20°、140°B.40°、40°、100°C.70°、70°、40°D.40°、40°、100°或70°、70°、40°3.如图,△ABC中,DE∥BC,FB,FC分别平分∠ABC和∠ACB,已知BC=20,AB=18,AC=16,则△ADE的周长是()A.30B.32C.34D.364.如图钢架BAC中,焊上等长的钢条来加固钢架,若P1A=P1P2,量得∠BP5P4=100°,则∠A=()度.A.10B.20C.15D.255.如图,为了加固屋顶的钢架,焊上等长的钢条(P1P2、P2P3等).若∠A=15°,AP1=P1P2,则这样的钢条最多只能焊上()条.A.4B.5C.6D.76.如图,AB=BC=CD=DE=EF=FG,则∠A的范围是()A.0°<∠A<15°B.0°<∠A<18°C.0°<∠A<20°D.0°<∠A<22.5°7.如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM 上;△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2021B2021A2022的边长为()A.4044B.4046C.22020D.220218.如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有()A.1个B.2个C.3个D.4个二.填空题(共7小题,满分28分)9.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是.10.如图,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长线上,且CE=1,∠E=30°,则BC=.11.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以A n为顶点的底角度数是.12.如图,在△ABC中,AB=AC,∠BAD=30°,AE=AD,则∠EDC的度数是.13.已知等腰三角形一腰上的高与另一腰的夹角为30°,则这个等腰三角形顶角为°.14.如图,线段OP的一个端点O在直线a上,以OP为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能有个.15.如果△ABM和△ACN分别是以△ABC的边AB、AC为边的形外等边三角形,MC交BN 于P,连P A,则∠APN=.三.解答题(共9小题,满分60分)16.如图,在△ABC中,已知AD平分∠BAC,过AD上一点P作EF⊥AD,交AB于E、交AC于F,交BC延长线于M,则有正确结论:∠M=(∠ACB﹣∠B).请说明理由.17.如图,在△ABC中,∠B=60°,延长BC到D,延长BA到E,使AE=BD,连接CE、DE,使EC=DE,求证:△ABC是等边三角形.18.如图,已知△ABC中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC.求证:DE+DF=BG.19.如图,已知∠EAC是△ABC的外角,AD平分∠EAC,AD∥BC,点F为BC中点.求证:AF⊥BC.20.如图,在等腰△ABC中,AB=AC,BD为∠ABC平分线,延长BC到点E,使CE=CD,作DH⊥BE于H,求证:H为BE的中点.21.已知:如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.求证:△DEF是等边三角形.22.如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,求证:△CMN是等边三角形.23.如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE 交CB于点P,点P为DE中点(1)求证:CD=BE;(2)若DE⊥AC,求BP的长.24.如图,过等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且P A=CQ,连PQ交AC边于D.(1)求证:PD=DQ;(2)若△ABC的边长为1,求DE的长.参考答案一.选择题(共8小题,满分32分)1.解:在三角形ABC中,设AB=AC,BD⊥AC于D.①若是锐角三角形,∠A=90°﹣36°=54°,底角=(180°﹣54°)÷2=63°;②若三角形是钝角三角形,∠BAC=36°+90°=126°,此时底角=(180°﹣126°)÷2=27°.所以等腰三角形底角的度数是63°或27°.故选:D.2.解:(1)当40°角是顶角时,另两个底角度数为70°,70°;(2)当40°角是底角时,另两个角度数为40°,100°.故选:D.3.解:∵DE∥BC,∴∠BFD=∠FBC,∠EFC=∠BCF,∵FC分别平分∠ABC和∠ACB,∴∠DBF=∠FBC,∠ECF=∠BCF,∴∠BFD=∠DBF,∠EFC=∠ECF,∴DF=DB,EF=EC,∵△ADE的周长=AD+AE+DE,DE=DF+EF,∴△ADE的周长=AD+BD+AE+EC=AB+AC,∵AB=18,AC=16,∴△ADE的周长=34.故选:C.4.解:∵AP1=P1P2,P1P2=P2P3,P3P4=P2P3,P3P4=P4P5,∴∠A=∠P1P2A,∠P2P1P3=∠P2P3P1,∠P3P2P4=∠P3P4P2,∠P4P3P5=∠P4P5P3,∴∠P3P5P4=4∠A,∵∠P3P5P4+∠BP5P4=180°,∠BP5P4=100°,∴∠P3P5P4=80°,∴∠A=20°.故选:B.5.解:∵∠A=∠P1P2A=15°∴∠P2P1P3=30°,∠P1P3P2=30°∴∠P1P2P3=120°∴∠P3P2P4=45°∴∠P3P2P4=45°∴∠P2P3P4=90°∴∠P4P3P5=60°∴∠P3P5P4=60°∴∠P3P4P5=60°∴∠P5P4P6=75°∴∠P4P6P5=75°∴∠P4P5P6=30°∴∠P6P5P7=90°,此时就不能在往上焊接了,综上所述总共可焊上5条.故选:B.6.解:采用排除法:①∵AB=BC=CD=DE=EF=FG,当∠A=15°,∴∠BCA=∠A=15°,∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,∴∠BCD=180°﹣(∠CBD+∠BDC)=180°﹣60°=120°,∴∠ECD=∠CED=180°﹣∠BCD﹣∠BCA=180°﹣120°﹣15°=45°,∴∠CDE=180°﹣(∠ECD+∠CED)=180°﹣90°=90°,∴∠EDF=∠EFD=180°﹣∠CDE﹣∠BDC=180°﹣90°﹣30°=60°,∴∠FGE=∠GEF=∠EFD+∠A=60°+15°=75°,即此时符合;①当∠A=18°时,同法求出∠FEG=∠FGE=90°,此时△FEG不存在,此时不符合,同样,当∠A取大于18°的角都不符合,当∠A=小于18°的数时,△FEG存在,即选项A、C、D错误,只有选项B正确;故选:B.7.解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∵∠MON=30°,∴OA1=A1B1=1,∴A2B1=1,∵△A2B2A3、△A3B3A4是等边三角形,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16,以此类推:△A2021B2021A2022的边长为22020.故选:C.8.解:如图,①当OP=OE时,这样的点E由2个,②当PE=OE时,这样的点E由1个,③当OP=PE时,这样的点E由1个,∴这样的点P有4个,故选:D.二.填空题(共7小题,满分28分)9.解:∵等边△ABC和等边△CDE,∴AC=BC,CD=CE,∠ACB=∠ECD=60°,∴180°﹣∠ECD=180°﹣∠ACB,即∠ACD=∠BCE,在△ACD与△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE,故①小题正确;∵△ACD≌△BCE(已证),∴∠CAD=∠CBE,∵∠ACB=∠ECD=60°(已证),∴∠BCQ=180°﹣60°×2=60°,∴∠ACB=∠BCQ=60°,在△ACP与△BCQ中,,∴△ACP≌△BCQ(ASA),∴AP=BQ,故③小题正确;PC=QC,∴△PCQ是等边三角形,∴∠CPQ=60°,∴∠ACB=∠CPQ,∴PQ∥AE,故②小题正确;∵AD=BE,AP=BQ,∴AD﹣AP=BE﹣BQ,即DP=QE,∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,∴∠DQE≠∠CDE,故④小题错误.综上所述,正确的是①②③.故答案为:①②③.10.解:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,BA=BC,∵BD平分∠ABC,∴∠DBC=∠E=30°,BD⊥AC,∴∠BDC=90°,∴BC=2DC,∵∠ACB=∠E+∠CDE,∴∠CDE=∠E=30°,∴CD=CE=1,∴BC=2CD=2,故答案为211.解:∵在△CBA1中,∠B=30°,A1B=CB,∴∠BA1C==75°,∵A1A2=A1D,∠BA1C是△A1A2D的外角,∴∠DA2A1=∠BA1C=×75°;同理可得∠EA3A2=()2×75°,∠F A4A3=()3×75°,∴第n个三角形中以A n为顶点的内角度数是()n﹣1×75°.故答案为:()n﹣1×75°.12.解:设∠EDC=x,∠B=∠C=y,∠AED=∠EDC+∠C=x+y,又因为AD=AE,所以∠ADE=∠AED=x+y,则∠ADC=∠ADE+∠EDC=2x+y,又因为∠ADC=∠B+∠BAD,所以2x+y=y+30,解得x=15,所以∠EDC的度数是15°.故答案是:15°.13.解:当高在三角形内部时(如图1),顶角是60°;当高在三角形外部时(如图2),顶角是120°.故答案为:60或120.14.解:△AOP,△BOP,△COP,△DOP就是所求的三角形.15.解:∵△ABM和△ACN都是等边三角形,∴AB=AM,AN=AC,∠BAM=∠CAN=60°,∴∠BAM+∠BAC=∠CAN+∠BAC,即∠CAM=∠BAN,在△ABN与△AMC中,,∴△ABN≌△AMC(SAS),∴∠ANP=∠ACP,又∵∠AEN=∠PEC(对顶角相等),∵∠AEP=∠NEC(对顶角相等),∴∠APN=∠ACN=60°.故答案为:60°.三.解答题(共9小题,满分60分)16.证明:∵EF⊥AD,AD平分∠BAC,∴∠1=∠2,∠APE=∠APF=90°,又∵∠AEF=180°﹣∠1﹣∠APE,∠AFE=180°﹣∠2﹣∠APF,∴∠AEF=∠AFE,∵∠CFM=∠AFE,∴∠AEF=∠AFE=∠CFM,∵∠AEF=∠B+∠M,∠MFC=∠ACB﹣∠M,∴∠B+∠M=∠ACB﹣∠M,即:∠M=(∠ACB﹣∠B).17.证明:延长BD至F,使DF=BC,连接EF,∵EC=ED,∴∠ECD=∠EDC,∴∠ECB=∠EDF,∴△ECB≌△EDF(SAS),∴BE=EF,∠B=60°,∴△BEF为等边三角形,∴BE=BF,∵AE=BD,∴DF=AB,BC=DF,∴AB=BC,∴△ABC是等边三角形.18.证明:连接AD.则△ABC的面积=△ABD的面积+△ACD的面积,AB•DE+AC•DF=AC•BG,∵AB=AC,∴DE+DF=BG.19.证明:∵AD∥BC,∴∠EAD=∠B,∠DAC=∠C,∵AD平分∠EAC,∴∠EAD=∠DAC,∴∠B=∠C,∴AB=AC,∵点F为BC中点,∴AF⊥BC.20.证明:∵AB=AC,∴∠ABC=∠SCB,∵BD平分∠ABC,∴∠ABD=∠CBD,∵CE=CD,∴∠CDE=∠E,∵∠ACB=∠E+∠CDE=2∠DBC,∴∠DBC=∠E,∴△BDE为等腰三角形,BD=ED,∵DH垂直于BE,∴H为BE中点(三线合一).21.证明:∵△ABC是等边三角形,∴AB=BC=AC,∵AD=BE=CF,∴AF=BD,在△ADF和△BED中,,∴△ADF≌△BED(SAS),∴DF=DE,同理DE=EF,∴DE=DF=EF.∴△DEF是等边三角形.22.证明:∵△ABC是等边三角形,△CDE是等边三角形,M是线段AD的中点,N是线段BE的中点,∴∠ACB=∠ECD=60°,∴∠ACB+∠BCD=∠ECD+∠BCD,即∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE,∴AD=BE,AM=BN;∴AC=BC,∠CAD=∠CBE,AM=BN,∴△AMC≌△BNC(SAS),∴CM=CN,∠ACM=∠BCN;又∵∠NCM=∠BCN﹣∠BCM,∠ACB=∠ACM﹣∠BCM,∴∠NCM=∠ACB=60°,∴△CMN是等边三角形.23.(1)证明:作DF∥AB交BC于F,如图所示:∵△ABC是等边三角形,∴∠A=∠ABC=∠C=60°,∵DF∥AB,∴∠CDF=∠A=60°,∠DFC=∠ABC=60°,∠DFP=∠EBP,∴△CDF是等边三角形,∴CD=DF,∵点P为DE中点,∴PD=PE,在△PDF和△PEB中,,∴△PDF≌△PEB(AAS),∴DF=BE,∴CD=BE;(2)解:∵DE⊥AC,∴∠ADE=90°,∴∠E=90°﹣∠A=30°,∴AD=AE,∠BPE=∠ACB﹣∠E=30°=∠E,∴BP=BE,由(1)得:CD=BE,∴BP=BE=CD,设BP=x,则BE=CD=x,AD=12﹣x,∵AE=2AD,∴12+x=2(12﹣x),解得:x=4,即BP的长为4.24.(1)证明:如图,过P做PF∥BC交AC于点F,∴∠AFP=∠ACB,∠FPD=∠Q,∠PFD=∠QCD ∵△ABC为等边三角形,∴∠A=∠ACB=60°,∴∠A=∠AFP=60°,∴△APF是等边三角形;∵AP=PF,AP=CQ,∴PF=CQ∴△PFD≌△QCD,∴PD=DQ.(2)△APF是等边三角形,∵PE⊥AC,∴AE=EF,△PFD≌△QCD,∴CD=DF,DE=EF+DF=AC,∵AC=1,DE=.。
13.3等腰三角形(同步练习)-2021-2022学年人教版数学八年级上册(含答案)

13.3等腰三角形一、单选题1.等腰三角形的两条边长分别为8和4,则它的周长等于( ) A .12 B .16 C .20 D .16或20 2.如图,ABC 中,AB AC =,D 是BC 中点,下列结论中不正确的是( )A .BC ∠=∠ B .AD BC ⊥ C .AD 平分BAC ∠ D .2AB BD = 3.等腰三角形的一个角比另一个角2倍少20度,等腰三角形顶角的度数是( ) A .140︒或44︒或80︒B .140︒或80︒C .44︒或80︒D .140︒或44︒4.如图,D 在AC 上,E 在AB 上,若AB=AC ,BC=BD ,AD=DE=BE ,则∠A 的度数为( )A .60°B .72°C .45°D .50° 5.在下列命题中:∠有一个外角是120°的等腰三角形是等边三角形;∠有两个外角相等的等腰三角形是等边三角形;∠有一边上的高也是这边上的中线的三角形是等边三角形;∠三个外角都相等的三角形是等边三角形.正确的命题有( ) A .4个 B .3个 C .2个 D .1个 6.如图,等腰ABC 中,,,AB AC P Q =分别为,AC AB 上的点,且AP PQ QB BC ===,则PCQ ∠的度数为( )A .30︒B .36︒C .45︒D .37.5︒ 7.如图,在∠AB C 中,AB =AC ,点D ,E 在边BC 上,∠BAD =∠CAE ,若BC =15,DE =6,则CE 的长为( )A .3.5B .4.5C .5D .5.5 8.已知ABC ∆的周长是l ,2AB l BC =-,则下列直线一定为ABC ∆的对称轴的是 A .ABC ∆的边BC 的中垂线B .ABC ∠的平分线所在的直线 C .ABC ∆的边AB 上的中线所在的直线D .ABC ∆的边AC 上的高所在的直线 9.如图,ABC ∆是等边三角形,0,20BC BD BAD =∠=,则BCD ∠的度数为( )A .50°B .55°C .60°D .65° 10.如图,过边长为1的等边ABC 的边AB 上一点,作PE AC ⊥于,E Q 为BC 延长线上一点,当PA CQ =时,连接PQ 交AC 于D ,则DE 的长为( )A .13B .12C .23D .34二、填空题 11.已知:如图所示,点D 在BC 的延长线上,120ACD AB AC ︒∠==,,则ABC ∆的形状为___________12.如图,已知48ECD ∠=︒,AB BC CD ==,则EAF ∠=______.13.等腰三角形的底角为15°,腰长为24cm ,则这个三角形的面积为____________. 14.如图,过边长为3的等边∠ABC 的边AB 上一点P ,作PE ∠AC 于E ,Q 为BC 延长线上一点,当P A =CQ 时,连PQ 交AC 边于D ,则DE 的长为_____.15.如图,在第一个1A BC 中,30B ∠=︒,1A B CB =,在边1A B 上任取一D ,延长1CA 到2A ,使121A A A D =,得到第2个12A A D ,在边2A D 上任取一点E ,延长12A A 到3A ,使232A A A E =,得到第三个23A A E △,…按此做法继续下去,第n 个等腰三角形的底角的度数是________________.三、解答题16.(1)已知等腰三角形的两边长分别为9cm 和15cm ,则周长为多少? (2)已知等腰三角形的两边长分别为6cm 和15cm ,则周长为多少?17.如图,ABC ∆为等边三角形,BD 平分ABC ∠交AC 于点D ,//DE BC 交AB 于点E . (1)求证:ADE ∆是等边三角形.(2)求证:12AE AB =.18.如图,在ABC △中,120BAC ∠=︒,40B ∠=︒,边AB 的垂直平分线与边AB 交于点E,与边BC交于点D.(1)求∠ADC的度数;(2)求证:∠ACD为等腰三角形.1.C2.D3.A4.C5.C6.A7.B8.C9.A10.B11.等边三角形12.1613.144 cm 214.32. 15.1752n -︒16.(1)33cm 或39cm ;(2)36cm . 17.(1)∠∠ABC 为等边三角形, ∠∠A=∠ABC=∠C=60°.∠DE∠BC ,∠∠AED=∠ABC=60°,∠ADE=∠C=60°. ∠∠ADE 是等边三角形(2)∠∠ABC 为等边三角形, ∠AB=BC=AC .∠BD 平分∠ABC , ∠AD=12AC ∠∠ADE 是等边三角形,∠AE=AD . ∠AE=12AB .18.(1)∠DE 垂直平分AB , ∠DB DA =,∠B DAB ∠=∠∠40∠=∠=︒,B DAB∠80ADC B DAB∠=∠+∠=︒.(2)∠∠BAC=120°,∠DAB=40°,∠1204080∠=∠-∠=︒-︒=︒,DAC BAC DAB∠80∠=︒,ADC∠ADC DAC∠=∠,∠CA CD=,∠ACD△为等腰三角形.。
人教版八年级上册数学 13.3 等腰三角形 同步习题(含答案)

13.3 等腰三角形同步习题一.选择题1.等腰三角形的两边长为3和7,则其周长为()A.17B.13C.13或17D.以上都不对2.等腰三角形的两边长分别为3cm和7cm,则周长为()A.13cm B.17cm C.13cm或17cm D.11cm或17cm 3.在△ABC中,∠A:∠B:∠C=1:2:3,最小边BC=4cm,则最长边AB的长为()A.8cm B.6cm C.cm D.5cm4.在△ABC中,AB=AC,若∠A=40°,则∠C为()A.40°B.70°C.40°或70°D.100°5.如图,在△ABC中,AB=AC,点D,点E分别是BC,AC上一点,且DE⊥AD,若∠BAD=55°,∠B=50°,则∠DEC的度数为()A.125°B.120°C.115°D.110°6.如图,将边长为7cm的等边△ABC沿边BC向右平移5cm得到△A'B'C',则四边形AA'C'B 的周长为()A.30cm B.31cm C.32cm D.33cm7.如图,在△ABC中,D、E分别为AB、AC边上的点,DA=DE,DB=BE=EC.若∠ABC =130°,则∠C的度数为()A.20°B.22.5°C.25°D.30°8.△ABC中,AB=AC,∠BAC=120°,BC=2,D为BC的中点,AE=AB,则△EBD 的面积为()A.B.C.D.9.如图,在△ABC中,AB=AC,点D,E在边BC上,∠BAD=∠CAE,若BC=15,DE =6,则CE的长为()A.3.5B.4.5C.5D.5.510.如图,在等边△ABC中,BC=4,D,E分别是AB,AC的中点,EF⊥BC于点F,连接DF.则DF等于()A.2B.3C.D.2二.填空题11.如图,AD、BE是等边△ABC的两条高线,AD、BE交于点O,则∠AOB=度.12.等腰三角形周长为20cm,则腰长xcm的取值范围是.13.在等腰三角形ABC中,BC边上的高恰好等于BC边长的一半,则∠BAC等于.14.如图,在△ABC中,AE=DE=BD,AD=EC,∠1=17°,则∠EBC的度数是.15.如图,点C为线段AB上一点,且CB=2,分别以AC、BC为边,在AB的同一侧作等边△ACD和等边△CBE,连接DE,AE,∠CDE=30°,则△ADE的面积为.三.解答题16.如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.(1)求证:∠BAD=∠CAD;(2)求∠ADB的度数.17.如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)(2)请选择(1)中的一种情形,说明你的理由.参考答案1.A2.B3.A4.B5.C6.B7.D8.B9.B10.C11.120.12.5<x<1013.90°或75°或15°14.56°15.416.(1)证明:∵∠BDC=90°,∠DBC=45°,∴∠BCD=180°﹣∠BDC﹣∠DBC=45°,∴∠DBC=∠BCD,∴DB=DC.在△ABD与△ACD中,,∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD;(2)解:∵△ABD≌△ACD(SSS),∴∠ADB=∠ADC,∵∠ADB+∠ADC+∠BDC=360°,∠BDC=90°,∴∠ADB=(360°﹣90°)=135°.17.解:(1)由①②或①③可以判定△ABC是等腰三角形;(2)由①②判定△ABC是等腰三角形,理由如下:在△BOE和△COD中,∵∠EBO=∠DCO,BE=CD,∠BOE=∠COD,∴△BOE≌△COD,∴OB=OC,∴∠OBC=∠OCB,∴∠OBC+∠EBO=∠OCB+∠DCO,即:∠ABC=∠ACB,∴AB=AC,即△ABC是等腰三角形.①③判定△ABC是等腰三角形,理由如下:∵OB=OC,∴∠OBC=∠OCB,又∵∠EBO=∠DCO,∴∠OBC+∠EBO=∠OCB+∠DCO,即:∠ABC=∠ACB,∴AB=AC,即△ABC是等腰三角形.。
人教版数学八年级上册13.3 等腰三角形同步练习(解析版)

人教版数学八年级上册13.3:等腰三角形同步练习一.选择题(共15小题)1.在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC长为()A.4 cm B.2 cm C.1 cm D.cm2.一个等腰三角形但不是等边三角形,它的角平分线、高线、中线总数共()条.A.9B.7C.6D.33.如图,△ABC是等边三角形,AE⊥BC于E,AD⊥CD于D,AB∥CD,则图中60°的角有()A.3个B.4个C.5个D.6个4.下列判断不正确的是()A.等腰三角形的两底角相等B.等腰三角形的两腰相等C.等边三角形的三个内角都是60°D.两个内角分别为120°、40°的三角形是等腰三角形5.在△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,若AC=6,则BD等于()A.6B.3C.9D.126.等腰三角形的对称轴,最多可以有()A.1条B.3条C.6条D.无数条7.等腰三角形两边的长分别为2cm和5cm,则这个三角形的周长是()A.9cm B.12cmC.9cm或12cm D.在9cm或12cm之间8.如图,在△ABC中,AB=AC,D为BC的中点,E为AC边上一点,且AE=AD,∠BAC =40°,则∠EDC的度数是()A.10°B.20°C.30°D.40°9.一个三角形有两条边相等,这个三角形一边等于5cm,一边等于10cm,则另一边等于()A.5cm B.10cm C.15cm D.12cm10.如图,△ABC是等腰三角形,AD是底边BC上的高线,DE⊥AB于E,DF⊥AC于F,图中除AB=AC外,相等的线段共有()A.1对B.2对C.3对D.4对11.等腰三角形一腰上的高与底边所夹的角为a,则这个等腰三角形的顶角为()A.a B.90°﹣a C.12a D.2a12.等腰三角形的底角为a,则a的取值范围是()A.a≤45°B.0°<a<90°C.45°<a<90°D.0°≤a<90°13.如图,在等边三角形ABC中,三条中线AE,BD,CF相交于点O,则等边三角形ABC 中,从△BOF到△COD需要经过的变换是()A.轴对称变换B.旋转变换C.平移变换D.相似变换14.如果以4cm长的线段为底组成一个等腰三角形,腰长x的取值范围是()A.x>4cm B.x>2cm C.x≥4cm D.x≥2cm15.等腰三角形周长是32cm,一边长为10cm,则其他两边的长分别为()A.10cm,12cm B.11cm,11cmC.11cm,11cm或10cm,12cm D.不能确定二.填空题(共6小题)16.若等腰三角形的一腰上的高与另一腰的夹角等于50°,则其顶角的度数为.若等腰三角形的一腰上的高与底边的夹角等于50°,则其顶角的度数为.17.一个等腰三角形的腰长为3cm,则底边长的取值范围是.18.如图,AB=AC,∠A=100°,AB∥CD,则∠BCD=度.19.等腰三角形的顶角与底角的度数之比为4:1,则它的各内角度数为.20.△ABC中,∠A:∠B:∠C=1:2:3,AB=10,则BC=.21.(1)等腰三角形的一个角为100°,那么另外两个角分别为.(2)等腰三角形的一个角为50°,则底角是.三.解答题(共9小题)22.已知等腰三角形的周长为28cm,其中的一边长是另一边长的倍,求这个等腰三角形各边的长.23.如图,已知AB=AC,D为BC边中点,你能说出AD与BC的位置关系吗?请说明理由.24.如图,△ABC是等腰三角形,且AB=AC,试作出BC边上的中线和高以及∠A的平分线,从中你发现了什么?与其他同学进行交流.25.如图,在△ABC中,AB=AC,∠C=2∠A,BD平分∠ABC.请找出图中其他的等腰三角形,并选择其中的一个说明理由.26.已知D是等腰△ABC底边BC上的一个点,DE⊥AB于E,DF⊥AC于F,当D点在什么位置时,DE=DF,并加以证明.27.如图,AD是等腰△ABC顶角的外角的平分线,那么AD与BC平行吗?为什么?28.如图,在△ABC中,AD平分∠BAC,G是CA延长线上一点,GE∥AD交AB于F.交BC于E,试判断△AGF的形状并加以证明.29.如图,在等腰△ABC中,AB=AC,AD是BC边上的高,点E、F分别是边AB、AC上的点,且EF∥BC.(1)试说明△AEF是等腰三角形;(2)试比较DE与DF的大小关系,并说明理由.30.已知:如图,△ABC中,AB=AC,D是BC延长线上一点,E是AC延长线上一点,且DE∥AB,求证:ED=EC.人教版数学八年级上册13.3:等腰三角形同步练习参考答案一.选择题(共15小题)1.在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC长为()A.4 cm B.2 cm C.1 cm D.cm【解答】解:∵∠C=90°,∠B=30°,∴AB=2AC,∵AB=2cm,∴AC=AB=1cm,故选:C.2.一个等腰三角形但不是等边三角形,它的角平分线、高线、中线总数共()条.A.9B.7C.6D.3【解答】解:由于任意一个三角形都有三条角平分线、三条高线、三条中线,而等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合,所以一个等腰三角形但不是等边三角形,它的角平分线、高线、中线总数共7条.故选:B.3.如图,△ABC是等边三角形,AE⊥BC于E,AD⊥CD于D,AB∥CD,则图中60°的角有()A.3个B.4个C.5个D.6个【解答】解:∵△ABC是等边三角形,∴∠ABC=∠ACB=∠CAB=60°∵AB∥CD,∴∠ACD=∠CAB=60°,∵AD⊥CD,∴∠DAB=90°,∵AE⊥BC,∴∠BAE=∠CAE=30°,∴∠DAE=60°∴图中60°的角有5个,故选:C.4.下列判断不正确的是()A.等腰三角形的两底角相等B.等腰三角形的两腰相等C.等边三角形的三个内角都是60°D.两个内角分别为120°、40°的三角形是等腰三角形【解答】解:A、等腰三角形的两底角相等,正确,故本选项错误;B、等腰三角形的两腰相等,正确,故本选项错误;C、等边三角形的三个内角都是60°,正确,故本选项错误;D、两个内角分别为120°、40°的三角形的第三个内角为20°,不是等腰三角形,故本选项正确.故选:D.5.在△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,若AC=6,则BD等于()A.6B.3C.9D.12【解答】解:∵∠ACB=90°,CD⊥AB,∴∠ACD=∠B=30°,∵AC=6,∴AD=AC=×6=3,AB=2AC=2×6=12,∴BD=AB﹣AD=12﹣3=9.故选:C.6.等腰三角形的对称轴,最多可以有()A.1条B.3条C.6条D.无数条【解答】解:等腰三角形为等边三角形时对称轴最多,可以有3条.故选:B.7.等腰三角形两边的长分别为2cm和5cm,则这个三角形的周长是()A.9cm B.12cmC.9cm或12cm D.在9cm或12cm之间【解答】解:当腰长是2cm时,因为2+2<5,不符合三角形的三边关系,应排除;当腰长是5cm时,因为5+5>2,符合三角形三边关系,此时周长是12cm.故选:B.8.如图,在△ABC中,AB=AC,D为BC的中点,E为AC边上一点,且AE=AD,∠BAC =40°,则∠EDC的度数是()A.10°B.20°C.30°D.40°【解答】解:∵在△ABC中,D为BC中点,AB=AC,∴AD⊥BC,AD是∠BAC的角平分线,又∵AD=AE,∠BAC=40°,∴∠ADE=80°∴∠EDC=∠ADC﹣∠ADE=90°﹣80°=10°.故选:A.9.一个三角形有两条边相等,这个三角形一边等于5cm,一边等于10cm,则另一边等于()A.5cm B.10cm C.15cm D.12cm【解答】解:当第三边是5cm时,则5+5=10,不能构成三角形,当另一边长是10cm时,能构成三角形.故选:B.10.如图,△ABC是等腰三角形,AD是底边BC上的高线,DE⊥AB于E,DF⊥AC于F,图中除AB=AC外,相等的线段共有()A.1对B.2对C.3对D.4对【解答】解:∵△ABC是等腰三角形,AD是底边BC上的高线,∴BD=CD,∠BAD=∠CAD,∵DE⊥AB,DF⊥AC,∴DE=DF,∠BED=∠DFC=90°,在Rt△BED和Rt△CFD中,,∴Rt△BED≌Rt△CFD(HL),∴BE=CF,∵AB=AC,∴AE=AF.故图中除AB=AC外,相等的线段共有4对.故选:D.11.等腰三角形一腰上的高与底边所夹的角为a,则这个等腰三角形的顶角为()A.a B.90°﹣a C.12a D.2a【解答】解:如图,AB=AC,BD是腰AC的高,则∠DBC=α∴∠C=90°﹣α∴∠A=180°﹣2(90°﹣α)=2α故选:D.12.等腰三角形的底角为a,则a的取值范围是()A.a≤45°B.0°<a<90°C.45°<a<90°D.0°≤a<90°【解答】解:∵等腰三角形的底角为a,且三角形的内角和等于180°,∴0°<2a<180°,∴0°<a<90°.故选:B.13.如图,在等边三角形ABC中,三条中线AE,BD,CF相交于点O,则等边三角形ABC 中,从△BOF到△COD需要经过的变换是()A.轴对称变换B.旋转变换C.平移变换D.相似变换【解答】解:∵△BOF与△COD是关于OE的轴对称图形,∴从△BOF到△COD需要经过轴对称变换.故选A14.如果以4cm长的线段为底组成一个等腰三角形,腰长x的取值范围是()A.x>4cm B.x>2cm C.x≥4cm D.x≥2cm【解答】解:此等腰三角形的底为4cm,则有2x>4,解得x>2,故选:B.15.等腰三角形周长是32cm,一边长为10cm,则其他两边的长分别为()A.10cm,12cm B.11cm,11cmC.11cm,11cm或10cm,12cm D.不能确定【解答】解:当该边是腰时,底边是32﹣20=12cm,则另外两边是10cm,12cm;当该边是底时,则腰的长为:(32﹣10)÷2=11cm,则另外两边是11cm,11cm;经检验,两种情况都符合三角形的三边关系.故选:C.二.填空题(共6小题)16.若等腰三角形的一腰上的高与另一腰的夹角等于50°,则其顶角的度数为40°或140°.若等腰三角形的一腰上的高与底边的夹角等于50°,则其顶角的度数为100°.【解答】解:(1)①当为锐角三角形时可以画图,高与右边腰成50°夹角,由三角形内角和为180°可得,顶角为40°;②当为钝角三角形时可画图,此时垂足落到三角形外面,因为三角形内角和为180°,由图可以看出等腰三角形的顶角的补角为40°,三角形的顶角为140°.(2)如图,①顶角是钝角时,∠B=90°﹣50°=40°,则顶角=180°﹣2×40°=100°,是钝角,符合;②顶角是锐角时,∠B=90°﹣50°=40°,∠A=180°﹣2×40°=100°,是钝角,不符合.故答案为:40°或140°;100°.17.一个等腰三角形的腰长为3cm,则底边长的取值范围是0<底边<6cm.【解答】解:∵3﹣3=0,3+3=6cm,∴底边的取值范围是0<底边<6cm.故答案为:0<底边<6cm.18.如图,AB=AC,∠A=100°,AB∥CD,则∠BCD=40度.【解答】解:∵AB=AC∴∠B=∠ACB=(180﹣∠A)=40°∵AB∥CD∴∠BCD=∠B=40°.故填40.19.等腰三角形的顶角与底角的度数之比为4:1,则它的各内角度数为120°,30°,30°.【解答】解:设等腰三角形的各角为4x,x,x∵4x+x+x=180°∴x=30°∴三个内角分别是120°,30°,30°.故填120°,30°,30°.20.△ABC中,∠A:∠B:∠C=1:2:3,AB=10,则BC=5.【解答】解:由∠A:∠B:∠C=1:2:3,可设∠A=x°,则∠B=2x°,∠C=3x°.∵∠A+∠B+∠C=180°,∴x+2x+3x=180,∴x=30,∴∠A=30°,∠B=60°,∠C=90°,∴BC=AB=×10=5.故答案为5.21.(1)等腰三角形的一个角为100°,那么另外两个角分别为40°,40°.(2)等腰三角形的一个角为50°,则底角是50°,65°.【解答】解:(1)∵等腰三角形的一个角为100°∴两底角的和=180°﹣100°=80°又∵等腰三角形的两底角相等∴两底角都为40°.(2)当50°的角是底角,则底角就为50°;当50°的角是顶角,则两底角的和等于130°,所以底角等于65°.故填40°,40°;50°,65°.三.解答题(共9小题)22.已知等腰三角形的周长为28cm,其中的一边长是另一边长的倍,求这个等腰三角形各边的长.【解答】解:设等腰三角形的一边长为xcm,则另一边长为xcm,则等腰三角形的三边有两种情况:xcm,xcm,xcm或xcm,xcm,xcm,则有:①x+x+x=28,得x=8cm,所以三边为:8cm、8cm、12cm;②x+x+x=28,得x=7cm,所以三边为7cm、10.5cm、10.5cm.因此等腰三角形的三边的长为:8cm,8cm,12cm或7cm,10.5cm,10.5cm.23.如图,已知AB=AC,D为BC边中点,你能说出AD与BC的位置关系吗?请说明理由.【解答】解:AD⊥BC.理由如下:∵AB=AC,D为BC边中点,∴AD⊥BC.24.如图,△ABC是等腰三角形,且AB=AC,试作出BC边上的中线和高以及∠A的平分线,从中你发现了什么?与其他同学进行交流.【解答】解:如图,过点A作AD⊥BC于点D,在Rt△ABD和Rt△ACD中,∵AB=AC,AD=AD,∴Rt△ABD≌Rt△ACD(HL)∴BD=CD,即AD也是中线,∴∠BAD=∠CAD,即AD又是高线,所以等腰三角形底边上的中线、高以及顶角的角平分线重合.25.如图,在△ABC中,AB=AC,∠C=2∠A,BD平分∠ABC.请找出图中其他的等腰三角形,并选择其中的一个说明理由.【解答】解:△ABD、△BCD.理由:∵在△ABC中,AB=AC,∠C=2∠A,∴∠ABC=∠C=2∠A,∵∠A+∠ABC+∠C=180°,∴∠A+2∠A+2∠A=180°,解得:∠A=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠DBC=36°,∴∠A=∠ABD=36°,∠BDC=∠C=72°,∴△ABD与△BCD是等腰三角形.26.已知D是等腰△ABC底边BC上的一个点,DE⊥AB于E,DF⊥AC于F,当D点在什么位置时,DE=DF,并加以证明.【解答】解:当D是BC中点时DE=DF,理由:∵AB=AC,∴∠B=∠C;∵∠BED=∠CFD=90°,BD=CD;∴△BDE≌△CDF;∴DE=DF.27.如图,AD是等腰△ABC顶角的外角的平分线,那么AD与BC平行吗?为什么?【解答】解:AD∥BC.∵△ABC是等腰三角形,∴∠B=∠C,又∵∠EAC是△ABC的一个外角,∴∠EAC=∠B+∠C=2∠B,∵AD是等腰△ABC顶角的外角的平分线,∴2∠DAC=∠EAC,∴∠C=∠DAC,∴AD∥BC(内错角相等,两直线平行).28.如图,在△ABC中,AD平分∠BAC,G是CA延长线上一点,GE∥AD交AB于F.交BC于E,试判断△AGF的形状并加以证明.【解答】解:△AGF是等腰三角形;理由:∵GE∥AD,∴∠G=∠CAD,∠BAD=∠GF A,∵AD平分∠BAC,∴∠CAD=∠BAD,∴∠G=∠GF A,∴AG=AF,∴△AGF是等腰三角形.29.如图,在等腰△ABC中,AB=AC,AD是BC边上的高,点E、F分别是边AB、AC上的点,且EF∥BC.(1)试说明△AEF是等腰三角形;(2)试比较DE与DF的大小关系,并说明理由.【解答】解:(1)∵EF∥BC,∴∠AEF=∠B,∠AFE=∠C.又∵AB=AC,∴∠B=∠C,∴∠AEF=∠AFE,∴AE=AF,即△AEF是等腰三角形;(2)DE=DF.理由如下:∵AD是等腰三角形ABC的底边上的高,∴AD也是∠BAC的平分线.又∵△AEF是等腰三角形,∴AG是底边EF上的高和中线,∴AD⊥EF,GE=GF,∴AD是线段EF的垂直平分线,∴DE=DF.30.已知:如图,△ABC中,AB=AC,D是BC延长线上一点,E是AC延长线上一点,且DE∥AB,求证:ED=EC.【解答】证明:∵AB=AC,∴∠B=∠ACB,∵AB∥ED,∴∠B=∠D,∴∠ACB=∠D,又∵∠ACB=∠ECD,∴∠ECD=∠D,∴ED=EC.。
第13章13.3等腰三角形(课堂练习)人教版数学八年级上册试题试卷含答案

1.一个等腰三角形的两边长分别为2,4,则它的周长为( )A .8B .10C .9D .8或102.等腰三角形一腰上的高与另一腰的夹角为30︒,则底角的度数为( )A .60︒B .120︒C .60︒或120︒D .60︒或30︒3.若等腰三角形的一个内角是另一个内角的2倍,则满足条件的形状不同的三角形有( )A .1个B .2个C .3个D .4个4.等腰三角形补充下列条件后,一定不会成为等边三角形的是( )A .有一个内角是60︒B .有一个外角是120︒C .其中一个角是另一个角的3倍D .腰与底边相等5.如图所示,在等边三角形ABC 中,AD BC ⊥,E 为AD 上一点,50CED ∠=︒,则ABE∠等于( )A .10︒B .15︒C .20︒D .25︒6.如图,在Rt ABC ∆中,90C ∠=︒,点D 在线段BC 上,且30B ∠=︒,60ADC ∠=︒,BC =则BD 的长度为__________.课堂练习:基础版题量: 10题 时间: 20min13.3等腰三角形7.如图,60AOB ∠=︒,OC 平分AOB ∠,如果射线OA 上的点E 满足OCE ∆是等腰三角形,那么OEC ∠的度数为__________.8.在ABC ∆中,40A ∠=︒,当C ∠=__________时,ABC ∆为等腰三角形.9.等腰三角形的腰长为17,底长为16,则其底边上的高为__________.10.如图,四边形ABCD 中,4AD =,1BC =,30A ∠=︒,90B ∠=︒,120ADC ∠=︒,求CD的长.【错误题号】【错因自查】 基础不牢 审题不清思路不清 计算错误 粗心大意【正确解答】【错误题号】【错因自查】 基础不牢 审题不清思路不清 计算错误 粗心大意【正确解答】1.B2.D3.B4.C5.C6.7.120︒或75︒或30︒.8.40︒或70︒或100︒.9.1510.延长AD 、BC 交于E ,30A ∠=︒ ,90B ∠=︒,60E ∴∠=︒,120ADC ∠=︒ ,60EDC ∴∠=︒,EDC ∴∆是等边三角形,设CD CE DE x ===,4AD = ,1BC =,2(1)4x x ∴+=+,解得2x =,2CD ∴=.1.一个等腰三角形的两边长分别为2,4,则它的周长为( )A .8B .10C .9D .8或102.等腰三角形一腰上的高与另一腰的夹角为30︒,则底角的度数为( )A .60︒B .120︒C .60︒或120︒D .60︒或30︒3.若等腰三角形的一个内角是另一个内角的2倍,则满足条件的形状不同的三角形有( )A .1个B .2个C .3个D .4个4.等腰三角形补充下列条件后,一定不会成为等边三角形的是( )A .有一个内角是60︒B .有一个外角是120︒C .其中一个角是另一个角的3倍D .腰与底边相等5.如图所示,在等边三角形ABC 中,AD BC ⊥,E 为AD 上一点,50CED ∠=︒,则ABE∠等于( )A .10︒B .15︒C .20︒D .25︒6.如图,在Rt ABC ∆中,90C ∠=︒,点D 在线段BC 上,且30B ∠=︒,60ADC ∠=︒,BC =则BD 的长度为__________.课堂练习:提升版题量: 10题 时间: 20min13.3等腰三角形7.(★)下列三角形:①有两个角等于60︒的三角形;②有一个角等于60︒的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )A .①②③④B .①②④C .①③D .②③④8.(★)如图,在ABC ∆中,AB AC =,BD ,CE 分别是ABC ∠,ACB ∠的平分线,且DE BC ,36A ∠=︒,则图中等腰三角形共有__________个.9.(★)如图,ABC ∆是等边三角形,沿图中的虚线剪去B ∠,则12∠+∠的度数等于__________.10.(★)求证:在直角三角形中,如果一个锐角等于30︒,那么它所对的直角边等于斜边的一半.【错误题号】【错因自查】 基础不牢 审题不清思路不清 计算错误 粗心大意【正确解答】1.B2.D 3.B 4.C5.C6.7.A 8.129.240︒10.已知,在Rt ABC ∆中,30A ∠=︒,90ACB ∠=︒.求证:12BC AB =.证明:证法一:如图所示,延长BC 到D ,使CD BC =,连接AD ,易证AD AB =,60BAD ∠=︒.ABD ∴∆为等边三角形,AB BD ∴=,12BC CD AB ∴==,即12BC AB =.证法二:如图所示,取AB 的中点D ,连接DC ,有12CD AB AD DB ===,30DCA A ∴∠=∠=︒,60BDC DCA A ∠=∠+∠=︒.DBC ∴∆为等边三角形,12BC DB AB ∴==,即12BC AB =.证法三:如图所示,在AB 上取一点D ,使BD BC =,60B ∠=︒ ,BDC ∴∆为等边三角形,60DCB ∴∠=︒,90906030ACD DCB A ∠=︒-∠=︒-︒=︒=∠.DC DA ∴=,即有12BC BD DA AB ===,12BC AB ∴=.证法四:如图所示,作ABC ∆的外接圆D ,90C ∠=︒,AB 为O 的直径,连DC 有DB DC =,223060BDC A ∠=∠=⨯︒=︒,DBC ∴∆为等边三角形,12BC DB DA AB ∴===,即12BC AB =.1.一个等腰三角形的两边长分别为2,4,则它的周长为( )A .8B .10C .9D .8或102.等腰三角形一腰上的高与另一腰的夹角为30︒,则底角的度数为( )A .60︒B .120︒C .60︒或120︒D .60︒或30︒3.若等腰三角形的一个内角是另一个内角的2倍,则满足条件的形状不同的三角形有( )A .1个B .2个C .3个D .4个4.等腰三角形补充下列条件后,一定不会成为等边三角形的是( )A .有一个内角是60︒B .有一个外角是120︒C .其中一个角是另一个角的3倍D .腰与底边相等5.如图所示,在等边三角形ABC 中,AD BC ⊥,E 为AD 上一点,50CED ∠=︒,则ABE∠等于( )A .10︒B .15︒C .20︒D .25︒6.如图,在Rt ABC ∆中,90C ∠=︒,点D 在线段BC 上,且30B ∠=︒,60ADC ∠=︒,BC =则BD 的长度为__________.课堂练习:培优版题量: 10题 时间: 20min13.3等腰三角形7.(★★)如图,已知:30MON ∠=︒,点1A ,2A ,3A ⋯⋯在射线ON 上,点1B ,2B ,3B ⋯⋯在射线OM 上,△112A B A ,△223A B A ,△334A B A ⋯⋯均为等边三角形,若11OA =,则△778A B A 的边长为( )A .64B .32C .16D .1288.(★★)如图,在ABC ∆中,90BAC ∠=︒,点D 在BC 上,AB AC =,BD BA =,点E 在BC的延长线上,CA CE =,连接AE ,则DAE ∠=__________.9.(★★)如图,在1ABA ∆中,28B ∠=︒,1AB A B =,在1A B 上取一点C ,延长1AA 到2A ,使得121A A A C =,连接2A C .完成下列问题:(1)12A A C ∠的度数等于__________度;(2)如果继续在2A C 上取一点D ,延长12A A 到3A ,使得232A A A D =,连接3A D ,⋯,依此进行下去,那么以n A 为顶点的锐角的度数等于__________度.10.(★★)如图,ABC ∆为等边三角形,AE CD =,AD 、BE 相交于点P , BQ AD ⊥于点Q ,3PQ =,1PE =.(1)求证:AD BE =;(2)求AD 的长.【错误题号】【错因自查】 基础不牢 审题不清思路不清 计算错误 粗心大意【正确解答】【错误题号】【错因自查】 基础不牢 审题不清思路不清 计算错误 粗心大意【正确解答】1.B2.D 3.B 4.C5.C6.7.A8.45︒9.(1)38;(2)1762n -.10.(1)证明:ABC ∆ 为等边三角形,AB CA BC ∴==,60BAE ACD ∠=∠=︒;在ABE ∆和CAD ∆中,60AB CA BAE ACD AE CD =⎧⎪∠=∠=︒⎨⎪=⎩,(SAS)ABE CAD ∴∆≅∆,AD BE ∴=;(2)解:ABE CAD ∆≅∆ ,CAD ABE ∴∠=∠,60BPQ ABE BAD BAD CAD BAE ∴∠=∠+∠=∠+∠=∠=︒;BQ AD ⊥ ,90AQB ∴∠=︒,906030PBQ ∴∠=︒-︒=︒,3PQ = ,∴在Rt BPQ ∆中,26BP PQ ==,又1PE = ,617AD BE BP PE ∴==+=+=.。
2022-2023学年人教版八年级数学上册《13-3等腰三角形》同步达标测试题(附答案)

2022-2023学年人教版八年级数学上册《13.3等腰三角形》同步达标测试题(附答案)一.选择题(共10小题,满分40分)1.已知等腰三角形三边的长分别为4,x,10,则x的值是()A.4B.10C.4 或10D.6 或102.已知等腰三角形ABC的周长为20cm,BC=8cm,则AB的长度是()A.8cm B.6cmC.8cm或6cm D.8cm或6cm或4cm3.已知等腰三角形的一个底角为70°,则其顶角为()A.50°B.60°C.30°D.40°4.等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为()A.65°B.105°C.55°或105°D.65°或115°5.如图,在△ABC中,D、E是两边AB、AC上的点,DE∥BC,DE=BE,若∠DBC=20°,∠C=65°,则∠A的度数是()A.60°B.65°C.70°D.75°6.如图,已知点B,C,D,E在同一直线上,△ABC是等边三角形,且CG=CD,DF=DE,则∠E=()A.35°B.30°C.25°D.15°7.三个等边三角形的摆放位置如图,若∠3=60°,则∠1+∠2的度数为()°A.150B.120C.90D.808.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD于点D.∠ABD=∠A,若BD=1,BC=3,则AC的长为()A.2B.3C.4D.59.如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是()A.10B.8C.6D.410.如图,在△ABC中,∠B=60°,∠EDC=∠BAC,且D为BC中点,DE=CE,则AE:AB的值为()A.B.C.D.无法确定二.填空题(共6小题,满分30分)11.等腰三角形一边长等于4,一边长等于9,它的周长是.12.已知△ABC中有一个内角是30°,AB=AC,AB边上的中垂线交直线BC于点D,连结AD,则∠DAC=.13.如图,AD是△ABC的高,且AB+BD=DC,∠BAD=40°,则∠C的度数为.14.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E =60°,若BE=4cm,DE=3cm,则BC=cm.15.如图,∠ABC的平分线BF与△ABC的相邻外角∠ACG的平分线CF相交于F,过F 作DF∥BC,交AB于D,交AC于E,若BD=8cm,CE=5cm,则DE的长为.16.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB 于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn.其中正确的结论是.(填序号)三.解答题(共5小题,满分50分)17.已知:如图,E为△ABC的外角平分线上的一点,AE∥BC,BF=AE,求证:(1)△ABC是等腰三角形;(2)AF=CE.18.如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)求证:∠B=∠DEF;(3)当∠A=40°时,求∠DEF的度数.19.如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.(1)求证:AE=BD;(2)求证:MN∥AB.20.已知:在△AOB和△COD中,OA=OB,OC=OD.(1)如图①,若∠AOB=∠COD=60°,求证:①AC=BD②∠APB=60°.(2)如图②,若∠AOB=∠COD=α,则AC与BD间的等量关系式为,∠APB 的大小为(直接写出结果,不证明)21.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.参考答案一.选择题(共10小题,满分40分)1.解:当x=4时,4+4<10,不符合三角形三边关系,舍去;当x=10时,4+10>10,符合三角形三边关系.故选:B.2.解:(1)当BC=8cm为底边时,AB为腰,由等腰三角形的性质,得AB=(20﹣BC)=6cm;(2)当BC=8cm为腰时,①若AB为腰,则BC=AB=8cm;②若AB为底,则AB=20﹣2BC=4cm,故选:D.3.解:∵等腰三角形的一个底角为70°,∴顶角=180°﹣70°×2=40°.故选:D.4.解:①如图1,当等腰三角形的顶角是钝角时,腰上的高在外部.根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+25°=115°;②如图2,当等腰三角形的顶角是锐角时,腰上的高在其内部,故顶角是90°﹣25°=65°.故选:D.5.解:∵DE=BE,∴∠EBD=∠EDB,∵DE∥BC,∴∠EDB=∠DBC=20°,∴∠DBE=∠BDE=20°,∴∠ABC=40°,∵∠C=65°,∴∠A=180°﹣∠ABC﹣∠C=180°﹣40°﹣65°=75°,故选:D.6.解:如图所示,∵△ABC是等边三角形,∴∠B=∠1=60°,∵CD=CG,∴∠CGD=∠2,∴∠1=2∠2,同理有∠2=2∠E,∴4∠E=60°,∴∠E=15°.故选:D.7.解:∵图中是三个等边三角形,∠3=60°,∴∠ABC=180°﹣60°﹣60°=60°,∠ACB=180°﹣60°﹣∠2=120°﹣∠2,∠BAC=180°﹣60°﹣∠1=120°﹣∠1,∵∠ABC+∠ACB+∠BAC=180°,∴60°+(120°﹣∠2)+(120°﹣∠1)=180°,∴∠1+∠2=120°.故选:B.8.解:延长BD交AC于E,如图,∵CD平分∠ACB,BD⊥CD,∴△BCE为等腰三角形,∴DE=BD=1,CE=CB=3,∵∠A=∠ABD,∴EA=EB=2,∴AC=AE+CE=2+3=5.故选:D.9.解:如图,延长BD交AC于点E,∵AD平分∠BAE,AD⊥BD,∴∠BAD=∠EAD,∠ADB=∠ADE,在△ABD和△AED中,,∴△ABD≌△AED(ASA),∴BD=DE,∴S△ABD=S△ADE,S△BDC=S△CDE,∴S△ABD+S△BDC=S△ADE+S△CDE=S△ADC,∴S△ADC=S△ABC=×12=6,故选:C.10.解:∵DE=CE∴∠EDC=∠C,∵∠EDC=∠BAC,∴∠EDC=∠BAC=∠C,∵∠B=60°,∴△ABC及△DCE是等边三角形,∵D为BC中点,∴DE是△ABC的中位线,∴AE:AB=1:2.故选:A.二.填空题(共6小题,满分30分)11.解:∵4+4=8<9,0<4<9+9=18∴腰的不应为4,而应为9∴等腰三角形的周长=4+9+9=22故填:22.12.解:∠B=30°是底角,如图1:∵AB=AC,∠B=30°,∴∠C=30°,∵AB边上的中垂线交直线BC于点D,∴∠BAD=∠B=30°,∴∠ADC=30°+30°=60°,∴∠DAC=180°﹣30°﹣60°=90°;∠BAC=30°的角是顶角,如图2:∵AB=AC,∠BAC=30°,∴∠B=∠ACB=(180°﹣30°)÷2=75°,∵AB边上的中垂线交直线BC于点D,∴∠BED=∠AED=90°﹣75°=15°,∴∠ADC=15°+15°=30°,∴∠DAC=75°﹣30°=45°.故∠DAC=90°或45°.故答案为:90°或45°.13.解:在线段DC上取一点E,使DE=DB,连接AE,∵AD是△ABC的高,∴AD⊥BC,∴AD垂直平分BE,∴AB=AE,∴∠EAD=∠BAD=40°,∠AEB=∠B=90°﹣∠BAD=50°,∵AB+BD=DC,DE+CE=DC,∴AB=CE,∴AE=CE,∴∠EAC=∠C,∵∠AEB=∠EAC+∠C=2∠C,∴∠C=∠AEB=25°,故答案为:25°.14.解:延长ED交BC于M,延长AD交BC于N,作DF∥BC,∵AB=AC,AD平分∠BAC,∴AN⊥BC,BN=CN,∵∠EBC=∠E=60°,∴△BEM为等边三角形,∴△EFD为等边三角形,∵BE=4cm,DE=3cm,∴DM=1cm,∵△BEM为等边三角形,∴∠EMB=60°,∵AN⊥BC,∴∠DNM=90°,∴∠NDM=30°,∴NM=cm,∴BN=cm,∴BC=2BN=7cm,故答案为7.15.解:∵BF、CF分别平分∠ABC、∠ACB的外角,∴∠DBF=∠CBF,∠FCE=∠FCG,∵DE∥BC,∴∠DFB=∠CBF,∠EFC=∠FCG,∴∠DBF=∠DFB,∠FCE=∠EFC,∴BD=FD=8cm,EF=CE=5cm,∴BD﹣CE=FD﹣EF=DE=8﹣5=3(cm),故答案为:3cm.16.解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故②正确;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF,∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=AE•OM+AF•OD=OD•(AE+AF)=mn;故④错误;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故③正确.故答案是:①②③三.解答题(共5小题,满分50分)17.证明:(1)∵AE∥BC,∴∠DAE=∠B,∠EAC=∠ACB,∵E为△ABC的外角平分线上的一点,∴∠DAE=∠EAC,∴∠B=∠ACB,∴AB=AC,∴△ABC是等腰三角形;(2)在△ABF和△CAE中,,∴△ABF≌△CAE(SAS),∴AF=CE.18.(1)证明:∵AB=AC,∴∠B=∠C,在△DBE和△ECF中,,∴△DBE≌△ECF,∴DE=FE,∴△DEF是等腰三角形;(2)∵△BDE≌△CEF,∴∠FEC=∠BDE,∴∠DEF=180°﹣∠BED﹣∠FEC=180°﹣∠DEB﹣∠EDB=∠B (3)∵由(2)知△BDE≌△CEF,∴∠BDE=∠CEF,∴∠CEF+∠DEF=∠BDE+∠B,∴∠DEF=∠B,∴AB=AC,∠A=40°,∴∠DEF=∠B==70°.19.证明:(1)∵△ACD和△BCE是等边三角形,∴AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,∵∠DCA=∠ECB=60°,∴∠DCA+∠DCE=∠ECB+∠DCE,∠ACE=∠DCB,在△ACE与△DCB中,∵,∴△ACE≌△DCB,∴AE=BD;(2)∵由(1)得,△ACE≌△DCB,∴∠CAM=∠CDN,∵∠ACD=∠ECB=60°,而A、C、B三点共线,∴∠DCN=60°,在△ACM与△DCN中,∵,∴△ACM≌△DCN(ASA),∴MC=NC,∵∠MCN=60°,∴△MCN为等边三角形,∴∠NMC=∠DCN=60°,∴∠NMC=∠DCA,∴MN∥AB.20.解:(1)①证明:∵∠AOB=∠COD=60°,∴∠AOB+∠BOC=∠COD+∠BOC,∴∠AOC=∠BOD.在△AOC和△BOD中,,∴△AOC≌△BOD(SAS),∴AC=BD;②证明:∵△AOC≌△BOD,∴∠OAC=∠OBD,∴∠OAC+∠AOB=∠OBD+∠APB,∴∠OAC+60°=∠OBD+∠APB,∴∠APB=60°;(2)AC=BD,∠APB=α.21.解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,∠BDA逐渐变小;故答案为:25°,115°,小;(2)当DC=2时,△ABD≌△DCE,理由:∵∠C=40°,∴∠DEC+∠EDC=140°,又∵∠ADE=40°,∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,又∵AB=DC=2,∴△ABD≌△DCE(AAS),(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,理由:∵∠BDA=110°时,∴∠ADC=70°,∵∠C=40°,∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,∴∠DAC=∠AED,∴△ADE的形状是等腰三角形;∵当∠BDA的度数为80°时,∴∠ADC=100°,∵∠C=40°,∴∠DAC=40°,∴∠DAC=∠ADE,∴△ADE的形状是等腰三角形.。
人教版数学八年级上册 第13章 13.3等腰三角形同步测试题(一)

等腰三角形同步测试题(一)一.选择题1.如图,△ABC是等腰三角形(AB=AC,∠B=30°),AD是底边BC上的高.BC=12米,则AD的长是()A.2米B.2米C.6米D.4米2.规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k,若k=,则该等腰三角形的顶角为()A.30°B.36°C.45°D.60°3.在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,以下说法错误的是()A.AC=2CD B.AD=2CD C.AD=3BD D.AB=2BC4.如图,等边三角形ABC的边长为4,则点C的坐标是()A.C.(﹣2,)D.(2,﹣2)5.如图,直线a∥b,等边三角形ABC的顶点B在直线b上,若∠1=34°,则∠2等于()A.84°B.86°C.94°D.96°6.如图,直线l1∥l2,且分别与等腰△ABC的两条腰相交,若∠1=40°,∠2=86°,则∠B的度数为()A.54°B.60°C.63°D.70°7.如图,直线l1∥l2,将等边三角形如图放置若∠α=25°,则∠β等于()A.35°B.30°C.25°D.20°8.如图,在Rt△ABC中,∠C=90°,∠A=30°,D是AC边的中点,DE⊥AC于点D,交AB于点E,若AB=16,则DE的长是()A.8B.6C.4D.29.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=4,点D、F分别是边AB,BC 上的动点,连接CD,过点A作AE⊥CD交BC于点E,垂足为G,连接GF,则GF+FB 的最小值是()A.B.C.D.10.如图,BD,CE分别是△ABC的高线和角平分线,且相交于点O.若AB=AC,∠A=40°,则∠BOE的度数是()A.60°B.55°C.50°D.40°二.填空题11.如图,等边三角形ABC的两条角平分线BD和CD交于点D,则∠BDC等于.12.如图,△ABC是边长为6cm的等边三角形,BP=4cm,点Q为射线BC边上一点,当CQ的长为时,△PBQ是直角三角形.13.如图,Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,DE垂直平分BC,垂足为E,则∠C的度数为°.14.如图,在△ABC中,AB=AC,∠BAC=120°,点D为△ABC外一点,连接BD、AD、CD,∠ADC=60°,BD=5,DC=4,则AD=.15.如图,CE平分∠ACB,且CE⊥BD,DA=DB,又知AC=18,△CDB的周长为28,那么BE的长为.三.解答题16.如图,△ABC中,AB=AC,AD=AE,∠CAD=60°,∠C=α(1)用α表示∠BAD,则∠BAD=;(2)求∠EDB的度数.17.已知:如图等边△ABC,D是AC的中点,且CE=CD,DF⊥BE.(1)求证:BF=EF.(2)若DE=5cm,求DF的长.18.如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,AD=3cm,求BC的长.19.已知:如图,△ABC是等边三角形,BD⊥AC,E是BC延长线上的一点,且∠CED=30°.(1)求证:DB=DE.(2)在图中过D作DF⊥BE交BE于F,若CF=3,求△ABC的周长.参考答案与试题解析一.选择题1.【解答】解:∵AB=AC,∠B=30°,AD是底边BC上的高,∴BD=CD=BC=6,∴AD=BD=2,故选:A.2.【解答】解:∵△ABC中,AB=AC,∴∠B=∠C,∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k,若k =,∴∠A:∠B=1:2,即5∠A=180°,∴∠A=36°,故选:B.3.【解答】解:∵△ABC中,∠ACB=90°,∠A=30°,∴AB=2BC;∵CD⊥AB,∴AC=2CD,∴∠B=60°,又CD⊥AB,∴∠BCD=30°,在Rt△BCD中,∠BCD=30°,CD=BD,在Rt△ABC中,∠A=30°,AD=CD=3BD,故选:B.4.【解答】解:过C作CD⊥OB于D,∵等边三角形ABC的边长为4,∴OD=2,CD=2,∴C(2,﹣2),故选:D.5.【解答】解:∵∠3=∠1=34°,∵△ABC是等边三角形,∴∠A=60°,∴∠4=∠A+∠3=94°,∵直线a∥b,∴∠2=∠4=94°,故选:C.6.【解答】解:∵∠3=∠2=86°,∠5=∠1=40°,∵直线l1∥l2,∴∠4=180°﹣∠3=94°,∴∠A=∠4﹣∠5=54°,∵AB=AC,∴∠B=(180°﹣∠A)=63°,故选:C.7.【解答】解:过点B作BD∥l1,如图,则∠ABD=∠α=25°.∵l1∥l2,∴BD∥l2,∵∠DBC=∠β.∵△ABC是等边三角形,∴∠ABC=60°,∴∠β=∠CBD=∠ABC﹣∠ABD=60°﹣25°=35°.故选:A.8.【解答】解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=16,∴BC=AB=8,∵DE⊥AC,∠C=90°,∴DE∥BC,∵D是AC边的中点,∴AD=CD,∴AE=BE,∴DE=BC=4,故选:C.9.【解答】解:延长AC到点P,使CP=AC,连接BP,过点F作FH⊥BP于点H,取AC 中点O,连接OG,过点O作OQ⊥BP于点Q,∵∠ACB=90°,∠ABC=30°,AB=4∴AC=CP=2,BP=AB=4∴△ABP是等边三角形∴∠FBH=30°∴Rt△FHB中,FH=FB∴当G、F、H在同一直线上时,GF+FB=GF+FH=GH取得最小值∵AE⊥CD于点G∴∠AGC=90°∵O为AC中点∴OA=OC=OG=AC∴A、C、G三点共圆,圆心为O,即点G在⊙O上运动∴当点G运动到OQ上时,GH取得最小值∵Rt△OPQ中,∠P=60°,OP=3,sin∠P=∴OQ=OP=∴GH最小值为故选:C.10.【解答】解:∵AB=AC,∠A=40°,∴∠ABC=∠ACB=70°,∵CE平分∠ACB,∴∠ACE=∠ACB=35°,∵BD⊥AC,∴∠ODC=90°,∴∠BOE=∠COD=90°﹣35°=55°,故选:B.二.填空题(共5小题)11.【解答】解:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵BD平分∠ABC,CD平分∠ACB,∴∠DBC=,∠DCB=ACB=30°,∴∠BDC=180°﹣30°﹣30°=120°,故答案为:120°.12.【解答】解:∵△ABC是等边三角形,∴∠B=60°,如图1,当∠PQB=90°时,BQ=BP=2cm,CQ=6﹣2=4cm;如图2,当∠BPQ=90°时,BQ=2BP=8cm,CQ=8﹣6=2cm.故当CQ的长为4cm或2cm时,△PBQ是直角三角形.故答案为:4cm或2cm.13.【解答】解:∵DE垂直平分BC,∴DC=DB,∴∠DBC=∠C,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠DBC=∠ABD=∠C,∵∠A=90°,∴∠C=∠DBC=∠ABD=30°,故答案为:3014.【解答】解:将△ABD绕点A逆时针旋转120°得到△ACE,∴∠DAE=120°,AD=AE,∴∠ADE=∠AED=30°,∵∠ADC=60°,∴∠CDE=90°,∵EC=BD=5,DC=4,∴DE===3,作AF⊥DE于F,∴DF=DE=,∵在Rt△ADF中,cos30°=,∴AD===,故答案为.15.【解答】解:∵CE平分∠ACB,且CE⊥BD,∴∠DCE=∠BCE,∠CED=∠CEB=90°,在△CED和△CEB中,,∴△CED≌△CEB(ASA),∴CD=CB,DE=BE,∵DA=DB,AC=18,△CDB的周长为28,∴BC=10,∴CD=10,∴BD=8,∴BE=4,故答案为:4.三.解答题(共4小题)16.【解答】解:(1)∵AB=AC,∴∠B=∠C=α,∴∠BAC=180°﹣2α,∵∠DAC=60°,∴∠BAD=120°﹣2α;故答案为:120°﹣2α;(2)∵AE=AD,∴∠ADE=(180°﹣∠BAD)=30°+α,∵∠ADB=∠DAC+∠C=60°+α,∴∠EDB=∠ADB﹣∠ADE=30°.17.【解答】证明:(1)∵在等边△ABC,且D是AC的中点,∴∠DBC=∠ABC=×60°=30°,∠ACB=60°,∵CE=CD,∴∠CDE=∠E,∵∠ACB=∠CDE+∠E,∴∠E=30°,∴∠DBC=∠E=30°,∴BD=ED,△BDE为等腰三角形,又∵DF⊥BE,∴F是BE的中点,∴BF=EF;(2)∵在直角三角形DFE中,∠E=30°,DE=5,∴DF=DE=×5=.18.【解答】解:∵AB=AC,∴∠B=∠C.∵∠BAC=120°,∠BAC+∠B+∠C=180°,∴∠B=∠C=30°.∵AD⊥AC,∴∠DAC=90°.∴DC=2AD,∠BAD=∠BAC﹣∠DAC=30°.∴∠BAD=∠B.∴BD=AD=3.∴BC=BD+DC=3BD=9.19.【解答】证明:(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.∵BD⊥AC,∴BD平分∠ABC,∴∠DBC=30°(等腰三角形三线合一).又∵∠CED=30°,∴DB=DE(等角对等边);(2)过D作DF⊥BE交BE于F,∵∠CDE=∠CED=∠BCD=30°,∴∠CDF=30°,∵CF=3,∴DC=6,∵AD=CD,∴AC=12,∴△ABC的周长=3AC=36.。
人教版八年级上册数学《等腰三角形》同步训练附答案

人教版八年级数学上册《13.3等腰三角形》同步训练1.如图,△ABC是等边三角形,△BCD是等腰三角形,且BD=CD,过点D作AB的平行线交AC于点E,若AB=8,DE=6,则BD的长为()A.6B.C.D.2.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.已知:如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.求证AB=AC.以下是排乱的证明过程:①又∠1=∠2,②∴∠B=∠C,③∵AD∥BC,④∴∠1=∠B,∠2=∠C,⑤∴AB=AC.证明步骤正确的顺序是()A.③→②→①→④→⑤B.③→④→①→②→⑤C..①→②→④→③→⑤D.①→④→③→②→⑤3.如图,△ABC是等边三角形,AD是BC边上的中线,点E在AD上,且DE=BC,则∠AFE=()A.100°B.105°C.110°D.115°4.如图,已知△ABC是等边三角形,D是BC边上的一个动点(异于点B、C),过点D作DE⊥AB,垂足为E,DE的垂直平分线分别交AC、BC于点F、G,连接FD,FE.当点D在BC边上移动时,有下列三个结论:①△DEF一定为等腰三角形;②△CFG一定为等边三角形;③△FDC可能为等腰三角形.其中正确的有()A.0个B.1个C.2个D.3个5.如图,在Rt△ABC中,∠A=90°,CM平分∠ACB交AB于点M,过点M作MN∥BC 交AC于点N,且MN平分∠AMC,若AN=2,则BC的长为()A.12B.16C.20D.86.如图,AB∥CD,CB平分∠ACD,点E在AB上,DE⊥CB,垂足为F,连接AF则下列结论中错误的是()A.AB=AC B.∠AFC=∠DC.∠AEF+∠D=180°D.∠AFC>∠FCD7.如果一个等腰三角形的两边长为2和5,那么这个三角形的周长是()A.9B.12C.9或12D.不确定8.若等腰三角形的一个内角比另一个内角大30°,则这个等腰三角形的底角度数是()A.50°B.80°C.50°或70°D.80°或40°9.若等腰三角形一边长9cm,另一边长4cm,则它的周长为()A.22cm B.17cm C.22cm或17cm D.22cm或19cm 10.等腰三角形一边长9cm,另一边长4cm,它的第三边是()cm.A.4 B.9 C.4或9 D.大于5且小于1311.下列对△ABC的判断,错误的是()A.若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形B.若AB=BC,∠C=50°,则∠B=50°C.若AB=BC,∠A=60°,则△ABC是等边三角形D.若∠A=20°,∠C=80°,则△ABC是等腰三角形12.已知等腰三角形的周长为19,一边长为8,则此等腰三角形的底边长为()A.3B.8C.3或8D.8或5.513.若等腰三角形的顶角是大于60°的锐角,则底角度数的取值范围是()A.x<60°B.x≤60°C.45°<x<60°D.45°≤x<60°14.△ABC中,∠BAC=∠BCA,AD平分∠BAC,DE∥AC,下列说法正确的是()A.∠B=36°B.∠ADB=108°C.∠ADB=3∠EDA D.∠AED=3∠B 15.等腰三角形的两边长为3和8,则这个等腰三角形的周长是()A.14B.19C.14或19D.2016.如图,在△ABC中,AB=AC,尺规作图:(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D;(2)作射线AD,连接BD,CD.则下列结论中错误的是()A.∠BAD=∠CAD B.△BCD是等边三角形C.AD垂直平分BC D.S四边形ABDC=AD⋅BC17.如图,在△ABC中,AB=AC,AC的垂直平分线l交BC于点D.若∠BAD=78°,则∠B的度数是()A.34°B.30°C.28°D.26°18.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM 交AB于点E.若AE=5,BE=1,则EC的长度是()A.B.C.9D.19.如图,在等腰△ABD中,∠A=32°,取大于AB的长为半径,分别以点A,B为圆心作弧相交于两点,过此两点的直线交AD边于点E(作图痕迹如图所示),连接BE,BD,则∠EBD的度数为.20.如图,在△ABC中,AB=AC,以点B为圆心,BC长为半径画弧交AC于点C和点D,再分别以点C和点D为圆心,大于DC长为半径画弧,两弧相交于点F,作射线BF交AC于点E.若∠A=40°,则∠EBC=度.21.如图,在边长为2的等边三角形ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,G为EF的中点,连接DG,则DG的长为.22.如图,在△ABC中,AB=AC,∠B=35°,D是BC边上的动点,连接AD,若△ABD 为直角三角形,则∠DAC的度数为.23.已知等腰三角形的一个内角为110°,则等腰三角形的底角的度数为.24.用三根木棒首尾相连围成一个等腰三角形,其中两根木棒的长度分别为3cm和6cm,则第三根木棒长为cm.25.如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,BC=16cm,则BD=cm.26.如图,在平面直角坐标系中,点A的坐标为(0,2),点B的坐标为(4,0),在y轴上取一点C使△ABC为等腰三角形,符合条件的C点有个.27.如图,在△ABC中,AB=AC,∠BAC=108°,AC的中垂线交BC于点D,交AC于点E,连接AD,则图中等腰三角形有个.28.如图,在△ABC中,以点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=32°,求∠DAC的度数.29.如图,已知△ABC中,AB=AC,∠ABC、∠ACB的平分线交于点E,直线AE交BC于点D,说明AD⊥BC的理由.30.若关于x,y的二元一次方程组的解都是正数.(1)求a的取值范围;(2)若此方程组的解是一个等腰三角形的一条腰和底边的长,且这个等腰三角形的周长为12,求a的值.31.如图,在△ABC中,D是三角形内一点,连接DA、DB、DC,且∠1=∠2,∠3=∠4,求证:AB=AC.参考答案1.解:连接AD交BC于点O,取AC中点N,连接ON,如图,∵△ABC是等边三角形,∴AB=AC=BC=8,∠ABC=60°,∵△BCD是等腰三角形,∴BD=DC,∴AD垂直平分BC,∴BO=CO=4,∵AN=CN,∴ON=AB=4,ON∥AB,∵AB∥DE,∴ON∥DE,∴OD=AO,∴AO=4,∴OD=2,在Rt△BOD中,BD==2.故选:B.2.解:∵③AD∥BC,∴④∠1=∠B,∠2=∠C,∵①∠1=∠2,∴②∠B=∠C,∴⑤AB=AC,故证明步骤正确的顺序是③→④→①→②→⑤,3.解:∵△ABC是等边三角形,∴∠BAC=60°,∵AD是BC边上的中线,∴∠BAD=BAC=30°,AD⊥BC,BD=CD=BC,∴∠CDE=90°,∵DE=BC,∴DE=DC,∴∠DEC=∠DCE=45°,∴∠AEF=∠DEC=45°,∴∠AFE=180°﹣∠BAD﹣∠AEF=180°﹣30°﹣45°=105°,故选:B.4.解:∵DE的垂直平分线分别交AC、BC于点F、G,∴FE=FD,∴△DEF一定为等腰三角形,故①正确;∵DE⊥AB,DE⊥FG,∴AB∥FG,∴∠FGC=∠B=60°,又∵△ABC是等边三角形,∴∠C=60°,∴△CFG中,∠C=∠CFG=∠CGF,∴△CFG一定为等边三角形;故②正确;∵∠FDC>∠FGC=60°,∠C=60°,∠CFD<∠CFG=60°,∴△FDC不可能为等腰三角形.故③错误;5.解:∵CM平分∠ACB交AB于点M,∴∠NCM=∠BCM,∵MN∥BC∴∠NCM=∠BCM=∠NMC,∵MN平分∠AMC,∴∠AMN=∠NMC=∠B,∴∠ACB=2∠B,NM=NC,∴∠B=30°;∵AN=2,∠AMN=∠B=30°,∴MN=2AN=4,∴NM=NC=4,∴AC=AN+NC=6,∴BC=2AC=12,故选:A.6.解:∵AB∥CD,∴∠B=∠BCD,∠AEF+∠D=180°,故C选项正确;∵CB平分∠ACD,∴∠ACB=∠BCD,∴∠ACB=∠B,∴AC=AB,故A选项正确;∵DE⊥CB,∴∠CFD=90°,∴∠D+∠BCD=90°,假如∠AFC=∠D,则∠CAF=∠CFD=90°,而∠CAF不一定是90°,∴∠AFC与∠D不一定相等,故B选项错误;∵∠AFC是△ABF的外角,∴∠AFC>∠B,∵∠B=∠FCD,∴∠AFC>∠FCD,故D选项正确,故选:B.7.解:∵2+2=4<5,∴腰的长不能为2,只能为5,∴等腰三角形的周长=2×5+2=12,故选:B.8.解:在△ABC中,设∠A=x,∠B=x+30°,分情况讨论:当∠A=∠C为底角时,2x+(x+30°)=180°,解得x=50°,底角∠A=50°;当∠B=∠C为底角时,2(x+30°)+x=180°,解得x=40°,底角∠B=70°.故这个等腰三角形的底角的度数为50°或70°.故选:C.9.解:①当腰为4cm时,三边为4cm,4cm,9cm,∵4+4<9,∴不符合三角形的三边关系定理,此种情况舍去;②当腰为9cm时,三边为4cm,9cm,9cm,此时符合三角形的三边关系定理,此时等腰三角形的周长是4cm+9cm+9cm=22cm,故选:A.10.解:①当腰为4cm时,三边为4cm,4cm,9cm,∵4+4<9,∴不符合三角形的三边关系定理,此种情况舍去;②当腰为9cm时,三边为4cm,9cm,9cm,此时符合三角形的三边关系定理,所以三角形的第三边为9cm,故选:B.11.解:A.若∠A:∠B:∠C=1:2:3,则∠A=30°,∠B=60°,∠C=90°,所以△ABC是直角三角形,故此选项正确,不符合题意;B.若AB=BC,∠C=50°,则∠A=∠C=50°,∠B=100°,故此选项错误,符合题意;C.若AB=BC,∠A=60°,则∠A=∠C=60°,∠B=60°,所以△ABC是等边三角形,故此选项正确,不符合题意;D.若∠A=20°,∠C=80°,则∠B=80°,∠C=∠B=80°,所以△ABC是等腰三角形,故此选项正确,不符合题意.故选:B.12.解:本题可分两种情况:①当腰长为8时,底边长=19﹣2×8=3;经检验,符合三角形三边关系;②底边长为8,此时腰长=(19﹣8)÷2=5.5,经检验,符合三角形三边关系;因此该等腰三角形的底边长为3或8.故选:C.13.解:设等腰三角形的底角为x°,则顶角为(180°﹣2x),由题意可得:60°<180°﹣2x<90°,∴45°<x<60°,∴底角度数的取值范围是45°<x<60°,故选:C.14.解:设∠CAD=x°,∵AD平分∠BAC,∠BAC=∠BCA,∴∠BCA=∠BAC=2x°,∵DE∥AC,∴∠BDE=∠BCA=2x°,∠ADE=∠CAD=x°,∴∠ADB=∠BDE+∠ADE=2x°+x°=3x°,即∠ADB=3∠EDA,故选:C.15.解:①若3是腰,则另一腰也是3,底是8,但是3+3<8,故不构成三角形,舍去.②若3是底,则腰是8,8.3+8>8,符合条件.成立.故周长为:3+8+8=19.故选:B.16.解:根据作图方法可得BC=BD=CD,∵BD=CD,∴点D在BC的垂直平分线上,∵AB=AC,∴点A在BC的垂直平分线上,∴AD是BC的垂直平分线,故C结论正确;∴O为BC中点,∴AO是△BAC的中线,∵AB=AC,∴∠BAD=∠CAD,故A结论正确;∵BC=BD=CD,∴△BCD是等边三角形,故B结论正确;∵四边形ABDC的面积=S△BCD+S△ABC=BC•DO+BC•AO=BC•AD,故D选项错误,故选:D.17.解:∵AB=AC,∴∠B=∠C,∵AC的垂直平分线l交BC于点D,∴AD=DC,∴∠DAC=∠C,∵∠ADB=∠DAC+∠C=2∠C,∴∠ADB=2∠B,∵∠BAD=78°,∴∠B+∠ADB+∠BAD=∠B+2∠B+78°=180°,∴∠B=34°,故选:A.18.解:由作法得CE⊥AB,则∠AEC=90°,AC=AB=BE+AE=5+1=6,在Rt△ACE中,CE==,故选:A.19.解:∵AD=AB,∠A=32°,∴∠ABD=∠ADB=(180°﹣∠A)=74°,由作图可知,EA=EB,∴∠ABE=∠A=32°,∴∠EBD=∠ABD﹣∠ABE=74°﹣32°=42°,故答案为:42°.20.解:∵AB=AC,∠A=40°,∴∠ACB=(180°﹣40°)÷2=70°,由题意可知,BC=BD,∴∠BDC=∠ACB=70°,∴∠CBD=180°﹣70°×2=40°,由题意可知,BF平分∠DBC,∴∠EBC=∠CBD=20°.故答案为:20.21.解:连接DE,∵在边长为2的等边△ABC中,D,E分别为AB,BC的中点,∴DE是△ABC的中位线,∴DE=1,且DE∥AC,BD=BE=EC=1,∵EF⊥AC于点F,∠C=60°,∴∠FEC=30°,∠DEF=∠EFC=90°,∴FC=EC=,故EF===,∵G为EF的中点,∴EG=,∴DG==,故答案为:.22.解:如图,∵AB=AC,∠B=35°,∴∠B=∠C=35°,∴∠BAC=110°,当∠BAD=90°时,∠DAC=110°﹣90°=20°;当∠ADB=90°时,∵AB=AC,AD⊥BC,∴∠DAC=∠BAD=55°.故答案为:20°或55°.23.解:∵等腰三角形的一个内角是110°,∴等腰三角形的顶角为110°,∴等腰三角形的底角为35°,故答案为:35°.24.解:组成等腰三角形的两根木棒的长度分别为3cm和6cm,根据三角形三边关系可得,组成等腰三角形的第三根木棒长为6cm,故答案为:6.25.解:∵AB=AC,AD平分∠BAC交BC于点D,∴BD=DC=BC,∵BC=16cm,故答案为:8.26.解:观察图形可知,若以点A为圆心,以AB为半径画弧,与y轴有2个交点,但其中一个与B点重合,故此时符合条件的点由1个;若以点B为圆心,以AB为半径画弧,与y轴有2个交点;线段AB的垂直平分线与y轴有1个交点;∴符合条件的C点有:1+2+1=4(个),故答案为:4.27.解:∵AB=AC,∠BAC=108°,∴△ABC是等腰三角形,∠B=∠C=(180°﹣∠BAC)÷2=36°,∵AC的中垂线交BC于点D,交AC于点E,∴AD=CD,∴△ADC是等腰三角形,∠DAC=∠C=36°,∴∠BAD=∠BAC﹣∠DAC=72°,∠ADB=∠DAC+∠C=72°,∴∠BAD=∠ADB,∴△BAD是等腰三角形.故图中等腰三角形有3个.故答案为:3.28.解:∵∠B=40°,∠C=32°,∴∠BAC=180°﹣∠B﹣∠C=108°,由作图可知:BA=BD,∴∠BAD=∠BDA=(180°﹣∠B)÷2=70°,∴∠DAC=∠BAC﹣∠BAD=38°.29.证明:∵AB=AC,∴∠ABC=∠ACB,∵BE平分∠ABC,CE平分∠ACB,∴∠EBC=,,∴∠EBC=∠ECB,∴EB=EC,∴AE垂直平分BC,∴AD⊥BC.30.解:(1)解得,∵若关于x、y的二元一次方程组的解都为正数,∴,解得:a>1;(2)∵二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,这个等腰三角形的周长为12,∴2(a﹣1)+a+2=12,解得:a=4,∴x=3,y=6,故3,3,6不能组成三角形,∴2(a+2)+a﹣1=12,解得:a=3,∴x=2,y=5,故2,5,5能组成等腰三角形,∴a的值是3.31.证明:∵∠1=∠2,∴DB=CD,在△ABD和△ACD中,,∴△ABD≌△ACD(SAS),∴AB=AC.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等腰三角形例1. 如图在在△ABC 中,AB=AC ,点D 在AC 上,且DB=BC=AD ,求△ABC 各角的度数。
DCB A例2. 如图:△ABC 中,AB=AC,PB=PC .求证:AD ⊥BC例3. 已知如图在△ABC 中,AB =AC ,BD 、CE 是两条角平分线,并且BD 、CE 相交于点 O 。
求证:OB=OC 。
O D E CBA21例4. 如图,ΔABC 是等腰直角三角形,∠BAC=90°,BD 平分∠ABC 交AC 于点D ,CE 垂直于BD ,交BD 的延长线于点E 。
求证:BD=2CE 。
演练方阵A 档(巩固专练)1.等腰直角三角形的底边长为5cm ,则它的面积是 ( )A .25cm 2B .12.5cm 2C .10cm 2D .6.25cm 2 2.等腰三角形的两边长分别为25cm 和13cm ,则它的周长是 ( )A .63cmB .51cmC .63cm 和51cmD .以上都不正确 3.△ABC 中,AB =AC ,D 是AC 上一点,且AD =BD =BC ,则∠A 等于 ( )A.36°B.45°C.90°D.135°4. 判定两个等腰三角形全等的条件可以是()。
A、有一腰和顶角对应相等B、有两边对应相等C、有顶角和一个底角对应相等D、有两角对应相等5. 等腰三角形一腰上的高线与底边的夹角等于()A、顶角B、底角C、顶角的一半D、底角的一半6. 在等腰三角形ABC中,∠A与∠B度数之比为5∶2,则∠A的度数是()A、100°B、75°C、150°D、75°或100°7. 在△ABC中,AB=AC,下列推理中错误的是()。
A、如果AD是中线,那么AD⊥BC,∠BAD=∠DACB、如果BD是高,那么BD是角平分线C、如果AD是高,那么∠BAD=∠DAC、BD=DCD、如果AD是角平分线,那么AD也是BC边的垂直平分线8. 如图,P、Q是△ABC边BC上的两点,且QC=AP=AQ=BP=PQ,则∠BAC=()A、1250B、1300C、900D、12009. 如图,△ABC中,AB=AC,BD、CE为中线,图中共有等腰三角形()个。
A、3个B、4个C、5个D、6个10. 如图,AB=AC,AE=EC,∠ACE=280,则∠B的度数是()A、600B、700C、760D、450B档(提升精练)1. 已知等腰三角形的一边长为5cm,另一边长为6cm,则它的周长为。
2. 已知等腰三角形的一边长为4cm,另一边长为9cm,则它的周长为。
3. 等腰三角形底边长为5cm,一腰上的中线把其周长分为两部分的差为3cm.则腰长为4. 在等腰三角形中,设底角为0x,顶角为0y,用含x的代数式表示y,得y= ;用含y的代数式表示x,则x= 。
5. 有一个角等于50°,另一个角等于__________的三角形是等腰三角形.6. 如图,∠A=15°,AB=BC=CD=DE=EF,则∠GEF=7. 有一个内角为40°的等腰三角形的另外两个内角的度数为 .140°呢8. 等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为9. 如果等腰三角形的三边均为整数且它的周长为10cm,那么它的三边长为10. 如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60 ,且DE=1,则边BC的长为.C档(跨越导练)1. 如图,△ABC中,AB=AC,∠A=36°,BD、CE分别为∠ABC与∠ACB的角平分线,且相交于点F,则图中的等腰三角形有()A. 6个B. 7个C. 8个D. 9个A36°E DFB C2. 选择题:等腰三角形底边长为5cm,一腰上的中线把其周长分为两部分的差为3cm,则腰长为()A. 2cmB. 8cmC. 2cm或8cmD. 以上都不对3. 如图,ABC ∆是等边三角形,BC BD 90CBD ==∠,,则1∠的度数是________。
CA 1DB2 34. 如图,已知在等边三角形ABC 中,D 是AC 的中点,E 为BC 延长线上一点,且CE =CD ,DM ⊥BC ,垂足为M 。
求证:M 是BE 的中点。
E5. 如图,已知:ABC ∆中,AC AB =,D 是BC 上一点,且CA DC DB AD ==,,求BA C ∠的度数。
ABCD6. 已知:如图,ABC ∆中,AB CD AC AB ⊥=,于D 。
求证:DCB 2BAC ∠=∠。
C7. 已知:如图,在△ABC 中,AB =AC ,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,E 、F 分别是垂足。
求证:AE =AF 。
AE FBD8. 如图,ABC ∆中,100=∠=A AC AB ,,BD 平分ABC ∠。
求证:BC BD AD =+。
E FC9. 求证:等腰三角形两腰中线的交点在底边的垂直平分线上.10. ABC ∆中,120A AC AB =∠=,,AB 的中垂线交AB 于D ,交CA 延长线于E ,求证:BC 21DE =。
等腰三角形参考答案例1 【答案】解:若等腰三角形的一个顶角为︒80,则设它的底角为x2x+︒80=︒180 x = ︒50所以其余两个角的大小分别为︒50、︒50。
若等腰三角形的一个底角为︒80,则设它的顶角为x x + 2︒⨯80=︒180 x = ︒20所以其余两个角的大小分别为︒20、︒80。
例2【答案】解:∵AB=AC ,DB=BC=AD (已知)∴∠ABC=C ∠=BDC ∠,ABD A ∠=∠(等边对等角)∵︒=∠+∠+∠180C ABC A ,︒=∠+∠+∠180DBC C BDC 又∵ABD A BDC ∠+∠=∠(三角形外角性质) ∴DBC ABD A ∠=∠=∠∴︒=∠=∠=∠362121C ABC A ∴︒=∠︒=∠︒=∠72,72,36C ABC A例3【答案】证明:在中和APC∆∆APB ⎪⎩⎪⎨⎧===PC PB AP AP ACAB∴APC APB ∆≅∆(SSS ) ∴CAP BAP ∠=∠即AD 为△ABC 中A ∠的平分线 又∵AB=AC ∴AD ⊥BC例4【答案】证明:延长BA,CE交于点F,在ΔBEF和ΔBEC中,∵∠1=∠2,BE=BE,∠BEF=∠BEC=90°,∴ΔBEF≌ΔBEC,∴EF=EC,从而CF=2CE。
又∠1+∠F=∠3+∠F=90°,故∠1=∠3。
在ΔABD和ΔACF中,∵∠1=∠3,AB=AC,∠BAD=∠CAF=90°,∴ΔABD≌ΔACF,∴BD=CF,∴BD=2CE。
演练方阵A档(巩固专练)1【答案】D2【答案】C3【答案】A4【答案】A5【答案】C6【答案】D7【答案】B8【答案】D9【答案】D10【答案】CB档(提升精练)1【答案】16 cm 17 cm2【答案】22 cm3【答案】8 cm4【答案】180-2x (180-y)/25【答案】50°或 65°6【答案】75°7【答案】40°,100°或70°,70°8【答案】50°或 130°9【答案】3cm,3cm,4cm或4cm,4cm,2cm10【答案】3C 档(跨越导练)1.【答案】C2.【答案】B3.【答案】解:因为ABC ∆是等边三角形所以60ABC BC AB =∠=,因为BC BD =,所以BD AB = 所以23∠=∠在ABD ∆中,因为60ABC 90CBD =∠=∠, 所以150ABD =∠,所以 152=∠ 所以75ABC 21=∠+∠=∠4.【答案】证明:因为三角形ABC 是等边三角形,D 是AC 的中点所以∠1=21∠ABC 又因为CE =CD ,所以∠CDE =∠E 所以∠ACB =2∠E 即∠1=∠E所以BD =BE ,又DM ⊥BC ,垂足为M所以M 是BE 的中点 (等腰三角形三线合一定理)5.【答案】解:因为AC AB =,所以C B ∠=∠因为DB AD =,所以C DAB B ∠=∠=∠;因为CD CA =,所以CDA CAD ∠=∠(等边对等角) 而 DAB B ADC ∠+∠=∠ 所以B DAC B ADC ∠=∠∠=∠22, 所以B 3BAC ∠=∠又因为180=∠+∠+∠BAC C B即180B 3C B =∠+∠+∠ 所以36B =∠ 即求得108BAC =∠6.【答案】证明:过点A 作BC AE ⊥于E ,AC AB =所以BAC 2121∠=∠=∠(等腰三角形的三线合一性质) 因为90B 1=∠+∠又AB CD ⊥,所以90CDB =∠所以90B 3=∠+∠(直角三角形两锐角互余) 所以31∠=∠(同角的余角相等) 即DCB 2BAC ∠=∠7.【答案】证明:因为AC AB =,所以C B ∠=∠又因为AC DF AB DE ⊥⊥, 所以90CFD BED =∠=∠ 又D 是BC 的中点,所以DC DB = 所以)AAS (CFD DEB ∆∆≅ 所以CF BE =,所以AF AE =8.【答案】 证明一:在BC 上截取BD BF BA BE ==,,连结DE 、DFE FC在ABD ∆和EBD ∆中,BD BD 21BE BA =∠=∠=,,80DEF 100A BED DE AD )SAS (EBD ABD =∠∴=∠=∠=∴∆≅∆∴,又100A AC AB =∠=, 40)100180(21C ABC =-=∠=∠∴ 20402121=⨯=∠=∠∴ 而BF BD = 80)20180(21)2180(21BDF BFD =-=∠-=∠=∠∴ADBD FC BF BC FCDF DE AD FC DF C FDC 404080C DFE FDC 40C 80DFE DFDE 80DFE DEF +=+=∴===∴=∴∠=∠∴=-=∠-∠=∠∴=∠=∠∴=∴=∠=∠∴,即BC BD AD =+证明二:延长BD 到E ,使DE =AD ,连结CE ,作DF 平分BDC ∠交BC 于F 。
E由证明一知:100A 2021=∠=∠=∠,则有12060180BDC 603660201001803=-=∠=∠=∠=--=∠,, DF 平分 6054BDC=∠=∠∴∠606543=∠=∠=∠=∠∴,在ABD ∆和FBD ∆中 43BD BD 21∠=∠=∠=∠,, )ASA (FBD ABD ∆≅∆∴100A BFD FD AD =∠=∠=∴,,而DE DF DE AD =∴=,在DEC ∆和DFC ∆中,DC DC 65DF DE =∠=∠=,, )SAS (DFC DEC ∆≅∆∴80100180BFD 180DFC E =-=∠-=∠=∠∴ 在BCE ∆中,803202=∠=∠, BCE E BCE ∠=∠∴=∠∴,80BC BD AD BE BC =+∴=∴,9.【答案】已知:如图,在ABC ∆中,AC AB =,D 、E 分别为AC 、AB 边中点,BD 、CE 交于O 点。
