冬雷-北京理工大学自动化学院

合集下载

基于灰色关联的雷达无源干扰识别方法[发明专利]

(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号 (43)申请公布日 (21)申请号 202010771680.2(22)申请日 2020.08.04(71)申请人北京理工大学地址 100081 北京市海淀区中关村南大街5号(72)发明人李阳　李枫　王楚媛　张洪纲　张哲　龙腾　(74)专利代理机构北京理工大学专利中心11120代理人代丽　郭德忠(51)Int.Cl.G01S 7/36(2006.01)G01S 7/41(2006.01)(54)发明名称基于灰色关联的雷达无源干扰识别方法(57)摘要本发明提供了一种基于灰色关联的雷达无源干扰识别方法，结合多种特征提取和分析，能够实现对雷达无源干扰的识别。

本发明基于灰色关联进行分类器构建，结合了特征提取的全面性和分类器设计的高效性，从而使得通过分类器的特征匹配结果的准确率和实时性很高，进而得到的识别结果准确性特别高，能够解决雷达对无源干扰识别的需求。

权利要求书1页说明书7页附图5页CN 112034428 A 2020.12.04C N 112034428A1.一种基于灰色关联的雷达无源干扰识别方法，其特征在于，包括如下步骤：以实测数据中的真实目标的雷达回波信号以及雷达无源干扰目标的回波信号作为样本数据，分别进行标记，对应不同属性；提取带标记样本数据的一维距离像的静态特征、多普勒频谱特征以及邓氏平均灰色关联度特征，构成带标记向量样本；将利用带标记向量样本构建分类器；根据待识别目标的距离多普勒量测信息，定位待识别目标在数据中的位置并截取相应的目标数据；提取目标数据的一维距离像的静态特征、多普勒频谱特征以及邓氏平均灰色关联度特征形成目标向量；将目标向量送入构建好的分类器，分类器对待识别目标的属性进行判别并输出，完成识别。

2.如权利要求1所述的基于灰色关联的雷达无源干扰识别方法，其特征在于，所述雷达真实目标为舰船；所述雷达无源干扰包括箔条和角反射器。

北理工-计算电磁学实验报告材料(2017.6)

本科实验报告实验名称：计算电磁学实验（MATLAB实现）2.1.1subplot(211);w=2;x = -2*pi/w:0.01:2*pi/w; x1=w*x;plot(x,cos(x1));title('cos(wx)');grid onsubplot(212);w=1;x = -2*pi/w:0.01:2*pi/w; x1=w*x;plot(x,sin(x1));title('sin(wx)');grid on2.1.2k=1;w=1;u=2*pi/k;T=2*pi/w;x=-u:0.01:u;plot(x,cos(x));title('cos(-kx)');grid on2.1.3k=10;w=1;u=2*pi/k;T=2*pi/w;x=-u:0.01:u;xlabel('x');ylabel('y(x)');for t=0:0.1:2*Ty=cos(w*t-k*x);plot(x,y);pause(0.1);end;2.1.4w=2;x = -20*pi/w:pi/2:20*pi/w;x1=w*x;plot(x,cos(x1),'.');ylim([-1.5,1.5]);title('cos(wx),¼ä¸ôÈ¡¦Ð/2'); grid on2.1.5n0=10;J0=2.35;dt=0.01;w=pi;i=1;for n=-10*n0:0.01:10*n0 %(U(ndt)if n<0u(i)=0; %iÊÇÊý×éµÄË÷Òý£¬Ö»ÄÜÊÇÕýÕûÊý,iÒªÉè³õÊ¼Öµ£¬³õÊ¼ÖµÖ»ÄÜÎª1 elseif n<=n0;u(i)=n/n0;elseu(i)=1;endi=i+1;endsubplot(211);n=-10*n0:0.01:10*n0;plot(n,u);xlabel('n');ylabel('U(n¡÷t)');axis([-50 50 -1.5 1.5]);grid onclear;%È¡n0=10µÄÊ±ºòÇ°ÃæµÄÊý¾ÝÒªÇåÁã£¬²»È»Êý×é¹æÄ£»á´ÓÉÏÃæ¼Ì³ÐÏÂÀ´n0=10;J0=2.35;dt=0.01;w=pi;i=1;for n=-100*n0:dt:100*n0;if n<0Jz(i)=0;elseif n*dt<0Jz(i)=0;elseif n*dt<=n0Jz(i)=J0*(n0-n)/n0*sin(w*n*dt);elseJz(i)=J0*sin(w*n*dt);endendi=i+1;endsubplot(212);n=-100*n0:0.01:100*n0;plot(n,Jz);xlabel('n');ylabel('Jz(n)');grid on;2.1.6dt=0.01;x=-10:dt:10;y=sin(x);i=1;for x=-10:dt:10dy=sin(x+dt/2)-sin(x-dt/2); d(i)=dy/dt;i=i+1;endx=-10:dt:10;plot(x,d);title('sin(x)的导数');xlabel('x');ylabel('dy/dx');2.1.7dt=0.01;x=-10:dt:10;i=1;y1=0;for x=-0:dt:pi-dt;s=sin(x+dt/2)*dt;y1=y1+si=i+1;endy1clear;dt=pi/120;x=-10:dt:10;y2=0;i=1;s=0;for x=-0:dt:2*pi-dt;s=sin(x+dt/2)*dty2=y2+s;i=i+1;endy2得y1=2，y2=4.0804e-16clear;dt=pi/60;i=1;j=1for x=0:dt:4*pi-dt;yt=0;for t=0:dt:x-dt;s=sin(t+dt/2);yt=yt+s;i=i+1;endy(j)=yt;j=j+1;endx=0:dt:4*pi-dt;plot(x,y);xlabel('x');ylabel('y(x)');grid on;2.1.8【用meshgrid】[x,y] = meshgrid(-1:0.4:5,-1:0.4:3); u = x.*y;v = 3.*x-y.^2;figurequiver(x,y,u,v)【不用meshgrid】x=-1:0.4:5;y=-1:0.4:3;m=length(x);%列n=length(y);%行u=zeros(n,m);for i=1:nu(i,:)=x*y(i);%':'表所有，u（列，行） v(i,:)=3*x-y(i)^2;endquiver(u,v)2.1.9（1）dt=-0.01;i=1;j=1;y1=0; %删双层循环的时候忘记移出来了for x=5:dt:3-dt;x0=x+dt/2;s=(1.5.*x0.*(x0-1)+(3.*x0-2.25.*(x0-1)^2).*1.5).*dt %大中小括号在Matl里含义不同，数学表达式一律用小括号y1=y1+s;i=i+1;endy1y1=-10.0000（2）dt=-0.01;i=1;y1=0;s=0;for y=6:dt:3-dt;y0=y+dt/2;s=(15-y0.^2).*dty1=y1+s;i=i+1;end%y1y2=0;s=0;for x=5:dt:3-dt;x0=x+dt/2;s=(3.*x0).*dty2=y2+s;i=i+1;end%y2y=y1+y2;yy = -6.00002.1.10dt=0.1;[x,y]=meshgrid(-1-dt:dt:5+dt,-1-dt:dt:3+dt);%meshgrid就是构建二维数组的函数dux=((x+dt).*y-(x-dt).*y)/(2*dt);dvy=((3.*x-(y+dt).^2)-(3.*x-(y-dt).^2))/(2.*dt);divF=dux+dvy;contour3(x,y,divF,250);title('É¢¶È');xlabel('x');ylabel('y');zlabel('z');figure(2); %单开一个网格dt=3.*dt;[x,y,z]=meshgrid(-1-dt:dt:5+dt,-1-dt:dt:3+dt,-10:dt:10);Size=size(x);%计算x矩阵每维的长度，将长度记在一个矩阵里empty=zeros(Size(1),Size(2),Size(3));%建立一个和Size矩阵一样大的空矩阵p=empty;q=empty;r=((3.*(x+dt)-y.^2)-(3.*(x-dt)-y.^2))/(2.*dt)-(x.*(y+dt)-x.*(y-dt))/( 2.*dt);quiver3(x,y,z,p,q,r,'color',[0,0,0]./255);%quiver3是建立向量三维坐标，contour3是普通三维网格或者标量图title('旋度');xlabel('x');ylabel('y');zlabel('z');grid off;2.1.11clear;f0=3e6;w0=2*pi*f0;T=1/f0;dt=1e-9*pi;t=-5*T-dt:dt:5*T+dt;y=sin(w0*t)+2*cos(2*w0*t);subplot(211);plot(t,y);set(gca,'XTick',[-5e-7*pi:1e-7*pi:5e-7*pi]);set(gca,'xtickLabel',{'-5¦ÐE-7','-4¦ÐE-7','-3¦ÐE-7','-2¦ÐE-7','-¦ÐE-7 ','0','¦ÐE-7','2¦ÐE-7','3¦ÐE-7','4¦ÐE-7','5¦ÐE-7'});%GCA用法示例set(gca,'box','on','xlim',[02*pi],'YDir','reverse')后，图形变成下图所示，出现坐标边界（box），x轴显示坐标范围缩小（xlim）,y轴方向反转（ydir）xlabel('t');ylabel('y(t)');subplot(212);i=0;for w=-5e7:1e5:5e7;%取值和之前的y计算的取值点必须相同，不然没法用上一问算出的y 矩阵i=i+1;dF(i,:)=y.*exp(-1j.*w.*t).*dt;%t和y都是上一问已经得到的矩阵，此处用上可以省略很多运算endF=sum(dF,2);%sum(x)列求和,sum(x,2)行求和,sum(x(:))矩阵求和w=-5e7:1e5:5e7;plot(w,abs(F));xlabel('w');ylabel('|F(w)|');2.1.12clear;F0=2;t0=0.1;d0=1;dt=0.01;i=0;for n=-10:dt:400;i=i+1;if n<0F(i)=0;elseF(i)=F0.*exp(-(n.*dt-t0).^2/(2.*d0.^2));endendn=-10:dt:400;plot(n,F);axis([-10 500 0 2.1]);title('F(n)');clear;F0=2;t0=4;d0=1;dt=0.1;i=0;for n=-10:1*dt:100 %老师讲n的步长要和dt相同i=i+1;if n<0F(i)=0;elseF(i)=F0.*exp(-(n.*dt-t0).^2/(2.*d0.^2));endendn=-10:1*dt:100;l=0;for w=-20:0.5*dt:20l=l+1;dF(l,:)=F.*exp(-1j.*w.*n.*dt).*dt;endFw=sum(dF,2);w=-20:0.5*dt:20;plot(w,abs(Fw));xlabel('w');ylabel('F(w)');2.1.13clear;subplot(211);F0=2;t0=4;d0=1;dt=0.1;i=0;w0=20;for n=-10:1*dt:100i=i+1;if n<0F(i)=0;elseF(i)=F0.*exp(-(n.*dt-t0).^2/(2.*d0.^2)).*cos(w0.*n.*dt);endendplot(F);title('时域');subplot(212);n=-10:1*dt:100;l=0;for w=-40:0.5*dt:40l=l+1;dF(l,:)=F.*exp(-1j.*w.*n.*dt).*dt; endFw=sum(dF,2);w=-40:0.5*dt:40;plot(w,abs(Fw));xlabel('w');ylabel('F(w)');title('频域');2.1.11FFTw0=128;Fs=256;%采样频率N=256; %采样点数n=[0:1/Fs:N/Fs]; %采样时间间隔作为坐标s=sin(w0.*n)+2.*cos(2.*w0.*n);Y=fft(s,N);Ayy=abs(Y); %取模Ayy=Ayy/(N/2); %换算实际幅度Ayy(1)=Ayy(1)/2;F=([1:N]-1)*Fs/N; %换算实际频率值stem(F(1:N/2),Ayy(1:N/2)); %显示换算后模值结果title('FFT算频谱');clear;f0=3e6;w0=2*pi*f0;T=1/f0;dt=1e-9*pi;t=-5*T-dt:dt:5*T+dt;Fs=f0; %这个就是保证FFT出来每个点的间隔<代表>1Fs/(2*times) // %所以Fs要关联时域点数即关联T 因为length(t)是通过T限定的 //times = 4;N = times * length(t) * 2;%最小取样点数1064*2 //y=sin(w0*t)+2*cos(2*w0*t); %【时域图】subplot(3,2,[1,2]);plot(t,y);set(gca,'XTick',[-5e-7*pi:1e-7*pi:5e-7*pi]);set(gca,'xtickLabel',{'-5πE-7','-4πE-7','-3πE-7','-2πE-7','-πE-7' ,'0','πE-7','2πE-7','3πE-7','4πE-7','5πE-7'});xlabel('t');ylabel('y(t)');subplot(3,2,[3,4]); %【以傅里叶法计算频谱】i=0;for w=-5e7:1e5:5e7;i=i+1;dF(i,:)=y.*exp(-1j.*w.*t).*dt;endF=sum(dF,2);w=-5e7:1e5:5e7;plot(w,abs(F));xlabel('ω');ylabel('|F(ω)|');% n=[-N/Fs:1/Fs:N/Fs];% s=sin(w0.*n)+2.*cos(2.*w0.*n);subplot(3,2,5); %【以FFT函数算频谱】Y=fft(y,N);A=abs(Y);A=A/(N/2);%xinhaozhenfuA(1)=A(1)/2;%zhiliuchuxinhaozhenfuF=(([1:N/2]-1))*Fs / ( 2 * times ) / 10;% Fs/(2*times)就是f轴间隔,所以不需要除以N,除以10因为时域点数是10个周期的 //plot(F(1:N/2),A(1:N/2));xlim([0 1e7]);xlabel('f / Hz');subplot(3,2,6); %【换成角频率的】FF = F * 2 * pi;plot(FF,A(1:N/2));xlim([0 5e7]);xlabel('ω');一维FDTDclear;cc = 3e8;m0 = 4*pi*1e-7;eps0 = 1/cc/cc/m0;freq = 3e6;%频率wavelength = cc/freq;%波长dx = wavelength/20;dt = dx/cc/2;maxz = 200;nmax = 300;%演示时间ex = zeros(maxz,1);hy = zeros(maxz,1);vc = 2:(maxz-1)for n = 1:nmax % 边界条件ex1=ex(1);ex2=ex(2);exmaxz_1=ex(maxz-1);exmaxz=ex(maxz);ex(vc)=ex(vc)-dt/eps0/dx*(hy(vc)-hy(vc-1));ex(1)=ex2+(cc*dt-dx)/(cc*dt+dx)*(ex(2)-ex1);ex(maxz)=exmaxz_1+(cc*dt-dx)/(cc*dt+dx)*(ex(maxz-1)-exmaxz);ex(src)=cos(2*pi*freq*n*dt);hy1=hy(1);hy2=hy(2);hymaxz_1=hy(maxz-1);hymaxz=hy(maxz);hy(vc)=hy(vc)-dt/m0/dx*(ex(vc+1)-ex(vc));hy(1)=hy2+(cc*dt-dx)/(cc*dt+dx)*(hy(2)-hy1);hy(maxz)=hymaxz_1+(cc*dt-dx)/(cc*dt+dx)*(hy(maxz-1)-hymaxz);figure(1)plot(ex);title('ex');axis([1 maxz -2 2])pause(0.05);end二维FDTDZ=200;c=3*10^8;dx=0.005;dt=dx/(2*c);u0=(4*pi)*1e-7;s=(1/(36*pi))*1e-9; n0=100;Ca=1;Cb=dt/(s*dx);Da=1;Db=dt/(u0*dx);Ex=zeros(Z+1,Z+1);Ey=zeros(Z+1,Z+1);Hz=zeros(Z+1,Z+1);Hzzz=zeros(Z+1,Z+1);for n=0:400for y=2:Z+1 %更新Exfor x=1:Z+1Ex(x,y)=Ca*Ex(x,y)+Cb*(Hz(x,y)-Hz(x,y-1));endendfor y=1:Z+1 %更新Eyfor x=2:Z+1Ey(x,y)=Ca*Ey(x,y)-Cb*(Hz(x,y)-Hz(x-1,y));endendfor y=1:Z %更新Hzfor x=1:ZHz(n0,n0)=sin(1.20*pi*10^11*n*dt);Hz(x,y)=Da*Hz(x,y)-Db*(Ey(x+1,y)-Ey(x,y)-Ex(x,y+1)+Ex(x,y));endendfor y=2:Z %边界条件Hz(1,y)=Hzzz(2,y)+(c*dt-dx)/(c*dt+dx)*(Hz(2,y)-Hzzz(1,y)); Hz(Z+1,y)=Hzzz(Z,y)+(c*dt-dx)/(c*dt+dx)*(Hz(Z,y)-Hzzz(Z+1,y));endfor x=2:ZHz(x,1)=Hzzz(x,2)+(c*dt-dx)/(c*dt+dx)*(Hz(x,2)-Hzzz(x,1)); Hz(x,Z+1)=Hzzz(x,Z)+(c*dt-dx)/(c*dt+dx)*(Hz(x,Z)-Hzzz(x,Z+1));endHz(1,1)=Hzzz(2,2)+(c*dt-sqrt(2)*dx)/(c*dt+sqrt(2)*dx)*(Hz(2,2)-Hzzz(1,1));Hz(Z+1,1)=Hzzz(Z,2)+(c*dt-sqrt(2)*dx)/(c*dt+sqrt(2)*dx)*(Hz(Z,2)-Hzzz (Z+1,1));Hz(1,Z+1)=Hzzz(2,Z)+(c*dt-sqrt(2)*dx)/(c*dt+sqrt(2)*dx)*(Hz(2,Z)-Hzzz (1,Z+1));Hz(Z+1,Z+1)=Hzzz(Z,Z)+(c*dt-sqrt(2)*dx)/(c*dt+sqrt(2)*dx)*(Hz(Z,Z)-Hzzz(Z+1,Z+1));for i=20:30; %加金属介质for j=80:120;Ex(i,j)=0;Ey(i,j)=0;endendHzzz=Hz;x=1:Z+1;y=1:Z+1;surf(Hz);colormap(winter);colorbar;shading interpaxis([1 Z+1 1 Z+1 -0.5 0.5]); xlabel('x'),ylabel('y');pause(0.00001);endHFSS模拟焦点处x坐标为5.732，截图的时候截早了。

决赛入围奖名单【全国第四届高等学校自制实验教学仪器设备评选活动】

全国第四届高等学校自制实验教学仪器设备评选活动
决赛入围奖公示
“全国第四届高等学校自制实验教学仪器设备评选活动”共计收到来自全国192所高等院校528个有效参赛作品。

经评审活动组委会74名专家评审，来自全国136所高等院校274个作品入围决赛。

现将“决赛入围奖”名单公示如下（见附件），公示期为10天。

在公示期内，任何单位或个人如对公示的参评作品持有异议，可以书面形式（邮寄或传真）向组委会具名提出（如实提供姓名、工作单位、联系电话）。

经查明确有弄虚作假者、或不符合参评条件者，取消其决赛资格。

中国高等教育学会
2016年9月18日
附件：全国第四届高等学校自制实验教学仪器设备评选活动“决赛入围奖”公示结果一、电类入围作品：102个（排序按照作品完成单位字母A~Z排列）
二、机类入围作品：70个（排序按照作品完成单位字母A~Z排列）
三、其他类入围作品：82个）（排序按照作品完成单位字母A~Z排列）
四、实验教学软件类入围作品：20个（排序按照作品完成单位字母A~Z排列）。

电偶极子模型在天体光谱中的应用

电偶极子模型在天体光谱中的应用王菲【摘要】与电介质中非极性分子的位移极化和极性分子的转向极化不同的是,天体致密大气层中的原子及分子间因碰撞也会产生电偶极矩,进而出现吸收过程,是研究带外行星和冷白矮星等天体光谱的重要理论基础.以冷白矮星为例,介绍其大气层中大量原子分子对之间的碰撞诱导偶极矩与电磁辐射相互作用产生的连续谱吸收.【期刊名称】《大学物理》【年(卷),期】2019(038)002【总页数】5页(P55-59)【关键词】碰撞诱导吸收;偶极矩;白矮星【作者】王菲【作者单位】北京理工大学物理学院,北京 100081【正文语种】中文【中图分类】P144.1在行星和恒星的致密大气层中，大量碰撞相互作用的原子、分子会以原子分子对的形式形成超分子复合体，它们之间的碰撞相互作用改变了电荷分布，从而产生电偶极矩，称为碰撞诱导偶极矩.是极性分子固有电偶极矩和非极性分子在外电场中出现感生电偶极矩之外，又一种产生电偶极矩的机制.1 天体大气层中的电偶极子在天体高密度大气层中形成的超分子复合体与单独存在的原子和分子性质不同，原本禁戒的跃迁和过程就有可能出现，因碰撞而产生的诱导偶极子还与电磁辐射相互作用产生吸收连续谱，在高温下可从微波、远红外区扩展至近红外、甚至可见光频率[1]，这一过程被称为碰撞诱导吸收(CIA)[2-5] .研究碰撞产生的电偶极子及其相关吸收过程对于天体光谱的研究乃至天体的演化过程都具有十分重要的价值.例如，冷白矮星高密度的氢氦大气层中的碰撞诱导吸收过程就强烈地抑制了红外发射[6]，导致其发射谱与预期的内核黑体谱有很大不同.在斯隆数字巡天(SDSS)中观测到大量白矮星，其中包括温度只有几千K的冷白矮星[7]，它们正在进一步冷却中，冷却率与其大气温度和组成以及大气不透明度有关，并直接决定着冷白矮星年龄.冷白矮星的大气层主要由氢分子、氦原子、氢原子、氢离子、氦离子和电子组成.其中，氦原子和氢分子都不吸收红外辐射，而在白矮星致密大气层中剧烈碰撞产生的一些分子对才是内核红外辐射被吸收的主要原因，这些分子对包括H2-H2，H2-He，H-He，D2-D2等.形成双分子复合体的普通分子与它们单独存在时的性质截然不同，即便对于那些非极性分子，只要气体密度足够高，当它们碰撞形成双分子复合体时，受到分子间和分子内动力学的影响，包括交换力，色散力，多极诱导和分子框架扭曲等的各种相互作用，就会改变电荷分布，从而产生碰撞诱导偶极矩，那些对于单个分子来说被选择定则所禁止的振转跃迁和电子谱带，在分子对系统中就会出现，进而吸收红外辐射.图1 给出了碰撞诱导产生的H-He分子对的偶极子吸收光子的过程.通过分析碰撞诱导吸收过程所产生的光谱不透明度随频率和温度的变化规律，可以揭示出冷白矮星的大气光谱规律和演化信息，也是天体物理学与原子分子物理学交叉的前沿课题.图1 碰撞诱导产生的H-He分子对的偶极子吸收光子示意图.图中μ为碰撞诱导偶极矩Saumon等人[8]结合褐矮星的观测光谱和大气模型，通过其近红外区碰撞诱导吸收谱研究分析了褐矮星的大气组成.Hodgkin等人[6]则进一步发现最古老亦即最冷的白矮星大气主要由氦和氢组成，白矮星氦核的大部分红外发射都被由氦-氢混合气体组成的薄而高密度的致密层过滤，导致白矮星的发射观测谱与熟悉的黑体谱显示出很大不同.因此高温宽频范围的碰撞诱导吸收谱的理论研究[9-12]成为研究天体光谱的重要依据.碰撞诱导吸收过程的实验室测量所用气体的密度通常比行星和恒星的吸收区大气密度还要高，这是因为实验室气室尺度比真实大气层的典型光程长度要小得多，要想观测到明显的碰撞诱导吸收过程就必须有足够长的光程长度或者足够高的气体密度.而实验室中为提高气体密度所采用的高压则有可能引入多体效应，这些多体效应对于分析行星和恒星大气是十分不利的.因此，碰撞诱导吸收过程的实验室测量十分困难.近年来发展的各种量子力学计算方法已可以很好地处理分子间弱范德瓦尔斯相互作用，我们与Frommhold等人合作[2-5]采用第一性原理计算并研究了H2-He和H2-H2体系的精确相互作用偶极面和碰撞诱导吸收谱，其中氢分子对在300 K的碰撞诱导吸收谱计算结果与实验室结果符合得非常好.本文将采用同一方法，计算高温高频下H2-H2的碰撞诱导吸收谱.2 计算白矮星大气吸收谱的理论方法白矮星大气吸收谱的理论研究方法通常基于第一性原理，结合从头算获得的诱导偶极矩和势能面，假定所有势能面和偶极面都与原子核运动无关，采用玻恩-奥本海默近似处理原子核和电子的运动，即可计算不同温度下冷白矮星及带外行星大气层分子对的碰撞诱导吸收谱及大气不透明度.以氢分子对H2-H2为例，碰撞相互作用下的两个氢分子会吸收一个光子：H2(ν1j1)+H2 (ν2j2)+KE+ћω→(1)这里ν和j分别表示分子的振转量子数，KE为相对移动的动能；ћω代表光子.为计算碰撞诱导吸收谱，需建立振转态—态分子散射过程，并在描述分子间散射的哈密顿量中加入微扰算符以描述分子复合体与弱电磁场间的耦合，即光子场通过微扰与碰撞诱导产生的分子对瞬间偶极子相耦合.偶极分量μx、μy、μz转换为球坐标系表示：μ0=μz，μ±1=∓(2)偶极球张量分量A即为(3)上式中矢量耦合函数定义为C(ΔL1;MΛMν)Yλ1M1(Ω1)Yλ2M2(Ω2)YLM(Ω)(4)式中Ylml(Ω)为球谐函数，C为C.G.系数.计算中考虑了15个A系数：λ1λ2ΛL= 0001、0221、0223、2021、2023、2211、2233、0443、0445、4043、4045、2465、2467、4265、4267.其中后4个系数是高阶球分量贡献，对于分析高温高频下的碰撞诱导吸收谱具有十分重要的价值，所有15个系数中，最大的偶极球分量是4级诱导分量0223和2023.处理涉及振转激发态的分子体系时，采用各向同性势能面，并在7个不同核间距R(R=4、5、6、7、8、9、10玻尔)和氢分子8个不同键距r1、r2(r1,r2=0.942、1.111、1.280、1.449、1.787、2.125、2.463、2.801玻尔)下进行了计算.对于氢分子对H2-H2的碰撞诱导吸收谱，各向异性相互作用非常微弱，可以忽略.碰撞诱导吸收谱由大量混杂、重叠的谱线构成，这些谱线来自母分子的振转跃迁：(5)每个跃迁的偶极算符为BC′Cλ1λ2ΛL(R)=〉(6)决定分子散射过程的分子间作用势为〈ν1j1ν2j2|V000(r1，r2,R)|ν1j1ν2j2〉(7)由式(7)可得到初态散射波函数，末态与初态形式相同.在各向同性相互作用近似下，单个谱线的谱轮廓为ћ(8)这里S表示是相对于频率中心ωC′C的2π倍频移.频率中心ωC′C：ћ(9)式中E(ν,j)表示量子数为ν和j的振转态能量.碰撞诱导吸收线非常宽.高温下，碰撞诱导吸收谱是由许多重叠谱线构成的准连续谱.通常可用气体密度ρ的维里级数形式来表示吸收系数α(ω，T)：α(ω，T)=A(ω，T)ρ+B(ω，T)ρ2+C(ω，T)ρ3+…(10)线性依赖于密度的第一项来自单个分子的吸收(贝尔定律)，在氢分子情况下，频率位于红外，这一项为零.式(10)右侧第二项代表分子对的吸收，对于氢气，这一项由式(11)给出.由于贝尔定律并不考虑分子复合体的吸收，这一项的存在将使贝尔定律失效.可通过不同气体密度的测量将式(10)右侧第三项的三级吸收从一级和二级贡献中分离出来.这里主要考虑二重复合体产生的二级碰撞诱导吸收.计算所得的吸收系数α将通过密度平方ρ2归一.吸收谱是所有谱线(C’C)和偶极分量(S)的叠加：(11)其中NA是阿佛加德罗常数，Vg(ω,T)是谱线叠加贡献，具体形式为Vg (ω,T)=(12)其中Pi(T)表示分子i=1,2的振转初态跃迁率.3 氢分子对的碰撞诱导吸收谱氢分子是非极性分子，但是在天体大气环境下，由于气体密度足够高，氢分子间碰撞相互作用而形成的氢分子对复合体与氢分子的性质截然不同，在碰撞诱导下产生电偶极矩，从而吸收红外辐射，这些复合体(即氢分子对)内的分子会发生从低能态到高能态的跃迁.在这些分子中，产生电偶极矩的机制与产生范德瓦尔斯力的机制相同，诱导偶极子与电磁辐射相互作用所导致的吸收谱通常为连续谱，在高温下可从微波、远红外区域扩展至近红外、甚至可见光频率.原子对、分子对所形成复合体的不同运动自由度对应着不同频率范围的光谱带.通常与振动跃迁无关的碰撞诱导吸收谱对应着微波和远红外光谱区的平移或转动谱带，而典型的振动谱带则位于近红外区.图 2 氢分子对碰撞诱导吸收谱的相对吸收系数(温度从500 K到2800 K，频率从0到20 000 cm-1)图2中给出了温度从500 K到2 800 K、频率从0到20 000 cm-1范围的碰撞诱导吸收谱.纵坐标是将计算所得的吸收系数α对密度平方ρ2归一所得到的相对吸收系数.在图2的计算中，考虑了15个贡献较为重要的A系数，其中λ1λ2ΛL=2 465、2 467、4 265、4 267的贡献是首次包括在计算中，它们在低温时的贡献并不明显，但对于高温碰撞吸收谱的贡献将变得不可忽略，在所有这些A系数中，最大的偶极球分量是四级诱导分量0223和2023.我们注意到，随着温度的升高，各温度下的吸收峰整体显示出相同的轮廓，但是在不同的频率范围内，不同温度的吸收峰值有着不同的变化规律，例如0到2 500 cm-1频段内，吸收峰值随着温度升高而逐渐降低，但在15 000 cm-1到17 500 cm-1的频段内，峰值显然是随着温度升高而变大的.在17 500 cm-1到20 000 cm-1的频率区间内的弱吸收峰值甚至低于低频的吸收谷，并且在2 100 K到2 800 K的高温下这些弱吸收峰值已不明显，表明高频高温下的吸收是非常弱的碰撞诱导吸收过程.而2 800 K温度下的吸收谱对研究M型矮星具有十分重要的价值[13]，图2显示随着频率增大，吸收在光谱蓝翼逐渐减小.在这一区域的光谱强度对于行星研究十分重要，旅行者号空间探测器的探测表明，带外行星在这一频率范围内的发射谱仍需进一步分析研究[14].图2中给出的该区域数据将有助于进一步对吸收系数带间极值开展研究.图 3 高温下氢分子对碰撞诱导吸收谱曲线(温度从2 800 K到7 000 K，频率从0到10 000 cm-1)图3中给出了0到10 000 cm-1频率范围内从2 800 K到7 000 K的高温吸收谱.各温度下的吸收谱曲线均在2 000 cm-1和4 000 cm-1频率附近出现了吸收峰，不难发现，在2 800 K以上的高温情况下，各温度下的吸收峰整体依然显示出相同的轮廓，但与低温情况不同的是，0到3 000 cm-1频段的吸收峰明显低于3 000 cm-1到6 000 cm-1的吸收峰，且在整个频率范围内都显示出吸收峰随着温度升高而依次降低的明显趋势.这一温度范围内的碰撞诱导吸收谱的研究对研究白矮星大气谱具有非常重要的价值.其中3 800 K的H2-H2吸收谱可用于分析英国施密特望远镜(UKST)在金牛座中观测到的低光度[15]冷白矮星WD0346 + 246发射谱与预期的内核黑体谱存在的巨大差异[6].从图2和图3各温度的吸收谱曲线可以看出，吸收峰之间都有很深的吸收谷极小值，我们称之为带间极小值.随着温度升高，无论峰谷均迅速展宽，因而带间极小也变得更加平缓.目前已知的实验室测量均只针对强吸收，由于弱吸收很难测量，尚无吸收极小值附近的实验数据报道，而在天体观测中，吸收路径长度比传统实验室装置要大得多，因此天文观测中会出现吸收极小附近的吸收谱.以往，由于这些弱吸收谱是大量非常弱的谱贡献的叠加，很难进行精确的理论计算，那些对吸收峰可忽略不计的高阶偶极球分量(λ1+λ2> 2)，正是形成弱吸收谱的主要贡献，但在以往的研究中通常未能充分考虑它们的贡献.我们进一步考虑了高阶分量的贡献，计算所得的结果对进一步研究弱吸收谱具有十分重要的价值.【相关文献】[1] Frommhold L. Collision-Induced Absorption in Gases [M]. Cambridge: Cambridge University Press,2006：371-374.[2] Li X,Hunt K L C,Wang F,et al. Collision-Induced Infrared Absorption by Molecular Hydrogen Pairs at Thousands of Kelvin [J]. Int J Spectroscopy,2010(371201): 1-11.[3] Frommhold L,Abel M,Wang F,et al. Infrared atmospheric emission and absorption by simple molecular complexes,from first principles [J]. Molecular Physics,2010,108 (17): 2265-2272.[4] Frommhold L,Abel M,Wang F,et al. Collision-induced absorption at temperatures ofthousands of kelvin,from first principles,for astrophysical applications [J]. AIP Conference Proceedings,2010,1290(1): 219-230.[5] Abel M,Frommhold L,Wang F,et al. Collision-Induced Absorption by Supermolecular Complexes from a New Potential Energy and Induced Dipole Surface,Suited for Calculations up to Thousands of Kelvin [J]. AIP Conference Proceedings,2010,1290(1): 251-257.[6] Hodgkin S T,Oppenheimer R R,Hambly N C,et al. Infrared spectrum of an extremely cool white-dwarf star [J]. Nature,2000,403(1): 57-59.[7] Heller R,Homeier D,Dreizler S,et al.Spectral analysis of 636 white dwarf-M star binaries from the sloan digital sky survey[J].Astronomy & Astrophysics,2009,496(1): 191-205. [8] Saumon D,Marley M S,Abel M,et al.New H2 Collision-induced absorption and NH3 opacity and the spectra of the coolest brown dwarfs[J]. The AstrophysicalJournal,2012,750(1): 74.[9] Meyer W,Frommhold L. Collision-induced rototranslational spectra of H2-He from an accurate ab initio dipole moment surface [J]. Physical Review A,1986,34(4): 2771-2779. [10] Meyer W,Frommhold L,Birnbaum G. Rototranslational absorption spectra of H2-H2pairs in the far infrared [J]. Physical Review A,1989,39(5): 2434-2448.[11] Meyer W,Borysow A,Frommhold L. Absorption spectra of H2-H2 pairs in the fundamental band [J]. Physical Review A,1989,40(12): 6931-6949.[12] Meyer W,Borysow A,Frommhold L. Collision-induced first overtone band of gaseous hydrogen from first principles [J]. Physical Review A,1993,47(5): 4065-4077.[13] Borysow A,Jørgensen U G,Fu Y. High-temperature (1000-7000 K) collision-induced absorption of H2 pairs computed from the first principles,with application to cool and dense stellar atmospheres[J]. Journal of Quantitative Spectroscopy & Radiative Transfer,2001,68(3): 235-255.[14] Marten A,Baluteau J.P,Gautier D,et al.About unidentified features in the Voyager far infrared spectra of Jupiter and Saturn[J].Can.J.Phys.1983,61(10): 1455-1461.[15] 赵峥.《相对论、宇宙与时空》连载⑥——恒星演化的归宿(白矮星、中子星和黑洞)[J].大学物理,2009,38(6): 57-65.。

北京理工大学自动化学院人工智能专业2024年考研攻略

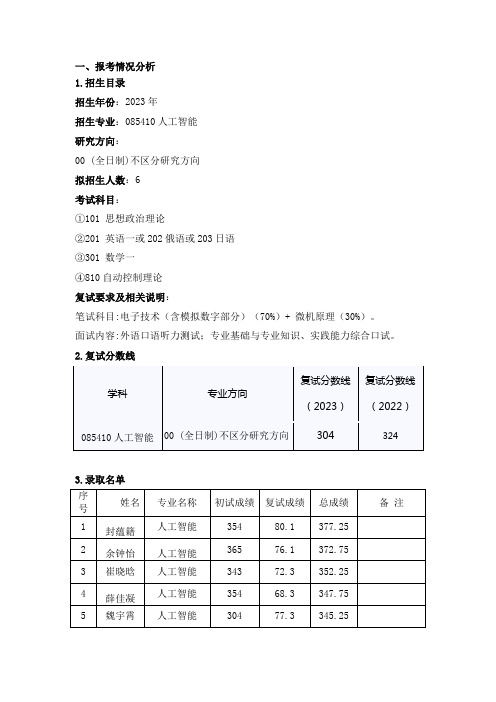
一、报考情况分析1.招生目录招生年份：2023年招生专业：085410人工智能研究方向：00 (全日制)不区分研究方向拟招生人数：6考试科目：①101 思想政治理论②201 英语一或202俄语或203日语③301 数学一④810自动控制理论复试要求及相关说明：笔试科目:电子技术（含模拟数字部分）（70%）+ 微机原理（30%）。

面试内容:外语口语听力测试；专业基础与专业知识、实践能力综合口试。

2.复试分数线3.录取名单二、考试大纲及参考书目810 自动控制理论考试内容及考试要求1.1 线性定常连续时间系统分析与设计1.1.1 系统的数学模型掌握：线性连续时间系统的概念；状态空间模型、微分方程模型、传递函数模型、方框图模型和信号流图模型；数学模型间的转换；方框图的化简。

1.1.2 系统的时域特性分析掌握：典型输入信号；由传递函数求系统的响应；系统的极点；一阶系统的响应；二阶系统的响应及时域性能指标；稳定性的基本概念；稳定性判据；稳态误差分析。

了解：高阶系统的响应；主导极点的概念。

1.1.3 根轨迹方法掌握：根轨迹的基本概念；绘制根轨迹的基本条件和规则；控制系统的根轨迹分析；广义根轨迹。

理解：控制系统的根轨迹校正方法及其原理。

1.1.4 频率响应方法掌握：频率响应的基本概念；典型环节的频率响应；开环系统的的频率响应；频率响应的图示法；最小相位系统；由频率响应求传递函数；基于开环频率响应的稳定性判据；稳定性裕量。

理解：闭环频率特性；基于频率响应的控制系统的串联校正。

1.1.4 状态空间方法掌握：状态转移矩阵的求取及其性质；状态方程的解；可控性和可观测性的基本概念及其判据；状态空间表达式的规范型；状态空间的分解；可镇定性和可检测性；状态反馈与极点配置；状态观测器的设计；带状态观测器的状态反馈。

1.2 线性定常采样控制系统的分析与设计掌握：连续时间信号的采样与复现；采样定理；零阶保持器；z变换；采样系统的脉冲传递函数；采样系统的响应；稳定性分析；稳态误差分析；最少拍采样控制系统的设计。

北京理工大学自动化学院2019年接收优秀应届本科毕业生推荐免试攻读硕士学..

一、申请条件1．拥护中国共产党的领导，愿为社会主义现代化建设服务，品德良好，遵纪守法，勤奋好学，思维敏捷，具有较强的创新能力和实践能力。

2．申请推荐免试的学生，须是取得就读高校推荐免试资格的优秀应届本科毕业生。

专业成绩或综合成绩位于本专业前列，国家大学英语四级考试成绩达到425分以上。

3.大学学习期间无不及格科目，未受过任何处分。

身心健康，符合所申请学科的体检及相关要求。

4.国家重点学科和优势学科的应届毕业生优先考虑。

5．大学学习期间在中文核心期刊及以上学术刊物发表论文，或获科研成果奖，或在全国重大科技竞赛中获奖者，优先考虑。

二、提交材料1.有效期内的学生证、身份证原件及复印件（提交复印件，复试时出示原件）。

2．加盖所在学校教务处公章的本科成绩单原件1份。

3．国家英语四级考试的成绩单（提交复印件，复试时出示原件）。

4．各类获奖证书复印件各1份。

5.体检合格的证明。

（体检可在我校校医院进行，时间为每周一、四上午8:00—11:00，抽血需在9:00前。

校外生源如不能到我校体检，需提供三级甲等医院体检证明）6、申请人还可提交体现学术水平的代表性学术论文、出版物或具有学术水平成果的复印件或证明。

所有材料均需使用A4纸，申请人的全部申请材料均在复试时提交学院审核备案，提交的材料恕不退还。

本直博学生除提交以上材料外，还须提交：《北京理工大学2019年招收优秀应届本科毕业生直接攻读博士学位研究生专家推荐书》一式两份（推荐人须是2名副教授或相当职称以上专家，推荐书须由推荐人密封并在封口处签字）。

三、申请程序1、推免生学院内预报名。

即日起有意愿报考我院的推免生即可联系相关导师并向导师提交相关证明材料，同时提交附件《2019年推免生报名信息表》电子版，发送至学院邮箱*************.cn，邮件主题2019推免生报名。

2、推免生复试。

复试由导师所在学科负责组织实施，复试时间和地点以导师电话通知为准。

（学院内完成预报名的学生复试全部在推免系统开放前完成）3、推免服务系统报名。

2015年北京理工大学自动化学院研究生入学考试“专业学位”拟录取名单

2015年北京理工大学自动化学院研究生入学考试“专业学位”拟录取名单序号考生编号姓名专业名称(或研究方向) 备注1100075000000192陈乾睿控制工程2100075000000225牟一旭控制工程3100075000000244赵婷控制工程4100075000000246孙大智控制工程5100075000000280刘吉祥控制工程6100075000000281李明霞控制工程7100075000000292杨华控制工程8100075000000294刘洋控制工程9100075000000295郑文控制工程10100075000000298王韫卓控制工程11100075000000300何砚高控制工程12100075000000303李瑞祥控制工程13100075000000305黄迪控制工程14100075000000307韩青松控制工程15100075000000308王楠控制工程16100075000000311明方博控制工程17100075000000315高源控制工程18100075000000320陈晓婧控制工程19100075000000321高冠强控制工程20100075000000322郝群控制工程21100075000000328周立杰控制工程22100075000000333孔祥煜控制工程23100075000000334张钟玉控制工程24100075000000337刘博涵控制工程25100075000000339仇斌控制工程26100075000000340高朝控制工程27100075000004369宋晓宁控制工程28100075000004383陈红学控制工程29100075000004398代艳胜控制工程30100075000004401董威控制工程31100075000004419黎霞霞控制工程32100075000004424范朝杰控制工程33100075000004432梁智控制工程34100075000004444赵立勋控制工程35100075000004457孟政控制工程36100075000004463凌艺菲控制工程37100075000004465张雪楠控制工程38100075000004477郝培言控制工程39100075000004495高瀚林控制工程40100075000004505刘要直控制工程41100075000004506王天控制工程42100075000004510张宗坤控制工程43100075000004516张亚男控制工程44100075000004526张双琪控制工程45100075000004530吴智高控制工程46100075000004543孙丙营控制工程47100075000004568李远军控制工程48100075000004569辛立伟控制工程49100075000004572李洁控制工程50100075000004572董浩控制工程51100075000004606付青山控制工程52100075000004621李响控制工程53100075000004631赵翰奕控制工程54100075000004638聂光涛控制工程55100075000004639吴金英控制工程56100075000004661张宇控制工程57100075000004669丁亚东控制工程58100075000004682王伟威控制工程。

探索智能优化技术研究的新路--记北京理工大学自动化学院辛斌教授

随着社会经济的发展，人工智能时代已经开启。

人工智能和多机器人二者相辅相成，并开始逐渐应用于我们生活中的诸多场景。

而人工智能和多机器人在计算机领域内，也愈发受到广泛重视。

在人工智能和多机器人领域，有一个人多年潜心研究、成绩斐然，而引领他走上这条路的只因儿时一个梦想，这个人就是辛斌。

人生要想充满无限可能，先让人生有一个梦想，再把想梦变成现实，而辛斌就是把梦想照进现实的人。

从小辛斌就喜欢机器人，只是那时还没有领域的概念。

机器人在年幼的辛斌看来，有点科幻，有点新奇、更充满了神秘的色彩。

对于每一个人来说，或许小时候的某一个人或事，或一件物品，对未来都可能会起到指引方向的作用。

长大后，辛斌的潜意识里便逐渐向梦想的方向靠拢。

“我相信大部分选择科研之路的人，如果不喜欢钻研，没有钻研的劲儿，也是不可能走上科研之路的。

无论你是做基础性的理论研究，还是理论和技术相结合，或者是侧重技术，从国家导向来看，都需要科研人员具备全方位的能力，这样才更适合做一个科研人。

”辛斌说。

开拓眼界，只为打开新世界的大门人生只有走出来的美丽，没有等出来的辉煌。

辛斌本科学的是电子工程，到了研究生阶段，他却选择了自动化专业。

为此，当时很多人都对他提出质疑，为什么要跨专业选择自动化领域。

在辛斌看来，换一个专业，只是想拓展一下自己的视野。

其实并没有跨越多大，都还在信息领域里，只不过是从弱电变成强电。

所以当时他义无反顾的选择了自动化领域，机缘巧合下，又遇到了陈杰教授。

多年来，一直跟随陈杰教授做科研，那时团队氛围非常好，大家一起协同奋进，攻克技术难关，随着团队的日益壮大，辛斌也在磨炼中迅速成长。

辛斌主要研究方向是计算智能和多机器人系统。

他说，虽然是两个方向，但是二者紧密关联，一个是内核所在，一个是外在逻辑呈现，可以概括为一软一硬。

计算智能其核心就是以算法为主，体现人工智能应用的领域，很多方法都是借鉴自然界规律，比如一些动物的社会性行为，建立创新性计算模式，去解决复杂问题。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

姓名冬雷
职务职称副教授所属学科电气工程
联系方式68918613 Pemc.bit@
通讯地址北京理工大学自动化学院中心教学楼1437室邮编：100081
个人简历北京理工大学自动化学院副教授，兼任中国自动化学会电气自动化专业委员会委员，中国电工技术学会电控系统与装置专业委员会委员。

学历：
1986年7月～1990年7月南京航空航天大学自动控制系，学士学位。

1995年7月～1997年3月南京航空航天大学测试工程系，提前攻博。

1997年3月～2000年5月南京航空航天大学自动控制系，博士学位。

研究工作经历：
1990年7月～1995年7月航空航天部第603研究所工作
2000年5月～2002年7月清华大学电机系博士后流动站工作
2003年6月～至今北京理工大学自动化学院，教学与科研工作
科研学术成果及获奖情况
先后参加了FBC－1（飞豹）飞机，以及运七－200A（新舟60）飞机的电气部分系统设计。

完成了两项国家自然科学基金项目：“异步电机极低速（包括零速）下速度辨识策略研究”和“大型风电场发电功率的建模与预测研究”。

讲授本科生必修课：电力电子技术、能源变换技术、DSP原理及应用，本科生实验选修课：智能车控制，研究生学位课∶现代电力电子技术，高等自动控制实验等课程。

负责大学生创新实验项目多项；指导大学生参加全国大学生智能车竞赛，获奖两项；成功组织大学生智能控制竞赛，取得了很好的成绩；参加教学改革项目一项，获校级优秀成果一等奖一项。

获2008年北京市教育教学成果二等奖一项。

近年来发表文章30多篇，其中EI检索10篇。

主编出版专著或教材2部，作为主编之一参编教材1部。

研究方向
主要从事电力电子与电力传动、风力发电与太阳能发电系统，微电网技术等方面的研究。

备注。