2017-2018学年高二3月月考数学(文)试卷
2017-2018学年安徽省淮南市第二中学高二上学期第二次月考数学试题(文创班,答案不全)

2017-2018学年安徽省淮南市第二中学高二上学期第二次月考数学测试卷一、选择题: 本题共12题,每小题5分1.已知两定点()1,0A -, ()1,0B ,动点(),P x y 满足()()2222112x y x y ++--+=,则点P 的轨迹是( )A. 椭圆B. 双曲线C. 一条线段D. 一条射线2.已知()(),f x g x 是定义在[],a b 上连续函数,则“()()f x g x <对一切[],x a b ∈成立”是“()f x 的最大值小于()g x 的最小值”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3.设函数()31(0)f x x ax a =++<,曲线()y f x =在点()(),a f a 处的切线方程为2y x b =+,则a b +=( )A. 1-B. 1C. 2D. 44.已知函数()y x f x =⋅'的图象如右下图,(其中()f x '是函数()f x 的导数),下面四个图像中, ()y f x =的图象大致是( )A. B. C. D.5.若函数()x tx x x f 323+-=在区间[]4,1上单调递减,则实数t 的取值范围是( )A. ⎥⎦⎤ ⎝⎛∞-851,B. (]3,∞-C. 51,8⎡⎫+∞⎪⎢⎣⎭D. [)3,+∞ 6. 已知不等式1<-m x 成立的一个充分不必要条件是2131<<x ,则实数m 的取值范围是( )A. ⎥⎦⎤⎢⎣⎡-21,34 B.⎥⎦⎤⎢⎣⎡-34,21 C. ⎪⎭⎫⎢⎣⎡+∞,34 D. ∅7. 已知抛物线28y x =的准线与双曲线221x y m-=交于,A B 两点,点F 为抛物线的焦点,若FAB ∆为直角三角形,则双曲线的离心率是( )A. 5B. 25C. 21D.2128. 已知椭圆和双曲线有共同焦点12,F F ,P 是它们的一个交点,且123F PF π∠=,记椭圆和双曲线的离心率分别12,e e ,则221213e e +的值为( ) A. 2 B. 3 C. 4 D. 59. 过抛物线24y x =的焦点F 的直线l 交抛物线于点,A B ,交其准线于点C ,若2BC BF =,则AB =( )A.83 B. 163C. 8D. 16 10.椭圆22154x y +=的左焦点为F ,直线x m =与椭圆相交于点,M N ,当FMN ∆的周长最大时,FMN ∆的面积是( ) A.55 B. 855 C. 655 D. 45511. 设函数()f x 的导函数为()'f x ,且在R 上()()'20f x xf x +<恒成立,则()1f ,()22f,()33f 的大小关系为( )A. ()()()12233f ff << B. ()()()33122f f f <<C. ()()()33221f f f <<D. ()()()13322f f f <<12.已知函数()22ln x e f x k x x x ⎛⎫=-+ ⎪⎝⎭,若2x =是函数()f x 的唯一一个极值点,则实数k的取值范围为 ( )A. (),e -∞B. [)0,eC. (],e -∞D. []0,e 二、填空题: 本题共4小题,每小题5分13. 已知双曲线2219y x m -=的一条渐近线方程为23y x =,则m = .14. 已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ,过点F 的直线交椭圆于,A B 两点.若AB 的中点坐标为()1,1-,则E 的方程为 .15.若函数()2ln 2-+=ax x x f 在区间⎪⎭⎫ ⎝⎛2,21内存在单调递增区间,则实数a 的取值范围是 .16.已知函数()4f x x x =+,()1a g x x x =++,若[]121,1,2,3,2x x ⎡⎤∀∈∃∈⎢⎥⎣⎦使得()()12f x g x ≥,则实数a 的取值范围是 .三、解答题:本题共6小题,第17题10分,第18至22题每小题12分17. 已知命题p : []13x ∀∈,,230x a -≥;命题q : 0x R ∃∈,使()20043110x a x +-+<.若“p 或q ”为真,“p 且q ”为假,求实数a 的取值范围.18. 已知12,F F 分别是椭圆2222:1(0)x y C a b a b+=>>的左右两个焦点,A 是椭圆C 的上顶点,B 是直线2AF 与椭圆C 的另一个交点,01260F AF ∠=.(1)求椭圆C 的离心率;(2)已知1AF B ∆的面积为403,求,a b 的值.19. 已知函数()2(2)ln f x ax a x x =-++. (1)若12x =是函数()f x 的一个极大值点,求a 的取值范围; (2)当0a >时,若()f x 在区间[]1,e 上的最小值为2-,求a 的取值范围.20. 已知函数()ln 1f x x x =+. (1)求()f x 的单调性;(2)设()()x g x e m x m R =+∈,若关于x 的方程()()f x g x =有解,求m 的取值范围.21. 已知抛物线()2:20C y px p =>的焦点F 与椭圆22:165x y E +=的一个焦点重合,点()0,2A x 在抛物线上,过焦点F 的直线l 交抛物线于,M N 两点. (1)求抛物线C 的方程以及AF 的值; (2)记抛物线C 的准线与x 轴交于点B ,若2240BM BN +=,求直线l 的方程.22. 已知函数2()ln(1)ln 2(0)f x ax x ax a =++--> (1)讨论()f x 在1,2⎡⎫+∞⎪⎢⎣⎭上的单调性;(2)若对(1,2)a ∀∈,总存在01,12x ⎡⎤∈⎢⎥⎣⎦使不等式20()(1)f x m a ≥-成立,求m 的范围.DBCBCB DCBBCC。
2020-2021学年浙江省高二下学期3月月考英语试题汇编-应用文写作专题Word版含答案

浙浙浙2020-2021浙浙浙浙浙浙浙浙3浙浙浙浙浙浙浙-浙浙浙浙浙浙浙浙江省湖州市德清县第三中学2020-2021学年高二3月月考英语试题七、应用文写作(共1小题,满分15 分)76. 假如你是李华,正在英国留学。
下周你所在的社区将举行以中医为主题的社区活动,目前正在招募志愿者。
请你用英文向主办方提出申请,内容包括:1. 提出申请;2. 介绍自己的优势;3. 期待加入。
注意:1.词数80 左右;2.可以适当增加细节,以使行文连贯。
参考词汇:中医traditional Chinese medicine (TCM)【答案】Dear Sir/Madam,I’m Li Hua, an international student from China. Hearing that you are recruiting volunteers for the activity about TCM, I cannot wait to apply to be one.I am competent for the job in that my parents happen to be TCM doctors. Brought up in the dense atmosphere of medicine, I’m equipped with abundant knowledge of how todistinguish various Chinese herbal medicines. Besides, I have the experience of being a volunteer guide for Americans. As a consequence, I’m convinced that I’ll live up to your expectations.I’d appreciate it if you could take my application into account. Looking forward to working with you.Y ours,Li Hua浙江省乐清市知临中学2020-2021学年高二下学期第一次月考英语试题第一节:应用文写作(满分15分)假如你是红星中学高三学生李华,你的英国笔友Jim获悉近年来中国的快递业发展迅速,想了解你身边的快递服务情况(delivery service)。
四川省成都市第七中学2017-2018学年高二上学期第一次月考数学(文)试题含解析

四川省成都市第七中学2017-2018学年高二上学期第一次月考数学(文)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,集合,则()A. B. C. D.【答案】B【解析】由题意得,,故选B.2. 在复平面,复数对应的点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】B3. 我国南宋数学家秦九韶所著《数学九章》中有“米谷粒分”问题:粮仓开仓收粮,粮农送来米1512 石,验得米内夹谷,抽样取米一把,数得216粒内夹谷27粒,则这批米内夹谷约()A. 164 石B. 178 石C. 189 石D. 196 石【答案】C【解析】试题分析:由已知,抽得样本中含谷27粒,占样本的比例为,则由此估计总体中谷的含量约为石. 故选C.考点:抽样中的用样本去估计总体.4. 下列选项中说法正确的是()A. 命题“为真”是命题“为真”的必要条件B. 若向量满足,则与的夹角为锐角C. 若,则D. “”的否定是“”【答案】A【解析】对于,若为真命题,则至少有一个为真命题,若为真命题,则为命题,则为真命题,是“p∧q为真命题”的必要不充分条件,正确;对于,根据向量积的定义,向量满足,则与的夹角为锐角或同向,故错误;对于,如果时,成立,不一定成立,故错误;对于“,”的否定是“,” 故错误,故选A.5. 设为等差数列的前项和,,则()A. B. C. D. 2【答案】A【解析】试题分析:由已知得解得.故选A.考点:等差数列的通项公式和前项和公式.6. 已知双曲线的离心率为,且抛物线的焦点为,点在此抛物线上,为线段的中点,则点到该抛物线的准线的距离为()A. B. 2 C. D. 1【答案】A【解析】试题分析:因为双曲线的离心率,所以,所以中点到该抛物线的准线的距离为.考点:双曲线及抛物线.7. 某产品的广告费用与销售额的统计数据如表:根据上表可得线性回归方程中的为9.4,据此模型预报广告费用为6万元时销售额为()A. 63.6 万元B. 65.5万元C. 67.7万元D. 72.0万元【答案】B【解析】∵,∵数据的样本中心点在线性回归直线上,回归方程中的为9.4∴线性回归方程是y=9.4x+9.1,∴广告费用为6万元时销售额为9.4×6+9.1=65.5,故选:B.8. 按照如图的程序框图执行,若输出结果为31,则处条件可以是()A. B. C. D.【答案】C【解析】试题分析:由已知,,,,,,,符合条件输出,故选C.考点:直到型循环结构程序框图运算.【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.9. 曲线在点处得切线与直线和围成的三角形的面积为()A. B. C. D. 1【答案】B【解析】由题意可得,曲线在点处的切线方程为:,则切线方程与的交点坐标为,则直线和围成的三角形的面积为,故选B10. —个三棱锥的三视图如图所示,其中正方形的边都是1,则该三棱锥的体积为()A. B. C. D.【答案】B【解析】由三棱锥的三视图可知,该三棱锥是一个直三棱锥,底面为边长为1的等腰直角三角形,高为2的直三棱锥,故,故选B.11. 已知双曲线的一条渐近线与圆相切,则双曲线的离心率等于()A. B. C. D.【答案】D.....................则圆心为M(3,1),半径R=1,由得,则双曲线的焦点在x轴,则对应的渐近线为,设双曲线的一条渐近线为,即ax−by=0,∵一条渐近线与圆相切,∴即圆心到直线的距离|3a−b|=c,平方得9a2−6ab+b2=c2=a2+b2,则离心率e=,故选:D.12. 如图,在边长为2的正六边形中,动圆的半径为1,圆心在线段(含端点)上运动,是圆上及内部的动点,设向量 (为实数),则的最大值是()A. 2B. 3C. 5D. 6【答案】C【解析】如图所示,①设点O为正六边形的中心,则当动圆Q的圆心经过点C时,与边BC交于点P,点P为边BC的中点。
【中小学资料】四川省广安第二中学校2017-2018学年高二数学下学期第二次月考试题 文
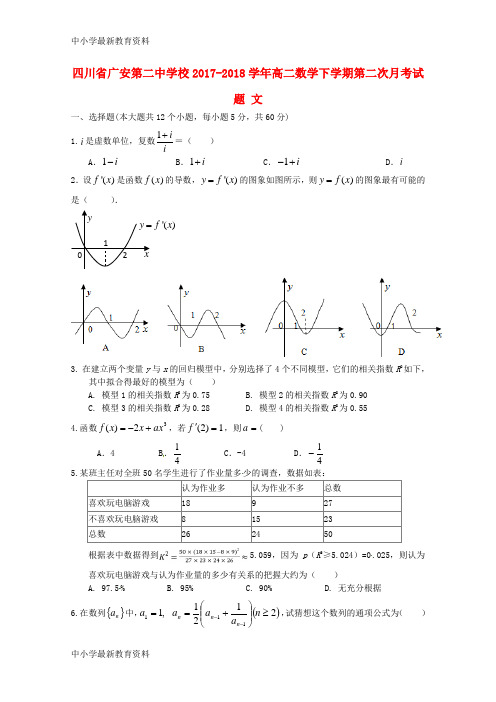
四川省广安第二中学校2017-2018学年高二数学下学期第二次月考试题 文一、选择题(本大题共12个小题,每小题5分,共60分) 1.i 是虚数单位,复数1ii+=( ) A .1i -B .1i +C .1i -+D .i2.设'()f x 是函数()f x 的导数,'()y f x =的图象如图所示,则()y f x =的图象最有可能的是( ).3. 在建立两个变量y 与x 的回归模型中,分别选择了4个不同模型,它们的相关指数R 2如下, 其中拟合得最好的模型为( ) A. 模型1的相关指数R 2为0.75 B. 模型2的相关指数R 2为0.90 C. 模型3的相关指数R 2为0.28 D. 模型4的相关指数R 2为0.554.函数32)(ax x x f +-=,若1)2(='f ,则=a ( )A .4B .41C .-4D .41-5.某班主任对全班50名学生进行了作业量多少的调查,数据如表:根据表中数据得到5.059,因为p (K 2≥5.024)=0.025,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( ) A. 97.5% B. 95% C. 90% D. 无充分根据6.在数列{}n a 中,()2121,1111≥⎪⎪⎭⎫⎝⎛+==--n a a a a n n n ,试猜想这个数列的通项公式为( ) '()f xA .n a n = B.1=n a C.n a n 1=D.21=n a7.已知,x y 是实数,且()01222=-+-+yi x i x (其中i 是虚数单位),则x yi +=( )A .i 21+B .5C .D .i +28. 参数方程(t 为参数)所表示的曲线是( )A. B. C. D.9.函数a ax x y +-=23在()1,0内有极小值,则实数a 的取值范围是( )A .()3,0B .()3,∞-C .()+∞,0D .⎪⎭⎫ ⎝⎛23,010 . 运行下图所示的程序框图,若输出结果为,则判断框中应该填的条件是( )A .k >5B .k >6C .k >7D .k >811.已知)(x f 满足1)2()4(=-=f f ,)(x f '为导函数,且导函数)(x f y '=的图象如右上图所示.则1)(<x f 的解集是( )A.)0,2(- B .)4,2(- C.(0,4) D.),4()2,(+∞⋃--∞ 12.已知函数()y f x =对于任意的(,)22x ππ∈-满足()()cos sin 0f x x f x x '+>(其中()f x '是函数()f x 的导函数),则下列不等式不成立的是( ) A .()()34f ππ< B .()()34f ππ-<- C .(0)()4f π<D .(0)2()3f f π<二、填空题(本大题共4小题,每小题5分,共20分) 13.化成极坐标方程为将直角坐标方程4=x .14.设曲线2xy xe x =+在原点处切线与直线10x ay ++=垂直,则a =15. 观察以下式子:按此规律归纳猜想第5个的等式为 .(不需要证明) 16.已知函数()e e x ea x x f ,1(2≤≤+-=是自然对数的底数)与()x x g ln 2=的图象上存在关于x 轴对称的点,则实数a 的取值范围是 .三、解答题(本大题共6小题,共70分)()()()().21:1210.17对应的复数向量所在的象限;点求,的对称点为关于原点点,对应点为的共轭复数为虚数单位在复平面内,复数分A B O A A Z i iiZ +=18.(12分)某人摆一个摊位卖小商品,一周内出摊天数x 与盈利y (百元),之间的一组数据关系见表:已知=90,=112.3,(1)计算,,并求出线性回归方程;(2)在第(Ⅰ)问条件下,估计该摊主每周7天要是天天出摊,盈利为多少? (参考公式:b ==,a =-b .)19.(12分)已知函数32()f x x ax bx c =+++在23x =-与1x =时都取得极值. (1)求,a b 的值;(2)若对[1,2]x ∈-,不等式2()f x c <恒成立,求c 的取值范围.20 .(12分)已知z y x ,,均为实数,且62,32,22222πππ+-=+-=+-=x z c z y b y x a .求证:c b a ,,中至少有一个大于0.()()()()().,0,121.cos 62321112.21的值求两点,交于与直线,曲线的直角坐标为若点的直角坐标方程;的普通方程和曲线写出直线为的极坐标方程极坐标系,曲线轴的正半轴为极轴建立以为极点,以原点,为参数的参数方程为中,已知直线在平面直角坐标系分PB PA B A l C P C l C x O t t y t x l xoy +=⎪⎪⎩⎪⎪⎨⎧=-=θρ22.(12分)已知函数.ln )2()(2x x a ax x f ++-=(1)当1=a 时,求曲线)(x f y =在点))1(,1f (处的切线方程;(2)当0>a 时,若)(x f 在区间],1[e 上的最小值为-2,其中e 是自然对数的底数, 求实数a 的取值范围.答案一、选择题(本大题共12个小题,每小题5分,共60分) A C B B A B C D D B B A 二、填空题(本大题共4小题,每小题5分,共20分)13. 二 14. 1 15.16. []212-e ,四、解答题(本大题共6小题,共70分)解:(Ⅰ)z ===1+i ,所以=1-i ,所以点A (1,-1)位于第四象限.…(5分)(Ⅱ)又点A ,B 关于原点O 对称. ∴点B 的坐标为B (-1,1).因此向量对应的复数为-1+i .…(10分)18.解:(Ⅰ)=4,=5.b ===1.23所以…故所求回归直线方程为.…(8分)(Ⅱ)当x =7时,y =1.23×7+0.08=8.69.所以,该摊主每周7天要是天天出摊,估计盈利为8.69(百元).…(12分)19.解:(1)因为32()f x x ax bx c =+++,所以'2()32f x x ax b =++由'2124()0393f a b -=-+=,'(1)320f a b =++=得12a =-,2b =-当1a =-,2b =-时,所以'2()32(32)(1)f x x x x x =--=+-,列表如下符合函数32()f x x ax bx c =+++在3x =-与1x =时都取得极值的要求,所以2a =-,2b =-(2)321()2,[1,2]2f x x x x c x =--+∈-由(1)可知max 2[()]max (),(2)3f x f f ⎧⎫=-⎨⎬⎩⎭当23x =-时,222()327f c -=+为极大值,而(2)2f c =+ 所以(2)2f c =+为最大值,要使2(),[1,2]f x c x <∈-恒成立,则只需2max [()]f x c <即2(2)2c f c >=+,解得1c <-或2c >.20 .证明:假设c b a ,,都不大于0,即0,0,0,0≤++≤≤≤c b a c b a 则 ① 而=++c b a 623222222πππ+-++-++-x z z y y x ,()()()3111222-+-+-+-=πz y x()()()0,,,00111,03222中至少有一个大于所以与①式矛盾c b a c b a z y x >++∴≥-+-+->-π 。
山西省太原师院附中、师苑中学2018-2019年高二年级第三次月考数学(文)试卷

太原师院附中 师苑中学2018~2019学年高二第三次月考数学试题(文)出题人:胡惠芝 审核人:白鹏恩 (考试时间:120分钟 试题满分:150分)一、选择题(本题共12小题,每题5分,共60分) 1.设复数z 满足(1)2i z i +=,则z =( )A .1i +B .1i -C .1i -+D .1i --2.甲、乙、丙、丁四位同学各自对,A B 两变量的线性相关性做试验,并用回归分析方法分别求得相关系数r 与残差平方和m 如下表:则哪位同学的试验结果体现,A B 两变量有更强的线性相关性( ) A .甲 B .乙 C .丙 D .丁 3.设曲线12xy e ax =+在点(0,1)处的切线与直线210x y +-=垂直,则实数a =( ) A .3 B .1 C .2 D .04.双曲线22:164y C x -=.经过3:2x x y yϕ'=⎧⎨'=⎩变换后所得到曲线的力程为( ) A .221916x y -= B .221169x y -= C .229116y x -= D .2291256y x -= 5.已知椭圆的参数方程为3cos 2sin x y θθ=⎧⎨=⎩(θ为参数),则椭圆的离心率为( )A B C .59 D .456.已知变量x 和y 的统计数据如下表:根据上表可得回归直线方程ˆˆ0.25ybx =-,据此可以预测当8x =时,ˆy =( )A .6.4B .6.25C .6.55D .6.45 7.在极坐标系中,点2,6π⎛⎫ ⎪⎝⎭到直线sin 16πρθ⎛⎫-= ⎪⎝⎭的距离为( ) A .3 B .4 C .2 D .18.参数方程()2t tt tx e ey e e --⎧=+⎪⎨=-⎪⎩(t 为参数)的普通方程为( ) A .221416x y -= B .221(2)416x y x -=≥ C .221(2)416x y x -=≤- D .221(2)416x y x -=≤-或(2)x ≥ 9.已知函数322()7f x x ax bx a a =++--在1x =处取得极大值为10,则ab的值为( ) A .23-B .2-C .2-或23-D .2或23- 10.设三次函数()f x 的导函数为()f x ',函数()y xf x '=的图像的一部分如图所示,则下列说法中正确的是( )A .()f x的极大值为f,极小值为(f B .()f x的极大值为(f,极小值为f C .()f x 的极大值为(3)f -,极小值为(3)f D .()f x 的极大值为(3)f ,极小值为(3)f -11.极坐标方程2(2sin )2sin 0ρρθθ-++=表示的图形为( ) A .一个圆与一条直线 B .一个圆 C .两个圆 D .两条直线12.()f x 是定义在R 上的偶函数,当0x <时,()()0xf x f x ''-<,且(3)0f -=,则不等式()0f x x>的解集为( )A .(,3)(3,)-∞-⋃+∞B .(,3)(0,3)-∞-⋃C .(3,3)-D .(3,0)(3,)-⋃+∞ 二、填空题(本题共4小题,每小题5分,共20分)13.复数(12)(3)z i i =+-,其中i 为虚数单位.则||z =________. 14.已知,M N 两点的极坐标分别是52,,3,66M N ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,则||MN =________.15.已知直线的参数方程为32545x t y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),且它与抛物线22y x =相交于,A B 两点,且线段AB的中点为M ,则点M 的坐标为_______________.16.已知函数3()1f x x ax =--.若()f x 在(1,1)-上为减函数,则实数a 的取值范围__________. 三、解答题(本题共6道大题,共70分)17.(本小题10分)已知定点(0,4),(6,0)Q P -,动点C 在椭圆22194x y +=上运动,求CPQ V 面积的最大值.18.(本小题12分)在直角坐标系xoy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知曲线2C :sin 2cos (0)a a ρθθ=>,过点(2,4)P --的直线2:42x l y ⎧=-+⎪⎪⎨⎪=-+⎪⎩(t为参数)与曲线C 相交于,M N 两点.(1)求曲线C 和直线l 的普通方程.(2)若||,||,||PM MN PN 成等比数列,求实数a 的值.19.(本小题12分)某种新产品投放市场一段时间后,经过调研获得了时间x (天数)与销售单价y (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).表中10111,10i i i i w w w x ===∑. (1)根据散点图判断,ˆˆˆy a bx =+与ˆˆˆd y c x=+哪一个更适合作价格y 关于时间x 的回归方程类型?(不必说明理由)(2)根据判断结果和表中数据,建立y 关于x 的回归方程. (3)若该产品的日销售量()g x (件)与时间x 的函数关系为()*100()120g x x N x-=+∈,求该产品投放市场第几天的销售额最高?最高为多少元?附:对于一组数据()()()()112233,,,,,,,n n u v u v u v u v ⋯,其回归直线v u αβ=+的斜率和截距的最小二乘法估计分别为()()()121ˆˆˆ,nii i nii vv u uav u u u ββ==--==--∑∑.20.(本小题12分)已知函数()cos xf x e x x =-. (1)求曲线()y f x =在点(0,(0))f 处的切线方程;(2)求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值. 21.(本小题12分)2018年11月21日,意大利奢侈品牌“&D G ”在广告中涉嫌辱华,中国明垦纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分別统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组[0,10),[10,20),[20,30),[30,40),[40,50),[50,60):得到如图所示的频率分布直方图:并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如下表.(1)在答题卡上补全列联表中数据;并判断能否有95%把握认为网友对此事件是否为“强烈关注”与性别有关?(2)现已从“强烈关注”的网友中按性别分层抽样选取了5人,再从这5人中选取2人,求这2人中至少有1名女性的概率.参考公式及数据:22()()()()()n ad bcKa b c d a c b d-=++++,23.(本小题12分)已知函数1()ln(0)f x a x ax=+>.(1)求函数()f x的极值.(2)是否存在实数a,使得函数()f x在[1,]e上的最小值为0?若存在,试求出a的值:若不存在,请说明理由.。
甘肃武威第十八中学2017-2018学年高二上学期第一次月考语文试题及答案 人教版高二上册

甘肃武威第十八中学2017-2018学年高二上学期第一次月考语文试题及答案人教版高二上册2017-2018学年度第一学期第一次月考试卷高二语文本试卷满分120分,考试时间:120分钟。
一、基础知识(每小题3分,共24分)1.下列注音全部正确的一组是( )A.赍发(jī) 迤逦(yǐlǐ)肉袒(tǎn)列观(guān)B.恁地(nèn)酒馔(zhuàn)尴尬(gāngà)昭然(zhāo)C.孱头(chàn)蹩进(bié)冠冕(guān)徘徊(huí)D.提防(tí) 仓廒(áo)央浼(měi)省亲(xǐng)2.下列句中加横线的词,解释不正确的一项是()A.求人可使报秦者报:报告B.相如因持璧却立却:后退几步C.武帝嘉其义嘉:赞许D.果引张胜引:牵攀,招供。
3.下列各句中的加点词语不是古今异义词的一项是()A、臣所以去亲戚而事君者B、传以示美人及左右C、臣等不肖,请辞去D、素与副张胜相知4.下列各组句子中,加点的词的意义和用法相同的一组是() A.秦贪,负其强,以空言求璧/臣诚恐见欺于王而负赵B.因宾客至蔺相如门谢罪/君因我降,与君为兄弟C.引赵使者蔺相如/左右或欲引相如去D.得璧,传之美人,以戏弄臣/赵王岂以一璧之故欺秦邪5.下列句子中,与例句句式相同的一项是()例:秦城恐不可得,徒见欺A.汉天子我丈人行也B.蚓无爪牙之利,筋骨之强C.饰以篆文山龟鸟兽之形D.六艺经传皆通习之,不拘于时,学于余6.下列句子不属于宾语前置句的一项是()A.子卿尚复谁为乎B.何以知之C.求人可使报秦者,未得D.自书典所记,未之有也7.下列句子断句正确的一项是()A.孺卿从祠河东\后土宦骑与黄门驸马争船\推堕驸马河中\溺死宦骑\亡诏使孺卿逐捕不得\惶恐饮药而死B.孺卿从祠河东后土\宦骑与黄门驸马\争船推堕驸马河中\溺死宦骑亡\诏使孺卿逐捕\不得\惶恐饮药而死C.孺卿从祠河东\后土宦骑与黄门驸马\争船推堕驸马河中\溺死宦骑\亡诏使孺卿逐捕\不得\惶恐饮药而死D.孺卿从祠河东后土\宦骑与黄门驸马争船\推堕驸马河中溺死\宦骑亡\诏使孺卿逐捕\不得\惶恐饮药而死8.下面对《拿来主义》内容的理解,不正确的一项是()A.对比的鲜明和反衬的强烈,是本文写作上的一个重要特点,比如开头大谈“闭关主义”“送去主义”,好像绕了一个大圈子,其实正好和“拿来主义”形成鲜明的对照。
安徽省临泉县第一中学2017-2018学年高二12月阶段考(第三次月考)数学(文)试题

临泉一中2017-2018高二上学期阶段考试试题数学(文科)命题人:郭辉 审题人:韦忠平一、选择题(本大题共12小题,每题5分,计60分,每小题只有一个正确选项) 1.命题“若0=a ,则0=ab ”的逆命题,否命题,逆否命题这三个命题中,真命题的个数是( )A.0B.1C.2D.3 2. 下列说法正确的是( ) A. ⎥⎦⎤⎝⎛∈+=2,0,sin 2sin πx x x y 没有最小值 B.当230<<x 时,()222323⎪⎭⎫ ⎝⎛-+≤-x x x x 恒成立C.已知5.40<<x ,则当x x 292-=时,()x x 292-的值最大D.当101<<x 时,xx y lg 1lg +=的最小值为2. 3.设{a n }是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,0212<+-n n a a ”的 ( )A.充要条件B.充分而不必要条件C.必要而不充分条件D.既不充分也不必要条件4.下列命题中正确的是( )A.“m=”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0互相平行”的充分不必要条件B.“直线l 垂直平面α内无数条直线”是“直线l 垂直于平面α”的充分条件C.已知a ,b ,c 为非零向量,则“a ·b =a ·c ”是“b =c ”的充要条件D.p:存在x∈R,x2+2x+2≤0.则¬p:任意x∈R,x2+2x+2>05.一元二次方程ax2+4x+3=0(a≠0)有一个正根和一个负根的充分不必要条件是( )A.a<0B.a>0C.a<-1D.a>16.下列4个命题:p1:存在x∈(0,+∞),<;p2:存在x∈(0,1),lo x>lo x;p3:任意x∈(0,+∞),>lo x;p4:任意x∈,<lo x.其中的真命题是( )A.p1,p3B.p1,p4C.p2,p3D.p2,p47.已知a,b,c为△ABC的三个内角A,B,C的对边,向量→m=(,-1),→n=(cosA,sinA).若→m⊥→n,且acosB+bcosA=csinC,则角A,B 的大小分别为( )A.,B.,C.,D.,8.某企业在今年年初贷款a万元,年利率为γ,从今年年末开始每年偿还一定金额,预计五年内还清,则每年应偿还( )A.万元B.万元C.万元D.万元9.变量x,y满足约束条件若z=2x-y的最大值为2,则实数m等于( )A.-2B.-1C.1D.210.若两个正实数x,y满足+=1,且不等式x+<m2-3m有解,则实数m 的取值范围( )A.(-1,4)B.(-∞,-1)∪(4,+∞)C.(-4,1)D.(-∞,0)∪(3,+∞)11.若a>b>1,0<c<1,则( )A.a c<b cB.ab c<ba cC.alog b c<blog a cD.log a c<log b c12.在△ABC中,a,b,c分别是角A,B,C的对边,且sinA+cosA=,a=7,3sinB=5sinC,则b+c的值为( )A.12B.8C.8D.8二、填空题(本大题共4小题,每题5分,计20分)13.不等式()()5243≥---xxx的解集为.____________.14.对于任意实数x,不等式sinx+cosx>m恒成立,则实数m的取值范围为________.15.已知命题p:“至少存在一个实数x∈,使不等式x2+2ax+2-a>0成立”为真,则a的取值范围是______________.16.要测量底部不能到达的东方明珠电视塔的高度,在黄浦江西岸选择甲、乙两观测点,在甲、乙两点测得塔顶的仰角分别为45°、30°,在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°,甲、乙两地相距500米,则电视塔在这次测量中的高度是________.三、解答题(本大题共6小题,17题10分,其余每题12分,计70分,每题请写出必要的解题步骤)17. 已知函数()2312-++=x x x f .(1)求不等式()5≥x f 的解集;(2)若关于x 的不等式()1-<m x f 的解集非空,求实数m 的取值范围.18.已知命题:p 方程012=++mx x 有两个不等的负实根,命题:q 方程01)2(442=+-+x m x 无实根.(1)若命题p 为真,求实数m 的取值范围;(2)若命题q p ∧为假,p q ∨为真,求实数m 的取值范围.19.已知命题:“[]1,1-∈∃x ,使等式x x m -=2成立”是真命题.(1)求实数m 的取值集合M ;(2)设不等式[]0)2()(<---a x a x 的解集为N ,若M N ⊆,求a 的取值范围.20. (1)已知1,1<<b a ,求证:11<--abba .(2)不等式11<--λλab ba 对满足1,1<<b a 的一切实数b a ,恒成立,求实数λ的取值范围.21.已知函数21()2cos ,()2f x x x x R --∈. (1)当5[,]1212x ππ∈-时,求函数()f x 的值域.(2)设ABC ∆的内角,,A B C 的对应边分别为,,a b c ,且()0c f C ==,若向量(1,sin )m A =. 与向量(2,sin )n B =共线,求,a b 的值.22.已知数列{a n }满足a n +2=qa n (q 为实数,且q ≠1),n ∈N*,a 1=1,a 2=2,且a 2+a 3,a 3+a 4,a 4+a 5成等差数列.(1)求q 的值和{a n }的通项公式. (2)设*2221log ,nn n a b n N a -=∈,求数列{b n }的前n 项和. .临泉一中2017-2018高二年级上学期(12月)考试试题数学(文科)答案一、选择题BBCDC DCBCB CD二、填空题13. 14. 1516.500m三、解答题17.(1)…………(5分)(2)…………(10分)18.解:(Ⅰ)…………(4分)(Ⅱ)命题成立:,………(6分)真假:………(8分)假真:………(10分)……………(12分)19.解:(1) 由题意知,方程在上有解,即m的取值范围为函数y=x2-x在上的值域,易得M=(6分)(2) 当a=1时,解集N为空集,满足题意;(7分)当a>1时,a>2-a,此时集合N={x|2-a<x<a},则(9分)当a<1时,a<2-a,此时集合N={x|a<x<2-a},则(11分)综上:(12分)20.解析:(1)证略…………(6分)…………(12分)21.解:(Ⅰ)。
语文-高二-江苏省宿迁市泗洪县兴洪中学2017至2018学年高二3月月考语文

兴洪中学2017—2018学年度第二学期高二年级月考语文试题2018.3分值:160分时间:150分钟一.语言文字运用(15分)1、在下面一段话的空缺处依次填入词语,最恰当的一组是(3分)( )尽管越来越多的人出国后选择去卢浮宫、大英博物馆、玛雅美术馆参观,但________式的参观却不在少数;尽管城市中的雕塑越来越多,但真正走入市民精神生活的却________;尽管文化市场上艺术品________,但泡沫也不少,个别收藏者连作者都不了解就举牌,一转身又投向下一场拍卖。
A.浅尝辄止所剩无几琳琅满目B.走马观花寥寥无几琳琅满目C.走马观花所剩无几鳞次栉比D.浅尝辄止寥寥无几鳞次栉比2、下列各句中,语言表达得体的一项是(3分)( )A.“这算得了什么,以后要是再有困难,可以继续到府上来找我。
”孙大款慷慨地说。
B.李烨对张进说:“非常感谢你这次帮我解决了一个大难题,下次如果你有什么困难,我一定会鼎力相助。
”C.主持人黄乐乐说:“感谢嘉宾吴小明,祝贺他荣幸地加入我们综艺之友俱乐部!”D.程一鸣教授将自己的学术专著送给爱徒王斌,他在扉页上写下“王斌同学惠存”的字样。
3、下列各句中,所引诗词最符合语境的一项是(3分)( )A.“明月不谙离别苦,斜光到晓穿朱户。
”长年累月出门在外的游子,又怎能体会到母亲对他们的思念和牵挂呢?B.“无可奈何花落去,似曾相识燕归来。
”事物的运动变化是有规律的,规律具有客观性,人们无法改变。
C.“花径不曾缘客扫,蓬门今始为君开。
”春节又将来临了,家家户户都忙着洒扫迎新,期待来年的好运。
D.“良辰美景奈何天,赏心乐事谁家院。
”中秋佳节,山塘街游人如织,怎奈天公不作美,突降的大雨让游客们扫兴而归。
4、下列歌词中,没有使用比喻手法的一项是(3分)( )A.山是山,水是水,往事恍然如云烟,流浪心已憔悴,谁在乎?英雄泪。
(《英雄泪》)B.过去的誓言,就像那课本里缤纷的书签,刻画着多少美丽的诗,可是终究是一阵烟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年下学期3月月考卷高二文科数学本试卷分为第I 卷(选择题)和第II卷(非选择题)两部分,全卷满分150分,考试用时120分钟。
一、选择题(本大题共12个小题,每小题5分,共60分。
)1.在数列55,,1,1x中,x等于(),8,5,3,2,,3421A.11B.12C.13D.142.从集合的所有子集中任取一个,这个集合恰是集合的子集的概率是()A. B. C. D.3.如图,程序执行后的结果是()A.3,5B.5,3C.5,5D.3,34.设a,b∈R,若a﹣|b|>0,则下面不等式中正确的是()A.b﹣a>0B.+<0C.b+a<0D.﹣>05.在平面直角坐标系中,若不等式组(a为常数)所表示平面区域的面积等于2,则a的值为()A.-5B.1C.2D.36.已知数列,,,且,则数列的第五项为()A.6B.-3C.-12D.-67.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c .若c=2a ,bsinB ﹣asinA=asinC ,则sinB 等于( )A. B. C. D.8.数列{a n }满足()1121nn n a a n ++-=-,则{a n }的前60项和为( ) A. 3690 B. 3660 C. 1845 D. 18309.已知点(n ,a n )在函数y=2x ﹣13的图象上,则数列{a n }的前n 项和S n 的最小值为( )A.36B.﹣36C.6D.﹣610.△ABC 的内角A 、B 、C 的对边分别是a ,b ,c ,且asinA ﹣csinC=(a ﹣b )sinB ,c=3.则△ABC 面积的最大值为( )A. B. C. D.11.已知 ,且满足 ,那么 的最小值为( )A.B.C.D.12.已知S n 是等差数列{a n }(n ∈N *)的前n 项和,且S 5>S 6>S 4 , 以下有四个命题:①数列{a n }中的最大项为S 10;②数列{a n }的公差d <0; ③S 10>0;④S 11<0;其中正确的序号是( )A.②③B.②③④C.②④D.①③④第II 卷(非选择题 90分)二、填空题(本大题共4个小题,每小题5分,共20分。
)13.在△ABC 中,设角A ,B ,C 所对的边分别为a ,b ,c ,若 sinA+cosA=2,a=3,C=,则b= .14.如图,设A ,B 两点在河的两岸,一测量者在A 的同侧,在A 所在的河岸边选定一点C ,测出AC 的距离为50m ,∠ACB=45°,∠CAB=105°后,则A ,B 两点的距离为 m .15.函数4(1)1y x x x =+>-的最小值为_________. 16.已知数列{}n a 中, 1111,n n n n a a a a a ++=-⋅=-,则n a =_________。
三、解答题(本大题共6个小题,共70分。
) 17. (10分)已知各项均为正数的数列{a n }满足a n+2+2=4a n+1﹣a n (n ∈N *),且a 1=1,a 2=4. 证明:数列{}是等差数列18. (12分)在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且满足 =,=3.(Ⅰ)求△ABC 的面积; (Ⅱ)若b+c=6,求a 的值.19. (12分)已知函数()()cos (0,0,)2f x A x A πωϕωϕ=+>><的部分图像如图所示.(Ⅰ)求函数()f x 的解析式;(Ⅱ)在ABC ∆中,角,,A B C 的对边分别是,,a b c ,若()2co s a B C =,求sin 2A f C ⎛⎫+ ⎪⎝⎭的取值范围.20. (12分)已知数列{a n }满足3(n+1)a n =na n+1(n ∈N *),且a 1=3, (1)求数列{a n }的通项公式;(2)求数列{a n }的前n 项和S n ;(3)若=,求证: ≤ + +…+<1.21. (12分)ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,已知ABC ∆的面积为cos ac B ,BC 的中点为D .(Ⅰ) 求cos B 的值;(Ⅱ) 若2c =, sin 5sin a A c C =,求AD 的长.22. (12分)有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:(Ⅰ)求频率分布直方图中m 的值;(Ⅱ)分别求出成绩落在[)[)[]70,80,80,90,90,100中的学生人数;(Ⅲ)从成绩在[]80,100的学生中任选2人,求所选学生的成绩都落在[)80,90中的概率参考答案1.C【解析】数列规律为21++=+n n n a a a ,所以218=+x ,解得:13=x ,故选C. 2.C【解析】因为的子集有:共8个(也可用公式计算的子集数:, 其中3表示集合中元素的个数),而集合的子集有:共4个,故所求的概率为 , 故选C. 3.C【解析】由程序语句知:执行A=5, B=5, ∴输出5,5. 故选:C . 4.D【解析】4.∵a﹣|b|>0,∴a>|b|,∴a 2>b 2 , 即a 2﹣b 2>0. 故选D . 5.D【解析】设直线与轴、轴分别交于点, 则.直线过点且与轴垂直,直线的过定点.依题意,该不等式组表示的平面区域即直线右上方、直线左方以及直线下方的区域,设直线与直线交于点C ,则点C必在点A 上方,又该平面区域的面积等于2,点B 到AC 的距离为1,所以AC=4,即C(1,4),代入直线方程中,得的值为3.6.D【解析】根据已知条件,由于数列,,,且有,将因此可知因此可知数列是有周期性的,并且数列的第五项为-6,故选D.7.A【解析】∵bsinB﹣asinA= asinC,∴由正弦定理可得:b2﹣a2= ,又∵c=2a,∴a2+c2﹣b2=4a2﹣ =3a2,∴利用余弦定理可得:cosB= = = ,∴由于0<B<π,解得:sinB= = = .故答案为:A.8.D【解析】∵a n+1+(-1)n a n=2n-1,∴当n=2k(k∈N*)时,a2k+1+a2k=4k-1①当n=2k+1(k∈N)时,a2k+2-a2k+1=4k+1②①+②得:a2k+a2k+2=8k.则a 2+a 4+a 6+a 8+…+a 60=(a 2+a 4)+(a 6+a 8)+…+(a 58+a 60)=8(1+3+…+29)=8×()151292⨯+=1800.由②得a 2k+1=a 2k+2-(4k+1),所以a 1+a 3+a 5+…+a 59=a 2+a 4+…+a 60-*4×(0+1+2+…+29)+30+=1800-(4×30292⨯+30)=30, ∴a 1+a 2+…+a 60=1800+30=1830. 9.B【解析】∵点(n ,a n )在函数y=2x ﹣13的图象上,则a n =2n ﹣13,a 1=﹣11=n 2﹣12n∵n∈N + , ∴当n=6时,S n 取得最小值为﹣36. 故选:B点(n ,a n )在函数y=2x ﹣13的图象上,的a n =2n ﹣13,a 1=﹣11,=n 2﹣12n 10.D【解析】∵asinA﹣csinC=(a ﹣b )sinB ,由正弦定理 ,得a 2=(a ﹣b )b+c 2,即a 2+b 2﹣c 2=ab .① 由余弦定理得cosC= = ,结合0<C <π,得C= . ∵c=3,∴由余弦定理可得:9=a 2+b 2﹣ab≥2ab﹣ab=ab ,当且仅当a=b 等号成立,∴S △ABC = ≤ = ,即△ABC 面积的最大值为 .故选:D . 11.C【解析】依题意 . 故答案为:C12.B【解析】∵S 5>S 6>S 4,∴a 6<0,a 5+a 6>0,a 5>0,∴d<0,数列{a n }中的最大项为S 5. S 10==5(a 5+a 6)>0,S 11==11a 6<0.因此只有②③④正确. 故答案为:B .先根据S 5>S 6>S 4判断相应项的正负,再利用等差数列前n 项和的特点判断S 10与S 11的大小. 13.【解析】∵sinA+cosA=2,∴2sin(A+ )=2,即sin (A+ )=1,∵A∈ ,∴(A+ )∈,∴A+ = ,解得A= .∴B=﹣ = ,在△ABC 中,则b= = = .故答案为:.sinA+cosA=2,化为2sin (A+ )=2,解得A ,再利用正弦定理即可得出. 14.50【解析】在△ABC 中,∵∠ACB=45°,∠CAB=105° ∴∠B=30°由正弦定理可得:∴=50 m故答案为:50先利用三角形的内角和求出∠B=30°,再利用正弦定理,即可得出结论. 15.5【解析】因为1x > ,所以10x -> ,函数()441+11511y x x x x =+=-+≥=-- ,当且仅当411x x -=- ,即3x = 时等号成立. 16.1n-【解析】11n n n n a a a a ++⋅=-变形为1111n n a a +-=- 1n a ⎧⎫∴⎨⎬⎩⎭为等差数列,首项为1-,公差1d =-,所以通项为11n n n a a n=-∴=- 考点:数列递推公式求通项公式17.解:∵且a n >0,∴(+)2=(2)2 ,∴+=2, ∴{}是首项为=1,公差为-=1的等差数列.【解析】通过已知条件,利用配方法推出等差数列的等差中项形式,判断数列是等差数列.18.解:(Ⅰ)因为,∴ ,又由=3,得bccosA=3,∴bc=5,∴(Ⅱ)对于bc=5,又b+c=6, ∴b=5,c=1或b=1,c=5,由余弦定理得a 2=b 2+c 2﹣2bccosA=20,∴【解析】(Ⅰ)利用二倍角公式利用 = 求得cosA ,进而求得sinA ,进而根据=3求得bc 的值,进而根据三角形面积公式求得答案.(Ⅱ)根据bc 和b+c 的值求得b 和c ,进而根据余弦定理求得a 的值.19.(Ⅰ)()2cos 23f x x π⎛⎫=- ⎪⎝⎭;(Ⅱ)(]0,3.【解析】(I )利用函数的图象,求出A ,通过函数的周期求出ω,通过函数的图象经过 26π(,),求出φ,即可解出函数f (x )的解析式;(II )利用()2cos cos a B C -=,结合正弦定理,求出cosB ,利用函数的解析式求sin 2A f C ⎛⎫+ ⎪⎝⎭的表达式,通过A 的范围求出函数的取值范围.解(Ⅰ)由图像知, 22,236A T πππ⎛⎫==-= ⎪⎝⎭,∴22T πω==, 由图像可知, 26f π⎛⎫= ⎪⎝⎭, ∴2cos 226πϕ⎛⎫⨯+= ⎪⎝⎭, ∴cos 13πϕ⎛⎫+= ⎪⎝⎭,∴23k πϕπ+=, 又∵2πϕ<, ∴3πϕ=-, ∴()2cos 23f x x π⎛⎫=- ⎪⎝⎭.(Ⅱ)依题设, ()2cos cos a B C =,∴()2sin cos cos A C B B C -=,即)2sin cos sin cos cos sin A B B C B C =+ ()B C A =+=,∴cos B =, 又()0,B π∈, ∴6B π=. ∴56A C π+=.由(Ⅰ)知, 5sin 2cos sin cos sin 236A f C A C A A A ππ⎛⎫⎛⎫⎛⎫+=-+=++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1cos cos 3sin 226A A A A A π⎛⎫=++=+ ⎪⎝⎭,又∵50,6A π⎛⎫∈ ⎪⎝⎭, ∴,66A πππ⎛⎫+∈ ⎪⎝⎭, ∴(]sin 0,16A π⎛⎫+∈ ⎪⎝⎭,∴sin 2A f C ⎛⎫+ ⎪⎝⎭的取值范围是(]0,3. 20.(1)解:∵数列{a n }满足3(n+1)a n =na n+1(n∈N *),且a 1=3,∴ = ,∴a n = •…• =3n ﹣1• … • ×3=n•3n (2)解:数列{a n }的前n 项和S n =3+2×32+3×33+…+n•3n ,3S n =32+2×33+…+(n ﹣1)•3n +n•3n+1,∴﹣2S n =3+32+…+3n ﹣n•3n+1=﹣n•3n+1, ∴S n = ×3n+1+(3)证明: =,∴ = = = ﹣. ∴ + +…+ =+ +…+ =1﹣ ∈ . ∴ ≤ + +…+ <1【解析】(1)数列{a n }满足3(n+1)a n =na n+1(n∈N *),且a 1=3,可得 = ,利用“累乘求积”方法即可得出.(2)利用“错位相减法”与等比数列的求和公式即可得出.(3) =,可得 = = =﹣.利用“裂项求和方法”与数列的单调性即可得出.21.(1) (2)【解析】(I )根据三角形面积公式得11sin cos ,sin cos ,224ac B ac B B B B π===,所以cos 2B =.(II )用正弦定理化简sin 5sin a A cC =,得225a c =,由此求得,a BD 的值,利用余弦定理可求得AD 的值.解: (Ⅰ) 由1sin cos 2ABC S ac B ac B ∆==,得sin 2cos B B =,①∵0B π<< ∴sin 0B > 故cos 0B >,又22sin cos 1B B +=,②①代入②得21cos5B =,∴cos B = (Ⅱ)由sin 5sin a A c C =及正弦定理得225a c =,∵2c =,∴a = 12BD a ==, 在△ABD 中,由余弦定理得:2222cos 4525AD c BD BD c B =+-⋅⋅=+-=,∴AD =.22.(Ⅰ)0.005m =(Ⅱ)6,4,2(Ⅲ)25【解析】(Ⅰ)由题意()10234561m m m m m ⨯++++=, 0.005m =(Ⅱ)成绩落在[)70,80中的学生人数为20100.036⨯⨯=,成绩落在[)80,90中的学生人数20100.024⨯⨯=成绩落在[]90,100中的学生人数20100.012⨯⨯=.(Ⅲ)设落在[)80,90中的学生为1234,,,a a a a ,落在[]90,100中的学生为12,b b , 写出所有事件,则可知基本事件个数为15n =, 而设A =“此2人的成绩都在[)80,90”,则事件A 包含的基本事件数6m =,所以事件A 发生概率()62155m P A n === 试题解析:(Ⅰ)由题意()10234561m m m m m ⨯++++=, 0.005m =. (Ⅱ)成绩落在[)70,80中的学生人数为20100.036⨯⨯=,成绩落在[)80,90中的学生人数20100.024⨯⨯=成绩落在[]90,100中的学生人数20100.012⨯⨯=. …(Ⅲ)设落在[)80,90中的学生为1234,,,a a a a ,落在[]90,100中的学生为12,b b , 则{}1121314111223242122343132414212,,,,,,,,,,,,,,a a a a a a a b a b a a a a a b a b a a a b a b a b a b bb Ω=, 基本事件个数为15n =设A =“此2人的成绩都在[)80,90”,则事件A 包含的基本事件数6m =,所以事件A 发生概率()62155m P A n ===。
