四川2005年高考全国卷(
2005年高考全国卷1英语(含答案)

英语作文常用谚语、俗语1、A liar is not believed when he speaks the truth. 说谎者即使讲真话也没人相信。
2、A little knowledge is a dangerous thing. 一知半解,自欺欺人。
3、All rivers run into sea. 海纳百川。
4、All roads lead to Rome. 条条大路通罗马。
5、All work and no play makes Jack a dull boy. 只会用功不玩耍,聪明孩子也变傻。
6、A bad beginning makes a bad ending. 不善始者不善终。
7、Actions speak louder than words. 事实胜于雄辩。
8、A faithful friend is hard to find. 知音难觅。
9、A friend in need is a friend indeed. 患难见真情。
10、A friend is easier lost than found. 得朋友难,失朋友易。
11、A A good good good beginning beginning beginning is is is half half half done. done. 良好的开端是成功的一半。
12、A good beginning makes a good ending. 善始者善终。
13、A good book is a good friend. 好书如挚友。
14、A good medicine tastes bitter. 良药苦口。
15、A mother's love never changes. 母爱永恒。
16、An apple a day keeps the doctor away. 一天一苹果,不用请医生。
一花独放不是17、A single flower does not make a spring.春,百花齐放春满园。
2005年高考物理试卷评价及备考策略
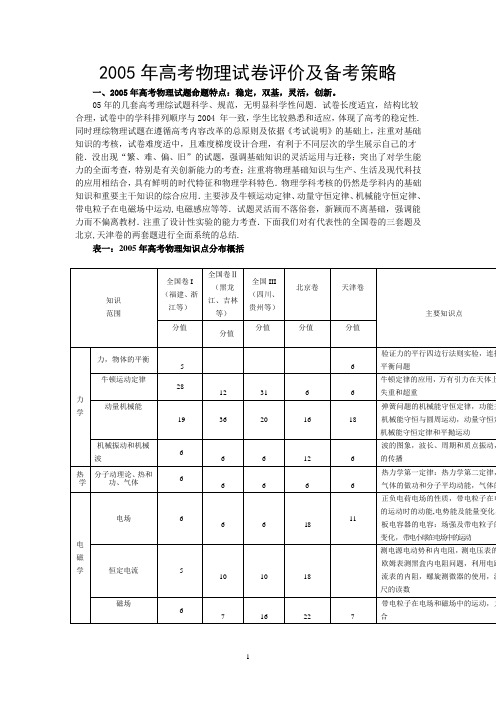
2005年高考物理试卷评价及备考策略一、2005年高考物理试题命题特点:稳定,双基,灵活,创新。
05年的几套高考理综试题科学、规范,无明显科学性问题.试卷长度适宜,结构比较合理,试卷中的学科排列顺序与2004 年一致,学生比较熟悉和适应,体现了高考的稳定性.同时理综物理试题在遵循高考内容改革的总原则及依据《考试说明》的基础上,注重对基础知识的考核,试卷难度适中,且难度梯度设计合理,有利于不同层次的学生展示自己的才能.没出现“繁、难、偏、旧”的试题,强调基础知识的灵活运用与迁移;突出了对学生能力的全面考查,特别是有关创新能力的考查;注重将物理基础知识与生产、生活及现代科技的应用相结合,具有鲜明的时代特征和物理学科特色.物理学科考核的仍然是学科内的基础知识和重要主干知识的综合应用.主要涉及牛顿运动定律、动量守恒定律、机械能守恒定律、带电粒子在电磁场中运动,电磁感应等等.试题灵活而不落俗套,新颖而不离基础,强调能力而不偏离教材.注重了设计性实验的能力考查.下面我们对有代表性的全国卷的三套题及北京,天津卷的两套题进行全面系统的总结.表一:2005年高考物理知识点分布概括表二:2005年高考物理能力测试概括重视理解能力、推理能力,同时突出分析综合能力和实验能力,对获取知识的能力也提出了一定的要求.3. 加强对实验能力的考查,特别是电学设计性实验的考查.二.典例分析研究1. 选择题部分从2005年高考理综卷来看,物理题共120分,其中选择题分值为48分,占40%,而且今年的物理选择题又增加了多选题,由此可知,做好物理选择题是取得高考突出成绩的关键,而要提高选择题解答的准确率,这就要求学生要在方法上下功夫,巧选方法快速解答选择题对于高考来说相当重要.下面我们以2005年高考试题中选择题为例进行类型归纳讨论快速解答物理选择题的常用方法.【例1】(2005年全国卷I )如图1所示,绝热隔板K 把绝热的气缸分隔成体积相等的两部分,K 与气缸的接触是光滑的.两部分中分别盛有相同质量、相同温度的同种气体a 和b ,气体分子之间相互作用势能可忽略.现通过电热丝对气体a 加热一段时间后,a 、b 各自达到新的平衡,则下列说法正确的A.A 的体积增大了,压强变小了B.B 的温度升高了C.加热后a 的分子热运动比b 的分子热运动更激烈 D.A 增加的内能大于b 增加的内能解析:先用假设法,假设K不动,则对a 加热,a 气体吸热,内能增加,温度升高,所以压强增大,故活塞K将向右移动,活塞对b 气体做功,b 不吸热不放热,所以b 的内能增加,不考虑分子势能,所以b 气体的温度升高,达到新的平衡后,a ,b 的压强相等,由于后来体积b a V V >,a 气体单位体积内分子数少,故要使a ,b 压强相等,则a 气体的温度必然要高于b 气体的温度b a T T >,故BCD选项正确.这里的关键是选准用假设法。
2005年高考理综(全国卷三_四川、贵州、云南、陕西、甘肃)

2005年普通高等学校招生全国统一考试理科综合能力测试(全国卷三)(四川、贵州、云南、陕西、甘肃)以下数据可供解题时参考:相对原子质量(原子量):H:1 He:4 C:12 N:14 O:16第I卷(选择题共126分)一、选择题(本题包括13小题。
每小题只有一个....选项符合题意)1.连续分裂的动物体细胞的生长即体积增大,发生在细胞周期的()A.分裂间期B.分裂前期C.分裂中期D.分裂后期2.右图表示在适宜的温度、水分和CO2条件下,两种植物光合作用强度的变化情况。
下列说法错误..的是()A.当光照强度增加到一定程度时,光合作用强度不再增加,即达到饱和B.C3植物比C4植物光合作用强度更容易达到饱和C.C4植物比C3植物光能利用率高D.水稻是阴生植物,玉米是阳生植物3.当人体处于饥饿状态时()A.肾上腺素分泌减少,胰高血糖素分泌增加B.肾上腺素分泌增加,胰高血糖素分泌增加C.肾上腺素分泌减少,胰高血糖素分泌减少D.肾上腺素分泌增加,胰高血糖素分泌减少4.关于抗体的产生、特性和作用等的叙述,错误..的是()A.抗毒素是抗体B.抗体都能被蛋白酶分解C.淋巴细胞都能产生抗体D.抗体在某些特殊情况下会对自身成分起免疫反应5.科学家通过基因工程的方法,能使马铃薯块茎含有人奶主要蛋白。
以下有关该基因工程的叙述,错误..的是()A.采用反转录的方法得到的目的基因有内含子B.基因非编码区对于目的基因在块茎中的表达是不可缺少的C.马铃薯的叶肉细胞可作为受体细胞D.用同一种限制酶,分别处理质粒和含目的基因的DNA,可产生黏性末端而形成重组DNA分子6.现有以下几种措施:①对燃烧煤时产生的尾气进行除硫处理,②少用原煤做燃料,③燃煤时鼓入足量空气、,④开发清洁能源。
其中能减少酸雨产生的措施的是()A .①②③B .②③④C .①②④D .①③④7.下列气体的制备可采用右图装置的是( ) A .铜与浓硝酸反应制NO 2 B .铜与稀硝酸反应制SO C .乙醇与浓硫酸反应制乙烯 D .氯化钠与浓硫酸反应制HCl8.在体积可变的密闭容器中,反应mA (气)+nB (固)pC (气)达到平衡后,压缩容器的体积,发现A 的转化率随之降低。
2005年全国各地高考各批次录取控制分数线

本科一批 文史类554分,理工类545分; 本科二批 文史类509分,理工类494分。
本科一批 文史类555分 理工类542分; 本科二批 文史类492分 理工类470分; 本科三批 文史类475分 理工类445分。
一本 文史类535分 理工类530分;
云南 陕西 甘肃 河南 天津 辽宁 贵州 江苏 山西
本科一批,文科565分,理科568分; 本科二批,文科522分,理科523分; 本科三批,文科493分,理科496分
理工类本科一批458分、本科二批(含A、B阶段)408分、本科 三批389分; 文史类本科一批498分、本科二批(含A、B阶段)460分、本 科三批443分
文理类:第一本科:530分;第二批本科:458分; 第三批本科405分;提前专科:445分;专科(高职):360 分
第一批本科院校最低投档控制线:理工类536分 分; 第二批本科院校最低投档控制线:理工类459分 分
文史类556 文史类476
普通类第一批本科录取最低控制分数线为560分; 普通类第二批本科录取最低控制分数线为529分
文史类本科:第一批为534分,第二批为497分; 理工类本科:第一批为532分,第二批为495分; 第三批本科最低控制分数线待第二批本科录取基本结束时根 据志愿划定
文史类 本科一批:536分,本科二批:500分,本科三批 : 416分,专科一批、二批:300分。 理工类 本科一批:551分,本科二批:511分,本科三批: 380分,专 科一批、二批:300分。
பைடு நூலகம்
文史类本科:第一批为534分,第二批为497分; 理工类本科:第一批为532分,第二批为495分; 体育类本科:体育(文)类:第一批为395分;体育(理)类:第 一批为395分。
提取关键词高考语文

3. 结构层次法:任何语各层次中 递进式语段关键词常出现在最后层次中 总分式语段关键词常出现在总说句中
[答案]书法 意象 体味 神髓
2.提取下面一段话的主要信息,写出四个关键词语。 (2006年高考广东卷)
从甲骨文到草书、行书的各种书法艺术,间接地反映了现 实某些方面的属性,将具体的形式集中概括为抽象的意象, 通过视觉来启发人们的想象力,调动人们的情感,使人们 从意象中体味到其间所蕴含的美。这也就是一些讲书法的 文章里常说的“舍貌取神”——舍弃客观事物的具体现象 特征,而摄取其神髓。
[答案] 开放时代 爱国主义 理性 深沉
7. 阅读下面的文段,提取四个关键词。 今天中国独特而强烈的爱国主义热情,直接源于“鸦片战争”以来的民族生 存危机。在开放时代,中国与世界的关系发生了巨大变化,中国不但摆脱了 民族生存危机,而且成为全球化竞争中的最大受益者之一。中国离不开世界, 世界也离不开中国。这时的爱国主义应当注入新的因子和意识。它不再应当 仅是一种内聚型的强烈感情,不应当是封闭的、种族的、排外的,而应当具 有理性、深沉的意识,即开放的世界观、积极的进取心、普世的价值观念。
一. 提取关键词的本质
1. 提取关键词本质上是对语段关键、主要、核心信息的集中。 2. 提取关键词本质上是压缩的压缩,精练的精练,关键的关键。 3. 提取关键词本质上是要淘汰掉次要的、支撑的、解说的信息。 4. 提取关键词本质上考查的语段信息筛选能力和梳理思路能力。
2005年高考文科综合能力测试(全国卷III)

绝密★启用前【考试时间:2005年6月8日9:00-11:30】2005年普通高等学校统一招生考试文科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分300分。
考试时间150分钟。
第Ι卷(选择题共140分)注意事项:1.答第Ⅰ卷前考生务必将自己的姓名、准考证号、考试科目、试卷类型涂写在答题卡上。
考试结束,将试题卷和答题卡一并交回。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试题卷上。
一、选择题本大题共35小题,每小题4分,共计140分。
在每小题列出的四个选项中,只有一项是最符合题目要求的。
2004年7月28日,我国第一个北极科学考察站——黄河站(78055’N,11056’,E)建成。
据此回答1-2题。
1.从黄河站往正南方,将到达A斯堪的纳维亚半岛B.西伯利亚C.阿拉斯加D.大不列颊岛2.黄河站至北极点的距离约为A.600千米B.900千米C.1200千米D.1500千米2005平3月28日23时9分(东7区区时),印度尼西亚的尼亚斯岛附近海域发生8.7级强烈地震。
不久又相继在该岛西略偏北l00千来海底和该岛正南约190千米海底发生强烈余震,这些地震均发生在靠近两大板姨界线的地方。
据此回答3-5题。
3.该8.7级地震发生时,纽约(西5区)为A.29日10时9分B.27日11时9分C.29日12时g分D.28日11时9分4.该岛附近作为板块边界的海沟的走向为A.东西向B.东北—西南向C.南北向D.西北—东南向5.该海沟两侧的板块是A.亚欧板块、太平洋板块B.南极洲板块、印度洋板块C.亚欧板块、印度洋板块D.印度详板块、非洲板块图1表示世界四个地点的气温降水状况。
据此回答6-9题。
6.位于热带气候区的地点是A.①B.②C.③D.④7.位于南半球的地点是A①B.②C.③D.④8.位于地中海气候区的地点是A.①②B.②③C.③④D.①④9.位于中高纬度大陆东岸的地点是A.①B.②C.③D.④。
并列短语中暗藏的语病透析

并列短语中暗藏的语病透析辨析并修改病句是每年高考必考的一个考点,笔者在整理往年的高考试题和模拟题时发现,命题人在“并列短语”上设置陷阱的病句特别多。
为了引起广大备考师生的的重视,今归类整理如下,以期为备战高考的师生提供帮助。
一、语序不当并列的短语之间都有一定的逻辑顺序,命题人设置的陷阱是,故意打乱并列短语之间的顺序,造成语序不当的语病。
如:1、任何一种文明的发展都是与其他文明碰撞、融合、交流的过程,完全封闭的环境不可能带来文明的进步,只会导致文明的衰落。
(2008年江苏卷)语序不当,“碰撞、融合、交流”应改为“碰撞、交流、融合”。
2、树立和落实科学发展观,发展和重视农业产后经济,应当成为解决我国:“三农”问题的重要组成部分。
(2007年安徽卷)语序不当,“发展和重视”应改为“重视和发展”。
3、这项基金,是对公益林管理者发生的管理、抚育、保护和营造等支出给予一定补助的专项资金。
(2006年安徽卷)语序不当,“公益林管理者发生的管理、抚育、保护和营造”应改为“公益林管理者所发生的营造、抚育、管理和保护”。
4、能抵抗诱惑、追求更远大目标、克制自己的孩子,长大之后会表现得更有自信,也更能面对挫折。
语序不当,“能抵抗诱惑、追求更远大目标、克制自己的孩子”应改为“能克制自己、抵抗诱惑、追求更远大目标的孩子”。
5、一个人从一些甜美的回忆中得到的某种难以言传的慰藉和快乐,恐怕不下于地质学家和历史学家追溯某个兴衰史和自然界的演化史所得到的乐趣。
语序不当,应改为“历史学家和地质学家”才能与后面的内容照应。
6、最该人民法院院长肖扬要求全国各级法院进一步完善和改革少年审判制度,充分发挥少年法庭的职能作用,为构建社会主义和谐社会做出新的贡献。
语序不当,“完善和改革”应改为“改革和完善”。
7、只要引导得当,学生上网,利大于弊,他们可以上网查询,扩大知识面,增长见识,获取信息。
语序不当,“扩大知识面,增长见识,获取信息”应为“获取信息,增长见识,扩大知识面”。
2005年高考全国卷1理科数学(含答案)

2005年普通高等学校招生全国统一考试理科数学(必修+选修Ⅰ)第I 卷一、选择题:1.设I 为全集,S 1、S 2、S 3是I 的三个非空子集且S 1∪S 2∪S 3=I ,则下面论断正确的是( ) A . I S I ∩(S 2∪S 3)= B .S 1⊆( I S 2∩ I S 3)C . I S I ∩ I S 2 ∩ I S 3=D .S 1⊆( I S 2∪ I S 3)2.一个与球心距离为1的平面截球所得的圆面面积为π,则球的表面积为 ( )A .8π2B .8πC .4π2D .4π3.已知直线l 过点(-2,0),当直线l 与圆x y x 222=+有两个交点时,其斜率k 的取值范围是( )A .)22,22(-B .)2,2(-C .)42,42( D .)81,81(-4.如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且△ADE 、△BCF 均为正三角形,EF//AB ,EF=2,则该多面体的体积为( )A .32 B .33C .34 D .23 5.已知双曲线)0(1222>=-a y ax 的一条准线与抛物线x y 62-=的准线重合,则该双曲线的离心率为( )A .23 B .23 C .26 D .332 6.当20π<<x 时,函数x xx x f 2sin sin 82cos 1)(2++=的最小值为( )A .2B .32C .4D .347.设0>b ,二次函数122-++=a bx ax y 的图象下列之一:则a 的值为( )A .1B .-1C .251-- D .251+- 8.设10<<a ,函数)22(log )(2--=xx a a a x f ,则使x x f 的0)(<取值范围是( )A .)0,(-∞B .),0(+∞C .)3log ,(a -∞D .),3(log +∞a9.在坐标平面上,不等式组⎩⎨⎧+-≤-≥1||3,1x y x y 所表示的平面区域的面积为( )A .2B .23 C .223 D .210.在ABC ∆中,已知C BA sin 2tan=+,给出以下四个论断:①1cot tan =⋅B A ②2sin sin 0≤+<B A ③1cos sin 22=+B A ④C B A 222sin cos cos =+其中正确的是( ) A .①③ B .②④ C .①④D .②③ 11.过三棱柱任意两个顶点的直线共15条,其中异面直线有( )A .18对B .24对C .30对D .36对 12.复数=--ii 2123( )A .iB .i -C .i -22D .i +-22第Ⅱ卷注意事项:1.用钢笔或圆珠笔直接答在试题卷中. 2.答卷前将密封线内的项目填写清楚. 3.本卷共10小题,共90分.二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上. 13.若正整数m 满足)3010.02.(lg ________,102105121≈=<<-m m m 则14.9)12(xx -的展开式中,常数项为 .(用数字作答)15.△ABC 的外接圆的圆心为O ,两条边上的高的交点为H ,)(OC OB OA m OH ++=,则实数m= .16.在正方体ABCD —A ′B ′C ′D ′中,过对角线BD ′的一个平面交AA ′于E ,交CC ′于F ,则①四边形BFD ′E 一定是平行四边形.②四边形BFD ′E 有可能是正方形.③四边形BFD ′E 在底面ABCD 内的投影一定是正方形. ④平面BFD ′E 有可能垂直于平面BB ′D.以上结论正确的为 .(写出所有正确结论的编号)三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)设函数)(),0)(2sin()(x f y x f =<<-+=ϕπϕπ图象的一条对称轴是直线.8π=x(Ⅰ)求ϕ;(Ⅱ)求函数)(x f y =的单调增区间;(Ⅲ)证明直线025=+-c y x 与函数)(x f y =的图象不相切.18.(本小题满分12分) 已知四棱锥P —ABCD 的底面为直角梯形,AB//DC ,∠DAB=90°,PA ⊥底面 ABCD ,且PA=AD=DE=21AB=1,M 是PB 的中点. (1)证明:面PAD ⊥面PCD ; (2)求AC 与PB 所成的角;(3)求面AMC 与面BMC 所成二面角的大小. 19.(本小题满分12分)设等比数列}{n a 的公比为q ,前n 项和S n >0(n=1,2,…)(1)求q 的取值范围; (2)设,2312++-=n n n a a b 记}{n b 的前n 项和为T n ,试比较S n 和T n 的大小. 20.(本小题满分12分) 9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为0.5,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑里的种子都没发芽,则这个坑需要补种,假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望.(精确到0.01) 21.(本小题满分14分) 已知椭圆的中心为坐标原点O ,焦点在x 轴上,斜率为1且过椭圆右焦点F 的直线交椭圆于A 、B 两点,OB OA +与)1,3(-=a 共线. (1)求椭圆的离心率;(2)设M 为椭圆上任意一点,且),(R OB OA OM ∈+=μλλλ,证明22μλ+为定值.22.(本小题满分12分)(1)设函数)10)(1(log )1(log )(22<<--+=x x x x x x f ,求)(x f 的最小值; (2)设正数n p p p p 2321,,,, 满足12321=++++n p p p p , 求证.log log log log 222323222121n p p p p p p p p n n -≥++++2005年普通高等学校招生全国统一考试理科数学(必修+选修I )参考答案一、选择题(本题考查基本知识和基本运算,每小题5分,满分60分)1.A 2.C 3.B 4.C 5.A 6.D 7.C 8.B 9.C 10.B 11.B 12.D 二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分. 13.155 14.672 15.1 16.①③④ 三、解答题17.本小题主要考查三角函数性质及图像的基本知识,考查推理和运算能力,满分12分. 解:(Ⅰ))(8x f y x ==是函数π的图像的对称轴,,1)82sin(±=+⨯∴ϕπ.,24Z k k ∈+=+∴ππππ.43,0πϕϕπ-=<<- (Ⅱ)由(Ⅰ)知).432sin(,43ππϕ-=-=x y 因此 由题意得.,2243222Z k k x k ∈+≤-≤-πππππ所以函数.],85,8[)432sin(Z k k k x y ∈++-=πππππ的单调增区间为(Ⅲ)证明:,2|)432cos(2||))432(sin(|||≤-='-='ππx x y所以曲线)(x f y =的切线斜率取值范围为[-2,2],而直线025=+-c y x 的斜率为225>,所以直线025=+-c y x 与函数)432sin(π-=x y 的图像不相切. 18.本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力.满分12分. 方案一:(Ⅰ)证明:∵PA ⊥面ABCD ,CD ⊥AD , ∴由三垂线定理得:CD ⊥PD.因而,CD 与面PAD 内两条相交直线AD ,PD 都垂直, ∴CD ⊥面PAD.又CD ⊂面PCD ,∴面PAD ⊥面PCD.(Ⅱ)解:过点B 作BE//CA ,且BE=CA ,则∠PBE 是AC 与PB 所成的角.连结AE ,可知AC=CB=BE=AE=2,又AB=2,所以四边形ACBE 为正方形. 由PA ⊥面ABCD 得∠PEB=90° 在Rt △PEB 中BE=2,PB=5, .510cos ==∠∴PB BE PBE.510arccos所成的角为与PB AC ∴ (Ⅲ)解:作AN ⊥CM ,垂足为N ,连结BN. 在Rt △PAB 中,AM=MB ,又AC=CB , ∴△AMC ≌△BMC,∴BN ⊥CM ,故∠ANB 为所求二面角的平面角. ∵CB ⊥AC ,由三垂线定理,得CB ⊥PC , 在Rt △PCB 中,CM=MB ,所以CM=AM. 在等腰三角形AMC 中,AN ·MC=AC AC CM ⋅-22)2(, 5625223=⨯=∴AN . ∴AB=2,322cos 222-=⨯⨯-+=∠∴BN AN AB BN AN ANB 故所求的二面角为).32arccos(-方法二:因为PA ⊥PD ,PA ⊥AB ,AD ⊥AB ,以A 为坐标原点AD 长为单位长度,如图建立空间直角坐标系,则各点坐标为A (0,0,0)B (0,2,0),C (1,1,0),D (1,0,0),P (0,0,1),M (0,1,)21. (Ⅰ)证明:因.,0),0,1,0(),1,0,0(DC AP DC AP DC AP ⊥=⋅==所以故由题设知AD ⊥DC ,且AP 与AD 是平面PAD 内的两条相交直线,由此得DC ⊥面PAD. 又DC 在面PCD 上,故面PAD ⊥面PCD. (Ⅱ)解:因),1,2,0(),0,1,1(-==PB AC.510||||,cos ,2,5||,2||=⋅⋅>=<=⋅==PB AC PBAC PB AC PB AC PB AC 所以故(Ⅲ)解:在MC 上取一点N (x ,y ,z ),则存在,R ∈λ使,MC NC λ=..21,1,1),21,0,1(),,1,1(λλ==-=∴-=---=z y x MC z y x NC要使.54,0210,==-=⋅⊥λ解得即只需z x MC AN MC AN),52,1,51(),52,1,51(,.0),52,1,51(,54=⋅-===⋅=MC BN BN AN MC AN N 有此时能使点坐标为时可知当λANB MC BN MC AN MC BN MC AN ∠⊥⊥=⋅=⋅所以得由.,0,0为所求二面角的平面角.).32arccos(.32||||),cos(.54,530||,530||--=⋅=∴-=⋅==故所求的二面角为BN AN BNAN BN AN BN AN BN AN19. 本小题主要考查等比数列的基本知识,考查分析问题能力和推理能力,满分12分. 解:(Ⅰ)因为}{n a 是等比数列,.0,0,011≠>=>q S a S n 可得 当;0,11>==na S q n 时),2,1(,011,01)1(,11 =>-->--=≠n qqq q a S q nn n 即时当上式等价于不等式组:),2,1(,01,01 =⎩⎨⎧<-<-n q q n① 或),2,1(,01,01 =⎩⎨⎧>->-n q q n②解①式得q>1;解②,由于n 可为奇数、可为偶数,得-1<q<1. 综上,q 的取值范围是).,0()0,1(+∞⋃-(Ⅱ)由得1223++-=n a n a a b .)23(),23(22n n n n S q q T q q a b -=-=于是)123(2--=-q q S S T n n n).2)(21(-+=q q S n.,0,2,21;,0,0221;,0,2211,,001,0n n n n n n n n n n n n n S T S T q q S T S T q q S T S T q q q q S ==-=-=<<-≠<<->>->-<<-><<->即时或当即时且当即时或当所以或且又因为 20.本小题主要考查相互独立事件和互斥事件有一个发生的概率的计算方法,考查运用概率知识解决实际问题的能力. 满分12分.(Ⅰ)解:因为甲坑内的3粒种子都不发芽的概率为81)5.01(3=-,所以甲坑不需要补种的概率为 .87811=-3个坑都不需要补种的概率,670.0)87()81(303=⨯⨯ C恰有1个坑需要补种的概率为,287.0)87(81213=⨯⨯C恰有2个坑需要补种的概率为,041.087)81(223=⨯⨯C3个坑都需要补种的概率为.002.0)87()81(0333=⨯⨯C补种费用ξ的分布为ξ的数学期望为75.3002.030041.020287.010670.00=⨯+⨯+⨯+⨯=ξE21.本小题主要考查直线方程、平面向量及椭圆的几何性质等基本知训,考查综合运用数学知识解决问题及推理的能力,满分14分.(I )解:设椭圆方程为),0,(),0(12222c F b a by a x >>=+则直线AB 的方程为1,2222=+-=by a x c x y 代入化简得02)(22222222=-+-+b a c a cx a x b a .令),,(),,(2211y x B y x A则 .,22222222122221ba b a c a x x b a c a x x +-=+=+),,(2121y y x x OB OA ++=+由a OB OA a 与+-=),1,3(共线,得.0)()(32121=+++x x y y.36,36.3,232.23,0)()2(3,,22222222121212211===-=∴==+=+∴=++-+∴-=-=a c e ab ac b a cba c a c x x x x c x x c x y c x y 故离心率所以即又 (II )证明:由(I )知223b a =,所以椭圆12222=+by a x 可化为22233b y x =+.),,(),(),(),,(2211y x y x y x y x OM μλ+==由已知得设 ⎩⎨⎧+=+=∴.,2121y y y x x x μλμλ ),(y x M 在椭圆上,.3)(3)(2221221b y y x x =+++∴μλμλ即 .3)3(2)3()3(221212222221212b y y x x y x y x =+++++λμμλ ①由(I )知.21,23,23222221c b c a c x x ===+))((33.8321212121222222221c x c x x x y y x x c ba b a c a x x --++=+∴=+-=∴ .0329233)(3422222121=+-=++-=c c c c c x x x x又222222212133,33b y x b y x =+=+又,代入①得 .122=+μλ 故22μλ+为定值,定值为1.22.本小题主要考查数学归纳法及导数应用等知识,考查综合运用数学知识解决问题的能力.满分12分.(Ⅰ)解:对函数)(x f 求导数:])1(log )1[()log ()(22'--+'='x x x x x f.2ln 12ln 1)1(log log 22-+--=x x ).1(log log 22x x --=于是.0)21(='f当)(,0)1(log log )(,2122x f x x x f x <--='<时在区间)21,0(是减函数, 当)(,0)1(log log )(,2122x f x x x f x >--='>时在区间)1,21(是增函数.所以21)(=x x f 在时取得最小值,1)21(-=f ,(Ⅱ)证法一:用数学归纳法证明.(i )当n=1时,由(Ⅰ)知命题成立.(ii )假定当k n =时命题成立,即若正数1,,,221221=+++k k p p p p p p 满足, 则.log log log 222222121k p p p p p p k k -≥+++当1+=k n 时,若正数,1,,,11221221=+++++k k p p p p p p 满足 令.,,,,222211221xp q x pq x p q p p p x k k k ===+++= 则k q q q 221,,, 为正数,且.1221=+++k q q q由归纳假定知.log log log 222222121k q q p p p q k k -≥+++kk k k q q q q q q x p p p p p p 222222121222222121log log log (log log log +++=+++,log )()log 22x x k x x +-≥+ ①同理,由x p p p k k k -=++++++1122212 可得1122212212log log ++++++k k k k p p p p).1(log )1())(1(2x x k x --+--≥ ②综合①、②两式11222222121log log log +++++k k p p p p p p).1()1(log )1(log ))](1([22+-≥--++--+≥k x x x x k x x即当1+=k n 时命题也成立.根据(i )、(ii )可知对一切正整数n 命题成立. 证法二:令函数那么常数)),,0(,0)((log )(log )(22c x c x c x c x x x g ∈>--+=],log )1(log )1(log [)(222c cxc x c x c x c x g +--+=利用(Ⅰ)知,当.)(,)2(21取得最小值函数时即x g cx c x == 对任意都有,0,021>>x x2log 22log log 21221222121x x x x x x x x ++⋅≥+ ]1)()[log (21221-++=x x x x . ① 下面用数学归纳法证明结论.(i )当n=1时,由(I )知命题成立.(ii )设当n=k 时命题成立,即若正数有满足,1,,,221221=+++k k p p p p p p11111122212212222121221221222222121log log log log .1,,,,1.log log log ++++++++++==++++=-≥+++--k k k k k k k k p p p p p p p p H p p p p p p k n k p p p p p p 令满足时当由①得到,1)()(],1)()[log (]1)()[log (11111121221212221221221=++++-++++-++≥++++++---k k k k k k p p p p p p p p p p p p H 因为由归纳法假设得到,)(log )()(log )(1111212221221221k p p p p p p p p k k k k -≥++++++++++-- ).1()(1121221+-=++++--≥+++k p p p p k H k k 即当1+=k n 时命题也成立. 所以对一切正整数n 命题成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2005年高考·全国卷Ⅲ(四川、云南、陕西等地区用)文科数学(含参考答案评分标准)2005年普通高等学校招生全国统一考试(四川)文科数学(必修+选修Ⅰ)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分. 共150分. 考试时间120分钟.第I 卷参考公式: 如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B )如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率P n (k)=C k n P k (1-P)n -k一、选择题:(1)已知α为第三象限角,则2α所在的象限是(A )第一或第二象限 (B )第二或第三象限(C )第一或第三象限 (D )第二或第四象限(2)已知过点A(-2,m)和B(m ,4)的直线与直线2x+y-1=0平行,则m 的值为(A )0 (B )-8 (C )2 (D )10 (3)在8(1)(1)x x -+的展开式中5x 的系数是(A )-14 (B )14 (C )-28 (D )28(4)设三棱柱ABC-A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B-APQC 的体积为(A )16V (B )14V (C )13V (D )12V(5)设173x=,则(A )-2<x<-1 (B )-3<x<-2 (C )-1<x<0 (D )0<x<1 (6)若ln 2ln 3ln 5,,235a b c ===,则(A)a<b<c (B)c<b<a (C)c<a<b (D)b<a<c (7)设02x π≤≤,sin cos x x =-,则球的表面积公式S=42R π其中R 表示球的半径, 球的体积公式V=334R π,其中R 表示球的半径(A) 0x π≤≤ (B) 744x ππ≤≤(C)544x ππ≤≤(D)322x ππ≤≤(8)22sin 21cos 2cos 2cos αααα⋅=+(A) tan α (B) tan 2α (C) 1 (D)12(9)已知双曲线2212yx -=的焦点为F 1、F 2,点M 在双曲线上且120,M F M F ⋅=则点M到x 轴的距离为(A )43(B )53(C)3(D(10)设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是 (A)2(B)12(C)2- (D1(11)不共面的四个定点到平面α的距离都相等,这样的平面α共有(A )3个 (B )4个 (C )6个 (D )7个(12)计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A ~F 共16个计数符号,这些符号与十进制的数的对应关系如下表:(A )6E (B )72 (C )5F (D )B0第Ⅱ卷二.填空题(16分)(13)经问卷调查,某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多 人(14)已知向量(,12),(4,5),(,10)O A k O B O C k ===-,且A 、B 、C 三点共线,则k=(15)曲线32y x x=-在点(1,1)处的切线方程为(16)已知在△ABC 中,∠ACB=90°,BC=3,AC=4,P 是AB 上的点,则点P 到AC 、BC 的距离乘积的最大值是 三.解答题:(17)(本小题满分12分)已知函数2()2sin 2,[0,2].sin f x x x x π=+∈求使()f x 为正值的x 的集合.(18)(本小题满分12分)设甲、乙、丙三台机器是否需要照顾相互之间没有影响。
已知在某一小时内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照顾的概率为0.125, (Ⅰ)求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少; (Ⅱ)计算这个小时内至少有一台需要照顾的概率. (19)(本小题满分12分)在四棱锥V-ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD . (Ⅰ)证明AB ⊥平面VAD .(Ⅱ)求面VAD 与面VDB 所成的二面角的大小.(20)(本小题满分12分)在等差数列241{},0,n d a a a a ≠在等差数列中公差与的等差中项,是已知数列1213,,,,n k k k a a a a a 成等比数列,求数列{}n k 的通项n k(21) (本小题满分12分)用长为90cm,宽为48cm 的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?(22) (本小题满分14分) 设1212(,),(,)A B yyx x 两点在抛物线22y x =上,l 是AB 的垂直平分线,(Ⅰ)当且仅当12x x+取何值时,直线l 经过抛物线的焦点F ?证明你的结论;(Ⅱ)当121,3x x ==-时,求直线l 的方程.2005年高考文科数学(四川)参考答案一.DBBCA ,CCBCD ,BA 二.13、3,14、23-,15、x+y-2=0,16、12三.解答题:解:∵()1cos 2sin 2f x x x =-+……………………………………………2分1)4x π=+-………………………………………………4分()012s i n (2)04f x x π∴>⇔->sin(2)42x π⇔->-…………………………………………6分5222444k x k πππππ⇔-+<-<+……………………………8分34k x k πππ⇔<<+………………………………………………10分又[0,2].x π∈ ∴37(0,)(,)44x πππ∈⋃………………………………………………12分(18)解:(Ⅰ)记甲、乙、丙三台机器在一小时需要照顾分别为事件A 、B 、C ,……1分 则A 、B 、C 相互独立, 由题意得:P (AB )=P (A )P (B )=0.05P (AC )=P (A )P (C )=0.1P (BC )=P (B )P (C )=0.125…………………………………………………………4分 解得:P (A )=0.2;P (B )=0.25;P (C )=0.5所以, 甲、乙、丙每台机器在这个小时内需要照顾的概率分别是0.2、0.25、0.5……6分 (Ⅱ)∵A 、B 、C 相互独立,∴A B C 、、相互独立,……………………………………7分 ∴甲、乙、丙每台机器在这个小时内需都不需要照顾的概率为()()()()0.80.750.50.3P A B C P A P B P C ⋅⋅==⨯⨯=……………………………10分∴这个小时内至少有一台需要照顾的概率为1()10.30.7p P A B C =-⋅⋅=-=……12分(19)证明:(Ⅰ)作AD 的中点O ,则VO ⊥底面ABCD .…………………………1分建立如图空间直角坐标系,并设正方形边长为1,…………………………2分 则A (12,0,0),B (12,1,0),C (-12,1,0),D (-12,0,0),V (0,02),∴1(0,1,0),(1,0,0),(,0,)22AB AD AV ===- ………………………………3分由(0,1,0)(1,0,0)0AB AD AB AD ⋅=⋅=⇒⊥……………………………………4分 1(0,1,0)(,0,)022AB AV AB AV ⋅=⋅-=⇒⊥ ……………………………………5分又AB ∩A V=A∴AB ⊥平面VAD …………………………………………………………………………6分(Ⅱ)由(Ⅰ)得(0,1,0)AB =是面VAD 的法向量………………………………7分设(1,,)n y z =是面VDB 的法向量,则110(1,,)(,1,0(1,1,2230(1,,)(1,1,0)03x n VB y z n z n BD y z =-⎧⎧⎧⋅=⋅--=⎪⎪⎪⇒⇒⇒=-⎨⎨⎨=-⋅=⎪⎪⎪⎩⋅--=⎩⎩……9分∴(0,1,0)(1,1,)cos ,73AB n ⋅-<>==-11分又由题意知,面VAD 与面VDB所成的二面角,所以其大小为arccos 7…………12分(20)解:由题意得:2214a a a=……………………………………………………1分即211(3)1()d da aa=++……………………………………………………………3分又0,d ≠∴1d a =…………………………………………………………………………4分 又1213,,,,n k k k a a a a a 成等比数列, ∴该数列的公比为3133d q da a===,……………………………………………………6分所以113n n k a a +=⋅…………………………………………………………………………8分又11(1)n k n nd a a k k a=+-=…………………………………………………………10分∴13n n k +=所以数列{}n k 的通项为13n n k +=…………………………………………………………12分(21)解:设容器的高为x ,容器的体积为V ,……………………………………………1分 则V=(90-2x )(48-2x )x,(0<V<24)…………………………………………………………5分 =4x 3-276x 2+4320x∵V ′=12 x 2-552x+4320………………………………………………………………………7分 由V ′=12 x 2-552x+4320=0得x 1=10,x 2=36 ∵x<10 时,V ′>0,10<x<36时,V ′<0, x>36时,V ′>0,所以,当x=10,V 有极大值V(10)=1960……………………………………………………10分 又V(0)=0,V(24)=0,…………………………………………………………………………11分 所以当x=10,V 有最大值V(10)=1960………………………………………………………12分(22)解:(Ⅰ)∵抛物线22y x =,即22y x =,∴14p =,∴焦点为1(0,)8F ………………………………………………………………1分 (1)直线l 的斜率不存在时,显然有12x x+=0………………………………3分(2)直线l 的斜率存在时,设为k , 截距为b即直线l :y=kx+b 由已知得:12121212221k bkyy x xy y xx⎧++⎪=⋅+⎪⎨-⎪=-⎪-⎩……………………………………………………5分2212122212122212222k b k x x x x x x x x ⎧++=⋅+⎪⎪⇒⎨-⎪=-⎪-⎩22121212212k bk x x x x x x +⎧+=⋅+⎪⎪⇒⎨⎪+=-⎪⎩………………………………………………7分2212104b xx⇒+=-+≥14b ⇒≥即l 的斜率存在时,不可能经过焦点1(0,)8F ……………………………………8分所以当且仅当12x x+=0时,直线l 经过抛物线的焦点F …………………………9分(Ⅱ)当121,3x x ==-时,直线l 的斜率显然存在,设为l :y=kx+b ………………………………10分则由(Ⅰ)得:22121212212k bk x x x x x x +⎧+=⋅+⎪⎪⎨⎪+=-⎪⎩ 12102122k b kxx+⎧⋅+=⎪⎪⇒⎨⎪-=-⎪⎩………………………………………………11分14414k b ⎧=⎪⎪⇒⎨⎪=⎪⎩………………………………………………………………13分 所以直线l 的方程为14144y x =+,即4410x y -+=………………14分。
