甘肃省瓜州县第二中学七年级数学下册 3.3 用图象表示的变量间关系课时作业1

合集下载

七年级数学下册第三章变量之间的关系用图象表示的变量间关系一课一练基础闯关(新版)北师大版

用图象表示的变量间关系一课一练·基础闯关题组用图象表示的变量间关系1.如图是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )A.凌晨4时气温最低为-3℃B.14时气温最高为8℃C.从0时至14时,气温随时间增长而上升D.从14时至24时,气温随时间增长而下降【解析】选C. A.因为由图象可知,在凌晨4时函数图象在最低点-3,所以凌晨4时气温最低为-3℃,故本选项正确;B.因为由图象可知,在14时函数图象在最高点8,所以14时气温最高为8℃,故本选项正确;C.因为由图象可知,从4时至14时,气温随时间增长而上升,不是从0点,故本选项错误;D.因为由图象可知,14时至24时,气温随时间增长而下降,故本选项正确.2.(2017·呼和浩特中考)如图是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )A.2010年至2014年间工业生产总值逐年增加B.2014年的工业生产总值比前一年增加了40亿元C.2012年与2013年每一年与前一年比,其增长额相同D.从2011年至2014年,每一年与前一年比,2014年的增长率最大【解析】选D.(40-20)÷20×100%=100%,∴2012年的增长率为100%,最大.3.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子的价格打6折,设购买种子数量x千克,付款金额为y元,则y与x的关系的图象大致是 ( )【解析】选B.可知2千克以下付款金额y元随购买种子数量x千克增大而增大,超过2千克的部分打6折,y 仍随x的增大而增大,不过增加慢了.4.(2017·南通中考)有一个进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )A.5LB.3.75LC.2.5LD.1.25L【解析】选B.第一阶段(0<x≤4),时间4分钟,水增加了20L,因此进水速度为5L/min;第二阶段(4<x<12),时间8分钟,水增加了10L,因此进水和出水合计速度为 1.25L/min;综合来看出水速度应为5-1.25=3.75L/min.题组路程-时间图象的应用1.小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会儿太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间x(分钟)之间关系的大致图象是( )【解析】选B.“爷爷从家里跑步到公园”,反映在图象上是一条斜线段,一端点是O;爷爷在公园“打了一会儿太极拳”,说明这段时间x(分钟)在增加,但爷爷离家的距离y(米)没变,反映在图象上是一条水平线段;然后“沿原路慢步走到家”,说明最终的距离y(米)为0,反映在图象上也是一条斜线段,其中一端点在x轴上,与第一条线段相比,线段的倾斜程度较为平缓。

用图象表示的变量间关系(第二课时)

第四章变量之间的关系
3.3用图象表示的变量间关系（第二课时）
【复习回顾】1、表示变量之间的关系常常用三种方法。 2、在关系式S=4t中,自变量是 ,因变量是 ,当t=1.5时,S= . 3、已知等腰三角形的底为3,腰长为x,则周长y可以表示为 . 4、如图是某地区一天的气温随时间变化的图像，根据图像回答，在这一天中，
s
s s
s
O A
t
OtO CFra bibliotektO
D
t
B
7、一辆在高速公路上以150千米/时的速度匀速行驶的汽车，下列哪一张图象能大致刻画汽车的速度与时间的关系（）
A
B
C
D
速度
0
速度
时间速度
0 0
A
B
时间
速度时间
C
0
D
时间
2、下列各情境分别可以用哪幅图来近似地刻画？、 1.一杯越来越凉的水(水温与时间的关系)； 2.一面冉冉上升的旗子(高度与时间的关系)； 3.足球守门员大脚开出去的球(高度与时间的关系)；
4.匀速行驶的汽车(速度与时间的关系)
s s t A O B t s O C t s O D t
时间
(4) 6 12 18 24
时间
0
5、某同学从第一中学走回家，在路上他碰到两个同学，于是在文化宫玩了一会儿，然后再回家，图中哪一幅图能较好地刻画出这位同学离家所剩的路程与时间的变化情况：
A
B
C
D
6、李明骑车上学，一开始以某一速度行进，途中车子发生故障，只好停下来修车，车修好后，因怕耽误上学时间，于是加快车速，在下图中给出的示意图中（s为距离，t为时间）符合以上情况的是（）

北师大版七年级数学下3.3用图像表示的变量关系同步练习含答案

3.3用图像表示的变量关系课后拓展训练1．如图6—13所示的是一游泳池断面图，分为深水区和浅水区，排空池里的水进行清理后，打开进水阀门连续向该池注水(此时已关闭排水阀门)．则游泳池的蓄水高度h(米)与注水时间t (时)之间的关系的大致图象是(如图6—14所示) ( )2．打开某洗衣机开关，在洗涤衣服时(洗衣机内无水)，洗衣机经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种变量关系，其图象(如图6—15所示)大致为 ( )3．早晨小强从家出发，以v1的速度前往学校，途中在一饮食店吃早点，之后以v2的速度向学校行进．已知v1> v2，如图6—16所示的图象中表示小强从家到学校的时间t(分钟)与路程s(千米)之间的关系的是( )4．如图6—17所示的是一位护士统计某病人的体温变化图，这位病人中午12时的体温约为 ( )A．39．0℃ B．38．5℃C．38．2℃ D．37．8℃5．小明根据邻居家的故事写了一首小诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还”．如果用纵轴y表示父亲与儿子行进中离家的距离，横轴x表示父亲离家的时间，那么如图6—18所示的图象中与上述诗的含义大致吻合的是 ( )6，如图6-19所示，向高为h的圆柱形水杯注水，已知水杯底面半径为2，那么水深y与注水量x之间关系的图象是 ( )7．甲、乙两个水桶内水面的高度y(cm)与放水(或注水)的时间x(分)之间关系的图象如图6-20所示，当两个水桶内水面的高度相同时，x约为分．(精确到0．1分)8．城镇人口占总人口比例的大小表示城镇化水平的高低，如图6-21所示，可知城镇化水平提高最快的时期是.9．四个容量相等的容器形状如图6—22所示，用同一流量的水管分别向这四个容器注水，所需时间都相同，如图6—23所示的是容器水位(h)与时间(t)的关系的图象．请把适当的图象序号与相应容器形状的字母代号用线段相连接．10．如图6—24所示的图象记录了某地一月份某天的温度随时间变化．的情况，请你仔细观察图象回答下面的问题：(1)20时的温度是℃，温度是0℃时的时刻是时，最暖和的时刻是时，温度在-3℃以下的持续时间为时；(2)从图象中还能获取哪些信息?(写出1~2条即可)11．如图6—25所示的是甲、乙两人在争夺冠军中的比赛图，其中t表示赛跑时所用时间，s表示赛跑的距离，根据图象回答下列问题：(1)图象反映了哪两个变量之间的关系?(2)他们进行的是多远的比赛?(3)谁是冠军?(4)乙在这次比赛中的速度是多少?参考答案1．D[提示：根据图形分析全部注水的过程是关键．]2．D[提示：洗衣机内原本无水，水量从0开始逐渐增加，清洗过程中，洗衣机中的水量不变，排水时，排出的水小于进入的水．故选D．]3．A4．C[提示：看图估计比38℃略高些．]5．C6．A7．2．7[提示：答案属于估算，是近似值，2．6或2．8也可以．]8．1990年～2002年9．解：如图6—26所示．10．(1)-l 12，18 8 (2)解：从图象中还能获取：从4时到14时，温度逐渐升高；最低气温约为-4．5℃；最高气温是2℃；温度在0℃以上的时刻是在12时到18时等信息．11．解：(1)反映了赛跑距离s 与时间t 之间的关系． (2)他们进行的是200 m 赛跑的比赛．(3)甲是冠军． (4)825200==乙v (m/s)．。

《同步课时卷》北师大版七年级数学(下册)3.3用图象表示的变量间关系(1)(附参考答案)

《同步课时卷》北师大版七年级数学（下册）3.3用图象表示的变量间关系（1）1.用图象表示自变量与因变量之间的关系的方法,叫做,这种方法明显的特点是.2.从表示两个变量关系的图象中,不仅能根据一个变量找出另一个变量的,而且能从图象上看出.3.海水受日月的引力而产生潮汐现象.早晨海水上涨叫潮,黄昏海水上涨叫汐,合称潮汐.下面是某港口从0时刻到10时的水深情况,根据图象回答.图3-3-1(1)在时到时, 时到时,港口的水深在增加;(2)大约在时,深度最深,大约m.4.学校升旗仪式上,徐徐上升的国旗的高度与时间的关系可以用一幅图近似地表示,这幅图是下列选项中的( )A.B.C.D.5.下列各情景可以用哪幅图来近似地刻画( )(1)一个球被竖直向上抛起,球上升到最高点,垂直下落,直到地面,在此过程中,球的高度与时间的关系;(2)将常温中的温度计插入一杯60℃的热水中,温度计的度数与时间的关系;(3)在长方体洗衣机放水的过程中,水的高度与时间的关系.A.③,②,①B.②,③,①C.②,①,③D.①,②,③6.下面的折线图描述了某地某日的气温变化情况,根据图中提供的信息,下列结论错误的是( )图3-3-2A.这一天的温差是10℃B.在0:00~4:00时气温在逐渐下降C.在4:00~14:00时气温一直在上升D.14:00时气温最高7.甲、乙两人在操场上赛跑,他们赛跑的路程s(米)与时间t(分钟)之间的关系如图3-3-3所示,则下列说法错误的是( )图3-3-3A.甲、乙两人进行1000米赛跑B.甲先慢后快,乙先快后慢C.比赛到2分钟时,甲、乙两人跑过的路程相等D.甲先到达终点8.光合作用是指绿色植物通过叶绿体,利用光能,把二氧化碳和水转化成储存着能量的有机物,并释放氧气的过程,如图3-3-4是某日某种绿色植物叶片光合作用强度的曲线图,分析曲线图回答:图3-3-4(1)大约从7时到时的光合作用的强度不断增强;(2)从时到时,光合作用强度不断减弱.9.某机动车出发前油箱中有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量Q(升)与行驶时间t(时)之间的关系如图3-3-5,根据所给图象回答问题:图3-3-5(1)机动车行驶小时后加油;(2)中途加油升;(3)机动车每小时耗油升;(4)如果加油站距目的地还有240千米,机动车车速为40千米/时,要到达目的地,油箱中的油是否够用?(说明理由)10.如图3-3-6所示的折线ABC是甲地向乙地打长途电话所需要付的电话费y与通话时间t之间的关系的图象.图3-3-6(1)通话1分钟,要付电话费多少元?通话5分钟,要付多少电话费?(2)通话在多少分钟内,所支付的电话费不变?(3)如果通话超过3分钟,电话费y与时间t的关系式是y=2.5+(t-3),那么通话4分钟的电话费是多少?11.向高为h的圆柱形空水杯中注水,表示注水量y与水深x的关系的图象是下列选项中的( )A.B.C.D.12.小明和小红练习射击,第一轮10枪打完后两人的成绩如图3-3-7所示,一般新手的成绩不太稳定,小明和小红二人中有一个是新手,估计小明和小红两人中新手是.图3-3-713.放假了,小明和小聪去蔬菜加工厂参加社会实践,两人同时工作了一段时间后,休息时小明对小聪说:“我已加工了28千克,你呢?”小聪思考了一会儿说:“我来考考你,图3-3-8①、图3-3-8②分别表示你和我的工作量与工作时间的关系,你能算出我加工了多少千克吗?”小明思考后回答:“你难不倒我,你现在加工了千克.”图3-3-814.某医院为一位病人记录三天的体温情况如图3-3-9所示.图3-3-9由图可知:(1)护士每隔小时给病人量一次体温;(2)这位病人的体温最高是,最低是;(3)4月8日18时这位病人的体温是℃;(4)该病人的体温在的时间段里下降最快,在的时间段里比较稳定;(5)图中的虚线表示;(6)从这幅图中你还能得到的信息是: .15.某报报道了某地“养老保险执行新标准”的信息,实验中学数学课外活动小组根据消息提供的数据,绘制出本地区企业职工养老保险个人月缴费y(元)随个人月工资x(元)变化的图象,如图3-3-10所示,请你根据图象回答下列问题:图3-3-10(1)张工程师本月工资是3000元,这月他个人应缴养老保险多少元?(2)小陈本月工资为500元,这月他个人应缴养老保险多少元?(3)李师傅本月个人缴了养老保险83元,请问他的工资大约在什么范围内?参考答案1.图象法直观2.对应数值因变量随自变量的变化趋势3.(1)0 3 9 10(2)3 64.A5.A6.C7.C8.(1)11(2)15 199.(1)5(2)24(3)6(4)解:因为行驶240千米所需时间是240÷40=6(小时),加油后油箱中的油能燃烧的时间为36÷6=6(小时),所以够用.10.解:(1)通话1分钟,要付电话费2.5元;通话5分钟,要付电话费4.5元;(2)通话在3分钟以内,所支付的电话费不变;(3)因为通话超过3分钟,电话费y与时间t的关系式是:y=2.5+(t-3),所以通话4分钟的电话费:y=2.5+(4-3)=3.5(元).11.A12.小红13.2014.(1)6(2)39.5℃36.5℃(3)37(4)4月7日6时~12时4月7日18时~4月8日0时(5)正常体温(6)在4月9日病人体温最高为37.5℃15.解:(1)195元;(2)39元;(3)因为39<83<195,所以李师傅工资应在557元至2786元之间.。

甘肃省瓜州县第二中学七年级数学下册 2.3 平行线的性

平行线的性质一、选择题:1.如图1所示,AB ∥CD,则与∠1相等的角(∠1除外)共有( )A.5个B.4个C.3个D.2个DCBA 1EDCBAOF E D C BA(1) (2) (3)2.如图2所示,已知DE ∥BC,CD 是∠ACB 的平分线,∠B=72°,∠ACB=40°,•那么∠BDC 等于( )A.78°B.90°C.88°D.92°3.下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;•③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( ) A.① B.②和③ C.④ D.①和④二、填空题:1.如图6所示,如果DE ∥AB,那么∠A+______=180°,或∠B+_____=180°,根据是______;如果∠CED=∠FDE,那么________∥_________.根据是________.2.如图7所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、•后的两条路平行,若第一次拐角是150°,则第二次拐角为________.D CBADCBA12(7) (8) (9)3.如图8所示,AB ∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=_______,∠ACD=•_______.三、训练平台:1.如图9所示,AD∥BC,∠1=78°,∠2=40°,求∠ADC的度数.2.如图所示,AB∥CD,AD∥BC,∠A的2倍与∠C的3倍互补,求∠A和∠D的度数.•D CAB。

七年级数学下课本习题第3章变量之间的关系

第三章变量之间的关系第1节用表格表示的变量间关系1. P63-随堂练习-1略2. P63-随堂练习-2研究表明，当每公顷钾服和磷服的施用量一定时，土豆的产量与氮肥的施用量有如下关系：（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）当氮肥的施用量是101kg/hm2（hm2是单位“公顷”的符号）时，土豆的产量是多少？如果不施氮肥呢?（3）根据表格中的数据，你认为氮肥的施用量是多少时比较适宜？说说你的理由。

（4）粗略说一说氮肥的施用量对土豆产量的影响。

3. P63-习题3.1-1据世界人口组织公布，地球上的人口1600年为5亿，1830年为10亿，1930年为20亿，1960年为30亿，1974年为40亿，1987年为50亿，1999年为60亿，而到2011年地球上的人口数达到了70亿。

用表格表示上面的数据，并说一说世界人口是怎样随时间推移而变化的。

婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍，6周岁、10周岁时体重分别约是1周岁时的2倍、3倍。

（1）上述的哪些量在发生变化？自变量和因变量各是什么？（2）某婴儿在出生时的体重是3.5kg，请把他在发育过程中的体重情况填入下表：（3）根据表格中的数据，说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的。

5. P64-习题3.1-3略6. P64-习题3.1-4小明在课余时间找了几副度数不同的老花镜，让镜片正对着太阳光，并上下移动镜片，直到地上的光斑最小。

此时他测量了镜片与光斑的距离，得到如下数据：（1）观察表中的数据，你发现了什么？（2）如果按上述方法测得一副老花镜的镜片与光斑的距离为0.7m，那么你估计这副老花镜的度数是多少？在高海拔（1 500--3 500m为高海拔，3 500--5 500为超高海拔，5 500m以上为极高海拔）地区的人有缺氧的感觉，下面是有关海拔高度与空气含氧量之间的一组数据：（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）在海拔高度0m的地方空气含氧量是多少？海拔高度4 000m的地方空气含氧量是多少？（3）你估计在5 500m海拔高度空气含氧量是多少？第2节用关系式表示的变量间关系8. P67-随堂练习-1在地球某地，温度T（℃）与高度d（m）的关系可以近似地用T=10 -d150来表示。

北师大七年级数学下《3.3.1用图象表示变量关系》课后作业含答案

3.3.1用图象表示变量关系
课后作业
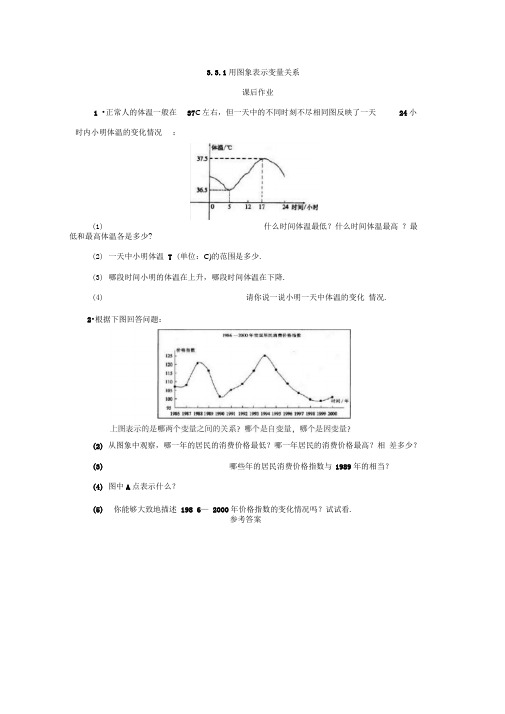
1 •正常人的体温一般在 37C 左右，但一天中的不同时刻不尽相同图反映了一天
时内小明体温的变化情况： (1)
什么时间体温最低？什么时间体温最高？最
低和最高体温各是多少? (2) 一天中小明体温 T (单位：C)的范围是多少.
(3) 哪段时间小明的体温在上升，哪段时间体温在下降.
(4)
请你说一说小明一天中体温的变化情况.
2•根据下图回答问题：
(2) 从图象中观察，哪一年的居民的消费价格最低？哪一年居民的消费价格最高？相差多少？
(3)
哪些年的居民消费价格指数与 1989年的相当？ (4) 图中A 点表示什么？
(5) 你能够大致地描述 198 6— 2000年价格指数的变化情况吗？试试看.
参考答案 24小
1.( 1) 5时最低，17时最高，最低气温为365C，最高气温为37.5 C.( 2) 365C至
375C之间.(3) 5时至17时体温上升，0时至5时和17时至24时体温在下降.(4)略
2.( 1)图象表示的是我国居民消费价格指数与时间之间的关系. 时间是自变量，居民消费价格指数是因变量.(2) 1994年最高，1999年最低，相差25.( 3) 1993年和1995
年.(4) 1998年的居民消费价格指数约为101.( 5)略，只要合理即可.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 用图像表示变量间的关系
1.在变化过程中，我们把变化着的量叫做变量，其中一个叫__________，一个叫_________.
2.表示两个变量之间的关系有______种，分别是_ .
3.在△ABC 中，当面积S 一定时，底边BC 的长度a 与
底边BC 上的高h 之间的关系式为________.
4.每周一，我们仰望国旗冉冉升起，请在图6－27中画
出国旗升高的高度h 与时间t 的大致图象.
5.图6－28表示一辆汽车行驶的速度和时间的图象，你
能用语言描述汽车的行驶情况吗？________ ________
图6－27 图6－28
6.已知关系式y=kx+2，且自变量x=－3时，因变量y=0,则当自变量x=9时，因变量y 的值是______.
7.（米
4
到发令枪的烟0.2秒后，听到了枪声，则由此可知，这个人距发令地点__________米.
二、选择题
1.汽车开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内余油量Q （升）与行驶时间t （时）的关系用图象表示应为图中的（）
2.弹簧的长度与所挂物体的质量的关系如图6－29所示，由图
可知不挂重物时弹簧的长度为（）
A.8 cm
B.9 cm
C.10 cm
D.11 cm
3.一根蜡烛长20 cm ，点燃后每小时燃烧5 cm,燃烧时剩下的高度y （cm ）与燃烧时间x （小时）的关系用下图中___ ____图象表示。