福建省晋江市季延中学2017_2018学年高二数学下学期期末考试试题理201808290222
福建省晋江市季延中学2017-2018学年高二下学期期末考试数学(理)试题 Word版含解析

季延中学2018年春高二年期末考试理科数学试卷考试时间 120分钟满分 150分一.填空题(12*5=60)1. 为了检查某超市货架上的奶粉是否含有三聚氰胺,要从编号依次为1到50的袋装奶粉中抽取5袋进行检验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的5袋奶粉的编号可能是()A. 5,10,15,20,25B. 2,4,8,16,32C. 1,2,3,4,5D. 7,17,27,37,47【答案】D【解析】利用系统抽样,把编号分为5段,每段10个,每段抽取1个,号码间隔为10,经验证只有选项D符合要求;故选D.2.下图是把二进制的数化成十进制数的一个程序框图,则判断框内应填入的条件是()A. B. C. D.【答案】C【解析】【分析】由题意输出的S=1+1×2+1×22+1×23+1×24,按照程序运行,观察S与i的关系,确定判断框内的条件即可.【详解】由题意输出的S=1+1×2+1×22+1×23+1×24,按照程序运行:S=1,i=1;S=1+1×2,i=2;S=1+1×2+1×22,i=3;S=1+1×2+1×22+1×23,i=4;S=1+1×2+1×22+1×23+1×24,i=5,此时跳出循环输出结果,故判断框内的条件应为i≤4.故选C.【点睛】本题主要考查的是程序框图,考查了进位制,本题是程序框图中的循环结构,是先进行了一次判断,实则是直到型性循环,这是一道基础题.首先将二进制数化为十进制数,得到十进制数的数值,然后假设判断框中的条件不满足,执行算法步骤,待累加变量的值为时,算法结束,此时判断框中的条件要满足,即可得到答案.3.用秦九韶算法求次多项式,当时,求需要算乘方、乘法、加法的次数分别为()A. B. C. D.【答案】D【解析】求多项式的值时,首先计算最内层括号内一次多项式的值,即然后由内向外逐层计算一次多项式的值,即..….这样,求n次多项式f(x)的值就转化为求n个一次多项式的值。
2017-2018学年福建省泉州市晋江二中高二(下)期末数学试卷(理科) Word版含解析

2017-2018学年福建省泉州市晋江二中高二(下)期末数学试卷(理科)一.选择题(每小题5分共60分)1.端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同,从中任意选取3个,则三种粽子各取到1个的概率是()A.B.C.D.2.函数y=x2sinx的导数为()A.y′=2xcosx+x2sinx B.y′=2xcosx﹣x2sinxC.y′=2xsinx+x2cosx D.y′=2xsinx﹣x2cosx3.“|x﹣1|<2成立”是“(x+2)(x﹣3)<0成立”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.函数f(x)=x﹣sinx在(﹣∞,+∞)内是()A.增函数B.减函数C.有增有减D.不能确定5.在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为()A.B.C.D.6.表中提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.根据下表提供的数据,求出y关于x的线性回归方程为=0.7x+0.35,那么表中t的值为()x 3 4 5 6y 2.5 t 4 4.5 A.3 B.3.15 C.3.5 D.4.57.已知ξ的分布列如下:ξ 0 1 2P并且η=3ξ+2,则方差Dη=()A.B.C.D.78.来晋江旅游的外地游客中,若甲、乙、丙三人选择去五店市游览的概率均为,且他们的选择互不影响,则这三人中至多有两人选择去五店市游览的概率为()A.B.C.D.9.设,则二项式的展开式的常数项是()A.12 B.6 C.4 D.210.数字“2015”中,各位数字相加和为8,称该数为“如意四位数”,则用数字0,1,2,3,4,5组成的无重复数字且大于2015的“如意四位数”有()个.A.21 B.22 C.23 D.2411.设y=f″(x)是y=f′(x)的导数.某同学经过探究发现,任意一个三次函数f(x)=ax3+bx2+cx+d (a≠0)都有对称中心(x0,f(x0)),其中x0满足f″(x0)=0.已知f(x)=﹣,则=()A.2012 B.2013 C.2014 D.20151+x)n的展开式中,x k的系数可以表示从n个不同物体中选出k个的方法总数.下列各式的展开式中x8的系数恰能表示从重量分别为1,2,3,4,…,10克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为8克的方法总数的选项是()A.(1+x)(1+x2)(1+x3)…(1+x10)B.(1+x)(1+2x)(1+3x)…(1+10x)C.(1+x)(1+2x2)(1+3x3)…(1+10x10)D.(1+x)(1+x+x2)(1+x+x2+x3)...(1+x+x2+ (x10)二.填空题(每小题4分共20分)13.计算=.14.已知随机变量X~N(3,σ2),若P(X<a)=0.8,则P(6﹣a<X<a)=.15.函数y=xe x在其极值点处的切线方程为.16.现有5种不同颜色的染料,要对如图中的四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色,则不同的着色方法的种数是(用数字作答).17.如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为.三.解答题(共70分)18.已知(﹣)n二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3(1)求n的值;(2)求展开式中x3项的系数(3)计算式子C﹣2C+4C﹣8C+…+1024C的值.19.已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.20.已知两个正数a,b满足a+b=1(1)求证:+≥4(2)若不等式|x﹣2|+|2x﹣1|≤+对任意正数a,b都成立,求实数x的取值范围.21.某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如表.优秀非优秀总计课改班50非课改班20 110合计210(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与课改有关”;(2)把全部210人进行编号,从编号中有放回抽取4次,每次抽取1个,记被抽取的4人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望Eξ.22.道路交通安全法中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q<80时,为酒后驾车;当Q≥80时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,依据上述材料回答下列问题:(Ⅰ)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;(Ⅱ)从违法驾车的8人中抽取2人,求取到醉酒驾车人数的分布列和期望,并指出所求期望的实际意义;(Ⅲ)饮酒后违法驾驶机动车极易发生交通事故,假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.1和0.25,且每位驾驶员是否发生交通事故是相互独立的.依此计算被查处的8名驾驶员中至少有一人发生交通事故的概率.(精确到0.01)并针对你的计算结果对驾驶员发出一句话的倡议.23.已知函数f(x)=﹣2alnx+(a﹣2)x,a∈R.(Ⅰ)当a=1时,求函数f(x)的最小值;(Ⅱ)当a≤0时,讨论函数f(x)的单调性;(Ⅲ)是否存在实数a,对任意的x1,x2∈(0,+∞),且x1≠x2,有>a,恒成立,若存在求出a的取值范围,若不存在,说明理由.2017-2018学年福建省泉州市晋江二中高二(下)期末数学试卷(理科)参考答案与试题解析一.选择题(每小题5分共60分)1.端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同,从中任意选取3个,则三种粽子各取到1个的概率是()A.B.C.D.考点:列举法计算基本事件数及事件发生的概率.专题:概率与统计.分析:从10个中任意选取3个,共有C103=120,其中三种粽子各取到1个有C21C31C51=30,根据古典概型的概率公式进行计算即可.解答:解:从10个中任意选取3个,共有C103=120,其中三种粽子各取到1个有C21C31C51=30,故从中任意选取3个,则三种粽子各取到1个的概率是=,故选:C.点评:本题考查了古典概率问题以及排列组合的问题,属于基础题.2.函数y=x2sinx的导数为()A.y′=2xcosx+x2sinx B.y′=2xcosx﹣x2sinxC.y′=2xsinx+x2cosx D.y′=2xsinx﹣x2cosx考点:导数的运算.专题:导数的概念及应用.分析:根据导数的运算法则求导即可.解答:解:y′=(x2sinx)′=(x2)′sinx+x2(sinx)′=2xsinx+x2cosx,故选:C.点评:本题考查了导数的运算法则,属于基础题.3.“|x﹣1|<2成立”是“(x+2)(x﹣3)<0成立”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据充分条件和必要条件的定义结合不等式的关系进行判断即可.解答:解:由|x﹣1|<2得﹣2<x﹣1<2,即﹣1<x<3,由(x+2)(x﹣3)<0得﹣2<x<3,∵(﹣1,3)⊊(﹣2,3),∴“|x﹣1|<2成立”是“(x+2)(x﹣3)<0成立”的充分不必要条件,故选:A.点评:本题主要考查充分条件和必要条件的判断,根据不等式的解法求出不等式的解集是解决本题的关键.4.函数f(x)=x﹣sinx在(﹣∞,+∞)内是()A.增函数B.减函数C.有增有减D.不能确定考点:利用导数研究函数的单调性.专题:导数的综合应用.分析:求出函数的导数,判断导数的符号,然后判断函数的单调性.解答:解:函数f(x)=x﹣sinx,可得f′(x)=1﹣cosx≥0,所以函数f(x)=x﹣sinx在(﹣∞,+∞)内是增函数.故选:A.点评:本题考查函数的单调性的判断,导数的应用,考查计算能力.5.在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为()A.B.C.D.考点:条件概率与独立事件.专题:计算题;概率与统计.分析:事件“第一次摸到红球且第二次也摸到红球”的概率等于事件“第一次摸到红球”的概率乘以事件“在第一次摸出红球的条件下,第二次也摸到红球”的概率.根据这个原理,可以分别求出“第一次摸到红球”的概率和“第一次摸到红球且第二次也摸到红球”的概率,再用公式可以求出要求的概率.解答:解:先求出“第一次摸到红球”的概率为:P1==,设“在第一次摸出红球的条件下,第二次也摸到红球”的概率是P2再求“第一次摸到红球且第二次也摸到红球”的概率为P==,根据条件概率公式,得:P2==,故选:D.点评:本题考查了概率的计算方法,主要是考查了条件概率与独立事件的理解,属于中档题.看准确事件之间的联系,正确运用公式,是解决本题的关键.6.表中提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.根据下表提供的数据,求出y关于x的线性回归方程为=0.7x+0.35,那么表中t的值为()x 3 4 5 6y 2.5 t 4 4.5A.3 B.3.15 C.3.5 D.4.5考点:回归分析的初步应用.专题:计算题.分析:先求出这组数据的样本中心点,样本中心点是用含有t的代数式表示的,把样本中心点代入变形的线性回归方程,得到关于t的一次方程,解方程,得到结果.解答:解:∵由回归方程知=,解得t=3,故选A.点评:本题考查回归分析的初步应用,考查样本中心点的性质,考查方程思想的应用,是一个基础题,解题时注意数字计算不要出错.7.已知ξ的分布列如下:ξ 0 1 2P并且η=3ξ+2,则方差Dη=()A.B.C.D.7考点:离散型随机变量的期望与方差.专题:概率与统计.分析:由题意及随机变量ξ的分布列,可以先利用期望定义求出期望Eξ的值,最后根据方差的定义求出其方差即可.解答:解:由于Eξ=0×+1×+2×=则Dξ=×(0﹣)2+×(1﹣)2+×(2﹣)2=又由η=3ξ+2,Dη=32Dξ故方差Dη=9×=7故选:D.点评:本题主要考查了离散型随机变量的期望公式与方差公式,同时考查了分布列等知识,属于中档题.8.来晋江旅游的外地游客中,若甲、乙、丙三人选择去五店市游览的概率均为,且他们的选择互不影响,则这三人中至多有两人选择去五店市游览的概率为()A.B.C.D.考点:相互独立事件的概率乘法公式.专题:计算题;排列组合.分析:根据题意,设“三人中至多有两人选择去五店市游览”为事件A,则A的对立事件为“三人都选择去五店市游览”,由相互独立事件的概率公式可得P(),结合对立事件的概率公式计算可得答案.解答:解:根据题意,设“三人中至多有两人选择去五店市游览”为事件A,则A的对立事件为“三人都选择去五店市游览”,又由甲、乙、丙三人选择去五店市游览的概率均为,且他们的选择互不影响,则P()=××=,则P(A)=1﹣P()=;故选:D.点评:本题考查互斥事件的概率计算,解题时利用对立事件的概率特点,先求出A的对立事件的概率.9.设,则二项式的展开式的常数项是()A.12 B.6 C.4 D.2考点:二项式定理;定积分.专题:计算题.分析:利用微积分基本定理求出n,利用二项展开式的通项公式求出通项,令x的指数等于0,求出常数项.解答:解:=4=4∴=展开式的通项为T r+1=(﹣1)r C4r x4﹣2r令4﹣2r=0得r=2故展开式的常数项是C42=6故选B点评:本题考查微积分基本定理、二项展开式的通项公式解决二项展开式的特定项问题.10.数字“2015”中,各位数字相加和为8,称该数为“如意四位数”,则用数字0,1,2,3,4,5组成的无重复数字且大于2015的“如意四位数”有()个.A.21 B.22 C.23 D.24考点:计数原理的应用.专题:应用题;排列组合.分析:分类讨论,利用排列知识,即可得出结论.解答:解:卡片上的四位数字之和等于8,四个数字为0,1,2,5;0,1,3,4.0,1,2,5组成的无重复数字且大于2015的“如意四位数”有,共1+2+2+=11个;0,1,3,4组成的无重复数字且大于2015的“如意四位数”有,共2=12个;故共23个.故选:C.点评:本题考查计数原理的应用,考查分类讨论的数学思想,考查学生分析解决问题的能力,比较基础.11.设y=f″(x)是y=f′(x)的导数.某同学经过探究发现,任意一个三次函数f(x)=ax3+bx2+cx+d (a≠0)都有对称中心(x0,f(x0)),其中x0满足f″(x0)=0.已知f(x)=﹣,则=()A.2012 B.2013 C.2014 D.2015考点:导数的运算.专题:导数的综合应用.分析:令f″(x)=0,解得函数f(x)的对称中心为M.设P,Q是函数f(x)的图象上关于M准线对称的两点,则f(x)+f(1﹣x)=2,即可得出.解答:解:f′(x)=x2﹣x+3,f″(x)=2x﹣1,令f″(x)=0,解得x=,=﹣+3×﹣=1,∴函数f(x)的对称中心为M.设P,Q是函数f(x)的图象上关于M中心对称的两点,则f(x)+f(1﹣x)=2,∴=++…+==2014.故选:C.点评:本题考查了利用导数研究三次函数的中心对称性、函数求和,考查了推理能力与计算能力,属于中档题.1+x)n的展开式中,x k的系数可以表示从n个不同物体中选出k个的方法总数.下列各式的展开式中x8的系数恰能表示从重量分别为1,2,3,4,…,10克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为8克的方法总数的选项是()A.(1+x)(1+x2)(1+x3)…(1+x10)B.(1+x)(1+2x)(1+3x)…(1+10x)C.(1+x)(1+2x2)(1+3x3)…(1+10x10)D.(1+x)(1+x+x2)(1+x+x2+x3)...(1+x+x2+ (x10)考点:二项式定理的应用;排列、组合及简单计数问题.专题:计算题.分析:x8是由x、x2、x3、x4、x5、x6、x7、x8、x9、x10中的、指数和等于8 的那些项的乘积构成,有多少种这样的乘积,就有多少个x8.而各个这样的乘积,分别对应从重量1、2、3、…10克的砝码(每种砝码各一个)中,选出若干个表示8克的方法,从而得出结论.解答:解:x8是由x、x2、x3、x4、x5、x6、x7、x8、x9、x10中的、指数和等于8 的那些项的乘积构成,有多少种这样的乘积,就有多少个x8.各个这样的乘积,分别对应从重量1、2、3、…10克的砝码(每种砝码各一个)中,选出若干个表示8克的方法.故“从重量1、2、3、…10克的砝码(每种砝码各一个)中选出若干个.使其总重量恰为8克的方法总数”,就是“(1+x)(1+x2)(1+x3)…(1+x10)”的展开式中x8的系数”,故选A.点评:本题主要考查排列、组合、二项式定理的应用,体现了转化的数学思想,属于中档题.二.填空题(每小题4分共20分)13.计算=120.考点:组合及组合数公式.专题:计算题.分析:直接利用组合数公式求解即可.解答:解:====120.故答案为:120.点评:本题考查组合数公式的应用,基本知识的考查.14.已知随机变量X~N(3,σ2),若P(X<a)=0.8,则P(6﹣a<X<a)=0.6.考点:正态分布曲线的特点及曲线所表示的意义.专题:计算题;概率与统计.分析:随机变量ξ服从正态分布N(3,σ2),得到曲线关于x=3对称,根据曲线的对称性得到结果.解答:解:随机变量X服从正态分布N(3,σ2),∴曲线关于x=3对称,∵P(X<a)=0.8,∴P(6﹣a<X<a)=1﹣2(1﹣0.8)=0.6,故答案为:0.6.点评:本题考查正态分布曲线的特点及曲线所表示的意义,考查概率的性质,是一个基础题,这种题目可以出现在选择或填空中,是一个送分题目.15.函数y=xe x在其极值点处的切线方程为y=﹣.考点:函数在某点取得极值的条件;利用导数研究曲线上某点切线方程.专题:计算题;导数的概念及应用.分析:求出极值点,再结合导数的几何意义即可求出切线的方程.解答:解:依题解:依题意得y′=e x+xe x,令y′=0,可得x=﹣1,∴y=﹣.因此函数y=xe x在其极值点处的切线方程为y=﹣.故答案为:y=﹣.点评:本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.16.现有5种不同颜色的染料,要对如图中的四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色,则不同的着色方法的种数是260(用数字作答).考点:排列、组合及简单计数问题.专题:计算题;分类讨论.分析:首先分析题目求5种不同颜色,对四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色的着色种数,故可以根据使用颜色的多少分情况讨论.情况1:用到4种颜色,情况2:用到3种颜色,情况3:用到2中颜色,分别求出它们的种数相加即可得到答案.解答:解,情况1:用到4种颜色:C54•A44=24×5=120情况2:用到3种颜色即AC或BD有一对同色:2×C53A33=120情况3:用到2中颜色即AC同色,BD也同色:C52×A22=20故有120+120+20=260种着色的方法.故答案为260.点评:此题主要考查排列组合及简单的计数原理在实际中的应用问题,对于此类对图形着色问题,在近几年的高考中多次出现,同学们需要很好的掌握做题方法.17.如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为 1.2.考点:直线与圆锥曲线的关系.专题:创新题型;圆锥曲线的定义、性质与方程.分析:建立直角坐标系,求出抛物线方程,然后利用定积分求出泥沙沉积的横截面面积,求出梯形面积,即可推出结果.解答:解:如图:建立平面直角坐标系,设抛物线方程为:y=ax2,因为抛物线经过(5,2),可得a=,所以抛物线方程:y=,横截面为等腰梯形的水渠,泥沙沉积的横截面的面积为:2×=2()=,等腰梯形的面积为:=16,当前最大流量的横截面的面积16﹣,原始的最大流量与当前最大流量的比值为:=1.2.故答案为:1.2.点评:本题考查抛物线的求法,定积分的应用,考查分析问题解决问题的能力,合理建系是解题的关键.三.解答题(共70分)18.已知(﹣)n二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3(1)求n的值;(2)求展开式中x3项的系数(3)计算式子C﹣2C+4C﹣8C+…+1024C的值.考点:二项式定理的应用;二项式系数的性质.专题:二项式定理.分析:(1)直接利用条件可得=,求得n的值.(2)在二项展开式的通项公式中,令x的幂指数等于03,求出r的值,即可求得展开式中x3项的系数.(3)在(﹣)10二项展开式中,令x=1,可得式子C﹣2C+4C﹣8C+…+1024C的值.解答:解:(1)由第4项的二项式系数与第3项的二项式系数的比为8:3,可得=,化简可得=,求得n=10.(2)由于(﹣)n二项展开式的通项公式为T r+1=(﹣2)r••x5﹣r,令5﹣r=3,求得r=2,可得展开式中x3项的系数为(﹣2)2•=180.(III)由二项式定理可得,所以令x=1得=(1﹣2)10=1.点评:本题主要考查二项式定理的应用,二项展开式的通项公式,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,属于基础题.19.已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.考点:参数方程化成普通方程;简单曲线的极坐标方程.专题:选作题;坐标系和参数方程.分析:(1)曲线的极坐标方程即ρ2=2ρcosθ,根据极坐标和直角坐标的互化公式得x2+y2=2x,即得它的直角坐标方程;(2)直线l的方程化为普通方程,利用切割线定理可得结论.解答:解:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x﹣1)2+y2=1;(2)直线l:(t为参数),普通方程为,(5,)在直线l上,过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,由切割线定理,可得|MT|2=|MA|•|MB|=18.点评:本题主要考查把极坐标方程化为直角坐标方程的方法,属于基础题.20.已知两个正数a,b满足a+b=1(1)求证:+≥4(2)若不等式|x﹣2|+|2x﹣1|≤+对任意正数a,b都成立,求实数x的取值范围.考点:绝对值不等式的解法;不等式的证明.专题:不等式的解法及应用.分析:(1)由条件利用基本不等式证得结论.(2)由题意可得|x﹣2|+|2x﹣1|≤4,分类讨论,去掉绝对值,求得它的解集.解答:解:(1)证明:∵两个正数a,b满足a+b=1,∴+=+=2++≥2+2=4,当且仅当a=b=时,取等号,∴+≥4成立.(2)由题意结合(1)可知,只须|x﹣2|+|2x﹣1|≤4,而当时,解不等式2﹣x+1﹣2x≤4得,当时,解不等式2﹣x+2x﹣1≤4得,当x≥2时,解不等式x﹣2+2x﹣1≤4得,综上|x﹣2|+|2x﹣1|≤4的解集为.点评:本题主要考查基本不等式的应用,绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.21.某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如表.优秀非优秀总计课改班50非课改班20 110合计210(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与课改有关”;(2)把全部210人进行编号,从编号中有放回抽取4次,每次抽取1个,记被抽取的4人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望Eξ.考点:离散型随机变量及其分布列;独立性检验的应用;离散型随机变量的期望与方差.专题:应用题;概率与统计.分析:(1)确定2×2列联表,计算K2,与临界值比较,即可得出结论;(2)随机变量ξ的所有取值为0,1,2,3,4,求出相应的概率,可得ξ的分布列及数学期望Eξ.解答:解:(1)优秀非优秀总计课改班50 50 100非课改班20 90 110合计70 140 210(2分)K2==23.86>6.635,(5分)所以按照99%的可靠性要求,能够判断成绩与课改有关.(6分)(2)随机变量ξ的所有取值为0,1,2,3,分)由于是有放回的抽取,所以可知每次抽取中抽到优秀的概率为=,(8分)P(ξ=0)=C40()0()4=;P(ξ=1)=C41()1()3=;P(ξ=2)=C42()2()2=;P(ξ=3)=C43()3()1=;P(ξ=4)=C44()4()0=.所以ξ的分布列为:ξ0 1 2 3 4P(10分)Eξ=0×+1×+2×+3×+4×=.(12分)点评:本题考查了独立性检验、分布列及其数学期望,正确计算是关键,属于中档题.22.道路交通安全法中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q<80时,为酒后驾车;当Q≥80时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,依据上述材料回答下列问题:(Ⅰ)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;(Ⅱ)从违法驾车的8人中抽取2人,求取到醉酒驾车人数的分布列和期望,并指出所求期望的实际意义;(Ⅲ)饮酒后违法驾驶机动车极易发生交通事故,假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.1和0.25,且每位驾驶员是否发生交通事故是相互独立的.依此计算被查处的8名驾驶员中至少有一人发生交通事故的概率.(精确到0.01)并针对你的计算结果对驾驶员发出一句话的倡议.考点:离散型随机变量的期望与方差;离散型随机变量及其分布列.专题:概率与统计.分析:(Ⅰ)由题意知检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,违法驾车发生的频率为,醉酒驾车占违法驾车总数的百分数为×100%.(Ⅱ)由题意得到醉酒驾车的人数为随机变量ξ,从违法驾车的8人中抽取2人,8人中最多有2人醉驾,得到ξ可能取到的值有0,1,2,根据古典概型概率公式得到结果.(Ⅲ)被查处的8名驾驶员中至少有一人发生交通事故的对立事件是没有人发生交通事故,由相互独立事件同时发生的概率和对立事件的概率得到要求的概率解答:解:(Ⅰ)由题意知检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,∴违法驾车发生的频率为=,醉酒驾车占违法驾车总数的百分数为×100%=25%(Ⅱ)解:设取到醉酒驾车的人数为随机变量ξ,则ξ可能取到的值有0,1,2,p(ξ=0)==,p(ξ=1)==,p(ξ=2)==.则分布列如下:ξ 0 1 2PEξ=1×+2×=,实际意义:在抽取的两人中平均含有0.5个醉酒驾车人员.(Ⅲ)被查处的8名驾驶员中至少有一人发生交通事故的对立事件是没有人发生交通事故,由相互独立事件同时发生的概率和对立事件的概率得到p=1﹣0.96•0.752≈0.70一句话倡议:远离酒驾,珍爱生命.点评:考查运用概率知识解决实际问题的能力,相互独立事件是指,两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式.23.已知函数f(x)=﹣2alnx+(a﹣2)x,a∈R.(Ⅰ)当a=1时,求函数f(x)的最小值;(Ⅱ)当a≤0时,讨论函数f(x)的单调性;(Ⅲ)是否存在实数a,对任意的x1,x2∈(0,+∞),且x1≠x2,有>a,恒成立,若存在求出a的取值范围,若不存在,说明理由.考点:利用导数求闭区间上函数的最值;函数单调性的判断与证明;利用导数研究函数的单调性.专题:综合题;压轴题.分析:(Ⅰ)显然函数f(x)的定义域为(0,+∞),当a=1 时,求导函数,确定函数的单调性,从而可得f(x)的最小值;(Ⅱ)∵,根据a≤0,将﹣a与2进行比较,分类讨论,从而可确定函数f(x)的单调性;(Ⅲ)假设存在实数a使得对任意的x1,x2∈(0,+∞),且x1≠x2,有恒成立,不妨设0<x1<x2,只要,即:f(x2)﹣ax2>f(x1)﹣ax1,构建函数(x)=f(x)﹣ax,只要g(x)在(0,+∞)为增函数,即使g'(x)≥0在(0,+∞)恒成立,从而可确定是否存在实数a解答:解:(Ⅰ)由题意,函数f(x)的定义域为(0,+∞),…(1分)当a=1 时,…(2分)∴当x∈(0,2)时,f′(x)<0,x∈(2,+∞),f'(x)>0.∴f(x)在x=2时取得极小值且为最小值,其最小值为f(2)=﹣2ln2…(4分)(Ⅱ)∵,…(5分)∴(1)当﹣2<a≤0时,若x∈(0,﹣a)时,f′(x)>0,f(x)为增函数;x∈(﹣a,2)时,f′(x)<0,f(x)为减函数;x∈(2,+∞)时,f′(x)>0,f(x)为增函数.(2)当a=﹣2时,x∈(0,+∞)时,f(x)为增函数;(3)当a<﹣2时,x∈(0,2)时,f′(x)>0,f(x)为增函数;x∈(2,﹣a)时,f′(x)<0,f(x)为减函数;x∈(﹣a,+∞)时,f′(x)>0,f(x)为增函数…(9分)(Ⅲ)假设存在实数a使得对任意的x1,x2∈(0,+∞),且x1≠x2,有恒成立,不妨设0<x1<x2,只要,即:f(x2)﹣ax2>f(x1)﹣ax1令g(x)=f(x)﹣ax,只要g(x)在(0,+∞)为增函数又函数.考查函数…(10分)要使g'(x)≥0在(0,+∞)恒成立,只要﹣1﹣2a≥0,即,…(12分)故存在实数a时,对任意的x1,x2∈(0,+∞),且x1≠x2,有恒成立,…(14分)点评:本题考查导数知识的运用,考查利用导数确定函数的单调区间,考查是否存在问题,考查分类讨论的数学思想,正确运用好导数工具是关键.。
福建省晋江市季延中学2017_2018学年高二数学下学期期中试题文20180829036

21.(12 分)在极坐标系中,曲线 C1 的极坐标方程为 4cos ,曲线 C2 的极坐标方程为
4sin ,以极点 O 为坐标原点,极轴为 x 的正半轴建立平面直角坐标系 xOy .
(1)求 C1 和 C2 的参数方程; (2)已知射线 l1 : (0
( ).A.
V 2K
S1 S 2 S3 S 4 K , H1 3 H 2 5 H 3 7 H 4 1 3 5 7 2V 3V V B. C. D. K K 3K
二.填空题(本大题共 4 小题,每小题 5 分) 13.在复平面内,复数 z m m 2m 8 i 对应的点位于第三象限,则
4 . 15
(2)是否有 99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. (3)4 名调查人员随机分成两组,每组 2 人,一组负责问卷调查,另一组负责数据处理, 求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
3
参考数据:
P( K 2 k )
0. 0.15 2.072
. . . . . . . . . . . . . .7 分
因此有 99.5%的把握认为肥胖与常喝碳酸饮料有关. (2)设其他工作人员为丙和丁,4 人分组的所有情况如下表 小组 收集数据 处理数据 1 甲乙 丙丁 2 甲丙 乙丁 3 甲丁 乙丙 4 乙丙 甲丁 5 乙丁 甲丙 6 丙丁 甲乙
分组的情况总有 6 中,工作人员甲 负责收集数据且工作人员乙负责处理数据占两种, 所以工作人员甲负责收集数据且工作人员处理数据的概率是 P 19. (本小题满分 12 分) (Ⅰ)曲线 C 的普通方程为: ( x 1) y 1 ,即 x y 2 x ,∴ 2 cos ,
福建省晋江市季延中学2017-2018学年高二下学期期末考试物理试题 Word版含答案

季延中学2017-2018学年春高二年期末考试物理科试卷(分值:100分时间:100分钟)者:一.单项选择题(每题4分)1汽车进行刹车试验,若速率从8 m/s匀减速至零,需用时间1 s,按规定速率为8 m/s的汽车刹车后拖行路程不得超过5.9 m,那么上述刹车试验的拖行路程是否符合规定( ) A.拖行路程为8 m,符合规定B.拖行路程为8 m,不符合规定C.拖行路程为4 m,符合规定D.拖行路程为4 m,不符合规定2.从同一地点同时开始沿同一直线运动的两个物体Ⅰ、Ⅱ的v-t图象如图所示,在0~t0时间内,下列说法中正确的是:()A.Ⅰ、Ⅱ两个物体所受的合外力都在不断减小B.Ⅰ物体的加速度不断增大,Ⅱ物体的加速度不断减小C.Ⅰ、Ⅱ两个物体在t1时刻相遇D.Ⅰ、Ⅱ两个物体的平均速度大小都是221vv3.如图,一质量为m的正方体物块置于风洞内的水平面上,其一面与风速垂直,当风速为v 时刚好能推动该物块。
已知风对物块的推力F正比于2Sv,其中v为风速、S为物块迎风面积。
当风速变为2v时,刚好能推动用同一材料做成的另一正方体物块,则该物块的质量为:()A.4m B.8m C.32m D.64m4.如图所示,穿在一根光滑固定杆上的小球A、B通过一条跨过定滑轮的细绳连接,杆与水平面成θ角,不计所有摩擦,当两球静止时,OA绳与杆的夹角为θ,OB绳沿竖直方向,则下列说法正确的是A.A可能受到2个力的作用B.B可能受到3个力的作用C.绳子对A的拉力大于对B的拉力D.A、B的质量之比为1∶tanθ5.光滑斜面上,当系统静止时,挡板C与斜面垂直,弹簧、轻杆均与斜面平行。
在突然撤去挡板的瞬间:()A.两图中两球加速度均为gsinθB.两图中A球的加速度均为零C.图甲中B球的加速度是为2gsinθD.图乙中B球的加速度为零6.如图所示,在倾斜的滑杆上套一个质量为m的圆环,圆环通过轻绳拉着一个质量为M的物体,在圆环沿滑杆向下滑动的过程中,悬挂物体的轻绳始终处于竖直方向.则( ).A.环只受三个力作用B.环一定受四个力作用C.物体做匀加速运动D.悬绳对物体的拉力小于物体的重力二.多项选择题(每题4分,选全得4分,漏选得2分,错选得0分)7.一遥控玩具小车在平直路上运动的位移-时间图象如图所示,则( )A.15 s末汽车的位移为300 mB.20 s末汽车的速度为-1 m/sC .前10 s 内汽车的速度为3 m /sD .前25 s 内汽车做单方向直线运动8.如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上。
晋江市2017_2018学年高二数学下学期期末联考试题理_3649

“两次点数相同”则只有一个,故=.故选:D.
4.盒子里共有 7 个除了颜色外完全相同的球,其中有 4 个红球 3 个白球,从盒子中任取 3
个球,则恰好取到 2 个红球1个白球的概率为( ).
24
A.
35
18
B.
35
12
C.
35
6
D.
35
4.B
【解析】由题意得所求概率为 P
C24 C13 C37
63 35
2.“ x 3 且 y 3 ”是“ x y 6 ”成立的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 即不充分也不必要条件
2.A 解析若“ x 3 且 y 3 ”成立,则“ x y 6 ”一定成立.反之,若“ x y 6 ”成
立时,但“ x 3 且 y 3 ”不一定成立.故“ x 3 且 y 3 ”是“ x y 6 ”成立的充分
A. 5
B. 3
23
C.
D. 2
3
10.设 a R ,函数 f x ex a ex 的导函数 f ' x 是奇函数,若曲线 y f x 的一条
3
切线的斜率是 ,则切点的横坐标为(
)
2
A. ln2 2
B. ln2
ln2
C.
2
D. ln2
11.已
知
双
曲
线
C1:
x2 a2
y2 b2
1(a
18 35
.选 B .
5.某校在高三第一次模拟考试中约有 1000 人参加考试,其数学考试成绩近似服从正态分布, 即,试卷满分分,统计结果显示数学考试成绩不及格(低于 90 分)的人数占总人数的,则 此次数学考试成绩在 100 分到 110 分之间的人数约为( ) A. 400 B. 500 C. 600 D. 800
福建省晋江市2017-2018学年高二12月段考(期末)数学(理)试题 Word版含答案

福建省晋江市2017-2018学年高二12月段考(期末)数学(理)试题时间:120分钟 总分:150分一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中, 只有一项符合题目要求)。
1、已知点(4,1,3),(2,5,1)A B -,若1,3AC AB = 则点C 的坐标为( )。
A. 715(,,)222- B. 107(,1,)33- C. 573(,,)222- D. 3(,3,2)8- 2、下面四个条件中,使a b >成立的充分不必要条件是( )。
A. 1a b >+B. 1a b >-C. 22a b >D. 33a b >3、在空间四边形ABCD 中,G 为CD 的中点,则1(+)2AB BD BC += ( ). A. AG B. CG C. BG D. 12BC 4、已知0,0,a b >>且24,a b +=则1ab的最小值为( )。
A. 14 B. 4 C. 12 D. 2 5、下列说法正确的是( )。
A. “若220,x y +=则,x y 全为0”的否命题为“若220,x y +≠则,x y 全不为0”B. 若命题p 为假命题,命题q ⌝为真命题,则命题“p q ∨” 为真命题C. “1a b>” 是“0a b >> ”的必要不充分条件 D.命题“若4,xy ≠则1x ≠或4y ≠”为假命题6、若0,a m a a b b m b+>>>+恒成立,则m 的取值范围是( )。
A. m b <- B. 0m > C. 0m < D. 0b m -<<7、已知(2,1,3),(1,4,2),(7,5,),a b c λ=-=--= 若,,a b c 三向量不能构成空间的一个基底,则实数λ的值为( )。
A. 0 B. 357 C. 9 D. 6578、已知{}n a 为等差数列,前n 项和为n S ,若258,4a a a π++=则9cos S =()。
福建省晋江市季延中学2017-2018学年高二下学期期末复习数学(理)试题 Word版无答案
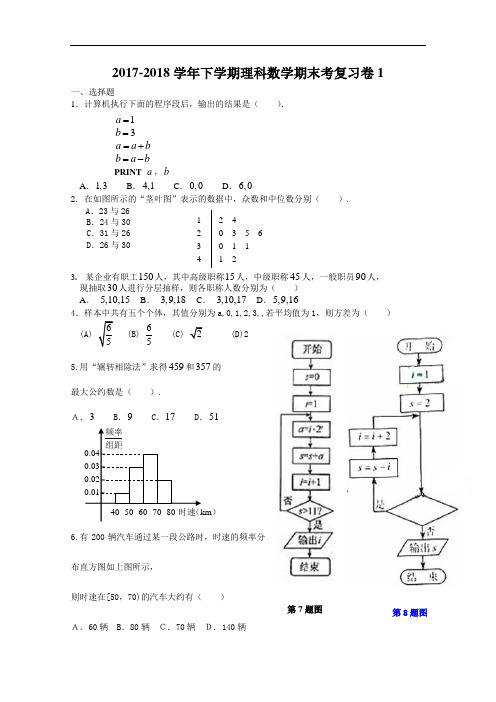
1a =3b = a a b =+ b a b =- PRINT a ,b2017-2018学年下学期理科数学期末考复习卷1一、选择题1.计算机执行下面的程序段后,输出的结果是( ).A .1,3B .4,1C .0,0D .6,02. 在如图所示的“茎叶图”表示的数据中,众数和中位数分别( ).A .23与26B .24与30C .31与26D .26与303 某企业有职工150人,其中高级职称15人,中级职称45人,一般职员90人, 现抽取30人进行分层抽样,则各职称人数分别为( ) A . 5,10,15 B . 3,9,18 C . 3,10,17 D .5,9,164.样本中共有五个个体,其值分别为a,0,1,2,3,,若平均值为1,则方差为( )655.用“辗转相除法”求得459和357的 最大公约数是( ).A.3 B .9 C .17 D .516.有200辆汽车通过某一段公路时,时速的频率分布直方图如上图所示,则时速在[50,70)的汽车大约有( )A.60辆 B .80辆 C.70辆 D.140辆1 2 4 2 0 3 5 6 3 0 1 1 4 1 2)7.阅读如图所示的程序框图,运行相应的程序,输出的i 值等于( ) A.2 B.3 C.4 D.58.阅读如图所示的程序框图,若输出S 的值为-7,则叛断框内可填写( ) (Ai<3? ( B)i<4? (C)i<5? (D)i<6?9.在方程sin ()cos 2x y θθθ=⎧⎨=⎩是参数所表示的曲线上的点是( )(A). 11(,)22 (B).(2,7)- (C). 12(,)33(D).(1,0)10.直线y x =D的圆,([0,2))1x y θθπθ⎧=⎪∈⎨=⎪⎩交于A 、B 两点,则直线AD 与BD 的倾斜角之和为( )(A )76π (B )54π (C ) 43π (D ) 53π 11.设曲线C 的参数方程为23cos 13sin x y θθ=+⎧⎨=-+⎩(θ为参数),直线l 的方程为320x y -+=,则曲线C 上到直线l的点的个数为( ) (A) 1 (B) 2 (C) 3 (D) 412. 两曲线22cos 2()()sin 2x x a t t y y tθθθ=⎧=+⎧⎨⎨==⎩⎩为参数与为参数有公共点的条件是( )(A) 22a -≤≤ (B) 01a ≤≤ (C) 52a ≤ (D) 52a ≥-二、填空题13.秦九韶算法求2346f()=1+5-8763x x x x x x +++的值, 当x =2时,4v =14.甲、乙两人在10天中每天加工零件的个数用茎叶图表示下图,中间一列的数字表示零件个数,两边的数字表示零件个数的位数。
福建省晋江市季延中学高二数学下学期期末考试试题 理(含解析)

福建省晋江市季延中学2012-2013学年高二数学下学期期末考试试题 理(含解析)一、选择题(5×10 = 50)1.设三次函数)(x f 的导函数为)(x f ',函数)(x f x y '⋅=的图象的一部分如图所示,则正确的是 ( )A.)(x f 的极大值为)3(f ,极小值为)3(-fB.)(x f 的极大值为)3(-f ,极小值为)3(fC.()f x 的极大值为(3)f ,极小值为(3)f -D.)(x f 的极大值为)3(-f ,极小值为)3(f 解:观察图象知,x <-3时,y=x•f′(x )>0, ∴f′(x )<0.-3<x <0时,y=x•f′(x )<0, ∴f′(x )>0. 由此知极小值为f (-3). 0<x <3时,y=x•f′(x )>0,∴f′(x )>0. x >3时,y=x•f′(x )<0, ∴f′(x )<0. 由此知极大值为f (3).故选D .2.如图,边长为2的正方形内有一不规则阴影部分,随机向正方形内投入200粒芝麻,恰有60粒落入阴影部分,则不规则图形的面积为( )A.35 B.45 C.65 D.323.曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为( )A. 430x y ++=B.450x y +-=C. 430x y -+=D. 430x y --=第2题图故选答案D4.函数x x x f 3)(3-=的递减区间是( )A.⎪⎪⎭⎫ ⎝⎛-∞-26,或⎪⎪⎭⎫ ⎝⎛+∞,26 B. ()1,1- C. ()1,-∞-或()+∞,1 D. ⎪⎪⎭⎫ ⎝⎛-26,26解:函数f (x )=x 3-3x 的导数为f'(x )=3x 2-3,由f'(x )<0,解得-1<x <1, 所以函数的单调递减区间为(-1,1).故选B .5.在某项体育比赛中,八位裁判为一选手打出的分数如下: 90 89 90 95 92 94 93 90 求此数据的众数和中位数分别为 ( )A .90,91B . 90 , 92C .93, 91D . 93 , 92 解:数据按从小到大排列:89,90,90,90,92,93,94,95. 中位数是(90+92)÷2=91;数据90出现3次,次数最多,所以众数是90.故选A .6.下表提供了某厂节能降耗技术改造后在生产A 产品过程中记录的产量x (吨)与相应的生产根据上表提供的数据,求出y 关于x 的线性回归方程为0.70.35y x =+,那么表中t 的值为A. 3B. 3. 15C. 3.5D. 4.5故选答案A7.若方程()20f x -=在(,0)-∞内有解,则()y f x =的图象是( )解:A :与直线y=2的交点是(0,2),不符合题意,故不正确; B :与直线y=2的无交点,不符合题意,故不正确;C :与直线y=2的在区间(0,+∞)上有交点,不符合题意,故不正确;D :与直线y=2在(-∞,0)上有交点,故正确. 故选D .8.圆2cos ,2sin 2x y θθ=⎧⎨=+⎩的圆心坐标是( )A. (0,2)B. (2,0)C.(0,2)-D. (2,0)-9.在同一坐标系中,将曲线x y 3sin 2=变为曲线x y sin =的伸缩变换是( )⎪⎩⎪⎨⎧==''213)(y y x x A ⎪⎩⎪⎨⎧==yy x x B 213)('' ⎪⎩⎪⎨⎧==''23)(y y x x C ⎪⎩⎪⎨⎧==y y x x D 23)(''10.已知{}()0101x y x y Ω=≤≤≤≤,,,A 是由直线0y =,(01)x a a =<≤和曲线3y x =围成的曲边三角形区域,若向区域Ω上随机投一点,点落在区域A 内的概率为164,则a 的值是( ) (A )164 (B )18 (C )14 (D )12故选答案D二、填空题(4×5 = 20)11.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分,已知某运动员罚球命中的概率为0.7,则他罚球2次(每次罚球结果互不影响)的得分的数学期望是 ;12.如图是甲、乙两班同学身高(单位:cm )数据的茎叶图,若从乙班身高不低于170cm 的同学中随机抽取两名,则身高为173cm 的同学被抽中的概率为 . 甲班 乙班2 18 19 9 1 0 17 0 3 6 8 9 8 8 3 2 16 2 5 8 8 15 913. 已知点A 是曲线2sin ρθ=上任意一点,则点A 到直线sin()43πρθ+=的距离的最小值是 ;14. 若以直角坐标系的x 轴的非负半轴为极轴,曲线1l 的极坐标系方程为sin 42πρθ⎛⎫-=⎪⎝⎭(0,ρ>02)θπ≤≤,直线2l 的参数方程为{1222x t y t =-=+(t 为参数),则1l 与2l 的交点A 的直角坐标是 ;15.设随机变量X ~B(2,p),Y ~B(4,p),若P(X≥1)=59,则P(Y≥1)=____ ____.三、解答题16. (本题满分13分)某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是34,23,14且各轮次通过与否相互独立. (I )设该选手参赛的轮次为ξ,求ξ的分布列和数学期望; (Ⅱ)对于(I )中的ξ,设“函数()3sin()2x f x x R ξπ+=∈是偶函数”为事件D ,求事件D 发生的概率.解:(I )ξ可能取值为1,2,3.记“该选手通过初赛”为事件A ,“该选手通过复赛”为事件B ,31(1)()1,44321(2)()()()(1),434P P A P P AB P A P B ξξ===-=====⨯-=321(3)()()().P P AB P A P B ξ====⨯= ξ的分布列为:ξ的数学期望123.4424E ξ=⨯+⨯+⨯=∴事件D 发生的概率是34. 17. (本小题满分13分)已知函数2()1xe f x ax =+,其中a为正实数,12x =是()f x 的一个极值点. (Ⅰ)求a 的值; (Ⅱ)当12b >时,求函数()f x 在[,)b +∞上的最小值. 解:2'22(21)()(1)xax ax e f x ax -+=+(Ⅰ)因为12x =是函数()y f x =的一个极值点, 所以'1()02f = 因此,1104a a -+= 解得43a =经检验,当34=a 时,21=x 是)(x f y =的一个极值点,故所求a 的值为34. (Ⅱ)由(Ⅰ)可知,2'2248(1)33()4(1)3xx x e f x x -+=+令'()0f x =,得1213,22x x == ()f x 与'()f x 的变化情况如下:所以,()f x 的单调递增区间是13(,),(,),22-∞+∞单调递减区间是13(,)22当1322b <<时,()f x 在3[,)2b 上单调递减, 在3(,)2+∞上单调递增所以()f x 在[,)b +∞上的最小值为3()24f =当32b ≥时,()f x 在[,)b +∞上单调递增, 所以()f x 在[,)b +∞上的最小值为223()134b be ef b ab b==++ 18.(本题满分13分)某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.(1)设所选3人中女生人数为ξ,求ξ的分布列及数学期望; (2)在男生甲被选中的情况下,求女生乙也被选中的概率. 解:(1)ξ的所有可能取值为0,1,2.依题意,得3436C 1(0)C 5P ξ===,214236C C 3(1)C 5P ξ===, 124236C C 1(2)C 5P ξ===. ∴ξ的分布列为∴ 0121555E ξ=⨯+⨯+⨯=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
季延中学2018年春高二年期末考试理科数学试卷
考试时间 120分钟 满分 150分
一.填空题(12*5=60)
1.为了检查某超市货架上的奶粉是否含有三聚氰胺,要从编号依次为1到50的袋装奶粉中抽取5袋进行检验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的5袋奶粉的编号可能是( )
A.5,10,15,20,25
B.2,4,8,16,32
C.1,2,3,4,5
D.7,17,27,37,47
2.下图是把二进制的数化成十进制数的一个程序框图,则判断框内应填入的条件是()211111( )
A. B. C. D. 4i >5i ≤4i ≤i >53、用秦九韶算法求n 次多项式,当时,求
011
1)(a x a x
a x a x f n n n
n ++++=-- 0x x =需要算乘方、乘法、加法的次数分别为( )
)(0x f A 、
B 、n,2n,n
C 、 0,2n,n
D 、 0,n,n
n n n n ,,2
)
1(+4. 某单位有职工160人,其中业务员有104人,管理人员32人,后勤服务人员24人,现用分层抽样法从中抽取一容量为20的样本,则抽取管理人员( ) A.3人 B.4人 C.7人 D.12人
5.抽查10件产品,设事件A :至少有两件次品,则A 的对立事件为 ( ) A.至多两件次品 B.至多一件次品 C.至多两件正品 D.至少两件正品
6.已知随机变量X 服从正态分布N (3,δ2),且P (x ≤6)=0.9,则P (0<x <3)=( )
A .0.4
B .0.5
C .0.6
D .0.7
7. 从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论哪个是正确的( ) A A,C 互斥 B B,C 互斥 C 任何两个都互斥 D 任何两个都不互斥
8. 已知x 与y 之间的一组数据:
x 0 1 2 3 y
1
3
5
7
则y 与x 的线性回归方程为y=bx+a 必过点 ( )
A (2,2)
B (1.5,0)
C (1.5,4)
D (1, 2)
9.甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场进球数为3.2,全年比赛进球个数的标准差为3;乙队平均每场进球数为1.8,全年比赛进球个数的标准差为0.3.下列说法正确的个数为( )
①甲队的技术比乙队好 ②乙队发挥比甲队稳定 ③乙队几乎每场都进球 ④甲队的表现时好时坏
A.1
B.2
C.3
D.4 10. 的展开式中的系数为( )
6
)12)(2(+-x x 4
x A . -160 B .320 C. 480 D .640
11.把四个不同的小球放入三个分别标有1〜3号的盒子中,不允许有空盒子的放法有( )
A .12种
B .24种
C .36种
D .48种
12. 考查正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( )
A. B. C. D. 175275375475二.填空题(4*5=20)
13.已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为________.
14.(N *)展开式中不含的项的系数和为 .
n
y x )234(+-∈n y 15. 某学校食堂早餐只有花卷、包子、面条和蛋炒饭四种主食可供食用,有5名同学前去就餐,每人只选择其中一种,且每种主食都至少有一名同学选择.已知包子数量不足仅够一人食用,甲同学肠胃不好不会选择蛋炒饭,则这5名同学不同的主食选择方案种数为________.(用数字作答)
16. 任取两个小于1的正数x 、y ,若x 、y 、1能作为三角形的三条边长,则它们能构成钝角三角形三条边长的概率是________. 三.解答题(70分)
17.(10分)已知平面直角坐标系xOy 中,直线l 的参数方程为(t 为参数,
0≤α<π且),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为
.已知直线l 与曲线C 交于A 、B 两点,且
.
(1)求α的大小;
(2)过A 、B 分别作l 的垂线与x 轴交于M ,N 两点,求|MN|.
18.(10分)某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工.根据这50名职工对该部门的评分,绘制频率分布直方图(如图321所示),其中样本数据分组区间为:[40,50),[50,60),…,[80,90),[90,100).
图321
(1)求频率分布直方图中a 的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60)的受访职工中,随机抽取2人,求此2人的评分都在[40,50)的概率.
19.(12分)已知直线(为参数),曲线(为参数).
⎪⎪⎩
⎪⎪⎨⎧=+=t
y t x l 222
2
1:t ⎩⎨⎧==θθsin 3cos 2:1y x C θ(1)求直线与曲线的普通方程;
l 1C
(2)已知点,若直线与曲线相交于两点(点在点的上方),)0,1(),0,1(1-F F l 1C B A ,A B 求的值. ||||11B F A F -
20.(12分)设事件A 表示“关于x 的一元二次方程x 2+ax+b 2=0有实根”,其中a ,b 为实常数.
(Ⅰ)若a 为区间[0,5]上的整数值随机数,b 为区间[0,2]上的整数值随机数,求事件A 发生的概率;
(Ⅱ)若a 为区间[0,5]上的均匀随机数,b 为区间[0,2]上的均匀随机数,求事件A 发生的概率.
21(13分)袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球. (Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X ,求随机变量X 的概率分布与数学期望.
22(13分)某市为迎接“国家义务教育均衡发展综合评估”,市教育
行政部门在全市范围内随机抽取了所学校,并组织专家对两n 个必检指标进行考核评分. 其中、分别表示“学校的基础设x y 施建设”和“学校的师资力量”两项指标,根据评分将每项指标划分为A (优秀)、B (良好)、C (及格)三个等级,调查结果如右表所示. 例如:表中“学校的基础设施建设”指标为B 等级的共有20+21+2=43所学校. 已知两项指标均为B 等级的概率为0.21.
x
y A B C
A 20 20 1
B 12 21 1
C
a 2
b
(I )在该样本中,若“学校的基础设施建设”优秀率是0.4,请填写下面2×2列联表,并根
据列联表判断是否有90﹪的把 握认为“学校的基础设施建设”和“学校的师资力量”有关;
师资力量(优秀) 师资力量(非优秀)
基础设施建设(优秀) 基础设施建设(非优秀)
(II )在该样本的“学校的师资力量”为C 等级的学校中,若,,记随8a ≥1115b ≤≤机变量,求的分布列和数学期望. b a -=ξξ 答案: 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案
D
C
D
B
B
A
B
C D
B
C
D
13. 0.25 14. 1 15. 132 16.
4
2
-π17. (1)由已知直线l 的参数方程为:(t 为参数,0≤α<π且
)
,
附表:()
2P K k …0.150.100.050
0.0250.010k 2.072
2.706
3.841
5.024
6.635
2
2
()()()()()
n ad bc K a b c d a c b d -=
++++。
