2020版高考数学人教版理科一轮复习课时作业:8 指数与指数函数 Word版含解析
2020版高考数学一轮复习课后限时集训8指数与指数函数理含解析北师大版2

课后限时集训(八) 指数与指数函数(建议用时:60分钟)A 组 基础达标一、选择题1.设a >0,将表示成分数指数幂的形式,其结果是( )a 2a ·3a 2A .a B .a 12 56C .aD .a 7632C [==Error!=Error!=a 2-=a .故选C.]a 2a ·3a 2a 2a ·a 56 762.已知a =20.2,b =0.40.2,c =0.40.6,则( )A .a >b >cB .a >c >bC .c >a >bD .b >c >aA [由0.2<0.6,0.4<1,并结合指数函数的图像可知0.40.2>0.40.6,即b >c .因为a =20.2>1,b =0.40.2<1,所以a >b.综上,a >b >c .]3.函数y =(0<a <1)的图像的大致形状是( )xa x|x | A B C DD [函数的定义域为{x |x ≠0},所以y ==Error!当x >0时,函数是指数函数,其底数0<a <xa x|x |1,所以函数递减;当x <0时,函数图像与指数函数y =a x (x <0)的图像关于x 轴对称,函数递增,所以应选D.]4.若2x 2+1≤x -2,则函数y =2x 的值域是( )(14)A. B.[18,2)[18,2]C. D .[2,+∞)(-∞,18]B [因2x 2+1≤x -2=24-2x ,则x 2+1≤4-2x ,即x 2+2x -3≤0,所以-3≤x ≤1,所以(14)18≤y ≤2.]5.若存在正数x 使2x (x -a )<1成立,则a 的取值范围是( )A .(-∞,+∞)B .(-2,+∞)C .(0,+∞)D .(-1,+∞)D [不等式2x (x -a )<1可变形为x -a <x.在同一平面直角坐标系中作出直线y =x -a 与y (12)=x 的图像.由题意知,在(0,+∞)内, 直线有一部分在y =x (12)(12)图像的下方.由图可知,-a <1,所以a >-1.]二、填空题6.计算:-×0+8×-Error!=________.(32)13(-76)14 422 [原式=Error!×1+2×2-Error!=2.](23)34 14 (23)7.已知函数f (x )=2|2x -m |(m 为常数).若f (x )在[2,+∞)上是增函数,则m 的取值范围是________.(-∞,4] [令t =|2x -m |,则t =|2x -m |在区间上递增,在区间上递[m 2,+∞)(-∞,m 2]减.而y =2t 在R 上递增,所以要使函数f (x )=2|2x -m |在[2,+∞)上递增,则有≤2,即m ≤4,m2所以m 的取值范围是(-∞,4].]8.(2019·西安八校联考)设函数f (x )=Error!则满足f (x )+f (x -1)>1的x 的取值范围是________.(0,+∞) [画出函数f (x )的大致图像如图,易知函数f (x )在(-∞,+∞)上递增.又x >x -1,且x -(x -1)=1,f (0)=1,所以要使f (x )+f (x -1)>1成立,则结合函数f (x )的图像知只需x -1>-1,解得x >0.故所求x 的取值范围是(0,+∞).]三、解答题9.已知函数f (x )=b ·a x (其中a ,b 为常量,且a >0,a ≠1)的图像经过点A (1,6),B (3,24).(1)求f (x )的表达式;(2)若不等式x +x-m ≥0在(-∞,1]上恒成立,求实数m 的取值范围.(1a )(1b )[解] (1)因为f (x )的图像过A (1,6),B (3,24),所以Error!所以a 2=4,又a >0,所以a =2,b =3.所以f (x )=3·2x .(2)由(1)知a =2,b =3,则x ∈(-∞,1]时,x +x -m ≥0恒成立,即m ≤x +x 在(-∞,1](12)(13)(12)(13)上恒成立.又因为y =x 与y =x 均为减函数,所以y =x +x 也是减函数,(12)(13)(12)(13)所以当x =1时,y =x +x有最小值.所以m ≤.(12)(13)5656即m 的取值范围是.(-∞,56]10.已知函数f (x )=-+3(-1≤x ≤2).14x λ2x -1(1)若λ=,求函数f (x )的值域;32(2)若函数f (x )的最小值是1,求实数λ的值.[解] (1)f (x )=-+314x λ2x -1=2x -2λ·x +3(-1≤x ≤2).(12)(12)设t =x ,(12)得g (t )=t 2-2λt +3.(14≤t ≤2)当λ=时,g (t )=t 2-3t +332=2+.(t -32)34(14≤t ≤2)所以g (t )max =g =,(14)3716g (t )min =g =.(32)34所以f (x )max =,f (x )min =,371634故函数f (x )的值域为.[34,3716](2)由(1)得g (t )=t 2-2λt +3=(t -λ)2+3-λ2,(14≤t ≤2)①当λ≤时,g (t )min =g =-+,14(14)λ24916令-+=1,得λ=>,不符合,舍去;λ2491633814②当<λ≤2时,g (t )min =g (λ)=-λ2+3,14令-λ2+3=1,得λ=;2(λ=-2<14,不符合,舍去)③当λ>2时,g (t )min =g (2)=-4λ+7,令-4λ+7=1,得λ=<2,不符合,舍去.32综上所述,实数λ的值为.2B 组 能力提升1.设函数f (x )=x (e x +e -x ),则f (x )( )A .是奇函数,且在(0,+∞)上是增函数B .是偶函数,且在(0,+∞)上是增函数C .是奇函数,且在(0,+∞)上是减函数D .是偶函数,且在(0,+∞)上是减函数A [∵f (-x )=-x (e -x +e x )=-[x (e -x +e x )]=-f (x ),∴f (x )是奇函数.任取x 2>x 1>0,则e x 2-e x 1>0,e x 2+x 1>1,e x 2+e -x 2-(e x 1+e -x 1)=(e x 1-e x 1)>0,(1-1e x 1+x 2)f (x 2)>f (x 1),∴f (x )在(0,+∞)上递增,故选A.]2.设函数f (x )=Error!则满足f (f (a ))=2f (a )的a 的取值范围是( )A. B .[0,1][23,1]C. D .[1,+∞)[23,+∞)C [令f (a )=t ,则f (t )=2t .当t <1时,3t -1=2t ,令g (t )=3t -1-2t ,则g ′(t )=3-2t ln 2,当t <1时,g ′(t )>0,g (t )在(-∞,1)上递增,即g (t )<g (1)=0,则方程3t -1=2t 无解.当t ≥1时,2t =2t 成立,由f (a )≥1,即当a <1时,3a -1≥1,解得≤a <1;或a ≥1时,2a ≥1,23解得a ≥1.综上可得a 的取值范围是a ≥.]233.若32+2x -3x 2+x>2+2x -x 2+x ,则x 的取值范围是________.(14)(14)(-1,2) [∵32+2x -3x 2+x>2+2x -x 2+x ,(14)(14)∴32+2x -2+2x >3x 2+x -x 2+x,(*)(14)(14)观察知,不等式两边结构相同,故构造函数F (t )=3t -t ,则F (t )为R 上的增函数,而(*)(14)式可以写成,F (2+2x )>F (x 2+x ),根据F (x )递增,得2+2x >x 2+x ,即x 2-x -2<0,解得x ∈(-1,2).]4.已知定义域为R 的函数f (x )=是奇函数.-2x +b 2x +1+a(1)求a ,b 的值;(2)解关于t 的不等式f (t 2-2t )+f (2t 2-1)<0.[解] (1)因为f (x )是定义在R 上的奇函数,所以f (0)=0,即=0,解得b =1,-1+b 2+a所以f (x )=.-2x +12x +1+a又由f (1)=-f (-1)知=-,解得a =2.-2+14+a -12+11+a(2)由(1)知f (x )==-+.-2x +12x +1+21212x +1由上式易知f (x )在(-∞,+∞)上为减函数(此处可用定义或导数法证明函数f (x )在R 上是减函数).又因为f (x )是奇函数,所以不等式f (t 2-2t )+f (2t 2-1)<0等价于f (t 2-2t )<-f (2t 2-1)=f (-2t 2+1).所以t 2-2t >-2t 2+1,即3t 2-2t -1>0.解得t >1或t <-,所以该不等式的解集为13.{tt >1或t <-13}。
2020版高考数学一轮复习教程学案第12课__指数函数 Word版含解析

第课指数函数. 理解指数函数的概念、图象和性质.. 能利用函数图象的平移与对称变换讨论指数函数的图象.. 会利用换元法及分类讨论的数学思想,求解一些复杂函数的值域..阅读必修第~页,理解指数函数的定义和图象特征,能用自己的语言概括第页表格的内容..理解教材第页例和例及第页思考,结合指数函数的图象特征理解左右平移和上下伸缩变换的关系.. 完成教材第页练习第、题,加深理解指数函数的图象和性质.基础诊断. 下列函数中是指数函数的有④.(填序号)①()=·;②()=;③()=+;④()=(-)(>,≠).解析:由指数函数的定义可知④是指数函数.. 不等式+-<的解集是(-,).解析:由题意得+-<,解得-<<..如图所示的曲线,,,分别是函数=,=,=,=的图象,则,,,的大小关系为<<<.解析:轴左、右两侧的图象对应函数的底数按逆时针方向增大,所以>>,>>>.. 已知函数()=-的图象如图,,为常数,则下列结论正确的是④.(填序号)①>,<;②>,>;③<<,>;④<<,<.解析:由()=-的图象知函数()=-在定义域上单调递减,所以<<;函数()=-的图象是在()=的基础上向左平移得到的,所以<.范例导航考向❶指数函数的图象及其应用例已知函数=.() 作出函数的图象(简图);() 由图象指出其单调区间;() 由图象指出当取什么值时函数=有最值,并求出最值.解析:() 方法一:由函数解析式可得==其图象由两部分组成:一部分是:=(≥)=(≥-);另一部分是:=(<)=+(<-).如图所示.方法二:①由=可知函数是偶函数,其图象关于轴对称,故先作出=的图象,保留≥的部分,当<时,其图象是将=(≥)图象关于轴对折,从而得出=的图象.②将=的图象向左平移个单位长度,即可得=的图象,如图所示.() 由图象知函数的单调增区间为(-∞,-),单调减区间为(-,+∞).() 由图象知当=-时,有最大值,无最小值.。
2020版高考数学人教版理科一轮复习课时作业:8 指数与指数函数 Word版含解析

课时作业8 指数与指数函数一、选择题1.化简4a ·b ÷的结果为( C )-(-23ab )A .-B .-2a 3b 8a b C .-D .-6ab6ab 2.设函数f (x )=Error!若f (a )<1,则实数a 的取值范围是( C )A .(-∞,-3) B .(1,+∞)C .(-3,1)D .(-∞,-3)∪(1,+∞)解析:当a <0时,不等式f (a )<1为a-7<1,(12)即a <8,即a <-3,(12)(12)(12)因为0<<1,所以a >-3,12此时-3<a <0;当a ≥0时,不等式f (a )<1为<1,所以0≤a <1.a 故a 的取值范围是(-3,1),故选C.3.(2019·湖南永州模拟)下列函数中,与函数y =2x -2-x 的定义域、单调性与奇偶性均一致的是( B )A .y =sin xB .y =x 3C .y =xD .y =log 2x(12)解析:y =2x -2-x 是定义域为R 的单调递增函数,且是奇函数.而y =sin x 不是单调递增函数,不符合题意;y =x 是非奇非偶(12)函数,不符合题意;y =log 2x 的定义域是(0,+∞),不符合题意;y =x 3是定义域为R 的单调递增函数,且是奇函数符合题意.故选B.4.二次函数y =-x 2-4x (x >-2)与指数函数y =x的图象的交(12)点个数是( C )A .3B .2C .1D .0解析:因为函数y =-x 2-4x =-(x +2)2+4(x >-2),且当x =-2时,y =-x 2-4x =4,y =x=4,则在同一直角坐标系中画出y =-x 2(12)-4x (x >-2)与y =x的图象如图所示,由图象可得,两个函数图象(12)的交点个数是1,故选C.5.(2019·福建厦门一模)已知a =0.3,b =log 0.3,c =a b ,则a ,b ,c(12)12的大小关系是( B )A .a <b <cB .c <a <bC .a <c <bD .b <c <a解析:b =log 0.3>log =1>a =0.3,c =a b <a .∴c <a <b .故选B.121212(12)6.已知a ,b ∈(0,1)∪(1,+∞),当x >0时,1<b x <a x ,则( C )A .0<b <a <1B .0<a <b <1C .1<b <aD .1<a <b解析:∵当x >0时,1<b x ,∴b >1.∵当x >0时,b x <a x ,∴当x >0时,x>1.(a b)∴>1,∴a >b .∴1<b <a ,故选C.ab7.如图,在面积为8的平行四边形OABC 中,AC ⊥CO ,AC 与BO 交于点E .若指数函数y =a x (a >0,且a ≠1)经过点E ,B ,则a 的值为( A )A. B.23C .2D .3解析:设点E (t ,a t ),则点B 的坐标为(2t,2a t ).因为2a t =a 2t ,所以a t =2.因为平行四边形OABC 的面积=OC ×AC =a t ×2t =4t ,又平行四边形OABC 的面积为8,所以4t =8,t =2,所以a 2=2,a =.2故选A.二、填空题8.不等式2x 2-x <4的解集为{x |-1<x <2}.解析:∵2x 2-x <4,∴2x 2-x <22,∴x 2-x <2,即x 2-x -2<0,解得-1<x <2.9.若直线y 1=2a 与函数y 2=|a x -1|(a >0且a ≠1)的图象有两个公共点,则a 的取值范围是.(0,12)解析:(数形结合法)当0<a <1时,作出函数y 2=|a x -1|的图象,由图象可知0<2a <1,∴0<a <;12同理,当a >1时,解得0<a <,与a >1矛盾.12综上,a 的取值范围是.(0,12)10.已知函数f (x )=2x -,函数g (x )=Error!则函数g (x )的最小12x 值是0.解析:当x ≥0时,g (x )=f (x )=2x -为单调增函数,所以g (x )≥g (0)12x =0;当x <0时,g (x )=f (-x )=2-x -为单调减函数,所以g (x )>g (0)12-x =0,所以函数g (x )的最小值是0.11.(2019·湖南益阳调研)已知函数f (x )=(a ∈R )的图象关2x1+a ·2x 于点对称,则a =1.(0,12)解析:由已知,得f (x )+f (-x )=1,即+=1,2x 1+a ·2x 2-x1+a ·2-x 整理得(a -1)[22x +(a -1)·2x +1]=0,所以当a -1=0,即a =1时,等式成立.三、解答题12.设a >0,且a ≠1,函数y =a 2x +2a x -1在[-1,1]上的最大值是14,求实数a 的值.解:令t =a x (a >0,且a ≠1),则原函数化为y =f (t )=(t +1)2-2(t >0).①当0<a <1,x ∈[-1,1]时,t =a x ∈,此时f (t )在上为[a ,1a ][a ,1a]增函数.所以f (t )max =f =2-2=14.所以2=16,解得a =(1a )(1a +1)(1a+1)-15(舍去)或a =.13②当a >1时,x ∈[-1,1],t =a x ∈,此时f (t )在上是增[1a ,a ][1a,a ]函数.所以f (t )max =f (a )=(a +1)2-2=14,解得a =3或a =-5(舍去).综上得a =或3.1313.(2019·河南八市第一次测评)设函数f (x )=x 2-a 与g (x )=a x (a >1且a ≠2)在区间(0,+∞)上具有不同的单调性,则M =(a -1)0.2与N =0.1的大小关系是( D )(1a)A .M =NB .M ≤NC .M <ND .M >N解析:因为f (x )=x 2-a 与g (x )=a x (a >1且a ≠2)在区间(0,+∞)上具有不同的单调性,所以a >2,所以M =(a -1)0.2>1,N =0.1<1,所(1a)以M >N ,故选D.14.已知函数f (x )=1-(a >0,a ≠1)且f (0)=0.42a x +a (1)求a 的值;(2)若函数g (x )=(2x +1)·f (x )+k 有零点,求实数k 的取值范围;(3)当x ∈(0,1)时,f (x )>m ·2x -2恒成立,求实数m 的取值范围.解:(1)对于函数f (x )=1-(a >0,a ≠1),由f (0)=1-=42a x +a 42+a 0,得a =2.(2)由(1)知f (x )=1-=1-.42·2x +222x +1因为函数g (x )=(2x +1)·f (x )+k =2x +1-2+k =2x -1+k 有零点,所以函数y =2x 的图象和直线y =1-k 有交点,∴1-k >0,即k <1.(3)∵当x ∈(0,1)时,f (x )>m ·2x -2恒成立,即1->m ·2x -222x +1恒成立,亦即m <-恒成立,32x 22x (2x +1)令t =2x ,则t ∈(1,2),且m <-==+.3t 2t (t +1)3t +1t (t +1)1t 2t +1由于y =+在t ∈(1,2)上单调递减,1t 2t +1∴+>+=,∴m ≤.1t 2t +11222+17676尖子生小题库——供重点班学生使用,普通班学生慎用15.已知实数a ,b 满足>a >b >,则( B )12(12)(22)14A .b <2B .b >2b -a b -aC .a <D .a >b -a b -a解析:由>a ,得a >1,由a >b,得2a >b ,故2a <b ,12(12)(12)(22)(22)(22)由b >,得b >4,得b <4.由2a <b ,得b >2a >2,a <<2,(22)14(22)(22)b2∴1<a <2,2<b <4.对于选项A ,B ,由于b 2-4(b -a )=(b -2)2+4(a -1)>0恒成立,故A 错误,B 正确;对于选项C ,D ,a 2-(b -a )=a +2-,12(b +14)由于1<a <2,2<b <4,故该式的符号不确定,故C ,D 错误.故选B.16.已知max(a ,b )表示a ,b 两数中的最大值.若f (x )=max(e |x |,e |x -2|),则f (x )的最小值为e.解析:由题意得,f (x )=Error!当x ≥1时,f (x )=e x ≥e(当x =1时取等号),当x <1时,f (x )=e |x -2|=e 2-x >e ,因此x =1时,f (x )有最小值f (1)=e.。
2020高考数学一轮复习考点规范练8指数与指数函数

D.-2X _4. 函数f(x)=1-e |x|的图象大致是(5. 若函数y=a x -b(a>0,且a 鬥)的图象经过第二、第三、第四象限A.(1, + 叼B. (0, +旳基础巩固i •化简 (x<O,y< 0)得(A.2xB.2xC.(0,1)D.无法确定 6.已知 a=20.2,b= O.40.2,C =O.40.6,则( )A.a>b>cB.a>c>bC.c>a>bD.b>c>a 7.若函数f(x)=a |2x-4|(a>0,a 为)满足f(1)=~,则f(x)的单调递减区间是(A.(-s ,2]B.[2, +旳C.-2xJ Lk1D3.已知f(x)=3x-b (2<x w 4,b 为常数)的图象经过点 (2,1),则f(x)的值域为(A.[9,81]B.[3,9]C.[1,9]D.[1, + 乡 a b 的取值范围为()2.函数f(x)=2|x-11的大致图象是 ),则C. [-2,+ 旳D. (a,-2]8. 函数 y= 2-2 x 是( )A. 奇函数,在区间(0, +乡内单调递增B. 奇函数,在区间(0,+旳内单调递减C. 偶函数,在区间(-x ,0)内单调递增D. 偶函数,在区间(-x ,0)内单调递减9. 曲线 y=2a |x-1|-1(a>0,a 鬥)过定点 __________10.函数f(x)= ____________ - 的值域为 .15.已知函数f(x)=|2x -1|,且当a<b<c 时有f(a)>f(c)>f(b),则下列结论一定成立的是 (A. a< 0,b< 0,c<0B.a< 0,b > 0,c>0 — -a cC. 2 <2 a c小D.2 +2 <216. _______________ 记X 2-X 1为区间[x 1,x 2]的长度,已知函数y=2|x|,x € [-2,a ](a > 0),其值域为[m,n ],则区间[m,n ]的长度的 最小值是.三、高考预测11.函数y= -+ 1在x € [-3,2]上的值域是_X、,12.已知函数 f(x)= (a-2)a (a>0,且 a 为),若对任意 x 1,x 2€ R ,>0,则a 的取值范围二、能力提升13.当x € (-a ,-1]时,若不等式(m 2-m) 4x -2x <0恒成立,则实数m 的取值范围是( )A.(-2,1)B.(-4,3)C.(-1,2)D.(-3,4)14.若存在正数 x 使2x (x-a)< 1成立,则a 的取值范围是 A. (a,+汨 B.(-2,+ 叼C. (0,+ a ) D. (-1,+a )17.设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c 的大小关系是()A.a<b<cB.a<c<bC.b<a<cD.b<c<a考点规范练8指数与指数函数1. D2. B 解析因为f(x)=2|x-1|= -所以f(x)在[1,+ x)内为增函数,在(-円1)内为减函数•3. C 解析由f(x)的图象经过点(2,1)可知b=2.因为f(x)=3x-2在区间[2,4]上是增函数,所以f(x)min =f (2) = 1,f(x)max=f (4) = 9.故f(X)的值域为[1,9]•4. A 解析因为函数f(x)= 1 -e|x|是偶函数,且值域是(-x,0],只有A满足上述两个性质.故选A.5. C 解析因为函数图象经过第二、第三、第四象限,所以函数单调递减且图象与y轴的交点在y轴负半轴上•令x=0,得y=a°-b= 1-b,由题意得解得故a b€ (0,1),故选C.6. A 解析由0.2<0.6,0<0.4<1,可知0.40.2>0.40",即b>c.又因为a=20.2>1,b=O.40.2<1,所以a>b.综上,a>b>c.7. B 解析由f(1) = 一得a2=-,故a=- -- 舍去,即f(x)= - .由于y=|2x-4|在(-x,2]上单调递减,在[2, + x)上单调递增,故f(x)在(-x,2]上单调递增,在[2, + X上单调递减■故选B.8. A 解析令f(x)=2x-2-x,则f(x)的定义域为R,且f(-x) = 2-x-2x=-f(x),所以函数f(x)是奇函数,排除C,D. 又函数y=-2-x,y=2x均是R上的增函数,所以y= 2x-2-x在R上为增函数.9. (1,1) 解析由|x-1|=0,即x= 1,此时y=1 故函数恒过定点(1,1).10. [0,1)解析由1-e x>0,可知e x w 1.又0<e x,所以-K -e x<0,即0W 1 -e x< 1.故函数f(x)的值域为[0,1).11•- 解析令匸-,由x€ [-3,2],得t €_.则y=t2-t+ 1=-一 - - .当t= -时,y min = -;当t=8 时,y max= 57.故所求函数的值域为一12. (0,1) U (2,+旳解析由题意知f(x)在R上是增函数•当0<a< 1时,a-2<0,y=a x单调递减,所以f(x)单调递增;当1<a< 2时,a-2<0,y=a x单调递增,所以f(x)单调递减;当a=2时,f(x)=0;当a>2时,a-2>0,y=a x 单调递增所以f(x)单调递增•故a的取值范围是(0,1) U (2,+旳.213. C 解析原不等式可变形为m -m< - •函数y= -在(-8,-1]上是减函数,当x€ (-8,-1]时,m2-m< -恒成立等价于m2-m<2,解得-1<m< 2.14. D 解析不等式2x(x-a)< 1可变形为x-a< - •在同一平面直角坐标系中作出直线y=x-a与y= 一的图象.由题意知,在(0,+ 8内,直线有一部分在y= -图象的下方.由图可知,-a< 1所以a>-1.15. D 解析作出函数f(x)=|2x-1|的图象,如图.T当a<b<c 时,有f(a)>f (c)>f (b),•••结合图象知0<f(a)<1,a<0,c>0.•••0<2a<l.•••f(a)=|2a-i|=i-2a<1.•••f(c)< 1, /.0<c< 1.• 1<2c<2,•f(c)=|2c-1|=2c-1,又f(a)>f (c), • 1-2a>2c-1,•2a+2c<2,故选D.16.3 解析令f(x)=y= 2|x|,则f(x)= _(1)当a=0时,f(x)=2-x在[-2,0]上为减函数值域为[1,4].⑵当a>0时,f(x)在[-2,0)上为减函数,在[0,a]上为增函数①当0<a < 2 时,f(x)max=f(-2)=4,值域为[1,4];②当a>2 时,f(x)max=f(a)=2a>4,值域为[1,2a].综上(1)(2),可知[m,n]的长度的最小值为 3.17. C解析函数y=0.6x在定义域R上为减函数,0 0.6 1.5•1=0.60>0.60.6>0.61.5.而函数y=1.5x为增函数,• 1.50.6> 1.5°= 1, • b<a<c.。
2020高三数学(人教版)一轮复习指数与指数函数

[跟踪训练]
1.函数 y=ax-1a(a>0,且 a≠1)的图象可能是(
)
解析:D [法一:当 0<a<1 时,函数 y=ax-1a是减函数,且其 图象可视为是由函数 y=ax 的图象向下平移1a个单位长度得到的,结 合各选项知选 D.
法二:因为函数 y=ax-1a(a>0,且 a≠1)的图象必过点(-1,0), 所以选 D.]
n am m,n∈N*,且 n>1);0 的正分数指数幂等于 0;0 的负分数指数幂 没有意义 .
(2)有理指数幂的运算性质:aras= ar+s ;(ar)s= ars ;(ab)r = arbr ,其中 a>0,b>0,r,s∈Q.
3.指数函数及其性质 (1)概念:函数 y=ax(a>0 且 a≠1) 叫做指数函数,其中指数 x 是自变量,函数的定义域是 R,a 是底数.
答案:(0,1)
[互动探究 2] 若将本例(3)改为:函数 y=|2x-1|在(-∞,k]上单调递减,则 k 的取值范围是 ________ . 解析:因为函数 y=|2x-1|的单调递减区间为(-∞,0],所以 k≤0, 即 k 的取值范围为(-∞,0].
答案:(-∞,0]
[互动探究 3] 若将本例(3)改为:直线 y=2a 与函数 y=|ax-1|(a> 且 a≠1)的 图象有两个公共点,则 a 的取值范围是________________.
(3)曲线|y|=2x+1 与直线 y=b 的图象如图所示,由图象可得:如 果|y|=2x+1 与直线 y=b 没有公共点,则 b 应满足的条件是 b∈[- 1,1].
[答案] (1)A (2)D (3)[-1,1]
[互动探究 1] 若将本例(3)中“|y|=2x+1”改为“y=|2x-1|”,且与直线 y=b 有两个公共点,则 b 的取值范围是 ________ . 解析:曲线 y=|2x-1|与直线 y=b 的图象如图所示,由图象可得, 如果曲线 y=|2x-1|与直线 y=b 有两个公共点,则 b 的取值范围是 (0,1).
高考数学一轮复习 第2章 函数概念与基本初等函数Ⅰ8 指数与指数函数课时训练 文(含解析)-人教版高
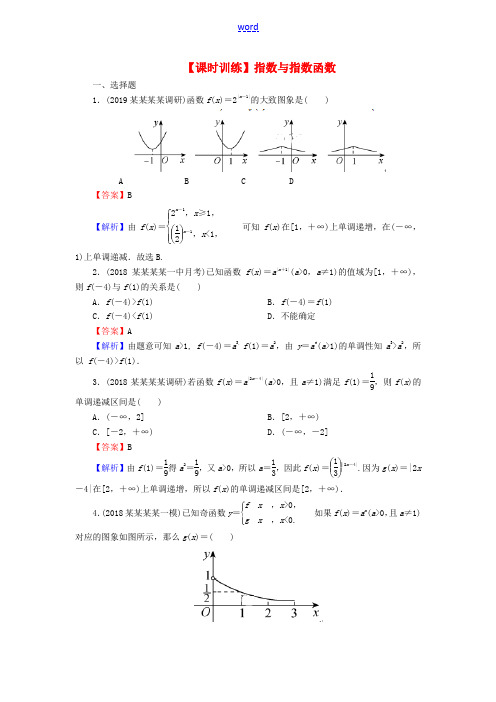
【课时训练】指数与指数函数一、选择题1.(2019某某某某调研)函数f (x )=2|x -1|的大致图象是( )A B C D 【答案】B【解析】由f (x )=⎩⎪⎨⎪⎧2x -1,x ≥1,⎝ ⎛⎭⎪⎫12x -1,x <1,可知f (x )在[1,+∞)上单调递增,在(-∞,1)上单调递减.故选B.2.(2018某某某某一中月考)已知函数f (x )=a |x +1|(a >0,a ≠1)的值域为[1,+∞),则f (-4)与f (1)的关系是( )A .f (-4)>f (1)B .f (-4)=f (1)C .f (-4)<f (1)D .不能确定【答案】A【解析】由题意可知a >1, f (-4)=a 3,f (1)=a 2,由y =a t(a >1)的单调性知a 3>a 2,所以 f (-4)>f (1).3.(2018某某某某调研)若函数f (x )=a |2x -4|(a >0,且a ≠1)满足f (1)=19,则f (x )的单调递减区间是( )A .(-∞,2]B .[2,+∞)C .[-2,+∞)D .(-∞,-2]【答案】B【解析】由f (1)=19得a 2=19,又a >0,所以a =13,因此f (x )=⎝ ⎛⎭⎪⎫13|2x -4|.因为g (x )=|2x -4|在[2,+∞)上单调递增,所以f (x )的单调递减区间是[2,+∞).4.(2018某某某某一模)已知奇函数y =⎩⎪⎨⎪⎧fx ,x >0,g x ,x <0.如果f (x )=a x(a >0,且a ≠1)对应的图象如图所示,那么g (x )=( )A .⎝ ⎛⎭⎪⎫12-x B .-⎝ ⎛⎭⎪⎫12xC .2-xD .-2x【答案】D【解析】由题图可知f (1)=12,∴a =12,f (x )=⎝ ⎛⎭⎪⎫12x .由题意得g (x )=-f (-x )=-⎝ ⎛⎭⎪⎫12-x=-2x.故选D.5.(2018某某省实验中学分校月考)函数y =16-2x的值域是( ) A .[0,+∞) B .[0,4] C .[0,4) D .(0,4)【答案】C【解析】函数y =16-2x中,因为16-2x≥0,所以2x≤16.因此2x∈(0,16],所以16-2x∈[0,16).故y =∈[0,4).故选C.6.(2018某某某某第一中学月考)已知集合A ={x |(2-x )·(2+x )>0},则函数f (x )=4x-2x +1-3(x ∈A )的最小值为( )A .4B .2C .-2D .-4【答案】D【解析】由题知集合A ={x |-2<x <2}.又f (x )=(2x )2-2×2x -3,设2x=t ,则14<t <4,所以f (x )=g (t )=t 2-2t -3=(t -1)2-4,且函数g (t )的对称轴为直线t =1,所以最小值为g (1)=-4.故选D.7.(2018某某某某联考)已知函数f (x )=e x,如果x 1,x 2∈R ,且x 1≠x 2,则下列关于f (x )的性质:①(x 1-x 2)[f (x 1)-f (x 2)]>0;②y =f (x )不存在反函数;③f (x 1)+f (x 2)<2f ⎝ ⎛⎭⎪⎫x 1+x 22;④方程f (x )=x 2在(0,+∞)上没有实数根.其中正确的是( )A .①②B .①④C .①③D .③④【答案】B8.(2018某某某某联考)若函数f (x )=2x -a +1+x -a -a 的定义域与值域相同,则a =( )A .-1B .1C .0D .±1【答案】B【解析】∵函数f (x )=2x -a +1+x -a -a ,∴函数f (x )的定义域为[a ,+∞). ∵函数f (x )的定义域与值域相同, ∴函数f (x )的值域为[a ,+∞).又∵函数f (x )在[a ,+∞)上是单调递增函数,∴当x =a 时,f (a )=2a -a +1-a =a ,解得a =1.故选B.二、填空题9.(2018某某某某一模)已知函数f (x )=e x -e -xe x +e -x ,若f (a )=-12,则f (-a )=________. 【答案】12【解析】∵f (x )=e x-e -xe x +e -x ,f (a )=-12,∴e a -e -a e a +e -a =-12.∴f (-a )=e -a -e a e -a +e a =-e a -e -ae a +e -a =-⎝ ⎛⎭⎪⎫-12=12. 10.(2018某某一中月考)若函数f (x )=a x-1(a >0,a ≠1)的定义域和值域都是[0,2],则实数a =________.【答案】 3【解析】当a >1时,f (x )=a x -1在[0,2]上为增函数,则a 2-1=2,∴a =± 3.又a >1,∴a = 3.当0<a <1时,f (x )=a x-1在[0,2]上为减函数,又f (0)=0≠2,∴0<a <1不成立.综上可知,a = 3.11.(2018某某十校联考)已知max (a ,b )表示a ,b 两数中的最大值.若f (x )=max {e |x |,e|x -2|},则f (x )的最小值为________.【答案】e【解析】由于f (x )=max {e |x |,e |x -2|}=⎩⎪⎨⎪⎧e x,x ≥1,e 2-x,x <1.当x ≥1时,f (x )≥e,且当x =1时,取得最小值e ;当x <1时,f (x )>e.故f (x )的最小值为f (1)=e.12.(2018某某某某海阳一中期中)已知函数f (x )=2|x -2|-1在区间[0,m ]上的值域为[0,3],则实数m 的取值X 围为________.【答案】[2,4] 【解析】函数f (x )=2|x -2|-1的对称轴为直线x =2,且在(-∞,2]上单调递减,在(2,+∞)上单调递增.由于函数f (x )=2|x -2|-1在区间[0,m ]上的值域为[0,3]且函数关于直线x =2对称,f (0)=f (4)=3,f (2)=0,所以结合图象可知m ∈[2,4].三、解答题13.(2018某某余姚中学月考)已知定义在R 上的函数 f (x )=2x-12|x |.(1)若f (x )=32,求x 的值;(2)若2tf (2t )+mf (t )≥0对于t ∈[1,2]恒成立,某某数m 的取值X 围. 【解】(1)当x <0时,f (x )=0,无解; 当x ≥0时,f (x )=2x-12x ,由2x -12x =32,得2·22x -3·2x-2=0,将上式看成关于2x的一元二次方程, 解得2x =2或2x=-12,∵2x>0,∴x =1.(2)当t ∈[1,2]时,2t ⎝ ⎛⎭⎪⎫22t-122t +m ⎝ ⎛⎭⎪⎫2t -12t ≥0,即m (22t-1)≥-(24t-1),∵22t-1>0, ∴m ≥-(22t+1),∵t ∈[1,2],∴-(22t+1)∈[-17,-5], 故实数m 的取值X 围是[-5,+∞).。
2020高考数学理科大一轮复习导学案《指数与指数》含答案

第五节指数与指数函数知识点一指数与指数幂的运算1.根式(1)根式的概念:(2)两个重要公式:①(na)n=a(n>1,且n∈N+).②na n=⎩⎪⎨⎪⎧a n为奇数,|a| n为偶数.2.有理指数幂(1)分数指数幂的含义:③0的正分数指数幂等于0,0的负分数指数幂没有意义.(2)有理指数幂的运算法则:设a>0,b>0,对任意有理数α,β,有以下运算法则aαaβ=aα+β,(aα)β=aαβ,(ab)α=aαbα.上述有理指数幂的运算性质,对于无理指数幂也适用.1.判断正误(1)(4-2)4=-2.(×)(2)na n=a.(×)2.(必修1P59A组第1题改编)化简416x8y4(x<0,y<0)得(D)A.2x2y B.2xy C.4x2y D.-2x2y解析:因为x<0,y<0,所以416x8y4=(16x8·y4)14=(16)14·(x8)14·(y4)14=2x2|y|=-2x2y.3.若x+x-1=3,则x2-x-2=±3 5.解析:由(x+x-1)2=x2+x-2+2=9,得x2+x-2=7.又(x-x-1)2=x2-2+x-2=5,所以x-x-1=±5,所以x2-x-2=(x+x-1)(x-x-1)=±3 5.知识点二指数函数的图象与性质4.函数y =1-⎝ ⎛⎭⎪⎫12x的定义域为[0,+∞). 解析:要使函数有意义,需1-⎝ ⎛⎭⎪⎫12x ≥0,即⎝ ⎛⎭⎪⎫12x ≤1,∴x ≥0,即定义域为[0,+∞).5.(必修1P56例6改编)若函数f (x )=a x (a >0,且a ≠1)的图象经过点A ⎝ ⎛⎭⎪⎫2,13,则f (-1)= 3. 解析:依题意可知a 2=13,解得a =33,所以f (x )=⎝ ⎛⎭⎪⎫33x ,所以f (-1)=⎝ ⎛⎭⎪⎫33-1= 3. 6.(必修1P58第2题改编)函数的定义域是(0,+∞).解析:要使该函数有意义,解得x >0,所以定义域为(0,+∞).1.指数函数图象的画法画指数函数y =a x (a >0,且a ≠1)的图象,应抓住三个关键点:(1,a ),(0,1),⎝ ⎛⎭⎪⎫-1,1a .2.指数函数的图象与底数大小的比较如图是指数函数(1)y =a x ,(2)y =b x ,(3)y =c x ,(4)y =d x 的图象,底数a ,b ,c ,d 与1之间的大小关系为c >d >1>a >b >0.由此我们可得到以下规律:在第一象限内,指数函数y =a x (a >0,a ≠1)的图象越高,底数越大.3.指数函数y=a x(a>0,a≠1)的图象和性质跟a的取值有关,要特别注意应分a>1与0<a<1来研究.考向一指数与指数幂的运算【例1】化简、求值:幂的运算的一般规律及要求(1)分数指数幂与根式根据a mn=na m(a>0,m,n∈N*,且n>1)可以相互转化.(2)分数指数幂中的指数不能随便约分,例如要将a 24写成a12必须认真考查a的取值才能决定,如(-1)24=4(-1)2=1,而(-1)12=-1无意义.(3)在进行幂的运算时,一般是先将根式化成幂的形式,并化小数指数幂为分数指数幂,再利用幂的运算性质进行运算.(4)结果不能同时含有根式和分数指数幂,也不能既有分母又有负分数指数幂.已知a ,b 是方程9x 2-82x +9=0的两根,且a <b ,求: (1)a -1+b -1(ab )-1;解:因为a ,b 是方程9x 2-82x +9=0的两根,且a <b , 所以a =19,b =9, (1)a -1+b-1(ab )-1=1a +1b 1ab=a +b=19+9=829.考向二 指数的图象及应用【例2】 (1)(2018·全国卷Ⅱ)函数f (x )=e x -e -xx 2的图象大致为()(2)已知函数f (x )=|2x -1|,a <b <c 且f (a )>f (c )>f (b ),则下列结论中,一定成立的是( )A .a <0,b <0,c <0B .a <0,b ≥0,c >0C .2-a <2cD .2a +2c <2【解析】 (1)解法1:因为f (x )的定义域关于原点对称且f (-x )=-f (x ), 所以f (x )为奇函数,排除A 选项;由f (2)=e 2-1e 24>1,排除C 、D 选项.故选B.解法2:当x <0时,因为e x -e -x <0, 所以此时f (x )=e x -e -xx 2<0, 故排除A 、D ;又f (1)=e -1e >2,故排除C,选B.(2)作出函数f(x)=|2x-1|的图象,如图,∵a<b<c且f(a)>f(c)>f(b),结合图象知,0<f(a)<1,a<0,c>0,∴0<2a<1.∴f(a)=|2a-1|=1-2a<1,∴f(c)<1,∴0<c<1.∴1<2c<2,∴f(c)=|2c-1|=2c-1,又∵f(a)>f(c),∴1-2a>2c-1,∴2a+2c<2,故选D.【答案】(1)B(2)D函数图象的识辨方法(1)由函数的定义域判断图象的左右位置,由函数的值域判断图象的上下位置;(2)由函数的单调性判断图象的变化趋势;(3)由函数的奇偶性判断图象的对称性;(4)由函数的周期性识辨图象;(5)由函数图象上的特征点排除不符合要求的图象.(1)函数f(x)=a x-b的图象如图,其中a,b为常数,则下列结论正确的是(D)A.a>1,b<0B.a>1,b>0C.0<a<1,b>0D.0<a<1,b<0(2)已知实数a,b满足等式2 018a=2 019b,下列五个关系式:①0<b <a ;②a <b <0;③0<a <b ;④b <a <0;⑤a =b . 其中不可能成立的关系式有( B ) A .1个 B .2个 C .3个D .4个解析:(1)由f (x )=a x -b 的图象可以观察出,函数f (x )=a x -b 在定义域上单调递减,所以0<a <1,函数f (x )=a x -b 的图象是在y =a x 的基础上向左平移得到的,所以b <0.(2)如图,观察易知,a ,b 的关系为a <b <0或0<b <a 或a =b =0.考向三 指数函数的性质及应用方向1 指数函数的单调性【例3】 (1)已知a =⎝ ⎛⎭⎪⎫35- 13,b =⎝ ⎛⎭⎪⎫35- 14 ,c =⎝ ⎛⎭⎪⎫32- 34 ,则a ,b ,c 的大小关系是( )A .c <a <bB .a <b <cC .b <a <cD .c <b <a(2)已知函数f (x )=(13)ax 2-4x +3 .①若a =-1,求f (x )的单调区间; ②若f (x )有最大值3,求a 的值. 【解析】 (1)因为-13<-14<0,所以⎝ ⎛⎭⎪⎫35-13 >⎝ ⎛⎭⎪⎫35-14 >⎝ ⎛⎭⎪⎫350=1,即a >b >1,且⎝ ⎛⎭⎪⎫32-34 <⎝ ⎛⎭⎪⎫320=1,所以c <1,综上,c <b <a .(2)①当a =-1时,f (x )=(13)-x 2-4x +3,令g (x )=-x 2-4x +3,由于g (x )在(-∞,-2)上单调递增,在(-2,+∞)上单调递减,而y =(13)t 在R 上单调递减,所以f (x )在(-∞,-2)上单调递减,在(-2,+∞)上单调递增,即函数f (x )的递增区间是(-2,+∞),递减区间是(-∞,-2).②令h (x )=ax 2-4x +3,则f (x )=(13)h (x ),由于f (x )有最大值3,所以h (x )应有最小值-1,因此必有⎩⎨⎧a >0,12a -164a =-1,解得a =1,即当f (x )有最大值3时,a 的值等于1.【答案】 (1)D (2)见解析 方向2 指数函数性质的综合应用【例4】 (1)函数f (x )=a +be x +1(a ,b ∈R )是奇函数,且图象经过点⎝⎛⎭⎪⎫ln3,12,则函数f (x )的值域为( )A .(-1,1)B .(-2,2)C .(-3,3)D .(-4,4)(2)若不等式1+2x +4x ·a >0在x ∈(-∞,1]时恒成立,则实数a 的取值范围是________.【解析】 (1)函数f (x )为奇函数,则f (0)=a +b2=0①,函数图象过点⎝⎛⎭⎪⎫ln3,12,则f (ln3)=a +b 4=12②.结合①②可得a =1,b =-2,则f (x )=1-2e x+1.因为e x >0,所以e x +1>1,所以0<2e x +1<2,所以-1<1-2e x +1<1,即函数f (x )的值域为(-1,1).(2)从已知不等式中分离出实数a ,得a >-⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫14x +⎝ ⎛⎭⎪⎫12x .∵函数y =⎝ ⎛⎭⎪⎫14x 和y =⎝ ⎛⎭⎪⎫12x 在R 上都是减函数,∴当x ∈(-∞,1]时,⎝ ⎛⎭⎪⎫14x ≥14,⎝ ⎛⎭⎪⎫12x ≥12,∴⎝ ⎛⎭⎪⎫14x+⎝ ⎛⎭⎪⎫12x ≥14+12=34,从而得-⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫14x +⎝ ⎛⎭⎪⎫12x ≤-34.故实数a 的取值范围为a >-34. 【答案】 (1)A (2)⎝ ⎛⎭⎪⎫-34,+∞1.比较指数式大小的问题:常化为同底或同指,利用指数函数的单调性,图象或1,0等中间量进行比较.2.解简单的指数方程或不等式问题时,应利用指数函数的单调性转化为一般方程或不等式求解.要特别注意底数a的取值范围,并在必要时进行分类讨论.3.对于指数函数性质的综合应用,应首先判断指数型函数的性质,再利用其性质求解,关键是指数型函数的单调性要抓住“同增异减”.1.(方向1)(2019·滕州模拟)下列各式比较大小正确的是(B)A.1.72.5>1.73B.0.6-1>0.62C.0.8-0.1>1.250.2D.1.70.3<0.93.1解析:A中,∵函数y=1.7x在R上是增函数,2.5<3,∴1.72.5<1.73.B中,∵y=0.6x在R上是减函数,-1<2.∴0.6-1>0.62.C中,∵0.8-1=1.25,∴问题转化为比较1.250.1与1.250.2的大小.∵y=1.25x在R上是增函数,0.1<0.2.∴1.250.1<1.250.2,即0.8-0.1<1.250.2.D中,∵1.70.3>1,0<0.93.1<1,∴1.70.3>0.93.1.2.(方向2)(2019·绍兴模拟)设偶函数f (x )满足f (x )=2x -4(x ≥0),则{x |f (x -2)>0}=( B )A .{x |x <-2或x >4}B .{x |x <0或x >4}C .{x |x <0或x >6}D .{x |x <-2或x >2} 解析:∵f (x )为偶函数, 当x <0时,f (x )=f (-x )=2-x -4.∴f (x )={ 2x-4,x ≥0,2-x -4,x <0,若f (x -2)>0,则有⎩⎪⎨⎪⎧ x -2≥0,2x -2-4>0,或⎩⎪⎨⎪⎧x -2<0,2-x +2-4>0,解得x >4或x <0. 3.(方向2)若函数f (x )=a |2x -4|(a >0,且a ≠1),满足f (1)=19,则f (x )的单调递减区间是( B )A .(-∞,2]B .[2,+∞)C .[-2,+∞)D .(-∞,-2]解析:由f (1)=19,得a 2=19,解得a =13或a =-13(舍去),即f (x )=⎝ ⎛⎭⎪⎫13|2x-4|.由于y=|2x-4|在(-∞,2]上递减,在[2,+∞)上递增,所以f(x)在(-∞,2]上递增,在[2,+∞)上递减,故选B.。
高考数学一轮复习考点规范练8指数与指数函数新人教A版

考点规范练8 指数与指数函数一、基础巩固1.化简(x<0,y<0)得()A.2xB.2xC.-2xD.-2x2.函数f(x)=2|x-1|的大致图象是()3.已知f(x)=3x-b( ≤x≤ ,b为常数)的图象经过点(2,1),则f(x)的值域为()A.[9,81]B.[3,9]C.[1,9]D.[1,+∞)4.函数f(x)=1-e|x|的图象大致是()5.若函数y=a x-b(a>0,且a≠1)的图象经过第二、第三、第四象限,则a b的取值范围为()A.(1,+∞)B.(0,+∞)C.(0,1)D.无法确定6.已知a=20.2,b=0.40.2,c=0.40.6,则()A.a>b>cB.a>c>bC.c>a>bD.b>c>a7.若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)=,则f(x)的单调递减区间是()A.(-∞,2]B.[2,+∞)C.[-2,+∞)D.(-∞,-2]8.函数y=2x-2-x是()A.奇函数,在区间(0,+∞)内单调递增B.奇函数,在区间(0,+∞)内单调递减C.偶函数,在区间(-∞,0)内单调递增D.偶函数,在区间(-∞,0)内单调递减9.曲线y=2a|x-1|-1(a>0,a≠1)过定点.10.函数f(x)=的值域为.11.函数y=+1在x∈[-3,2]上的值域是.12.已知函数f(x)=(a-2)a x(a>0,且a≠1),若对任意x1,x2∈R,(-(->0,则a的取值范围是.二、能力提升13.当x∈(-∞,-1]时,若不等式(m2-m)·4x-2x<0恒成立,则实数m的取值范围是()A.(-2,1)B.(-4,3)C.(-1,2)D.(-3,4)14.若存在正数x使2x(x-a)<1成立,则a的取值范围是()A.(-∞,+∞)B.(-2,+∞)C.(0,+∞)D.(-1,+∞)15.已知函数f(x)=|2x-1|,且当a<b<c时,有f(a)>f(c)>f(b),则下列结论一定成立的是()A.a<0,b<0,c<0B.a<0,b≥0,c>0C.2-a<2cD.2a+2c<216.记x2-x1为区间[x1,x2]的长度,已知函数y=2|x|,x∈[-2,a](a≥0 ,其值域为[m,n],则区间[m,n]的长度的最小值是.三、高考预测17.设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系是()A.a<b<cB.a<c<bC.b<a<cD.b<c<a考点规范练8指数与指数函数1.D2.B解析因为f(x)=2|x-1|=-,-,,所以f(x)在[1,+∞)内为增函数,在(-∞,1)内为减函数.3.C解析由f(x)的图象经过点(2,1)可知b=2.因为f(x)=3x-2在区间[2,4]上是增函数,所以f(x)min=f(2)=1,f(x)max=f(4)=9.故f(x)的值域为[1,9].4.A解析因为函数f(x)=1-e|x|是偶函数,且值域是(-∞,0],只有A满足上述两个性质.故选A.5.C解析因为函数图象经过第二、第三、第四象限,所以函数单调递减且图象与y轴的交点在y轴负半轴上.令x=0,得y=a0-b=1-b,由题意得0,解得0,故a b∈(0,1),故选C.6.A解析由0.2<0.6,0<0.4<1,可知0.40.2>0.40.6, 即b>c.又因为a=20.2>1,b=0.40.2<1,所以a>b.综上,a>b>c.7.B解析由f(1)=得a2=,故a=舍去,即f(x)=-.由于y=|2x-4|在(-∞,2]上单调递减,在[2,+∞)上单调递增,故f(x)在(-∞,2]上单调递增,在[2,+∞)上单调递减.故选B.8.A解析令f(x)=2x-2-x,则f(x)的定义域为R,且f(-x)=2-x-2x=-f(x),所以函数f(x)是奇函数,排除C,D.又函数y=-2-x,y=2x均是R上的增函数,所以y=2x-2-x在R上为增函数.9.(1,1)解析由|x-1|=0,即x=1,此时y=1,故函数恒过定点(1,1).10.[0,1)解析由1-e x≥0,可知e x≤ .又0<e x,所以- ≤-e x<0,即0≤ -e x<1.故函数f(x)的值域为[0,1).11., 解析令t=,由x∈[-3,2],得t∈, .则y=t2-t+1=-∈, .当t=时,y min=;当t=8时,y max=57.故所求函数的值域为, .12.(0,1)∪(2,+∞)解析由题意知f(x)在R上是增函数.当0<a<1时,a-2<0,y=a x单调递减,所以f(x)单调递增;当1<a<2时,a-2<0,y=a x单调递增,所以f(x)单调递减;当a=2时,f(x)=0;当a>2时,a-2>0,y=a x单调递增,所以f(x)单调递增.故a的取值范围是(0,1)∪(2,+∞).13.C解析原不等式可变形为m2-m<.∵函数y=在(-∞,-1]上是减函数,∴-=2.当x∈(-∞,-1]时,m2-m<恒成立等价于m2-m<2,解得-1<m<2.14. D解析不等式2x(x-a)<1可变形为x-a<.在同一平面直角坐标系中作出直线y=x-a与y=的图象.由题意知,在(0,+∞)内,直线有一部分在y=图象的下方.由图可知,-a<1,所以a>-1.15.D解析作出函数f(x)=|2x-1|的图象,如图.∵当a<b<c时,有f(a)>f(c)>f(b),∴结合图象知0<f(a)<1,a<0,c>0.∴0<2a<1.∴f(a)=|2a-1|=1-2a<1.∴f(c)<1,∴0<c<1.∴1<2c<2,∴f(c)=|2c-1|=2c-1,又f(a)>f(c),∴1-2a>2c-1,∴2a+2c<2,故选D.16.3解析令f(x)=y=2|x|,则f(x)=,0≤, -,- ≤0(1)当a=0时,f(x)=2-x在[-2,0]上为减函数,值域为[1,4].(2)当a>0时,f(x)在[-2,0)上为减函数,在[0,a]上为增函数,①当0<a≤ 时,f(x)max=f(-2)=4,值域为[1,4];②当a>2时,f(x)max=f(a)=2a>4,值域为[1,2a].综上(1)(2),可知[m,n]的长度的最小值为3.17.C解析函数y=0.6x在定义域R上为减函数,∴1=0.60>0.60.6>0.61.5.而函数y=1.5x为增函数,∴1.50.6>1.50=1,∴b<a<c.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业8 指数与指数函数一、选择题1.化简4a23 ·b - 13 ÷⎝⎛⎭⎪⎪⎫-23a- 13 b 23 的结果为( C )A .-2a 3bB .-8ab C .-6a bD .-6ab2.设函数f (x )=⎩⎨⎧⎝ ⎛⎭⎪⎫12x -7,x <0,x ,x ≥0,若f (a )<1,则实数a 的取值范围是( C )A .(-∞,-3)B .(1,+∞)C .(-3,1)D .(-∞,-3)∪(1,+∞)解析:当a <0时,不等式f (a )<1为⎝ ⎛⎭⎪⎫12a-7<1,即⎝ ⎛⎭⎪⎫12a <8,即⎝ ⎛⎭⎪⎫12a <⎝ ⎛⎭⎪⎫12-3, 因为0<12<1,所以a >-3, 此时-3<a <0;当a ≥0时, 不等式f (a )<1为a <1,所以0≤a <1. 故a 的取值范围是(-3,1),故选C.3.(2019·湖南永州模拟)下列函数中,与函数y =2x -2-x 的定义域、单调性与奇偶性均一致的是( B )A .y =sin xB .y =x 3C .y =⎝ ⎛⎭⎪⎫12xD .y =log 2x解析:y =2x -2-x 是定义域为R 的单调递增函数,且是奇函数.而y =sin x 不是单调递增函数,不符合题意;y =⎝ ⎛⎭⎪⎫12x是非奇非偶函数,不符合题意;y =log 2x 的定义域是(0,+∞),不符合题意;y =x 3是定义域为R 的单调递增函数,且是奇函数符合题意.故选B.4.二次函数y =-x 2-4x (x >-2)与指数函数y =⎝ ⎛⎭⎪⎫12x的图象的交点个数是( C )A .3B .2C .1D .0解析:因为函数y =-x 2-4x =-(x +2)2+4(x >-2),且当x =-2时,y =-x 2-4x =4,y =⎝ ⎛⎭⎪⎫12x=4,则在同一直角坐标系中画出y =-x 2-4x (x >-2)与y =⎝ ⎛⎭⎪⎫12x的图象如图所示,由图象可得,两个函数图象的交点个数是1,故选C.5.(2019·福建厦门一模)已知a =⎝ ⎛⎭⎪⎫120.3,b =log 120.3,c =a b ,则a ,b ,c 的大小关系是( B )A .a <b <cB .c <a <bC .a <c <bD .b <c <a解析:b =log 12 0.3>log 1212=1>a =⎝ ⎛⎭⎪⎫120.3,c =a b <a .∴c <a <b .故选B.6.已知a ,b ∈(0,1)∪(1,+∞),当x >0时,1<b x <a x ,则( C ) A .0<b <a <1 B .0<a <b <1 C .1<b <aD .1<a <b解析:∵当x >0时,1<b x ,∴b >1. ∵当x >0时,b x <a x ,∴当x >0时,⎝ ⎛⎭⎪⎫a b x >1.∴ab >1,∴a >b .∴1<b <a ,故选C.7.如图,在面积为8的平行四边形OABC 中,AC ⊥CO ,AC 与BO 交于点E .若指数函数y =a x (a >0,且a ≠1)经过点E ,B ,则a 的值为( A )A. 2B. 3 C .2D .3解析:设点E (t ,a t ),则点B 的坐标为(2t,2a t ).因为2a t =a 2t ,所以a t =2.因为平行四边形OABC 的面积=OC ×AC =a t ×2t =4t ,又平行四边形OABC 的面积为8,所以4t =8,t =2,所以a 2=2,a = 2.故选A.二、填空题8.不等式2x 2-x <4的解集为{x |-1<x <2}. 解析:∵2x 2-x <4,∴2x 2-x <22, ∴x 2-x <2,即x 2-x -2<0,解得-1<x <2.9.若直线y 1=2a 与函数y 2=|a x -1|(a >0且a ≠1)的图象有两个公共点,则a 的取值范围是⎝ ⎛⎭⎪⎫0,12.解析:(数形结合法)当0<a <1时,作出函数y 2=|a x -1|的图象,由图象可知0<2a <1,∴0<a <12;同理,当a >1时,解得0<a <12,与a >1矛盾. 综上,a 的取值范围是⎝⎛⎭⎪⎫0,12. 10.已知函数f (x )=2x-12x ,函数g (x )=⎩⎪⎨⎪⎧f (x ),x ≥0,f (-x ),x <0,则函数g (x )的最小值是0.解析:当x ≥0时,g (x )=f (x )=2x -12x 为单调增函数,所以g (x )≥g (0)=0;当x <0时,g (x )=f (-x )=2-x -12-x为单调减函数,所以g (x )>g (0)=0,所以函数g (x )的最小值是0.11.(2019·湖南益阳调研)已知函数f (x )=2x1+a ·2x(a ∈R )的图象关于点⎝⎛⎭⎪⎫0,12对称,则a =1.解析:由已知,得f (x )+f (-x )=1, 即2x1+a ·2x+2-x1+a ·2-x =1, 整理得(a -1)[22x +(a -1)·2x +1]=0,所以当a -1=0,即a =1时,等式成立.三、解答题12.设a >0,且a ≠1,函数y =a 2x +2a x -1在[-1,1]上的最大值是14,求实数a 的值.解:令t =a x (a >0,且a ≠1),则原函数化为y =f (t )=(t +1)2-2(t >0). ①当0<a <1,x ∈[-1,1]时,t =a x ∈⎣⎢⎡⎦⎥⎤a ,1a ,此时f (t )在⎣⎢⎡⎦⎥⎤a ,1a 上为增函数.所以f (t )max =f ⎝ ⎛⎭⎪⎫1a =⎝ ⎛⎭⎪⎫1a +12-2=14.所以⎝ ⎛⎭⎪⎫1a +12=16,解得a =-15(舍去)或a =13.②当a >1时,x ∈[-1,1],t =a x∈⎣⎢⎡⎦⎥⎤1a ,a ,此时f (t )在⎣⎢⎡⎦⎥⎤1a ,a 上是增函数.所以f (t )max =f (a )=(a +1)2-2=14,解得a =3或a =-5(舍去).综上得a =13或3.13.(2019·河南八市第一次测评)设函数f (x )=x 2-a 与g (x )=a x (a >1且a ≠2)在区间(0,+∞)上具有不同的单调性,则M =(a -1)0.2与N=⎝ ⎛⎭⎪⎫1a 0.1的大小关系是( D ) A .M =N B .M ≤N C .M <ND .M >N解析:因为f (x )=x 2-a 与g (x )=a x (a >1且a ≠2)在区间(0,+∞)上具有不同的单调性,所以a >2,所以M =(a -1)0.2>1,N =⎝ ⎛⎭⎪⎫1a 0.1<1,所以M >N ,故选D.14.已知函数f (x )=1-42a x +a (a >0,a ≠1)且f (0)=0.(1)求a 的值;(2)若函数g (x )=(2x +1)·f (x )+k 有零点,求实数k 的取值范围; (3)当x ∈(0,1)时,f (x )>m ·2x -2恒成立,求实数m 的取值范围. 解:(1)对于函数f (x )=1-42a x +a (a >0,a ≠1),由f (0)=1-42+a =0,得a =2.(2)由(1)知f (x )=1-42·2x +2=1-22x +1.因为函数g (x )=(2x +1)·f (x )+k =2x +1-2+k =2x -1+k 有零点,所以函数y =2x 的图象和直线y =1-k 有交点,∴1-k >0,即k <1.(3)∵当x ∈(0,1)时,f (x )>m ·2x -2恒成立,即1-22x +1>m ·2x -2恒成立,亦即m <32x -22x (2x +1)恒成立,令t =2x,则t ∈(1,2),且m <3t -2t (t +1)=3t +1t (t +1)=1t +2t +1.由于y =1t +2t +1在t ∈(1,2)上单调递减,∴1t +2t +1>12+22+1=76,∴m ≤76.尖子生小题库——供重点班学生使用,普通班学生慎用 15.已知实数a ,b 满足12>⎝ ⎛⎭⎪⎫12a >⎝ ⎛⎭⎪⎫22b >14,则( B )A .b <2b -aB .b >2b -aC .a <b -aD .a >b -a解析:由12>⎝ ⎛⎭⎪⎫12a,得a >1,由⎝ ⎛⎭⎪⎫12a >⎝ ⎛⎭⎪⎫22b ,得⎝ ⎛⎭⎪⎫222a >⎝ ⎛⎭⎪⎫22b ,故2a <b ,由⎝ ⎛⎭⎪⎫22b >14,得⎝ ⎛⎭⎪⎫22b >⎝ ⎛⎭⎪⎫224,得b <4.由2a <b ,得b >2a >2,a <b2<2, ∴1<a <2,2<b <4.对于选项A ,B ,由于b 2-4(b -a )=(b -2)2+4(a -1)>0恒成立,故A 错误,B 正确;对于选项C ,D ,a 2-(b -a )=a +122-⎝ ⎛⎭⎪⎫b +14,由于1<a <2,2<b <4,故该式的符号不确定,故C ,D 错误.故选B.16.已知max(a ,b )表示a ,b 两数中的最大值.若f (x )=max(e |x |,e |x -2|),则f (x )的最小值为e.解析:由题意得,f (x )=⎩⎨⎧e x ,x ≥1,e |x -2|,x <1.当x ≥1时,f (x )=e x ≥e(当x =1时取等号),当x<1时,f(x)=e|x-2|=e2-x>e,因此x=1时,f(x)有最小值f(1)=e.。
