全等三角形及其判定复习提高训练
全等三角形判定综合训练
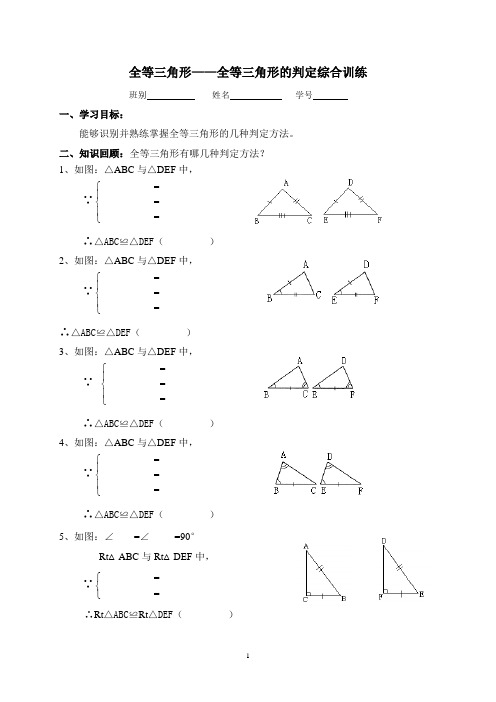
全等三角形——全等三角形的判定综合训练班别 姓名 学号一、学习目标:能够识别并熟练掌握全等三角形的几种判定方法。
二、知识回顾:全等三角形有哪几种判定方法? 1、如图:△ABC 与△DEF 中,∵⎪⎩⎪⎨⎧===__________________________________________________________ ∴△ABC ≌△DEF ( )2、如图:△ABC 与△DEF 中,∵⎪⎩⎪⎨⎧===__________________________________________________________ ∴△ABC ≌△DEF ( )3、如图:△ABC 与△DEF 中,∵ ⎪⎩⎪⎨⎧===__________________________________________________________∴△ABC ≌△DEF ( )4、如图:△ABC 与△DEF 中,∵⎪⎩⎪⎨⎧===__________________________________________________________ ∴△ABC ≌△DEF ( )5、如图:∠____=∠_____=90°Rt △ABC 与Rt △DEF 中,∵⎩⎨⎧==______________________________________∴Rt △ABC≌Rt △DEF( )三、练习:1、已知AB=CD,BE=DF,AF=CE,则AB与CD有怎样的位置关系?2、已知O是AB中点,OC=OD,AOD BOC∠=∠,求证:AC BD=3、已知:如图, ∠1=∠2 , ∠3=∠4求证:AC=AB.4、已知:如图, E、D、B、F在同一条直线上, AD∥CB , ∠BAD=∠BCD , DE=BF.求证:AE∥CF.5、如图,△ABC中,D是BC上一点,DE⊥AB,DF⊥AC,E、F分别为垂足,且AE=AF,试说明:DE=DF,AD平分∠BAC.6、如图,△ABC中,∠C=90°,AB=2AC,M是AB的中点,点N在BC上,MN⊥AB。
三角形全等判定专题训练题

三角形全等判定专题训练题1.给定三角形ABC,AD垂直于BC,垂足为D,且BD=CD。
证明△ABD≌△ACD。
2.给定平行四边形ABCD,AC=EF,AC平行于EF,且F在AD上。
证明△ABC≌△EDF。
3.给定三角形ABC和DEF,DF=CE,AD=BC,∠D=∠C。
证明△AED≌△BFC,其中AE=BD。
4.给定等腰直角三角形ABC,AB=AC,AD=AE,AB垂直于AC,AD垂直于AE。
证明∠B=∠C且BD=CE。
6.给定四边形ABCDE,CG=CF,BC=DC,AB=ED,且A、B、C、D、E在同一直线上。
证明AF=EG且BF平行于DG。
7.给定三角形ABC,AC垂直于BC,___平分∠ABC,且交AC于点M,N是AB的中点,且BN=BC。
证明___平分∠AMB且∠A=∠___。
8.给定四边形ABCD,AC=DB,BE平行于CF,AE平行于DF。
证明△ABE≌△DCF。
9.给定三角形ABC,AE和BC相交于点M,F在AM上,BE平行于CF,且BE=CF。
证明AM是△ABC的中线。
10.给定四边形ABCD,且∠BAC=∠DAE,∠ABD=∠ACE,BD=CE。
证明AB=AC。
11.给定三角形ABC和△DBC,且∠1=∠2,∠3=∠4,P是BC上的任意一点。
证明PA=PD。
12.给定四边形ABCD,AB平行于CD,OA=OD,且F、D、O、A、E在同一直线上,AE=DF。
证明EB平行于CF。
13.给定三角形ABC和△EDC,且△ABC≌△EDC。
证明BE=AD。
14.给定等腰直角三角形ABC,AC=BC,AE是BC的中线,CF⊥AE于F,BD⊥CB交CF的延长线于点D。
证明AB=BD。
15、证明:由图可知,∠BAC=90°,且AB=2AC,因此由勾股定理可得BC=√5AC,而DE=AC,BF=2AC,EF=BC-AC=√5AC-AC=(√5-1)AC,因此AE=AC+EF=2AC+(√5-1)AC=(1+√5)AC,所以△ABC≌△AED。
(完整)全等三角形提高练习精选27题及答案

全等三角形提高练习精选27题及答案1•如图所示,△ ABC ^A ADE , BC 的延长线过点 E,/ ACB= / AED=105 / CAD=10 ° ,Z B=50。
,求/DEF 的度数。
2•如图,△ AOB 中,/ B=30。
,将A AOB 绕点O 顺时针旋转52。
,得到厶A'OB ', 边A 'B '与边OB 交于点C (A '不在OB 上),则/ A 'CO 的度数为多少?3•如图所示,在△ ABC 中,/ A=90 ° ,D 、E 分别是 AC 、 若厶ADB ◎△ EDB ^A EDC ,则/ C 的度数是多少?4•如图所示,把△ ABC 绕点C 顺时针旋转35°,得到△ A'B'C , A '' 交 AC 于点 D ,若/ A 'DC=90 °,^U/A= ____________6•如图,Rt A ABC 中,/ BAC=90 ° ,AB=AC ,分别过点 B C 作过点A 的垂线BC 、CE,垂足分另【J 为 D 、E , 若 BD=3 , CE=2,贝U DE= ____________7•如图,AD 是厶ABC 的角平分线,DE 丄AB , DF 丄AC ,垂足分别是 E 、F ,连接EF, 交AD 于G , AD 与EF 垂直吗?证明你的结论。
AE G5•已知,如图所示, 则AD 是多AB=AC , AD 丄 BC 于 D ,且 AB+AC+BC=50cm,ABA'B'AO14. 如图所示,已知△ ABC 和厶BDE 都是等边三角形,下列结论:① AE=CD ;②BF=BG ; ③BH 平分/ AHD ; ④/ AHC=60 ° ;⑤厶BFG 是等边三角形; ⑥FG// AD , E其中正确的有()A . 3 个 B. 4 个 C. 5 个 D. 6 个C H8•如图所示,在△ ABC 中,AD 为/ BAC 的角平分线,2积是 28cm ,AB=20cm , AC=8cm ,求 DE 的长。
全等三角形的提高拓展训练典范题型50题(含答案解析)

全等三角形的提高拓展训练知识点睛全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等.寻找对应边和对应角,常用到以下方法:(1) 全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.(2) 全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.(3) 有公共边的,公共边常是对应边.(4) 有公共角的,公共角常是对应角.(5) 有对顶角的,对顶角常是对应角.(6) 两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键.全等三角形的判定方法:(1)边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.⑵角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.(3) 边边边定理(SSS):三边对应相等的两个三角形全等.(4) 角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.(5) 斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线.拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系. 而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.例题精讲板块一、截长补短【例1】(06年北京中考题)已知ABC中,A 60 , BD、CE分别平分ABC和.ACB ,BD、CE交于点0,试判断BE、CD、BC的数量关系,并加以证明.N【例2】 如图,点 M 为正三角形 ABD 的边AB 所在直线上的任意一点 (点B 除外),作DMN 60,射线MN 与/ DBA 外角的平分线交于点 N , DM 与MN 有怎样的 数量关系? 【例4】以 ABC 的AB 、AC 为边向三角形外作等边【变式拓展训练】如图,MN DM 且与Z ABC 外角的平分线交 【例3】已知:如图,ABCD 是正方形,/ FAD = /FAE 求证: B C于点0 .求证:OA 平分 DOE •【例 6】 五边形 ABCDE 中,AB = AE ,BC + DE = CD ,/ABC + ZAED = 180求证:AD 平分Z CDE 【例5】(北京市、天津市数学竞赛试题)如图所示, ABC 是边长为1的正三角形, BDC 是 顶角为120的等腰三角形,以 D 为顶点作一个60的AB 、AC 上,求 AMN 的周长.MDN ,板块二、全等与角度【例7】如图,在ABC 中, 求 ABC 的度数.【例8】在等腰 ABC 中,AB AC ,顶角 A 20,在边AB 上取点D ,使AD BC ,求 BDC .【例9】(“勤奋杯”数学邀请赛试题 )如图所示,在 ABC 中,AC BC , 又M 在AC 上,N 在BC 上,且满足 BAN 50, ABM 60,求 NMB • 例 10】在四边形 ABCDBAC 60 , AD 是 BAC 的平分线,且 AC AB BD ,C A中,已知AB AC,ABD 60 ,ADB 76 ,BDC 28 ,求DBC 的度数.【例11】(日本算术奥林匹克试题)如图所示,在四边形ABCD中,DAC 12 , CAB 36 ,ABD 48 ,DBC 24 ,求ACD 的度数.【例12】(河南省数学竞赛试题)在正ABC内取一点D,使DA DB,在ABC 外取一点E,使DBE DBC,且BE BA,求BED.【例13】(北京市数学竞赛试题)如图所示,在ABC中,BAC BCA 44 , M为ABC 内一点,使得MCA 30 , MAC 16,求BMC的度数.全等三角形证明经典20题(含答案)1. 已知:AB=4,AC=2,D是BC中点,AD是整数,求ADA延长AD到E使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数则AD=52. 已知:/ 1= Z2 , CD=DE , EF//AB,求证:EF=AC 证明:过E点,作EG//AC,交AD延长线于G贝U/DEG= Z DCA,/DGE= Z2又VCD=DE•••zADC BzGDE (AAS )•••EG=ACTEF//AB•••ZDFE= Z1•/Z1= Z2•••ZDFE= ZDGE•••EF=EG•••EF=AC3. 已知:AD 平分/ BAC, AC=AB+BD ,求证:/ B=2 ZCA证明:在AC上截取AE=AB,连接EDVAD 平分Z BAC•••ZEAD= /BAD又V AE=AB , AD=AD• zAED Bz ABD ( SAS)•••ZAED= ZB,DE=DB•/AC=AB+BDAC=AE+CE•••CE=DE•••ZC= /EDCV Z AED= ZC+ Z EDC=2 ZC•••ZB=2 Z C4. 已知:AC 平分Z BAD , CE丄AB ,Z B+ /D=180 °,求证:AE=AD+BE 证明:在AE上取F,使EF= EB,连接CF因为CE丄AB所以/CEB =/CEF = 90因为 EB = EF , CE = CE ,所以△ CEB ^z CEF所以/B =Z CFE因为/B +/D = 180 ° ,z CFE +/CFA = 180所以/D = /CFA因为AC 平分/BAD所以 /DAC =/FAC又因为AC = AC所以△ADC ^ZAFC (SAS )5. 如图,四边形 ABCD 中,AB //DC , BE 、CE 分别平分/ ABC 、/BCD ,且点E 在AD 上。
三角形全等的判定专题训练50题

三角形全等的判定专题训练题1、如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:△ABD ≌△ACD 。
2、如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
3、 如图(3):DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
4、 如图(4):AB=AC ,AD=AE ,AB ⊥AC ,AD ⊥AE 。
求证:(1)∠B=∠C ,(2)BD=CE.(图1)D CBA F E (图2)DCB A F E (图3)DCB A E (图4)D C B A5、如图(5):AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE 。
求证:AC ⊥CE 。
6、如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF=EG ,(2)BF ∥DG 。
7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M ,N 是AB 的中点且BN=BC 。
求证:(1)MN 平分∠AMB ,(2)∠A=∠CBM 。
8、如图(8):A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
GF E(图6)D CBA N M(图7)CBA F E (图8)D CBA E (图5)DC B A9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
10、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE 。
求证:AB=AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA=PD 。
12、如图(12)AB ∥CD ,OA=OD ,点F 、D 、O 、A 、E 在同一直线上,AE=DF 。
求证:EB ∥CF 。
经典全等三角形各种判定(提高版)
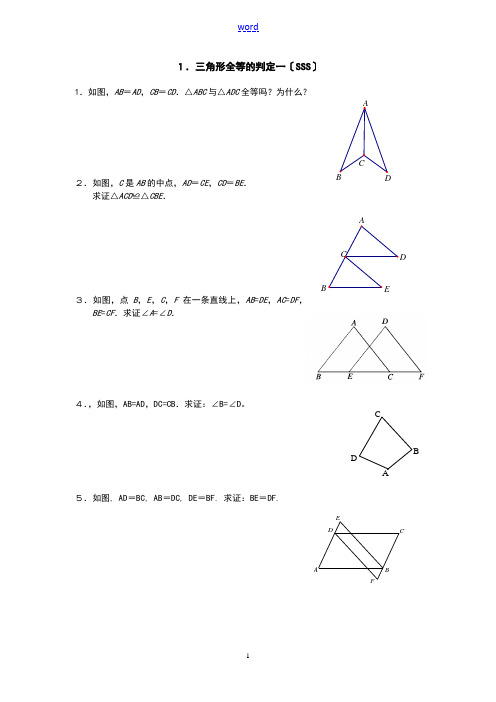
FE DCBA1.如图,AB =AD ,CB =CD .△ABC 与△ADC 全等吗?为什么?2.如图,C 是AB 的中点,AD =CE ,CD =BE .求证△ACD ≌△CBE .3.如图,点B ,E ,C ,F 在一条直线上,AB =DE ,AC =DF ,BE =CF .求证∠A =∠D . 4.,如图,AB=AD ,DC=CB .求证:∠B=∠D 。
5.如图, AD =BC, AB =DC, DE =BF. 求证:BE =DF.CA B A C EAD C B1.如图,AC 和BD 相交于点O ,OA =OC ,OB =OD .求证DC ∥AB . 2.如图,△ABC ≌△A B C ''',AD ,A D ''分别是△ABC ,△A B C '''的对应边上的中线,AD 与A D ''有什么关系?证明你的结论.3.如图,AC ⊥AB ,DB ⊥AB ,AC =BE ,AE =BD ,试猜测线段CE 与DE 的大小与位置关系,并证明你的结论.4.:如图,AD ∥BC ,AD=CB ,求证:△ADC ≌△CBA .5.:如图AD ∥BC ,AD=CB ,AE=CF 。
求证:△AFD ≌△CEB .6.,如图,AB=AC ,AD=AE ,∠1=∠2。
求证:△ABD ≌△ACE .AC EDBAE B CFDAB CD2 A CBE1H F ED CB A 7.:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF.求证:AC ∥DF .8.:如图,AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF . 9.如图, 在△ABC 中, 分别延长中线BE 、CD 至F 、H, 使EF =BE, DH =CD, 连结AF 、AH . 求证:(1) AF =AH ;(2)点A 、F 、H 三点在同一直线上; (3)HF ∥BC.10.如图, 在△ABC 中, AC ⊥BC, AC =BC, 直线EF 交AC 于F, 交AB 于E, 交BC 的延长线于D, 连结AD 、BF, CF =CD. 求证:BF =AD, BF ⊥AD.11.证明:如果两个三角形有两条边和其中一边上的中线对应相等,那么这两个三角形全等.〔提示:首先分清和求证,然后画出图形,再结合图形用数学符号表示和求证〕AB C DE F12.证明:如果两个三角形有两条边和第三边上的中线对应相等,那么这两个三角形全等.13.:如图,正方形ABCD ,BE =CF ,求证:(1)AE =BF ; 〔2〕AE ⊥BF . 14.:E 是正方形ABCD 的边长AD 上一点,BF 平分∠EBC ,交CD 于F ,求证BE=AE+CF.〔提示:旋转构造等腰〕15.如图,△ABD 和△ACE 是△ABC 外两个等腰直角三角形,∠BAD=∠CAE=900.〔1〕判断CD 与BE 有怎样的数量关系;〔2〕探索DC 与BE 的夹角的大小.〔3〕取BC 的中点M ,连MA ,探讨MA 与DE 的位置关系。
全等三角形的判定和性质专题训练

全等三角形判定与性质专题训练一、全等三角形实际应用问题1如图,要测量河两岸相对的两点A、B间的距离,先在过B点的AB的垂线L上取两点C、D,使CD=BC,再在过D点的垂线上取点E,使A、C、E在一条直线上,ED=AB这时,测ED的长就得AB得长,判定△ACB≌△ECD的理由是()A. SASB. ASAC. SSS D .AAS2.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是()A.PO B.PQ C.MO D.MQ3、如图所示,将两根钢条AA′,BB′的中点O连在一起,使A A′,BB′可以绕着点O自由转动,就做成了一个测量工具,则A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是()A、SSS B、SAS C、ASA D、HL4、如图:工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是()A、SSSB、SASC、ASAD、HL5、如图,有两个长度相等的滑梯靠在一面墙上.已知左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,则这两个滑梯与地面的夹角∠ABC+∠DFE= 度6、如图,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是:( )A 、带①去,B 、带②去C 、带③去D 、①②③都带去二、证两次全等相关问题1:如图:已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证: CF=DF2:如图已知AD∥BC,AB∥CD BF=DE,求证:AE=CF,3:如图AB⊥AC,AD⊥AE AB=AD,BC=DE,求证AM=AN三、探索两线段的关系问题1.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB 至点D,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE交CD于点F,试探索线段BE与AD的关系,并证明。
全等三角形的判定提高(含答案)

全等三角形的性质及判定【知识点归纳】全等三角形的认识与性质全等图形:能够完全重合的两个图形就是全等图形.全等多边形:能够完全重合的多边形就是全等多边形.相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.全等多边形的对应边、对应角分别相等.如下图,两个全等的五边形,记作:五边形ABCDE ≌五边形A 'B 'C 'D 'E' .这里符号“≌”表示全等,读作“全等于”.A A'E E'B D B' D'C C'全等三角形:能够完全重合的三角形就是全等三角形.全等三角形的对应边相等,对应角分别相等;反之,如果两个三角形的边和角分别对应相等,那么这两个三角形全等.全等三角形对应的中线、高线、角平分线及周长面积均相等.全等三角形的概念与表示:能够完全重合的两个三角形叫作全等三角形.能够相互重合的顶点、边、角分别叫作对应顶点、对应边、对应角.全等符号为“≌”.全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等.寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.(3)有公共边的,公共边常是对应边.(4)有公共角的,公共角常是对应角.(5)有对顶角的,对顶角常是对应角.FDE(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边 (或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键.板块一、全等三角形的认识与性质【例 1】 ① 判定两个三角形全等的方法是:⑴ ;⑵;⑶;⑷;⑸;⑹. 全等三角形的性质是对应边、对应角、周长、面积都分别.② 两个三角形具备下列()条件,则它们一定全等.A .两边和其中一边的对角对应相等B .三个角对应相等C .两角和一组对应边相等D .两边及第三边上的高对应相等③ 下列命题错误的是()A .全等三角形对应边上的高相等B .全等三角形对应边上的中线相等C .全等三角形对应角的角平分线相等D .有两边和一个角对应相等的两个三角形全等【解析】①⑴定义,⑵ SAS ,⑶ ASA ,⑷ AAS ,⑸ SSS ,⑹ HL ;相等.②C ;③D .【例 2】 ⑴ 考查下列命题:①有两边及一角对应相等的两个三角形全等;②两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等;③两角和其中一角的角平分线(或第三角的角平分线) 对应相等的两个三角形全等;④两边和其中一边上的高(或第三边上的高)对应相等的两个三角形全 等.其中正确命题的个数有个.⑵已知 ∆ABC 中, AB = BC ≠ AC ,作与 ∆ABC 只有一条公共边,且与 ∆ABC 全等的三角形,这样的三角形一共能作出个.⑶如图,在 Rt ∆ABC 中, AB = AC ,AD ⊥ BC ,垂足为 D . E 、F 分别是CD 、AD 上的点,且CE = AF .如果 ∠AED = 62︒ ,那么∠DBF = .⑷如图,已知 ∆ABC 中,∠ABC = 90︒ ,AB = BC ,三角形的顶点在相互平行的三条直线l 1 ,l 2 ,l 3 上,且l 1 ,l 2 之间的距离为 2 , l 2 ,l 3 之间的距离为3 ,则 AC 的长是.Al 12BC【解析】⑴ 2 ,注:正确的是②③;⑵ 7 ;⑶ 28︒ ;⑷ 2 ACl Bl317E P F【例 3】 ⑴ 如左下图所示, ∆ABC 中, D 、 E 分别在 AC 、 AB 上, BD 与CE交于点O ,给出下列四个条件:① ∠EBO = ∠DCO ;② ∠BEO = ∠CDO ;③ BE = CD ;④ OB = OC上述四个条件中,哪两个条件可判定, ∆ABC 是等腰三角形(用序号写出所有情形);A A BO FEBC C D⑵ 如右上图所示, AB ∥CD , AC ∥ DB , AB = CD , AD 与 BC 交于O , AE ⊥ BC 于 E , DF ⊥ BC 于 F , 那么图中全等的三角形有哪几对?并简单说明理由. 【解析】⑴ ①③、①④、②③、②④.⑵ 7 对: ∆AOB ≌ ∆DOC ; ∆AOC ≌ ∆DOB ; ∆AEO ≌ ∆DFO ;∆AEC ≌ ∆DFB ; ∆ABC ≌ ∆DCB ; ∆ABD ≌ ∆DCA ; ∆AEB ≌ ∆CFD .理由略.【例 4】 在 AB 、AC 上各取一点 E 、D ,使 AE = AD ,连接 BD 、CE 相交于O 再连结 AO 、BC ,若 ∠1 = ∠2 ,则图中全等三角形共有哪几对?并简单说明理由.BAC【解析】有5 对: ∆AEO ≌ ∆ADO ; ∆AEC ≌ ∆ADB ; ∆EOB ≌ ∆DOC ; ∆AOB ≌ ∆AOC ; ∆CDB ≌ ∆BEC ;理由略.【巩固】如图所示, AB = AD , BC = DC , E 、F 在 AC 上, AC 与 BD 相交于 P .图中有几对全等三角形?请一一找出来,并简述全等的理由.BACD【解析】共 10 对全等三角形.∆ABC ≌ ∆ADC ; ∆ABE ≌ ∆ADE ; ∆ABP ≌ ∆ADP ;EOD⎪⎩已知一边一角⎪⎩ ⎩ ∆ABF ≌ ∆ADF ; ∆BCF ≌ ∆DCF ; ∆BCP ≌ ∆DCP ; ∆BCE ≌ ∆DCE ; ∆BEP ≌ ∆DEP ; ∆BEF ≌ ∆DEF ; ∆BPF ≌ ∆DPF .板块二、三角形全等的判定与应用全等三角形的判定方法:(1) 边角边定理(SAS ):两边和它们的夹角对应相等的两个三角形全等. (2) 角边角定理(ASA ):两角和它们的夹边对应相等的两个三角形全等. (3) 边边边定理(SSS ):三边对应相等的两个三角形全等.(4) 角角边定理(AAS ):两个角和其中一个角的对边对应相等的两个三角形全等. (5) 斜边、直角边定理(HL ):斜边和一条直角边对应相等的两个直角三角形全等.全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线.奥数赛点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础. 判定三角形全等的基本思路: ⎧ 找夹角→ SAS 已知两边⎨ 找直角→ HL⎪ 找另一边→ SSS⎧ 边为角的对边→找任意一角→ AAS ⎪⎧ 找这条边上的另一角→ ASA ⎨ ⎪⎪ 边就是角的一条边⎨ 找这条边上的对角→ AAS ⎪ ⎩ ⎧ 找两角的夹边→ ASA已知两角⎨找任意一边→ AAS⎪ 找该角的另一边→ SAS全等三角形的图形归纳起来有以下几种典型形式: ⑴ 平移全等型FB⑵ 对称全等型⑶ 旋转全等型由全等可得到的相关定理:⑴ 角的平分线上的点到这个角的两边的距离相等. ⑵ 到一个角的两边的距离相同的点,在这个角的平分线上.⑶ 等腰三角形的性质定理:等腰三角形的两个底角相等 (即等边对等角). ⑷ 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合.⑸ 等腰三角形的判定定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边). ⑹ 线段垂直平分线上的点和这条线段两个端点的距离相等. ⑺ 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.【例 5】 如图, AC ∥ DE , BC ∥ EF , AC = DE .求证: AF = BD .EADC【解析】∵ AC ∥ DE ,∴ ∠A = ∠D∵ BC ∥ EF ,∴ ∠EFD = ∠CBA 又∵ AC = DE ∴ ∆ABC ≌ ∆DFE ∴ AB = DFO⎨ ⎩ADO∴ AB - FB = DF - BF 即 AF = BD【巩固】如图所示: AB ∥CD , AB = CD .求证: AD ∥ BC .D CA B【解析】连接 BD ,∵ AB ∥CD ,∴ ∠ABD = ∠CDB ,利用 SAS 证明∆ABD ≌ ∆CDB ,∴ ∠ADB = ∠CBD ,∴ AD ∥ BC .【例 6】 已知:如图, AD = BC , AC = BD ,求证: ∠C = ∠D .DC DCABAB【解析】连结 AB在∆ADB 与∆BCA 中 ⎧ AD = B C ⎪AB = B A ⎪BD = AC ∴ ∆ADB ≌ ∆BCA ∴ ∠D = ∠C【例 7】 已知:如图,B 、E 、F 、C 四点在同一条直线上,AB = DC ,BE = CF ,∠B = ∠C .求证:OA = OD .B EF C【解析】∵ BE = CF ,∴ BE + EF = EF + CF ,∴ BF = CE在∆ABF 与∆DCE 中ODEF⎨ ⎩⎧ A B = DC ⎪∠B = ∠C ⎪BF = CE ∴ ∆ABF ≌ ∆DCF∴ AF = DE , ∠AFB = ∠DEC∴ OF = OE∴ AF - OF = DE - OE∴ O A = OD【巩固】如图所示,已知 AD = AE , DF = EF .求证: AB = AC .ABC【解析】连接 AF ,根据 SSS 易得∆ADF ≌ ∆AEF ,进而得∠C = ∠B根据 AAS 易得∆ABE ≌ ∆ACD ,进而得 AB = AC .【例 8】 如图, AC 、 BD 相交于O 点,且 AC = BD , AB = CD ,求证: OA = OD .DCAB【解析】连接 AD ,根据 SSS 易得∆ABD ≌ ∆DCA ,进而得∠ABD =∠DCA . 根据 AAS 易得∆AOB ≌ ∆DOC ,进而得OA = OD .【巩固】如图,在梯形 ABCD 中, AD ∥ BC , E 为CD 中点,连结 AE 并延长 AE 交 BC 的延长线于点 F .求证: FC = AD .CF【解析】∵ AD ∥ BC∴ ∠F = ∠DAEOE F ⎨ ⎩⎨ ⎩又∵ ∠FEC = ∠AED CE = DE ∴ ∆FEC ≌ ∆AED ∴ FC = AD【例 9】 已知,如图, AB = AC , CE ⊥ AB , BF ⊥ AC ,求证: BF = CE .ABC【解析】在∆BCE 和∆CBF⎧∠BEC = ∠CFB ⎪∠CBE = ∠BCF ⎪BC = CB∴ ∆BCE ≌ ∆CBF , BF = CE .另一方法:面积法.S ∆ABC = 1 AB ⋅ CE = 1AC ⋅ BF ,∵ AB = AC ,∴BF = CE . 2 2 等腰三角形两腰上的高相等.【巩固】如图,AB ,CD 相交于点O ,OA = OB ,E 、F 为CD 上两点,AE ∥ BF ,CE = DF .求证:AC ∥ BD .CD【解析】∵ AE ∥ BF ,∴ ∠AEO = ∠BFO在△AEO 和△BFO 中 ⎧∠AOE = ∠BOF ⎪∠AEO = ∠BFO ⎪OA = OB ∴ △AEO ≌△BFO (AAS) ,∴ OE = OF ∵ CE = DF ,∴ OC = OPAOE FBE ⎨ ⎩⎨ ⎩在△AOC 和△BOD 中 ⎧OA = OB ⎪∠AOC = ∠BOD ⎪OC = OD ∴ △AOC ≌△BOD (SAS) ,∴ ∠C = ∠D ,∴ AC ∥ BD【例 10】如图,设 ∆ABC 和 ∆CDE 都是正三角形,且 ∠EBD = 62︒ ,则 ∠AEB A的度数是()BCD 图1A .124︒B .122︒C .120︒D .118︒【解析】分析 既然题目这样问,说明这两个角之间必然能找到一定的联系. 解 易知∠ACE = ∠BCD , ∆AEC ≌ ∆BDC ,于是∠AEC = ∠BDC , 从而∠AEB = 360 - ∠AEC - ∠DEC - ∠BED . 注意到∠BDC = 60︒ + ∠BDE , ∠BDE + ∠BED = 180︒ - 62︒ , ∠AEB = 360︒ - ∠BDC - 60︒ - ∠BED ,可算出∠AEB = 122 ,选 B .【例 11】如图所示, 已知 AB = DC , AE = DF , CE = BF ,证明: AF = DE .ADCEFB【解析】∵ CE = FB , ∴ CE + EF = FB + EF , 即CF = BE .⎧CF = BE在∆AEB 和∆DFC 中, ⎪DC = AB ,∴ ∆AEB ≌ ∆DFC ( SSS )⎪DF = AEP⎨ ⎩ ⎨ ⎩⎧ AE = DF ∴ ∠AEF = ∠DFE ,在∆AEF 和∆DFE 中, ⎪∠AEF = ∠DFE⎪EF = FE∴ ∆AEF ≌ ∆DFE ( SAS ),∴ AF = DE .【例 12】E 、F 分别是正方形 ABCD 的 BC 、CD 边上的点,且 BE = CF .求证: AE ⊥ BF .ADFBEC【解析】在∆ABE 和∆BCF 中 ⎧ AB = BC ⎪∠ABE = ∠BCF ⎪BE = CF∴ ∆ABE ≌ ∆BCF∴ ∠BAE = ∠CBF∵ ∠BAE + ∠AEB = 90︒ ∴ ∠CBF + ∠AEB = 90︒∴ AE ⊥ BF【巩固】 E 、 F 、 G 分别是正方形 ABCD 的 BC 、 CD 、 AB 边上的点, GE ⊥ EF , GE = EF .求证:BG + CF = BC .ADGFBEC【解析】显然, ∆BEG ≌ ∆CFE ,∴ BG = CE , BE = CF ∴ BG + CF = BC【例 13】如图所示: AF = CD , BC = EF , AB = DE , ∠A = ∠D .求证: BC ∥ EF .BECD【解析】分别连接 BF 、CE 、 BE ,利用 SAS 证得∆ABF ≌ ∆DEC ,⎨⎩⎨⎩∴ BF = CE ,利用 SSS 证得∆BFE ≌ ∆ECB , ∴ ∠BEF = ∠EBC ,∴ BC ∥ EF .可先讲解变式,通过此例体会添加辅助线的基本切入点.【例 14】在凸五边形中, ∠B = ∠E , ∠C = ∠D , BC = DE , M 为CD 中点.求证: AM ⊥ CD .AABECM D F C M D G【解析】延长 AB , AE ,交直线CD 于 F , G .∵ ∠ABC = ∠AED . ∴ ∠FBC = ∠GED . ∵ ∠BCM = ∠EDM . ∴ ∠BCF = ∠EDG . ∴在∆BCF 与∆EDG 中 ⎧∠FBC = ∠GED ⎪BC = ED ⎪∠BCF = ∠EDG ∴ ∆BCF ≌ ∆EDG (ASA) ∴ ∠F = ∠G . FC = GD . ∴ AG = AF ∵ CM = MD ∴ FM = MG∴在∆AMF 与∆AMG 中 ⎧ AM = AM ⎪FM = M G ⎪ AF = AG ∴ ∆AMF ≌ ∆AMG (SSS ) ∴ ∠AMF = ∠AMG = 180︒= 90︒ 2∴ AM ⊥ CDB ED【例 15】如图,∆ABC 中,AB = BC ,∠ABC = 90︒ ,D 是 AC 上一点,且CD = CB = AB ,DE ⊥ AC 交 AB 于 E 点.求证: AD = DE = EB .AAEEBC B C【解析】解法一:如图,连结CE .∵ ED ⊥ AC ,∴ ∠EDC = ∠EDA = 90︒ . ∵ ∠B = 90︒ ,∴ ∠EDC = ∠B .在∆CDE 与∆CBE 中, CD = CB , CE 公共, ∠EDC = ∠B , ∵ AB = BC , ∠A = 45︒ . ∵ ∠AED = 45︒ , ∠A = ∠AED . ∴ AD = DE .∴ AD = DE = EB . 解法二:连结 DB . ∵ C D = CB , ∴ ∠CBD = ∠CDB . ∵ ED ⊥ AC , ∠CDE = 90︒ . ∵ ∠ABC = 90︒ , ∴ ∠CDE = ∠ABC . ∴ ∠EBD = ∠EDB , ∴ DE = EB .∵ AB = AC ,∴ ∠A = 45︒ . ∵ ∠ADE = 90︒ , ∴ ∠AED = 45︒ . ∴ AD = DE = EB .【例 16】 ∆ABC 中, ∠B = 90︒ , M 为 AB 上一点,使得 AM = BC , N 为 BC 上一点,使得CN = BM ,连 AN 、CM 交于 P 点.试求 ∠APM 的度数,并写出你的推理证明的过程.D⎨ ⎩ADB NC【解析】 ∠APM 的度数为 45︒证明过程如下:如图过点 M 作 AB 的垂线 MD ,使 MD = CN ,连接 DA 、 DN , 于是因为 MD ∥CN 且 MD = CN ,所以四边形 MDNC 是平行四边形. 从而∠MDN = ∠MCN ,又因为CN = BM ,得到 DM = BM ,进而在∆MDA 与∆MBC 中, ⎧DM = BM ⎪∠DMA = ∠MBC = 90︒ , ⎪MA = BC 所以∆DMA ≌ ∆MBC , 这样 DA = MC ,而 MC = DN , 所以 DN = DA .又因为∠ADN = ∠ADM + ∠MDN = ∠ADM + ∠DAM = 90︒ , 所以得到∆ADN 是一个等腰直角三角形,所以∠AND = 45︒ ,利用 MC ∥ DN ,从而得到∠APM = ∠AND = 45︒ .【例 17】如图, I 是△ABC 的内心,且CA + AI = BC .若 ∠BAC = 80︒ ,求∠ABC 和∠AIB 的大小.CBA【解析】因为有内心,故可以用角平分线构造全等三角形,从而使问题容易解决. 如图,在 BC 上取点 D ,使CD = AC ,连接 DI . 因为CA + AI = BC , 所以 BD = AI . 在△ACI 和△DCI 中,IM PAC =DC ,∠ACI =∠DCI ,CI =CI .所以△ACI ≌△DCI .于是AI =DI .所以DI =BD .因为∠BAC = 80︒,所以∠CAI = 40︒,∠CDI =40︒.又∠CDI 是等腰△BDI 的外角,所以∠DBI =∠DIB =∠CDI = 20︒,∠ABC =40︒.在△AIB 中,∠BAI = 40︒,∠ABI = 20︒,所以∠AIB = 180︒-(20︒+ 40︒)= 120︒.【例18】已知:BD、CE 是∆ABC 的高,点P 在BD 的延长线上,BP =AC ,点Q 在CE 上,CQ =AB ,求证:⑴AP =AQ ;⑵AP ⊥AQ .【解析】如图,设CE 交BD 于F .⑴由BD ⊥CA ,CE ⊥AB ,知∠BEF = 90︒=∠CDF .而∠BFE =∠CFD ,故∠ABD =∠QCA .由已知,有AB =QC ,BP =CA ,从而∆ABP ≌∆QCA ,即有AP =AQ .⑵由⑴可得∠AQC =∠PAB ,而∠AQC =∠QEA +∠QAE = 90︒+∠QAE .∠PAB =∠PAQ +∠QAE .从而可得∠PAQ = 90︒ ,即 AP ⊥ AQ .【例 19】⑴ 如左下图,在矩形 ABCD 中, E 为CB 延长线上一点且 AC = CE , F 为 AE 的中点.求证:BF ⊥ FD .⑵ 如右下图,在 ∆ABC 中,BE 、CF 分别为边 AC 、AB 的高,D 为 BC 的中点,DM ⊥ EF 于 M .求证: FM = EM .AADE BCBDCAADE BCBD C【解析】⑴ 如图,连结CF .∵ AC = CE , F 为 AE 的中点 ∴ CF ⊥ AE∴ ∠EFB + ∠BFC = 90︒ ∵四边形 ABCD 是矩形∴ BC = AD , AB ⊥ CE , ∠ABC = ∠BAD = 90︒ ∵ F 为 AE 的中点 ∴ E F = AF ∴ ∠FBA = ∠FAB∴ ∠FAB + ∠BAD = ∠FBA + ∠ABC ,即∠FBC = ∠FAD ∵ AD = BC , FA = FB ∴ ∆FBC ≌ ∆FADFFMEFMEF∴ ∠AFD = ∠BFC ∴ ∠AFD + ∠EFB = 90︒ ∴ BF ⊥ FD .⑵ 如图,连结 DF 、 DE .∵ BE 、CF 分别为边 AC 、 AB 上的高 ∴ ∠BEC = ∠BFC = 90︒ 又∵ D 为 BC 上的中点 ∴ BD = CD∵ DE = 1 BC , DF = 1 BC2 2 ∴ DE = DF又∵ DM ⊥ EF ,∴ EM = FM .【例 20】如图,在 ∆ABC 中,∠B ,∠C 为锐角,M , N , D 分别为边 AB 、AC 、BC 上的点,满足 AM = AN ,BD = DC ,且∠BDM = ∠CDN .求证: AB = AC .AAB D CB D C【解析】分析 若∆BDM ≌ ∆CDN ,则问题迎刃而解.直接证明困难,可考虑反证法.解 若 DM > DN ,则在 DM 上取一点 E ,使 DN = DE ,连接 BE 交 AC 于 F ,连接 EN . 在∆BED 与∆CND 中, BD = DC , ∠BDE = ∠CDN , DE = DN ,故∆BDE ≌ ∆CDN . 于是有∠EBD = ∠NCD , BE = NC . 所以 FB = FC ,从而 BE = NC,故 EN ∥ BC .FB FC 从而有∠ENF = ∠ACB .但另一方面,由于 DM > DN ,知∠ABC > ∠FBC = ∠ACB ,所以∠ANM = 1 (180︒ - ∠BAC ) = 1(∠ABC + ∠ACB ) 2 2 > 1 (∠ACB + ∠ACB ) = ∠ACB .2 从而∠ENF > ∠MNA > ∠ACB .矛盾.故假设不成立. 若 DM < DN ,同法可证假设不成立.MNF M NEN MNMC综上所述DM =DN ,于是由∆BDM ≌∆CDN 知∠DBM =∠DCN ,从而AB = AC .说明:在某些平面几何问题的证明中,反证法也是常用的方法.【例21】如图,已知∠ABD =∠ACD = 60︒,且∠ADB = 90︒-1∠BDC .求证:∆ABC 是等腰三角形.2A AB B D EC C【解析】延长BD 到E ,使得DE =CD ,连接AE .∵∠ADB = 90︒-1∠BDC ,∴2∠ADB +∠BDC = 180︒,2即∠ADC +∠ADB = 180︒.∵∠ADE +∠ADB = 180︒,∴∠ADC =∠ADE ,∵CD =DE ,AD =AD ,∴∆ADC ≌∆ADE (SAS),∴∠ACD =∠E = 60︒,AC =AE ,∵∠ABD =∠ACD = 60︒,∴∠ABD =∠E ,∴AB =AE ,∴AB =AC ,∴∆ABC 是等腰三角形.【例22】如图,∆ABC 为边长是1 的等边三角形,∆BDC 为顶角(∠BDC) 是120︒的等腰三角形,以D 为顶点作一个60︒角,角的两边分别交AB 于M ,AC 于N ,连接MN ,形成一个∆AMN .求∆AMN 的周长.A AB C BED D【解析】分析考虑特殊情况,MN ∥BC ,此时不难计算出∆AMN 的周长为 2 ,于是可考虑证明:BD AB + AC = AM + MN + AN ,即证 BM + NC = MN 解 延长 AC 到E ,使CE = BM ,连接 DE ..采用截长补短法可解之. 易知在∆BMD 与∆CED 中有 BD = CD , ∠MBD = ∠ECD = 90︒ , BM = CE ,从而∆BMD ≌ ∆CED . ∴ MD = DE , ∠MDB = ∠EDC .于是在∆DMN 与∆DEN 中有: DN = DN , MD = ED , ∠MDN = 60︒ = ∠MDB + ∠CDN = ∠EDC + ∠CDN = ∠EDN . 从而∆MDN ≌ ∆EDN ,故 EN = MN .∴ AM + MN + AN = AM + NE + AN = AM + NC + CE + AN = AM + MB + NC + AN = AB + AC = 2 .说明 本题通过考虑特殊情况得到可能的结论,然后进行一般的证明.从特殊性看问题,从极端情况考虑问题,从特殊到一般是数学中常用的思想方法.【例 23】我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下, 它们会全等?⑴ 阅读与证明:对于这两个三角形均为直角三角形,显然它们全等. 对于这两个三角形均为钝角三角形,可证它们全等(证明略). 对于这两个三角形均为锐角三角形,它们也全等,可证明如下:已知: ∆ABC 、 ∆A 1B 1C 1 均为锐角三角形, AB = A 1B 1 , BC = B 1C 1 , ∠C = ∠C 1 . 求证: ∆ABC ≌ ∆A 1B 1C 1 . (请你将下列证明过程补充完整.)证明:分别过点 B , B 1 作 BD ⊥ AC 于 D , B 1D 1 ⊥ A 1C 1 于 D 1 .则 ∠BDC = ∠B 1D 1C 1 = 90︒ ,∵ BC = B 1C 1 , ∠C = ∠C 1 , ∴ ∆BCD ≌ ∆B 1C 1D 1 ∴ BD = B 1D 1C⑵ 归纳与叙述:DA C 11B 1A 1⎩由⑴可得到一个正确结论,请你写出这个结论.【解析】⑴ 又∵ AB = A 1B 1 , ∠ADB = ∠A 1D 1B 1 ,∴ ∆ADB ≌ ∆A 1D 1B 1 = 90︒ ∴ ∠A = ∠A 1 ,又∵ ∠C = ∠C 1 , BC = B 1C 1 ,∴ ∆ABC ≌ ∆A 1B 1C 1 .⑵ 若∆ABC 、 ∆A 1B 1C 1 均为锐角三角形或均为直角三角形或均为钝角三角形,且 AB = A 1B 1 ,BC = B 1C 1 , ∠C = ∠C 1 ,则∆ABC ≌ ∆A 1B 1C 1 .练习 1:1、如图,已知 AC = BD , AD ⊥ AC , BC ⊥ BD ,求证: AD = BC .A B A BCD C【解析】连结CD在Rt ∆ADC 和Rt ∆BCD 中 ⎧ AC = BD ⎨DC = CD∴ Rt ∆ADC ≌ Rt ∆BCD ∴ AD = BC2、已知:如图, AB ∥ DE , AC ∥ DF , BE = CF . 求证: AB = DE .ADBECF【解析】∵ AB ∥ DE ,∴ ∠B = ∠DEF∵ AC ∥ D F ,∴ ∠F = ∠ACB∵ BE = CF ,∴ BE + EC = CF + EC 即 BC = EF ∴ ∆ABC ≌ ∆DEF ,∴ AB = DE .3、如图,矩形 ABCD 中,E 是 AD 上一点,CE ⊥ EF 交 AB 于 F 点,若 DE = 2 ,矩形周长为16 ,且CE = EF , 求 AE 的长.A E DFB C【解析】∵FE ⊥EC ,∴∠AEF +∠DEC = 90︒.∵∠AEF +∠AFE = 90︒,∴∠AFE =∠DEC .在三角形AFE 与∆DEC 中,FE =CE ,∠A =∠D = 90︒,∠AFE =∠DEC ,∴∆AFE ≌∆DEC .∴AE =DC .∵矩形周长为16 ,∴AD +DC = 8 .∵AD =AE +DE ,∴且DE = 2 .∴2 AE = 8 -DE .即AE = 3 .4、在四边形ABCD 中,AD ∥BC ,∠A 的平分线AE 交DC 于E .求证:当BE 是∠B 的角平分线时,有AD +BC =AB .【解析】在AB 上截取AF ,使AF =AD ,连EF ,则可得∆ADE ≌∆AFE .∴∠ADE =∠AFE .∵AD ∥BC ,知∠ADE +∠C = 180︒.∵∠EFB +∠AFE = 180︒.∴∠EFB =∠C .注意到BE 平分∠B ,BE 公用,∴∆EFB ≌∆ECB ,∴BF =BC .∴AD +BC =AF +BF =AB .215、如图所示: AB = AC , AD = AE , CD 、 BE 相交于点O .求证: OA 平分∠DAE .EA B D【解析】利用 SAS 证得∆ABE ≌ ∆ACD ,∴ ∠E = ∠D ,根据已知可得 BD = CE ,利用 AAS 证得∆BOD ≌ ∆COE ,∴ OD = OE ,利用 SAS 证得∆AOD ≌ ∆AOE ,∴ ∠OAD = ∠OAE ,∴ OA 平分∠DAE .6、如图所示,在△ABC 中, AD ⊥ BC 于点 D , ∠B = 2∠C .求证: AB + BD = CD .A ACD B CE D B 【解析】由已知 AD ⊥ BC ,∠B = 2∠C 知如果我们在CD 上截取 DE = DB ,连接 AE ,就可以构造出两个等腰三角形△ABE 和△AEC .如图,在CD 上截取 DE = DB ,连接AE . 因为 AD ⊥ BC , DE = DB ,所以 AE = AB ,于是∠B = ∠AEB ,又因为∠AEB = ∠C + ∠CAE , ∠B = 2∠C ,所以∠CAE = ∠C ,于是 AE = EC ,故 AB + BD = AE + ED = EC + ED = CD .CO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形及其判定复习提高
一、知识梳理:1、全等三角形概念:两个能完全重合的三角形叫做全等三角形. 2、全等三角形性质: (1)全等三角形的对应边相等,对应角相等.
(2)全等三角形的对应边上的高相等,对应边上的中线相等,对应角的平分线相等.
(3)全等三角形的面积和周长分别相等. 3、全等三角形判定方法: (1) “边角边”或“SAS ”(2) “角边角”或“ASA ”
(3) “边边边”或“SSS ” (4) “角角边”或“AAS ” 二、证明两个三角形全等的思路: (1)已知两边分别相等⎧⎨
⎩找第三边( )找夹角( )
(2)已知一边一角分别相等⎧⎧⎪⎪
⎨⎪⎨⎪⎩⎪
⎪⎩
找这边的另一邻角( )
已知一边与邻角找这边的对角( )找这个角的另一边( )已知一边与对角:找另一角( )
(3)已知两角分别相等⎧⎨
⎩找夹边( )找夹边外任意一边( ) (注意:公共边、公共角、对顶角是对应角) 三、典型例题: 例题1:如图所示,某同学把一块三角形玻璃打碎成了三块,现在要到玻璃店去配一
块完全一样的玻璃,那么最省事的办法是( )
A. 带①去
B.带②去
C.带③去
D.带①和②去 结论:把实际问题转化为数学中判定三角形全等问题。
训练:1.下列是利用了三角形的稳定性的有( )个 ①自行车的三角形车架 ②长方形门框的斜拉条 ③照相机的三脚架 ④塔吊上部的三角形结构。
A 、1 B 、2 C 、3 D 、4 2.判断题:①两边和一角对应相等的两个三角形全等.( )②两角和一边对应相等的两个三角形全等.( )③两条直角边对应相等的两个三角形全等. ( )
④腰长相等,顶角相等的两个等腰三角形全等. ( )⑤三角形中的一条中线
把三角形分成的两个小三角形全等.( )⑥两个等边三角形全等( ). ⑦一腰和底边对应相等的两个等腰三角形全等. ( )⑧腰长相等,且都有一个40°角的两个等腰三角形全等.( )⑨.腰长相等,且都有一个100°角的两个等腰三角形全等.( )⑩有两边和第三边上的中线对应相等的两个三角形全等. ( )
例2. 已知:如图,AD =AE ,AB =AC ,∠DAE =∠BAC . 求证:BD =CE .
例3. 已知:如图,△ABC 中,AD ⊥BC 于D ,E 是AD 上一点,BE 的延长线交AC 于F ,若BD=AD ,DE=DC 。
求证:BF ⊥AC 。
A
B C D E F
例4. 如图,等腰直角三角形ABC 中,∠ACB =90°,AD 为腰CB 上的中线,CE ⊥AD
交AB 于E .求证∠CDA =∠EDB .
例5.如图:AE=BD ,AB=DE ,求证:∠A=∠D
例6.在△ABC 中,∠ACB=90°,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .试问DE ,AD ,BE 具有怎样的等量关系?并加以证明.
四、测试训练:一、选择题(48分) 1、下列说法正确的是( )
A :全等三角形是指形状相同的两个三角形
B :全等三角形的周长和面积分别相等
C :全等三角形是指面积相等的两个三角形
D :所有的等边三角形都是全等三角形 2、如图:若△AB
E ≌△AC
F ,且AB=5,AE=2,则EC 的长为( )
A :2
B :3
C :5
D :2.5
3、如图:若△ABC ≌△EAC ,则∠EAC 等于( )
A :∠AC
B B :∠BAF
C :∠CAF
D :∠BAC
4、如图:AB=AD ,AE 平分∠BAD ,则图中有( )对全等三角形。
A :2
B :3
C :4
D :5
5、如图:△ABC ≌△DEF ,△ABC 的周长等于40㎝,
AB=10㎝,BC=16㎝,则DF 的长为( ) A :10㎝ B :14㎝ C :16㎝ D :40㎝ 6、能判断△ABC ≌△DEF 的是( )
A :AB=DE ,BC=EF ,∠A=∠D
B :∠A=∠E ,∠C=∠F ,AC=EF
C :∠B=∠E ,∠A=∠
D ,AC=DF D :∠A=∠D ,∠B=∠
E ,∠C=∠F
7、如图:EA ∥DF ,AE=DF ,要使△AEC ≌△DBF ,则只要( ) A :AB=CD B :EC=BF C :∠A=∠D D :AB=BC
8、如图:AD=AC ,AB 平分∠DAC ,下列结论错误的是( )
A :△AD
B ≌△ACB B :△ADE ≌△ACE
C :△EDB ≌△ECB
D :△AED ≌△CEB 9、下页图中全等的三角形是( )A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ
10、如图:△ABC 中,∠C=90°,AC=BC ,AD 平分∠CAB 交BC
于D ,DE ⊥AB 于E ,且AB=6㎝,则△DEB 的周长是( )
1 2
A
B C D
E
(第2题)
F
E
C
B
A
(第3题)
E
C
B A
(第4题)
E
D
C
B
A
(第5题)
F
E D
C B
A
(第7题)
F
E
D
C
B A
(第8题)E
D
C
B
A
(第10题)E
D
C
B
A
A :6㎝
B :4㎝
C :10㎝
D :以上都不对
11、 AD=AE , AB=AC , BE 、CD 交于F , 则图中相等的角共有 (除去∠DFE=∠BFC )( ) A.5对 B.4对 C.3对 D.2对 12、如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED 的度数 是( ) A.70° B. 85° C. 65° D. 以上都不对 二、填空:(32分)
13、如图:△AEC ≌△ADB ,则∠AEC= ,EC= ; 14、△ABC 中,∠BAC ∶∠ACB ∶∠ABC =4∶3∶2, 且△ABC ≌△DEF ,则∠DEF =______.
15、如图:在△ABC 中,AD=AE ,BD=EC ,∠ADB=∠AEC=105
°, ∠B=40°,则∠CAE= ;
16、如图,AE=BF ,AD ∥BC ,AD=BC ,则有ΔADF ≌
,且DF= 。
17、工人师傅砌门时,如图所示,常用木条EF 固定矩形木框ABCD ,使其不变形,这是利用
,用菱形做活动铁门是利用四边形的 。
18、如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,
④ ∠B=∠E,其中能使ΔABC ≌ΔAED 的条件有 个. 19、如图所示,AD 是△ABC 中BC 边上的中线,若AB=2,AC=4,则AD 的取值范围是 20、如图:在△ABC 中,∠B=∠C=50°,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,则∠BAD= 。
21、已知:如图,点C 在线段AB 上,以AC 和BC 为边在AB 的同侧作等边三角形
△ACM 和△BCN ,连结AN 、BM ,分别交CM 、CN 于点P 、Q .求证:CP=CQ .
22、已知:四边形ABCD 是正方形,M 为BC 上任意一点,MN ⊥AM ,且MN 交∠ECD 的平
分线于N.求证:AM=MN
第11题图
第12题图
C
E
D
B
O
A
第9题图
(第13题)
E
D
C
B
A
E (第15题)
D C
B
A
F
E
(第20题)
D C B
A
16题图
17题图
2
1
E
D
C
B
A
18题图
19题图。
