四连杆增力合模机构
契贝谢夫四连杆机构的优化设计与应用

契贝谢夫四连杆机构的优化设计与应用
契贝谢夫四连杆机构是一种常用的机构,其由四根连杆和一个滑块组成。
契贝谢夫四连杆机构的优化设计和应用可以涉及以下方面:
1. 运动学分析和优化设计:可以通过对契贝谢夫四连杆机构的运动学特性进行分析和优化设计,以提高机构的性能。
通过优化连杆的长度和角度,可以实现所需的运动轨迹和位移,并最小化驱动力和摩擦损失。
2. 动力学分析和优化设计:可以通过对契贝谢夫四连杆机构的动力学特性进行分析和优化设计,以实现所需的力学性能。
通过优化连杆的惯量和刚度,可以提高机构的响应速度和精度,并最大限度地减小振动和动态载荷。
3. 结构强度分析和优化设计:可以通过对契贝谢夫四连杆机构的结构强度进行分析和优化设计,以确保机构在工作过程中的安全和可靠性。
通过优化连杆的剖面和材料,可以提高机构的承载能力和抗疲劳性,以应对不同工况和环境的要求。
4. 仿真和测试分析:可以通过使用计算机辅助设计和仿真软件,对契贝谢夫四连杆机构进行仿真分析,并验证优化设计的有效性。
同时,可以进行实际测试和试验,以验证优化设计参数和模型的准确性和可行性。
契贝谢夫四连杆机构在工程上有广泛的应用,例如在机械工程中可以应用于机器人、汽车发动机、传输机器和减速器等领域。
在机械设计和制造过程中,优化设计和应用契贝谢夫四连杆机构可以提高机械系统的性能、效率和可靠性。
此外,契贝谢夫四连杆机构也可以应用于模拟和教学实验,用于解决实际问题和培养学生的设计和创新能力。
四连杆受力分析

时间:二O二一年七月二十九日
四连杆受力分析之答禄夫天创作
时间:二O二一年七月二十九日
不计摩擦时机构的受力分析根据机构所受已知外力(包括惯性力)来确定个运动副中的反力和需加于该机构上的平衡力.由于运动副反力对机构来说是内力,必需将机构分解为若干个杆组,然后依次分析.平衡力(矩)——与作用于机构构件上的已知外力和惯性力相平衡的未知外力(矩)相平衡的未知外力(矩)已知生产阻力平衡力(矩)——求解保证原动件按预定运动规律运动时所需要的驱动力(矩)已知驱动力(矩)平衡力(矩)——求解机构所能克服的生产阻力一. 构件组的静定条件——该构件组所能列出的自力的力平衡方程式的数目.
时间:二O二一年七月二十九日
时间:二O二一年七月二十九日。
液压支架四连杆建模及优化设计资料

四连杆机构的建模及优化设计四连杆机构的建模及优化设计摘要四连杆是掩护式支架和支撑掩护式支架的最重要部件之一,其作用概括起来主要有两。
一是当支架由高到低变化时,借助四连杆机构使支架顶梁前端点的运动轨迹近似双纽线。
从而使支架顶梁前端点与煤壁间距离的变化大大减小,提高了管理顶板的性能;二是使支架承受较大的水平力。
这篇文章就是讨论液压支架四连杆机构的。
在文章里,我们研究了液压支架四连杆机构所面临的问题,及可以从几个方面考虑解决的方法。
文章研究的是液压支架四连杆机构,液压支架四连杆机构是矿上机械——液压支架的关键部件。
文章对四连杆机构和液压支架整体进行了研究。
文章还对四连杆机构的动态特性进行分析,在此过程中运用了SolidWorks中的COSMOSMotion 进行建模和运动仿真。
关键词:四连杆,SolidWorks,COSMOSMotion,运动仿真FOUR-BAR LINKAGE DESIGN OF THEMODELING AND OPTIMIZATIONABSTRACTFour-link is the shield support bracket and support shield one of the most important components, its role can be summarized as two. First, when the support changes from high to low, with four-bar linkage so that the front support beam trajectory point approximation lemniscates. So that the front support beam points away from the wall of the changes with the coal greatly reduced, improving the management performance of the roof; Second, the level of support to withstand greater force. This article is to discuss four hydraulic linkage mechanisms.In the article, we study the four-bar linkage hydraulic problems, and can be considered from several aspects of the solution. This paper studies the four hydraulic linkage, hydraulic four-bar linkage is mine machinery - the key hydraulic components. Article on the four-bar linkage and hydraulic support the overall studied.Paper also the dynamic characteristics of four-bar linkage analysis, in the process of the Application of the SolidWorks COSMOSMotion in modeling and motion simulation.KEYWARDS:Four-link, SolidWorks, COSMOSMotion, motion simulation.目录摘要 (I)ABSTRACT (II)1.1引言 (1)1.2 SolidWorks软件简介 (1)1.2.1 SolidWorks功能描述 (1)1.2.2 CAD技术概述 (3)1.2.3 CAD系统 (4)1.2.4 CAD技术的应用 (4)1.2.5 COSMOSmotion简介 (6)2四连杆机构建模 (7)2.1四连杆机构的作用 (7)2.2四连杆机构的几何作图法 (8)2.3 四连杆机构优选方法 (12)2.3.1 目标函索的确定 (12)2.3.2 四连杆机构的几何特征 (12)2.4运用SolidWorks建立四连杆机构模型 (12)2.5 本章小结 (15)3 对四连杆机构进行COSMOSMotion运动分析 (16)3.1COSMOSMotion软件的应用 (16)3.2四连杆机构的运动仿真过程 (17)3.2.1选择马达和设置马达参数 (18)3.2.2仿真机构的运动设置 (19)3.2.3 仿真机构的参数设置 (19)3.3 仿真数据处理 (20)结论 (32)参考文献 (33)致谢 (34)1绪论1.1引言液压传动时一项新兴技术,他被引用到工业领域只有很短的时间,液压支架已广泛应用于我国煤矿井下支护,它具有初撑力大、恒阻、安全和高效等特性,是适合我国国情的一种有效的工作面支护设备。
常用机构(四连杆机构)1

机构演化方法
础
平 改变杆件长度,用移动副取代回转副
面 连 杆
扩大回转副 变更机架等
机
构
连架杆 B
连杆 2
C 连架杆
3
1
A
4
D
机 (1)改变杆件长度 —— 曲柄滑块机构
械
设 计
曲线导轨曲柄滑块机构
基
C
础
C
平
2
面
连
B
杆1
机
构A
4
对CD杆等效转化
B2
3
1
转动副变成移动副 A
4 D
lCD
3 D
e
b+c >a+d 、 b+d >a+c 、 c+d >a+b
B
a
A
并可得: a<b 、 a<c 、 a<d .
b f
d
C
c
D
曲柄存在的条件: (1)最短杆与最长杆长度之和小于或等于其余两杆长度和。 (2)曲柄是最短杆。
机 曲柄存在的条件:
械 设
(1)最短杆与最长杆长度之和小于或等于其余两杆长度之和
2
BD
b2
c2
2b c cosd
基 础
b
平 面
cosd
b2 c 2 2 a d cosj a 2 d 2
2bc
B
a
j
连 杆
分析
A
机
构 j =0 cos j =1 cos d d min
j =180° cos j = –1 cos d d max
C
d c
d
D
四连杆机构

函 数 生 成 机 构
组 合 功 能 机 构
轨迹生成机构
刚体导引机构
刚体导引机构
搅拌机
冲床
B’’
F2
90-
Cγ
F
b
B
C’’
F1 δ
vc
γ
c
C’
a δmax
δmin
A
D
d
B’
O
γ
四、运动的连续性 连杆机构的运动连续性:指该机构在运动中能够连续实现给定的各个位置。
(B’) B
C1
C
C2
1
D
B3
A
B1
2 A
C’2
C’1
C’
连杆机构的运动不连续的问题:错位不连续;错序不连续。
C1 B2
C3 C2 D
§2-3平面四杆机构的设计 一、平面连杆机构的功能及应用 1、实现刚体给定位置的设计: 机构具有能引导刚体通过一系列给定位置的功能。刚体导引机构 。
二、平面四杆机构的设计方法
三、平面四杆机构的设计(几何法) 1、根据给定连杆上两铰链中心的位置设计四杆机构。
B1
B2
B3
A
C1
C2 C3
D
2、按给定行程速度变化系数设计四杆机构
C1
A
B2
A1 B1
90-
D
γ O
C2 θ=
180°(K-1) (K+1)
AC1=BC-AB AC2=BC+AB
AB=(AC2-AC1)/2 BC=(AC1+AC2)/2
三、平面四杆机构的演变
1)取不同构件为机架(机构的倒置) 2)转动副转化为移动副
3) 扩大转动副(教材P33自学)
平面连杆机构——四连杆机构的类型
曲柄摇杆机构 曲柄摇杆机构的应用
双曲柄机构及其应用
天平中的平行四边形机构
反平行四边形机构及其应用
双摇杆机构 双摇杆机构及其在鹤式起重机中的应用
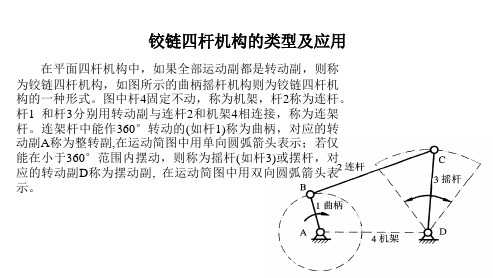
铰链四杆机构的类型及应用
在平面四杆机构中,如果全部运动副都是转动副,则称 为铰链四杆机构,如图所示的曲柄摇杆机构则为铰链四杆机 构的一种形式。图中杆4固定不动,称为机架,杆2称为连杆。 杆1 和杆3分别用转动副与连杆2和机架4相连接,称为连架 杆。连架杆中能作360°转动的(如杆1)称为曲柄,对应的转ห้องสมุดไป่ตู้动副A称为整转副,在运动简图中用单向圆弧箭头表示;若仅 能在小于360°范围内摆动,则称为摇杆(如杆3)或摆杆,对 应的转动副D称为摆动副, 在运动简图中用双向圆弧箭头表 示。
液压支架四连杆建模及优化设计方案资料

四连杆机构的建模及优化设计四连杆机构的建模及优化设计摘要四连杆是掩护式支架和支撑掩护式支架的最重要部件之一,其作用概括起来主要有两。
一是当支架由高到低变化时,借助四连杆机构使支架顶梁前端点的运动轨迹近似双纽线。
从而使支架顶梁前端点与煤壁间距离的变化大大减小,提高了管理顶板的性能;二是使支架承受较大的水平力。
这篇文章就是讨论液压支架四连杆机构的。
在文章里,我们研究了液压支架四连杆机构所面临的问题,及可以从几个方面考虑解决的方法。
文章研究的是液压支架四连杆机构,液压支架四连杆机构是矿上机械——液压支架的关键部件。
文章对四连杆机构和液压支架整体进行了研究。
文章还对四连杆机构的动态特性进行分析,在此过程中运用了SolidWorks中的COSMOSMotion 进行建模和运动仿真。
关键词:四连杆,SolidWorks,COSMOSMotion,运动仿真FOUR-BARLINKAGEDESIGNOFTHEMODELINGANDOPTIMIZATIONABSTRACTFour-link is the shield support bracket and support shield one of the most important components, its role can be summarized as two. First, when the support changes from high to low, with four-bar linkage so that the front support beam trajectory point approximation lemniscates. So that the front support beam points away from the wall of the changes with the coal greatly reduced, improving the management performance of the roof。
机械原理四连杆机构(借鉴材料)

能实现预期的运动规律,而且希望运转轻
便、效率高。图4-5所示的曲柄摇杆机构,
如不计各杆质量和运动副中的摩擦,则连
杆BC为二力杆,它作用于从动摇杆3上的
力P是沿BC方向的。作用在从动件上的驱
动力P 与该力作用点绝对速度vc之间所夹
的锐角称为压力角。由图可见,力P在vc 方向的有效分力为Pt=Pcos,
柄。仅能在某一角度摆动的连架杆,称 为摇杆。
教学教资
5
对于铰链四杆机构来说,机架和连杆 总是存在的,因此可按照连架杆是曲柄还 是摇杆,将铰链四杆机构分为三种基本型 式:
曲柄摇杆机构
双曲柄机构
双摇杆机构
教学教资
6
一、 曲柄摇杆机构
在铰链四杆机构中,若两个连架杆,
一个为曲柄,另一个为摇杆,则此铰链 四杆机构称为曲柄摇杆机构。
教学教资
34
图4-11 起重机起重机构
教学教资
35
两摇杆长度相等的双摇杆机构,称 为等腰梯形机构。
图4-12所示,轮式车辆的前轮转向 机构就是等腰梯形机构的应用实例。
教学教资
36
图4-12 汽车前轮转向机构
教学教资
37
当车转弯时,与前轮轴固联的两个
摇杆的摆角和不等。如果在任意位置
都能使两前轮轴线的交点P落在后轮轴 线的延长线上,则当整个车身绕P点转 动时,四个车轮都能在地面上纯滚动, 避免轮胎因滑动而损伤。等腰梯形机构 就能近似地满足这一要求。
BCD分别最小和最大(见图4-4)。
当BCD为锐角时,传动角=BCD, 是传动角的最小值,也即BCD(min) ;
当BCD为钝角时,传动角=180-
BCD ,BCD(max)对应传动角的另一 极小值。
