山东省滕州市洪绪中学七年级数学上册 1.4.1从不同方向看导学案(无答案) 北师大版
北师大版数学七年级上册1.4《从不同的方向看》教学设计

北师大版数学七年级上册1.4《从不同的方向看》教学设计一. 教材分析《从不同的方向看》是北师大版数学七年级上册第一章第四节的内容。
本节课主要让学生掌握利用方向和距离来描述物体的位置,学会从不同的方向观察物体,培养学生的空间想象能力和抽象思维能力。
教材通过丰富的图片和实例,引导学生感知和理解从不同方向观察物体的方法,并能够运用到实际问题中。
二. 学情分析七年级的学生已经具备了一定的空间想象能力和抽象思维能力,通过对现实生活中的物体和图形进行观察和操作,他们能够感知和理解从不同方向观察物体的重要性。
然而,部分学生可能对抽象的概念理解较困难,需要通过具体的实例和实践活动来帮助他们掌握。
三. 教学目标1.知识与技能:使学生掌握利用方向和距离来描述物体的位置的方法,学会从不同的方向观察物体。
2.过程与方法:通过观察实例和实际操作,培养学生的空间想象能力和抽象思维能力。
3.情感态度与价值观:培养学生对数学的兴趣,培养学生的观察能力和思维能力。
四. 教学重难点1.重点:利用方向和距离来描述物体的位置,从不同方向观察物体。
2.难点:对抽象概念的理解和运用。
五. 教学方法1.情境教学法:通过展示现实生活中的实例,引导学生感知和理解从不同方向观察物体的重要性。
2.互动教学法:引导学生参与课堂讨论和实践活动,培养学生的空间想象能力和抽象思维能力。
3.激励评价法:鼓励学生积极思考和表达,给予及时的反馈和激励。
六. 教学准备1.教学课件:制作课件,展示实例和练习题。
2.教学道具:准备一些实际物体,如玩具、图片等,用于展示和操作。
3.练习题:准备一些相关的练习题,用于巩固和拓展学生的知识。
七. 教学过程1.导入(5分钟)利用多媒体展示一些实际物体,如教室里的桌子、椅子等,引导学生观察并思考如何描述它们的位置。
通过提问的方式,引起学生对从不同方向观察物体的兴趣。
2.呈现(10分钟)展示教材中的实例,引导学生感知和理解从不同方向观察物体的重要性。
七年级数学上《从不同方向看立体图形》导学案

___ 年___ 月____日组长检查:教师评价:课题:从不同方向看立体图形学习目标:1、经历“从不同方向观察物体”的活动过程,发展空间观念;2、能描述简单立体图形的视图,能画出草图,并能识别见到视图形状与类别。
学习重难点:从不同方向观察几何物体得到正确的结果并画出来。
学习过程:(阅读教材第117至119页,并完成学前准备的内容)一.学前准备:1.观察:如下图所示,电视台的摄像机①、②、③、④在不同位置拍摄了四幅画面,则A 图像是______号摄像机所拍,B图像是______号摄像机所拍,C图像是______号摄像机所拍,D 图像是______号摄像机所拍.2.体会从正面、左面、上面看下面几何体得到平面图形的过程。
从正面看到的平面图形叫,从左面看到的平面图形叫,从上面看到的平面图形叫.二.自主探究3.画出下列立体图形的三视图:三.课后巩固4.如图,从上面观察,看到的图形是()A.B.C.D.第2题图5.一个几何体从正面看、从左面看、从上面看到的形状图如图所示,该几何体是__________.6.从不同方向看一只茶壶,你认为是俯视效果图的是()A.B.C.D.7.如图所示的几何体的左视图是(),主视图是(),俯视图是()A.B.C.D.8.如图所示几何体的俯视图是()A.B.C.D.9.如图是几个小立方块所搭的几何体俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是()A.B.C.D.10.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是__________.11.(2011•广州)5个棱长为1的正方体组成如图的几何体.(1)该几何体的体积是________(立方单位),表面积是________(平方单位).(2)画出该几何体的主视图和左视图.四.教学反思。
数学初一上1.4.1从不同方向看导学案

数学初一上1.4.1从不同方向看导学案本卷须知1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2、选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3、请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4、保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
主备人:郭金红备课组成员:杨宝华任广田颜伟课题:1.4.1从不同的方向看〔第一课时〕导学目标:1、在观察的过程中初步体会从不同方向观察物体可能看到不同的图形、2、能识别简单物体的三视图、导学重点:1、经历从不同方向观察物体和与他人合作交流,发展空间观念、2、初步体会从不同方向观察同一物体可能看到的不同的图形、3、能识别简单的三视图,会画立方体及其简单组合体的三视图、导学难点:识别简单的三视图,会画立方体及其简单组合体的三视图温故:从不同的方向观察一个正方体,看到的图形是否相同?如果是圆柱呢,圆锥、球呢?链接:认真仔细的观察课本P20_21,并按要求回答以下问题知新:1、主视图、左视图、俯视图的定义从不同方向观察同一物体,从________________叫主视图,从_____________叫左视图,从________________叫做俯视图、2画出下图的三视图巩固练习:1、回答以下问题〔1〕正方体:三视图都是_____________、主视图左视图俯视图〔2〕球:三视图都是___________、主视图左视图俯视图提醒:在所有几何体中,只有正方体与球这两种几何体的三视图是_____的、〔3〕圆柱体:主视图左视图俯视图〔4〕圆锥体:主视图左视图俯视图2、分辨和画出一些几何体的三视图1】桌子上放着一个长方体和圆柱〔如下图〕,说出以下三幅图分别是:〔〕〔〕〔〕2】画出以下几何体的主视图、左视图和俯视图主视图左视图俯视图注意:照片中的几何体为了使大家看清前后情况,因此照片中的物体一般朝左偏的位置是正面、3】一辆汽车从小明面前经过,小明拍摄了一组照片。
七年级数学上册 1.4 从不同方向看

1.4从不同方向看教学目标:1.经历"从不同方向观看物体"的活动进程,进展空间思维,能在与他人交流的进程中,合理清楚地表达自己的思维进程.2.在观看的进程中,初步体会从不同方向观看同一物体可能看到不一样的结果.3.能识别简单物体的三视图,会画立方体及其简单组合体的三视图.教学重点:识别简单物体的三视图,会画立方体及其简单组合体的三视图.教学难点:画立方体及其简单组合体的三视图.教学进程:一、设疑自探一、创设问题情境,从学生熟悉的古诗入手,引出课题.横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.哪位同窗能说说苏东坡是如何观看庐山的吗?这首诗隐含着一些数学知识.它教会了我们如何观看物体,这也是咱们这节课将要学习的内容——《从不同方向看》.在此,我想先请同窗们一路来做一个小实验.二、观看实物、利用小实验,使学生初步体会从不同方向观看同一物体,可能看到不一样的结果.水壶、杯子、乒乓球先用布盖好.三名学生从不同角度进行观看,回答别离看到了什么?试探:什么缘故三名学生看到的不一样?二、解疑合探一、观看几个简单几何体的组合,讨论得出"观看同一物体时,可能看到不同的图形"的结论.拿出前两节课自制的模型(三棱柱).看三棱柱的侧面是什么图形?底面呢?是不是同一物体,从不同方向看结果必然不一样呢?由此,咱们取得如此的结论:从不同方向观看同一物体时,可能看到不同的图形.在几何中,咱们把从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫俯视图.二、讨论立方体及其简单组合的三视图.通过讨论,让学生能在与他人交流的进程中,合理清楚地表达自己的思维进程.给定一个几何体。
说说你从正面、左面、上面别离看到什么图形?主视图、左视图、俯视图是相关于观看者而言的,相关于不同的观看者,其三视图可能不同.假设从右下角往左上角的方向看是从正面看,那么从左向看为从左看,站在观看主视图的位置从上往下看为从上面看.请同窗们试探一下从这三个方向看别离看到什么图形?(1)(2)(3)图(1)是从左侧看到的图,即左视图.图(2)是从正面看到的图,即主视图.图(3)是从上面看到的图,即俯视图.适才咱们从不同方向观看了实物、几何体,还学习了简单几何体的三视图,为了巩固这些知识,下面咱们来做几道练习.三、质疑再探说说你还有什么疑惑或问题(由学生或教师来解答所提出的问题)。
人教版七年级数学上册 导学案:4.1.1 第2课时 从不同方向看立体图形和立体图形的展开图【精品】

第四章几何图形初步4.1 几何图形4.1.1 立体图形与平面图形第2课时从不同的方向看立体图形和立体图形的展开图学习目标:1. 了解立体图形与平面图形之间的联系.2. 能画出简单立体图形从不同方向看得到的平面图形.3. 了解研究立体图形的方法,体会一个立体图形按照不同方式展开可得到不同的平面展开图.4. 通过展开与折叠,了解棱柱、棱锥、圆柱、圆锥、长方体、正方体的表面展开图或根据展开图判断立体图形.重点:了解立体图形从不同方向看能够得到平面图形,了解基本几何体与其展开图的关系,体会一个立体图形可以有多种展开图.难点:会画简单立体图形从不同方向看得到的平面图形,能够画出简单立体图形的展开图,或根据展开图判断立体图形.一、要点探究探究点1:从不同的方向看立体图形合作探究:画出正方体、长方体、圆柱体、圆锥、四棱锥、三棱柱从正面、左面、上面看得到的平面图形.各能得到什么平面图形?针对训练图中的几何体从正面看得到的平面图形是____,从左面看得到的平面图形是____,从上面看得到的平面图形是____.探究点2:立体图形的展开图 合作探究:将一个正方体的表面沿某些棱剪开,能展成哪些平面图形?思考:正方体展开图可以分为几种?这些展开图有没有什么规律?哪些展开图可以分为一类,为什么?要点归纳:1.巧记正方体的展开图口诀:正方体盒巧展开,六个面儿七刀裁,十一类图记分明; 一四一呈6种,二三一有3种,二二二与三三各1种;对面相隔不相连,识图巧排“凹”和“田”.2.一个多面体的展开图中,在同一直线上的相邻的三个线框中,首尾两个线框是立体图形中相对的两个面. 针对训练1. 下列图形中,不是正方体表面展开图的是 ()2. “坚”在下,“就”在后,“胜”和“利”在哪里?3. 下面图形是一些多面体的表面展开图,?4. 下列立体图形的平面展开图是什么?二、课堂小结常见几何体的展开图:2. 下图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞, 又可以堵住方形空洞的是( )3. 下图是由一些相同的小正方体构成的几何体的从正面、左面、上面看得到的三个平面 图形,这些相同的小正方体的个数是 ( ) A .4个 B .5个C.6个D.7个4. 下列的三幅平面图是三棱柱的表面展开图的有(多选) ( )5. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ;b= ;c= .。
山东省滕州市洪绪中学七年级数学上册 2.4有理数的加法导学案(无答案) 北师大版

2.4有理数的加法导学目标1.使学生掌握有理数加法法则,并能运用法则进行计算;2导学重点:有理数加法法则.导学难点:异号两数相加的法则.导学过程温故:绝对值的特点有哪些?(1)一个正数的绝对值是;例如,|4|= , |+7.1| =。
(2)一个负数的绝对值是;例如,|-2|= ,|-5.2|=。
(3)0的绝对值是.链接:互为相反数的一对有理数有什么特点?知新:一.两个有理数相加,有多少种不同的情形?为此,我们来看一个大家熟悉的实际问题:足球比赛中赢球个数与输球个数是相反意义的量.若我们规定赢球为“正”,输球为“负”.比如,赢3球记为+3,输2球记为-2.学校足球队在一场比赛中的胜负可能有以下各种不同的情形:(1)上半场赢了3球,下半场赢了2球,那么全场共赢了5球.也就是(+3)+(+2)=+5.①(2)上半场输了2球,下半场输了1球,那么全场共输了3球.也就是(-2)+(-1)=-3.②现在,请同学们看下其他可能的情形.上半场赢了3球,下半场输了2球,全场赢了1球,也就是③上半场输了3球,下半场赢了2球,全场输了1球,也就是④上半场赢了3球下半场不输不赢,全场仍赢3球,也就是⑤上半场输了2球,下半场两队都没有进球,全场仍输2球,也就是上半场打平,下半场也打平,全场仍是平局,也就是⑥归纳出有理数加法法则:1.2.3. 。
练一练:计算下列算式的结果,并说明理由:(1)(+4)+(+7); (2)(-4)+(-7); (3)(+4)+(-7);(4)(+9)+(-4);(5)(+4)+(-4); (6)(+9)+(-2); (7)(-9)+(+2);(8)(-9)+0;(9)0+(+2); (10)0+0.计算下列各题:(1)[8+(-5)]+(-4); (2)8+[(-5)+(-4)];(3)[(-7)+(-10)]+(-11); (4)(-7)+[(-10)+(-11)];(5)[(-22)+(-27)]+(+27); (6)(-22)+[(-27)+(+27)].二、学生共同研究形成有理数运算律交换律——两个有理数相加,交换加数的位置,和不变.用代数式表示上面一段话:a+b=b+a.运算律式子中的字母a,b表示任意的一个有理数,可以是正数,也可以是负数或者零.在同一个式子中,同一个字母表示同一个数.结合律——三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.用代数式表示上面一段话:(a+b)+c=a+(b+c).这里a,b,c表示任意三个有理数.练一练:例1.计算(要求注理由)16+(-25)+24+(-32).解:16+(-25)+24+(-32)= (加法交换律) = (加法结合律)=(同号相加法则)= .(异号相加法则)2.10袋小麦称重记录如图所示,以每袋90千克为准,超过的千克数记作正数,不足的千克数记作负数.7 ,5,-4,6,4,3,-3,-2,8,1。
数学初一上北师大版1.4.1从不同方向看导学案

数学初一上北师大版1.4.1从不同方向看导学案主备人:郭金红备课组成员:杨宝华任广田颜伟课题:1.4.1从不同的方向看〔第一课时〕导学目标:1、在观看的过程中初步体会从不同方向观看物体可能看到不同的图形、2、能识别简单物体的三视图、导学重点:1、经历从不同方向观看物体和与他人合作交流,进展空间观念、2、初步体会从不同方向观看同一物体可能看到的不同的图形、3、能识别简单的三视图,会画立方体及其简单组合体的三视图、导学难点:识别简单的三视图,会画立方体及其简单组合体的三视图温故:从不同的方向观看一个正方体,看到的图形是否相同?假如是圆柱呢,圆锥、球呢?链接:认真认真的观看课本P20_21,并按要求回答以下问题知新:1、主视图、左视图、俯视图的定义从不同方向观看同一物体,从________________叫主视图,从_____________叫左视图,从________________叫做俯视图、2画出下图的三视图巩固练习:1、回答以下问题(1)正方体:三视图基本上_____________、主视图左视图俯视图(2)球:三视图基本上___________、主视图左视图俯视图提醒:在所有几何体中,只有正方体与球这两种几何体的三视图是_____的、(3)圆柱体:主视图左视图俯视图(4)圆锥体:主视图左视图俯视图2、分辨和画出一些几何体的三视图1]桌子上放着一个长方体和圆柱〔如下图〕,说出以下三幅图分别是:〔〕〔〕〔〕2]画出以下几何体的主视图、左视图和俯视图主视图左视图俯视图注意:照片中的几何体为了使大伙看清前后情况,因此照片中的物体一般朝左偏的位置是正面、3]一辆汽车从小明面前通过,小明拍摄了一组照片。
请按照汽车被摄人镜头的先后顺序给下面的照片编号,〔照片见课本第22页“随堂练习”第1题〕拓展:1、画出下图几何体的主视图、左视图与俯视图。
主视图左视图俯视图2、如图是一个水管接头请写出上面三幅图〔1〕〔2〕〔3〕分别是从哪个方向看到的。
北师大版七年级数学上册 1.4 从不同方向看导学案(1)(2)
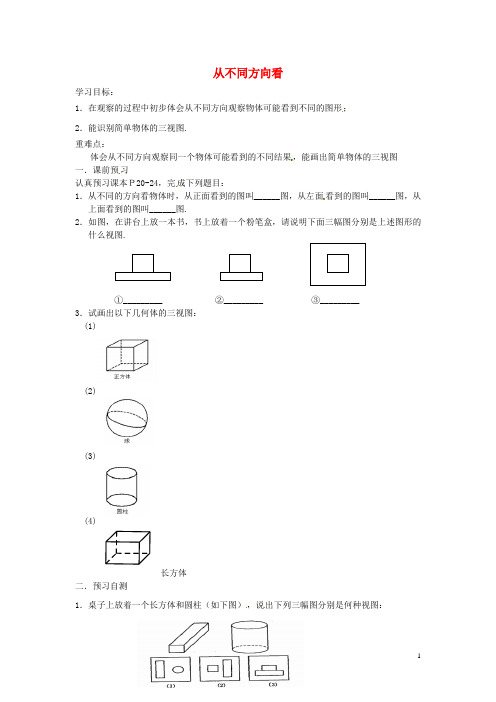
从不同方向看学习目标:1.在观察的过程中初步体会从不同方向观察物体可能看到不同的图形;2.能识别简单物体的三视图.重难点:体会从不同方向观察同一个物体可能看到的不同结果,能画出简单物体的三视图一.课前预习认真预习课本P20-24,完成下列题目:1.从不同的方向看物体时,从正面看到的图叫______图,从左面看到的图叫______图,从上面看到的图叫______图.2.如图,在讲台上放一本书,书上放着一个粉笔盒,请说明下面三幅图分别是上述图形的什么视图.①_________ ②_________ ③_________3.试画出以下几何体的三视图:(1)(2)(3)(4)长方体二.预习自测1.桌子上放着一个长方体和圆柱(如下图),说出下列三幅图分别是何种视图:①_________ ②_________ ③_________2.一个直立在水平面上的圆柱体的主视图、俯视图、左视图分别是()A.长方形、圆、长方形B.长方形、长方形、圆C.圆、长方形、长方形D.长方形、长主形、圆3.试画出以下几何体的三视图:(1)(2)棱锥三.拓展与探究1.如图的几何体,左视图是()A B C D2.画出下列几何体的三视图:3.猜谜语:正看三条边,侧看三条边;上看圆圈圈,中间小圆点.(打一几何体)从不同方向看学习目标:1.观察并会画由小立方块组成的不同的几何体的三视图;2.根据每个位置的小立方块的个数及其中一种视图画出另外两种视图 .重难点: 根据几何体其中一个视图确定它的另外两个视图;根据视图确定立体图形一.课前预习认真预习课本P25-27,完成下列题目:1. 从不同的方向看物体时,_______________叫主视图, ___________叫左视图,_______________叫俯视图.2.试画出以下组合几何体的三视图:(1)(2)(3)3.如图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数请画出这个几何体的主视图和左视图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:1 . 4 . 1 从不同的方向看(第一课时)
导学目标:1、在观察的过程中初步体会从不同方向观察物体可能看到不同的图形.
2 、能识别简单物体的三视图.
导学重点:
1 、经历从不同方向观察物体和与他人合作交流,发展空间观念.
2、初步体会从不同方向观察同一物体可能看到的不同的图形.
3 、能识别简单的三视图,会画立方体及其简单组合体的三视图.
导学难点:识别简单的三视图,会画立方体及其简单组合体的三视图
温故:从不同的方向观察一个正方体,看到的图形是否相同?如果是圆柱呢,圆锥、球呢?
链接:认真仔细的观察课本P20_21,并按要求回答问题
知新:1、主视图、左视图、俯视图的定义
从不同方向观察同一物体,从________________叫主视图,从_____________叫左视图,从________________叫做俯视图.
2画出下图的三视图
巩固练习:1、回答下列问题
(1)正方体:三视图都是_____________.
主视图左视图俯视图
(2)球:三视图都是___________.
主视图左视图俯视图
提醒:在所有几何体中,只有正方体与球这两种几何体的三视图是_____的.
(3)圆柱体:
主视图左视图俯视图
(4)圆锥体:
主视图左视图俯视图
2、分辨和画出一些几何体的三视图
1]桌子上放着一个长方体和圆柱(如下图),说出下列三幅图分别是:
()()()
2]画出下列几何体的主视图、左视图和俯视图
主视图左视图俯视图
注意:照片中的几何体为了使大家看清前后情况,因此照片中的物体一般朝左偏的位置是正面.
3] 一辆汽车从小明面前经过,小明拍摄了一组照片。
请按照汽车被摄人镜头的先后顺序给下面的照片编号,(照片见课本第 22 页“随堂练习”第1题)
拓展:1、画出下图几何体的主视图、左视图与俯视图。
主视图左视图俯视图
2、如图是一个水管接头
请写出上面三幅图(1)(2)(3)分别是从哪个方向看到的。
3 、下图是两个立体图的三视图,根据视图写出立体图形的名称。
(1)(2)
解:
4 画出一个三棱锥的三视图:。
