梁静力计算系数表讲解
静水力报表讲解
修改记录日期编号.描述编制校对审定船号建造设计详细设计基本性能m2静水力表Heel = 0.000(deg.) Trim=0.000(m)舯吃水(m)净体积(m3)排水体积(m3)排水量(t)浮心Z(m)浮心X(m)水线面面积(m2)漂心X(m)横稳心高(m)纵稳心高(m)方形系数0.522.322.423.00.290-0.55266.5420.418 5.14256.8770.2480.50022.322.423.00.290-0.55266.5420.418 5.14256.8770.2481.00061.862.163.70.5910.14689.2670.557 3.72635.4260.3431.500110.4111.0113.80.8840.288104.4380.360 3.21027.9420.4092.000165.7166.7170.9 1.1750.263116.6630.0623.02824.7420.4602.500227.8229.2234.9 1.4710.108136.509-1.0843.07328.2910.5063.000301.9303.7311.3 1.785-0.368153.475-2.009 3.22629.6890.559 3.5379.8382.1391.6 2.083-0.697157.526-1.908 3.28925.7760.603舯吃水(m)水线面系数中剖面系数菱形系数每厘米吃水吨数吨/厘米每厘米纵倾力矩吨米/厘米湿表面面积(m2)0.50.3700.7200.3440.70.474.2160.5000.3700.7200.3440.70.474.2161.0000.4960.8340.4110.90.8107.4361.5000.5800.8870.461 1.1 1.0136.2592.0000.6480.9150.503 1.2 1.4164.7522.5000.7590.9320.543 1.4 2.1203.2323.0000.8530.9440.593 1.6 2.9241.945 3.50.8750.9520.634 1.6 3.1270.719T/m 012345678910111213141516171819200.511.522.533.5Aft Fore净体积(m3)1格=20.0(m3)排水体积(m3)1格=20.0(m3)排水量(t)1格=20.0(t)浮心Z(m)1格=0.850(m)横稳心高(m)1格=1.500(m)水线面面积(m2)1格=50.000(m2)每厘米吃水吨数吨/厘米1格=0.5吨/厘米每厘米纵倾力矩吨米/厘米1格=1.0吨米/厘米纵稳心高(m)1格=15.000(m)湿表面面积(m2)1格=15.000(m2)漂心X(m)1格=1.350(m)浮心X(m)1格=1.350(m)方形系数1格=0.1菱形系数1格=0.1水线面系数1格=0.1中剖面系数1格=0.100.10.20.30.40.50.60.70.80.91稳性横截曲线Cross Curve At Trim 0(m)舯吃水(m)/横倾0.0 5.010.015.020.030.040.050.060.070.0(deg)0.5000.0000.4380.825 1.148 1.423 1.855 2.176 2.338 2.425 2.5140.5000.0000.4380.825 1.148 1.423 1.855 2.176 2.338 2.425 2.5141.0000.0000.3230.6380.934 1.201 1.6512.031 2.378 2.639 2.7511.5000.0000.2800.5570.830 1.095 1.5832.013 2.398 2.648 2.7122.0000.0000.2640.5270.792 1.057 1.576 2.044 2.365 2.544 2.6102.5000.0000.2680.5360.804 1.071 1.596 2.009 2.278 2.436 2.4953.0000.0000.2810.5600.836 1.108 1.556 1.897 2.148 2.314 2.3963.5000.0000.2870.5730.822 1.038 1.412 1.724 1.978 2.171 2.296舯吃水(m)稳性力臂 l φ(m )00.51 1.52 2.53 3.50.511.522.53邦京T X = -15.150 X = -14.650 X = -14.150 X = -13.650 X = -13.150AREAMOM BL AREAMOM BL AREAMOM BL AREAMOM BL AREAMOM BL0.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 2 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 2.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.048 0.119 3 0.000 0.000 1.922 5.403 2.128 5.946 2.323 6.453 2.491 6.890 3.50.0000.0004.81714.8215.04815.4435.26816.0335.45916.542T X = -12.650X = -12.150X = -11.650X = -11.150X = -10.650AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.50.0000.0000.0000.0000.0000.0000.0000.0000.0000.000 10.0000.0000.0000.0000.0000.0000.0000.0000.0000.000 1.50.0000.0000.0000.0000.0000.0000.0000.0000.0000.000 20.0000.0000.0000.0000.0000.0000.0000.0000.0000.0002.50.1330.3300.2440.6000.454 1.1100.828 1.994 1.5683.6593 2.6697.346 2.8697.854 3.1668.593 3.6189.688 4.42811.539 3.5 5.65817.066 5.87517.627 6.18418.407 6.64819.5387.46621.415T X = -10.150X = -9.650X = -9.150X = -8.650X = -8.150AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.50.2710.0260.2670.0290.2620.0330.2830.0420.3350.059 10.4440.1560.4680.1820.5320.2420.6640.3390.8650.4731.50.6560.4250.8270.643 1.1170.995 1.545 1.4752.109 2.0742 1.262 1.522 1.922 2.618 2.724 3.870 3.600 5.123 4.501 6.2972.53.495 6.6074.4228.2825.4059.9276.41311.4697.41012.8523 6.41114.6387.38516.4368.40318.1769.43619.78510.44921.212 3.59.45524.53210.43226.34111.45128.08412.48529.69513.49831.121T X = -7.650X = -7.150X = -6.650X = -6.150X = -5.650AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.50.4180.0820.5270.1140.6590.1530.8150.200 1.0030.2561 1.1520.657 1.5280.899 1.976 1.184 2.466 1.484 2.960 1.7681.52.802 2.7713.569 3.4964.325 4.1555.024 4.708 5.664 5.1682 5.4227.383 6.3438.3687.2049.2057.9729.8758.65610.409 2.58.39614.0809.35615.15010.23816.03411.01816.72911.70817.275 311.44422.46412.40723.54213.28924.42414.06725.11514.75725.661 3.514.49432.37515.45733.45516.33934.33517.11735.02817.80735.574T X = -5.150X = -4.650X = -4.150X = -3.650X = -3.150AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.5 1.2130.318 1.4240.379 1.6110.433 1.7980.484 1.9460.5261 3.432 2.020 3.850 2.229 4.190 2.393 4.488 2.523 4.715 2.621 1.5 6.244 5.549 6.741 5.8547.137 6.0847.471 6.2577.719 6.380 29.26110.8339.77311.16210.17711.40610.51611.58610.76611.711 2.512.31417.70112.82418.02713.22718.26913.56618.44913.81618.574 315.36326.08715.87426.41416.27726.65616.61626.83616.86626.962 3.518.41336.00018.92436.32719.32736.56919.66636.74919.91636.874T X = -2.650X = -2.150X = -1.650X = -1.150X = -0.650AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.5 2.0600.559 2.1360.583 2.1850.598 2.1970.606 2.1740.6071 4.884 2.691 4.995 2.739 5.065 2.769 5.087 2.785 5.064 2.785 1.57.900 6.4658.019 6.5228.093 6.5578.118 6.5758.093 6.574 210.94711.79711.06711.85611.14311.89411.16911.91411.14211.911 2.513.99718.66014.11718.71914.19218.75614.21918.77614.19218.773T X = -2.650X = -2.150X = -1.650X = -1.150X = -0.650AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL317.04727.04817.16727.10617.24227.14317.26927.16417.24227.161 3.520.09736.96020.21737.01920.29237.05620.31937.07620.29237.073T X = -0.150X = 0.350X = 0.850X = 1.350X = 1.850AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.5 2.1170.601 2.0360.591 1.9370.575 1.8300.556 1.7120.5311 4.997 2.772 4.897 2.748 4.769 2.712 4.625 2.665 4.456 2.604 1.58.021 6.5557.916 6.5247.778 6.4767.617 6.4107.426 6.321 211.06911.88810.96411.85910.82611.81110.66211.73810.46411.639 2.514.11918.75114.01418.72113.87618.67313.71018.59813.51218.496 317.16927.13817.06427.10916.92627.06016.76126.98616.56226.884 3.520.21937.05120.11437.02119.97636.97319.81136.89919.61236.797T X = 2.350X = 2.850X = 3.350X = 3.850X = 4.350AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.5 1.5930.504 1.4620.472 1.3270.438 1.1880.401 1.0450.3611 4.275 2.531 4.068 2.445 3.844 2.345 3.604 2.235 3.348 2.112 1.57.213 6.210 6.963 6.071 6.685 5.906 6.381 5.716 6.048 5.499 210.23811.5079.97111.3369.66611.1269.32710.8758.94810.579 2.513.28418.36013.01418.18412.70117.95712.34617.67011.94217.318 316.33526.74916.06426.57315.75126.34315.39126.04614.97725.666 3.519.38536.66119.11436.48518.80136.25518.44235.96218.02535.573T X = 4.850X = 5.350X = 5.850X = 6.350X = 6.850AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.50.9030.3200.7860.2840.6570.2430.5370.2030.4350.1681 3.083 1.981 2.832 1.846 2.561 1.700 2.293 1.551 2.037 1.401 1.5 5.698 5.262 5.350 5.007 4.970 4.727 4.583 4.429 4.197 4.118 28.53910.2408.1199.8607.6559.4357.1728.971 6.6778.468 2.511.49716.89911.03016.41410.50515.8519.94815.2219.36314.518 314.51425.19714.01824.63513.45223.96012.84123.18212.18722.290 3.517.55535.08117.04634.47716.45733.72815.81132.83615.10831.787T X = 7.350X = 7.850X = 8.350X = 8.850X = 9.350AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.50.3510.1380.2800.1120.2220.0900.1770.0720.1400.0581 1.791 1.250 1.557 1.101 1.3380.956 1.1350.8180.9470.6881.5 3.808 3.789 3.414 3.441 3.021 3.0792.633 2.710 2.251 2.3352 6.1647.924 5.6287.327 5.071 6.678 4.502 5.994 3.918 5.266 2.58.74513.7388.08612.8657.38311.892 6.64610.827 5.8679.660 311.48421.27710.72220.1219.89818.8149.01017.3368.04715.665 3.514.34130.56713.49729.14412.57127.50811.55525.61410.43023.418T X = 9.850X = 10.350X = 10.850X = 11.350X = 11.850AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BLT X = 9.850X = 10.350X = 10.850X = 11.350X = 11.850AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.50.1000.0430.0750.0320.0540.0230.0330.0150.0000.000 10.7670.5630.6060.4470.4540.3350.3080.2280.0940.0791.5 1.865 1.952 1.491 1.567 1.120 1.1790.7640.8070.3420.3942 3.307 4.488 2.691 3.679 2.063 2.840 1.440 2.0000.736 1.091 2.5 5.0318.379 4.1687.012 3.268 5.562 2.352 4.060 1.330 2.435 37.00313.810 5.89911.783 4.7279.587 3.5067.246 2.140 4.673 3.59.19520.9457.86618.185 6.43315.140 4.90911.815 3.1898.092T X = 12.350X = 12.850X = 13.350X = 13.850X = 14.350AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL AREA MOM BL0.50.0000.0000.0000.0000.0000.0000.0000.0000.0000.000 10.0000.0000.0000.0000.0000.0000.0000.0000.0000.000 1.50.0000.0000.0000.0000.0000.0000.0000.0000.0000.000 20.0680.1270.0000.0000.0000.0000.0000.0000.0000.000 2.50.3210.7040.0000.0000.0000.0000.0000.0000.0000.000 30.751 1.8930.0250.0730.0000.0000.0000.0000.0000.000 3.5 1.404 4.0270.2560.8340.0000.0000.0000.0000.0000.000T X = 14.850AREA MOM BL0.50.0000.000 10.0000.000 1.50.0000.000 20.0000.000 2.50.0000.000 30.0000.000 3.50.0000.000Bonjean Area4.53.7532.251.50.75-16.5-15-13.5-12-10.5-9-7.5-6-4.5-3-1.50 1.53 4.567.5910.51213.515Bonjean Mom4.53.7532.251.50.75-16.5-15-13.5-12-10.5-9-7.5-6-4.5-3-1.50 1.53 4.567.5910.51213.515。
常见梁静动态测试及模态测试教学说明书

(2)
分析式(附 2) 可得: (1) 衰减振动周期 T
T
2 0 1
2
T0 1 2
(3)
式中: T0 — 无阻尼系统周期;
n — 阻尼比 0
8
安正软件
在小阻尼ζ<<1 时, T T0 (2) 对数减幅系数
CRASV 7.0
若 t1 时刻振幅为 A 1 Ae nt1 , t 1 T 时刻振幅为 A 2 Ae n ( T t1 ) , 经过 1 个周期振幅衰减为 e nT , 对其取自然对数, 定义为对数减幅系数 , 即
CRASV 7.0
阻尼比测定
(3) 学习 CRAS 数据采集软件操作方法。 2. 实验对象
在悬臂梁自由端安装一个加速度计。悬臂梁材质不锈钢。
3. 实验框图和仪器
图 1. 脉冲锤击法测固有频率和阻尼比的实验框图 加速度计: 将被测系统的机械振动量(加速度)转换成电压量。 AZ 信号调理仪。 AZ 采集箱: 数据采集硬件。 计算机、打印机。 AdCras 和 SsCras 软件: 与采集箱、计算机和打印机一道完成数据采集、分析和打印的功能
ln(
A1 ) nT nT0 A2
(4)
因为 T0
2 n , , 故由上式还可得: 0 0 2
(5)
为保证测试精度, 一般取 k 个周期计算对数减幅系数 , 若第 1 和第 k 周期的振幅分别记作 A 1 和
A k , 则对数减幅系数为 ln(A1 / A k ) / k
2
; A5 = ;
m s 2 ;
ln(A 1 / A 5 ) = 5
。
2
共振峰的纵坐标(振幅的最大值) A max A (f1 ) 半功率点的纵坐标
结构动力学的刚度系数柔度系数ppt课件
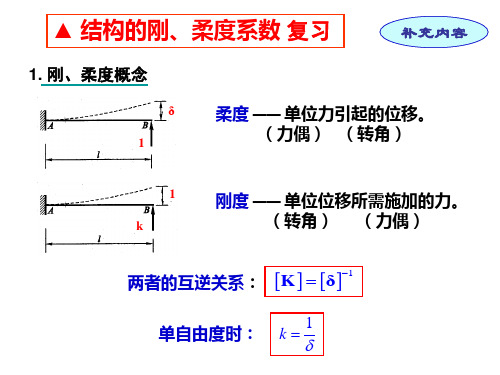
三、自由振动微分方程的解
y(t) Asin( t )
四、结构的自振周期和频率
静定结构,图乘法求δ
k 1 m m
T 2
五、例题
m EI
l /2
l /2
1
[例1] 计算图示结构的频率和周期。
解:(柔度法)
1 m
l3
48EI
48EI ml 3
T 2 ml3
2 结构约束越强,则刚度越大, 其自振动频率也越大。
SUCCESS
THANK YOU
•
[例4] 图示桁架,E=206GPa , A=0.002m2 , mg=40KN , 计算自振频率。( g取10m/s2 )
1
m
4
4
解:(柔度法)
3
5 (Fn )i2li 243
i1 EA 18EA
一、自由振动
二、振动微分方程的建立 my ky 0
y 2y 0
(1)刚度法 —— 研究作用于被隔离的质量上的力,建立 平衡方程,需要用到刚度系数。
(2)柔度法 —— 研究结构上质点的位移,建立位移协调方程, 需要用到柔度系数。
超静定结构,查表(形常数)
刚度系数 取决于结构的
柔度系数
谁较容易求得。
3EI h3
3EI h3
6EI h3
h1
i1
i2 h2
∞
h i1
i2
总侧移刚度:
k
k左柱
k右柱
3 h
i1
2 1
3 h
i2
2 2
总侧移刚度:
k
变截面预应力混凝土箱梁径向力计算

153.76
6
8 仅有径向力 I[6]
55.2
-57.71
6
8 仅有径向力 J[7]
55.2
-0.0355.2
-0.03
7
8 仅有径向力 J[8]
55.2
57.65
8
8 仅有径向力 I[8]
55.2
57.65
8
8 仅有径向力 J[9]
55.2
129.75
9
8 仅有径向力 I[9]
55.2
129.75
9
8 仅有径向力 J[10] 55.2
201.85
10
8 仅有径向力 I[10] 155.05 140.53
10
8 仅有径向力 J[11] 155.05 140.53
11
8 仅有径向力 I[11] 55.2
201.85
11
8 仅有径向力 J[12] 55.2
201.85
12
8 仅有径向力 I[12]
19 1 64 -189 -316 316 189 -64
-19 1
-369-291
-293-369
-1
-218
-218
169
203
203
169
-1
主+附+径向弯矩图
CB: 7含径向力组
MAX : 14 MIN : 2 文件: 牛角坪环框计藒 单位: kN*m 日期: 12/08/2007
表示-方向 X: 0.000
箍筋时会导致底板产生纵向裂缝,正确的设计是按此径向分布荷载设置平衡箍
筋,将这部分力通过平衡箍筋传递于上层钢筋,使全底板共同参与受力,有效防
止底板劈裂。
基于狄拉克δ函数的梁静力挠度分析

基于狄拉克δ函数的梁静力挠度分析
刘彦辉;冯新
【期刊名称】《科技信息》
【年(卷),期】2009(000)14X
【摘要】本文提出了一种基于狄拉克δ函数的静力挠度分析方法,建立了一种Euler裂纹梁的分析模型,并且获得了闭合形式的挠度解析解。
在一致梁的理论框架下,通过引入δ函数模拟裂纹导致的局部柔度,建立用广义函数表示的Euler裂纹梁的微分控制方程,进而得到挠度的闭合形式的解答。
通过数值算例证实了基于狄拉克δ函数的Euler裂纹梁的分析模型,具有较高的计算精度和效率,在结构模型修正和损伤识别中具有良好的应用前景。
【总页数】0页(P99-101)
【作者】刘彦辉;冯新
【作者单位】大连理工大学土木水利学院;大连理工大学海岸与近海工程国家重点实验室
【正文语种】中文
【中图分类】O413.1
【相关文献】
1.预应力梁开裂后的静力挠度特性分析 [J], 余静静
2.千米级斜拉桥主梁挠度非线性随机静力分析 [J], 刘晓銮;张杨永;周云岗
3.预应力混凝土简支梁的桥静力挠度可靠度分析 [J], 杜斌;向天宇;黄质宏
4.基于静力挠度的简支梁桥刚度识别模型试验研究 [J], 于奇;杜隆基
5.基于静力挠度的简支梁桥刚度识别模型试验研究 [J], 于奇;杜隆基
因版权原因,仅展示原文概要,查看原文内容请购买。
钢筋混凝土梁抗冲击性能和设计方法研究

钢筋混凝土梁抗冲击性能和设计方法研究赵德博;易伟建【摘要】In order to study the behavior of reinforced concrete (RC)beams under impact loading,drop hammer tests were performed for 4 RC beams and test variables were impact mass and impact velocity.Impactforce,reaction force and mid-span deflection were measured.The crack propagation was recorded using a high-speed video camera.The specimens revealed two different failure patterns of the beam-hammer contact zone.It was shown that with increase in impact velocity and decrease in impact mass,the proportion of the hammer kinetic energy to be converted into the beam's strain energy reduces,more energy is consumed for the local damage of the beam-hammer contact zone.Based on the statistical analysis of these tests'results and those of the tests conducted by previous researchers,an empirical formula to estimate the maximum deflection of RC beams was derived considering influence of impact mass and its accuracy was better than that of the empirical formula proposed by previous researchers.%为研究钢筋混凝土梁在冲击荷载作用下的性能,进行了4根钢筋混凝土梁的落锤冲击试验,试验变量为冲击质量和冲击速度。
25m20m箱梁预应力钢绞线张拉力与伸长值计算表(1)
参数 k=0.0015 x(mm) μ =0.25 θ (rad) kx+μ θ 钢绞线名 分段编 称 号 N1控制应力
1395 1 793.6 349 90.7 0 0.043625 0 0.0011904 0.998810308 195300 195067.6532 195183.8036 193957.1011 140 140 140
参数k00015025钢绞线名称分段编号xmmradkxekx起点张拉力终点张拉力平均张拉力ppnap理论mm2ep理论limml理论mm备注n1控制应力139517936000011904099881030819530019506765321951838036140195000567直线段23490043625001142975098863532119506765321928507721939571011140195000248曲线段39070000013605099986395919285077219282453651928376539140195000064直线段n2控制应力1395163100000946509990539481953001951152361952076034140195000451直线段2349004362500114297509886353211951152361928978141194004413140195000248曲线段3252900000379350999620722192897814119282465221928612308140195000179直线段n3控制应力1395146800000702099929824619530019516294751952314657140195000335直线段234900436250011429750988635321195162947519294498331940518529140195000248曲线段3415100000622650999377544192944983319282488351928849272140195000293直线段n4控制应力1395192200000138309998617119530019527299191952864956140195000066直线段2977001628330004217383099579149719527299191944511851948617996140195000070曲线段3104010000156015099844106619445118519414804851942995773140195000740直线段交底
20m箱梁(后张法)计算参数
20m箱梁(后张法)计算参数=1860MPa,单根面积140mm2,钢绞线为高强度、低松弛φj15.24钢绞线,标准强度R by管道摩擦系数μ=0.25,管道影响系数k=0.0015,钢筋回缩和锚具变形为6mm,锚下控制应力为σk=0.75R b=1395MPa。
y钢绞线下料长度:中跨:钢束编号下料长度伸长值计算长度曲线长度直线长度(cm) (cm) (cm) (cm) N1 2075 1945 813.3 159.2N2 2080 1950 624.4 350.6N3 2052 1922 179.8 781.2边跨:钢束编号下料长度伸长值计算长度曲线长度直线长度(cm) (cm) (cm) (cm) N1 2083 1953 809.1 167.4N2 2085 1955 621.7 355.8N3 2069 1939 171.4 798.1钢束编号下料长度伸长值计算长度曲线长度直线长度(cm) (cm) (cm) (cm) T1 761 701 87.8 262.7T2 1361 1301 87.8 562.7T3 1361 1301 87.8 562.7=1395MPa,各束钢控制应力:依据设计规定所有钢束锚下控制应力均为σk=0.75R by绞线控制张拉力如下:中跨:钢束编号每束根数控制应力(KN) 张拉方式N1 3 585.9 两端张拉N2 3 585.9 两端张拉N3 4 781.2 两端张拉边跨:钢束编号每束根数控制应力(KN) 张拉方式N1 4 781.2 两端张拉N2 4 781.2 两端张拉N3 4 781.2 两端张拉钢束编号每束根数控制应力(KN) 张拉方式T1 4 195.3(781.2) 两端单根张拉T2 5 195.3(976.5) 两端单根张拉T3 4 195.3(781.2) 两端单根张拉张拉程序:依据<<公路桥规>>JTJ041-2000及设计之规定对N1、N2、N3钢束采用两端整体张拉,对T1、T2、T3钢束采用两端单根对称张拉,张拉程序均采用0→初应力→σk(持荷2min 锚固)依据<<公路桥规>>JTJ041-2000规定拟定初应力为0.15σk张拉步骤:0→0.15σk→0.3σk→1.0σk张拉顺序:N1→N2→N3 T1→T2→T3张拉采用YDC1500A-200型千斤顶张拉钢束时,张拉缸活塞面积为28510mm2,千斤顶的摩阻为0.32%和0.36%。
梁静力计算系数表..
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=A dA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y IW =3.i 称截面回转半径(mm ),其基本计算公式如下:AI i = 4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
预应力梁承载能力计算说明
根据名义拉应力法计算有粘结预应力梁承载能力
k ct pc M W σσ=
- []ct p c d h ct k k k k k λσσ=⋅⋅⋅⋅⋅
2P pn P pc n n n n n N e N M y y A I I σ=
±± 由以上公式,当不考虑次弯矩的影响,则推导出()k ct pc M W σσ=+。
[]ct σ——设预应力混凝土构件最大裂缝宽度w max 所对应的名义拉应力,
及名义拉应力限值。
ct σ——根据预应力梁的具体条件,修正后的某一裂缝宽度的名义拉应力允许值。
,,,,p c d h k k k k k λ——分别为非预应力筋配筋率、混凝土强度等级、非预应力筋直径、预应力度及截面高度对名义拉应力允许值的修正系数。
有粘结预应力混凝土大梁名义拉应力限值
钢筋直径影响系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用截面几何与力学特征表表2-5
注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=A dA y
I 2
2.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y I
W =
3.i 称截面回转半径(mm ),其基本计算公式如下:A
I i = 4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
(1)简支梁的反力、剪力、弯矩、挠度表2-6
(2)悬臂梁的反力、剪力、弯矩和挠度表2-7
(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8
(4)两端固定梁的反力、剪力、弯矩和挠度表2-9
(5)外伸梁的反力、剪力、弯矩和挠度表2-10
3.等截面连续梁的内力及变形表
(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)
1)二跨等跨梁的内力和挠度系数表2-11
注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EI
w 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)
=(-36.75)+(-27.64)=-64.39kN ·m
V B 左=(-0.625×11.76×5)+(-0.688×29.4)
=(-36.75)+(-20.23)=-56.98kN
[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN ·m 。
2)三跨等跨梁的内力和挠度系数 表2-12
注:1.在均布荷载作用下:M =表中系数×ql 2
;V =表中系数×ql ;EI
w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EI
w 100Fl 表中系数3
⨯=。
3)四跨等跨连续梁内力和挠度系数表2-13
注:同三跨等跨连续梁。
4)五跨等跨连续梁内力和挠度系数表2-14
注:1.M=表中系数×ql21;V=表中系数×ql1;2.(M max)、(V max)表示它为相应跨内的最大内力。
注:1.M=表中系数×ql21;V=表中系数×ql1;2.(M max)、(V max)为荷载在最不利布置时的最大内力。
4.双向板在均布荷载作用下的内力及变形系数表(表2-17~表2-22) 符号说明如下:
刚度 )1(1223
υ-=Eh K
式中 E ——弹性模量;
h ——板厚; ν——泊松比;
ω、ωmax ——分别为板中心点的挠度和最大挠度;
M x ——为平行于l x 方向板中心点的弯矩; M y ——为平行于l y 方向板中心点的弯矩; M x 0——固定边中点沿l x 方向的弯矩; M y 0——固定边中点沿l y 方向的弯矩。
正负号的规定:
弯矩——使板的受荷面受压者为正; 挠度——变位方向与荷载方向相同者为正。
四边简支 表2-17
两边简支,两边固定表2-19
四边固定表2-21
两边简支,两边固定表2-22
5.拱的内力计算表(表2-23)
各种荷载作用下双铰抛物线拱计算公式表2-23
注:表中的K为轴向力变形影响的修正系数。
(1)无拉杆双铰拱
1)在竖向荷载作用下的轴向力变形修正系数
式中I c——拱顶截面惯性矩;
A c——拱顶截面面积;
A——拱上任意点截面面积。
当为矩形等宽度实腹式变截面拱时,公式I=I c/cosθ所代表的截面惯性矩变化规律相当于下列的截面面积变化公式:
此时,上式中的n可表达成如下形式:
下表中列出了矩形等宽度实腹式变截面拱的n值。
f/l 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 n 1.67 1.59 1.51 1.43 1.36 1.29 1.23 1.17 1.12 2)在水平荷载作用下的轴向力变形修正系数,近似取
K=1
(2)带拉杆双铰拱
1)在竖向荷载作用下的轴向力变形修正系数
式中E——拱圈材料的弹性模量;
E1——拉杆材料的弹性模量;
A1——拉杆的截面积。
2)在水平荷载作用下的轴向力变形修正系数(略去拱圈轴向力变形影响)
式中f——为矢高;
l——为拱的跨度。
6.刚架内力计算表
内力的正负号规定如下:
V——向上者为正;
H——向内者为正;
M——刚架中虚线的一面受拉为正。
(1)“┌┐”形刚架内力计算(表2-24、表2-25)
“┌┐”形刚架内力计算表(一)表2-34
“┌┐”形刚架内力计算表(二)表2-35
(2)“”形刚架的内力计算(表2-26)
“”形刚架的内力计算表表2-26。
