初一-有理数的乘除法、乘方运算-练习题

合集下载

初一数学有理数的加减乘除以及乘方试题答案及解析

初一数学有理数的加减乘除以及乘方试题答案及解析1.小华利用计算器计算0.0000001295×0.0000001295时，发现计算器的显示屏上显示如下图的结果，对这个结果表示正确的解释应该是（）．A．1.677025×10—14B．1.677025×1014C．（1.677025×10）—14D．1.677025×10×（—14）【答案】A．【解析】0.0000001295×0.0000001295，=0.00000000000001677025，=1.677025×10-14．故选A．【考点】计算器—有理数．2.计算：【答案】41．【解析】针对有理数的乘方、绝对值分别进行计算，然后根据实数的运算法则求得计算结果．原式=．【考点】1.有理数的乘方；2..绝对值；3.实数的运算法则．3.人一根头发的直径大约为0.00072分米，用科学记数法表示正确的是（）A．B．C．D．【答案】D.【解析】根据科学记数法的定义，科学记数法的表示形式为a×10n，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值。

在确定n的值时，看该数是大于或等于1还是小于1.当该数大于或等于1时，n为它的整数位数减1；当该数小于1时，－n为它第一个有效数字前0的个数（含小数点前的1个0）.0.00072第一个有效数字前有4个0（含小数点前的1个0），从而.故选D.【考点】科学记数法.4.中学数学中，我们知道加减运算是互逆运算，乘除运算也是互逆运算；其实乘方运算也有逆运算，如式子可写成，式子也可写成；已知式子表示为，则用表示时，＝（）A．6B．C．D．【答案】B.【解析】根据观察式子23=8可以变形为3=log28，2=log525也可以变形为52=25，可发现规律，根据同底数幂的乘法，可得答案．由y=log318，得3y=183x=2，32=932×3x=32+x=183y=18=32+x所以y=2+x．故选B.【考点】有理数的乘方．5.计算（1）[(x+y)2-(x-y)2]÷(2xy)（2）（3）【答案】（1）2；（2）-0．1；（3）-4．【解析】（1）原式中括号中利用完全平方公式展开，再利用多项式除以单项式法则计算即可得到结果．（2）先算积的乘方，再进行除法运算即可；（3）根据乘方、零次幂、负整数指数幂的意义进行计算即可求出答案．试题解析：（1）原式=（x2+2xy+y2-x2+2xy-y2）÷（2xy）=4xy÷（2xy）=2；(2) 原式====-0．1；（3）原式=-4+4×1-4=-4+4-4=-4【考点】1．完全平方公式；2．整式的除法；3．实数的混合运算．6.用小数表示2.014×10－3是 .【答案】0.002014.【解析】把数据2.014×10－3中2.014的小数点向左移动3位就可以得到．试题解析：2.014×10－3=0.002014.考点: 科学记数法—原数．7.已知，则=_______.【答案】-3.【解析】把变形为3-3，即可求出m的值.试题解析：∵∴m=-3.考点: 负整数指数幂.8.根据下图所示的程序计算代数式的值,若输入n的值为5,则输出的结果为（）A．16B．2.5C．18.5D．13.5【答案】A【解析】由程序图可知输出的结果为3.9.明近期几次数学测试成绩如下：第一次85分，第二次比第一次高8分，第三次比第二次低12分，第四次又比第三次高10分．那么小明第四次测验的成绩是（）A．90分B．75分C．91分D．81分【答案】C【解析】小明第四次测验的成绩是故选C.10.小彬从家里步行到学校需100步，他到学校的距离可能是（）A．250 m B．200 m C．150 m D．50 m【答案】D【解析】0.5×100=50(m)．故选D．11.计算（－2.5）×0.37×1.25×（－4）×（－8）=_________.【答案】-37【解析】原式=[(－2.5)×(－4)]×[1.25×(－8)]×0.37=10×(－10)×0.37=－37.12.比较下列各对数的大小．（1）与；（2）与；（3）与.【答案】（1）＜（2）＜（3）＜【解析】解：（1）因为|－4＋5|=1，|－4|＋|5|=9，所以|－4＋5|＜|－4|＋|5|.（2）因为，所以.（3）因为，，所以.13.务川电视台天气预报，12月20日的气温是﹣2℃～7℃，则这一天的温差是℃【答案】9【解析】用最高气温减去最低气温，然后根据减去一个数等于加上这个数的相反数进行计算即可得解．7﹣（﹣2）=7+2=9℃．故答案为：9．【考点】有理数的减法．14.）计算：（1）（2）；（3）；（4）．【答案】（1）－2.5；（2）；（3）－15；（4）1．【解析】（1）原式＝＝0.5＋(－3)＝－2.5．（2）原式＝＝(－1)×＝．（3）原式＝－25＋＝－25＋12＋16－18＝－15（4）原式＝=1【考点】有理数的运算．15.一振子从点A开始左右振动8次，如果规定向右为正，向左为负，这8次振动记录为（单位：毫米）：＋10，－9，＋8，－6，＋7.5，－6，＋8，－7．（1）求振子停止时所在位置距A点有多远？（2）如果每毫米需时0.22秒，则共用时多少秒？【答案】（1）5.5；（2）13.53．【解析】（1）将8次的记录相加，得到的数就是停止时所在位置距A点的距离，如果是“正”则在A点右边，如果是“负”则在A点左边；（2）将8次记录的绝对值相加就是它振运8次的距离，再乘以0.22，即可得到共用时间．试题解析：（1）＋10－9＋8－6＋7.5－6＋8－7＝5.5；答：振子停止时位于A点右边5.5毫米处．（2）10＋9＋8＋6＋7.5＋6＋8＋7＝61.5，61.5×0.22＝13.53（秒）答：振子共用时13.53秒．【考点】正数和负数．16.温家宝总理在十届全国人大四次会议上谈到解决“三农”问题时说，2006年中央财政用于“三农”的支出将达到33970000万元，这个数据用科学记数法可表示为万元.【答案】3.397×107【解析】科学记数法的表示方法：科学记数法的表示形式为，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数.解：．【考点】科学记数法的表示方法点评：本题属于基础应用题，只需学生熟练掌握科学记数法的表示方法，即可完成.17. (-2)4表示A．(-2)×4B．(-2)×(-2)×(-2)×(-2)C．-4×4D．(-2)+(-2)+(-2)+(-2)【答案】B【解析】有理数的乘方的定义：几个相同因数的积叫做有理数的乘方.(-2)×(-2)×(-2)×(-2)，故选B.【考点】有理数的乘方点评：本题属于基础应用题，只需学生熟练掌握有理数的乘方的定义，即可完成.18.按四舍五入法则取近似值：2.096≈（精确到百分位）.-0.03445≈（精确到0.001）.【答案】2.10，-0.034【解析】精确到百分位即是对千分位四舍五入，精确到0.001即是对0.0001位四舍五入.按四舍五入法则取近似值：2.096≈2.10（精确到百分位）.-0.03445≈-0.034（精确到0.001）.【考点】近似数和有效数字点评：本题属于基础应用题，只需学生熟练掌握取近似数的方法，即可完成.19.下表是小明记录的10月份某一周内每天中午12时的气温的变化情况（气温比前一天上升记为正数，下降记为负数）星期一二三四五六日（2）本周的最高气温与最低气温相差多少摄氏度？【答案】（1）由题意得【解析】（1）根据气温比前一天上升记为正数，下降记为负数即可依次计算出各天的实际气温；（2）根据（1）中得到的结果即可计算出本周的最高气温与最低气温的差.（1）由题意得13111614131716【考点】有理数的减法法则的应用点评：解题的关键是读懂气温比前一天上升记为正数，下降记为负数，分别计算出各天的实际气温.20.研究下列算式，你会发现什么规律?……问题探究(1)请你找出规律并计算=_____________=( ).(2)用含有的式子表示上面的规律：_____________________________.问题解决(3)用找到的规律解决下面的问题：计算: =_______________.写出运算过程：【答案】（1）8（2）（3）【解析】1）=64=8（2）n（n+2）+1=（3）解：原式==【考点】找规律-数字的变化点评：解答本题的关键是仔细分析题意得到规律，再把这个规律应用于解题.21. 2008年全国人民共向四川地震灾区捐款约43681000000元，这笔款额用科学记数法表示（保留三个有效数字）正确的是（）A．0.437×1011B．4.4×1010C．4.37×1010D．43．7×109【答案】C【解析】科学记数法的表示形式为，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．43681000000，故选C.【考点】科学记数法的表示方法，近似数与有效数字点评：解题的关键是熟练掌握从左边第一个不为0的数开始到末尾数字为止，所有的数字都是这个数的有效数字，注意有效数字的个数与乘方的次数无关.22.钓鱼岛自古以来是中国的领土，岛屿周围的海域面积约170 000平方公里，相当于五个台湾本岛面积. 这里的“170 000”用科学记数法表示为 .【答案】【解析】科学记数法的表示形式为，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【考点】本题考查的是科学记数法的表示方法点评：本题属于基础应用题，只需学生熟练掌握科学记数法的表示方法，即可完成.23.有理数3.645精确到百分位的近似数为A．3.6B．3.64C．3.7D．3.65【答案】D【解析】由题意精确到百分位就是对千分位四舍五入取近似值.有理数3.645精确到百分位的近似数为3.65，故选D.【考点】近似数和有效数字点评：本题属于基础应用题，只需学生熟练掌握四舍五入取近似值的方法，即可完成.24.计算：（1）（2）（3）（4）【答案】（1）0；（2）-1；（3）7；（4）6【解析】有理数的混合运算的顺序：先算乘方，再算乘除，最后算加减，同级运算按从左向右的顺序依次计算；有括号的先算括号里的.同时注意运算过程中可以运用运算律计算的要运用运算律简化计算.（1）原式=-3+3=0；（2）原式==；（3）原式==；（4）原式==.【考点】有理数的混合运算点评：本题属于基础应用题，只需学生熟练掌握有理数的混合运算的顺序，即可完成.25.若a、b互为相反数，c、d互为倒数，∣m∣=2，求+m2-3cd的值.【答案】-2【解析】由题意可得，，，再整体代入求值即可.由题意得，，则【考点】代数式求值点评：解题的关键是熟记相反数之和为0，倒数之积为1，相反数的两个数的绝对值相等.26.计算：（1）4―－3×；（2）【答案】（1）-1；（2）【解析】有理数的混合运算的顺序：先算乘方，再算乘除，最后算加减，同级运算按从左向右的顺序依次计算；有括号的先算括号里的.同时注意运算过程中可以运用运算律计算的要运用运算律简化计算.（1）原式=4-6+1=-1；(2) 原式=-1-=.【考点】有理数的混合运算点评：本题属于基础应用题，只需学生熟练掌握有理数的混合运算，即可完成.27.的个位数字是（）A．2B．4C．6D．8【答案】C【解析】∵一个数的乘方的个位数字＝这个数的个位数字的乘方的个位数字。

七年级有理数的加减乘除乘方计算训练(80小题)-有解析

有理数的加减乘除乘方计算（80小题）1.计算：(1)(−37)−(−47)；(2)(−53)−16；(3)(−210)−87；(4)1.3−(−2.7)．【答案】解：(1)(−37)−(−47)=−37+47=10；(2)(−53)−16=−69；(3)(−210)−87=−297；(4)1.3−(−2.7)=1.3+2.7=4．【解析】此题主要考查有理数的减法，解题关键是掌握有理数的减法法则，据此求解即可．(1)根据有理数的减法法则计算即可；(2)根据有理数的减法法则计算即可；(3)根据有理数的减法法则计算即可；(4)根据有理数的减法法则计算即可．2.计算：(1)−7+3−5+20；(2)223+(−223)+513−(−512)；(3)4.25+(−2.18)−(−2.75)+5.18；(4)43−(−87)−2−13−17【答案】解：(1)原式=−12+23=11；(2)原式=0+163+112=326+336=656=1056；(3)原式=(4.25+2.75)+(5.18−2.18)=7+3=10；(4)原式=(43−13)−2+(87−17)=1−2+1=0．【解析】此题考查有理数的加减混合运算，熟练掌握有理数的加减混合运算法则和运算律是解题关键．(1)根据结合律和交换律先同号相加，再异号相加即可求解；(2)根据结合律和相反数的定义算223+(−223)并将513和512化成假分数，然后通分后算加法得出结果再化成带分数即可；(3)根据结合律和交换律先算4.25−(−2.75)和(−2.18)+5.18，再算加法即可求解；(4)根据结合律和交换律先算43−13和87−17，再算加减即可求解．3. 计算：(1)|−7|+|−9715|； (2)(+4.85)+(−3.25)；(3)(−3.1)+6.9；(4)−(−15)+(−645)；(5)(−3.125)+(+318)．【答案】解：(1)原式=7+9715=16715；(2)原式=4.85−3.25=1.6；(3)原式=−(6.9−3.1)=−3.8；(4)原式=15−645=−635；(5)原式=−3.125+3.125=0．【解析】本题考查有理数的加法，以及绝对值，掌握运算法则是解题关键．(1)先化简绝对值，再计算加法即可；(2)先化简括号，再计算即可；(3)根据异号两数相加，取绝对值较大的符号，再用较大的绝对值减较小的绝对值即可；(4)先化简括号，再计算即可；(5)将分数化为小数，再计算即可．4. 用简便方法计算：(1)−13×23−0.34×27+13×(−13)−57×0.34；(2)(−13−14+15−715)×(−60)．【答案】解：(1)原式=(−13)×(23+13)+0.34×(−17−57)=−13×1+0.34×(−1)=−13−0.34=−13.34；(2)原式=−13×(−60)−14×(−60)+15×(−60)−715×(−60)=20+15−12+28=51【解析】本题主要考查了有理数的混合运算，关键是熟练掌握乘法运算律．(1)运用乘法分配律进行计算可得结果；(2)利用乘法分配律进行计算，最后计算加减可得结果．5. 计算：(1)(−8)×9×(−1.25)×(−19)；(2)−113×214÷(−112)；(3)(−132)÷(134−58+12)；(4)(−3)÷134×0.75×|−213|÷9．【答案】解：(1)原式=(−8)×(−1.25)×[9×(−19)]=10×(−1)=−10；(2)原式=−43×94×(−23) =2；(3)原式=(−132)÷(148−58+48)=(−132)÷138 =−132×813=−152；(4)原式=−3×47×34×73×19=−13．【解析】本题主要考查的是有理数的乘法，有理数的混合运算的有关知识．(1)利用有理数的乘法的计算法则进行计算即可；(2)利用混合运算的运算法则进行计算即可；(3)利用混合运算的运算法则进行计算即可；(4)利用混合运算的运算法则进行计算即可．6.计算：(1)−2.2+(−4.3)(2)−(−334)+(−15.5)(3)−(−5)−|−4|(4)−21−12+33+12−67．【答案】解：(1)−2.2+(−4.3)=−(2.2+4.3)=−6.5(2)−(−334)+(−15.5)=3.75−15.5=−(15.5−3.75)=−11.75(3)−(−5)−|−4|=5−4=1(4)−21−12+33+12−67=−100+45=−55．【解析】此题主要考查有理数的加减及混合运算(1)根据同号两数相加，取相同的符号，并把绝对值相加求解(2)先求出相反数，根据异号两数相加，取绝对值较大加数的符号，并用较大的绝对值减去较小的绝对值求解(3)先求出相反数和绝对值，再相减(4)利用分组法，符号相同的加在一起，再根据异号两数相加，取绝对值较大加数的符号，并用较大的绝对值减去较小的绝对值求解7.计算：(1)(−99)+(−103)；(2)(−16)+9；(3)3+(−8)+(−1)．(4)|−18|+|−6|；(5)|−36|+|+24|．【答案】解：(1)(−99)+(−103)=−(99+103)=−202(2)(−16)+9=−(16−9)=−７；(3)3+(−8)+(−1)=3+(−9)=−(9−3)=−6．(4)|−18|+|−6|=18+6=24；(5)|−36|+|+24|=36+24=60．【解析】此题主要考查有理数的加法，根据同号两数相加，取相同的符号，并把绝对值相加，异号两数相加，取绝对值较大加数的符号，并用较大的绝对值减去较小的绝对值求解(1)根据同号两数相加，取相同的符号，并把绝对值相加求解(2)根据异号两数相加，取绝对值较大加数的符号，并用较大的绝对值减去较小的绝对值求解(3)先同号相加，再异号相加求解较简便(4)先求个数的绝对值，再相加(5)先求个数的绝对值，再相加8.计算题(1)−(−8)+(−32)+(−|−16|)+(+28)(2)0.36+(−7.4)+0.3+(−0.6)+0.64；。

有理数的加减乘除乘方混合运算专题训练(带答案)

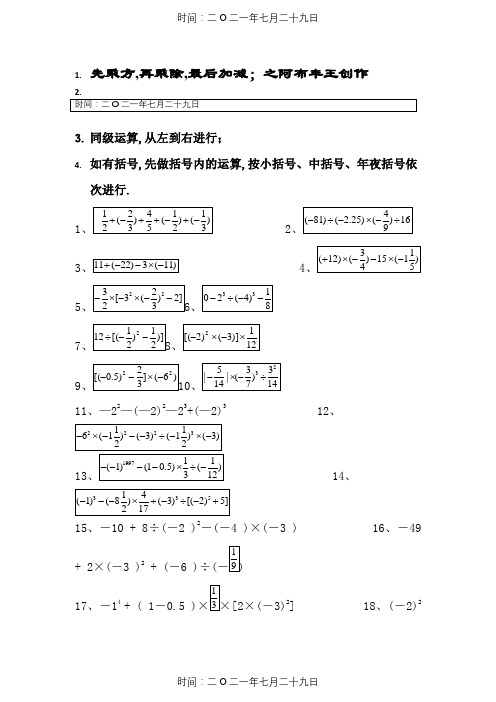
1.先乘方,再乘除,最后加减；之阿布丰王创作3.同级运算,从左到右进行；4.如有括号,先做括号内的运算,按小括号、中括号、年夜括号依次进行.1357911、—22—(—2)2—23+(—2)3 12、13、15、－10 + 8÷(－2 )2－(－4 )×(－3 ) 16、－49+ 2×(－3 )2 + (－6 )÷(17、－14 + ( 1－0.5 )[2×(－3)2] 18、(－2)2－2×[(2－3192123、 24、25、6－（－12、（-48）÷ 8 －（-5）27、420.25 2829、(－5)×6＋(－125) ÷(－5)3311、【基础题】计算：（1÷（2）（3（4（1（2（3（4（1（34（5（6（7（8；（9）10（1）11＋（－22）－3×（－11）；（2）（34；（5（6（7）（－6）（8）（1（2（34（5（6）－10＋84×3；（7（81－0.5）（1）（－8）×5－40；（2）（）÷（-（-2）；（3）-20÷5×（-3）÷15；（4）-3[-5+（÷-2）]；（5）－23÷2÷（2；（6×(－2.4)参考谜底1、-1/52、-13、224、95、96、 07、-48 8、-1 9、-15 10、-15/34311、-24 12、-89 13、3 14、215、-2016、23 17、2 18、24 19、-2820、9/1621、1 22、10 23、-1/12 24、104/325、926、1427、-3128、-81又1/81 29、-9 30、-2931、-1/5 32、91、【谜底】（1）17；（2（3）31；（4）－112、【谜底】（1）－10；（2）22；（3）－16；（4）3、【谜底】（1）1；（2）0；（3）42；（4（5）18；（6）0；（7）－4.64；（8（9）8；（104、【谜底】（1）22；（2）0；（3）－17；（4（5（6）－95；（7）－85；（8）6 .5、【谜底】（1）3；（2）1；（3）－54；（4）0；（5）（6）－20；（7）－2；（86、【谜底】（1）－80；（2）5.6；（3）－2；（4）16；（5）－复习有理数的乘除、乘方运算测试题一、填空题（每小题3分,共30分）1．3×（－2）=________,（－6=________．2．（－3）2的底数是________,；－32的底数是________,结果是________．3=________=________；（+8）÷（－=________．4．233=________2=________．5________=1________=－162．4=________．7．－32×（－5）23=________．83600平方公里,________．9．________；________10①23________222________3③32________22）3________）2二、判断题（每小题1分,共5分）11．零除以任何数都得零（）12．互为相反数的两个数的积为负数（）13．如果ab＞0,则a＞0且b＞0（）14．1除以一个非零数的商叫做这个数的倒数（）15．（－3）5暗示5个－3相乘（）三、选择题（每小题3分,共21分）16．下列说法,其中毛病的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘,符号不变．A．1个B．2个C．3个D．4个17．下列各对数：①1与1；②－1与1；③a－b与b－a；④－1与－1；⑤－5与|6|,其中互为倒数的是A．①②③B．①③⑤C．①③④D．①④18．下列各题中两个式子的值相等的是A．－23与（－2）3 B．32与23C．（－2）2与－22 D．|－2|与－|－2|19．下列结论中,其中正确的个数为①0的倒数是0；②一个不即是0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数即是自身的数是±1；④若a,b互为倒数,则－ab=－1．A．4 B．3C．2 D．120．下列各式中结果年夜于0的是A．1－910×3 B．（1－910）×3C．1－（9×3）10 D．（1－9）10×3 21．下列说法中正确的是A．一个数的平方必为正数B．一个数的平方必小于这个数的绝对值C．一个数的平方必年夜于这个数D．一个数的平方不成能为负数22．用科学记数法暗示的数2．89×104,原来是A．2890 B．2890000 C．28900 D．289000四、计算题（共35分）23．（3分）（－3）×（－5）×（+1224．（3分）－6÷（+3）÷（－4）×（+2）25．（3分）－5－626．（3分）（－81）÷16）27．（3分）－22×（－328．（3分）（－1）2000200120021）200329．（3分）（－2）×（－20011－200230．（331．（332．（3分）（－2.53）33．（5分）30五、解答题（934．已知A=a+a2+a3+……+a2000（1）若a=1,求A的值．（2）若a=－1,求A的值．一、1．－6 2 2．－3 9 3 －9 3－3245103平方公里9．＞＞＞＜13．×14．√15．√三、16．A 17．D 18．A 19．B 21．D 22．C四、23．－90 24．1 25．－3 2627．15 28．1 29．－200230．1 31．30 3233．－4五、34．（1）2000 （2）0。

有理数乘除法及乘方运算(较难)

有理数乘法及乘方练习题一、填空题1、我市六月份连续五天的日最高气温（单位：）分别为35，33，37，34，39，则我市这五天的日最高气温的平均值为.2、我们规定一种运算法则“※”，对任意两个有理数a、b，有a※b＝2a＋6．若有理数x满足(2x＋1)※(－4)＝5※(3－x)，则x＝．3、若“!”是一种数学运算符号，并且1!＝1，2!＝2×1＝2，3!＝3×2×1＝6，4!＝4×3×2×1=24，……则÷99的值为________。

4、若与互为相反数，、互为倒数，则的值为 .5、若的相反数是2，则的值是 .6、已知A=a+ a2+ a3+……+ a2000若a=1,则A= ，若a=-1，则A= ，7、若+(b+4)=0,则b a=________.8、已知：，，，…若（、为正整数），则；9、若，那么= ，=10、我们知道，，，，，……那么：=___________．利用上面规律解答下面问题：算一算：=___________．二、选择题11、若( )×(-2)＝1，则括号内填一个实数应该是 ( )A. B.2 C.-2 D.-12、按100分制60分及格来算，满分是150分的及格分是（）A.60分B.72分C.90分D.105分13、若|a+b+1|与（a-b+1）2互为相反数，则a与b的大小关系是（）A．a＞b B．a=b C．a＜b D．a≥b三、简答题14、观察下面的变形规律：=1﹣；=﹣；=﹣；…解答下面的问题：（1）若n为正整数，请你猜想= ；（2）证明你猜想的结论；（3）求和：+++…+．15、有若干个数，第一个数记为a1，第二个数记为a2，…，第n个数记为a n。

若a1=，从第二个数起，每个数都等于“1与它前面那个数的差的倒数”。

试计算：a2=______，a3=____，a4=_____，a5=______。

有理数的加减乘除乘方混合运算专题训练(带答案)

有理数的加减乘除乘方混合运算专题训练(带答案)1）+（－3）×2答案：20改写：先做除法，再乘法和乘法，最后加减。

18-3*2*(-1)-6/(-2)=202）（－3）²+1/2÷（－2/3）×（－6/5）答案：8/5改写：先做除法，再乘法和乘法，最后加减。

(-3)^2+1/2/(-2/3)*(-6/5)=8/53）（－1/2）²－（－2/3）³×（－3/4）²－2/5答案：-49/144改写：同级运算，从左到右进行。

(-1/2)^2-(-2/3)^3*(-3/4)^2-2/5=-49/1444）（－1/2）²×（－2/3）³÷（－3/4）²－2/5答案：-25/162改写：先做乘方，再做乘除法，最后加减。

(-1/2)^2*(-2/3)^3/(-3/4)^2-2/5=-25/1625）（－5）×6＋（－125）÷（－5）³答案：-24改写：先做除法，再乘法和乘法，最后加减。

-5*6+(-125)/(-5)^3=-246）（－4）²÷（－2/3）³×（－3/4）²－2/5答案：-51/4改写：先做乘方，再做乘除法，最后加减。

(-4)^2/(-2/3)^3*(-3/4)^2-2/5=-51/47）（－7）÷6－（－5）÷（－12）²答案：-191/216改写：先做乘方，再做除法，最后加减。

-7/6-(-5)/(-12)^2=-191/2168）（－81）÷（－2.25）×（－1）÷16答案：9/8改写：先做乘除法，最后加减。

(-81)/(-2.25)*(-1)/16=9/89）（－1/4）²－2/3×（－6/5）³答案：-217/200改写：先做乘方，再做乘除法，最后加减。

有理数的加减乘除乘方混合运算专题训练(带答案)

1.先乘方,再乘除,最后加减；之樊仲川亿创作3. 同级运算,从左到右进行；4.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷ 3、11(22)3(11)+--⨯- 4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、33102(4)8-÷--7、)]21)21[(122--÷8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯--10、23533||()14714-⨯-÷11、—22—(—2)2—23+(—2)3 12、2223116(1)(3)(1)(3)22-⨯---÷-⨯-13、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、－10 + 8÷(－2 )2－(－4 )×(－3 ) 16、－49 + 2×(－3 )2 + (－6 )÷(－91)17、－14 + ( 1－0.5 )×31×[2×(－3)2] 18、(－2)2－2×[(－21)2－3×43]÷51．19、)8()4()6(52-÷---⨯20、0)132()43(2⨯+-+- 21、6)12()4365127(÷-⨯+-22、22)4()5(25.0)4()85(-⨯-⨯--⨯-23、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6－（－12）÷2)2(- 26、（-48）÷ 8 －（-5）÷2)21(- 27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯-30、(－5)×6＋(－125) ÷(－5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算：（1）618－÷）（－）（－312⨯；（2））（－＋51232⨯；（3））（－）（－49⨯＋）（－60÷12；（4）23）（－×[ ）＋（－－9532 ]. （1））（－）＋（－2382⨯；（2）100÷22）（－－）（－2÷）（－32；（3））（－4÷）（－）（－343⨯；（4））（－31÷231）（－－3214）（－⨯. （1）36×23121）－（；（2）12.7÷）（－1980⨯；（3）6342＋）（－⨯；（4））（－43×）－＋（－31328；（5）1323－）（－÷）（－21；（6）320－÷34）（－81－；（7）236.15.02）－（－）（－⨯÷22）（－；（8））（－23×[ 2322－）（－ ]；（9）[ 2253）－（－）（－ ]÷）（－2；（10）16÷）（－）－（－）（－48123⨯. （1）11＋（－22）－3×（－11）；（2）0313243⨯⨯）－（－）（－；（3）2332－）（－；（4）23÷[ ）－（－）（－423]；（5））－（8743÷）（－87；（6））＋（）（－654360⨯；（7）－27+2×()23-+（－6）÷()231-；（8））（－）－＋－（－4151275420361⨯⨯. （1））－（－258÷）（－5；（2）－33121）（－－⨯；（3）223232）－（－）（－⨯⨯；（4）0132432⨯⨯）＋（－）（－；（5））（－＋51262⨯；（6）－10＋8÷()22-－4×3；（7）－51－()()[]55.24.0-⨯-；（8）()251-－（1－0.5）×31；（1）（－8）×5－40；（2）（-1.2）÷（-13）-（-2）；（3）-20÷5×14+5×（-3）÷15；（4）-3[-5+（1-0.2÷35）÷（-2）]；（5）－23÷153×（-131）2÷（132）2；（6）－52＋(1276185+-)×(－2.4) 参考答案1、-1/52、-13、224、95、96、 07、-48 8、-1 9、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-2016、23 17、2 18、24 19、-28 20、9/1621、1 22、10 23、-1/12 24、104/3 25、926、1427、-3128、-81又1/81 29、-9 30、-29 31、-1/5 32、9 1、【答案】（1）17；（2）511；（3）31；（4）－11 2、【答案】（1）－10；（2）22；（3）－16；（4）－25 3、【答案】（1）1；（2）0；（3）42；（4）423；（5）18；（6）0；（7）－4.64；（8）37；（9）8；（10）－25.4、【答案】（1）22；（2）0；（3）－17；（4）－423；（5）71；（6）－95；（7）－85；（8）6 .5、【答案】（1）3；（2）1；（3）－54；（4）0；（5）526；（6）－20；（7）－2；（8）－67.6、【答案】（1）－80；（2）5.6；（3）－2；（4）16；（5）－516；（6）－2.9温习有理数的乘除、乘方运算测试题一、填空题（每小题3分,共30分） 1．3×（－2）=________,（－6）×（－31）=________． 2．（－3）2的底数是________,结果是________；－32的底数是________,结果是________．3．（－61）÷（+23）=________；－493÷（－176）=________；（+8）÷（－41）=________． 4．23×（－41）3=________；（－91）÷（+34）2=________．5．（－32）×________=1；（－32）×________=－16．－65×（－2．4）×（－53）=________．7．－32×（－5）2÷（－21）3=________．8．我国台湾省的面积约为3600平方千米,用科学记数法暗示为________． 9．+121的倒数是________；________的倒数是－54． 10．用“＞”“＜”填空： ①23________22②（21）2________（21）3 ③32________22④（－2）3________（－2）2二、判断题（每小题1分,共5分） 11．零除以任何数都得零（）12．互为相反数的两个数的积为正数（） 13．如果ab ＞0,则a ＞0且b ＞0（）14．1除以一个非零数的商叫做这个数的倒数（） 15．（－3）5暗示5个－3相乘（）三、选择题（每小题3分,共21分） 16．下列说法,其中错误的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘,符号不变．A ．1个B ．2个C ．3个D ．4个17．下列各对数：①1与1；②－1与1；③a －b 与b －a ；④－1与－1；⑤－5与|6|,其中互为倒数的是A ．①②③B ．①③⑤C ．①③④D ．①④ 18．下列各题中两个式子的值相等的是A ．－23与（－2）3B ．32与23C ．（－2）2与－22D ．|－2|与－|－2| 19．下列结论中,其中正确的个数为①0的倒数是0；②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数等于自身的数是±1；④若a,b 互为倒数,则－ab=－1．A ．4B ．3C ．2D ．1 20．下列各式中结果大于0的是 A ．1－910×3 B ．（1－910）×3 C ．1－（9×3）10 D ．（1－9）10×3 21．下列说法中正确的是 A ．一个数的平方必为正数B ．一个数的平方必小于这个数的绝对值C ．一个数的平方必大于这个数D ．一个数的平方不成能为正数22．用科学记数法暗示的数2．89×104,原来是 A ．2890 B ．2890000 C ．28900 D ．289000 四、计算题（共35分）23．（3分）（－3）×（－5）×（+12）×（－21） 24．（3分）－6÷（+3）÷（－4）×（+2） 25．（3分）－5－6÷（－3）26．（3分）（－81）÷241×91÷（－16） 27．（3分）－22×（－3）÷5428．（3分）（－1）2000×（－1）2001×（－1）2002÷（－1）200329．（3分）（－2）×（－2001）×［－21－（－21）］×1－2002 30．（3分）－)45()45(5222-÷-⨯⨯ 31．（3分）（－5）2÷5×632．（3分）（－2.5）÷（－310）×（－3） 33．（5分）30×（21－31+53－109）五、解答题（9分）34．已知A=a+a2+a3+……+a2000 （1）若a=1,求A 的值．（2）若a=－1,求A 的值．参考答案一、1．－6 2 2．－3 9 3 －9 3．－91913－32 4．－81 －161 5．－2323 6．－1.2 7．1800 8．3.6×103平方千米 9．32 －14110．＞＞＞＜二、11．× 12．× 13．× 14．√ 15．√三、16．A 17．D 18．A 19．B 20．D 21．D 22．C 四、23．－90 24．1 25．－3 26．4127．15 28．1 29．－2002 30．1 31．30 32．－4933．－4。

有理数的乘、除、乘方、混合运算习题

有理数的乘法、除法、乘方练习一、有理数的乘法运算法则：（一）没有0因数相乘的情况下：1、由负因数的个数确定符号----------+⎧⎨⎩奇数（如1，3，5，）个负因数,积为“—”偶数（如2，4，6，）个负因数，积为“”，可省略，再把绝对值相乘---------- （二）有一个以上的0因数相乘，积为0（三）适用的运算律： 1.2.()3.()a b b a a b c a b c a b c d a b a c a d ⨯=⨯⎧⎪⨯⨯=⨯⨯⎨⎪ ⨯+-=⨯+⨯-⨯⎩（四）策略：在有理数的乘、除中，碰到小数就，碰到带分数就练习：1、（–4）×（–9）= 2、（–52）×81 = 3、（–253）×135=4、（–12）×2.45×0×9×1005、10.12512(16)(2)2-⨯⨯-⨯- 6、（-6）×（-4）－（-5）×107、（0.7－103－254+ 0.03）×（－100） 8、（–11）×52+（–11）×953二、有理数的倒数：（一）定义：如，则称a 与b 互为倒数；其中一个是另一个的倒数。

（二）几种情况下的倒数：1、整数：2的倒数是；12-的倒数是；0没有倒数2、分数：12的倒数是；23-的倒数是；112的倒数是；223-的倒数是；发现：求倒数时，碰到带分数，必须化为3、小数：0.25的倒数是； 1.125-的倒数是；发现：求倒数时，碰到小数，必须化为，练习：求下列各数的倒数： 4.25-是 235是 1.14-是三、有理数的除法法则：(a b a b ÷=⨯的）即看到除法，就转化为练习：1、（－18）÷（－9）2、－3÷（－31） 3、0÷（–105） 4、（－2）÷（－1.5）×（－3）5、－0.2÷（-151）×（－261） 6、[65÷(－21－31)+281]÷(－181)四、乘方：（一）在n a 中，a 称为；n 称为；n a 称为。

初一数学有理数的加减乘除以及乘方试题答案及解析

初一数学有理数的加减乘除以及乘方试题答案及解析1.“十二五”期间，我国将新建保障性住房36 000 000套，用于解决中低收入人群和新参加工作的大学生住房的需求，将36 000 000用科学记数法表示应是（）A．B．C．D．【答案】A.【解析】科学计数法的定义：将一个数字表示成（×10的n次幂的形式），其中1≤＜10，n表示整数.对于10的指数大于0的情形，数出“除了第一位以外的数位”的个数，即代表0的个数；本题中第一个数为3,3后面有7位数.故选A．【考点】科学计数法．2.若正整数使得在计算的过程中，各数位均不产生进位现象，则称为“本位数”．例如：2和30是“本位数”，而5和91不是“本位数”．在不超过100的所有本位数中，全体奇数的和为 .【答案】64.【解析】先确定出所有大于0且小于100的“本位数”，再确定奇数后，再求和.试题解析：所有大于0且小于100的“本位数”有：1、2、10、11、12、20、21、22、30、31、32共有11个，但奇数只有：1，11，21，31四个，故和为1+11+21+31=64.【考点】有理数的概念与运算.3.（）A．2B．C．D．【答案】B.【解析】.故选B.考点: 1.负整数指数幂；2.积的乘方.4.如果a－3与a+1互为相反数，那么a＝ .【答案】1【解析】若a－3与a+1互为相反数，则a－3+a+1＝0，解得a＝1.5.计算（－2.5）×0.37×1.25×（－4）×（－8）=_________.【答案】-37【解析】原式=[(－2.5)×(－4)]×[1.25×(－8)]×0.37=10×(－10)×0.37=－37.6.已知：且，求的值.【答案】-125【解析】解：因为=3，所以=±3.因为=2，所以=±2.又因为，所以=－3，=±2.所以或.7.某股民上周五收盘时买进某公司股票1000股，每股27元.股票交易时间是周一到周五上午9：30-11:30，下午1：00-3：00. 下表为本周内每日股票的涨跌情况：（单价：元）星期一二三四五（1）根据上表填空：星期三收盘时，每股是元；本周内最高价是每股元，最低价是每股元；（2）已知该股民买进股票时付了0.15％的手续费，卖出时需付成交额0.15％的手续费和0.1％的交易税，如果他一直观望到星期五收盘时才将股票全部卖出，请算算他本周的收益如何.【答案】（1）34.5，35.5，28；（2）889.5元．【解析】（1）先根据题意列出式子解出结果即可；（2）先算出刚买股票后去掉手续费剩余的钱是多少，然后再算出周五卖出股票后所剩的钱，最后再减去当时的钱，剩下的钱就是所收益的．试题解析：（1）根据题意得：每股价（元）；最高价（元）；最低价（元）.（2）∵27×1000×（1+0.15%）=27000×（1+0.15%）=27040.5（元），28×1000-28×1000×0.15%-28×1000×0.1%=28000-28000×0.15%-28000×0.1%=28000-42-28=27930（元），∴他本周的收益为27930-27040.5=889.5（元）【考点】有理数的混合运算．8.已知，，则、、按从小到大的顺序排列为（）A．B．C．D．【答案】B.【解析】∵，，∴，，∴．故选B．【考点】有理数大小比较．9.如果三个有理数的积是负数，那么这三个有理数中（）.A．只有一个负数B．有两个负数C．三个都是负数D．有一个或三个负数【答案】D【解析】几个不相等0的数相乘，积得符号由负因数的个数决定，当负因数有奇数个时，积为负，当负因数有偶数个时，积为正.解：如果三个有理数的积是负数，那么这三个有理数中有一个或三个负数，故选D.【考点】有理数乘法的符号法则点评：本题属于基础应用题，只需学生熟练掌握有理数乘法的符号法则，即可完成.10.有理数0.0050400的有效数字的个数是（）.A．3个B．4个C．5个D．6个【答案】C【解析】有效数字是从左边第一个不是0的数字起，后面所有的数字都是有效数字．解：有理数0.0050400的有效数字有5、0、4、0、0这5个，故选C.【考点】近似数和有效数字点评：本题是基础应用题，只需学生熟练掌握有效数字的定义，即可完成.11.计算：（1）（2）（3）【答案】（1）；（2）；（3）【解析】（1）先算有理数的乘方，再算加减即可；（2）先算幂的乘方、同底数幂的乘法，再合并同类项即可；（3）先根据完全平方公式、多项式乘多项式法则去括号，再合并同类项即可.（1）原式；（2）原式；（3）原式.【考点】有理数的乘方，整式的化简点评：计算题是中考必考题，一般难度不大，学生要特别慎重，尽量不在计算上失分.12.经专家估算，整个南海属我国传统海疆线的油气资源约合15000亿美元，开采前景甚至要超过英国的北海油田，用科学记数法表示15000亿美元是【】美元．A．1.5×104B．1.5×105C．1.5×1012D．1.5×1013【答案】C【解析】科学记数法的表示形式为，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．15000亿，故选C.【考点】科学记数法的表示方法点评：本题属于基础应用题，只需学生熟练掌握科学记数法的表示方法，即可完成.13.（1）；（2）解方程：【答案】（1）101；（2）【解析】（1）有理数的混合运算的顺序：先算乘方，再算乘除，最后算加减，同级运算按从左向右的顺序依次计算；有括号的先算括号里的.同时注意运算过程中可以运用运算律计算的要运用运算律简化计算；（2）解一元一次方程的一般步骤：去分母，去括号，移项，合并同类项，系数化为1（1）；（2）.【考点】有理数的混合运算，解一元一次方程点评：有理数的混合运算及解方程是中考必考题，一般难度不大，要特别慎重，尽量不在计算上失分.14.在，，，这四个数中，最大的数比最小的数要大A．13B．10C．8D．5【答案】A【解析】先根据有理数的乘方法则计算出各个数的值，再用最大的数减最小的数即可.∵=-1，=1，=-4，=9∴最大的数比最小的数要大故选A.【考点】有理数的乘方，有理数的减法点评：解题的关键是熟记正数的任何次幂均为正数，负数的奇数次幂为负，负数的偶数次幂为正.15.若x＝（－4），则x=【答案】±4【解析】先计算出（－4）＝16，再根据有理数的乘方法则即可求得结果.x＝（－4）x＝16x＝±4.【考点】有理数的乘方点评：解题的关键是熟练掌握互为相反数的两个数的平方相同.16.据科学家估计，地球的年龄大约是4600000000年，这个数用科学记数法表示为A．4.6×108B．46×108C．4.6×109D．0.46×1010【答案】C【解析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．有效数字的计算方法是：从左边第一个不是0的开始，后面所有的数都是有效数字．所以4600000000=4.6×109【考点】科学计数法点评：任何一个数都可以用科学记数法表示成a×10n（1≤|a|＜10，n是整数）的形式，表示时关键要正确确定a的值以及n的值17.计算：（1）－2＋6÷(－2)×；（2）（－2）3－(1－)×．【答案】（1）－；（2）－12【解析】有理数的混合运算的顺序：先算乘方，再算乘除，最后算加减，同级运算按从左向右的顺序依次计算；有括号的先算括号里的.同时注意运算过程中可以运用运算律计算的要运用运算律简化计算.（1）原式=－2＋6×(－)×=－2－=－；（2）原式=－8－×6=－8－4=－12.【考点】有理数的混合运算点评：本题属于基础应用题，只需学生熟练掌握有理数的混合运算，即可完成.18.下列式子中，正确的是A．5－|－5|=10B．(－1)99= －99C．－102 = (－10)×(－10)D．－(－22)=4【答案】D【解析】解：A中，5－|－5|=0B中，(－1)99= －1C中，－102 = -100，故不选D中，正确故选D【考点】绝对值，平方的符号点评：负数的绝对值是其相反数，正数的绝对值是其本身。

初一数学有理数的加减乘除以及乘方试题答案及解析

初一数学有理数的加减乘除以及乘方试题答案及解析1.有一种原子的直径为0.000000503米，它用科学记数法表示为____________米。

【答案】5.03×10-7【解析】解：将0.000000503用科学记数法表示为5.03×10-7；故答案为5.03×10-7【考点】科学记数法—表示较小的数2. PM2.5是指大气中直径小于或等于2.5（0.0000025）的颗粒物，含有大量有毒、有害物质，也称可入肺颗粒物．将0.0000025用科学记数法表示为A．B．C．D．【答案】D.【解析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．所以：0.0000025表示为：.故选D.【考点】科学记数法——表示较小的数.3.计算：= ．【答案】.【解析】针对负整数指数幂，零指数幂2个考点分别进行计算，然后根据实数的运算法则求得计算结果：.【考点】1.负整数指数幂；2.零指数幂.4.计算2-（-3）的结果是（）A．-5B．5C．-1D．1【答案】B【解析】有理数的减法法则：减去一个数等于加上这个数的相反数本题是对有理数减法的考查，减去一个数等于加上它的相反数．解：2-（-3）=2+3=5．【考点】有理数的减法．5.已知在0摄氏度及一个标准大气压下1cm3空气的质量是0.001293克，数0.001293用科学计数法表示为__________ .【答案】.【解析】用科学记数法表示绝对值小于的数，只要将小数定向右移到第一个不为零的数后，若共移动位，则最后乘以即可，如本题中向右移了位，变为，在后乘以，最后.【考点】科学记数法.6.有一组等式：请观察它们的构成规律，用你发现的规律解答下面的问题：（1）写出第8个等式为；（2）试用含正整数的等式表示你所发现的规律；（3）说明你在（2）中所写等式成立的理由．【答案】（1）82+92+722=732；（2）（n为正整数）（3）证明见解析.【解析】（1）观察不难发现，两个连续自然数的平方和加上它们积的平方，等于比它们的积大1的数的平方，然后写出即可．（2）找到规律后，即可用含有n的等式来表示规律；（3）证明左边=右边即可.试题解析：（1）∵12+22+22=32，22+32+62=72，32+42+122=132，42+52+202=212，…，∴第8个等式为：82+92+（8×9）2=（8×9+1）2，即82+92+722=732（2）（n为正整数）（3）理由：∵∴即：∴（2）中的等式成立.【考点】规律型：数字的变化类.7.如下数表是由从1开始的连续自然数组成，则自然数2014所在的行数是A．第45行B．第46行C．第47行D．第48行【答案】A．【解析】由数列知第n行第一个数为（n-1）2+1，第n行最后一个数为n2,而：1937＜2014＜2025即（45-1）2＜2014＜452所以：n=45．故选A．【考点】数字变化规律．8.在一次水灾中，大约有个人无家可归，假如一顶帐篷占地100米，可以放置40个床位(一人一床位)，为了安置所有无家可归的人，需要多少顶帐篷？这些帐篷大约要占多少地方？若某广场面积为5000米2。

有理数的加减乘除乘方混合运算专题训练带答案

1. 先乘方，再乘除，最后加减；2. 同级运算，从左到右进行；3. 如有括号，先做括号的运算，按小括号、中括号、大括号依次进行。

1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷3、11(22)3(11)+--⨯-4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、 33102(4)8-÷--7、)]21)21[(122--÷ 8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯-- 10、23533||()14714-⨯-÷22231113、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、－10 + 8÷(－2 )2 －(－4 )×(－3 ) 16、－49 + 2×(－3 )2 + (－6 )÷(－91)17、－14 + ( 1－0.5 )×31×[2×(－3)2] 18、(－2)2－2×[(－21)2－3×43]÷51．19、)8()4()6(52-÷---⨯ 20、0)132()43(2⨯+-+-35722523、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6－（－12）÷2)2(- 26、（-48）÷ 8 －（-5）÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯- 30、(－5)×6＋(－125) ÷(－5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算：（1）618－÷）（－）（－312⨯；（2））（－＋51232⨯；（3））（－）（－49⨯＋）（－60÷12；（4）23）（－×[ ）＋（－－9532 ].（1））（－）＋（－2382⨯；（2）100÷22）（－－）（－2÷）（－32；（3））（－4÷）（－）（－343⨯；（4））（－31÷231）（－－3214）（－⨯.（1）36×23121）－（；（2）12.7÷）（－1980⨯；（3）6342＋）（－⨯；（4））（－43×）－＋（－31328；（5）1323－）（－÷）（－21；（6）320－÷34）（－81－；（7）236.15.02）－（－）（－⨯÷22）（－；（8））（－23×[ 2322－）（－ ]；（9）[ 2253）－（－）（－ ]÷）（－2；（10）16÷）（－）－（－）（－48123⨯.（1）11＋（－22）－3×（－11）；（2）0313243⨯⨯）－（－）（－；（3）2332－）（－；（4）23÷[ ）－（－）（－423]；（5））－（8743÷）（－87；（6））＋（）（－654360⨯；（7）－27+2×()23-+（－6）÷()231-；（8））（－）－＋－（－4151275420361⨯⨯.（1））－（－258÷）（－5；（2）－33121）（－－⨯；（3）223232）－（－）（－⨯⨯；（4）0132432⨯⨯）＋（－）（－；（5））（－＋51262⨯；（6）－10＋8÷()22-－4×3；（7）－51－()()[]55.24.0-⨯-；（8）()251-－（1－0.5）×31；（1）（－8）×5－40；（2）（-1.2）÷（-13）-（-2）；（3）-20÷5×14+5×（-3）÷15；（4）-3[-5+（1-0.2÷35）÷（-2）]；（5）－23÷153×（-131）2÷（132）2；（6）－52＋(1276185+-)×(－2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】（1）17；（2）511；（3）31；（4）－11 2、【答案】（1）－10；（2）22；（3）－16；（4）－25 3、【答案】（1）1；（2）0；（3）42；（4）423；（5）18；（6）0；（7）－4.64；（8）37；（9）8；（10）－25. 4、【答案】（1）22；（2）0；（3）－17；（4）－423；（5）71；（6）－95；（7）－85；（8）6 .5、【答案】（1）3；（2）1；（3）－54；（4）0；（5）526；（6）－20；（7）－2；（8）－67. 6、【答案】（1）－80；（2）5.6；（3）－2；（4）16；（5）－516；（6）－2.9复习有理数的乘除、乘方运算测试题一、填空题（每小题3分，共30分） 1．3×（－2）=________，（－6）×（－31）=________． 2．（－3）2的底数是________，结果是________；－32的底数是________，结果是________．3．（－61）÷（+23）=________；－493÷（－176）=________；（+8）÷（－41）=________．4．23×（－41）3=________；（－91）÷（+34）2=________． 5．（－32）×________=1；（－32）×________=－16．－65×（－2．4）×（－53）=________．7．－32×（－5）2÷（－21）3=________．8．我国省的面积约为3600平方公里，用科学记数法表示为________． 9．+121的倒数是________；________的倒数是－54． 10．用“＞”“＜”填空： ①23________22 ②（21）2________（21）3 ③32________22 ④（－2）3________（－2）2二、判断题（每小题1分，共5分） 11．零除以任何数都得零（）12．互为相反数的两个数的积为负数（） 13．如果ab ＞0，则a ＞0且b ＞0（）14．1除以一个非零数的商叫做这个数的倒数（） 15．（－3）5表示5个－3相乘（）三、选择题（每小题3分，共21分） 16．下列说法，其中错误的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘，符号不变．A ．1个B ．2个C ．3个D ．4个17．下列各对数：①1与1；②－1与1；③a －b 与b －a ；④－1与－1；⑤－5与|6|，其中互为倒数的是A ．①②③B ．①③⑤C ．①③④D ．①④18．下列各题中两个式子的值相等的是A ．－23与（－2）3B ．32与23C ．（－2）2与－22D ．|－2|与－|－2| 19．下列结论中，其中正确的个数为①0的倒数是0；②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数等于自身的数是±1；④若a ，b 互为倒数，则－ab=－1．A ．4B ．3C ．2D ．1 20．下列各式中结果大于0的是 A ．1－910×3 B ．（1－910）×3C ．1－（9×3）10D ．（1－9）10×3 21．下列说法中正确的是 A ．一个数的平方必为正数B ．一个数的平方必小于这个数的绝对值C ．一个数的平方必大于这个数D ．一个数的平方不可能为负数22．用科学记数法表示的数2．89×104，原来是 A ．2890 B ．2890000 C ．28900 D ．289000四、计算题（共35分）23．（3分）（－3）×（－5）×（+12）×（－21） 24．（3分）－6÷（+3）÷（－4）×（+2） 25．（3分）－5－6÷（－3）26．（3分）（－81）÷241×91÷（－16）27．（3分）－22×（－3）÷5428．（3分）（－1）2000×（－1）2001×（－1）2002÷（－1）200329．（3分）（－2）×（－2001）×［－21－（－21）］×1－200230．（3分）－)45()45(5222-÷-⨯⨯31．（3分）（－5）2÷5×632．（3分）（－2.5）÷（－310）×（－3）33．（5分）30×（21－31+53－109）五、解答题（9分）34．已知A=a+a 2+a 3+……+a 2000（1）若a =1，求A 的值．（2）若a =－1，求A 的值．参考答案一、1．－6 2 2．－3 9 3 －9 3．－91 913 －32 4．－81 －161 5．－23 23 6．－1.2 7．1800 8．3.6×103平方公里 9．32 －141 10．＞＞＞＜二、11．× 12．× 13．× 14．√ 15．√三、16．A 17．D 18．A 19．B 20．D 21．D 22．C四、23．－90 24．1 25．－3 26．41 27．15 28．1 29．－2002 30．1 31．30 32．－49 33．－4 五、34．（1）2000 （2）0。

七年级上册数学有理数乘除法练习题

七年级上册数学有理数乘除法练习题
1. 将下列各数的绝对值写出来：
a) -6 b) 3 c) -9 d) 0
2. 计算下列各题的积或商：
a) (-2) × (4) b) (-5) ÷ (-1) c) 18 ÷ (3) d) (-8) × (-
6)
3. 将下列各题填入适当的符号（>, <, =）使等式成立：
a) (-9) __ (-5) b) (-7) __ (-10) c) (-2) __ (-2) d) (-3) __ (-2)
4. 编写一个算式，只使用以下数的绝对值：3, 6, 9, 12
5. 根据所给的数，找到一个相反数和绝对值都相同的数：
a) 4 b) -8 c) -1
6. 如果可行，请找到两个数，其中一个的相反数等于另一个数的倒数，总和为0：
7. 判断下列各式是否正确，正确的用"√"标注，错误的用"×"标注：
a) (-1) × (-5) = 5 b) 3 × (-8) = (-24) c) (-6) ÷ 2 = 3
8. 电影院票价为35元，小明购买了5张电影票，他支付了多
少钱？
9. 一个工人每小时赚20元，他工作了8个小时，他一共赚了
多少钱？
10. 某商品原价100元，打了8折后出售，现在的价格是多少？。

初一数学有理数的加减乘除以及乘方试题

初一数学有理数的加减乘除以及乘方试题1.计算：= ．【答案】-1．【解析】原式=．【考点】平方差公式．2.若规定，则的值为 .【答案】-9【解析】.3.如果，则的值是（）A．4B．－2C．4或－2D．－4或2【答案】C【解析】由，得或，所以或.故选C.4.下列说法中正确的有（）①同号两数相乘，符号不变；②异号两数相乘，积取负号；③互为相反数的两数相乘，积一定为负；④两个有理数的积的绝对值，等于这两个有理数的绝对值的积．A．1个B．2个C．3个D．4个【答案】B【解析】①错误，如，符号改变; ③错误，如0×0，积为0；②④正确.5.计算=______.【答案】-4【解析】6.计算：；【答案】【解析】先根据有理数的除法法则统一为乘，再根据有理数的乘法法则计算，最后算减即可得到结果.解：原式.【考点】有理数的混合运算点评：计算题是中考必考题，一般难度不大，学生要特别慎重，尽量不在计算上失分.7.有一种原子的直径约为0.00000053米, 用科学记数法表示为 .【答案】5.3×10-7【解析】较小的数的科学记数法的一般形式为：a×10-n，在本题中a应为5.3，10的指数为-7．0.000 000 53=5.3×10-7．【考点】科学计数法点评：本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．8.计算：.【答案】13【解析】原式【考点】简单有理数的混合运算点评：本题难度不大，考查的是学生对于有理数的混合运算的掌握，先进行乘除的运算，再进行加减的运算9.计算：2+（－3）的结果是（）A．－1B．1C．－5D．5【答案】A【解析】2+（－3）去括号得2-3=-1.【考点】实数运算点评：本题难度较低，主要考查学生对实数的运算学习。

10.计算：（4分×2=8分）(1).14-（-12）+（-25）-7 (2).（－+－）×12+（－1）2011【答案】①②-12.5【解析】（1）14-（-12）+（-25）-7=14+12-25=-6（2）（－+－）×12+（－1）2011=【考点】代数式的运算点评：代数式的运算中，通分和化简是其中的重中之重，要学会很好的去区分11.）下列叙述中，出现近似数的是A．七年级（4）班有40名学生B．小李买了5支铅笔C．晶晶向希望工程捐款100元D．小明的体重为46千克【答案】D【解析】A、B、C都是确切数字，只有D是大约的数字，即近似数。

初一数学有理数的加减乘除以及乘方试题

初一数学有理数的加减乘除以及乘方试题1.计算；（1）（2）（-）2007×1.52008×（－1）2008【答案】（1）0 （2）-【解析】有理指数幂运算，注意负指数幂.（1）原式==4+1-5=0（2）原式=（-）2007×（）2008×1=（-）2007×（）2007×=（-×）2007×=(-1)2007×=-【考点】指数幂运算.2.月球距离地球约为3.84×105千米，一架飞机速度为8×102千米/时，•若坐飞机飞行这么远的距离需 _________ 小时【答案】4.8×102.【解析】先根据时间=路程÷速度，算出时间为（3.84×105）÷（8×102），利用单项式除单项式的法则计算，然后再按照科学记数法的方法的形式表示即可．试题解析：依题意得（3.84×105）÷（8×102），=0.48×103=4.8×102（小时）．∴坐飞机飞行这么远的距离需4.8×102小时．考点: 1.整式的除法；2科学记数法—表示较大的数．3.李强靠勤工俭学的收入维持上大学费用，表中是李强某一周的收支情况表，记收入为正，支出为负（单位：元）：星期一二三四五六日（2）照这个情况估计，李强一个月（按30天计算）能有多少节余？（3）按以上的支出水平，李强一个月（按30天计算）至少有多少收入才能维持正常开支？【答案】（1）到这个周末，李强有14元节余.（2）照这个情况估计，李强一个月（按30天计算）能有60元节余.（3）按以上的支出水平，李强一个月（按30天计算）至少有360元收入才能维持正常开支.【解析】分析：（1）七天的收入总和减去支出总和即可；（2）首先计算出平均一天的节余，然后乘30即可；（3）计算出这7天支出的平均数，即可作为一个月中每天的支出，乘30即可求得．解：（1）由题意可得：（元）.（2）由题意得：14÷7×30=60（元）.（3）根据题意得：10+14+13+8+10+14+15=84，84÷7×30=360（元）．答：（1）到这个周末，李强有14元节余.（2）照这个情况估计，李强一个月（按30天计算）能有60元节余.（3）按以上的支出水平，李强一个月（按30天计算）至少有360元收入才能维持正常开支.4.（1）|﹣4|﹣（﹣2）2+（﹣1）2011﹣1÷2；（2）（﹣2）2+3×（﹣2）﹣1÷（）2．【答案】（1）﹣1（2）﹣18【解析】（1）根据运算顺序先算乘方运算，（﹣2）2表示两个﹣2的乘积，（﹣1）2011表示2011个﹣1的乘积，其结果为﹣1，同时根据负数的绝对值等于它的相反数化简原式的第一项，根据互为相反数的两数和为0化简，然后利用同号两数相加的法则即可得到结果；（2）根据运算顺序先算乘方运算，（﹣2）2表示两个﹣2的乘积，（）2表示两个的乘积，然后利用除以一个数等于乘以这个数的倒数把除法运算化为乘法运算，利用两数相乘，同号得正、异号得负，并把绝对值相乘来计算乘法运算，利用减法法则：减去一个数等于加上这个数的相反数把减法运算化为加法运算，利用同号及异号两数相加的法则即可得到结果．解：（1）|﹣4|﹣（﹣2）2+（﹣1）2011﹣1÷2=4﹣4+（﹣1）﹣=﹣1+（﹣）=﹣1；（2）（﹣2）2+3×（﹣2）﹣1÷（）2=4+（﹣6）﹣1÷=4+（﹣6）﹣1×16=4+（﹣6）+（﹣16）=4+（﹣22）=﹣18．点评：此题考查了有理数的混合运算，有理数的混合运算首先弄清运算顺序：先乘方，再乘除，最后算加减，有括号先算括号里边的，然后利用各种运算法则进行计算，有时可以利用运算律来简化运算，注意（﹣2）2与﹣22的区别，前者表示两个﹣2的乘积，后者表示2平方的相反数．5.2003年10月15日，航天英雄杨利伟乘坐“神舟五号”载人飞船，于9时9分50秒准确进入预定轨道，开始巡天飞行.飞船绕地球飞行了十四圈后，返回舱与推进舱于16日5时59分分离，结束巡天飞行.飞船共用了20小时49分10秒，巡天飞行了约6×105千米，则“神舟五号”飞船巡天飞行的平均速度约为________千米／秒.（结果精确到0.1）【答案】8.0【解析】仔细分析题意，再根据平均速度=总里程÷总时间列式计算即可.解：10月15日9时50秒到16日5时59分期间共有20小时50分10秒，共计75 010秒．6×105÷75 010=7.99千米/秒≈8.0千米/秒．答：“神舟五号”飞船巡天飞行的平均速度是8.0千米/秒．【考点】有理数的除法的应用点评：计算题是中考必考题，一般难度不大，学生要特别慎重，尽量不在计算上失分.6.计算：（1）；（2）【答案】（1）；（2）1【解析】（1）先根据积的乘方、幂的乘方法则化简，再算同底数幂的乘法，最后合并同类项；（2）先根据有理数的乘方法则计算，再算加减即可.（1）原式；（2）原式.【考点】整式的混合运算，实数的运算点评：计算题是中考必考题，一般难度不大，要特别慎重，尽量不在计算上失分.7.用“＜”号，将、、、连接起来______【答案】【解析】先根据有理数的乘方法则依次计算出各个数的值，再根据有理数的大小比较法则比较. ∵，，，∴.【考点】有理数的乘方点评：计算题是中考必考题，一般难度不大，要特别慎重，尽量不在计算上失分.8.今年3月26日20：30至21：30，在参与“地球一小时”活动中，南京全城节约用电约10万度．约可以减少二氧化碳排放量99700千克，这个排放量用科学记数法表示为千克．【答案】9.97´104【解析】99700有效数字为9.97.小数点向左移动4位。

[苏教版七年级第一章有理数的乘除、乘方测试题(含答案)] 有理数乘方

[苏教版七年级第一章有理数的乘除、乘方测试题（含答案）] 有理数乘方苏教版七年级第一章有理数的乘除、乘方测试题（含答案）一、填空题（每小题3分，共30分）1．3×（－2）=________，（－6）×（－）=________．2．（－3）2的底数是________，结果是________；－32的底数是________，结果是________．3．（－）÷（+ ）=________；－÷（－1 ）=________；（+8）÷（－）=________．4．23×（－）3=________；（－）÷（+ ）2=________．5．（－）×________=1；（－）×________=－16．－×（－2．4）×（－）=________．7．－32× （－5）2÷（－）3=________．8．我国台湾省的面积约为3600平方公里，用科学记数法表示为________．9．+1 的倒数是________；________的倒数是－．10．用“＞”“＜”填空：①23________22 ②（）2________（）3③32________22 ④（－2）3________（－2）2二、判断题（每小题1分，共5分）11．零除以任何数都得零（）12．互为相反数的两个数的积为负数（）13．如果ab＞0，则a＞0且b＞0（）14．1除以一个非零数的商叫做这个数的倒数（）15．（－3）5表示5个－3相乘（）三、选择题（每小题3分，共21分）16．下列说法，其中错误的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘，符号不变．A．1个 B．2个C．3个 D．4个17．下列各对数：①1与1；②－1与1；③a－b与b－a；④－1与－1；⑤－5与|6|，其中互为倒数的是A．①②③ B．①③⑤C．①③④ D．①④18．下列各题中两个式子的值相等的是A．－23与（－2）3 B．32与23C．（－2）2与－22 D．|－2|与－|－2|19．下列结论中，其中正确的个数为①0的倒数是0；②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数等于自身的数是±1；④若a，b互为倒数，则－ab=－1．A．4 B．3C．2 D．120．下列各式中结果大于0的是A．1－910×3 B．（1－910）×3C．1－（9×3）10 D．（1－9）10×321．下列说法中正确的是A．一个数的平方必为正数B．一个数的平方必小于这个数的绝对值C．一个数的平方必大于这个数D．一个数的平方不可能为负数22．用科学记数法表示的数2．89×104，原来是A．2890 B．2890000C．28900 D．289 000四、计算题（共35分）23．（3分）（－3）×（－5）×（+12）×（－） 24．（3分）－6÷（+3）÷（－4）×（+2）25．（3分）－5－6÷（－3）26．（3分）（－81）÷2 × ÷（－16）27．（3分）－22× （－3）÷28．（3分）（－1）20 00×（－1）20xx×（－1）20xx÷（－1）20xx29．（3分）（－2）×（－20xx）×［－－（－）］×1－20xx30．（3分）－ 31．（3分）（－5）2÷5×632．（3分）（－2.5）÷（－）×（－3）33．（5分）30×（－ + －）五、解答题（9分）34．已知A=a+a2+a3+……+a2000（1）若a=1，求A的值．（2）若a=－1，求A的值．参考答案一、1．－6 2 2．－3 9 3 －9 3．－－32 4．－－5．－6．－1.2 7．1800 8．3.6×103平方公里9．－1 10．＞＞＞＜二、11．×12．×13．×14．√15．√三、16．A 17．D 18．A 19．B 20．D 21．D 22．C四、2 3．－90 24．1 25．－3 26．27．15 28．1 29．－20xx 30．1 31．30 32．－33．－4五、34．（1）2000 （2）0。

初一数学《有理数的乘除、乘方运算》测试题(苏教版)

初一数学《有理数的乘除、乘方运算》测试题（苏教版）有理数的乘除、乘方运算测试题〔含答案苏教版〕一、填空题〔每题3分，共30分〕1．3×〔－2〕=________，〔－6〕×〔－〕=________．2．〔－3〕2的底数是________，结果是________；－32的底数是________，结果是________．3．〔－〕÷〔+〕=________；－÷〔－1〕=________；〔+8〕÷〔－〕=________．4．23×〔－〕3=________；〔－〕÷〔+〕2=________．5．〔－〕×________=1；〔－〕×________=－16．－×〔－2．4〕×〔－〕=________．7．－32×〔－5〕2÷〔－〕3=________．8．我国台湾省的面积约为3600平方公里，用迷信记数法表示为________．9．+1的倒数是________；________的倒数是－．10．用〝＞〞〝＜〞填空：①23________22②〔〕2________〔〕3③32________22④〔－2〕3________〔－2〕2二、判别题〔每题1分，共5分〕11．零除以任何数都得零〔〕12．互为相反数的两个数的积为正数〔〕13．假设ab＞0，那么a＞0且b＞0〔〕14．1除以一个非零数的商叫做这个数的倒数〔〕15．〔－3〕5表示5个－3相乘〔〕三、选择题〔每题3分，共21分〕16．以下说法，其中错误的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘，符号不变．A．1个B．2个C．3个D．4个17．以下各对数：①1与1；②－1与1；③a－b与b－a；④－1与－1；⑤－5与|6|，其中互为倒数的是A．①②③B．①③⑤C．①③④D．①④18．以下各题中两个式子的值相等的是A．－23与〔－2〕3B．32与23C．〔－2〕2与－22D．|－2|与－|－2|19．以下结论中，其中正确的个数为①0的倒数是0；②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数等于自身的数是±1；④假定a，b互为倒数，那么－ab=－1．A．4B．3C．2D．120．以下各式中结果大于0的是A．1－910×3B．〔1－910〕×3C．1－〔9×3〕10D．〔1－9〕10×321．以下说法中正确的选项是A．一个数的平方必为正数B．一个数的平方必小于这个数的相对值C．一个数的平方必大于这个数D．一个数的平方不能够为正数22．用迷信记数法表示的数2．89×104，原来是A．2890B．2890000C．28900D．289000四、计算题〔共35分〕23．〔3分〕〔－3〕×〔－5〕×〔+12〕×〔－〕24．〔3分〕－6÷〔+3〕÷〔－4〕×〔+2〕25．〔3分〕－5－6÷〔－3〕26．〔3分〕〔－81〕÷2×÷〔－16〕27．〔3分〕－22×〔－3〕÷28．〔3分〕〔－1〕2021×〔－1〕2021×〔－1〕2021÷〔－1〕202129．〔3分〕〔－2〕×〔－2021〕×［－－〔－〕］×1－2021 30．〔3分〕－31．〔3分〕〔－5〕2÷5×632．〔3分〕〔－2.5〕÷〔－〕×〔－3〕33．〔5分〕30×〔－+－〕五、解答题〔9分〕34．A=a+a2+a3+……+a2021〔1〕假定a=1，求A的值．〔2〕假定a=－1，求A的值．参考答案一、1．－622．－393－93．－－324．－－5．－6．－1.27．18008．3.6×103平方公里9．－110．＞＞＞＜二、11．×12．×13．×14．√15．√三、16．A17．D18．A19．B20．D21．D22．C四、23．－9024．125．－326．27．1528．129．－2021 30．131．3032．－33．－4五、34．〔1〕2021〔2〕0。

有理数的乘除乘方运算(含答案)

有理数的运算(乘、除、乘方)教学目的:1、理解有理数的乘法法则；掌握异号两数的乘除运算的规律：2、会进行有理数的乘法、除法、乘方的运算，能灵活运用运算律进行简化运算。

教学重点:1、有理数的乘法、除法法则：2、熟练的进行有理数乘法、除法、乘方运算。

教学难点:若干个有理数柑乘，积的符号的确定，乘方的符号确世。

有理数的乘法有理数的乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘。

例题目的：掌握有理数的乘法法则。

有理数乘法法则的推广：(1) 几个不等于0的数相乘，积的符号由负因数的个数决定。

当负数的个数为奇数时，积为负，当负因数为偶数个时，积为正。

(2) 几个数相乘，有一个因数为0,积为0. ⑵ 1^X (-1)X (-2.5)X (-A) 3 9 25例®目的：会算两个以上有理数的乘法，并能判定积的符号。

有理数乘法的运算律：衽有理数运算中，乘法的交换律，结合律以及乘法对加法的分配律仍然成立。

乘法交换律：两个数相乘，交换因数的位S,积不变，用式子表示为a b=b a例1：计算⑴(-5)x(-3)⑵(一7)x41 7例 2： (I) -X(--)x(-4)乘法结合律：三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积不变.用式子表示成(a ・b)・c=a ・(b ・c)乘法分配律：一个数同两个数的和相乘，等于把这个数分别同这两个数相乘. 用字母表示成-a(b+c)=a ・b+a ・c⑶7唏心)例題目的：掌握有理数乘法的运算律。

有理数的除法法则两个有理数相除，同号得正，异号向负，并把绝对值相除。

0除以任何非0的数都得0。

倒数与负倒数的概念：乘积为1的两个有理数互为倒数，即若a, b 互为倒数，则ah = l ；乘积为一1的两个有理数互为负倒数，即若互为负倒褻则a b = -l法则2：除以一个数等于乘以这个数的倒数，即《4 ="・一0式0) b 例4： 1.求下列各■数的倒数，负倒数。

初一-有理数的乘除法、乘方运算-练习题

初一-有理数的乘除法、乘方运算-练习题(总4页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2有理数的乘除法、乘方运算练习题一、有理数的乘除法1、有理数乘法法则：（1）两数相乘，同号得正，异号得负，并把绝对值相乘；（2）任何数同0相乘都得0；（3）多个有理数相乘：a ：只要有一个因数为0，则积为0。

b ：几个不为零的数相乘，积的符号由0的个数决定，当0的个数为奇数，则积为负，当0的个数为偶数，则积为正。

2、乘法运算律：（1）乘法交换律；（2）乘法结合律；（3）乘法分配律。

3、有理数除法法则：（1）法则：除以一个数等于乘以这个数的倒数（2）符号确定：两数相除，同号得正，异号得负，并把绝对值相除。

（3）0除以任何一个非零数，等于0；0不能作除数！二、有理数乘方：1、n 个相同因数的积的运算，叫做乘方。

乘方的结果叫做幂；用字母表示an a a a a 个⋅⋅⋅⋅记作n a ，其中a 叫做底数，n 叫做指数，n a 的结果叫做幂；读法：na 读作a 的n 次方。

2、正数的任何次幂都是正数，负数的奇次幂是负数，负数的偶次幂是正数。

练习题一、选择题：1、一个有理数和它的相反数之积（）A ．符号必为正B ．符号必为负C ．一定不大于零D ．一定不小于零2、若0ab >，则下列说法中，正确的是（）A ．a ，b 之和大于0B ．a ，b 之和小于0C ．,a b m 同号D ．无法确定3、下列说法中，正确的是（）A ．两个有理数的乘积一定大于每一个因数。

B ．若一个数的绝对值等于它本身，这个数一定是正数。

3C ．有理数的乘法就是求几个加数的和的运算。

D ．两个连续自然数的积一定是一个偶数。

4、下列说法中，正确的是（）A ．若两个有理数在数轴上的对应点分别在原点的两侧，那么这两个有理数的积一定为负数B ．若两个有理数的积是负数，则这两个数一定互为相反数C ．若两个有理数互为相反数，则这两个有理数的积一定为负数D ．若a 是任意有理数，则1a是它的倒数5、若ab ＝0，那么a ，b 的值为（）A ．都为0B ．都不为0C ．至少有一个为0D ．无法确定6、几个不等于0的有理数相乘，它们的积的符号（）A ．由因数的个数而定B ．由正因数的个数而定C ．由负因数的个数而定D ．由负因数的大小而定7、下列说法中，正确的是（）A ．若0a b +=，那么0a b ==B ．或0ab =，则0a b ==C ．若0ab ≠，则a ，b 都不等于0D ．若0a b +≠，则a ，b 都不等于0二、填空题：1、n 个相同因数a 相乘，即个n a a a a ⋅⋅记作________.这种求n 个相同_________的运算叫做乘方，乘方的结果叫________，在n a 中，a 叫_________，_________叫指数.2、平方得9的数有________个，分别是________.3、正数的任何次幂都是________；负数的________次幂是负数，偶次幂是________；0的任何次幂都是________.4、若a 为有理数，则2a ________0.5、若22a b =，则a 与b 的关系是_________.6、计算()()()()()234200311111-+-+-+-+⋅⋅⋅+-=____________.三、计算： 1、（1）()()3223-⨯- （2）()232714⎛⎫-+-÷- ⎪⎝⎭ （3）2342293⎛⎫-÷⨯ ⎪⎝⎭4（4）()2411[23]6---- （5）22122243⎛⎫⎛⎫-÷-⨯- ⎪ ⎪⎝⎭⎝⎭（6）()()()23540.25548⎛⎫-⨯--⨯-⨯- ⎪⎝⎭ （7）(()221420325⎛⎫⎡⎤-⨯÷--- ⎪⎣⎦⎝⎭2、（1）()200120020.254-⨯ （2）求()20033-的个位数字.3、（1）3482773⎛⎫⎛⎫÷-⨯÷- ⎪ ⎪⎝⎭⎝⎭ （2）31121422⎛⎫⎛⎫⎛⎫-⨯-÷- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（3）()()510.25564816⎛⎫-÷-⨯-⨯- ⎪⎝⎭ （4）1111735105⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+---+÷- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦5(5) 63999177⎛⎫÷- ⎪⎝⎭ (6) ()3.1435.2 6.2823.3 1.5736.4-⨯+⨯--⨯(7) ()1111603456⎛⎫-÷-+- ⎪⎝⎭ (8) ()()220.2518133⎛⎫⎛⎫-÷-⨯-⨯+ ⎪ ⎪⎝⎭⎝⎭(9) －14－(1－×31×[2－(－3)2](10) －5 2－(－5) 2×{(－1)50－[(－1)51－1÷(－21)×2]}6 (11) [－21×(－1)3 + |－6|÷31×3－(－5)2]×71。

有理数的加减乘除乘方混合运算专题训练(带答案)

1. 先乘方，再乘除，最后加减；2. 同级运算，从左到右进行；3. 如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行。

1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷3、11(22)3(11)+--⨯-4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、 33102(4)8-÷--7、)]21)21[(122--÷ 8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯-- 10、23533||()14714-⨯-÷11、—22—(—2)2—23+(—2)3 12、2223116(1)(3)(1)(3)22-⨯---÷-⨯-13、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、－10 + 8÷(－2 )2 －(－4 )×(－3 ) 16、－49 + 2×(－3 )2 + (－6 )÷(－91)17、－14 + ( 1－0.5 )×31×[2×(－3)2] 18、(－2)2－2×[(－21)2－3×43]÷51．19、)8()4()6(52-÷---⨯ 20、0)132()43(2⨯+-+-21、6)12()4365127(÷-⨯+- 22、22)4()5(25.0)4()85(-⨯-⨯--⨯-23、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6－（－12）÷2)2(- 26、（-48）÷ 8 －（-5）÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯- 30、(－5)×6＋(－125) ÷(－5)3 31、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+- 1、【基础题】计算：（1）618－÷）（－）（－312⨯；（2））（－＋51232⨯；（3））（－）（－49⨯＋）（－60÷12；（4）23）（－×[ ）＋（－－9532 ]. （1））（－）＋（－2382⨯；（2）100÷22）（－－）（－2÷）（－32；（3））（－4÷）（－）（－343⨯；（4））（－31÷231）（－－3214）（－⨯. （1）36×23121）－（；（2）12.7÷）（－1980⨯；（3）6342＋）（－⨯；（4））（－43×）－＋（－31328；（5）1323－）（－÷）（－21；（6）320－÷34）（－81－；（7）236.15.02）－（－）（－⨯÷22）（－；（8））（－23×[ 2322－）（－ ]；（9）[ 2253）－（－）（－ ]÷）（－2；（10）16÷）（－）－（－）（－48123⨯. （1）11＋（－22）－3×（－11）；（2）0313243⨯⨯）－（－）（－；（3）2332－）（－；（4）23÷[ ）－（－）（－423]；（5））－（8743÷）（－87；（6））＋（）（－654360⨯；（7）－27+2×()23-+（－6）÷()231-；（8））（－）－＋－（－4151275420361⨯⨯. （1））－（－258÷）（－5；（2）－33121）（－－⨯；（3）223232）－（－）（－⨯⨯；（4）0132432⨯⨯）＋（－）（－；（5））（－＋51262⨯；（6）－10＋8÷()22-－4×3；（7）－51－()()[]55.24.0-⨯-；（8）()251-－（1－0.5）×31；（1）（－8）×5－40；（2）（-1.2）÷（-13）-（-2）；（3）-20÷5×14+5×（-3）÷15；（4）-3[-5+（1-0.2÷35）÷（-2）]；（5）－23÷153×（-131）2÷（132）2；（6）－52＋(1276185+-)×(－2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】（1）17；（2）511；（3）31；（4）－112、【答案】（1）－10；（2）22；（3）－16；（4）－253、【答案】（1）1；（2）0；（3）42；（4）23；（5）18；（6）0；（7）－4.64；（8）37；（9）8；（10）－25. 4、【答案】（1）22；（2）0；（3）－17；（4）－423；（5）71；（6）－95；（7）－85；（8）6 .5、【答案】（1）3；（2）1；（3）－54；（4）0；（5）526；（6）－20；（7）－2；（8）－67. 6、【答案】（1）－80；（2）5.6；（3）－2；（4）16；（5）－516；（6）－2.9复习有理数的乘除、乘方运算测试题一、填空题（每小题3分，共30分） 1．3×（－2）=________，（－6）×（－31）=________． 2．（－3）2的底数是________，结果是________；－32的底数是________，结果是________．3．（－61）÷（+23）=________；－493÷（－176）=________；（+8）÷（－41）=________． 4．23×（－41）3=________；（－91）÷（+34）2=________．5．（－32）×________=1；（－32）×________=－16．－65×（－2．4）×（－53）=________．7．－32×（－5）2÷（－21）3=________．8．我国台湾省的面积约为3600平方公里，用科学记数法表示为________． 9．+121的倒数是________；________的倒数是－54． 10．用“＞”“＜”填空： ①23________22②（21）2________（21）3③32________22④（－2）3________（－2）2二、判断题（每小题1分，共5分） 11．零除以任何数都得零（）12．互为相反数的两个数的积为负数（） 13．如果ab ＞0，则a ＞0且b ＞0（）14．1除以一个非零数的商叫做这个数的倒数（）15．（－3）5表示5个－3相乘（）三、选择题（每小题3分，共21分） 16．下列说法，其中错误的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘，符号不变．A ．1个B ．2个C ．3个D ．4个17．下列各对数：①1与1；②－1与1；③a －b 与b －a ；④－1与－1；⑤－5与|6|，其中互为倒数的是A ．①②③B ．①③⑤C ．①③④D ．①④ 18．下列各题中两个式子的值相等的是A ．－23与（－2）3B ．32与23C ．（－2）2与－22D ．|－2|与－|－2| 19．下列结论中，其中正确的个数为①0的倒数是0；②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数等于自身的数是±1；④若a ，b 互为倒数，则－ab=－1．A ．4B ．3C ．2D ．1 20．下列各式中结果大于0的是A ．1－910×3B ．（1－910）×3C ．1－（9×3）10D ．（1－9）10×3 21．下列说法中正确的是 A ．一个数的平方必为正数B ．一个数的平方必小于这个数的绝对值C ．一个数的平方必大于这个数D ．一个数的平方不可能为负数22．用科学记数法表示的数2．89×104，原来是A ．2890B ．2890000C ．28900D ．289000 四、计算题（共35分）23．（3分）（－3）×（－5）×（+12）×（－21） 24．（3分）－6÷（+3）÷（－4）×（+2） 25．（3分）－5－6÷（－3）26．（3分）（－81）÷241×91÷（－16） 27．（3分）－22×（－3）÷5428．（3分）（－1）2000×（－1）2001×（－1）2002÷（－1）200329．（3分）（－2）×（－2001）×［－21－（－21）］×1－2002 30．（3分）－)45()45(5222-÷-⨯⨯ 31．（3分）（－5）2÷5×632．（3分）（－2.5）÷（－310）×（－3） 33．（5分）30×（21－31+53－109）五、解答题（9分） 34．已知A=a+a 2+a 3+……+a 2000（1）若a =1，求A 的值．（2）若a =－1，求A 的值．参考答案一、1．－6 2 2．－3 9 3 －9 3．－91 913 －32 4．－81 －161 5．－23 23 6．－1.2 7．1800 8．3.6×103平方公里9．32 －14110．＞＞＞＜二、11．× 12．× 13．× 14．√ 15．√三、16．A 17．D 18．A 19．B 20．D 21．D 22．C 四、23．－90 24．1 25．－3 26．4127．15 28．1 29．－2002 30．1 31．30 32．－4933．－4 五、34．（1）2000 （2）0。