金属晶体金属堆积方式(20200706105355)
合集下载
金属晶体堆积方式

金属晶体堆积方式 的研究意义和展望
提高材料的力学性能,如强度、硬度、韧性等 优化材料的电学、热学和磁学性能 实现材料的功能化与智能化,如传感器、驱动器等 探索新型材料,推动科技进步和产业发展
金属晶体堆积方 式的研究有助于 深入理解物质结 构和性质
金属晶体堆积方 式的多样性是决 定金属材料性能 的重要因素
添加标题
添加标题
添加标题
添加标题
金属晶体的堆积方式会影响其物理 性质,如导电性、热导率等。
了解金属晶体的堆积方式对于材料 性能的优化和新型材料的开发具有 重要的意义。
特点:金属晶体堆积方式具有高度 的对称性和规则性,不同金属晶体 堆积方式的差异较大。
影响因素:金属晶体堆积方式受金 属原子半径、金属键类型等因素影 响。
添加标题
添加标题
添加标题
添加标题
应用:金属晶体堆积方式对金属的 物理性质和化学性质有重要影响, 如导电性、耐腐蚀性等。
实验研究:通过X射线衍射、中子 衍射等实验手段研究金属晶体堆积 方式。
金属晶体堆积方式在材料科学中的应用 金属晶体堆积方式在电子器件制造中的应用 金属晶体堆积方式在航空航天领域的应用 金属晶体堆积方式在生物医学领域的应用
金属晶体堆积方式的形成原因 是为了实现空间利用率的最大 化。
通过合理的堆积方式,金属晶 体可以获得更高的密度和更强
的机械性能。
金属晶体堆积方式的形成还受 到金属原子间相互作用力的影
响。
金属晶体堆积方式 的特点和应用
金属晶体堆积方式的特点包括周期 性、对称性和密堆积等。
金属晶体的堆积方式在材料科学和 工程领域具有广泛的应用,如金属 材料、催化剂等。
热性能。
金属晶体的堆 积方式决定了 其物理和化学
金属晶体金属堆积方式

钠晶体的晶胞
如某晶体是右图六棱柱状晶胞, 则晶胞中的原子数是12×1/6+2×.1/2 + 3 = 6
练习
2. 最近发现一种由某金属原子M和非金 属原子N构成的气态团簇分子,如图所 示.顶角和面心的原子是M原子,棱的 中心和体心的原子是N原子,它的化学
式为( C )
A. M4N4 B.MN
C. M14N13
12
6
3
54
12
6
3
54
12
6
3
54
Ⅳ.面心立方 金、银、铜、铝等属于面心立方堆积
堆积(铜型)
第四层再排 A,于是形成
A
ABC ABC 三层一个周期。
这种堆积方式可划分出面心
C
立方晶胞。
B
12
6
3
54
配位数 12 ( 同层 6, 上下层各 3 )
A
C B A 此种立方紧密堆积的前视图
堆积方式及性质小结
金属晶体
Ti
金属样品 Ti
1、金属共同的物理性质
容易导电、导热、有延展性、有金属光泽等。
金属为什么具有这些共同性质呢? 2、金属的结构
㈠、金属键
(1)定义: 金属离子和自由电子之间的相互作用。 (2)成键微粒: 金属阳离子和自由电子
(3)键的存在: 金属单质和合金中
(4)方向性: 无方向性
(5)键的本质: 电子气理论
自由电子在运动时经常与金属离子碰撞, 引起两者能量的交换。当金属某部分受热时, 那个区域里的自由电子能量增加,运动速度加 快,通过碰撞,把能量传给金属离子。
金属容易导热,是由于自由电子运动时与 金属离子碰撞把能量从温度高的部分传到温度 低的部分,从而使整块金属达到相同的温度。
如某晶体是右图六棱柱状晶胞, 则晶胞中的原子数是12×1/6+2×.1/2 + 3 = 6
练习
2. 最近发现一种由某金属原子M和非金 属原子N构成的气态团簇分子,如图所 示.顶角和面心的原子是M原子,棱的 中心和体心的原子是N原子,它的化学
式为( C )
A. M4N4 B.MN
C. M14N13
12
6
3
54
12
6
3
54
12
6
3
54
Ⅳ.面心立方 金、银、铜、铝等属于面心立方堆积
堆积(铜型)
第四层再排 A,于是形成
A
ABC ABC 三层一个周期。
这种堆积方式可划分出面心
C
立方晶胞。
B
12
6
3
54
配位数 12 ( 同层 6, 上下层各 3 )
A
C B A 此种立方紧密堆积的前视图
堆积方式及性质小结
金属晶体
Ti
金属样品 Ti
1、金属共同的物理性质
容易导电、导热、有延展性、有金属光泽等。
金属为什么具有这些共同性质呢? 2、金属的结构
㈠、金属键
(1)定义: 金属离子和自由电子之间的相互作用。 (2)成键微粒: 金属阳离子和自由电子
(3)键的存在: 金属单质和合金中
(4)方向性: 无方向性
(5)键的本质: 电子气理论
自由电子在运动时经常与金属离子碰撞, 引起两者能量的交换。当金属某部分受热时, 那个区域里的自由电子能量增加,运动速度加 快,通过碰撞,把能量传给金属离子。
金属容易导热,是由于自由电子运动时与 金属离子碰撞把能量从温度高的部分传到温度 低的部分,从而使整块金属达到相同的温度。
金属晶体的四种堆积模型

金属晶体的四种堆积模型
金属晶体是由金属原子按照一定的排列构成的固体,它们具有规则的晶体结构,其中最常见的是四种堆积模型:面心立方模型、面心六方模型、空心六方模型和空心八方模型。
面心立方模型是最常见的金属晶体堆积模型,它由八个原子组成,每个原子都位于晶体的八个顶点上,形成一个立方体。
这种模型的特点是,每个原子都与其他七个原子有相同的距离,因此它具有良好的稳定性。
面心六方模型是一种比面心立方模型更复杂的晶体堆积模型,它由十二个原子组成,每个原子都位于晶体的六个面上,形成一个六面体。
这种模型的特点是,每个原子都与其他五个原子有不同的距离,因此它具有较高的热稳定性。
空心六方模型是一种比面心六方模型更复杂的晶体堆积模型,它由十八个原子组成,每个原子都位于晶体的六个面上,形成一个空心六面体。
这种模型的特点是,每个原子都与其他十一个原子有不同的距离,因此它具有较高的热稳定性和机械稳定性。
空心八方模型是一种比空心六方模型更复杂的晶体堆积模型,它由二十四个原子组成,每个原子都位于晶体的八个面上,形成一个空心八面体。
这种模型的特点是,每个原子都与其他十七个原子有不同的距离,同样具有较高的热稳定性和机械稳定性。
总之,金属晶体的四种堆积模型是面心立方模型、面心六方模型、空心六方模型和空心八方模型,它们各自具有不同的特点,可以满足不同的应用需求。
金属晶体中原子堆积方式

(三)三维堆积
非密置层 密置层
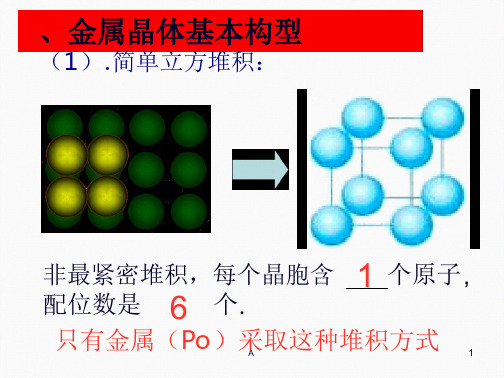
三、金属晶体基本构型
1.简单立方堆积:
非最紧密堆积, 空间利用率低
边长 = 2r
(2)体心立方堆积(A2):
例:金属钾 K 的体 心立方堆积
体对角线 = 4r 边长=4 3 r/3
(3)六方紧密堆积(A3)
1 2
6 5 4
3
各层均为密置层
于是每两层形成一个周期,即:AB、 AB 堆积方式,形成六方紧密堆积。
边长 = 2 2 r 面对角线 = 4r
四、晶体中有关计算
1.晶胞中微粒数的计算 (1)简单立方:在立方体顶点的微 粒为8个晶胞共享, 微粒数为:8×1/8 = 1 空间利用率: 4лr3/3 (2r)3
= 52.36%
(2)体心立方:在立方体顶 点的微粒为8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。 微粒数为:8×1/8 + 1 = 2
(3)六方晶胞:在六方体顶 点的微粒为6个晶胞共有,在 面心的为2个晶胞共有,在体 内的微粒全属于该晶胞。
微粒数为:12×1/6 + 2×1/2 + 3 = 6
(4)面心立方:在立方体顶点的微粒为8 个晶胞共有,在面心的为2个晶胞共有。 微粒数为: 8×1/8 + 6×1/2 = 4 空间利用率: 4×4лr3/3 (2×1.414r)3
= 74.05%
2.配位数:
每个小球周围距离最近的小球数 简单立方堆积: 体心立方堆积: 六方紧密堆积: 6 8 12 12
面心立方紧密堆积:
(3)六方紧密堆积
A B A B A
A A B B A A
密 置 层
边长 = 2r 高 = 4 6 r/3
金属晶体金属堆积方式

其他金属堆积方式
六方堆积:如 镁、锌等金属 的堆积方式, 原子密排程度 高,强度大,
塑性好。
面心立方堆积: 如铝、铜等金 属的堆积方式, 原子密排程度 较高,强度较 大,导电性好。
体心立方堆积: 如铁、铬等金 属的堆积方式, 原子密排程度 较低,强度较 小,导电性较
差。
简单立方堆积: 如铅、锡等金 属的堆积方式, 原子密排程度 低,强度小,
金属堆积方式的稳定性与其在高温 下的性能表现密切相关,稳定性较 高的堆积方式可以提高金属在高温 下的抗氧化性能和抗蠕变性能。
添加标题
添加标题
添加标题
添加标题
紧密堆积方式可以提高金属晶体的 硬度和稳定性,而开放堆积方式则 有利于金属的塑性和延展性。
金属堆积方式的形成还受到原子间 相互作用力和晶体结构的影响,这 些因素可以影响金属的化学性质和 反应活性。
金属晶体的金属堆积方式
汇报人:XX
金属晶体的基本概念 金属晶体的金属堆积方式 金属堆积方式的形成与特点 金属堆积方式的实际应用 金属堆积方式的研究进展与展望
金属晶体的基本概念
金属晶体的定义
金属晶体是由金属原子或金属离子通过金属键结合而成的晶体。 金属晶体具有金属光泽和良好的导电、导热性能。 金属晶体的结构取决于金属原子的半径和堆积方式。 金属晶体的性质与金属键的强度和方向有关,受到温度、压力等因素的影响。
密排六方堆积
定义:密排六方 堆积是一种金属 晶体的堆积方式, 其中金属原子在 三维空间中以六 方最密堆积的方 式排列。
特点:具有高度 的空间利用率和 稳定性,是金属 晶体中最常见的 堆积方式之一。
应用:广泛存在 于各种金属晶体 中,如镁、锌、 镉等。
形成过程:金属 原子在结晶过程 中,首先形成二 维平面排列,然 后逐渐堆积形成 三维结构。
金属晶体的堆积模型

二、 金属晶体的原子堆积模 型
精品课件
金属晶体原子平面排列方式有几种?
探究
2 1A3
4
2
1
3
A
6
4
5
配位数为4 非密置层
精品课件
配位数为6 密置层
非密置层层层堆积情况1: 相邻层原子在同一直线上的堆积
金属晶体的堆积方式──简单立方堆积
精品课件
简单立方堆积
配位数:6 晶胞含金属原子数 1
例: (Po) 精品课件
精品课件
2).立方面心结构 立方面心结构的配位数=12(即每个圆球有12个最
近的邻居,同一层有六个,上一层三个,下一层三 个)。立方密堆积中可以取出一个立方面心的单位 来,每个单位中有四个圆球,球心的位置是000;0 1/2 1/2;1/2 0 1/2;1/2 1/2 0。
等径圆球的最紧密堆积方式,在维持每个球的周围 的情况等同的条件下,就只有上述两种,它们的空 间利用率最高(74.05%)。
精品课件
立方体边长=a';
立方体对角线=
a';
四面体边长=
a';
精品课件
精品课件
设圆半径为R,晶胞棱长为a,晶胞面对角
线长
则
晶胞体
积
立方面心晶胞中含4个圆球,每个球体积
为:
立方最密堆积虽晶胞大小不同,每个晶胞中 含球数不同。但计算得到空间占有率相同。
精品课件
而体心立方堆积(bcp)则空间占有率低一些。 体对角线长为 晶胞体积 体心立方晶胞含2个球
精品课件
2、某些金属晶体(Cu、Ag、Au)的原子按面心 立方的形式紧密堆积,即在晶体结构中可以 划出一块正立方体的结构单元,金属原子处 于正立方体的八个顶点和六个侧面上,试计 算这类金属晶体中原子的空间利用率。
精品课件
金属晶体原子平面排列方式有几种?
探究
2 1A3
4
2
1
3
A
6
4
5
配位数为4 非密置层
精品课件
配位数为6 密置层
非密置层层层堆积情况1: 相邻层原子在同一直线上的堆积
金属晶体的堆积方式──简单立方堆积
精品课件
简单立方堆积
配位数:6 晶胞含金属原子数 1
例: (Po) 精品课件
精品课件
2).立方面心结构 立方面心结构的配位数=12(即每个圆球有12个最
近的邻居,同一层有六个,上一层三个,下一层三 个)。立方密堆积中可以取出一个立方面心的单位 来,每个单位中有四个圆球,球心的位置是000;0 1/2 1/2;1/2 0 1/2;1/2 1/2 0。
等径圆球的最紧密堆积方式,在维持每个球的周围 的情况等同的条件下,就只有上述两种,它们的空 间利用率最高(74.05%)。
精品课件
立方体边长=a';
立方体对角线=
a';
四面体边长=
a';
精品课件
精品课件
设圆半径为R,晶胞棱长为a,晶胞面对角
线长
则
晶胞体
积
立方面心晶胞中含4个圆球,每个球体积
为:
立方最密堆积虽晶胞大小不同,每个晶胞中 含球数不同。但计算得到空间占有率相同。
精品课件
而体心立方堆积(bcp)则空间占有率低一些。 体对角线长为 晶胞体积 体心立方晶胞含2个球
精品课件
2、某些金属晶体(Cu、Ag、Au)的原子按面心 立方的形式紧密堆积,即在晶体结构中可以 划出一块正立方体的结构单元,金属原子处 于正立方体的八个顶点和六个侧面上,试计 算这类金属晶体中原子的空间利用率。
金属晶体堆积模型及计算公式
A
3
5
6
8
7
1
2
4
3
这种堆积晶胞是一个体心立方,每个晶胞含
2 个原子,属于非密置层堆积,配位数
8 为
,许多金属(如 Na、K、Fe等)采取这种堆
积方式。
A
4
空间利用率的计算
(2)体心立方:在立方体顶
点的微粒为 8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。
微粒数为: 8×1/8 + 1 = 2
空间利用率:
4×4л r3/3
= 74.05%
(2 ×1.414r)
3 A
8
堆积方式及性质小结
简单立 方堆积
体心立方 堆积
六方最
密堆积
面心立方
最密堆积
简单立方
体心立方 六方
面心立方
52%
68%
74% 74%
A
6
Po
8
Na 、K、Fe
12 Mg 、Zn 、Ti
12 Cu 、 Ag、Au
9
A
10
小结:三种晶体类型与性质的比较
A
5
1200
平行六面体
每个晶胞含 2 个原子
A
6
铜型(面心立方紧密堆积)
7
1 9
6
8 2
3
5
4
12
10
11
这种堆积晶胞属于最密置层堆集,配位数
为 12 ,许多金属(如 Cu、Ag、Au等)采取这
种堆积方式。
A
7
(3)面心立方:在立方体顶点的微粒为 8个
晶胞共有,在面心的为 2个晶胞共有。
微粒数为: 8×1/8 + 6 ×1/2 = 4
金属晶体中原子堆积方式ppt课件

面对角线 = 4r
15
四、晶体中有关计算
1.晶胞中微粒数的计算
(1)简单立方:在立方体顶点的微 粒为8个晶胞共享,
微粒数为:8×1/8 = 1
空间利用率:
4лr3/3 (2r)3
= 52.36%
16
(2)体心立方:在立方体顶 点的微粒为8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。
微粒数为:8×1/8 + 1 = 2
物质结构与性质
金属晶体的堆积方式
1
一、理论基础:
由于金属键没有方向性,每个金属原 子中的电子分布基本是球对称的,所以 可以把金属晶体看成是由直径相等的圆 球的三维空间堆积而成的。
二、金属堆积方式
(一)一维堆积
2
(二)二维堆积
I型
II 型
非密置层
行列对齐四球一 空 非最紧密排列
密置层
行列相错三球一 空最紧密排列
(3)六方晶胞:在六方体顶 点的微粒为6个晶胞共有,在 面心的为2个晶胞共有,在体 内的微粒全属于该晶胞。
微粒数为:12×1/6 + 2×1/2 + 3 = 6 17
(4)面心立方:在立方体顶点的微粒为8个 晶胞共有,在面心的为2个晶胞共有。
微粒数为: 8×1/8 + 6×1/2 = 4
空间利用率:
3
(三)三维堆积
非密置层
密置层
4
三、金属晶体基本构型
1.简单立方堆积:
非最紧密堆积, 空间利用率低
边长 = 2r
5
(2)体心立方堆积(A2):
例:金属钾 K 的体 心立方堆积
体对角线 = 4r 边长=4 3r/3
6
(3)六方紧密堆积(A3)
15
四、晶体中有关计算
1.晶胞中微粒数的计算
(1)简单立方:在立方体顶点的微 粒为8个晶胞共享,
微粒数为:8×1/8 = 1
空间利用率:
4лr3/3 (2r)3
= 52.36%
16
(2)体心立方:在立方体顶 点的微粒为8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。
微粒数为:8×1/8 + 1 = 2
物质结构与性质
金属晶体的堆积方式
1
一、理论基础:
由于金属键没有方向性,每个金属原 子中的电子分布基本是球对称的,所以 可以把金属晶体看成是由直径相等的圆 球的三维空间堆积而成的。
二、金属堆积方式
(一)一维堆积
2
(二)二维堆积
I型
II 型
非密置层
行列对齐四球一 空 非最紧密排列
密置层
行列相错三球一 空最紧密排列
(3)六方晶胞:在六方体顶 点的微粒为6个晶胞共有,在 面心的为2个晶胞共有,在体 内的微粒全属于该晶胞。
微粒数为:12×1/6 + 2×1/2 + 3 = 6 17
(4)面心立方:在立方体顶点的微粒为8个 晶胞共有,在面心的为2个晶胞共有。
微粒数为: 8×1/8 + 6×1/2 = 4
空间利用率:
3
(三)三维堆积
非密置层
密置层
4
三、金属晶体基本构型
1.简单立方堆积:
非最紧密堆积, 空间利用率低
边长 = 2r
5
(2)体心立方堆积(A2):
例:金属钾 K 的体 心立方堆积
体对角线 = 4r 边长=4 3r/3
6
(3)六方紧密堆积(A3)
