金属原子堆积的4种基本模式
金属晶体的原子空间堆积模型

A
配位数 12 ( 同层 6, 上下层各 3 )
此种立方紧密堆积的前视图
金属晶体的原子空间堆积模型
(2).密置层的堆积方式
b、面心立方堆积
Hale Waihona Puke 金属晶体的原子空间堆积模型 六方密堆积可抽出六方晶胞,晶胞中心两个球的分
数坐标为(0,0,0,)、(2/3、1/3、1/2),密 置层的晶面坐标为(001)。(如图4(b)(c))
a
(b)
b
六 方 晶 胞
1 b 3
2 a 3
(C)六方晶胞中的圆球位置
由下面的(d)、(e)图我们可清楚看出A3 型堆积中的四面体空隙和八面体空隙
第三层的另一种排列方式, 是将球对准第一层的 2,4,6 位 ,不同于 AB 两层的位置,这是 C 层。 1 2
6 5
4
3
第二层
1 6 5 4 2 3 6 5 4
第三层
1
2 3
面心立方密堆积金、银、铜、铝等属于面心立方堆积 A
第四层再排 A,于是形成 ABC ABC 三层一个周期。 这种堆积方式可 划分出面心立方晶胞。 C B A 1 6 5 4 2 3 C B
图4(d)、(e)
二、金属晶体结构密堆积的几种常见形式 3、六方最密堆积(A3)型
在密置双层AB的基础上 将第3层球堆上去,第3层与B 层接触,其球心的投影与A球 A
B 的球心重合,称第3层为A层。 A 同理第四层为B层,依此类推。 B A3型堆积记为ABAB…型 A 堆积。 B
图4(a)
第一层
金属原子堆积方式

金属原子堆积方式
金属原子的排列方式通常是以晶格为单位进行堆积。
晶格是一种具有规则重复结构的三维点阵,其中每个点代表一个原子。
金属的晶体结构可以分为三类:面心立方(fcc)、体心立方(bcc)和简单立方(sc)。
面心立方结构中,原子在晶格的每个面的中心和每个角上都有一个原子,对于每个原子,其周围都有12个最近邻原子。
铜、铝、金、银等都是面心立方结构。
体心立方结构中,原子位于晶格的每个面的中心和晶格的每个立方体的中心,对于每个原子,其周围有8个最近邻原子。
铁、钴、铬、钛等都是体心立方结构。
简单立方结构中,原子只位于晶格的顶点,对于每个原子,其周围只有6个最近邻原子。
钠、铅、锌、铜等都是简单立方结构。
金属原子的堆积方式是由晶体结构所决定的。
不同的晶体结构会影响金属的物理性质和化学性质。
例如,面心立方结构的金属通常具有良好的延展性和导电性,而体心立方结构的金属则通常具有高强度和硬度。
- 1 -。
金属晶体的三种密堆积方式

金属晶体的三种密堆积方式金属晶体的三种密堆积方式中,原子排列的密堆积方式是指原子在三维空间中紧密排列,以使得晶体的空间利用率达到最大。
密堆积方式可以有效影响金属的密度、强度、硬度等物理性质,因此在材料科学和固体物理中具有重要意义。
通常,金属晶体的密堆积方式主要分为以下三种:面心立方堆积(FCC)、六方最密堆积(HCP)和体心立方堆积(BCC)。
一、面心立方堆积(FCC)面心立方堆积(Face-Centered Cubic, FCC)是一种常见的密堆积方式,其中每个立方体的面上都有一个原子,且每个顶点上也有一个原子。
FCC结构可以看作是由许多面心立方单元重复堆积而成,其代表性金属包括铜(Cu)、铝(Al)、银(Ag)和金(Au)等。
1. 结构特点:在FCC结构中,每个原子都有12个最近邻原子,即配位数为12。
该结构单胞中包含4个原子(8个顶点上的原子分别与相邻单元共享,6个面的原子与邻近单元共享),堆积因子达到0.74,即约74%的空间被原子占据,属于最密堆积结构。
2. 性质:FCC结构由于其紧密的堆积方式,具有较高的塑性和延展性。
因此,FCC金属在室温下一般较易发生滑移,从而产生延展变形。
例如,铜和铝具有良好的延展性,易于加工成型。
3. 堆积方式:在面心立方堆积中,原子在平面上形成紧密的六边形排列,层间顺序为ABCABC 的排列模式。
这意味着每三层后结构重复,形成周期性排列。
4. 应用:FCC结构的金属由于其良好的延展性和抗冲击性,常用于制造电线、金属薄膜和结构材料等。
二、六方最密堆积(HCP)六方最密堆积(Hexagonal Close-Packed, HCP)是一种与面心立方相似的密堆积方式,但其晶体结构为六方柱体,且具有不同的堆积顺序。
HCP结构的代表性金属包括镁(Mg)、钛(Ti)、锌(Zn)和钴(Co)等。
1. 结构特点:在HCP结构中,原子的配位数同样为12,说明其紧密度与FCC相似。
金属晶体堆积模型及计算公式课件

第四页,共28页幻灯片
4、金属晶体基本构型
(1).简单立方堆积:
非最紧密堆积,每个晶胞含 1个原子,配位
数是
个6.
只有金属(Po)采取这种堆积方式
第五页,共28页幻灯片
空间利用率的计算
(1)简单立方:在立方体顶点的微粒 为8个晶胞共享,
微粒数为:8×1/8 = 1
空间利用率:
4лr3/3 (2r)3
堆积方式晶胞类型空间利用率配位数实例面心立方最密堆积简单立方堆积体心立方堆积密堆积面心立方体心立方简单立方747468521212cuagaumgzntinakfepo遵循设计文件施工规范和质量验收标准的原则
关于金属晶体堆积模 型及计算公式
第一页,共28页幻灯片
一、金属晶体的原子堆积模型
1、理论基础
7
1 9
6
5
8 2
3 4
12
10
11
这种堆积晶胞属于最密置层堆集,配位数为
,许1多2金属(如Cu、Ag、Au等)采取这种堆积方式
。
第十九页,共28页幻灯片
铜型
第二十页,共28页幻灯片
第二十一页,共28页幻灯片
第二十二页,共28页幻灯片
第二十三页,共28页幻灯片
12
6
3
54
第二十四页,共28页幻灯片
5
8 2
3 4
10
11
12
这种堆积晶胞属于最密置层堆集,配位数为
12 ,许多金属(如Mg、Zn、Ti等)采取这种堆积方式
。
第十四页,共28页幻灯片
1200
平行六面体
每个晶胞含 2 个原子
第十五页,共28页幻灯片
六方最密堆积的空间利用率计算
金属晶体堆积方式
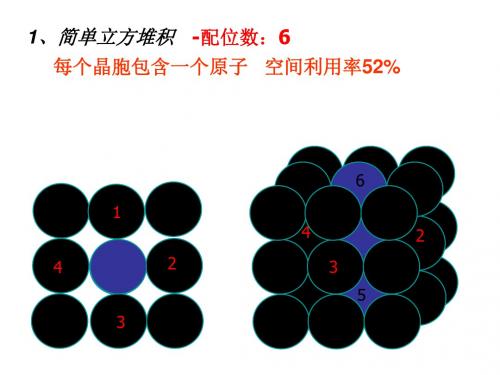
每个晶胞包含一个原子 空间利用率52%
ห้องสมุดไป่ตู้
1
4
2
3
6
1
4
2
3 5
2、钾型(体心立方堆积) -配位数:8
每个晶胞包含2个原子 空间利用率68%
5
6
8
7
1
2
4
3
密堆积原理:原子、离子、分子的排布总是 趋向于配位数高,空间利用率大的紧密堆 积结构方式,最紧密的堆积往往是最稳定 的结构。
密置堆:第三层球放在第二层球的空隙上有两种方式
A B C A
重复ABC的堆积叫A1堆积,重复单位⃒ABC⃒。
A B A
重复AB的堆积叫A3堆积,重复单位⃒AB⃒。
3、六方最密堆积 A3堆积: 抽出六方晶胞,又叫六方最密堆积(hexagonal
closest packing)简写为hcp 。
A B A
分数坐标: 配位数:12 空间利用率74% 晶胞内含有2个球。
4、面心立方最密堆积
A1堆积:
抽出立方面心晶胞,又叫面心立方最密堆积 (cubic closest packing)简写为ccp 。
z
A
B
C
y
x
A
配位数12 空间利用率74% 晶胞内含有4个球。
第3节金属晶体之金属晶体的原子堆积模型

2.1
面心立方最密堆积(A1)和六方最密堆积(A3)
第一层球排列
46
从上面的等径圆球密堆积图中可以看出:
1. 只有1种堆积形式;
2. 每个球和周围6个球相邻接,配位数位6,形 成6个三角形空隙;
3. 每个空隙由3个球围成;
4. 由N个球堆积成的层中有2N个空隙,
即球数:空隙数=1:2。
两层堆积情况分析
②该晶胞称为________(填序号)。
A.六方晶胞 C.面心立方晶胞 B.体心立方晶胞 D.简单立方晶胞
③此晶胞立方体的边长为a cm,Cu的相对原子质 量为64 g· mol-1,金属铜的密度为ρ g/cm3,则阿伏 加德罗常数为________(用a、ρ表示)。
解析: (1)由图中直接相邻的原子数可以求得 a、 b 中两类原子数之比分别为 1∶2、1∶3,求出化学式 分别为 AX2、AX3,故答案为 b。(2)①用“均摊法” 1 1 求解,8× +6× =4;②该晶胞为面心立方晶胞; 8 2 4 256 3 ③ · 64=ρ· a ,NA= 3。 NA ρ· a
必须把球放在第一层的空隙上。这样,仅有半数 的三角形空隙放进了球,而另一半空隙上方是第 二层的空隙。
1. 在第一层上堆积第二层时,要形成最密堆积,
2. 第一层上一半的三角形空隙被第二层球堆积,
被 4 个球包围,形成四面体空隙;另一半其上方
是第二层球的空隙,被 6 个球包围,形成八面体
空隙。
48
三层球堆积情况分析
(2)堆积特点
层的垂直方向为三次象转轴。
既是立方体的空间对角线。 原胞当中包含一个粒子,是 布拉菲格子。
c
120o
a
a
b、面心立方最密堆积
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金属原子堆积的4种基本模式
金属晶体可看成金属原子在三维空间中堆积而成。
、简单立方堆积:
1
不难理解,这种堆积方式形成的晶胞是一个立方体,每个晶胞含1个原子,被称为简单立方堆积。
这种堆积方式的空间利用率太低,只有金属钋(Po)采取这种堆积方式。
晶胞:一个立方体,1个原子,如金属钋。
、钾型
2
非密置层的另一种堆积方式是将上层金属原子填人下层的金属原子形成的凹穴中,每层均照此堆积,如图3—24所示。
与立方堆积相比空间利用率那一个高?
晶胞:体心立方,两个原子。
如碱金属。
动手:把非密置层的小球黏合在一起,再一层一层地堆积起来,使相邻层的球紧密接触。
试一试,除了上述两种堆积方式外,是否可能有第三种方式?
3、镁型和铜型
密置层的原子按上述钾型堆积方式堆积,会得到两种基本堆积方式——镁型和铜型。
镁型如图3—25左所示,按ABABABAB……的方式堆积;铜型如图3—25右所示,按ABCADCABC……的方式堆积。
分别用代表性金属命名为镁型和铜型①,这两种堆积方式都是金属晶体的最密堆积,配位数均为12,空间利用率均为74%,但所得晶胞的形式不同。
金属晶体的两种堆积方式:
b e
i n g
a 镁型:按ABABABAB……方式堆积;铜型:ABCADCABC……方式堆积;配位数均为12,空间利用率均为74%。
小结:金属晶体的四种模型对比:堆积模型采纳这种堆积的典型代表空间利用率配位数简单立方Po
52%6钾型(bcp)Na 、K 、Fe 68%8镁型(hcp)Mg 、Zn 、Ti 74%12铜型(ccp)
Cu 、Ag 、Au
74%
12。
