北邮 大学物理 吴百诗 Chapter-6-热力学基础
合集下载
热学-统计物理6 第6章 热力学第二定律

热功转换
3. 热传导
两个温度不同的物体放在一起,热量将自动地由高温物体 传向低温物体,最后使它们处于热平衡,具有相同的温度。 温度是粒子无规热运动剧烈程度即平均平动动能大小的宏观 标志。初态温度较高的物体,粒子的平均平动动能较大,粒 子无规热运动比较剧烈,而温度较低的物体,粒子的平均平 动动能较小,粒子无规热运动不太剧烈。若用粒子平均平动 动能的大小来区分它们是不可能了,也就是说末态与初态比 较,两个物体的系统的无序度增大了,这种自发的热传导过 程是向着无规热运动更加无序的方向进行的。
热机Q2
A , A
E
Q1
Q1
T1
A Q2
Q1 可
逆 热 机
T2 E’
用反证法,假设
得到
A A Q1 Q1
Q1 Q1
Q1 Q2 Q1 Q2
Q2 Q2
两部热机一起工作,成为一部复合机,结果外界不对复合
机作功,而复合机却将热量 Q1 Q2 Q1 Q2 从低温热源送到高温热源,违反热力学第二定律。
自然界中的自发热传导具有方向性。
通过某一过程,一个系统从某一状态变为另一状态, 若存在另一过程,能使系统与外界同时复原,则原来的过 程就是一个可逆过程。否则,若系统与外界无论怎样都不 能同时复原,则称原过程为不可逆过程。单摆在不受空气 阻力和摩擦情况下的运动就是一个可逆过程。
注意:不可逆过程不是不能逆向进行,而是说当过程逆向 进行时,逆过程在外界留下的痕迹不能将原来正过程的痕 迹完全消除。
现在考虑4个分别染了不同颜色的分子。开始时,4个分 子都在A部,抽出隔板后分子将向B部扩散并在整个容器内无 规则运动。隔板被抽出后,4分子在容器中可能的分布情形如 下图所示:
大学物理_热力学基础PPT课件

C Mc
摩尔热容量:1mol物质的热容量(Cm) J K 1 mol 1
C
M
Cm
第11页/共60页
热容量CY与过程有关:
CY
(
dQ dT
)Y
热容量C的可能值:
C 0 吸热且升温 T 0
C 0 放热且升温 T 0 C 0 Q 0 绝热过程
C 等温过程 T 0
稳定性要求 C 0
第1页/共60页
§7-1 热力学第一定律
一 功 宏观运动能量
热运动能量 (过程量)
功是能量传递和转换的量度,它引起系统热运动
状态的变化 .
准静态过程功的计算
dW Fdl pSdl
dW pdV
W V2 pdV V1
注意:作功与过程有关 .
第2页/共60页
二 热 量(过程量)
通过传热方式传递能量的量度,系统和外界之间
第5页/共60页
理想气体内能 : 表征系统状态的单值函数 , 理想气体的内能仅是温度的函数 .
E E(T )
系统内能的增量只与系统起始和终了状态有
关,与系统所经历的过程无关 .
p
p
A*
1
A*
1
2 *B
o
V
2 *B
o
V
EAB C
EA1B2 A 0
改变系统内能的两种等效方式: 作功, 传递热量
第6页/共60页
双原子理想气体
7 Cp 2 R
多原子理想气体 Cp 4R
第14页/共60页
3、比热容比 理想气体
Cp
CV C p CV R
i CV 2 R
i2
i 例7-1 教材 P230
第15页/共60页
大学物理-热力学基础-课件
Wa
CV m (T2
T1)
p1V1 p2V2
1
本题用 Wa E 计算较方便
关键用绝热方程
T2
T1
( V1 V2
)
1
先求出 T2
p
p2
2 T2
T2' T1
Q0
p2'
2'
p1
TC
T1
1
o V2 V2' V1 10 V1 V
18.
*四. 多方过程 — 实际过程( 满足 PV n C)
绝热 n = ( CPm / CVm )
等温 n = 1 等压 n = 0
W p1V1 p2V2 n 1
满足 E CV (T2 T1)
Q Cn (T2 T1)
等体 n = ∞
p
可以证明
n= n=∞
n=1
Cn
(
n
n 1
)CV
n=0
o
V
19.
13 – 5 循环过程 卡诺循环
一. 循环过程
1. 特点 E 0 W = Q ( 热功转换 )
1
2
W
(2)热一定律 dQP dE PdV
o V1
V2 V
QP
E
V2 PdV
V1
v
i 2
R(T2
T1 )
P(V2
V1 )
7.
2.摩尔定压热容 CPm
1mol
:
CPm
dQp dT
理论值:
CPm
dE pdV dT
CVm
R
i2R 2
(近似)
实验值:查表 (精确)
QP
dQP
2024年度大学物理热力学基础PPT课件

18
绝热过程和多方过程
绝热过程
系统与外界无热量交换,内能变化只由做功引起。
多方过程
系统状态变化遵循一定的规律,如压强与体积的特定关系,可用于描述某些实 际过程。
2024/2/2
19
循环过程与热机效率
循环过程
系统经历一系列状态变化后回到初始状态,完成一个循环。
热机效率
热机从高温热源吸收的热量与向低温热源放出的热量之差与吸收的热量之比,反映了热机的性能。
15
热力学函数的计算与应用
热力学函数的计算
根据系统的状态方程和状态参量,可以计算各种热力学函数的值。此外,还可以通过实验测量某些热 力学函数的值。
热力学函数的应用
热力学函数在能源、环境、材料等领域有广泛应用。例如,利用热力学函数可以评估能源利用效率、 预测材料性能、优化工艺过程等。同时,热力学函数也为理解自然现象和生命过程提供了重要工具。
未来趋势
03
关注非平衡态热力学、微观热力学等领域的研究,探索新的理
论和应用。
5
本课程的学习目标和方法
学习目标
掌握热力学基本概念、定律和理论,了解热力学在各 个领域的应用。
学习方法
理论学习与实验相结合,注重理解和应用热力学原理 。
学习建议
多做习题,加强理解和记忆;关注热力学前沿动态, 拓宽知识面。
2024/2/2
铁磁物质的居里点转变。
2024/2/2
23
相平衡条件与相图分析
相平衡条件
多相系统中各相之间达到动态平衡的条 件,包括热平衡、力平衡和化学平衡。
单组分系统相图
2024/2/2
如水的P-T相图,展示了水的固、液 、气三相在不同温度和压力下的平衡
大学物理 第六章

一定的时间, 系统达到一个稳定的, 宏观性质不随 时间变化的状态称为平衡态 .(理想状态)
真空膨胀 p
( p,V ,T )
p,V ,T
( p',V ',T )
o
V
p',V ',T
第六章热力学基础
平衡态的特点
( p,V ,T )
p
*( p,V ,T )
o
V
1)单一性( p,T 处处相等);
2)物态的稳定性—— 与时间无关; 3)自发过程的终点; 4)热动平衡(有别于力平衡).
第六章热力学基础
第六章热力学基础
燧人氏又称“燧人”,远古人“茹毛饮血”,他钻木 取火,教人熟食,是人工取火的发明者。关于他 的神话反映了中国原始时代从利用自然火,进化 到人工取火的情况。
第六章热力学基础
教学基本要求
一 掌握内能、功和热量等概念 . 理解准静 态过程 .
二 掌握热力学第一定律,能分析、计算理 想气体在等体、等压、等温和绝热过程中的功、 热量和内能的改变量 .
p
A*
1
p
A*
1
2 *B
o
V
EAB C
2 *B
o
V
EA1B2 A 0
第六章热力学基础
二 热力学第一定律
Q E2 E1 A
p
1*
系统从外界吸收的热量,
*2
一部分使系统的内能增加, 另
一部分使系统对外界做功 .
o V1
V2 V
Q E2 E1 A E A
准静态过程 微小过程
1atm 1.013 105 Pa
2 体积 V : 气体所能达到的最大空间(几何
真空膨胀 p
( p,V ,T )
p,V ,T
( p',V ',T )
o
V
p',V ',T
第六章热力学基础
平衡态的特点
( p,V ,T )
p
*( p,V ,T )
o
V
1)单一性( p,T 处处相等);
2)物态的稳定性—— 与时间无关; 3)自发过程的终点; 4)热动平衡(有别于力平衡).
第六章热力学基础
第六章热力学基础
燧人氏又称“燧人”,远古人“茹毛饮血”,他钻木 取火,教人熟食,是人工取火的发明者。关于他 的神话反映了中国原始时代从利用自然火,进化 到人工取火的情况。
第六章热力学基础
教学基本要求
一 掌握内能、功和热量等概念 . 理解准静 态过程 .
二 掌握热力学第一定律,能分析、计算理 想气体在等体、等压、等温和绝热过程中的功、 热量和内能的改变量 .
p
A*
1
p
A*
1
2 *B
o
V
EAB C
2 *B
o
V
EA1B2 A 0
第六章热力学基础
二 热力学第一定律
Q E2 E1 A
p
1*
系统从外界吸收的热量,
*2
一部分使系统的内能增加, 另
一部分使系统对外界做功 .
o V1
V2 V
Q E2 E1 A E A
准静态过程 微小过程
1atm 1.013 105 Pa
2 体积 V : 气体所能达到的最大空间(几何
北邮大物上10热力学基础20100528

各种热机的效率 液体燃料火箭 48% 柴油机 汽油机 蒸气机
37%
25%
8%
热机 : 持续地将热量转变为功的机器 .
冰箱循环示意图
一 循环过程
系统经过一系列变化状态过程后,又 回到原来的状态的过程叫热力学循环过程 . p 特征 E 0 A c W 由热力学第一定律 d B Q W
o
VA
VB V
净功 W Q1 Q2 Q 总吸热 总放热 净吸热
Q1
Q2
(取绝对值)
Q
二 热机效率和致冷机的致冷系数
热机(正循环) W 0 致冷机(逆循环) W 0
p
A
c
W
d
高温热源 Q1
B
VB V
o
VA
热机 Q2 低温热源
W
W Q1 Q2 Q2 1 热机效率 Q1 Q1 Q1
b c d
T↓
ΔE 0
ΔE1 ΔE2 ΔE3 A1 A2 A3
O
V0
2V0
V
(3) 又
且 故
Q ΔE A
Q1 Q2 Q3
例2 氮气液化, 把氮气放在一个绝热 的汽缸中.开始时,氮气的压强为50个标准大 气压、温度为300K;经急速膨胀后,其压 强降至 1个标准大气压,从而使氮气液化. 试问此时氮的温度为多少?
Q E2 E1 W E W
第一定律的符号规定
Q
E
内能增加
内能减少
W
系统对外界做功
外界对系统做功
+
系统吸热
系统放热
物理意义 (1)能量转换和守恒定律. 第一类永动机 是不可能制成的. (2)实验经验总结,自然界的普遍规律.
大学物理上册第六章-功 热量

二 等压过程 摩尔定压热容
特 性 p 常量
过程方程 VT 1 常量
功 W p(V2 V1)
p
p
( p,V1,T1) ( p,V2,T2)
1
2
W
热一律 dQp dE dW o V1 V2 V
摩尔定压热容: 1mol 理想气体在等压过程中吸
收的热量dQp ,温度升高 dT,其摩尔定压热容为
C p,m
第一类永动机是不可能制成的 .
2)实验经验总结,自然界的普遍规律 .
第六章 热力学基础
6 – 1 功 热量
物理学教程 (第二版)
计算各等值过程的热量、功和内能的理论基础
(1) pV m RT (理想气体的共性) M
(2)
dQ dE pdV
Q E V2 pdV V1
解决过程中能 量转换的问题
o
V
WA1B QA1B WA2B QA2B WA1B2 A QA1B2 A 0
第六章 热力学基础
6 – 1 功 热量
物理学教程 (第二版)
理想气体内能 : 表征系统状态的单值函数 ,
理想气体的内能仅是温度的函数 .
E E(T )
系统内能的增量只与系统起始和终了状态有 关,与系统所经历的过程无关 .
V
摩尔定体热容: 1mol理想气体在等体过程中吸
收的热量 dQV,使温度升高 dT, 其摩尔定体热容为
CV ,m
dQV dT
dQV CV ,mdT
单位 J mol1 K1
第六章 热力学基础
6 – 1 功 热量
物理学教程 (第二版)
CV ,m
dQV dT
dQV
dE
m' M CV ,mdT
大学物理 热力学基础详解

解:等压过程 A= pΔV=(M /Mmol)RΔT
内能增量
双原子分子 ∴
i i E ( M / M ) R T A mal 2 2
1 J Q E A iA A 7 2
i 5
3、等温过程:(dT=0) 内能: E=0
M P M V 1 2 RT ln A PdV RT ln V M P 1 M V mol 2 m ol 1
理想极限:将砝码无限 细分,足够缓慢地取走 它们,在 PV 图上
可得一曲线。
P
1
2
V
砂子 活塞 气体
p
p1
p2
1 (p , V , T ) 1 1 1
, V , T ) 2 (p 2 2 2
o
V1
V2
V
这种进行得足够缓慢, 以至于连续经过的每一 个中间过程
近似地看成平衡态的过 程称为准静态过程。
对于准静态过程,系统所经历
(3)、(4)、(5)式称为绝热方程 (或泊松公式)。
注意:式中的各常数不相同!!!
绝热线比等温线陡 (1)、等温:PV=const
0 (2)、绝热: PV const
PA dp A点的斜率: dVa V A
PA dp A点的斜率: VA dV T
一、内能 E(焦耳J)
理想气体内能:
内能是状态参量
M i E RT Mmol 2
T 的单值函数。
p Ⅰ E
内能的增量 E = E - E 2 1
只取决于系统的始末状态, 而与过程无关。
E
Ⅱ V
系统内能改变的两种方式: 做功 热传递
1、 功是能量传递与转化的量度。 功是过程量而非态函数。两个平衡态之间可经历 不同的过程,系统所做的功不同。 2、热量是系统与外界存在温度差而传递的能量
内能增量
双原子分子 ∴
i i E ( M / M ) R T A mal 2 2
1 J Q E A iA A 7 2
i 5
3、等温过程:(dT=0) 内能: E=0
M P M V 1 2 RT ln A PdV RT ln V M P 1 M V mol 2 m ol 1
理想极限:将砝码无限 细分,足够缓慢地取走 它们,在 PV 图上
可得一曲线。
P
1
2
V
砂子 活塞 气体
p
p1
p2
1 (p , V , T ) 1 1 1
, V , T ) 2 (p 2 2 2
o
V1
V2
V
这种进行得足够缓慢, 以至于连续经过的每一 个中间过程
近似地看成平衡态的过 程称为准静态过程。
对于准静态过程,系统所经历
(3)、(4)、(5)式称为绝热方程 (或泊松公式)。
注意:式中的各常数不相同!!!
绝热线比等温线陡 (1)、等温:PV=const
0 (2)、绝热: PV const
PA dp A点的斜率: dVa V A
PA dp A点的斜率: VA dV T
一、内能 E(焦耳J)
理想气体内能:
内能是状态参量
M i E RT Mmol 2
T 的单值函数。
p Ⅰ E
内能的增量 E = E - E 2 1
只取决于系统的始末状态, 而与过程无关。
E
Ⅱ V
系统内能改变的两种方式: 做功 热传递
1、 功是能量传递与转化的量度。 功是过程量而非态函数。两个平衡态之间可经历 不同的过程,系统所做的功不同。 2、热量是系统与外界存在温度差而传递的能量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( p1 ,V , T1 )
p
o
等 体 降 p2 压
p1
1 ( p1,V , T1 )
( p2 ,V , T2 )
V
2
V
V
V
o
QV
E1
E2
QV
E1
E2
30
二 等压过程 摩尔定压热容
特性
p 常量
过程方程 VT 1 常量 p ( p,V1, T1 ) ( p,V2 ,T2 ) p 功 W p(V2 V1 ) 2 1 由热力学第一定律 W
18
热力学理论
19
一 热力学第一定律
p
1*
*2
Q E2 E1 W
系统从外界吸收的热 量,一部分使系统的内能 增加,另一部分使系统对 外界做功 .
o
V1
V2 V
Q E2 E1 W E W
20
准静态过程
Q E
微变过程
V2
V1
pdV
dQ dE dW dE pdV
dp pA ( )T dV VA
pA
o
V A V V B
V
绝热线的斜率大于等温线的斜率.
48
例1 设有 5 mol 的氢气,最初温度20 C , 压强 1.013105 Pa ,求下列过程中把氢气压缩 为原体积的 1/10 需作的功: (1)等温过程 (2)绝热过程 (3)经这两过程后,气体的 p 2 压强各为多少? T T' T
o V1 dV
dE CV ,mdT
绝热的汽缸壁和活塞
41
W pdV
V1
V2
CV ,mdT
T1
T2
CV ,m (T2 T1 )
由热力学第一定律有
p
p1
1 ( p1, 1, 1 ) V T
W E
W CV ,m (T1 T2 )
p2
( p2 , 2 ,T2 ) V
dQT dW pdV
38
QT W
V2
V1
pdV
RT p V
RT V2 QT W dV RT ln V1 V V1
V2
p1 RT ln p2
39
等温膨胀
等温压缩
p p1
p2
V T 1 ( p1, 1, )
p p1
2
V2
1 ( p1, 1, ) V T
E1
W
p
Qp
E2
E1
W
Qp
E2
36
* 比热容
dQ 热容 C dT
比热容
dQ C c mdT m
37
三 等温过程
T 常量 过程方程 pV 常量
特征
p p1
p2
1 ( p1,V1,T )
( p2 , 2 ,T ) V
2
V1
dE 0
由热力学第一定律
o
恒 温 热 源 T
dV
V2 V
dQ 0 , dW dE
p
p1
V T 1 ( p1, 1, 1 )
pdV CV ,mdT pV RT
RT dV CV ,m dT V
Q0
( p2 , 2 ,T2 ) V 2
V1
V2 V
p2
o
44
CV ,m dT dV 分离变量得 V R T dV 1 dT V 1 T
原理性理论
由现象出发
永动机是不可能成功的
自然遵循什么法则
4
3)相互关系:互相补充,相辅相成
热力学- 宏观理论,基本结论来自实验事实,普 解释 验证
遍可靠,但不能解释其本质
统计物理- 微观理论,揭示热现象本质
热力学第一定 律的创始人
热力学第二定 律的创始人
5
大量粒子组成的宏观、有限的体系称为热力学系统。 与其比邻的环境称为外界。
1
1
(3)对等温过程
V1 p2 p1 ( ) V2 1.01 106 P a
p
p2
' p2
2T 2
2'
对绝热过程, 有
V1 p2 p1 ( ) V2 2.5510 P a
6
T2' T1 Q0
p1
T1
o
T 常量
1
V2 V2' V1 10 V1 V
51
例2 一汽缸内有一定的水,缸壁由良导 热材料制成. 作用于活塞上的压强1.013105 Pa 摩擦不计. 开始时,活塞与水面接触. 若环境 (热源) 温度非常缓慢地升高到100 C . 求把单 位质量的水汽化为水蒸气,内能改变多少?
V1 1 T2 T1 ( ) 753K V2
' p2
2T 2
2'
T2' T1 Q0
p1
T1
o
T 常量
1
V2 V2' V1 10 V1 V
50
W12 CV ,m (T2 T1 )
W12 4.70 104 J
CV ,m 20.44 J mol K
热力学基础
1
当一个科学家发现,自然界 的结构有这么多不可思议的奥妙, 他会有一个触及灵魂的震动。而 这个时候的感觉,我想是和最真 诚的宗教信仰很接近的。 ---杨振宁
2
结构框图
热力学系统 内能变化的 两种量度
等值过程
功
热量
应用 热力学 第一定律 (理想气体) 热力学 第二定律
(对热机效率的研究)
WA1B 2 A QA1B 2 A 0
16
理想气体内能 :
表征系统状态的单值函数 ,理想气体 的内能仅是温度的函数 .
E E (T )
17
系统内能的增量只与系统的初态和末 态有关,与系统所经历的过程无关 .
p
A*
2 1 *B
p
A*
2 1 *B
o
V
o
V
E AB C
E A1B 2 A 0
已知 汽化热 密度
L 2.26106 J kg1
水 1 040kg m3
V1
V2
dA
系统对外 界做功
若
外界对系 统做功
循环过程 的功
dV 0 dA 0 dV 0 dA 0 dV 0 dA 0
三 热 量(过程量)
通过传热方式传递能量的量度,系统 和外界之间存在温差而发生的能量传递 .
T1 T2
T1 Q T2
11
系统比热的定义
c dQ / mdT
绝热过程
循环过程 卡诺循环物理——技术模式 •两种研究方法——两种理论
1)微观理论-《统计物理》
物质的微观结构 统计方法 确定宏观量与微观量的联系, 平均效果 描述热现象的规律和本质 粒子的热运动 由基本假设 构造性理论
2)宏观理论-《热力学》
观测 实验
归纳
热现象基本定律,宏观过程进行的 方向和限度,不涉及微观本质
13
作机械功改变系统 状态的焦耳实验
作电功改变系统 状态的实验
A
V
14
四 内能 (状态量)
实验证明系统从状态A 变化到状态B, 可以采用做功和传热的方法,不管经过 什么过程,只要始末状态确定,做功和 传热之和保持不变.
15
p
A*
2
1
p
A*
*B
2 1
*B
o
V
o
V
WA1B QA1B WA2 B QA2 B
可得摩尔定压热容和摩尔定体热容的关系
C p,m = CV ,m + R
摩尔热容比
= C p,m CV ,m
泊松比
33
补充 *理想气体等容摩尔热容
*理想气体等压摩尔热容
i CV R 2
3 R 刚性单原子 2 5 R 刚性双原子 2 6 R 刚性多原子 2
i2 CP R 2
CP CV R 迈耶公式
V
1
T
常量
绝 V 1T 常量 热 pV 常量 方 1 程 p T 常量
45
绝热膨胀
p
p1
V T 1 ( p1, 1, 1 )
绝热压缩
p
p2
2 ( p , ,T ) 2 V2 2
p2
W
( p2 ,V2 ,T2 ) 2
p1
W
( p1, 1, 1 ) V T 1
dQV = CV ,mdT
单位 J mol1 K 1
28
mol 理想气体
CV ,m dQV = dT
dQV = dE = CV ,mdT
由热力学第一定律
QV CV ,m (T2 T1 ) E2 E1
29
p
等 体 升 p1 压
p2
2 ( p ,V , T ) 2 2 1
开放系统:
与外界有 m、E 交换
封闭系统: 与外界有 E 交换,无 m 交换 孤立系统:
与外界无 E、m 交换
绝 热 开放系统 封闭系统 孤立系统
6
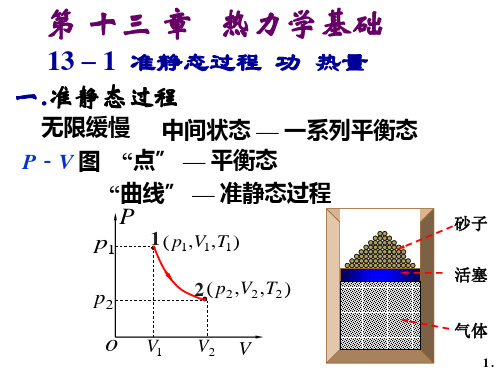
一 准静态过程(理想化的过程)
从一个平衡态到另一平衡态所经过的每 一中间状态均可近似当作平衡态的过程 .
p
砂子 活塞
p1
p2
1 ( p ,V , T ) 1 1 1
o
V1
dQ p dE dW
V2
V
31
摩尔定压热容: 1 mol 理想气体在等压 过程中吸收热量 dQ p ,温度升高 dT ,其 摩尔定压热容为:
p
o
等 体 降 p2 压
p1
1 ( p1,V , T1 )
( p2 ,V , T2 )
V
2
V
V
V
o
QV
E1
E2
QV
E1
E2
30
二 等压过程 摩尔定压热容
特性
p 常量
过程方程 VT 1 常量 p ( p,V1, T1 ) ( p,V2 ,T2 ) p 功 W p(V2 V1 ) 2 1 由热力学第一定律 W
18
热力学理论
19
一 热力学第一定律
p
1*
*2
Q E2 E1 W
系统从外界吸收的热 量,一部分使系统的内能 增加,另一部分使系统对 外界做功 .
o
V1
V2 V
Q E2 E1 W E W
20
准静态过程
Q E
微变过程
V2
V1
pdV
dQ dE dW dE pdV
dp pA ( )T dV VA
pA
o
V A V V B
V
绝热线的斜率大于等温线的斜率.
48
例1 设有 5 mol 的氢气,最初温度20 C , 压强 1.013105 Pa ,求下列过程中把氢气压缩 为原体积的 1/10 需作的功: (1)等温过程 (2)绝热过程 (3)经这两过程后,气体的 p 2 压强各为多少? T T' T
o V1 dV
dE CV ,mdT
绝热的汽缸壁和活塞
41
W pdV
V1
V2
CV ,mdT
T1
T2
CV ,m (T2 T1 )
由热力学第一定律有
p
p1
1 ( p1, 1, 1 ) V T
W E
W CV ,m (T1 T2 )
p2
( p2 , 2 ,T2 ) V
dQT dW pdV
38
QT W
V2
V1
pdV
RT p V
RT V2 QT W dV RT ln V1 V V1
V2
p1 RT ln p2
39
等温膨胀
等温压缩
p p1
p2
V T 1 ( p1, 1, )
p p1
2
V2
1 ( p1, 1, ) V T
E1
W
p
Qp
E2
E1
W
Qp
E2
36
* 比热容
dQ 热容 C dT
比热容
dQ C c mdT m
37
三 等温过程
T 常量 过程方程 pV 常量
特征
p p1
p2
1 ( p1,V1,T )
( p2 , 2 ,T ) V
2
V1
dE 0
由热力学第一定律
o
恒 温 热 源 T
dV
V2 V
dQ 0 , dW dE
p
p1
V T 1 ( p1, 1, 1 )
pdV CV ,mdT pV RT
RT dV CV ,m dT V
Q0
( p2 , 2 ,T2 ) V 2
V1
V2 V
p2
o
44
CV ,m dT dV 分离变量得 V R T dV 1 dT V 1 T
原理性理论
由现象出发
永动机是不可能成功的
自然遵循什么法则
4
3)相互关系:互相补充,相辅相成
热力学- 宏观理论,基本结论来自实验事实,普 解释 验证
遍可靠,但不能解释其本质
统计物理- 微观理论,揭示热现象本质
热力学第一定 律的创始人
热力学第二定 律的创始人
5
大量粒子组成的宏观、有限的体系称为热力学系统。 与其比邻的环境称为外界。
1
1
(3)对等温过程
V1 p2 p1 ( ) V2 1.01 106 P a
p
p2
' p2
2T 2
2'
对绝热过程, 有
V1 p2 p1 ( ) V2 2.5510 P a
6
T2' T1 Q0
p1
T1
o
T 常量
1
V2 V2' V1 10 V1 V
51
例2 一汽缸内有一定的水,缸壁由良导 热材料制成. 作用于活塞上的压强1.013105 Pa 摩擦不计. 开始时,活塞与水面接触. 若环境 (热源) 温度非常缓慢地升高到100 C . 求把单 位质量的水汽化为水蒸气,内能改变多少?
V1 1 T2 T1 ( ) 753K V2
' p2
2T 2
2'
T2' T1 Q0
p1
T1
o
T 常量
1
V2 V2' V1 10 V1 V
50
W12 CV ,m (T2 T1 )
W12 4.70 104 J
CV ,m 20.44 J mol K
热力学基础
1
当一个科学家发现,自然界 的结构有这么多不可思议的奥妙, 他会有一个触及灵魂的震动。而 这个时候的感觉,我想是和最真 诚的宗教信仰很接近的。 ---杨振宁
2
结构框图
热力学系统 内能变化的 两种量度
等值过程
功
热量
应用 热力学 第一定律 (理想气体) 热力学 第二定律
(对热机效率的研究)
WA1B 2 A QA1B 2 A 0
16
理想气体内能 :
表征系统状态的单值函数 ,理想气体 的内能仅是温度的函数 .
E E (T )
17
系统内能的增量只与系统的初态和末 态有关,与系统所经历的过程无关 .
p
A*
2 1 *B
p
A*
2 1 *B
o
V
o
V
E AB C
E A1B 2 A 0
已知 汽化热 密度
L 2.26106 J kg1
水 1 040kg m3
V1
V2
dA
系统对外 界做功
若
外界对系 统做功
循环过程 的功
dV 0 dA 0 dV 0 dA 0 dV 0 dA 0
三 热 量(过程量)
通过传热方式传递能量的量度,系统 和外界之间存在温差而发生的能量传递 .
T1 T2
T1 Q T2
11
系统比热的定义
c dQ / mdT
绝热过程
循环过程 卡诺循环物理——技术模式 •两种研究方法——两种理论
1)微观理论-《统计物理》
物质的微观结构 统计方法 确定宏观量与微观量的联系, 平均效果 描述热现象的规律和本质 粒子的热运动 由基本假设 构造性理论
2)宏观理论-《热力学》
观测 实验
归纳
热现象基本定律,宏观过程进行的 方向和限度,不涉及微观本质
13
作机械功改变系统 状态的焦耳实验
作电功改变系统 状态的实验
A
V
14
四 内能 (状态量)
实验证明系统从状态A 变化到状态B, 可以采用做功和传热的方法,不管经过 什么过程,只要始末状态确定,做功和 传热之和保持不变.
15
p
A*
2
1
p
A*
*B
2 1
*B
o
V
o
V
WA1B QA1B WA2 B QA2 B
可得摩尔定压热容和摩尔定体热容的关系
C p,m = CV ,m + R
摩尔热容比
= C p,m CV ,m
泊松比
33
补充 *理想气体等容摩尔热容
*理想气体等压摩尔热容
i CV R 2
3 R 刚性单原子 2 5 R 刚性双原子 2 6 R 刚性多原子 2
i2 CP R 2
CP CV R 迈耶公式
V
1
T
常量
绝 V 1T 常量 热 pV 常量 方 1 程 p T 常量
45
绝热膨胀
p
p1
V T 1 ( p1, 1, 1 )
绝热压缩
p
p2
2 ( p , ,T ) 2 V2 2
p2
W
( p2 ,V2 ,T2 ) 2
p1
W
( p1, 1, 1 ) V T 1
dQV = CV ,mdT
单位 J mol1 K 1
28
mol 理想气体
CV ,m dQV = dT
dQV = dE = CV ,mdT
由热力学第一定律
QV CV ,m (T2 T1 ) E2 E1
29
p
等 体 升 p1 压
p2
2 ( p ,V , T ) 2 2 1
开放系统:
与外界有 m、E 交换
封闭系统: 与外界有 E 交换,无 m 交换 孤立系统:
与外界无 E、m 交换
绝 热 开放系统 封闭系统 孤立系统
6
一 准静态过程(理想化的过程)
从一个平衡态到另一平衡态所经过的每 一中间状态均可近似当作平衡态的过程 .
p
砂子 活塞
p1
p2
1 ( p ,V , T ) 1 1 1
o
V1
dQ p dE dW
V2
V
31
摩尔定压热容: 1 mol 理想气体在等压 过程中吸收热量 dQ p ,温度升高 dT ,其 摩尔定压热容为:
