信息论试题6
信息论考试题

一.填空1.设X的取值受限于有限区间[a,b ],则X 服从 均匀 分布时,其熵达到最大;如X 的均值为μ,方差受限为2σ,则X 服从 高斯 分布时,其熵达到最大。
2.信息论不等式:对于任意实数0>z ,有1ln -≤z z ,当且仅当1=z 时等式成立。
3.设信源为X={0,1},P (0)=1/8,则信源的熵为 )8/7(log 8/78log 8/122+比特/符号,如信源发出由m 个“0”和(100-m )个“1”构成的序列,序列的自信息量为)8/7(log )100(8log22m m -+比特/符号。
4.离散对称信道输入等概率时,输出为 等概 分布。
5.根据码字所含的码元的个数,编码可分为 定长 编码和 变长 编码。
6.设DMS 为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡03.007.010.018.025.037.0.654321u u u u u u P U U ,用二元符号表}1,0{21===x x X 对其进行定长编码,若所编的码为{000,001,010,011,100,101},则编码器输出码元的一维概率=)(1x P 0.747 , =)(2x P 0.253 。
12设有DMC,其转移矩阵为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2/16/13/13/12/16/16/13/12/1|XY P ,若信道输入概率为[][]25.025.05.0=X P ,试确定最佳译码规则和极大似然译码规则,并计算出相应的平均差错率。
解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=8/124/112/112/18/124/112/16/14/1][XYP最佳译码规则:⎪⎩⎪⎨⎧===331211)()()(ab F a b F a b F ,平均差错率为1-1/4-1/6-1/8=11/24;极大似然规则:⎪⎩⎪⎨⎧===332211)()()(ab F a b F a b F ,平均差错率为1-1/4-1/8-1/8=1/2。
信息论试题6

一、填空题(共15分,每空1分)1、当 时,信源与信道达到匹配。
2、若高斯白噪声的平均功率为6 W ,则噪声熵为 。
如果一个平均功率为9 W 的连续信源的熵等于该噪声熵,则该连续信源的熵功率为 。
3、信源符号的相关程度越大,信源的符号熵越 ,信源的剩余度越 。
4、离散无记忆信源在进行无失真变长信源编码时,码字长度是变化的。
根据信源符号的统计特性,对概率 的符号用短码,对概率 的符号用长码,从而减少平均码长,提高编码效率。
8、香农第一编码定理指出平均码长的理论极限值为 ,此时编码效率为 。
4、在下面空格中选择填入数学符号“=,≥,≤,>”或“<” (1)()()2212X X H H =X ()X 3H = ()3321X X X H(2)()XY H ()()Y X H Y H |+ ()()X H Y H +。
9、有一信源X ,其概率分布为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡818141214321xx x x P X ,若对该信源进行100次扩展,则每扩展符号的平均信息量是 。
11、当时,信源熵为最大值。
8进制信源的最大熵为。
二、判断题(正确打√,错误打×)(共5分,每小题1分)1)噪声功率相同的加性噪声信道中以高斯噪声信道的容量为最大。
()2)即时码可以在一个码字后面添上一些码元构成另一个码字。
()3)连续信源的熵可正、可负、可为零,()4)平均互信息始终是非负的。
()5)信道容量C只与信道的统计特性有关,而与输入信源的概率分布无关。
()三、(10分)计算机终端发出A 、B 、C 、D 、E 五种符号,出现概率分别为1/16,1/16,1/8,1/4,1/2。
通过一条带宽为18kHz 的信道传输数据,假设信道输出信噪比为2047,试计算:1) 香农信道容量;2) 无误码传输的最高符号速率。
四、(10分)有一信源发出恒定宽度,但不同幅度的脉冲,幅度值x 处在1a 和2a 之间。
(完整word版)信息论试卷

一、选择题1、下列那位创立了信息论.(C)A.牛顿B.高斯C.香农D.哈夫曼2、下列不属于消息的是。
(B)A.文字B.信号C.图像D.语言3、同时扔两个正常的骰子,即各面呈现的概率都是1/6,若点数之和为2,则得到的自信息量为(B)。
A.-log36 bitB.log36 bitC.-log18 bitD.log18 bit4、下列说法不正确的是(C)A.异字头码肯定是唯一可译的B.逗点码是唯一可译的C.唯一可译码不必满足Kraft 不等式D.无逗点码可以唯一可译5、下述编码中那个可能是任何概率分布对应的Huffman编码(A)A.{0,10,11}B.{00,01,10,110}C.{01,10}D.{001,011,100,101}6、下列物理量不满足非负性的是(D)A.H(X)B.I(X;Y)C.H(Y|X)D.I(x j;y j)7、信源的输出与信道的输入匹配的目的不包括(D)A.符号匹配B.信息匹配C.降低信道剩余度D.功率匹配8、在串联系统中,有效信息量的值(B)A.趋于变大B.趋于变小C.不变D.不确定二、判断题1、信息论研究的主要问题是在通信系统设计中如何实现信息传输、存储和处理的有效性和可靠性。
(T)2、信息是先验概率和后验概率的函数,信息量是事件数目的指数函数。
(F)提示:对数函数3、两个事件之间的互信息量可正,可负,也可能为0。
(T)4、在通讯系统中,无论对接收到的信息怎样处理,信息只会减少,绝不可能增加。
(T )5、Huffman 编码是唯一的.(F)提示:不唯一6、概率大的事件自信息量大。
(F )提示:小7、在事件个数相同条件下,事件等概率出现情况下的熵值最大。
(T)8、平稳的离散无记忆信道不可用一维概率描述。
(F)提示:可以三、填空题1、必然事件的自信息是 0 .2、根据码字所含的码元的个数,编码可分为 等长 编码和 不等长 编码。
3、不等长D 元码,码字最长限定为N,则至多有 D(D N - 1)/(D — 1) 个码字。
信息论测试题及答案

一、设X 、Y 就是两个相互统计独立的二元随机变量,其取-1或1的概率相等。
定义另一个二元随机变量Z,取Z=YX(一般乘积)。
试计算:1、H(Y)、H(Z);2、H(YZ);3、I(X;Y)、I(Y;Z); 二、如图所示为一个三状态马尔科夫信源的转移概率矩阵1. 绘制状态转移图; 2、 求该马尔科夫信源的稳态分布;3、 求极限熵;三、在干扰离散对称信道上传输符号1与0,已知P(0)=1/4,P(1)=3/4,试求:1. 信道转移概率矩阵P 2、信道疑义度 3、信道容量以及其输入概率分布 四、某信道的转移矩阵⎥⎦⎤⎢⎣⎡=1.006.03.001.03.06.0P ,求信道容量,最佳输入概率分布。
五、求下列各离散信道的容量(其条件概率P(Y/X)如下:)六、求以下各信道矩阵代表的信道的容量答案一、设X 、Y 就是两个相互统计独立的二元随机变量,其取-1或1的概率相等。
定义另一个二元随机变量Z,取Z=YX(一般乘积)。
试计算:1、H(Y)、H(Z);2、H(XY)、H(YZ);3、I(X;Y)、I(Y;Z); 解:1、 2i 11111H Y P y logP y log log 2222i i =⎡⎤=-+⎢⎥⎣⎦∑()=-()()=1bit/符号 Z=YX 而且X 与Y 相互独立∴ 1(1)(1)(1)PP X P Y P X ⋅=+=-⋅=-(Z =1)=P(Y=1)= 1111122222⨯+⨯= 2(1)(1)(1)P P X P Y P X ⋅=-+=-⋅=(Z =-1)=P(Y=1)= 1111122222⨯+⨯=故H(Z)= i2i1(z )log (z )i P P =-∑=1bit/符号2、从上式可以瞧出:Y 与X 的联合概率分布为:H(YZ)=H(X)+H(Y)=1+1=2bit/符号 3、X 与Y 相互独立,故H(X|Y)=H(X)=1bit/符号∴I(X;Y)=H(X)-H(X|Y)=1-1=0bit/符号I(Y;Z)=H(Y)-H(Y|Z)=H(Y)-[H(YZ)-H(Z)]=0 bit/符号 二、如图所示为一个三状态马尔科夫信源的转移概率矩阵2. 绘制状态转移图; 2、 求该马尔科夫信源的稳态分布; 3、 求极限熵;解:1、状态转移图如右图 2、由公式31()()(|)j iji i p E P E P EE ==∑,可得其三个状态的稳态概率为:1123223313123111()()()()22411()()()2211()()()24()()()1P E P E P E P E P E P E P E P E P E P E P E P E P E ⎧=++⎪⎪⎪=+⎪⎨⎪=+⎪⎪⎪++=⎩1233()72()72()7P E P E P E ⎧=⎪⎪⎪⇒=⎨⎪⎪=⎪⎩ 3、其极限熵:3i i 13112112111H = -|E =0+0+72272274243228=1+1+ 1.5=bit/7777i P H H H H ∞=⨯⨯⨯⨯⨯⨯∑(E )(X )(,,)(,,)(,,)符号三、在干扰离散对称信道上传输符号1与0,已知P(0)=1/4,P(1)=3/4,试求:2. 信道转移概率矩阵P 2、信道疑义度 3、信道容量以及其输入概率分布解:1、该转移概率矩阵为 P=0.90.10.10.9⎡⎤⎢⎥⎣⎦2、根据P(XY)=P(Y|X)⋅P(X),可得联合概率由P(X|Y)=P(X|Y)/P(Y)可得H(X|Y)=-i jiji j(x y )log x |y =0.09+0.12+0.15+0.035=0.4bit/P P∑,()符号 3、该信道就是对称信道,其容量为:C=logs-H=log2-H(0、9,0、1)=1-0、469=0、531bit/符号这时,输入符号服从等概率分布,即0111()22X P X ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦四、某信道的转移矩阵⎥⎦⎤⎢⎣⎡=1.006.03.001.03.06.0P ,求信道容量,最佳输入概率分布。
信息论试题

信息论试题一、选择题1. 信息论的创始人是()。
A. 克劳德·香农B. 艾伦·图灵C. 约翰·冯·诺伊曼D. 阿兰·麦席森2. 下列哪个选项是信息论中信息熵的计算公式?()。
A. H(X) = -ΣP(x)log_2P(x)B. H(X) = ΣP(x)xC. H(X) = 1/ΣP(x)D. H(X) = log_2(1/P(x))3. 在信息论中,互信息用于衡量两个随机变量之间的()。
A. 独立性B. 相关性C. 非线性D. 周期性4. 以下哪个不是信息论的应用领域?()。
A. 通信系统B. 密码学C. 机器学习D. 生物遗传学5. 香农极限是指()。
A. 信息传输的最大速率B. 信息压缩的最小冗余度C. 信道容量的理论上限D. 编码长度的最优解二、填空题1. 信息论中的信息熵是衡量信息的不确定性或________的度量。
2. 互信息表示两个随机变量之间共享的信息量,它是衡量两个变量之间________的指标。
3. 香农在1948年发表的论文《________》奠定了信息论的基础。
4. 在数字通信中,信道容量可以通过公式________来计算。
5. 信息论不仅在通信领域有广泛应用,它还对________、数据分析等产生了深远影响。
三、简答题1. 简述信息论的基本原理及其在现代通信中的作用。
2. 描述香农信息论中的主要概念及其相互之间的关系。
3. 说明信息论如何应用于数据压缩技术,并给出一个实际例子。
4. 讨论信息论对于密码学和信息安全的贡献。
四、论述题1. 论述信息论对于人工智能和机器学习领域的影响及其潜在的应用前景。
2. 分析信息论在生物信息学中的应用,以及如何帮助我们更好地理解生物系统的复杂性。
3. 探讨信息论在社会网络分析中的应用,以及它如何帮助我们理解和预测社会行为模式。
4. 评述信息论在量子通信和量子计算中的潜在作用及其对未来科技发展的意义。
信息论典型试题及答案

第五章
5.1将下表所列的信源进行六种不同的二进制编码。
(1)求这些码中哪些是惟一可译码。
(2)哪些码是非延长码
(3)对所有惟一可译码求出其平均码长 。
消息
C1
C2
C3
C4
C5
C6
1/2
000
0
0
0
0
0
1/4
001
01
10
10
10
100
1/16
010
011
110
110
1100
101
27.能够描述无失真信源编码定理
例1:.黑白气象传真图的消息只有黑色和白色两种,求:
1)黑色出现的概率为0.3,白色出现的概率为0.7。给出这个只有两个符号的信源X的数学模型。假设图上黑白消息出现前后没有关联,求熵H(X);
2)假设黑白消息出现前后有关联,其依赖关系为:P(白/白)=0.9,P(黑/白)=0.1,P(白/黑)=0.2,P(黑/黑)=0.8,求其熵H2(X);
10.互信息的性质是什么?
11.熵的表达式、单位、含义是什么?
12.单符号离散信源最大熵是多少?信源概率如何分布时能达到?
13.熵的性质是什么?
14.联合熵、条件熵和熵的关系。
15.平均互信息的定义是什么?平均互信息的表达式怎么推导?
16.平均互信息的含义?
17.信道疑义度、损失熵和噪声熵的含义?
18.平均互信息的性质?(能够证明,并说明每个性质的含义)
解:
由题意可知该二元信道的转移概率矩阵为:
为一个BSC信道
所以由BSC信道的信道容量计算公式得到:
3.14电视图像编码中,若每帧为500行,每行划分为600个像素,每个像素采用8电平量化,且每秒传送30帧图像。试求所需的信息速率(bit/s)。
信息论往年试卷

试题编号:重庆邮电大学2009/2010学年2学期《信息论基础》试卷(期末)(B卷)(开卷)一、填空题(共15分,每空1分)1、若一连续消息通过某放大器,该放大器输出的最大瞬时电压为b,最小瞬时电压为a。
若消息从放大器中输出,则该信源的绝对熵是;其能在每个自由度熵的最大熵是。
2、高斯白噪声信道是指。
3、若连续信源的平均功率为5 W,则最大熵为,达到最大值的条件是。
4、离散信源存在剩余度的原因是和。
5、离散无记忆信源在进行无失真变长信源编码时,编码效率最大可以达到。
6、离散无记忆信源在进行无失真变长信源编码时,码字长度是变化的。
根据信源符号的统计特性,对概率大的符号用码,对概率小的符号用码,这样平均码《信息论基础》试卷第1页《信息论基础》试卷第2页长就可以降低,从而提高编码效率。
7、八进制信源的最小熵为 ,最大熵为 。
8、一个事件发生概率为0.125,则自信息量为 。
9、在下面空格中选择填入数学符号“=,≥,≤,>”或“<”()XY H ()()Y X H Y H |+ ()()X H Y H +。
二、判断题(正确打√,错误打×)(共5分,每小题1分)1)离散无记忆等概信源的剩余度为0。
( ) 2)离散无记忆信源N 次扩展源的熵是原信源熵的N 倍。
( ) 3)互信息可正、可负、可为零。
( ) 4)信源的真正功率P 永远不会大于熵功率P ,即P P ≤。
( ) 5)信道容量与信源输出符号的概率分布有关。
( ) 三、(5分)已知信源的概率密度函数)(x p 如下图所示,求信源的相对熵。
《信息论基础》试卷第3页四、(15分)设一个离散无记忆信源的概率空间为它们通过干扰信道,信道输出端的接收符号集为[]21,b b Y =,已知信道传输概率如下图所示。
试计算:(1)信源X 中事件1x 的自信息量;(3分) (2)信源X 的信息熵;(3分) (3)共熵)(XY H (3分) (4)噪声熵(|)H Y X ;(3分)(5)收到消息Y 后获得的关于信源X 的平均信息量。
信息论考试卷及答案
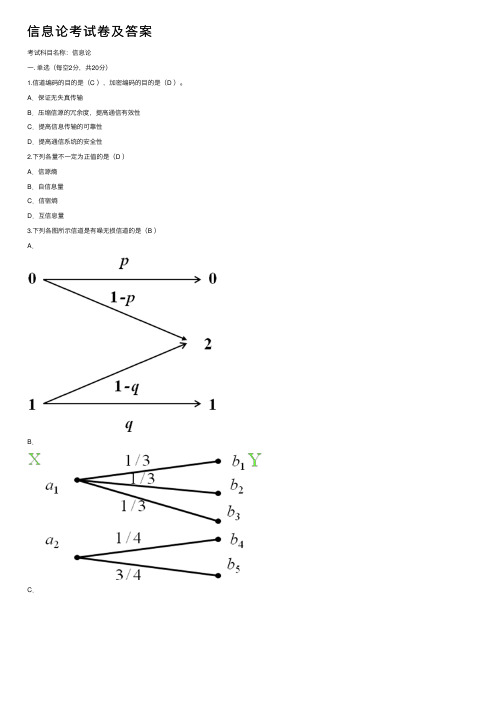
信息论考试卷及答案考试科⽬名称:信息论⼀. 单选(每空2分,共20分)1.信道编码的⽬的是(C ),加密编码的⽬的是(D )。
A.保证⽆失真传输B.压缩信源的冗余度,提⾼通信有效性C.提⾼信息传输的可靠性D.提⾼通信系统的安全性2.下列各量不⼀定为正值的是(D )A.信源熵B.⾃信息量C.信宿熵D.互信息量3.下列各图所⽰信道是有噪⽆损信道的是(B )A.B.C.D.4.下表中符合等长编码的是( A )5.联合熵H(XY)与熵H(X)及条件熵H(X/Y)之间存在关系正确的是(A )A.H(XY)=H(X)+H(Y/X)B.H(XY)=H(X)+H(X/Y)C.H(XY)=H(Y)+H(X)D.若X和Y相互独⽴,H(Y)=H(YX)6.⼀个n位的⼆进制数,该数的每⼀位可从等概率出现的⼆进制码元(0,1)中任取⼀个,这个n位的⼆进制数的⾃信息量为(C )A.n2B.1 bitC.n bitnD.27.已知发送26个英⽂字母和空格,其最⼤信源熵为H0 = log27 = 4.76⽐特/符号;在字母发送概率不等时,其信源熵为H1 = 4.03⽐特/符号;考虑字母之间相关性时,其信源熵为H2 = 3.32⽐特/符号;以此类推,极限熵H=1.5⽐特/符号。
问若⽤⼀般传送⽅式,冗余度为( B )∞A.0.32B.0.68C .0.63D .0.378. 某对称离散信道的信道矩阵为,信道容量为( B )A .)61,61,31,31(24log H C -= B .)61,61,31,31(4log H C -= C .)61,61,31,31(2log H C -= D .)61,31(2log H C -= 9. 下⾯不属于最佳变长编码的是( D )A .⾹农编码和哈夫曼编码B .费诺编码和哈夫曼编码C .费诺编码和⾹农编码D .算术编码和游程编码⼆. 综合(共80分)1. (10分)试写出信源编码的分类,并叙述各种分类编码的概念和特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《信息论基础》试卷第1页
《信息论基础》试卷答案
一、填空题(共15分,每空1分)
1,当(R=C 或信道剩余度为0)时,信源与信道达到匹配。
2,若高斯白噪声的平均功率为6W ,则噪声熵为(1/2log12πe=3。
337bit/自由度) 如果一个平均功率为9W 的连续信源的熵等于该噪声熵,则该连续信源的熵功率为(6W )
3,信源符号的相关程度越大,信源的符号熵越(小),信源的剩余度越(大) 4,离散无记忆信源在进行无失真变长信源编码时,码字长度是变化的。
根据信源符号的统计特性,对概率(大)的符号用短码,对概率(小)的符号用长码,从而减少平均码长,提高编码效率。
8,香农第一编码定理指出平均码长的理论极限值为(信源熵H(S)/logr 或H R (S)), 此时编码效率为(1)
9,在下面空格中选择填入数学符号“=,<,>,≤≥,” 9.1 H 2(X)=H(X 1X 2)/2 ≥ H 3(x)=H(X 1X 2X 3)/3 9.2 H (XY) = H(Y)+H(X/Y) ≤ H(Y)+H(X)
10,有一信源X ,其概率分布为1234x x x x 1/21/41/81/8X P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦
,
若对该信源进行100次扩展, 其每扩展符号的平均信息量是(175bit/扩展符号)
11当(概率为独立等概)时,信源熵为最大值,8进制信源的最大熵为(3bit/符号) 二、判断题(本大题共5小题,每小题1分,共5分)
1)噪声功率相同的加性噪声信道中以高斯噪声信道的容量为最大(⨯) 2)即时码可以在一个码字后面添上一些码元构成另一个码字(⨯) 3)连续信源的熵可正可负可零(∨) 4)平均互信息始终是非负的(∨)
5)信道容量C 只与信道的统计特性有关,而与输入信源概率分布无关(∨) 三、(10分)计算机终端发出 A.B.C.D.E 五种符号,出现概率分别为1/16,1/16,1/8,1/4,1/2.通过一条带宽为18KHz 的信道传输数据,假设信道输出信噪比为2047,试计算:
1)香农信道容量;
2)无误码传输的最高符号速率。
(1) 22log 118log 2048198/t S C B kbit s N ⎛
⎫=+== ⎪⎝
⎭
《信息论基础》试卷第2页
(2)()()
max t
B C R H x =,
()1111115,,,,16168428
H x H ⎛⎫==
⎪⎝⎭
()5198max 1.05610158
B k
R Baud =
=⨯ 四、(10分)有一信源发出恒定宽度,但不同幅度的脉冲,幅度值x 处在a1,a2之间。
此信源连至信道,信道接收端接收脉冲的幅度y 处在b1,b2之间。
已知随机变量x 和y 的联合概率密度函数(,)1/(21)(21)p x y a a b b =-- 试计算h (x ),h (y )h (xy )和I(x;y)
由(,)p x y 得 12211
()0,a x a a a p x ⎧≤≤⎪
-=⎨⎪⎩
其他
()22211
,0,b x b b b p y ⎧≤≤⎪-=⎨⎪⎩
其他 可见,()()()p xy p x p y =,x 和y 相互独立,且均服从均匀分布, 21()log()/h x a a bit =-自由度 21()log()/h y b b bit =-自由度
2121()()()log()()h xy h x h y a a b b =+=-- (,)0I x y =
五、(10分)设某信道的传递矩阵为
0.80.10.10.10.10.8p ⎡⎤
=⎢⎥⎣⎦
计算该信道的信道容量,并说明达到信道容量的最佳输入概率分布,该信道为准对称信道,
(1)两个对称信道矩阵为
0.80.10.80.10.10.80.10.8⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦和0.10.1⎡⎤⎢⎥⎣⎦
N1=0.8+0.1=0.9,N2=0.1; M1=0.9,M2=0.2
∴log 2(0.8,0.1,0.1)0.9log0.90.1log0.20.447/C H bit =---=符号
《信息论基础》试卷第3页
最佳输入概率分布为输入等概率,即 (1)(2)p x p x ==1/2 六、(10分)设随机变量x 和y
已知随机变量z=xy,计算H(X),H(Z),H(XY),H(X/Z),I(x
;y ) 1) H(x)=H(1/3,1/3)=0.9183bit/符号 2)
H(z)=H(2/3,1/3)=0.9183bit/符号
3)H(xy)=H(1/3,1/3,0,1/3)=1.58496 bit/每对符号 4)
xz P(xz) 00 2/3
01 0 10 0 11
1/3
H(xz)=H(2/3,1/3)bit/每对符号 H(x|z)=H(xz)-H(z)=0 5)
I(x,y)=H(x)+H(y)-H(xy) =0.25164bit/符号 七 (20) 一个离散无记忆信源
1
23456()1/161/161/161/161/41/2x x x x x x x p x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦
1) 求H(x)和冗余度;(4分) 2) 编成Fano 码,计算编码效率;(8分) 3) 编成Huffman 码,计算编码效率。
(8分)
1) H(x)=H(1/16,1/16,1/16,1/16,1/4,1/2)=2bit
()122.6log 6
H x v =-=﹪
2)
《信息论基础》试卷第4页
12
6
x 5x 14
116
116116116
4x 3x 2
x 1
x 0
1
1
1
1
1
10
11001101
1111
1110
3)
x6x2
x3x4x5x1
1/16
1/161/161/161/4
1/21/16
1/161/8
1/41/21/21/41/81/8
1/21/41/4
1/2
1/20
10
1
10
11
010111111001101
1110 111
12442
242
L =⨯+⨯+⨯⨯= ()
100H x L
η=
=% 八 (10分) 设一个离散无记忆信源的概率空间为12()0.20.8x x x p x ⎡⎤⎡⎤
=⎢⎥⎢⎥⎣⎦⎣⎦,它们通过干扰信道,信道矩阵为0.90.10.30.7P ⎡⎤=⎢⎥⎣⎦。
信道输出符号集[]12Y y y =,试计算: (1)信源X 的信息熵;(2分)
(2)收到信息y2后,获得关于x1的信息量;(2分) (3) 共熵H(XY);(2分) (4)信道疑义度H(X|Y);(2分)
(5) 收到消息Y 后获得的关于信源X 的平均信息量。
(2分)
P(xy) y1 y2
x2 0.3×0.8 0.7×0.8
(1) H(x)=H(0.2,0.8)=0.722bit/符号
(2) I(x1;y2)=I(x1)-I(x1|y2)=log1/0.2-log0,58/0.02=-2.536bit/符号
(3) H(xy)=H(0.18,0.02,0.24,0.56)=1.52076bit/每对符号
(4) H(x|y)=H(xy)-H(y)=1.52076-H(y)
H(y)=H(0.42,0.58)=0.98145
H(x|y)=0.53936bit/符号
(5)I(X:Y)=H(x)+H(y)-H(xy)
=H(x)-H(x|y)
=0.722-0.5393=0.1827bit/符号
九(10分)有一个二元马尔科夫信源,其状态转移概率如图所示,括号中的数表示转移时发出的符号。
试计算
(1)达到稳定后状态的极限概率
(2)该马尔科夫信源的极限熵H
∞。
(1)
012 000.50.5
10.50.50
200.50.5
s s s
s
p
s
s
=
P(s0)=0.5P(s1)
0.5(p(s0)+p(s1)+p(s2))=p(s1)
0.5(p(s0)+p(s2))=p(s2)
P(s0)+p(s1)+p(s2)=1
得 p(s0)=0.25;
P(s1)=0.5;
P(s2)=0.25;
(2)
H
∞
=1/4H(0.5,0.5)+1/2H(0.5,0.5)+1/4H(0.5,0.5)
《信息论基础》试卷第5页
1/4+1/2+1/4=1bit/符号
《信息论基础》试卷第6页。
