第5章 习题解答
5第五章习题解答

习题解答5-1 电路中存在有正反馈,且AF >1,是否一定会发生自激振荡?说明理由。
解答:不一定。
因为AF>1仅满足了自激振荡的振幅起振条件,此时,只有当πϕϕn F A 2=+即同时满足相位起振条件时才会发生自激振荡。
5-2 为什么晶体管LC 振荡器总是采用固定偏置与自生偏置混合的偏置电路?解答:晶体管LC 振荡器采用固定的正向偏置是为了使振荡器起振时为软激励状态,无须再外加强的激励下能起振,也不致停振。
而采用自生反向偏置则可以稳幅。
若两者不结合,则两个优点不可兼而有之。
5-3 什么是间歇振荡现象?试分析间歇振荡产生的原因?简述如何防止和消除间歇振荡。
解答:间歇振荡是指振荡器工作时,时而振荡,时而停振的现象。
原因是振荡器的自偏压电路参数选择不当。
防止和消除间歇振荡的方法是正确选择工作点以及ReCe 的数值。
5-4 反馈式自激振荡器由哪几部分组成?各自的功能是什么? 解答:反馈型自激振荡器的电路由三部分组成:(1) 包含两个或两个以上储能元件的振荡回路,完成能量交换。
(2) 直流电源,补充振荡回路电阻产生的损耗,维持等幅振荡。
(3) 有源器件和正反馈电路,控制能量在正确的时间内补充到电路中。
5-5 LC 振荡器的工作频率是严格等于调谐回路的谐振频率吗?为什么?解答:LC 振荡器的工作频率近似等于调谐回路的谐振频率,严格说,它的工作频率还应该与管子的参数有关,如0h 、i h 等。
5-6 LC 振荡器的静态工作点应如何选择?根据是什么?解答:振荡器静态工作点设计在甲类工作状态,采用自给偏压电路,如下图所示:随着振荡幅度的增加,振荡管便由线性状态很快地过渡到甲乙类乃至丙类的非线性状态,这时放大器的增益会下降,最终达到平衡状态。
5-7 一个振荡器,因为某种原因,使反馈电压v f 比输入信号v s 滞后于340︒,试问该振荡器还能否振荡?若能振荡,则振荡频率比原来相比是升高了,还是降低了? 解答:若此时反馈电压分量,使得反馈系数F>A1时,即可振荡,因v f 滞后v s 340︒,即产生一个负相角ϕ∆,频率与相位的关系为dtd ϕω=,因此频率降低了。
化工热力学第五章习题解答

第五章 习题解答1. 在一定压力下,组成相同的混合物的露点温度和泡点温度不可能相同。
(错,在共沸点时相同) 2. 在(1)-(2)的体系的汽液平衡中,若(1)是轻组分,(2)是重组分,则11x y >,22x y <。
(错,若系统存在共沸点,就可以出现相反的情况) 3. 纯物质的汽液平衡常数K 等于1。
(对,因为111==y x ) 4. 在(1)-(2)的体系的汽液平衡中,若(1)是轻组分,(2)是重组分,若温度一定,则体系的压力,随着1x 的增大而增大。
(错,若系统存在共沸点,就可以出现相反的情况)5. 下列汽液平衡关系是错误的i i Solvent i v i i x H Py *,ˆγϕ=。
(错,若i 组分采用不对称归一化,该式为正确)6. 对于理想体系,汽液平衡常数K i (=y i /x i ),只与T 、P 有关,而与组成无关。
(对,可以从理想体系的汽液平衡关系证明) 7. 对于负偏差体系,液相的活度系数总是小于1。
(对) 8. 能满足热力学一致性的汽液平衡数据就是高质量的数据。
(错) 9. 逸度系数也有归一化问题。
(错) 10. EOS +γ法既可以计算混合物的汽液平衡,也能计算纯物质的汽液平衡。
(错) 二、选择题1. 欲找到活度系数与组成的关系,已有下列二元体系的活度系数表达式,βα,为常数,请决定每一组的可接受性 。
(D ) A 2211;x x βγαγ== B 12211;1x x βγαγ+=+=C 1221ln ;ln x x βγαγ==D 212221ln ;ln x x βγαγ==2. 二元气体混合物的摩尔分数y 1=0.3,在一定的T ,P 下,8812.0ˆ,9381.0ˆ21==ϕϕ,则此时混合物的逸度系数为 。
(C ) A 0.9097 B 0.89827C 0.8979D 0.9092三、填空题1. 说出下列汽液平衡关系适用的条件(1) l i v i f f ˆˆ= ______无限制条件__________; (2)i l i i v i x y ϕϕˆˆ= ______无限制条件____________; (3)i i si i x P Py γ= _________低压条件下的非理想液相__________。
机械设计基础第5章 轮系习题解答1
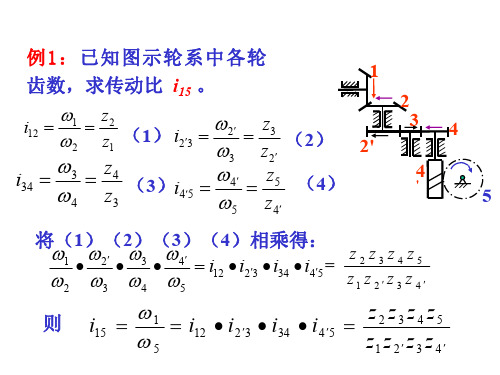
45 30 34 15 15 17
12
例2:在下图所示的轮系中,已知z1=20,z2=40,
z2'=20,z3=30,z4=80,试求传动比i1H。
解: i12
n1 n2
z2 z1
40 20
2
i2H4
n2 n4
nH nH
z4 z2
80 4 20
n2 n2
n4 0
联立求解得:
i1H
解: 将轮系分解
4 13
1-2为定轴轮系 2-2’共轴
2
H
H-4-3-2’为周转轮系
2’
定轴轮系: i12=ω1/ω2 =-z2/ z1
周转轮系: iH2’4=(1- i2’H) =-z4 /z2’
连接条件: ω2=ω2’
i12 • i2’HBiblioteka 联立解得 i1H1 H
z2 (1 z4 ) 40 (1 20) 10 z1 z2 20
n1 1 991909100
nH
1010000000
n1 19091909011 1100 1 nH 1100000 1010000000 100
iH 1
1 i1H
10100000
例题5.4:如图所示的轮系中 ,已知若 z1=20, z2=40,
z2’=20, z3=30,z4=80,试求传动比i1H。
z2=25,z2'=20,z3=75,齿轮1的转速为200r/min(箭头朝
上),齿轮3的转速为50r/min,求行星架转速的nH大小和
方向。
解: i13H
n1H n3 H
n1 nH n3 nH
z2z3 z1 z2
25 75 25 30 20 8
量子力学习题解答-第5章

第五章全同粒子本章主要内容概要1. 全同粒子:质量、电荷、自旋等固有性质完全相同的微观粒子称为全同粒子。
在一个量子体系中全同粒子是不可区分的,两全同粒子相互交换不会引起物理性质的改变(全同性原理)。
所有的微观粒子可以分为两类:波色子和费米子。
所有自旋为 整数倍的粒子称为波色子,而所有自旋为/2 奇数倍的粒子称为费米子。
由费米子组成的量子体系,不能有两个或两个以上的费米子处于同一个状态(泡利不相容原理),体系的波函数在交换任意两个费米子时是反对称的。
对由波色子组成的量子体系,则不受泡利不相容原理的限制,两个或两个以上的波色子可以处于同一个状态,体系的波函数在交换任意两个波色子时是对称的。
如果体系的波函数可以由归一化的单粒子波函数()i q αφ的积表示,其中i 表示不同的单粒子态,q α表示第α个粒子的量子数(包括空间与自旋),则由N 个费米子组成体系的反对称波函数可以用N 阶行列式表示为12121212()()()()()()(,,...,,...,)()()()i i i N j j j N A N k k k N q q q q q q q q q q q q q αφφφφφφΦ=交换任何两个粒子就是交换行列式中的两列,这使行列式改变符号,即波函数A Φ在交换两粒子时是反对称的。
当任两粒子处于相同状态,即行列式中两行相同,行列式为零,表示不能有两个或两个以上的费米子处于同一个状态。
对由N 个波色子组成的体系,体系的对称波函数可以表示为 1212(,,...,,...,)()()...()A N i j k N Pq q q q C P q q q αφφφΦ=∑其中P 表示N 个粒子在波函数中的某一种排列,P∑表示对所有可能排列求和,由于波色子可以处于相同的状态,,,...,i j k 可以相等,C 是归一化常数为求和的项数,,,...,i j k 完全相等时为1,全不相等时为1/2.交换力:以两粒子体系为例,若体系的波函数可以表示为空间部分和自旋部分之积,对称和反对称的空间波函数为121212(,)()()()()]a b b a x x x x x x ψψψψψ±=±这种波函数对称化的要求会使两粒子间出现一种力的作用,称为交换力。
机械设计第5-7章习题解答汇总

第5章 带传动与链传动5-1 带传动的弹性滑动是怎样产生的?能否防止?对传动有何影响?它与打滑有何不同?答:带传动的弹性滑动是由于带的弹性和拉力差而引起的带和带轮面间的局部的、微小的相对滑动,这是摩擦型带传动正常工作时的固有特性,是不可防止的。
弹性滑动导致传动效率降低、带磨损、传动比不准确。
打滑是由过载引起的带在带轮上的全面滑动,使传动失效。
打滑为非正常的工作状态,是必须防止也是可以防止的。
5-2带传动的中心距为什么要限制在一定的范围?答:带传动的中心距之所以要限制在一定的范围,是因为:1〕假设中心距过小,虽结构紧凑,但小带轮的包角太小,导致摩擦力和传动能力降低;2〕中心距过小,使带的长度过短,带的工作频率增加,降低带的疲劳强度和工作寿命;3〕中心距假设过大,不仅结构不紧凑,且皮带松边下垂,高速传动时易引起带的颤抖。
5-3.多根V 带传动时,假设发现一根已坏,应如何处置?答:多根V 带传动时,即使只发现一根已坏,也应该同时更换新的V 带,不可新旧混用。
5-4 已知一V 带传动,小带轮直径d 1d =160mm,大带轮直径d 2d =400mm ,小带轮转速n 1=960min r ,滑动率2=ε00,试求由于弹性滑动引起的大带轮的转速损失。
解: 假设无弹性滑动,大带轮的理想转速n 2应为:1122n d 960160n 384(r /min)d 400⨯=== 所以,由弹性滑动引起的大带轮的转速损失为:2n =3840.02=7.68(r /min)ε⨯5-5 为什么链传动具有运动不平稳性?答:由于链传动的多边形效应,使其瞬时速度和瞬时传动比周期性变化,从而引起动载荷,所以链传动具有运动不平稳性。
5-6 为什么链条节数常取偶数,而链轮齿数取为奇数?答: 因为假设链节数为奇数,则需要采用过渡链节,当链条受拉时,过渡链节的弯链板承受附加的弯矩作用,强度降低,所以链节数常取为偶数。
正因为链节数常为偶数,为使磨损均匀,链轮齿数一般取为奇数。
电工技术习题答案第5、6章 习题

第5章 习题解答5.1 在图5.1所示电路中,12100V,1,99,10F E R R C μ==Ω=Ω=,试求:(1)S 闭合瞬间,各支路电流及各元件端电压的值;(2)S 闭合后到达稳定状态时中各电流和电压的值;(3)当用电感元件L =1H 替换电容元件后再求(1),(2)两种情况下各支路的电流及各元件端电压的值。
解:(1)S 闭合瞬间,由于电容C 的电荷0)0(,0C 0==-u q ,所以0)0()0(C C ==-+u u ,即C 可视为短路,2R 被短接,20i =。
此时(2)S 闭合后,电路达到稳定状态时,由于E 为直流电动势,所以C 视为开路,则10i =1R 11A 11V u iR ==⨯Ω=2C R 21A 9999V u u iR ===⨯Ω=(3)当用电感元件替换电容元件后,S 闭合瞬间,由于S 闭合前电感中电流为零,即L (0)0i -=,且电感元件中电流不能跃变,所以L L 1(0)(0)0i i i +-===电感在S 闭合瞬间L 视为开路,所以此时212100V1A 199E i i R R ====+Ω+Ω1R 11A 11V u iR ==⨯Ω=2R 21A 9999V u iR ==⨯Ω=11100V100A 1E i i R ====Ω2R C (0)0u u +==212100V1A199E i i R R ====+Ω+Ω1R 1100A 1100Vu iR ==⨯Ω=22L R 99V u u ==S 闭合后,且电路达到稳定状态时,在直流电动势E 作用下,电感元件L 视为短路,则2R 被短路。
所以,11100V 100A 1E i i R ====Ω 20i = 2L R 0u u ==1R 1100A 1100V u iR ==⨯Ω=5.2 在图5.2所示电路中,已知126V,6A ,3E I R R ====Ω。
当电路稳定后,在t =0时将两个开关同时闭合。
结构化学习题解答5(北大)

NH3 N(CH3)3 C6H5NH2 CH3CONH2
[解]: 碱性的强弱和提供电子对能力大小有关,当N原子提供孤
对电子的能力大,碱性强。分子的几何够习惯内和有关性质主 要决定于分子中骨干原子的成键情况。下面将分析4个分子中的 骨干原子特别是N原子的成键轨道以及所形成的化学键的类型, 并结合有关原子或基团的电学性质,比较N原子上电荷密度的大 小,从而推断出4个分子碱性强弱的次序。
=-152.2 KJ•mol-1 [5.20] 试分析下列分子中的成键情况,指出C—Cl键键长大小
次序,并说明理由。
(a)H3CCl (b)H2C=CHCl (c)HC≡CCl [解]: (a)H3CCl:该分子为CH4分子的衍生物。同时CH4分子一样, C原子也采用sp3杂化轨道成键。4个sp3杂化轨道分别与3个H原 子的1s轨道及Cl原子的3p轨道重叠共形成4个σ键。分子呈四面 体构型,属C3v点群。 (b) H2C=CHCl:该分子为H2C=C H2分子的衍生物,其成键情况 与C2H4分子的成键情况即有相同之处又有差别。在C2H3Cl分子 中,C原子(1)的3个sp2杂化轨道分别与两个H原子的1s轨道
H
H
βc1+(α-E) c2+βc3=0
βc1+βc2+(α-E)c3=0 用β除各式并令x = (α-E)/β,则得:
xc1+c2+c3=0 c1+xc2+c3=0
c1+c2+xc3=0
欲使ci为非0解,则必须师其系数行列式为零,即:x 1 1
解此行列式,得:
1 x 10
x1=-2,x2=1,x3=1 将x值代入x=(α-E)/β,得: E1=α+2β,E2=α-β,E3=α-β 能级及电子分布简图如下:
何子述信号与系统习题解答第5章拉普拉斯变换(2012新)

1 L , 1 f1 t et u (t ) s 1
j t
dt
不存在 使上式积分收敛,故信号 f (t ) e 2t 的拉普拉斯变换不存在。 (f)由拉普拉斯变换的定义式
F s
题 5.3 解: (a)有拉普拉斯变换对
2δ t δ t 2 e
j t
5
s 2
2
25
s 2 j 30 s 2 j 30 s 2 4 s 34 , 2 2 s 4s 29 s 2 j5 s 2 j5
158
第5章
习题解答
信号与系统
何子述
高等教育出版社
零极点图如图 J5.3.2 所示。 (c)有拉普拉斯变换对
零极点图如图 J5.3.1 所示。 (b)有拉普拉斯变换对 L e2t sin 5t u t
L δ t 1,
5
s 2
2
25
, 2
由拉普拉斯变换的线性,信号 f t 的拉普拉斯变换为
L f t 1
F s e2t sin 3t u t e
-
dt
e2t
0
e j3t e j3t t jt e e dt 2j
