六年级用比例解决问题
六年级数学下册用比例解决问题
用比例解决问题班级姓名1、在比例尺是1：30000000的地图上量得甲乙两面地相距12厘米，一架飞机从早上的8：30以每小时800千米的速度从甲地飞往乙地。
到达乙地的时间是几时几分？2、甲乙两地相距300千米，在比例尺是的地图上应画多少厘米？如果画在比例尺是1：6000000的地图上应画多少厘米？3、在比例尺是1：4000的图纸上量得一个圆形运动场的直径是8厘米，这个圆形运动场的实际面积是多少平方米？4、在比例尺是1：2000的图纸上量得一块长方形菜地的周长是25厘米，且长与宽的比是3：2，这块长方形菜地的实际面积是多少平方米？5、一个篮球场的长是28米，宽是15米。
请选择一个合适的比例尺画出这个篮球场的平面图？6、一辆汽车5小时行驶140千米，照这样的速度，从甲地到乙地行了8小时，甲乙两地相距多少千米？（用比例解）7、用一批纸装订同样的练习本，每本40页，可装订90本，现在要装订100本，每本多少页？（用比例解）8、一个自来水龙头3天要浪费600升水，照这样计算六月份要浪费多少升水？（用比例解）9、一本书3天看了51，照这样计算剩下的还要多少天看完？（用比例解）10、一辆汽车从甲地到乙地去时每小行40千米，10小时到达，返回时，速度提高41，可节约几小时？（用比例解）11、给教室铺方砖，用面积是4平方分米的方砖需要200块，若改用面积是5平方分米的方砖需要多少块？（用比例解）0 40 80km12、给教室铺方砖，用边长是4分米的方砖需要200块，若改用面积是8平方分米的方砖需要多少块？（用比例解）13、给教室铺方砖，用边长是4分米的方砖需要200块，若改用边长是5分米的方砖需要多少块？（用比例解）14、一件商品原价80元，现打七五折出售，原来买12件商品的钱，现在可以买多少件？（用比例解）15、两个圆柱体积相等，一个圆柱的底面积是30平方米，高6米，另一个圆柱的底面积是45平方米，它的高是多少米？（用比例解）16、一段木料锯成3段要12分钟，照这样，锯成8段要多少分钟？（用比例解）17、一个服装店的所有服装都打同样的折扣销售①、李阿姨买了一件上衣，原价250元，现价150元，李阿姨还想买一条裤子，原价180元，现价多少钱？（用比例解）②、张伯伯有一笔钱，如果买现价90元一件的衬衫，正好买4件，如果想买原价200元一件的夹克衫，能买多少件？（用比例解）18、一个长方形长8厘米，宽6厘米，按3:1放大后，它的面积是多少平方厘米？19、在一幅比例尺是1:2000000的地图上，量得甲乙两地的距离是厘米，如果画在比例尺是1:5000000的地图上，应画多少厘米？20、希望小学装修多媒体教室。
六年级下4.3用比例解决问题
六年级下4.3用比例解决问题《六年级下 43 用比例解决问题》在六年级的数学学习中，用比例解决问题是一个非常重要的知识点。
它不仅能够帮助我们更轻松地解决一些实际的数学问题，还能培养我们的逻辑思维和分析能力。
比例，简单来说，就是两个比相等的式子。
比如，2:3 ＝ 4:6，这就是一个比例。
而用比例解决问题，就是根据题目中给出的条件，找出其中的比例关系，然后通过设未知数、列比例式、解比例等步骤来求出答案。
我们先来看一个常见的例子。
比如，一辆汽车 2 小时行驶了 100 千米，按照这样的速度，5 小时可以行驶多少千米？在这个问题中，我们知道汽车行驶的速度是一定的，也就是路程和时间的比值是不变的。
那么，我们可以设5 小时行驶的路程为x 千米。
因为速度＝路程÷时间，所以第一次行驶的速度为 100÷2 ＝ 50（千米/小时），第二次行驶的速度为 x÷5。
由于速度不变，所以可以列出比例式：100:2 ＝ x:5接下来，我们就可以根据比例的性质来解这个比例。
在比例里，两个内项的积等于两个外项的积。
所以 2x ＝ 100×5，2x ＝ 500，x ＝ 250。
这就求出了 5 小时行驶的路程是 250 千米。
再来看另一个例子。
小明买 5 本同样的练习本用了 10 元，那么买 8 本这样的练习本需要多少钱？同样的，我们设买 8 本需要 x 元。
因为练习本的单价是一定的，所以可以列出比例式：5:10 ＝ 8:x根据比例的性质，5x ＝ 10×8，5x ＝ 80，x ＝ 16所以买 8 本练习本需要 16 元。
用比例解决问题的时候，关键是要找到题目中不变的量，以及与之相关的两个变量，然后判断它们是成正比例还是反比例关系。
正比例关系是指两个量的比值一定，比如上面汽车行驶的例子，速度一定，路程和时间成正比例。
反比例关系则是指两个量的乘积一定，比如做一项工作，工作总量一定，工作效率和工作时间成反比例。
苏教版数学六年级下册专项～比例解决问题【含答案】
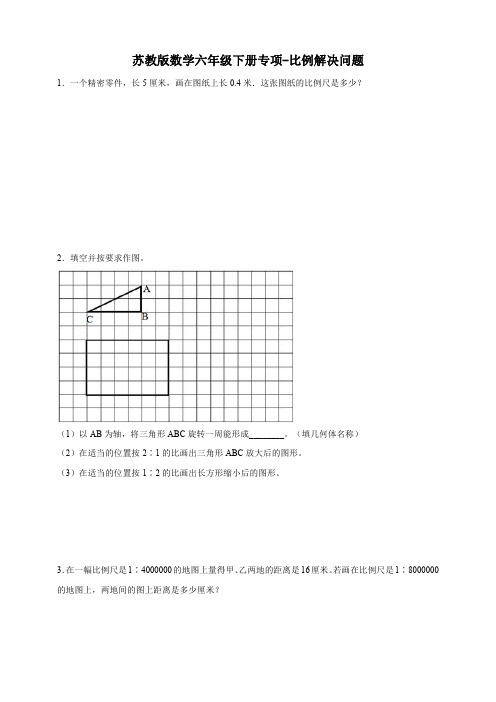
苏教版数学六年级下册专项-比例解决问题1．一个精密零件，长5厘米，画在图纸上长0.4米．这张图纸的比例尺是多少？2．填空并按要求作图。
（1）以AB为轴，将三角形ABC旋转一周能形成________。
（填几何体名称）（2）在适当的位置按2∶1的比画出三角形ABC放大后的图形。
（3）在适当的位置按1∶2的比画出长方形缩小后的图形。
3．在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。
若画在比例尺是1∶8000000的地图上，两地间的图上距离是多少厘米？4．画一画，填一填。
（1）按3∶1的比画出图形A放大后得到的图形B。
（2）按1∶2的比画出图形B缩小后得到的图形C。
我发现：放大或缩小前后的图形（）变了，但（）没有变，而且图形各部分长度是按一定的比变化的。
5．在一张比例尺是1∶150的建筑图纸上，量得一座大楼的长是6分米，这座大楼的实际长与宽的比是3∶1，这座大楼的实际宽是多少米？6．下图中小平行四边形按比放大后得到大平行四边形，求大平行四边形的高。
（单位：分米）12．根据图中提供的信息，完成下列问题。
（1）自来水厂要从水库取水，取水管道怎样铺最短，请在图中画出来。
（2）自来水厂到城区的送水管道经测算最短是2000米，请你测算：自来水厂到水库的取水管道最短需多少米？13．在一幅地图上，用5厘米长的线段表示实际距离100千米，这幅地图的比例尺是多少？如果甲市至乙市的铁路线路长150千米，那么这段铁路线路在这幅地图上的长度是多少厘米？14．江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。
广场绿地面积与铺装面积的比是6∶5，其中铺装面积共5000平方米，绿地面积有多少平方米？15．甲乙两城相距150千米，在一幅地图上量得甲乙两城之间的距离是5厘米，同时在这幅地图上量得乙丙两城之间的距离是8厘米。
乙丙两城之间的实际距离是多少千米？20．下图中A点是游乐场所在的位置，B点是电影院所在的位置，两地实际距离相距2千米。
数学六年级下册《用比例解决问题》教案
数学六年级下册《用比例解决问题》教案一、教学目标1.知识与技能:理解比例意义，掌握解比例的方法，能够运用比例解决简单的实际问题。
能够区分正比例和反比例关系，并能根据实际问题选择合适的比关系进行解答。
2.过程与方法:通过观察、分析、比较、归纳等活动，经历用比例解决问题的过程体会数学与生活的联系，发展学生的分析问题和解决问题的能力。
能够运用多种方法（例如：方程法、比例法）解决同一个问题，并比较不同方法的优缺点。
3.情感态与价值观:培养学生认真细致的学习态度，增强学生运用数学知识解决实际问题的自信心，体会数学的应用价值。
二、教学重点运用比例解决实际问题，区分正比和反比例关系。
三、教学难点分析实际问题中的数量关系，选择合适的比例式列式解答。
四、教学准备多媒体课件、练习题、比例尺模型、实物投影仪五、教学过程(一复习旧知 (5分钟)1.什么是比例？比例的基本性质是什么？2.如何解比例？举例说明。
3.举例说明正比例和反比例的意义。
(二) 导入新课 (5分钟)教师展示一些生活中的图片例如：地图、比例模型、工程进度图等，引导学生思考这些图片中蕴含的数学知识，引出比例的应用。
(三) 探究新知 (30分钟)1.例题讲解:选择几个不同类型的例题进行讲解，例如：•例题1 (正比例):如果5个苹果重1千克，那么15个苹果重多少千克？引导学生分析题意，找出题中的数量关系，列出比例式并解答。
讲解解题步骤，并强调单位的统一。
•例题2 (反比例): 5个人完成一项工程需要10天，如果增加到10个人，完成这项工程需要多少天？引导学生分析题意，找出题中的数量关系，列出比例式并解答。
比较正比例和反比例的区。
o例题3 (稍复杂的应用题):某地图的比例尺是1:50000，地图上两地相距4厘米，实际距离是多少千米？引导学生理解比例尺的意义，并运用比例解决问题。
2.*小组合作:** 将学生分成小组，让学生尝试解决课本上的练习题，教师巡视指导，帮助学生解决遇到的问题。
六年级-人教版-数学-下册-[教学设计]用比例解决问题(二)
![六年级-人教版-数学-下册-[教学设计]用比例解决问题(二)](https://img.taocdn.com/s3/m/2591f0684b7302768e9951e79b89680203d86b9a.png)
用比例解决问题（二）教学内容教科书第60页例6及相关内容。
教学目标1．能正确判断情境中的两种量是否成反比例关系，并利用反比例的意义解决实际问题。
掌握用反比例知识解决问题的解题思路。
2．能够类比正比例的相关知识，学习反比例的对应内容，培养学生的知识迁移能力。
3．在数学活动的深度体验中，体会解决问题的成功和喜悦，感受数学的无穷魅力，激发学生学习数学的热情。
教学重点能够利用反比例的意义解决问题。
教学难点能够正确利用反比例关系列出含有未知数的等式。
教学准备多媒体课件。
教学过程一、复习旧知师：我们已经能够判断什么叫作成正比例的量，什么叫作成反比例的量，也学会了用正比例的知识解决问题，下面看这几道题。
课件出示：1．判断下面每题中的两种量成什么比例关系。
（1）一根线截成同样的小段，截成的段数和每段的长度。
（2）每块地砖的面积一定，所需地砖的块数和所铺面积。
（3）给一间教室铺地砖，每块地砖的面积与所需的块数。
2．小花买5支圆珠笔用了8元，明明想买3支同样的圆珠笔，要用多少钱？（用比例的知识解答）教师指名学生逐题汇报，注意引导学生说出为什么。
在学生汇报完第2题之后，引导学生回顾用正比例知识解决问题的步骤：（1）找：找出题目中相关联的两种量。
（2）判：判断它们是否成正比例关系。
（3）列：根据正比例的意义列出比例式。
（4）解：解比例。
（5）检：检验、写答语。
师：这节课我们继续学习运用比例知识来解决实际问题。
二、探究新知（一）教学例61．阅读与理解。
课件出示：某办公楼原来平均每天照明用电100千瓦时。
改用节能灯以后，平均每天只用电25千瓦时。
原来5天的用电量现在可以用多少天？师：从题目中你知道了哪些数学信息？要解决的问题是什么？预设：知道了原来平均每天照明用电100千瓦时，改用节能灯以后，现在平均每天只用电25千瓦时。
要解决的问题是原来5天的用电量现在可以用多少天。
根据学生回答，课件出示表格：师：要解决这个问题必须要知道什么？预设：要求“原来5天的用电量现在可以用多少天”，就要知道现在每天的用电量和总用电量。
《用比例解决问题》说课稿(通用10篇)
《用比例解决问题》说课稿（通用10篇）《用比例解决问题》说课稿篇1教学目标：1、使学生掌握用比例知识解答以前学过的用归一、归总方法解答的应用题的解题思路，能进一步熟练地判断成正、反比例的量，加深对正、反比例概念的理解，沟通知识间的联系。
2、提高学生对应用题数量关系的分析能力和对正、反比例的判断能力。
3、培养学生良好的解答应用题的习惯。
教学重点：用比例知识解答比较容易的归一、归总应用题。
教学难点：正确分析题中的比例关系，列出方程。
教学过程：一、复习铺垫，引入新课。
（课件出示）1、判断下面每题中的两种量成什么比例？（1）速度一定，路程和时间．（2）路程一定，速度和时间．（3）单价一定，总价和数量．（4）每小时耕地的公顷数一定，耕地的总公顷数和时间．（5）全校学生做操，每行站的人数和站的行数．2、下面各题中各有哪三种量？那种量一定？哪两种量是变化的？变化的规律怎样？它们成什么比例？你能列出等式吗？（1）用一批纸装订练习本，每本30页，可装订200本，每本50页，可装订120本。
（2）一列火车从甲地到乙地，2小时行驶60千米，照这样的速度，8小时可行240千米。
（3）读一本书，每天读20页，6天可以读完，如果每天读5页，需要x天读完。
3、课件出示例5情境图，问：你能说出这幅图的意思吗？（指名回答）李奶奶家上个月的水费是多少钱？想请我们帮她算一算，你们能帮这个忙吗？（1）学生自己解答，然后交流解答方法。
（2）引入新课：象这样的问题也可以用比例的知识来解决，我们今天这节课就来讨论如何运用比例的知识来解决这类问题。
板书课题：用比例解决问题二、探究新知。
1、教学例5（1）学生再次读题，理解题意。
思考和讨论下面的问题：①问题中有哪三种量？哪一种量一定？哪两种量是变化的？②它们成什么比例关系？你是根据什么判断的？③根据这样的比例关系，你能列出等式吗？（2）根据上面三个问题，概括：因为水价一定，所以水费和用水的吨数成正比例。
六年级数学下册用比例解决问题
六年级数学下册用比例解决问题姓名：班级：1、学校食堂买来900千克大米，6天吃了180千克，照这样计算，剩下的还能吃几天？2、两根同样长的钢筋，其中一根锯成3段用了12分钟，另一根要锯成6段，需要多少分钟？3、电信公司要铺设一条通信光缆线，计划由20人工作12天完成。
因任务紧急，现在必须提前2天完成，如果工作效率不变，应增加多少人才能按时完成任务？4、某小区维修线路，需停电半小时，妈妈找来一根长20厘米的蜡烛，蜡烛燃烧8分钟后，还剩15厘米，请问：这根蜡烛能够燃烧到来电吗？5、一块圆柱形钢坯的底面半径是3cm，高是36cm。
如果把它熔铸成一个底面积是113.04平方厘米的圆锥，那么高是多少厘米？6、如果教室要用方砖铺地，用边长为3分米的方砖，需要96块，如果改用边长是4分米的方砖，需要多少块？7、如果教室要用方砖铺地，用面积为9平方分米的方砖，需要96块，如果改用面积是16平方分米的方砖，需要多少块？8、8、如果教室要用方砖铺地，用面积为9平方分米的方砖，需要96块，如果改用边长是4分米的方砖，需要多少块？9、聪聪在图书馆借到了《三体》第三册，计划每天看10页，需要51天刚好全部看完。
如果聪聪最后还书时共交了0.4元的延时服务费，那么他平均每天看了多少页？10、某工程队铺一段铁路，原计划每天铺3.6千米，实际每天比原计划多铺25%，实际铺完这段铁路用了8天。
原计划用多少天铺完？11、加工一批零件，若每天加工200个，则比原计划提前3天就能完成任务；若每天加工150个，则比原计划延迟5天才能完成任务。
原计划多少天完成任务？这批零件一共有多少个？12、甲乙两人骑自行车从A，B两地同时出发，相向而行。
甲行完全程要6小时，甲、乙相遇时所行的路程比是3：2，乙行完全程要多少小时？（甲、乙速度均保持不变）13、如图，平行四边形ABCD的周长为50厘米，以AD为底边时，高CE是8厘米；以AB 为底边时，高CF是12厘米，那么平行四边形ABCD的面积是多少平方厘米？14、甲、乙两车同时从A，B两城相对开出，经过8小时相遇，相遇后甲车继续开到B城还要4小时。
六年级数学用比例解决问题练习
六年级数学用比例解决问题练习学校：姓名：用比例知识解决下面问题：1、用边长40厘米的方砖给教室铺地，需要432块，如果用边长60厘米的方砖铺地，需要多少块方砖？解答：由于铺地面积不变，所以两种方砖的面积成比例。
设用60厘米边长的方砖需要x块，则有：40×40×432=60×60×x解得：x=192，所以需要192块60厘米边长的方砖。
2、一辆客车3小时行135千米，照这样计算，如果行315千米，需要多少小时？解答：客车的行驶速度不变，所以行驶时间与行驶距离成反比例。
设需要的时间为x，则有：3×135=315×x解得：x=1.35，所以需要1.35小时。
3、一种农药，用药液和水按1:1500配制而成。
如果只有3千克的药液，应加水多少千克？解答：药液和水的重量成比例。
设应加水x千克，则有：3:1500=x:(3+x)解得：x=4497，所以应加4497千克水。
4、运一批药品，每箱装36瓶，需要40只箱子，如果每箱装24瓶，需要多少只箱子？解答：药品的总瓶数不变，所以需要的箱子数与每箱装瓶数成反比例。
设需要的箱子数为x，则有：36×40=24×x解得：x=60，所以需要60只箱子。
5、一块长方形地长120米，宽90米。
把它画在比例尺是1:1000的图纸上，长和宽各应画多少厘米？解答：地的长度和宽度与图纸上的长度和宽度成比例。
设地在图纸上的长度为x厘米，则有：120:1000=x:1解得：x=12，所以地在图纸上的长度为12厘米。
同理可得，地在图纸上的宽度为9厘米。
6、在一幅比例尺是1:的地图上，量得甲乙两地的距离是12厘米，甲乙两地的实际距离是多少千米？解答：地图上的长度与实际长度成比例。
设甲乙两地的实际距离为x千米，则有：1:=12:x解得：x=420，所以甲乙两地的实际距离为420千米。
7、___用24元买了6本笔记本，___也想买几本，可是他妈妈只给他16元，他最多可以买到多少本笔记本？解答：笔记本的数量与钱数成正比例。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《用比例解决问题》教学设计
【教学目标】：
1．掌握用正比例知识解答含有正比例关系问题的步骤和方法。
2．使学生熟练地判断两种相关联的量是否成正比例，从而加深对正比例意义的理解。
3．发展学生探究解决问题策略的能力，帮助其构建相应的知识结构。
【教学重点】：
1．判断题中相对应的两个量和它们的比例关系。
2．利用正比例的关系列出含有未知数的等式，运用比例知识正确解决问题。
【教学难点】：
1．掌握用比例知识解答解答应用题的步骤和方法。
2．理解“用比例解决问题”的结构特点，从而构建知识结构。
【教学准备】：多媒体课件
【教学过程】：
一、激发兴趣，回忆旧知
1．师：我们先来回忆一下已经学过的知识吧！
（课件出示：）我会判断：判断下列每题中的两个量是不是成比例，成什么比例？
（1）购买课本的单价一定，总价和数量。
（成正比例）
（2）差一定，减数与被减数。
（不成比例）
（3）总路程一定，速度和时间。
（成反比例）
（4）零件总数一定，生产的天数和每天生产的件数。
（成反比例）
2．师：如果用字母x和y表示两种相关联的量，用k表示它们的比值（一定），正比例关系可以用哪个式子来表示？（板书：（一定））
3. 师：如果用字母x和y表示两种相关联的量，用k表示它们的乘积（一定），反比例关系可以用哪个式子来表示？（板书：x×y=k（一定））
4. 师：看来同学们正比例和反比例的知识学得都很不错，下面我们就一起来学习今天的新知识吧！今天我们就一起来研究——用比例解决问题。
（板书课题：用比例解决问题）
二、揭示课题、探索新知。
（一）教学例5（课件出示：情境图）
1．回顾旧知
师：从这幅图中你能知道哪些信息？（指名回答）李奶奶家上个月的水费是多少钱？想请我们帮她算一算，你们能帮这个忙吗？
（1）学生自己解答，然后交流解答方法。
（学生可以先求出单价，再求总价或先求出用水量的倍数关系再求总价。
）
【设计意图：用以往学过的方法解决例题，有助于从旧知跳跃到新知的学习，同时有利于用比例解决问题的检验，帮助学生在后面的学习中构建知识结构。
】（2）师：像这样的问题也可以用比例的知识来解决。
【设计意图：点明主题，鼓励学生以积极的态度投入新课的学习。
】
2. 探究解法
（1）梳理两种相关联的量
师：用比例解决这个问题之前，我们先来思考（课件出示）
①问题中有哪两种量？它们对应的数据分别是多少？
②它们成什么比例关系？你是根据什么判断的？
③根据这样的比例关系，你能列出等式吗？
（）一定，所以（）和（）成（）比例。
也就是说，两家的（）和（）的（）相等。
3.用比例解答。
如果设李奶奶家上个月的水费是x元，请根据表中相对应的数据和判断列出比例式，然后解答。
知道每吨水的价钱一定，所以水费和用水量成正比例。
也就是说，两家的水费和用水量的比值相等。
设李奶奶家上个月的水费是x元。
列出比例是：（12.8:8=x:10），比例的解是x=16。
（板书解法1）
师：你是怎么想的？（根据上面的数据，概括：因为每吨水的价钱一定，所以水费和用水的吨数成正比例。
也就是说，两家的水费和用水的吨数的比值是相等的。
）
12.8︰8=x︰10
板书: 解：设李奶奶家上个月的水费是χ元。
12.8 ：8 ＝χ：10 或12.8
8=
x
10
8χ＝12.8×10 8χ= 12.8×10
χ＝χ=
χ＝16 χ=16
答：李奶奶家上个月的水费是16元。
师：12.8︰8和x︰10 分别表示什么？（水费单价）
让学生再思考，看看有没有出现其它比例的解法，如果有，教师也要进行评析。
（学生可能通过复习题3的复习，想出不同的解法。
）
如果列出的比例是8︰12.8=10︰x可以吗？为什么？（可以，因为8︰12.8和10︰x都表示1元可以用水多少吨，是一定的，板书解法2）
师：这个问题我们用比例的知识解决了，你有什么方法检验自己的解答是正确的呢？（启发学生自主选择检验方法。
如：将结果代入原题、运用比例的基本性质、用算术方法或一般方程方法解答来检验等。
）
【设计意图：在教师引导下，学生通过合作、交流从而解决问题，能使他们增强学习的信心、能给他们自信。
在交流中，让学生充分地表达自己的见解，培养学生的辩证思维能力和口语交际能力。
】
4．即时练习
师：同学们很了不起，帮李奶奶解决完了问题，能再帮王大爷解决一个问题吗？课件出示：“王大爷家上个月的水费是19.2元，他们家上个月用了多少吨水？”让学生进行变式练习。
）
5. 提炼方法
师：解决了两个问题，我们一起来反思一下刚才的学习过程，归纳出用比例解决问题的步骤，好吗？
得出用比例解决问题的“五步曲”（板书）：
一梳（梳理相关联的两种量）
二判（判断相关联的两种量成什么比例）
三列（设未知x，根据判断列出比例）
四解（解比例）
五检（用自己熟练的方法来检验）。
【设计意图：“检验反思”有利于培养学生良好的学习习惯，同时提高解决问题的正确率。
归纳解题的策略，有助于提高学生解决问题的能力。
】
三、巩固提高。
1. 教材60页的做一做：1题。
2. 教材练习九的第3、5题。
【设计意图：通过练习的巩固，提高学生解决问题的能力。
同时从学生的生活实际入手，引导学生把所学的知识运用与生活实践，从中体会所学知识的生活价值。
】
四、全课总结。
1. 今天你们有什么收获？
【设计意图：通过练习的巩固，提高学生解决问题的能力。
】
数学教师每人一堂课教案
用比例解决问题
济南市段店小学
于耀宗。