一线三角模型及例题
备战中考数学二轮专题归纳提升真题几何模型—一线三等角模型(解析版)

专题13 几何模型3—一线三等角模型【模型介绍】一线三等角:两个三角形中相等的两个角落在同一条直线上,另外两条边所构成的角与这两个角相等,这三个相等的角落在同一直线上,故称“一线三等角”如下图所示,一线三等角包括一线三直角、一线三锐角、一线三钝角【解题关键】构造相似或是全等三角形【典型例题】【题型一:一线三直角模型】如图,若∠1、∠2、∠3都为直角,则有△ACP ∽△BP D .【例1】如图1所示,已知△ABC 中,∠ACB =90°,AC =BC ,直线m 经过点C ,过A 、B 两点分别作直线m 的垂线,垂足分别为E 、F .(1)如图1,当直线m 在A 、B 两点同侧时,求证:EF =AE +BF ;(2)若直线m 绕点C 旋转到图2所示的位置时(BF <AE ),其余条件不变,猜想EF 与AE ,BF 有什么数量关系?并证明你的猜想;(3)若直线m 绕点C 旋转到图3所示的位置时(BF >AE )其余条件不变,问EF 与AE ,BF 321DBP AC的关系如何?直接写出猜想结论,不需证明.【答案】(1)见解析;(2)EF=AE−BF,证明见解析;(3)EF=BF−AE,证明见解析【解析】(1)证明:∵AE⊥EF,BF⊥EF,∠ACB=90°,∴∠AEC=∠BFC=∠ACB=90°,∴∠EAC+∠ECA=90°,∠FCB+∠ECA=90°,∴∠EAC=∠FCB,在△EAC和△FCB中,{∠AEC=∠CFB ∠EAC=∠FCBAC=BC,∴△EAC≌△FCB(AAS),∴CE=BF,AE=CF,∵EF=CF+CE,∴EF=AE+BF;(2)解:EF=AE−BF,理由如下:∵AE⊥EF,BF⊥EF,∠ACB=90°,∴∠AEC=∠BFC=∠ACB=90°,∴∠EAC+∠ECA=90°,∠FCB+∠ECA=90°,∴∠EAC=∠FCB,在△EAC和△FCB中,{∠AEC=∠CFB ∠EAC=∠FCBAC=BC,∴△EAC≌△FCB(AAS),∴CE=BF,AE=CF,∵EF=CF−CE,∴EF=AE−BF;(3)解:EF=BF−AE,理由如下:∵AE⊥EF,BF⊥EF,∠ACB=90°,∴∠AEC=∠BFC=∠ACB=90°,∴∠EAC+∠ECA=90°,∠FCB+∠ECA=90°,∴∠EAC=∠FCB,在△EAC和△FCB中,{∠AEC=∠CFB ∠EAC=∠FCBAC=BC,∴△EAC≌△FCB(AAS),∴CE=BF,AE=CF,∵EF=CE−CF,∴EF=BF−AE.【练1】如图,在平面直角坐标系中,将直线y=−3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形AB C.若反比例函数y=kx(x>0)的图象经过点C,则k的值为()A.2B.3C.4D.6【答案】C【解析】解:过点C作CE⊥x轴于点E,作CF⊥y轴于点F,如图所示,∵CE⊥x轴,CF⊥y轴,∴∠ECF=90°.∵△ABC为等腰直角三角形,∴∠ACF+∠FCB=∠FCB+∠BCE=90°,AC=BC,∴∠ACF=∠BCE.在△ACF和△BCE中,{∠AFC =∠BEC =90°∠ACF =∠BCEAC =BC, ∴△ACF ≌△BCE (AAS ),∴S △ACF =S △BCE ,∴S 矩形OECF =S 四边形OBCA =S △AOB +S △AB C .∵将直线y =−3x 向上平移3个单位可得出直线AB ,∴直线AB 的表达式为y =−3x +3,∴点A (0,3),点B (1,0),∴AB =√OA 2+OB 2=√10,∵△ABC 为等腰直角三角形,∴AC =BC =√22AB =√5, ∴S 矩形OECF =S △AOB +S △ABC =12×1×3+12×√5×√5=4.∵反比例函数y =k x (x >0)的图象经过点C ,∴k =4,故选C .【练2】如图,直角三角形的直角顶点在坐标原点,∠OBA =60°,若点A 在反比例函数y =3x (x >0)的图象上,则经过点B 的反比例函数表达式为( )A .y =−3xB .y =3xC .1y x =-D .y =1x【答案】C 【解析】解:作AD ⊥x 轴于D ,BC ⊥x 轴于C ,如图,∵∠AOB=90°,∠ABO=60°,∴∠BAO=30°,∴OB=√33OA.∵点A在反比例函数y=3x(x>0)的图象上,∴xy=OD∙AD=3.∵∠AOD+∠BOC=90°,∠AOD+∠DAO=90°,∴∠BOC=∠DAO,∴Rt△BOC∽Rt△OAD,∴S△BOCS△DAO =(OBOA)2=13.∵S△DAO=12OD∙AD=12×3=32,∴S△BOC=12,即12|k|=12,∴|k|=1.∵k<0,∴k=−1,∴经过点B的反比例函数解析式为y=−1x.故选:C.【练3】如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是()A.13B. 617C.√55D. √1010【答案】D【解析】如图,过点A作AD⊥l1于点D,过点B作BE⊥l1于点B,设l1,l2,l3之间的距离为1∵∠CAD+∠ACD=90°,∠BCE+∠ACD=90°∴∠CAD=∠BCE在等腰直角△AB C中,AC=BC,∠ADC=∠BEC=90°∴△ACD≌△CBE∴CD=BE=1在Rt△AC D中AC=√AD2+CD2=√22+12=√5在等腰直角△AB C中AB=√2AC=√2×√5=√10∴sinα=1√10=√1010故选:D【练4】如图1,等腰Rt△AB C中,∠ABC=90°,CB=BA,直线ED经过点B,过A作AD ⊥ED于D,过C作CE⊥ED于E.则易证△ADB≌△BE C.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角,所以在平面直角坐标系中被大量使用.模型应用:(1)如图2,点A(0,4),点B(3,0),△ABC是等腰直角三角形.①若∠ABC=90°,且点C在第一象限,求点C的坐标;②若AB为直角边,求点C的坐标;(2)如图3,长方形MFNO,O为坐标原点,F的坐标为(8,6),M、N分别在坐标轴上,P 是线段NF上动点,设PN=n,已知点G在第一象限,且是直线y=2x一6上的一点,若△MPG 是以G为直角顶点的等腰直角三角形,请直接写出点G的坐标.【答案】(1)①(7,3);②(7,3)、(4,7)、(-4,1)、(-1,-3);(2)(4,2)、(203,22 3).【解析】解:(1)①如图,过C作CD垂直于x轴,根据“一线三垂直”可得△AOB≌△BDC,∴AO=BD,OB=CD,∵点A(0,4),点B(3,0),∴AO=4,OB=3,∴OD=3+4=7,∴点C的坐标为(7,3);②如图,若AB为直角边,点C的位置可有4处,a、若点C在①的位置处,则点C的坐标为(7,3);b、若点C在C1的位置处,同理可得,则点C1的坐标为(4,7);c、若点C在C2的位置处,则C1、C1关于点A对称,∵点A(0,4),点C1(4,7),∴点C2的坐标为(-4,1);d、若点C在C3的位置处,则C3、C关于点B对称,∵点B(3,0),点C(7,3),∴点C3的坐标为(-1,-3);综上,点C的坐标为(7,3)、(4,7)、(-4,1)、(-1,-3);(2)当点G位于直线y=2x-6上时,分两种情况:①当点G在矩形MFNO的内部时,如图,过G作x轴的平行线AB,交y轴于A,交直线NF于点B,设G(x,2x-6);则OA=2x-6,AM=6-(2x-6)=12-2x,BG=AB-AG=8-x;则△MAG≌△GBP,得AM =BG,即:12-2x=8-x,解得x=4,∴G(4,2);当点G在矩形MFNO的外部时,如图,过G作x轴的平行线AB,交y轴于A,交直线NF 的延长线于点B,设G(x,2x-6);则OA=2x-6,AM=(2x-6)-6=2x-12,BG=AB-AG=8-x;则△MAG≌△GBP,得AM =BG,即:2x-12=8-x,解得x=203,∴G(203,223);综上,G点的坐标为(4,2)、(203,22 3).【题型二:一线三锐角与一线三钝角】如图,若∠1、∠2、∠3都为锐角,则有△ACP ∽△BP D .证明:∵∠DPB =180°-∠3-∠CP A ,∠C =180°-∠1-∠CP A ,而∠1=∠3∴∠C =∠DPB ,∵∠1=∠2,∴△ACP ∽△BPD如图,若∠1、∠2、∠3都为钝角,则有△ACP ∽△BP D .(证明同锐角)【例2】如图,在等腰三角形AB C 中,∠BAC =120°,AB =AC =2,点D 是BC 边上的一个动点(不与B 、C 重合),在AC 上取一点E ,使∠ADE =30°.(1)设BD =x ,AE =y ,求y 关于x 的函数关系式并写出自变量x 的取值范围;(2)当△ADE 是等腰三角形时,求AE 的长.【答案】(1)y =12x 2−√3x +2(0<x <2√3)(2) AE =4-2√3或AE =23 【解析】解(1)∵△ABC 是等腰三角形,且∠BAC =120°,∴∠ABD =∠ACB =30°,∴∠ABD =∠ADE =30°,∵∠ADC =∠ADE +∠EDC =∠ABD +∠DAB ,∴∠EDC =∠DAB ,∴△ABD ∽△DCE ;∵AB =AC =2,∠BAC =120°,过A 作AF ⊥BC 于F ,3CDBP A 231DB P A CEC DB A∴∠AFB =90°,∵AB =2,∠ABF =30°,∴AF =12AB =1, ∴BF =√3,∴BC =2BF =2√3,则DC =2√3−x ,EC =2-y∵△ABD ∽△DCE ,∴AB BD =DC CE , ∴2x =2√3−x 2−y, 化简得:y =12x 2−√3x +2(0<x <2√3).(2)①当AD =DE 时,如图,△ABD ≌△DCE ,则AB =CD ,即2=2√3−x ,x =2√3−2,代入y =12x 2−√3x解得:y =4−2√3,即AE =4−2√3,②当AE =ED 时,如图,∠EAD =∠EDA =30°,∠AED =120°,所以∠DEC =60°,∠EDC =90°则ED = 12 EC ,即y =12 (2-y )解得y =23,即AE =23;③当AD =AE 时,有∠AED -∠EDA =30°,∠EAD =120° 此时点D 和点B 重合,与题目不符,此情况不存在. EC DB AAB C所以当△是ADE等腰三角形时,AE=4-2√3或AE=23【练1】如图,在△AB C中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=115°时,∠EDC=______°,∠AED=______°;(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由.【答案】(1)25°,65°;(2)2,理由见解析;(3)可以,110°或80°.【解析】解:(1)∵∠B=40°∠ADB=115°,∴∠BAD=180°-∠B-∠ADB=180°-115°-40°=25°,∵AB=AC,∴∠C=∠B=40°,∵∠EDC=180°-∠ADB-∠ADE=25°,∴∠DEC=180°-∠EDC-∠C=115°,∴∠AED=180°-∠DEC=180°-115°=65°;(2)当DC=2时,△ABD≌△DCE,理由:∵∠C=40°,∴∠DEC+∠EDC=140°,又∵∠ADE=40°,∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,又∵AB=DC=2,在△ABD和△DCE中,{∠ADB =∠DEC∠B =∠CAB =DC∴△ABD ≌△DCE (AAS );(3)当∠BDA 的度数为110°或80°时,△ADE 的形状是等腰三角形,∵∠BDA =110°时,∴∠ADC =70°,∵∠C =40°,∴∠DAC =70°,∴△ADE 的形状是等腰三角形;∵当∠BDA 的度数为80°时,∴∠ADC =100°,∵∠C =40°,∴∠DAC =40°,∴△ADE 的形状是等腰三角形.【练2】阅读材料:小胖同学遇到这样一个问题,如图1,在△AB C 中,∠ABC =45°,AB =2√2,AD =AE ,∠DAE =90°,CE =√5,求CD 的长;小胖经过思考后,在CD 上取点F 使得∠DEF =∠ADB (如图2),进而得到∠EFD =45°,试图构建“一线三等角”图形解决问题,于是他继续分析,又意外发现△CEF ∽△CDE .(1)请按照小胖的思路完成这个题目的解答过程.(2)参考小胖的解题思路解决下面的问题:如图3,在△AB C 中,∠ACB =∠DAC =∠ABC ,AD =AE ,12∠EAD +∠EBD =90°,求BE :E D .【答案】CD=5;(1)证明见解析;(2)12【解析】解:(1)在CD 上取点F ,使∠DEF =∠ADB ,∵AD=AE,∠DAE=90°,∴DE=√2AD=√2AE,∵∠ABC=45°,∠ADE=45°,且∠ADC=∠ADE+∠EDC,∴∠BAD=∠EDC,∵∠BDA=∠DEF,∴△ADB∽△DEF,∴DFAB =DEAD=√2,∵AB=2√2,∴DF=4,又∵∠CDE+∠C=45°,∴∠CEF=∠CDE,∴△CEF∽△CDE,∴CECF =DCCE,又∵DF=4,CE=√5,∴√5CF =√5,∴CF=1或CF=5(舍去),∴CD=CF+4=5;(2)如图3,作∠DAT=∠BDE,作∠RAT=∠DAE,∵∠ACB=∠DAC=∠ABC,∴AB=AC,AD=CD,∵AD=AE,∴∠AED=∠ADE,∵12∠EAD+∠EBD=90°,∴∠EAD+2∠EBD=180°,且∠EAD+2∠AED=180°,∴∠EBD=∠AED=∠ADE,∵∠BDA=∠DAT+∠ATD=∠BDE+∠ADE,∴∠ADE=∠ATD=∠EBD,且∠BDE=∠DAT,∴△DBE∽△ATD,∴BEDT =DEAD,∠ADT=∠BED,∴BEDE =DTAD,且AD=DC,∴BEDE =DTCD,∵∠RAT=∠DAE,∠ADE=∠ATD,∴∠RAE=∠DAT,∠AED=∠ART=∠ADE=∠ATD,∴AR=AT,且∠RAE=∠DAT,∠ARE=∠ATD,∴△ARE≌△ATD(ASA)∴∠ADT=∠AER,DT=ER,∴∠BED=∠AER,∴∠AED=∠BER=∠EBD,∴RE=RB=DT,∵AB=AC,∠ABC=∠ACB,∠ARB=∠ATC,∴△ABR≌△ACT(AAS)∴BR=TC,∴DT=TC,∴CD=2DT,∴BEDE =DTCD=12【练3】数学模型(“一线三等角”模型)(1)如图1,∠BAC=90°,AB=AC,BD⊥AD于点D,CE⊥AD于点E.求证:△ABD≌△CAE.(2)如图2,在△AB C中,AB=AC,点D,A,E都在直线l上,并且∠BDA=∠AEC=∠BAC =α.若CE=a,BD=b,求DE的长度(用含a,b的代数式表示);(3)如图3,D,E是直线l上的动点,若△ABF和△ACF都是等边三角形,且∠BDA=∠AEC =∠BAC=α,试判断△DEF的形状,并说明理由.【答案】(1)见解析(2)a+b(3)△DEF是等边三角形,理由见解析.【解析】(1)证明:∵∠1+∠2=∠2+∠C=90°,∴∠1=∠C,在△ABD和△CAE中,{∠1=∠C∠ADB=∠CEA=90°AB=AC,∴△ABD≌△CAE(AAS),(2)解:∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=180°﹣α=∠BAD+∠CAE,∴∠CAE=∠ABD,在△ABD和△CAE中,{∠ABD=∠CAE ∠BDA=∠AEC AB=AC∴△ABD≌△CAE(AAS),∴AD=CE,BD=AE,∵CE=a,BD=b,∴DE=AD+AE=BD+CE=a+b;(3)解:△DEF是等边三角形,理由如下:∵△ABF和△ACF都是等边三角形∴AB=AC,由(2)知:△ABD≌△CAE,∴BD=AE,∠ABD=∠CAE,∵△ACF是等边三角形,△ABF是等边三角形,∴∠CAF=60°,AB=AF,∴∠ABD+∠ABF=∠CAE+∠CAF,即∠DBF=∠F AE,在△BDF和△AEF中,{FB=FA∠FBD=∠FAEBD=AE,∴△BDF≌△AEF(SAS),∴DF=EF,∠BFD=∠AFE,∴∠DFE=∠AFD+∠AFE=∠AFD+∠BFD=60°,∴△DEF是等边三角形.【练4】数学模型学习与应用.【学习】如图1,∠BAD=90°,AB=AD,BC⊥AC于点C,DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D;又∠ACB=∠AED=90°,可以通过推理得到△ABC≌△DAE.我们把这个数学模型称为“一线三等角”模型;(1)【应用】如图2,点B,P,D都在直线l上,并且∠ABP=∠APC=∠PDC=α.若BP=x,AB=2,BD=5,用含x的式子表示CD的长;(2)【拓展】在△ABC中,点D,E分别是边BC,AC上的点,连接AD,DE,∠B=∠ADE=∠C,AB=5,BC=6.若△CDE为直角三角形,求CD的长;(3)如图3,在平面直角坐标系xOy中,点A的坐标为(2,4),点B为平面内任一点.△AOB是以OA为斜边的等腰直角三角形,试直接写出点B的坐标.【答案】(1)CD=−12x2+52x(2)3(3)(3,1)或(−1,3)【解析】(1)解:∵∠ABP=∠APC=∠PDC=α,∴∠A+∠APB=∠APB+∠CPD,∴∠A=∠CPD,又∵∠ABP=∠PDC,∴△ABP∽△PDC,∴ABPD =BPCD,即xCD =25−x,∴CD=−12x2+52x.(2)解:如图4,当∠CED=90°时,∵∠ADE=∠C,∠CAD=∠DAE,∴△ACD∽△ADE,∴∠ADC=∠AED=90°,∵∠B=∠C,∠ADC=90°∴点D为BC的中点,∴CD=12BC=12×6=3.如图5,当∠EDC=90°时,∵∠B=∠C,∴∠BAD=∠EDC=90°,过点A作AF⊥BC,交BC于点F,∴BF=12BC=3,cos B=BFAB=ABBD=35,BD=253>6,不合题意,舍去,∴CD=3.(3)解:分两种情况:①如图6所示,过A作AC⊥y轴于D,过B作BE⊥x轴于E,DA与EB相交于C,则∠C =90°,∴四边形OECD是矩形∵点A的坐标为(2,4),∴AD=2,OD=CE=4,∵∠OBA=90°,∴∠OBE+∠ABC=90°,∵∠ABC+∠BAC=90°,∴∠BAC=∠OBE,在△ABC与△BOE中,{∠C=∠BEO=90°∠BAC=∠OBEAB=BO∴△ABC≌△BOE(AAS),∴AC=BE,BC=OE,设OE=x,则BC=OE=CD=x,∴AC=BE=x-2,∴CE=BE+BC=x-2+x=OD=4,∴x=3,x-2=1,∴点B的坐标是(3,1);②如图7,同理可得,点B的坐标(-1,3),综上所述,点B的坐标为(3,1)或(-1,3).。
一线三等角全等模型例题

一线三等角全等模型例题
一线三等角全等模型是指在三角形中,如果两个三角形的三条
边分别相等(一线)、三个角分别相等(三等角),那么这两个三
角形就是全等的。
这个模型在几何学中是非常重要的,因为它可以
帮助我们解决许多三角形的性质和问题。
让我们来看一个例题来说明一线三等角全等模型的应用:
假设有两个三角形ABC和DEF,且已知AB=DE, BC=EF, ∠A=∠D, ∠B=∠E。
我们需要证明三角形ABC和DEF全等。
首先,根据一线三等角全等模型,我们已经知道AB=DE, BC=EF, ∠A=∠D, 这满足了一线三等角全等模型的条件之一。
接下来,我们
需要证明∠B=∠E。
根据三角形内角和定理,三角形内角和为180度。
因此,
∠A+∠B+∠C=180度,∠D+∠E+∠F=180度。
由于∠A=∠D,我们可
以得出∠B+∠C=∠E+∠F。
又因为BC=EF,根据等角等边定理,
∠B=∠E。
所以,我们证明了∠B=∠E。
综上所述,根据一线三等角全等模型的条件和证明,我们可以
得出结论,三角形ABC和DEF是全等的。
在这个例题中,我们通过应用一线三等角全等模型成功地证明
了两个三角形全等的方法。
这个模型在解决三角形问题时非常有用,因为它可以帮助我们简化证明过程,从而更轻松地得出结论。
希望
这个例题能够帮助你更好地理解一线三等角全等模型的应用。
专题12.25 三角形全等几何模型-“一线三直角”模型(专项练习)(培优篇)

C D E B A 专题12.25 三角形全等几何模型-“一线三直角”模型(专项练习)(培优篇)知识储备:1、模型一: 三垂直全等模型图一如图一,∠D=∠BCA=∠E=90°,BC=AC 。
结论:Rt △BDC ≌Rt △CEA2、拓展:模型二: 三等角全等模型图二如图二,∠D=∠BCA=∠E ,BC=AC 。
结论:△BEC ≌△CDA一、单选题1.如图,Rt△ABC 中,△C=90°,BC=6,DE 是△ABC 的中位线,点D 在AB 上,把点B 绕点D 按顺时针方向旋转α(0°<α<180°)角得到点F ,连接AF ,BF .下列结论:△△ABF 是直角三角形;△若△ABF 和△ABC 全等,则α=2△BAC 或2△ABC ;△若α=90°,连接EF ,则S△DEF=4.5;其中正确的结论是( )A .△△B .△△C .△△△D .△△二、填空题2.如图,点A 的坐标为()4,0,点B 的坐标为()0,1-,分别以OB ,AB 为直角边在第三、第四象限作等腰Rt OBF △,等腰Rt ABE △,连接EF 交y 轴于P 点,点P 的坐标是______.3.如图,AO△OM ,OA=7,点B 为射线OM 上的一个动点,分别以OB ,AB 为直角边,B 为直角顶点,在OM 两侧作等腰Rt△OBF 、等腰Rt△ABE ,连接EF 交OM 于P 点,当点B 在射线OM 上移动时,则PB 的长度____________.三、解答题4.在Rt AOB ∆中,AOB 90∠=.(1)如图△,以点A 为直角顶点,AB 为腰在AB 右侧作等腰Rt ABC ∆,过点C 作CD OA ⊥交OA 的延长线于点D .求证:A AOB CD ∆∆≌.(2)如图△,以AB 为底边在AB 左侧作等腰Rt ABC ∆,连接OC ,求AOC ∠的度数.(3)如图△,Rt AOB ∆中,,OA OB OD AB =⊥,垂足为点D ,以OB 为边在OB 左侧作等边OBC ∆,连接AC 交OD 于E ,2OE =,求AC 的长.5.已知Rt△ABC 中,△BAC =90°,AB =AC ,点E 为△ABC 内一点,连接AE ,CE ,CE △AE ,过点B 作BD △AE ,交AE 的延长线于D .(1)如图1,求证BD=AE ;(2)如图2,点H 为BC 中点,分别连接EH ,DH ,求△EDH 的度数;(3)如图3,在(2)的条件下,点M 为CH 上的一点,连接EM ,点F 为EM 的中点,连接FH ,过点D 作DG △FH ,交FH 的延长线于点G ,若GH :FH =6:5,△FHM 的面积为30,△EHB =△BHG ,求线段EH 的长.6.如图1,在Rt ACB ∆中,90BAC ∠=︒,AB AC =,分别过B 、C 两点作过点A 的直线l 的垂线,垂足为D 、E ;(1)如图1,当D 、E 两点在直线BC 的同侧时,猜想,BD 、CE 、DE 三条线段有怎样的数量关系?并说明理由.(2)如图2,当D 、E 两点在直线BC 的两侧时,BD 、CE 、DE 三条线段有怎样的数量关系?并说明理由.(3)如图3,90BAC ∠=︒,22AB =,28AC =.点P 从B 点出发沿B A C →→路径向终点C 运动;点Q 从C 点出发沿C A B →→路径向终点B 运动.点P 和Q 分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P 和Q 作PF l ⊥于F ,QG l ⊥于G .问:点P 运动多少秒时,PFA ∆与QAG ∆全等?(直接写出结果即可)7.如图,在△ABC 中,△ACB =90°,AC =6,BC =8.点P 从点A 出发,沿折线AC—CB以每秒1个单位长度的速度向终点B 运动,点Q 从点B 出发沿折线BC—CA 以每秒3个单位长度的速度向终点A 运动,P 、Q 两点同时出发.分别过P 、Q 两点作PE△l 于E ,QF△l 于F .设点P 的运动时间为t (秒):(1)当P 、Q 两点相遇时,求t 的值;(2)在整个运动过程中,求CP 的长(用含t 的代数式表示);(3)当△PEC 与△QFC 全等时,直接写出所有满足条件的CQ 的长.8.(1)如图1,已知:在ABC ∆中,90BAC ∠=︒,AB AC =,直线l 经过点A ,BD l ⊥,CE l ⊥垂足分别为点D 、E .证明:△CAE ABD ∠=∠;△DE BD CE =+.(2)如图2,将(1)中的条件改为:在ABC ∆中,AB AC =,D 、A 、E 三点都在l 上,并且有BDA AEC BAC α∠=∠=∠=,其中α为任意锐角或钝角.请问结论DE BD CE =+是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)如图3,过ABC ∆的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.9.如图,A (-2,0),B (0,4)以B 点为直角顶点在第二象限作等腰直角△ABC (1)求C 点的坐标;(2)如图2点E 为y 轴正半轴上一动点,以E 为直角顶点作等腰直角△AEM ,过M 作MN△x 轴于N ,求OE -MN 的值.10.如图,OA OB =,OA OB ⊥,135ACO ∠=︒,求ACB ∠的度数.11.综合与实践.积累经验我们在第十二章《全等三角形》中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.例如:我们在解决:“如图1,在ABC ∆中,90ACB ∠=︒,AC BC =,线段DE 经过点C ,且AD DE ⊥于点D ,BE DE ⊥于点E .求证:AD CE =,CD BE =”这个问题时,只要证明ADC CEB ∆∆≌,即可得到解决,(1)请写出证明过程;类比应用(2)如图2,在平面直角坐标系中,ABC ∆中,90ACB ∠=︒,AC BC =,点A 的坐标为()0,2,点C 的坐标为()1,0,求点B 的坐标.拓展提升(3)如图3,ABC ∆在平面直角坐标系中,90ACB ∠=︒,AC BC =,点A 的坐标为()2,1,点C 的坐标为()4,2,则点B 的坐标为____________.12.问题背景:(1)如图1,已知△ABC 中,△BAC =90°,AB =AC ,直线m 经过点A ,BD△直线m ,CE△直线m ,垂足分别为点D 、E .求证:DE =BD +CE .拓展延伸:(2)如图2,将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有△BDA =△AEC =△BAC .请写出DE 、BD 、CE 三条线段的数量关系.(不需要证明)实际应用:(3)如图,在△ACB 中,△ACB =90°,AC =BC ,点C 的坐标为(-2,0),点A 的坐标为(-6,3),请直接写出B 点的坐标.13.如图,Rt ACB △中,90ACB ∠=︒,AC BC =,E 点为射线CB 上一动点,连结AE ,作AF AE ⊥且AF AE =.(1)如图1,过F 点作FD AC ⊥交AC 于D 点,求证:FD BC =;(2)如图2,连结BF 交AC 于G 点,若3AG =,1CG =,求证:E 点为BC 中点. (3)当E 点在射线CB 上,连结BF 与直线AC 交于G 点,若4BC =,3BE =,则AG CG =______.(直接写出结果)14.如图,以ABC 的边AB 和AC ,向外作等腰直角三角形ABE △和ACF ,连接 EF ,AD 是ABC 的高,延长DA 交EF 于点G ,过点F 作DG 的垂线交DG 于点H .(1)求证:FHA ADC ≌△△;(2)求证:点G 是EF 的中点.15.如图,等腰Rt ABC 中,90ABC ∠=︒,AB BC =,点A ,B 分别在坐标轴上. (1)如图1,若点C 的横坐标为5,直接写出点B 的坐标_______;图1(2)如图2,若点A 的坐标为()6,0-,点B 在y 轴的正半轴上运动时,分别以OB ,AB 为边在第一、第二象限作等腰Rt OBF ,等腰Rt ABE △,连接EF 交y 轴于点P ,当点B 在y 轴的正半轴上移动时,PB 的长度是否发生改变?若不变,求出PB 的值;若变化,求PB 的取值范围.图216.提出问题:如图1,将三角板放在正方形ABCD 上,使三角板的直角顶点P 在对角线AC 上,一条直角边经过点B ,另一条直角边交边DC 与点E ,求证:PB=PE分析问题:学生甲:如图1,过点P 作PM△BC ,PN△CD ,垂足分别为M ,N 通过证明两三角形全等,进而证明两条线段相等.学生乙:连接DP ,如图2,很容易证明PD=PB ,然后再通过“等角对等边”证明PE=PD ,就可以证明PB=PE 了.解决问题:请你选择上述一种方法给予证明.问题延伸:如图3,移动三角板,使三角板的直角顶点P 在对角线AC 上,一条直角边经过点B ,另一条直角边交DC 的延长线于点E ,PB=PE 还成立吗?若成立,请证明;若不成立,请说明理由.17.(提出问题)如图1,在直角ABC 中,△BAC =90°,点A 正好落在直线l 上,则△1、△2的关系为(探究问题)如图2,在直角ABC 中,△BAC =90°,AB =AC ,点A 正好落在直线l 上,分别作BD △l 于点D ,CE △l 于点E ,试探究线段BD 、CE 、DE 之间的数量关系,并说明理由.(解决问题)如图3,在ABC 中,△CAB 、△CBA 均为锐角,点A 、B 正好落在直线l 上,分别以A 、B 为直角顶点,向ABC 外作等腰直角三角形ACE 和等腰直角三角形BCF ,分别过点E 、F 作直线l 的垂线,垂足为M 、N .△试探究线段EM 、AB 、FN 之间的数量关系,并说明理由;△若AC =3,BC =4,五边形EMNFC 面积的最大值为18.如图,在平面直角坐标系中,点()()3,01,0B A --、分别是x 轴上两点,点()0,P h 是y 轴正半轴上的动点,过点P 作,DP PB CP PA ⊥⊥,且,PD PB PC AP ==.(1)如图1,连接AD BC 、相交于点E ,求证:PCB PAD ≌;(2)如图1,连接PE ,求证:PE 平分CED ∠;(3)如图2,连CD 与y 轴相交于点Q ,当动点P 在y 轴正半轴上运动时,线段PQ 的长度是否改变?如果不变,请求出其值;如果改变,请求出其变化范围.19.在Rt ABC △中,90CAB ∠=︒,AB AC =,点O 是BC 的中点,点P 是射线CB 上的一个动点(点P 不与点C 、O 、B 重合),过点C 作CE AP ⊥于点E ,过点B 作BF AP⊥于点F ,连接EO ,OF .(问题探究)如图1,当P 点在线段CO 上运动时,延长EO 交BF 于点G ,(1)求证:AEC △BFA ;(2)BG 与AF 的数量关系为:______(直接写结论,不需说明理由);(拓展延伸)(3)△如图2,当P 点在线段OB 上运动,EO 的延长线与BF 的延长线交于点G ,OFE ∠的大小是否变化?若不变,求出OFE ∠的度数;若变化,请说明理由;△当P 点在射线OB 上运动时,若2AE =,5CE =,直接写出OEF 的面积,不需证明. 20.如图,线段AB=4,射线BG△AB ,P 为射线BG 上一点,以AP 为边作正方形APCD ,且点C、D与点B在AP两侧,在线段DP上取一点E,使△EAP=△BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).(1)求证:AEP△CEP;(2)判断CF与AB的位置关系,并说明理由;(3)请直接写出AEF的周长.参考答案1.C【分析】△根据直角三角形斜边中线的性质和旋转的性质得出AD BD DF ==,然后利用等腰三角形的性质和三角形内角和定理即可判断;△分两种情况讨论:ABF ABC ∠=∠或ABF BAC ∠=∠,分别求α即可 ; △先根据题意画出图形,首先证明FDG ADE ≅ ,然后得出3FG DE ==,最后利用12DEF S DE FG =⋅即可求解. 【详解】△△DE 是△ABC 的中位线,AD DB ∴=.由旋转可知DF DB =,AD BD DF ∴==,,DAF AFD DBF DFB ∴∠=∠∠=∠ .180DAF AFB ABF ∠+∠+∠=︒ ,90AFD DFB ∴∠+∠=︒ ,即90AFB ∠=︒ ,△△ABF 是直角三角形,故△正确;90C ∠=︒ ,90BAC ABC ∴∠+∠=︒ .若△ABF 和△ABC 全等,当ABF ABC ∠=∠时,180218022(90)2ABF ABC ABC BAC α=︒-∠=︒-∠=︒-∠=∠ ;当ABF BAC ∠=∠时,180218022(90)2ABF BAC BAC ABC α=︒-∠=︒-∠=︒-∠=∠,综上所述,若△ABF 和△ABC 全等,则α=2△BAC 或2△ABC ,故△正确;过点F 作FG DE ⊥交ED 的延长线于点G ,△DE 是ABC 的中位线,//DE BC ∴ ,90AED ACB ∴∠=∠=︒ .FG DE ⊥,90FGE ∴∠=︒.90FDB ∠=︒,90ADF ∴∠=︒,90FDG ADE ∴∠+∠=︒.90DAE ADE ∠+∠=︒ ,FDG DAE ∴∠=∠.90AFB ∠=︒,D 为AB 中点,FD AD ∴=.在FDG △和ADE 中,FGD AED FDG DAE FD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩()FDG ADE AAS ∴≅3FG DE ∴==,1133 4.522DEF S DE FG ∴=⋅=⨯⨯=,故△正确; 所以正确的有:△△△.故选:C .【点拨】本题主要考查三角形中位线的性质,直角三角形斜边中线的性质,全等三角形的判定及性质,掌握三角形中位线的性质,直角三角形斜边中线的性质,全等三角形的判定及性质是解题的关键.2.()0,3-【分析】作EN y ⊥轴于N ,求出NBE BAO ∠=∠,证ABO BEN ≅△△,得BN =AO ,再由90OBF FBP BNE ∠=∠=∠=︒,证BFP NEP ≅△△,推出BP NP ==2,由点B 的坐标为()0,1-即可得出点P 的坐标为()0,3-.【详解】解:如图,作EN y ⊥轴于N ,90ENB BOA ABE ∠=∠=∠=︒,90OBA NBE ∴∠+∠=︒,90OBA OAB ∠+∠=︒,NBE BAO ∴∠=∠,在ABO 和BEN 中,AOB BNE BAO NBE AB BE ∠=∠⎧⎪∠=∠⎨⎪=⎩()ABO BEN AAS ∴≅△△,OB NE BF ∴==,OA=BN90OBF FBP BNE ∠=∠=∠=︒,在BFP △和NEP △中,FPB EPN FBP ENP BF NE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BFP NEP AAS ∴≅△△,BP NP ∴=,又因为点A 的坐标为(4,0),4OA BN ∴==,122BP NP BN ∴===, 又△点B 的坐标为()0,1-,△点P 的坐标为()0,3-.故答案为:()0,3-.【点拨】本题考查了全等三角形的性质和判定,坐标与图形性质等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,有一定的难度,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS ,全等三角形的对应角相等,对应边相等.3.72【分析】根据题意过点E 作EN△BM ,垂足为点N ,首先证明△ABO△△BEN ,得到BO=ME ;进而证明△BPF△△MPE 并分析即可得出答案.【详解】解:如图,过点E 作EN△BM ,垂足为点N ,△△AOB=△ABE=△BNE=90°,△△ABO+△BAO=△ABO+△NBE=90°,△△BAO=△NBE ,△△ABE 、△BFO 均为等腰直角三角形,△AB=BE ,BF=BO ;在△ABO 与△BEN 中,BAO NBE AOB BNE AB BE ∠⎪∠⎧⎩∠⎪∠⎨===,△△ABO△△BEN (AAS ),△BO=NE ,BN=AO ;△BO=BF ,△BF=NE ,在△BPF 与△NPE 中,FBP ENP FPB EPN BF NE ∠⎪∠⎧⎩∠⎪∠⎨===,△△BPF△△NPE (AAS ), △BP=NP=12BN ,BN=AO , △BP= 12AO= 12×7=72. 故答案为:72. 【点拨】本题考查三角形内角和定理以及全等三角形的性质和判定的应用,解题的关键是作辅助线,构造全等三角形并灵活运用有关定理进行分析.4.(1)见解析;(2)135AOC ∴∠=;(3)【分析】(1)根据“一线三垂直”模型,可以证得A AOB CD ∆∆≌;(2)过点C 作CM△CO 交BO 于M ,AC 与BO 交于点N ,利用旋转模型证明BCM ∆△()ACO ASA ∆,由外角的性质计算即可;(3)在CE 上截取一点H ,使CH=AE ,连接OH ,利用等腰直角△AOB ,等边△BOC 证得OAE ∆△()OCH SAS ∆,通过等角代换证明HOE ∆为等边三角形,由线段和计算即可得到结果.【详解】(1)△△BAC=△AOB=90°,△△BAO+△DAC=△BAO+△ABO=90°,△△DAC=△ABO ,△△ABC 是等腰直角三角形,△AB=AC ,在△AOB 和△CDA 中,ABO DAC AOB CDA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△AOB△△CDA (AAS )(2)如图△,过点C 作CM△CO 交BO 于M ,AC 与BO 交于点N ,90MCO ACB ∴∠=∠=,BCM ACO ∴∠=∠,90BCA AOB ∠=∠=,BNC ANO ∠=∠,CBM OAC ∴∠=∠,△AC=BC ,BCM ∴∆△()ACO ASA ∆,CM CO ∴=,45COM CMO ∴∠=∠=,9045135AOC ∴∠=+=,故答案为:135°.(3)如图△,在CE 上截取一点H ,使CH=AE ,连接OH ,△△AOB 是等腰直角三角形,△BOC 是等边三角形,所以AO BO CO ==,OAE OCH ∴∠=∠,OAE ∴∆△()OCH SAS ∆,OH OE ∴=,AE=CH=3,△AOE=△COH ,OD AB ⊥,△AOB=90°,45AOE BOE ∴∠=∠=,45COH ∴∠=,△BOH=△BOC -△COH=60°-45°=15°,154560HOE ∴∠=+=,HOE ∴∆为等边三角形,2HE EO ∴==,Rt△ADE 中,△DAE=45°-15°=30°,△AE=2DE ,设DE=x ,则AE=2x ,,△AD=OD ,,,,.故答案为:.【点拨】本题考查了“一线三垂直”模型,三角形全等的判定和性质,等边三角形的判定和性质,等腰直角三角形的性质,等角代换的应用,计算线段和的应用,掌握三角形全等的判定和性质是解题的关键.5.(1)见解析;(2)△EDH=45°;(3)EH=【分析】(1)根据全等三角形的判定得出△CAE△△ABD,进而利用全等三角形的性质得出AE=BD 即可;(2)根据全等三角形的判定得出△AEH△△BDH,进而利用全等三角形的性质解答即可;(3)过点M作MS△FH于点S,过点E作ER△FH,交HF的延长线于点R,过点E作ET△BC,根据全等三角形判定和性质解答即可.【详解】证明:(1)△CE△AE,BD△AE,△△AEC=△ADB=90°,△△BAC=90°,△△ACE+CAE=△CAE+△BAD=90°,△△ACE=△BAD,在△CAE与△ABD中ACE BAD AEC ADB AC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩△△CAE △△ABD (AAS ),△AE =BD ;(2)连接AH△AB =AC ,BH =CH ,△△BAH =11904522BAC ∠=⨯︒=︒,△AHB =90°, △△ABH =△BAH =45°,△AH =BH ,△△EAH =△BAH ﹣△BAD =45°﹣△BAD ,△DBH =180°﹣△ADB ﹣△BAD ﹣△ABH =45°﹣△BAD ,△△EAH =△DBH ,在△AEH 与△BDH 中AE BD EAH DBH AH BH =⎧⎪∠=∠⎨⎪=⎩△△AEH △△BDH (SAS ),△EH =DH ,△AHE =△BHD ,△△AHE +△EHB =△BHD +△EHB =90°即△EHD =90°,△△EDH =△DEH =18090452︒-︒=︒; (3)过点M 作MS △FH 于点S ,过点E 作ER △FH ,交HF 的延长线于点R ,过点E 作ET △BC ,交HR 的延长线于点T .△DG △FH ,ER △FH ,△△DGH =△ERH =90°,△△HDG +△DHG =90°△△DHE =90°,△△EHR +△DHG =90°,△△HDG =△HER在△DHG 与△HER 中HDG HER DGH ERH DH EH ∠=∠⎧⎪∠=∠⎨⎪=⎩△△DHG △△HER (AAS ),△HG =ER ,△ET △BC ,△△ETF =△BHG ,△EHB =△HET ,△ETF =△FHM ,△△EHB =△BHG ,△△HET =△ETF ,△HE =HT ,在△EFT 与△MFH 中ETF FHM EFT MFH EF FM ∠=∠⎧⎪∠=∠⎨⎪=⎩,△△EFT △△MFH (AAS ),△HF =FT , △22HF MS FT ER =, △ER =MS ,△HG =ER =MS ,设GH =6k ,FH =5k ,则HG =ER =MS =6k , 563022HF MS k k ==, k△FH =△HE =HT =2HF =【点拨】本题考查全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会利用数形结合的思想思考问题,属于压轴题.6.(1)+DE CE BD =(2)CE DE BD =+(3)当P 点运动6秒或10秒时PFA ∆与QAG ∆全等【分析】(1)根据题意首先证明()ABD ACE AAS ∆≅∆,在采用等量替换即可证明+DE CE BD =. (2)根据题意首先证明()ABD CAE AAS ∆≅∆,在采用等量替换即可证明CE BD DE =+.(3)根据PFA ∆与QAG ∆全等,列方程即可,注意要分类讨论.【详解】(1)+DE CE BD =.理由如下:△在Rt ABC ∆中,90BAC ∠=︒,△90BAD EAC ∠+∠=︒,又△90ADB AEC ∠=∠=︒,△90BAD ABD ∠+∠=︒,△EAC ABD ∠=∠,△AB AC =,△()ABD ACE AAS ∆≅∆,△AD CE =,BD AE =,△DE AD AE CE BD =+=+.(2)CE DE BD =+..理由如下:△BD AE ⊥,CE AE ⊥,△90ADB AEC ∠=∠=︒,△90ABD BAD ∠+∠=︒,△90BAC ∠=︒,△90BAD EAC ∠+∠=︒,△ABD EAC ∠=∠,在ABD ∆和CAE ∆中,△ABD CAE ∠=∠,ADB CEA ∠=∠,AB AC =,△()ABD CAE AAS ∆≅∆,△BD AE =,AD CE =,△AD AE DE =+,△AD BD DE =+,△CE BD DE =+;(3)解:△当点P 在AB 上,点Q 在AC 上时,222283t t -=-,解得6t =,△当点P 在AB 上,点Q 在AC 上时,222328t t -=-,解得10t =.△当点P 在AC 上,点Q 在AB 上时,(t>11)222328t t -=-解得:t=6(舍)△当点Q 运动到B 点,点P 在AC 上时,(11<t≤503) 22222t -=,解得22t =(舍).所以当P 点运动6秒或10秒时PFA ∆与QAG ∆全等.【点拨】本题主要考查三角形的全等证明,关键在于第三问的分类讨论思想,这是数学的一个重要思想,应当熟练掌握.7.(1)t 的值为72秒;(2)CP 的长为6(6)6(614)t t t t -≤⎧⎨-<≤⎩;(3)当△PEC 与△QFC 全等时,满足条件的CQ的长为5或2.5或6【分析】(1)由题意得t+3t=6+8,即可求得P、Q两点相遇时,t的值;(2)根据题意即可得出CP的长为6(6)6(614)t tt t-≤⎧⎨-<≤⎩;(3)分两种情况讨论得出关于t的方程,解方程求得t的值,进而即可求得CQ的长.【详解】解:(1)由题意得t+3t=6+8,解得:t=72(秒),当P、Q两点相遇时,t的值为72秒;(2)由题意可知AP=t,则CP的长为6(6)6(614)t tt t-≤⎧⎨-<≤⎩;(3)当P在AC上,Q在BC上时,△△ACB=90,△△PCE+△QCF=90°,△PE△l于E,QF△l于F.△△EPC+△PCE=90°,△PEC=△CFQ=90°,△△EPC=△QCF,△△PCE△△CQF,△PC=CQ,△6﹣t=8﹣3t,解得t=1,△CQ=8﹣3t=5;当P在AC上,Q在AC上时,即P、Q重合时,则CQ=PC,由题意得,6﹣t=3t﹣8,解得:t=3.5,△CQ=3t﹣8=2.5,当P在BC上,Q在AC上时,即A、Q重合时,则CQ=AC=6,综上,当△PEC与△QFC全等时,满足条件的CQ的长为5或2.5或6.【点拨】本题考查了三角形全等的判定和性质,线段的动点问题,根据题意得出关于t 的方程是解题的关键.8.(1)△见解析;△见解析;(2)成立:DE=BD+CE ;证明见解析;(3)见解析【分析】(1)△根据平行线的判定与性质即可求解;△由条件可证明△ABD△△CAE ,可得DA =CE ,AE =BD ,可得DE =BD +CE ;(2)由条件可知△BAD +△CAE =180°−α,且△DBA +△BAD =180°−α,可得△DBA =△CAE ,结合条件可证明△ABD△△CAE ,同(1)可得出结论;(3)由条件可知EM =AH =GN ,可得EM =GN ,结合条件可证明△EMI△△GNI ,可得出结论I 是EG 的中点.【详解】(1)△△BD△直线l ,CE△直线l△△BDA=△CEA=90°△△BAC=90°△△BAD+△CAE=90°△△BAD+△ABD=90°△△CAE=△ABD△在△ADB 和△CEA 中ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△ADB△△CEA (AAS )△AE=BD ,AD=CE△DE=AE+AD=BD+CE ;(2)成立:DE=BD+CE 证明如下:△△BDA=△BAC=α△△DBA+△BAD=△BAD+△CAE=180°﹣α△△DBA=△CAE在△ADB 和△CEA 中ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△ADB△△CEA (AAS )△AE=BD 、AD=CE△DE=AE+AD=BD+CE ;(3)如图过E 作EM△HI 于M ,GN△HI 的延长线于N△△EMI=GNI=90°由(1)和(2)的结论可知EM=AH=GN△EM=GN在△EMI 和△GNI 中GIH EIM EM GNGHI EMI ∠=∠⎧⎪=⎨⎪∠=∠⎩△△EMI△△GNI (AAS )△EI=GI△I 是EG 的中点.【点拨】本题主要考查全等三角形的判定和性质,由条件证明三角形全等得到BD =AE 、CE =AD 是解题的关键.9.(1)C (-4,6);(2)OE -MN=2.【分析】(1)作CE△y 轴于E ,易证△CBE△△BAO ,即可得点C 的坐标;(2)作MF△y 轴于F ,易证△AOE△△EFM ,可得OE -MN=EF=OA 即可求得答案.【详解】(1)作CE△y 轴于E ,如图1,△A (-2,0),B (0,4),△OA=2,OB=4,△△CBA=90°,△△CEB=△AOB=△CBA=90°,△△ECB+△EBC=90°,△CBE+△ABO=90°,△△ECB=△ABO ,在△CBE 和△BAO 中ECB ABO CEB AOB BC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩△△CBE△△BAO ,△CE=BO=4,BE=AO=2,即OE=2+4=6,△C (-4,6).(2)如图2,作MF△y 轴于F ,则△AEM=△EFM=△AOE=90°,△△AEO+△MEF=90°,△MEF+△EMF=90°,△△AEO=△EMF ,在△AOE 和△EMF 中,AOE EFM AEO EMF AE EM ∠=∠⎧⎪∠=∠⎨⎪=⎩△△AEO△△EMF ,△EF=AO=2,MF=OE ,△MN△x 轴,MF△y 轴,△△MFO=△FON=△MNO=90°,△四边形FONM 是矩形,△MN=OF ,△OE -MN=OE -OF=EF=OA=2.考点:全等三角形的判定及性质.10.△ACB=90°.【分析】作AM△直线OC 于M ,BN△直线OC 于N .通过AAS 证明△AOM△△OBN ,根据全等三角形的性质和等腰直角三角形的性质即可求得答案.【详解】作AM△直线OC 于M ,BN△直线OC 于N .△△ACO=135°,△△ACM=45°,△AM=CM ,在△AOM 与△OBN 中,90()AMO ONB AOM OBN BON OA OB ∠∠︒⎧⎪∠∠∠⎨⎪=⎩===均为的余角,△△AOM△△OBN(AAS),△OM=BN ,ON=AM=CM ,△NC=OM=BN ,又△BN△NS .△△BCN=45°,△△ACB=△ACO -△BCN=90°.【点拨】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,有一定的综合性,难点是作出辅助线.11.(1)见解析;(2)B 的坐标(3,1);(3)(3,4)【分析】(1)根据AD△DE 、BE△DE 得到△D=△E=90°再根据直角三角形的性质以及同角的余角相等,推出△DAC=△BCE ,进而证明ADC CEB ≅,最后再根据全等三角形对应边相等得出AD=CE ,CD=BE ;(2)如图4,过点B 作BE△x 轴于点E ,通过证明AOC CEB ≅,进而得出AO=CE ,CO=BE ,再根据点A 的坐标为(0,2),点C 的坐标(1,0),求得OE=3,最后得出B 的坐标(3,1);(3)如图5,过点C 做CF△x 轴与点F ,再过点A 、B 分别做AE△CF ,BD△CF ,通过证明CDB AEC ≅,进而得出BD=CE=,AE=CD ,最后根据点A 的坐标为()2,1,点C 的坐标为()4,2,得出B 坐标(3,4).【详解】(1)证明:△AD△DE ,BE△DE△△D=△E=90°△△DAC+△ACD=90°又△△ACB=90°△△ACD+△BCE=90°△△DAC=△BCE在△ADC 和△CEB 中D E DAC BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△ADC△△CEB△AD=CE ,CD=BE(2)解:如图,过点B 作BE△x 轴于点E△△AOC=90°△△OAC+△ACO=90°又△△ACB=90°△△ACO+△BCE=90°△△OAC=△BCE在△AOC 和△CEB 中90AOC CEB OAC ECBAC BC ⎧∠=∠=⎪∠=∠⎨⎪=⎩△△AOC△△CEB△AO=CE ,CO=BE又△点A 的坐标为(0,2),点C 的坐标(1,0)△AO=2,CO=1△CE=2,BE=1△OE=3△B 的坐标(3,1)(3)(3,4)解:如图5,过点C 做CF△x 轴与点F ,再过点A 、B 分别做AE△CF ,BD△CF , △AE△CF ,BD△CF△90AEC CDB ∠=∠=︒,△90ACE CAE ∠+∠=︒,又△90ACB ∠=︒,△90ACE BCD ∠+∠=︒,△CAE BCD ∠=∠,△在ACE △和BCD △中AEC CDB CAE BCD AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,△ACE BCD ≅(AAS )△BD=CE ,AE=CD ,又△A 的坐标为()2,1,点C 的坐标为()4,2,△CE=BD=2-1=1,CD=AE=4-2=2设B 点坐标为(a ,b ),则a =4-1=3,b =2+2=4,△B 坐标(3,4).【点拨】本题综合考查了全等三角形的证明以及平面直角坐标系中求点坐标的综合应用问题;通过构建“一线三等角”模型,再利用直角三角形的性质以及同角的余角相等解决角关系是本题的关键.12.(1)证明见解析;(2)DE =BD +CE ;(3)B(1,4)【分析】(1)证明△ABD△△CAE ,根据全等三角形的性质得到AE=BD ,AD=CE ,结合图形解答即可;(2)根据三角形内角和定理、平角的定义证明△ABD=△CAE ,证明△ABD△△CAE ,根据全等三角形的性质得到AE=BD ,AD=CE ,结合图形解答即可;(3)根据△AEC△△CFB ,得到CF=AE=3,BF=CE=OE -OC=4,根据坐标与图形性质解答.【详解】(1)证明:△BD△直线m ,CE△直线m ,△△ADB =△CEA =90°△△BAC =90°△△BAD +△CAE =90°△△BAD +△ABD =90°△△CAE =△ABD△在△ADB 和△CEA 中ABD CAE ADB CEA AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩△△ADB△△CEA (AAS )△AE =BD ,AD =CE△DE =AE +AD =BD +CE即:DE =BD +CE(2)解:数量关系:DE =BD +CE理由如下:在△ABD 中,△ABD=180°-△ADB -△BAD ,△△CAE=180°-△BAC -△BAD ,△BDA=△AEC ,△△ABD=△CAE ,在△ABD 和△CAE 中,ABD CAE BDA AEC AB CA ∠∠⎧⎪∠∠⎨⎪⎩===△△ABD△△CAE (AAS )△AE=BD ,AD=CE ,△DE=AD+AE=BD+CE ;(3)解:如图,作AE△x 轴于E ,BF△x 轴于F ,由(1)可知,△AEC△△CFB ,△CF=AE=3,BF=CE=OE -OC=4,△OF=CF -OC=1,△点B 的坐标为B (1,4).【点拨】本题考查的是全等三角形的判定和性质、坐标与图形性质,掌握全等三角形的判定定理和性质定理是解题的关键.13.(1)见解析;(2)见解析;(3)113或53 【分析】(1)证明△AFD△△EAC ,根据全等三角形的性质得到DF=AC ,等量代换证明结论; (2)作FD△AC 于D ,证明△FDG△△BCG ,得到DG=CG ,求出CE ,CB 的长,得到答案;(3)过F 作FD△AG 的延长线交于点D ,根据全等三角形的性质得到CG=GD ,AD=CE=7,代入计算即可.【详解】解:(1)证明:△FD△AC ,△△FDA=90°,△△DFA+△DAF=90°,同理,△CAE+△DAF=90°,△△DFA=△CAE ,在△AFD 和△EAC 中, AFD EAC ADF ECA AF AE ∠=∠⎧⎪∠=∠⎨⎪=⎩,△△AFD△△EAC (AAS ),△DF=AC ,△AC=BC ,△FD=BC ;(2)作FD△AC 于D ,由(1)得,FD=AC=BC,AD=CE,在△FDG和△BCG中,90 FDG BCG FGD BGCFD BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩,△△FDG△△BCG(AAS),△DG=CG=1,△AD=2,△CE=2,△BC=AC=AG+CG=4,△E点为BC中点;(3)当点E在CB的延长线上时,过F作FD△AG的延长线交于点D,BC=AC=4,CE=CB+BE=7,由(1)(2)知:△ADF△△ECA,△GDF△△GCB,△CG=GD,AD=CE=7,△CG=DG=1.5,△4 1.5111.53 AGCG+==,同理,当点E在线段BC上时,4 1.551.53 AGCG-==,故答案为:113或53.【点拨】本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.14.(1)证明见解析;(2)证明见解析.【分析】(1)先利用同角的余角相等得到一对角相等,再由一对直角相等,且AF AC =,利用AAS 得到AFH CAD ∆≅∆;(2)由(1)利用全等三角形对应边相等得到FH AD =,再EK AD ⊥,交DG 延长线于点K ,同理可得到AD EK =,等量代换得到FK EH =,再由一对直角相等且对顶角相等,利用AAS 得到FHG EKG ≅△△,利用全等三角形对应边相等即可得证.【详解】证明:(1) △FH AG ⊥,90AEH EAH ∴∠+∠=︒,90FAC ∠=︒,90FAH CAD ∴∠+∠=︒,AFH CAD ∴∠=∠,在AFH ∆和CAD ∆中,90AHF ADC AFH CADAF AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ()AFH CAD AAS ∴∆≅∆,(2)由(1)得AFH CAD ∆≅∆,FH AD ∴=,作FK AG ⊥,交AG 延长线于点K ,如图;同理得到AEK ABD ∆≅∆,EK AD ∴=,FH EK ∴=,在EKG ∆和FHG ∆中,90EKG FHG EGK FGHEK FH ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ()EKG FHG AAS ∴∆≅∆,EG FG ∴=.即点G 是EF 的中点.【点拨】此题考查了全等三角形的判定与性质,熟练掌握K 字形全等进行证明是解本题的关键.15.(1)()05,;(2)不变,PB 的值为3【分析】(1)作CD△BO ,可证△ABO 全等于△BCD ,根据全等三角形对应边相等的性质即可解题; (2)作EG△y 轴,可证△BAO 全等于△EBG 全等于△EGP 全等于△FBP ,可得BG=OA 和PB=PG,即可求得PB 是AO 的2倍,即可得到结论.【详解】(1)如图,作CD△BO 于D ,△△CBD+△ABO=90°,△ABO+△BAO=90°,△△CBD=△BAO,在△ABO 和△BCD 中,90BOA BDC CBD BAOAB BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩△△ABO△△BCD,△CD=BO=5,△B 点的坐标(0,5)故答案为:()05,. (2)不发生改变,理由如下:作EG y ⊥轴于G ,90BAO OBA ∠+∠=︒,90OBA EBG ∠+∠=︒,BAO EBG ∴∠=∠.在BAO ∆和EBG ∆中,90AOB BGE BAO EBGAB BE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()BAO EBG AAS ∴∆≅∆AO BG ∴=,OB EG =OB BF =,BF EG ∴=在EGP ∆和FBP ∆中,90EPG FPB EGP FBP EG FB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩()EGP FBP AAS ∴∆≅∆PG PB ∴=.11322PB BG AO ∴===. △不变,PB 的值为3.【点拨】本题考查三角形全等、等腰直角三角形性质、勾股定理、角平分线性质,熟练掌握添加辅助线证明三角形全等是解题的关键.16.解决问题:证明见解析;问题延伸:成立,证明见解析.【分析】解决问题:对于图1,根据正方形的性质得△BCD=90°,AC 平分△BCD ,而PM△BC ,PN△CD ,则四边PMCN 为矩形,根据角平分线性质得PM=PN ,根据四边形内角和得到△PBC+△CEP=180°,再利用等角的补角相等得到△PBM=△PEN ,然后根据“AAS”证明△PBM△△PEN ,则PB=PE ;对于图2,连结PD ,根据正方形的性质得CB=CD ,CA 平分△BCD ,根据角平分线的性质得△BCP=△DCP ,再根据“SAS”证明△CBP△△CDP ,则PB=PD ,△CBP=△CDP ,根据四边形内角和得到△PBC+△CEP=180°,再利用等角的补角相等得到△PBC=△PED ,则△PED=△PDE ,所以PD=PE ,于是得到PB=PD ;问题延伸:对于图3,过点P 作PM△BC ,PN△CD ,垂足分别为M ,N ,根据正方形的性质得△BCD=90°,AC 平分△BCD ,而PM△BC ,PN△CD ,得到四边PMCN 为矩形,PM=PN ,则△MPN=90°,利用等角的余角相等得到△BPM=△EPN ,然后根据“AAS”证明△PBM△△PEN ,所以PB=PE .【详解】解决问题:如图1,△四边形ABCD 为正方形,△△BCD=90°,AC 平分△BCD ,△PM△BC ,PN△CD ,△四边PMCN 为矩形,PM=PN ,△△BPE=90°,△BCD=90°,△△PBC+△CEP=180°,而△CEP+△PEN=180°,△△PBM=△PEN ,在△PBM 和△PEN 中PMB PNE PBM PEN PM PN ∠=∠∠=∠=⎧⎪⎨⎪⎩△△PBM△△PEN (AAS ),△PB=PE ;如图2,连结PD ,△四边形ABCD 为正方形,△CB=CD ,CA 平分△BCD ,△△BCP=△DCP ,在△CBP 和△CDP 中CB CD BCP DCP CP CP =∠=∠=⎧⎪⎨⎪⎩,△△CBP△△CDP (SAS ),△PB=PD ,△CBP=△CDP ,△△BPE=90°,△BCD=90°,△△PBC+△CEP=180°,而△CEP+△PEN=180°,△△PBC=△PED ,△△PED=△PDE ,△PD=PE ,△PB=PD ;问题延伸:如图3,PB=PE 还成立.理由如下:过点P 作PM△BC ,PN△CD ,垂足分别为M ,N ,△四边形ABCD 为正方形,△△BCD=90°,AC 平分△BCD ,△PM△BC ,PN△CD ,△四边PMCN 为矩形,PM=PN ,△△MPN=90°,△△BPE=90°,△BCD=90°,△△BPM+△MPE=90°,而△MEP+△EPN=90°,△△BPM=△EPN ,在△PBM 和△PEN 中PMB PNE BPM EPN PM PN ∠=∠∠=∠=⎧⎪⎨⎪⎩,△△PBM△△PEN (AAS ),△PB=PE .17.提出问题:1290∠+∠=︒;探究问题:BD CE DE +=,理由见解析;解决问题:△EM FN AB +=,理由见解析;△492. 【分析】 提出问题:根据平角的定义、角的和差即可得;探究问题:先根据垂直的定义可得90ADB CEA ∠=∠=︒,再根据直角三角形的两锐角互余、角的和差可得2ABD ∠=∠,然后根据三角形全等的判定定理与性质可得,BD AE AD CE ==,最后根据线段的和差即可得;解决问题:△如图(见解析),同探究问题的方法可得,EM AD FN BD ==,再根据线段的和差即可得;△如图(见解析),同探究问题的方法可得,ACD EAM BCD FBN ≅≅,再根据三角形全等的性质可得,ACD EAM BCD FBN S S S S ==,然后利用三角形的面积公式将五边形EMNFC 面积表示出来,由此即可得出答案.【详解】提出问题:12180,90BAC BAC ∠+∠+∠=︒∠=︒,2190∴∠+∠=︒,故答案为:1290∠+∠=︒;探究问题:BD CE DE +=,理由如下:,BD l CE l ⊥⊥,90ADB CEA ∴∠=∠=︒,190ABD ∴∠+∠=︒,由提出问题可知,1290∠+∠=︒,2ABD ∴∠=∠,在ABD △和CAE 中,2ADB CEA ABD AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ABD CAE AAS ∴≅,,BD AE AD CE ∴==,DE AE AD BD CE ∴=+=+,即BD CE DE +=;解决问题:△EM FN AB +=,理由如下:同探究问题的方法可证:,EM AD FN BD ==,AB AD BD EM FN ∴=+=+,即EM FN AB +=;△如图,过点C 作CD l ⊥于点D ,同探究问题的方法可证:,ACD EAM BCD FBN ≅≅,,ACD EAM BCD FBN S S S S ∴==, ACE 和BCF △都是等腰直角三角形,且3,4AC BC ==,3,4AE AC BF BC ∴====, 191,8222ACE BCF S AC AE S BC BF ∴=⋅==⋅=, ∴五边形EMNFC 面积为EAM ACE ACD BCD BCF FBN SS S S S S +++++, 982ACD ACD BCD BCDS S S S =+++++, ()2522ACD BCD SS =++, 2522ABC S =+, 则当ABC 面积取得最大值时,五边形EMNFC 面积最大, 设ABC 的BC 边上的高为h ,则122ABC S BC h h =⋅=, 在ABC 中,CAB ∠、CBA ∠均为锐角,∴当90ACB ∠=︒时,h 取得最大值,最大值为3AC =,ABC ∴面积的最大值为236ABC S =⨯=,则五边形EMNFC 面积的最大值为25492622⨯+=, 故答案为:492.【点拨】本题考查了垂直的定义、三角形全等的判定定理与性质、等腰直角三角形的定义等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.18.(1)见解析;(2)见解析;(3)不变,1.【分析】(1)根据题意直接证明即可;(2)作PM D A ⊥,PN BC ⊥,运用角平分线的判定定理证明;(3)通过“一线三垂直”模型,证得SDQ CTQ △△≌,进而结合边长数量关系求解.【详解】(1)90DPB APC ∠=∠=︒,DPA BAC ∴∠=∠,在PCB 与PAD △中,PD PB DPA BAC PC AP =∠=∠=⎧⎪⎨⎪⎩()PCB PAD SAS ∴△≌△(2)如图,作PM D A ⊥,PN BC ⊥,则90PMA PNC ∠=∠=︒,由PCB PAD ≌,得PCN PAM ∠=∠,在PMA △与PNC △中,PMA PNC PCN PAM PA PC ∠=∠⎧⎪∠=∠⎨⎪=⎩()PMA PNC AAS ∴△△≌,PM PN ∴=,PE ∴平分CED ∠(3)如图,作DS CT 、分别垂直于y 轴,垂足为S T 、,90APO TPC ∠+∠=︒,90TPC TCP ∠+∠=︒,APO PCT ∴∠=∠(余角的性质)在APO △与PCT △中,POA CTP APO PCT PA PC ∠=∠⎧⎪∠=∠⎨⎪=⎩()APO PCT AAS ∴△△≌,1OA TP ∴==,PO CT =,同理可证:PBO DPS △△≌,3OB SP ∴==,4ST SP PT =+=,∴ PO SD =,CT SD =,在SDQ △与CTQ △中,CQT SQD CTQ DSQ CT SD ∠=∠⎧⎪∠=∠⎨⎪=⎩()SDQ CTQ AAS ∴△△≌122SQ TQ ST ∴===, 1PQ QT PT ∴=-=.。
相似三角形的基本模型(一线三等角)

【根本模子】
1.如图 , ∽ (一线三等角)
如图 , ∽ (一线三直角)
如图 ,特殊地,当 是 中点时: ∽ ∽ 等分 , 等分 .
2.一线三等角帮助线添加:一般情形下,已知一条直线上有两个等角(直角)或一个直角时,可结构“一线三等角”型类似.
【巩固进步】
1.已知 中 , 是 的中点, 边上有一点 延伸线上有一点 ,使 已知 ,则
提醒:作过点 作 ∥ ,分离交 . 于 . .
∵ ,
∴
设 ,由翻折可得:
∵ ∽
∴ ,即
∴ ,∴
5.已知△ , , ,边长 ,点 在 上,且 ,点 是 上一动点,联络 ,将线段 绕点 逆时针扭转 得到线段 ,要使点 正好落在 上,则 的长是 .
提醒:结构“一线三等角”
∴△ ≌△
∴ , ,
∴
6.如图,已知 ∥ , , ,点 是射线 上的一个动点(点 与点 不重合),点 是线段 上的一个动点(点 与点 . 不重合),联络 ,过点 作 的垂线,交射线 于点 ,联络 .设 , .
提醒: , 是 的中点
∴
由 ∽
∴ ,
2.如图,等边 中, 是边 上的一点,且 ,把 折叠,使点 落在 边上的点 处.那么 的值为 .
提醒:由翻折可得:
设: 则
∵ ∽ ,
∴
3.在矩形 中, , ,把矩形 沿直线 翻折,点 落在边 上的 点处,若 ,那么 的长等于
提醒:作 于 ,则
∵ ∽ ,
∴
∵
∴
4.在矩形 中, ,点 在边 上,联络 ,△ 沿直线 翻折后点 落到点 ,过点 作 ,垂足为点 ,假如 ,那么 .
(1)当 时,求 关于 的函数关系式,并写出它的界说域;
一线三角模型及例题

相似三角形判定的复习:1.相似三角形的预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。
2.相似三角形的判定定理:(1)两角对应相等两三角形相似。
(2)两边对应成比例且夹角相等,两个三角形相似。
(3)三边对应成比例,两个三角形相似。
3.直角三角形相似的判定定理:(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
(2)一直角三角形的斜边和一条直角边与另一直角三角形的斜边和一条直角边对应成比例,那么这两三角形相似。
相似三角形的性质:要点1:相似三角形的性质:相似三角形的对应角相等,对应边成比例要点2:相似三角形的性质定理:相似三角形的性质定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比相似三角形的性质定理2:相似三角形的周长的比等于相似比相似三角形的性质定理3:相似三角形的面积的比等于相似比的平方要点3:知识架构图1、如图,锐角∆ABC 的高CD 和BE 相交于点O ,图中相似三角形有多少对?请分别写出.AB C DE O2、如图,在锐角∆ABC 中,∠ADE=∠ACB ,图中相似三角形有多少对?请分别写出.AB C DE O周长之比等于相似比相似三角形的性质 对应角相等、对应边成比例面积之比等于相似比的平方 对应高之比、对应中线之比、对应角平分线之比都等于相似比.3、如图已知∠BAC=∠BDC=90°,8,16==∆∆ADE EBC S S . 问:∠BEC 的大小确定吗?若确定,求期度数;若不确定,请说明理由.4、如图,在ABC △中,90BAC ∠=,AD 是BC 边上的高,点E 在线段DC 上,EF AB ⊥,EG AC ⊥,垂足分别为F G ,.求证:(1)EG CG AD CD=; (2)FD ⊥DG .GFE D C B A5、如图,四边形ABCD 中,AC 与BD 交于点E ,AC ⊥AB ,BD ⊥CD. S ∆EBC =16,S ∆AED =8.(1)求AD BC的值; (2)问:∠BEC 是不是定角?如果是,把它求出来;如果不是,请说明理由. AB C DE5、如图,在△ABC 中,角ACB 为直角,CD⊥AB 于点D ,又△ACE 与△BCF 都是等边三角形,连结DE 、DF ;求证:DE⊥DFEA D C FBAB C DE中考热点:一线三等角型的相似三角形一、问题引入如图,ABC ∆中,90B ∠=︒,CD AC ⊥,过D 作DE AB ⊥交BC 延长线与E 。
一线三等角模型

4图B A E C D 图3C D E B A 一线三等角模型一、直角形“一线三等角”——“一线三直角”三垂直图形变形如下图③、图④,这也是由弦图演变而来的。
二、锐角形“一线三等角C D E B A E D C B A A B C D E F 三、钝角形“一线三等角例1.如图,AB ⊥BC ,CD ⊥BC ,AE ⊥DE ,AE=DE 。
求证:AB+CD=BC 。
例2.如图,∠ACB-90°,AC=BC ,BE ⊥CE 于点D ,AD=2.5cm ,BE=0.8cm 。
求DE 的长。
热搜精练 1.如图,正方形ABCD ,BE=CF 。
求证:(1)AE=BF ;(2)AE ⊥BF 。
2.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.3.如图(1),AB⊥AD,ED⊥AD,AB=CD,AC=DE,试说明BC⊥CE的理由;如图(2),若△ABC向右平移,使得点C移到点D,AB⊥AD,ED⊥AD,AB=CD,AD =DE,探索BD⊥CE的结论是否成立,并说明理由.4.如图,在△ABC中,∠ACB=90°,AC=BC,CE⊥BE,CE与AB相交于点F,且CD =BE,请探索∠ACD,∠CBA,∠DAF之间的数量关系,并说明理由.5.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC =∠CF A=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图1,若∠BCA=90°,∠α=90°,则BE CF;EF|BE﹣AF|(填“>”,“<”或“=”);②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).6.在Rt△AOB中,∠AOB=90°.(1)如图①,以点A为直角顶点,AB为腰在AB右侧作等腰Rt△ABC,使∠BAC=90°,BA=AC,过点C作CD⊥OA交OA的延长线于点D.求证:△BOA≌△ADC;(2)如图②,以AB为底边在AB左侧作等腰Rt△ABC,使∠ACB=90°,CB=CA,连接OC.若∠ACO=26°,则∠CBO=度(直接填空);(3)如图③,以OB为边在OB左侧作等边△OBC,DO⊥AB于点D,连接AC交OD 于E,交OB于F.若OA=OB,OE=3.5,则AC的长为.(直接填空)7.在四边形ABCD中,∠ABC=∠DAB=90°.AB=BC,E为平面内的一个动点.(1)如图1,连接BD,当点E在BD上且CE⊥BD,过点A作AF⊥BD于点F,连接AC,点O为AC中点,连接FO并延长,交CE于点M,①求证:AF=CM;②若AF=3,CE=8,则△EFM的面积为.(2)如图2,当点E在直线CD上运动时,连接BE,过点B作BN⊥BE,且BN=BE,(B、E、N按逆时针排列),若DE=2,点B到线段CD的距离为8,点D到线段BC的距离为10,请直接写出线段AN的长度.。
专题 相似三角形一线三等角模型(学生版)
专题04相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
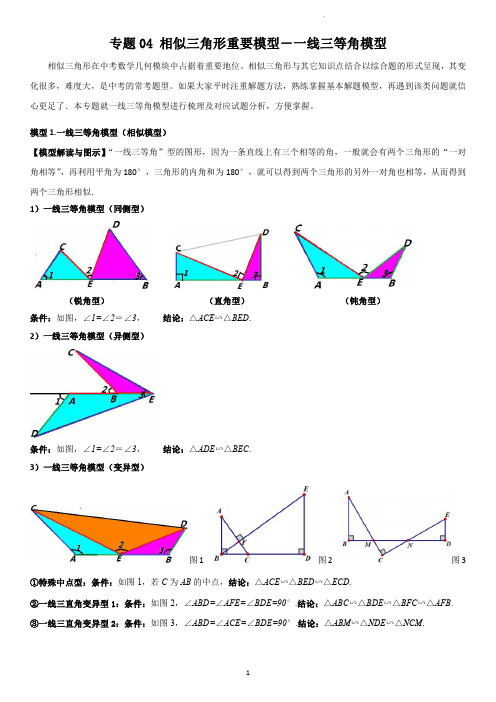
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.是边A.3B.5C.2D.1B (1)如图2,在53⨯个方格的纸上,小正方形的顶点为格点、边长均为1,AB 为端点在格点的已知线段.请用三种不...同连接格点.....的方法,作出以线段AB 为等联线、某格点P 为等联点的等联角,并标出等联角,保留作图痕迹;(2)如图3,在Rt APC △中,90A ∠=,AC AP >,延长AP 至点B ,使AB AC =,作A ∠的等联角CPD ∠和PBD ∠.将APC △沿PC 折叠,使点A 落在点M 处,得到MPC ,再延长PM 交BD 的延长线于E ,连接CE 并延长交PD 的延例5.(2022·浙江·嘉兴一中一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC 中,∠ACB =90°,AC =BC ,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:△ADC ≌△CEB .(1)探究问题:如果AC ≠BC ,其他条件不变,如图②,可得到结论;△ADC ∽△CEB .请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线y =12x 与直线CD 交于点M (2,1),且两直线夹角为α,且tanα=32,请你求出直线CD 的解析式.(3)拓展应用:如图④,在矩形ABCD 中,AB =4,BC =5,点E 为BC 边上一个动点,连接AE ,将线段AE 绕点E 顺时针旋转90°,点A 落在点P 处,当点P 在矩形ABCD 外部时,连接PC ,PD .若△DPC 为直角三角形时,请你探究并直接写出BE 的长.例6.(2023·浙江·九年级专题练习)在Rt ABC 中,90BAC ∠=︒,2AB AC ==,点D 在BC 所在的直线上运动,作45ADE ∠=︒(A 、D 、E 按逆时针方向).(1)如图,若点D 在线段BC 上运动,DE 交AC 于E .①求证:ABD DCE △△∽;②当ADE V 是等腰三角形时,求AE 的长;(2)如图,若点D 在BC 的延长线上运动,DE 的反向延长线与AC 的延长线相交于点E ',是否存在点D ,使ADE '△是等腰三角形?若存在,求出线段CD 的长度;若不存在,请简要说明理由;(3)若点D 在BC 的反向延长线上运动,是否存在点D ,使ADE V 是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由.上一点,轴9,23A.()9,3B.()3.(2023·湖南长沙·九年级专题练习)如图,在矩形4.(2021·浙江台州·中考真题)如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=_____.分别在边6.(2022秋·安徽淮北·九年级校考阶段练习)如图,在四边形分别在线段AD、DC上(点E与点A、CD=,在BC边上取中点E,连接DE,过点E 8.(2023·山东烟台·九年级统考期末)如图,在正方形ABCD中,4做EF ED⊥与AB交于点G,与DA的延长线交于点F.(1)求证:BEG CDE△∽△;(2)求AFG的面积.⊥交AB于点M,9.(2023·上海·九年级假期作业)在矩形ABCD中,3AB=,4=AD,点E是边AD上一点,EM EC∠=∠.(1)求证:AE是AM和AN的比例中项;(2)当点N在线段AB的延点N在射线MB上(如图),且ANE DCE长线上时,联结AC,且AC与NE互相垂直,求MN的长.的两个等腰直角三角形,(3)【拓展探究】在整个运动过程中,请直接写出N点运动的路径长,及CN的最小值.312.(2023·广东深圳·九年级校考阶段练习)如图,在ABC 中6cm AB AC ==,8cm BC =,点E 是线段BC 边上的一动点(不含B 、C 两端点),连接AE ,作AED B ∠=∠,交线段AB 于点D .(1)求证:BDE CEA△∽△(2)设BE x =,AD y =,请求y 与x 之间的函数关系式.(3)E 点在运动的过程中,ADE V 能否构成等腰三角形?若能,求出BE 的长;若不能,请说明理由.13.(2023春·广东深圳·八年级校考期中)【操作发现】如图1,在边长为1个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.①请按要求画图:将ABC 绕点A 顺时针方向旋转90︒,点B 的对应点为点B ',点C 的对应点为点C ',连接BB ';②在①中所画图形中,AB B '∠=______︒.【问题解决】如图2,在Rt ABC △中,190BC C =∠=︒,,延长CA 到D ,使1CD =,将斜边AB 绕点A 顺时针旋转90︒到AE ,连接DE ,求ADE ∠的度数.【拓展延伸】如图3,在四边形ABCD 中,AE BC ⊥,垂足为E ,BAE ADC ∠=∠,1BE CE ==,3CD =,2=AD AB ,求BD 的长.14.(2023·浙江·九年级专题练习)在平面直角坐标系中,O 为坐标原点,直线AB 与y 轴交于点A ,与x 轴交于点B ,2OA =,AOB 的面积为2.(1)如图1,求直线AB 的解析式.(2)如图2,线段OA 上有一点C ,直线BC 为2(0)y kx k k =-<,AD y ⊥轴,将BC 绕点B 顺时针旋转90︒,交AD 于点D ,求点D 的坐标.(用含k 的式子表示)(3)如图3,在(2)的条件下,连接OD ,交直线BC 于点E ,若345ABC BDO ∠-∠=︒,求点E 的坐标.九年级专题练习)某数学兴趣小组在学习了尺规作图、等腰三角形和相似三角形的有关知识后,在BC=.点E是线段AD上的动点(点E不与18.(2022·湖南郴州·中考真题)如图1,在矩形ABCD中,4AB=,6⊥,交AB于点F.点A,D重合),连接CE,过点E作EF CE∽;(1)求证:AEF DCE⊥,垂足为G,连接AG.点M是线段BC的中点,连接GM.(2)如图2,连接CF,过点B作BG CF①求AG GM+的最小值;②当AG GM+取最小值时,求线段DE的长.。
中考必会几何模型:K型(一线三垂直)模型
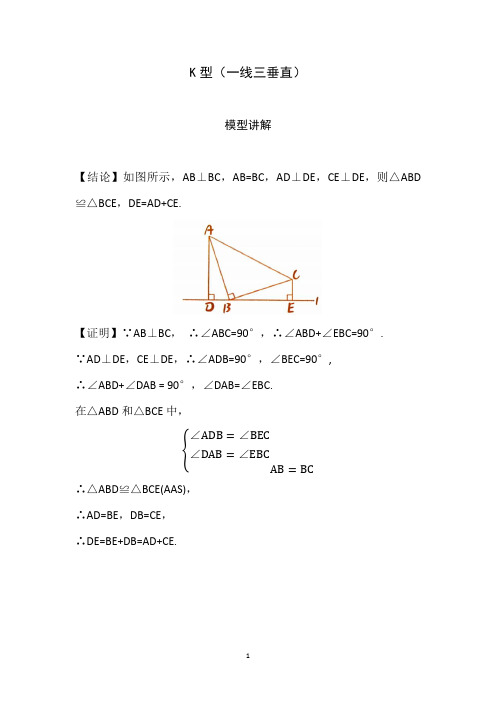
K 型(一线三垂直)模型讲解【结论】如图所示,AB ⊥BC ,AB=BC ,AD ⊥DE ,CE ⊥DE ,则△ABD ≌△BCE ,DE=AD+CE.【证明】∵AB ⊥BC , ∴∠ABC=90°,∴∠ABD+∠EBC=90°. ∵AD ⊥DE ,CE ⊥DE ,∴∠ADB=90°,∠BEC=90°,∴∠ABD+∠DAB = 90°,∠DAB=∠EBC.在△ABD 和△BCE 中,{∠ADB =∠BEC∠DAB =∠EBCAB =BC∴△ABD ≌△BCE(AAS),∴AD=BE ,DB=CE ,∴DE=BE+DB=AD+CE.其他形状的K型(一线三等角)模型【结论】如图所示,AB⊥BC,AB=BC,AD⊥DE,CE⊥DE,则△ABD ≌△BCE,DE = AD - CE.典型例题典例1如图所示,AC=CE,∠ACE=90°,AB⊥BD,ED⊥BD,AB=5cm,DE=3cm,则BD=( ).A.6 cmB.8 cmC.10 cmD.4 cm典例2如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE 于点D. 若DE=6cm,AD=9cm,则BE的长是( ).A.6 cmB.1.5 cmC.3 cmD.4.5 cm初露锋芒1. 如图所示,在△ABC中,AB=CB,∠ABC=90°,AD⊥BD于点D,CE⊥BD于点E. 若CE=5,AD=3,则DE的长是________.2.如图,△ABC中,AC=BC,∠ACB=90°,A(0,3),C(1,0),则点B 的坐标为________.感受中考1.(2018山东临沂中考真题)如图,△ACB=90°,AC=BC,AD⊥CE,BE ⊥CE,垂足分别是点D,E,AD=3,BE=1,则DE的长是( ).A.32B. 2C. 2√2D. √102. (2020四川南充中考真题)如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.参考答案典型例题典例1【答案】B【解析】易知本题为K型(一线三垂直)模型.根据K型(一线三垂直)模型的结论,可知两条手臂之间的距离=长手+短手,即BD=AB+DE,∴BD=5+3=8(cm).故选B.典例2【答案】C【解析】易知本题为K型(一线三垂直)模型根据K型(一线三垂直)模型的结论,可知两条手臂之间的距离=长手-短手即DE = AD - BE,∴BE=AD - DE= 9 - 6 = 3(cm).故选C.初露锋芒1.【答案】2【解析】由题图易知为K型(一线三垂直)模型,根据K型(一线三垂直)模型的结论,可知两条手臂之间的距离= 长手-短手,即DE = CE - AD = 5 - 3 = 2.2.【答案】(4,1)【解析】如图,作BD⊥x轴于点D.∵BD⊥x轴于点D,由K型(一线三垂直)模型容易得△AOC≌△CDB,∴CD=AO,OC=BD.∵点C(1,0),A(0,3),∴OC=1,BD=1,CD=3.∴OD=4,∴点B的坐标为(4,1).感受中考1.【答案】B【解析】由题图易知为K型(一线三垂直)模型,根据K型(一线三垂直)模型的结论,可知:两条手臂之间的距离=长手-短手,即DE = AD - BE = 3 - 1=2 .故选B.2.【解析】∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠ACE=∠ABC=∠CDE=90°,∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,∴∠ACB=∠CED.在△ABC和△CDE中,{∠ACB=∠CED BC=DE∠ABC=∠CDE∴△ABC≌△CDE(ASA),∴AB=CD.【小结】1. 遇到K型(一线三垂直)模型问题时,注意找“长手”“短手”.2. 在选择题或填空题中,运用模型结论可以快速解题,而在大题中,需要先找到全等三角形,根据全等三角形对应边相等来解题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形判定的复习:1.相似三角形的预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。
2.相似三角形的判定定理:(1)两角对应相等两三角形相似。
(2)两边对应成比例且夹角相等,两个三角形相似。
(3)三边对应成比例,两个三角形相似。
3.直角三角形相似的判定定理:(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
(2)一直角三角形的斜边和一条直角边与另一直角三角形的斜边和一条直角边对应成比例,那么这两三角形相似。
相似三角形的性质:要点1:相似三角形的性质:相似三角形的对应角相等,对应边成比例要点2:相似三角形的性质定理:相似三角形的性质定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比相似三角形的性质定理2:相似三角形的周长的比等于相似比相似三角形的性质定理3:相似三角形的面积的比等于相似比的平方要点3:知识架构图1、如图,锐角∆ABC的高CD和BE相交于点O,图中相似三角形有多少对?请分别写出.2、如图,在锐角∆ABC中,∠ADE=∠ACB,图中相似三角形有多少对?请分别写出.3、如图已知∠BAC=∠BDC=90°,8,16==∆∆ADE EBC S S . 问:∠BEC 的大小确定吗?若确定,求期度数;若不确定,请说明理由.4、如图,在ABC △中,90BAC ∠=,AD 是BC 边上的高,点E 在线段DC 上,EF AB ⊥,EG AC ⊥,垂足分别为F G ,.求证: (1)EG CGAD CD=; (2)FD ⊥DG .GF EDCBA5、如图,四边形ABCD 中,AC 与BD 交于点E ,AC ⊥AB ,BD ⊥CD. S ∆EBC =16,S ∆AED =8.(1)求ADBC的值; (2)问:∠BEC 是不是定角?如果是,把它求出来;如果不是,请说明理由.5、如图,在△ABC 中,角ACB 为直角,CD⊥AB 于点D ,又△ACE 与△BCF 都是等边三角形,连结DE 、DF ;求证:DE⊥DFEADCFBABCDE中考热点:一线三等角型的相似三角形一、问题引入如图,ABC ∆中,90B ∠=︒,CD AC ⊥,过D 作DE AB ⊥交BC 延长线与E 。
求证:ABCCED ∆∆B EADC三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示:其他常见的一线三等角图形(等腰三角形中底边上一线三等角) (等腰梯形中底边上一线三等角)A B DCEF(直角坐标系中一线三等角) (矩形中一线三等角)等角的顶点在底边上的位置不同得到的相似三角形的结论也不同,当顶点移动到底边的延长线时,形成变式图形,图形虽然变化但是求证的方法不变。
此规律需通过认真做题,细细体会。
(1)等腰三角形中一线三等角例1、 如图,已知在△ABC 中, AB =AC =6,BC =5,D 是AB 上一点,BD =2,E 是BC 上一动点,联结DE ,并作DEF B ∠=∠,射线EF 交线段AC 于F .(1)求证:△DBE ∽△ECF ; (2)当F 是线段AC 中点时,求线段BE 的长; (3)联结DF ,如果△DEF 与△DBE 相似,求FC 的长.FBACD E讲解:1、本题中,第一问的结论是这类题共同的特性,只要等腰三角形底边上有三等角,必有三角形相似;2、第二问中根据相似求线段的长,也很常见;有时候会反过来问,线段的长是多少是,三角线相似。
变式练习1就是这类题型;3、第三问中间的三角形与左右两个形似时有两种情况,一种是DF 与底边平行,一种是E 为中点;4、在等腰三角形,将腰延长会交于一点,也构成等腰三角形,故而以上三点,在等腰梯形中也适用。
D变式练习1 (浦东新区22题)如图,已知等边△ABC 的边长为8,点D 、F 、E 分别在边AB 、BC 、AC 上,3BD =,E 为AC 中 点,当△BPD 与△PCE 相似时,求BP 的值.变式练习2(宝山22题)如图6,已知ΔABC 中,AB AC =,点E 、F 在边BC 上,满足∠EAF =∠C .求证:2BF CE AB ⋅=;FE CBA变式练习3如图,在三角形ABC 中,AB=4,AC=2,∠A =900,点D 为腰AC 中点,点E 在底边BC 上,且DE ⊥BD ,求△CED 的面积。
变式练习4已知∠ABC=90°,AD ∥BC ,P 为线段BD 上的动点,点Q 在射线AB 上,且满足PQ ADPC AB=,当AD AB ,且点Q 在线段AB 的延长线上时,求QPC ∠的大小.(2)等腰梯形中一线三等角例1、(长宁区18题)如图,等腰梯形ABCD 中,AD ∥BC ,2AD =,42BC =,∠45B =˚,直角三角板含45度角的顶点E 在边BC 上移动,一直角边始终经过点A ,斜边与CD 交于点F .若△ABE 为等腰三角形,则CF 的长等于 .第18题E FDCB A例2、如图,梯形ABCD 中,AB ∥DC , ∠B =90°,E 为BC 上一点,且△ABE ∽△ECD 。
(1)若BC =8,AB=3,DC =4,求BE 的长 (2)若BC = 43 ,AB=3,DC =4,求BE 的长. (3)若BC =6,AB=3,DC =4,求BE 的长.例3、如图,梯形ABCD 中,AB ∥CD ,∠ABC=900,AB=8,CD=6,在AB 上取动点P ,连结DP ,作PQ ⊥DP ,使得PQ 交射线BC 与点E ,设AP=x ,BE=y 。
(1)当BC=4时,试求y 关于x 的函数关系式;(2)当BC 在什么范围时,存在点P ,使得PQ 经过点C (直接写出结果)。
例4、(徐汇区25).如图,在梯形ABCD 中,AD ∥BC ,6AB CD BC ===,3AD =.点M 为边BC 的中点,以M 为顶点作EMF B ∠=∠,射线ME 交腰AB 于点E ,射线MF 交腰CD 于点F ,联结EF . (1)求证:△MEF ∽△BEM ;(2)若△BEM 是以BM 为腰的等腰三角形,求EF 的长; (3)若EF CD ⊥,求BE 的长.例4、(杨浦区基础考)四边形ABCD 中,AD ∥BC ,()090ABC αα∠=<<,3AB DC ==,5BC =.点P 为射线BC 上动点(不与点B 、C 重合),点E 在直线DC 上,且APE α∠=.记1PAB ∠=∠,2EPC ∠=∠,BP x =,CE y =.(1)当点P 在线段BC 上时,写出并证明1∠与2∠的数量关系;(2)随着点P 的运动,(1)中得到的关于1∠与2∠的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的x 的取值范围; (3)若cos α=13,试用x 的代数式表示y .(3)坐标系中一线三等角例1、(金山区24)如图,住平面直角系中,直线AB :()440y x a a=+≠分别交x 轴、y 轴于B 、A 两点,直线AE 分别交x 轴、y 轴于E 、A 两点,D 是x 轴上的一点,OA OD =,过D 作CD ⊥x 轴交AE 于C ,连接B C ,当动点B 在线段OD 上运动(不与点O 点D 重合)且AB BC ⊥时(1)求证:ABO ∆∽BCD ∆;(2)求线段CD 的长(用a 的代数式表示); (3)若直线AE 的方程是1316y x b =-+,求tan BAC ∠的值.例2、如图,在直角坐标系中,直线122y x =+与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作矩形ABCD,使5AD = ,求点D的坐标.变式练习1在平面直角坐标系XOY 中,AOB ∆的位置如图所示,已知0060,90=∠=∠A AOB ,点A 的坐标为()1,3-(1) 求点B 的坐标;(2) 若抛物线c bx ax y ++=2经过A 、O 、B 三点,求函数解析式。
变式练习2如图所示:RT △AOB 中∠AO B =90°,OA=4,OB=2,点B 在反比例函数2y x=图像上,求过点A 的双曲线解析式。
变式练习3如图,在平面直角坐标系中,OB ⊥OA ,且OB =2OA ,点A 的坐标是(-1,2).求过点A 、O 、B 的抛物线的表达式;(4)矩形中一线三等角如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,将边BC折叠,使点B落在边OA的点D 处.已知折叠线CE 且55CE =, 3tan 4EDA ∠=,求直线CE与x轴交点的坐标;例6、(长宁区24题).如图,在矩形ABCD 中,4AB =,6AD =,点P 是射线DA 上的一个动点,将三角板的直角顶点重合于点P ,三角板两直角中的一边始终经过点C ,另一直角边交射线BA 于点E . (1)判断△EAP 与△PDC 一定相似吗?请证明你的结论;(2)设PD x =,AE y =,求y 与x 的函数关系式,并写出它的定义域;(3)是否存在这样的点P ,是△EAP 周长等于△PDC 周长的2倍?若存在,请求出PD 的长度;若不存在, 请简要说明理由.EPDCBA“一线三等角”专题练习一、知识梳理:1、如图1,AB =AC ,∠ B =∠ADE ,那么一定存在的相似三角形有 ;2、如图2,AB =AC ,∠ B =∠EDF ,那么一定存在的相似三角形有 ;B图1 图23、在等腰△ABC 中,腰长10厘米,底边长16厘米,点P 在底边上以0.5厘米/秒的速度从点B 向点C 移动.当点P 运动到PA 与腰垂直的位置时,点P 的运动时间为 秒. 二、经典例题解析1、如图,在ΔABC 中, AB =AC=4,BC =6,∠ B =∠ADE ,点D 、E 分别在BC 、AC 上(点D 与B 、C 不重合),设BD =x ,AE =y ,求y 关于x 的函数解析式及x 的取值范围。
B2、如图:在直角梯形ABCD 中,AD ∥BC ,∠B = 90°,DH ⊥BC 于H ,AB = 6,BC = 16,DC = 10,线段BC 上有一动点E (不与点C 重合),过点E 作EF ⊥DC 交线段DC 于点F. (1)求CH 的长;(2)设BE = x ,EF = y ,求y 关于x 的函数解析式及x 的取值范围; (3)当以E 、F 、C 为顶点的三角形与△ABE 相似时,求BE 的长.3、如图,在Rt △ABC 中,∠ACB =90º,AB =10,AC =6,点E 、F 分别是边AC 、BC 上的动点,过点E 作ED ⊥AB 于点D ,过点F 作FG ⊥AB 于点G ,DG 的长始终为2. (1)当AD =3时,求DE 的长;(2)当点E 、F 在边AC 、BC 上移动时,设x AD =,y FG =,求y 关于x 的函数解析式,并写出函数的定义域;B(3)在点E 、F 移动过程中,△AED 与△CEF 能否相似,若能,求AD 的长;若不能,请说明理由.4、已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且BC =6,AB =DC =4,点E 是AB 的中点. (1)如图3,P 为BC 上的一点,且BP =2.求证:△BEP ∽△CPD ;(2)如果点P 在BC 边上移动(点P 与点B 、C 不重合),且满足∠EPF =∠C ,PF 交直线CD 于点F ,同时交直线AD 于点M ,那么①当点F 在线段CD 的延长线上时,设BP =x ,DF =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当BEP DMF S S ∆∆=49时,求BP 的长.5、(2009闸北22题)(本题满分10分,第(1)小题满分3分,第(2)小题满分7分)如图七,在平面直角坐标中,四边形OABC 是等腰梯形,CB∥OA, OA=7,AB=4,∠COA=60°,点P 为x 轴上的—个动点,但是点P 不 与点0、点A 重合.连结CP , D 点是线段AB 上一点,连结PD. (1)求点B 的坐标; (2)当∠C PD=∠OAB,且AB BD =85,求这时点P 的坐标. A BC ED G FEDCBA P6、如图,已知在△ABC 中,AB=AC=8,cosB=58,D 是边BC 的中点,点E 、F 分在边AB 、AC 上,且∠EDF=∠B ,连接EF .(1)如果BE=4,求CF 的长; (2)如果EF ∥BC ,求EF 的长.7、(徐汇2009年 25题)如图,ABC ∆中,10==AC AB ,12=BC ,点D 在边BC 上,且4=BD ,以点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ,交射线CA 于点F . (1)当6=AE 时,求AF 的长;(2)当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长; (3)当以边AC 为直径的⊙O 与线段DE 相切时,求BE 的长.知识总结:补 充:关于“一线三等角”图形的提炼及变式:A BC DEFABCD当α为锐角时:BBB当α为直角时:当α为钝角时:E总结:在教学中要突出重点、深化学生对于“一线三等角”模型的理解;把握难点:“一线三等角”模型变式; 通过问题建构,关注课堂再生资源的挖掘,引导学生对于几何综合习题的有效分解具体的1.在教学中通过“回忆旧知”环节的师生互动过程让95%学生掌握解函数型综合题需要的必备知识储备. 2.在教学中通过一个“一线三等角”模型综合题的有效分析引导过程,让95%的学生树立几何型综合题的解决的信心,让75%的学生能够顺利解决前两小题,培养更多的学生具备解决最后压轴点一小题的能力. 3.在教学中通过有效分解策略的实施,打破他们对综合题的畏惧心理,让同学们加深对于题目条件的使用:条件用完,即使题目没有求解完毕,也得到相应的分数,提高问题解决的能力,在这个师生共同探讨的过程中鼓励学生尝试着加强解后反思与培养他们欣赏试题的能力.【课后作业】1、如图,已知正方形ABCD 的边长为4,P 是射线CD 上一动点. 将一把三角尺的直角顶点与P 重合,一条直角边始终经过点B ,另一条直角边所在直线与射线AD 相交于点E. 设CP=x ,DE=y. (1)当点P 在线段CD 上时,求证:△BPC ∽△PED ;(2)当点P 在线段CD 的延长线上时,求y 与x 的函数解析式及自变量x 的取值范围; (3)当DE=1时,求CP 的长.2、如图,在矩形ABCD 中,E 为AD 的中点,EF EC ⊥交AB 于点F ,联结()FC AB AE >. (1)AEF △与EFC △是否相似?若相似,证明你的结论;若不相似,请说明理由; (2)设ABk BC=,是否存在这样的k 值,使得AEF BFC △∽△?若存在,证明你的结论并求出k 的值;若不存在,请说明理由.(第12题)FBCA ED3、等腰△ABC ,AB=AC=8,∠BAC=120°,P 为BC 的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P ,三角板绕P 点旋转.(1)如图a ,当三角板的两边分别交AB 、AC 于点E 、F 时.求证:△BPE ~△CFP ;(2)操作:将三角板绕点P 旋转到图b 情形时,三角板的两边分别交BA 的延长线、边AC 于点E 、F . ① 探究1:△BPE 与△CFP 还相似吗?(只需写出结论) ② 探究2:连结EF ,△BPE 与△PFE 是否相似?请说明理由; ③ 设EF=m ,△EPF 的面积为S ,试用m 的代数式表示S .4、如图,在边长为1的正方形ABCD 中,点E 在边BC 上(与端点不重合),点F 在射线DC 上. (1)若AF =AE ,并设CE =x ,△AEF 的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (2)当CE 的长度为何值时,△AEF 和△ECF 相似? (3)若41=CE ,延长FE 与直线AB 交于点G ,当CF 的长度为何值时,△EAG 是等腰三角形? BCB5、如图,在△ABC 中,AC =BC =2,∠C =900,点D 为腰BC 中点,点E 在底边AB 上,且DE ⊥AD ,则BE 的长为 .6、如图,∆ABC 中,∠ACB=90°,∠A=60°,AC=2,CD ⊥AB ,垂足为D.任意作∠EDF=60°,点E 、F 分别在AC 、BC 上.设AE=x ,BF=y.(1)求y 关于x 的函数关系式,并指出它的定义域; (2)当x 为何值时,∆BDF 是等腰三角形.7、如图:AB 是等腰直角三角形ABC 的斜边,点M 在边AC 上,点N 在边BC 上,沿直线MN 将△MCN 翻折,使点C 落在AB 上,设其落点为P.(1)当P 是边AB 中点时,求证:PA CMPB CN =; (2)当P 不是边AB 中点时,PA CMPB CN=是否仍然成立?请证明你的结论.8、如图第13题图-1,在Rt △ABC 中,∠C =90°,AC =BC ,D 是AB 边上一点,E 是在AC 边上的一个动点(与点A 、C 不重合),DF ⊥DE ,DF 与射线BC 相交于点F 。
