第二讲问题求解
第二讲 和倍问题
第二讲和倍问题专题简析：已知两个数的和与它们之间的倍数关系，求这两个数是多少的应用题，叫做和倍问题。
解答和倍应用题的基本数量关系是：和÷（倍数＋1）=小数小数×倍数=大数（和－小数=大数）例1：学校有科技书和故事书共480本，科技书的本数是故事书的3倍。
两种书各有多少本？分析与解答：为了便于理解题意，我们画图来分析：由图可知，如果把故事书的本数看作一份，那么科技书的本数就是这样的3份，两种书的总本数就是这样的1＋3=4份。
把480本书平均分成4份，1份是故事书的本数，3份是科技书的本数。
480÷（1＋3）=120（本）120×3=360（本）课堂练习：1，用锡和铝制成的合金是720千克，其中铝的重量是锡的5倍。
铝和锡各用了多少千克？2，甲、乙两数的和是112，甲数除以乙数的商是6，甲、乙两数各是多少？例2：果园里有梨树、桃树和苹果树共1200棵，其中梨树的棵数是苹果树的3倍，桃树的棵数是苹果树的4倍。
求梨树、桃树和苹果树各有多少棵？分析与解答：如果把苹果树的棵数看作1份，三种树的总棵数是这样的1+3+4=8份。
所以，苹果树有1200÷8=150（棵），梨树有150×3=450（棵），桃树有150×4=600（棵）课堂练习：1，李大伯养鸡、鸭、鹅共960只，养鸡的只数是鹅的3倍，养鸭的只数是鹅的4倍。
鸡、鸭、鹅各养了多少只？2，甲、乙、丙三数之和是360，已知甲是乙的3倍，丙是乙的2倍。
求甲、乙、丙各是多少。
例3：有三个书橱共放了330本书，第二个书橱里的书是第一个的2倍，第三个书橱里的书是第二个的4倍。
每个书橱里各放了多少本书？分析与解答：把第一个书橱里的本数看作1份，那么第二个书橱里的本数是这样的2份，第三个就是这样的2×4=8份，三个书橱里的总本数就是这样的1+2+8=11份。
所以，第一个书橱里放了330÷11=30（本），第二个书橱里放了30×2=60（本），第三个书橱里放了60×4=240（本）。
第二讲页码问题(解答)
第二讲页码问题我们的课本，每页上都有页码，页码都是由一列连续的自然数组成的，每个页码都是由一个或几个数字（数码）组成的。
页码问题就是根据图书的页码而编制出的一类应用题。
编一本书的页码，一共需要多少个数码呢？反过来，知道编一本书的页码所需的数码数量，求这本书的页数。
这是页码问题中的两个基本内容。
为了顺利地解答页码问题，我们先看一下“数”与“组成它的数码个数”之间的关系。
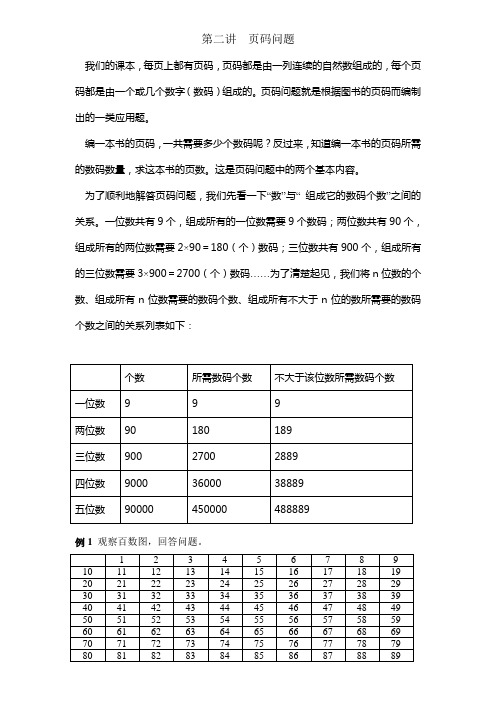
一位数共有9个，组成所有的一位数需要9个数码；两位数共有90个，组成所有的两位数需要2×90＝180（个）数码；三位数共有900个，组成所有的三位数需要3×900＝2700（个）数码……为了清楚起见，我们将n位数的个数、组成所有n位数需要的数码个数、组成所有不大于n位的数所需要的数码个数之间的关系列表如下：例1观察百数图，回答问题。
分析：将这100个数分成一位数、两位数、三位数三部分分别计算。
（结合此题分析表一）9+180+3=192（个）（2）数字“0”一共出现了多少次？数字“1”出现了多少次？其他的数字呢？分析： 0出现了11次，其他的数字分别出现了21次，追问：为什么0出现的次数与众不同？从而总结计算一个数字出现次数的方法是：将不同数位出现的次数进行累加。
例2一本科幻小说共320页，问：编印这本科幻小说的页码共要用多少个数字？分析：1～9页每页上的页码是一位数，共需数码1×9=9（个）；10～99页每页上的页码是两位数，共需数码2×90＝180（个）；100～320页每页上的页码是三位数，共需数码（320-100＋1）×3＝663（个）。
综上所述，这本书共需数码9＋180＋663＝852（个）。
例3 一本小说的页码，在排版时必须用2211个数码。
问：这本书共有多少页？分析：因为189＜2211＜2889，所以这本书有几百页。
由前面的分析知道，这本书在排三位数的页码时用了数码（2211-189）个，所以三位数的页数有（2211-189）÷3＝674（页）。
第二讲 和差、和倍问题
第二讲和差、和倍问题1、某校六年级一班有学生49人，其中男生比女生多5人，这个班男、女生各多少人？（49－5）÷2=22人22＋5=27人2、把325分成两个数，使两数的和是两数差的5倍，两数各是多少？325÷5=65 （65＋5）÷2=195 325－195=1303、少先队员种柳树和杨树共148棵，柳树的棵数比杨树棵数的2倍多4棵。
求两种树各种了多少棵？（148－4）÷（1＋2）=48 148－48=1004、甲、乙两数的和是32，甲数的3倍与乙数的5倍的和是122。
求甲乙两数各是多少？（122－32×3）÷（5－3）=13 32－13=195、甲、乙两打字员合打一份稿件，按分工，平均每人每小时打14页，3小时即可打完。
当两人打完稿件时，乙发现甲比自己多打了12页。
甲、乙两打字员打这份稿件时各打字多少页？（14×2×3－12）÷2=36 36＋12=486、甲站有汽车192辆，乙站有汽车48辆。
每天从甲站开往乙站的汽车是21辆，从乙站开往甲站的是24辆。
经过几天后，甲站的汽车辆数是乙站的7倍？（192＋48）÷（1＋7）=30 （48－30）÷（24－21）=67、有甲、乙、丙三袋化肥。
甲、乙两袋共重32千克，乙、丙两袋共重30千克，甲、丙两袋共重22千克。
甲、乙、丙三袋各重多少千克？（32＋30＋22）÷2=42 42－30=12 42－22=20 42－32=108、六年级有四个班，不算甲班，其余三个班的总人数是131人，不算丁班，其余三个班的总人数是134人，乙、丙两班的总人数比甲、丁两班的总人数少1人，四个班的总人数是多少人？（131＋134－1）÷3×2＋1=1779、甲、乙两数的和是15.2，如果甲数减少3.1，乙数增加2.1，那么这时甲数还比乙数的2倍多1。
第2讲 和倍问题
第2讲 和倍问题（五年级奥数班）专题引导：和信问题是已知几个数和以及它们的信数关系，求这几个数各是多少的典型习题。
解答和信问题时，一般确定小数为标准量、即信量，再根据其他几个数与小数的信数关系，确定倍数和。
常用的数量关系式： 和÷（倍数+1）=1倍量，1倍量×倍数=几倍数。
典型例题：例1．甲、乙两个车间共有职工784人，甲车间的人数是乙车间的3倍，两个车间各有职工多少人？ 解析：可以用下面的线段图来表示题目的已知条件和所求问题：甲车间：乙车间： 把乙车间人数看成是1倍数，甲车间人数就是3倍数，784人相当于3+1=4（倍）数，所以，先求1倍数，也就是先求乙车间的人数。
乙车间的人数：784÷（3+1）=196（人）甲车间的人数：784-196=588（人）或196×3=588（人）答：甲车间有职工588人，乙车间有职工196人。
模仿训练1：一个长方形，长是宽的2倍，周长是54厘米，这个长方形的长和宽各是多少厘米？例2．有两堆棋子，第一堆有67个，第二堆有53个，问从第二堆中拿出多少个棋子放入第一堆，就能使第一堆的棋子是第二堆的2倍？解析：根据题意知道，两堆棋子移来移去之后，总数没有改变，只是第一堆棋子数增加了，第二堆棋子数减少了。
要想使第一堆棋子数是第二堆棋子数的2倍，就要把67+53=120（个）棋子平均分成1+2=3（份），每份就可以求出来，这1份恰好是第二堆留下的棋子数，其余的棋子拿到第一堆去了。
67+53=120（个） 120÷（2+1）=40（个）53-40=13（个）答：要从第二堆中拿出13个棋子放入第一堆。
模仿训练2：水果店原来有苹果和橘子一共有320千克，后来苹果卖出40千克，橘子又运进20千克，这时苹果是橘子的2倍，水果店原来各有苹果、橘子多少千克？3倍 1倍 ？人784人例3．三篮苹果共有126个，第一篮的苹果个数是第二篮的2倍，第三篮的苹果个数是第一篮的3倍。
第二讲---方阵问题(一)
第二讲方阵问题（一）姓名在我们的日常生活中常遇到一些有关正方形的问题, 如: 运动会上大型团体操表演队的正方形队列, 解放军的方形仪仗队, 正方形棋盘上摆棋子等有趣的数学问题, 我们称为方阵问题。
方阵可以分为实心方阵（图①）和空心方阵（图②、③）。
方阵问题的基本特点是: 方阵中, 内一层总比外一层的一边少个物体；内一层物体的总个数一定比外一层物体总个数少。
解答方阵问题的关键是: 判断此方阵是实心方阵还是空心方阵。
1、方阵问题每边数与每层数之间的数量关系为:每层数＝（每边数－1）×4 、每边数＝每层数÷4＋1 .2.实心方阵的数量关系为: 总数＝外层每边数×外层每边数＝（外层每边数）23、空心方阵的数量关系为: 总数＝（外层每边数－层数）×层数×4或总数＝实心方阵总数－中间空心方阵总数最内层每边数＝外层每边数－2×（层数－1）最外层每边数＝总数÷4÷层数＋层数【例1】一个实心方阵, 最外一层每边12人。
（1）那么整个方阵一共有。
（2）最外面一层共有。
（3）从外向内数, 第二层每边有人, 一共有人。
（4）如果考虑最外面三层, 那么这三层共有人。
（5）如果将方阵外面增加一层, 那么一共增加人。
随堂练习1用64枚棋子摆成一个实心方阵。
（1）每边有枚棋子。
（2）最外层有枚棋子。
（3）从外向内数, 第二层每边有枚棋子, 第二层共有枚棋子。
【例2】有一块空地在进行种树绿化, 打算把树种成实心方阵的样子, 方阵最外面一周有60棵树, 问这个方阵最外层每边有多少棵树？这块空地一共需要多少棵树？随堂练习2 三年级学生排成一个实心方阵, 最外一层的人数为36人, 问: 方阵最外层每边有多少人？这个方阵共有三年级学生多少人【例3】小刚在用棋子摆好的实心方阵上又添了17枚棋子, 它的横竖各增加了一排, 成了大一点的实心方阵。
求原来实心方阵有多少枚棋子？随堂练习3 军训的学生进行队列表演, 排成了一个5行5列的正方形队形, 如果去掉一行一列, 要去掉多少人？【例4】有一个正方形的稻田, 四个角上都放1个稻草人, 如果每边放5个, 四边一共放多少个稻草人？解析：可以按每边5个计算, 四个角各多1次；可以按每边4个计算, 恰好分4组；可以按每边3个计算, 四个角各少算1次。
第二讲 相遇问题
第二讲相遇问题知识点1.行程问题中的相遇问题涉及到三个数量：路程、速度和时间，其关系为路程=速度×时间2.甲、乙两人在行程中相遇，就有甲走的路程+乙走的路程=甲的速度×时间+乙的速度×时间=（甲的速度+乙的速度）×时间通俗地说，“相遇问题”要考虑两人的速度和。
3.多次相遇问题两个物体从不同地点相向而行，第一次相遇后走1个全程，第二次相遇是合走3个全程，以后每相遇一次都是多走了2个全程。
4.流水问题（注意流水的影响）、钟表问题（注意时针和分针两者重合成直线）都属于相遇问题。
顺水速度=船速+水速逆流速度=船速—水速顺流行程=（船速+水速）×顺水时间逆水行程=（船速—水速）×逆水时间静水行程=（顺水速度+逆水速度）÷2水速=（顺水速度—逆水速度）÷2经典例题例1 快、慢车分别从A、B两地同时相向而行，快车每小时行78千米，慢车每小时行58千米，两车在离中点25千米处相遇。
那么A 、B两地相距多少千米？及时巩固1.小张从甲地到乙地步行需要36分钟，小王骑自行车从乙地到甲地需要12分钟。
他们同时出发，几分钟后两人相遇？例2 甲、乙两车分别从A、B两地同时出发，相向而行，6小时后相遇于点C。
如果甲车的速度不变，乙车每小时多行5千米，且两车还从A、B两地同时出发，相向而行，则相遇地点距点C处12千米，如果乙车速度不变，甲车每小时多行5千米，且两车还从A、B两地同时出发，相向而行，则相遇地点距C处16千米。
求A、B两地间的距离。
及时巩固2.小张和小王各以一定速度,在周长为500米的环形跑道上跑步。
小王的速度是每分钟180米。
（1）小张和小王同时从同一地点出发，反向跑步，75秒后两人第一次相遇，小张的速度是每分钟多少米？（2）小张和小王同时从同一地点出发，同向跑步，小张跑多少圈后，才能第一次追上小王？例3 甲、乙两人同时从A、B两地出发，相向而行，第一次在距A地25千米处相遇，相遇后两个继续前进，到达目的地后又立即返回，在距B地15千米处第二次相遇。
第二讲盈亏问题
『第二讲』盈亏问题例题1：将一些糖果分给幼儿园小班的小朋友，如果每人分3粒，就会余下糖果17粒；如果每人分5粒，就会缺少糖果13粒。
问：幼儿园小班有多少个小朋友？这些糖果共有多少粒？分析：用作图的方法来分析。
我们知道糖果的总数相等，小朋友的人数也是相等的。
3粒3粒3粒 (17)······5粒5粒5粒…………缺少13粒······………………·想：每个小朋友分3粒与5粒，相差5－3=2（粒）；分的糖果的总数就要相差17+13=30（粒）所以小班的人数是30÷2=15（人），这批糖果的总数是3×15+17=62（粒）或5×15－13=62（粒）。
这是盈亏问题中的“一盈一亏”的问题，解答这类问题的数量关系是：（盈数+亏数）÷两次分得的差= 人数解：（17+13）÷（5－3）=30÷2=15（人）3×15+17=62（粒）或：5×15－13=62（粒）答：有15个小朋友，62粒糖。
例题2：学生搬一批砖，每人搬4块，其中5人要搬两次；如果每人搬5块，就有两人没有砖可搬。
搬砖的学生有多少人？这批砖共有多少块？分析：用作图的方法来分析。
我们知道砖的总数相等，学生的人数也是相等的。
4块 4块 4块………… 余下的还需要5人搬一次······也就是多余（4×5）块5块 5块 5块…………就有两人没有搬······………………·也就是缺少（5×2）块通过分析，我们把问题转化为盈亏问题的一般情形。
每人搬砖数相差5－4=1（块），搬砖的总数就相差（4×5）+（5×2）=30（块）所以，搬砖的学生数是30＋1=30（人），砖的总数是4×30+20=140（块）。
第二讲 和倍问题(思维拓展讲义)四年级数学学生版
第2讲和倍问题已知两个数的和与两个数的倍数关系，求两个数各是多少的应用题，通常把它们叫做“和倍问题”。
和倍问题也是典型应用题的一种。
解答和倍问题，一般是在已知条件中确定小数为标准，假设小数为1倍或1份，再根据其他几个数与小数的倍数关系，确定总和相当于1倍数的多少倍，然后用除法求出1倍数，再求出其他各数。
和倍问题的数量关系是:和÷(倍数+1)=小数;小数x倍数=大数例1某超市食品柜卖出水果糖和巧克力共120千克，卖出的巧克力是水果糖的4倍，水果糖每千克16元，巧克力每千克25元，卖出的水果糖和巧克力各值多少元?【思路点拨】要求卖出的水果糖和巧克力各值多少元，首先要求出巧克力和水果糖各卖出了多少千克。
从条件中已知水果糖是1份数，求1份数用除法，但120千克是水果糖和巧克力一共的千克数，它所对应的份数应该是4+1=5。
同学们解答这道题时，千万要注意 120 千克是相当于5份水果糖的千克数。
例2花园小学买来足球和篮球共48个，已知买来足球的个数比篮球的2倍少3个，学校买来足球和篮球各多少个?【思路点拨】已经知道足球和篮球共48个，倍数关系也知道了，可后面却跟了个尾巴: 足球的个数比篮球的2倍少3个，因为足球的个数并不正好是篮球的2倍，它比篮球个数的2倍少3个，只有再买上3个足球，才是篮球的2倍。
例3有两堆棋子，第一堆有66枚，第二堆有54枚。
问从第二堆中拿出多少枚棋子放入第一堆，就能使第一堆的棋子数是第二堆的2倍?【思路点拨】 根据题意知道，两堆棋子移来移去之后，总数没有发生变化。
对!要想使第一堆棋子数是第二堆的2倍就要把 66+54=120(枚)棋子平均分成2+1=3(份)，每份恰好是第二堆留下的棋子数，其余的棋子拿到第一堆去了。
例4 三个书橱共放了330本书，第二个书橱里的书是第一个的2倍，第三个书橱里的书是第二个的4倍，每个书橱里各放了多少本书?【思路点拨】这道题里第一个书橱的本数和第二个书橱的本数都可以看做1份数。
第二讲 差倍问题
第二讲：差倍问题姓名：例1甲桶汽油的质量是乙桶汽油质量的5倍，如果从甲桶倒出25千克到乙桶，则甲桶还比乙桶汽油重10千克。
甲、乙两桶汽油的质量各重多少千克？体验训练1、植树节那天，五年级同学计划植树的棵树是三年级同学计划植树棵数的3倍，实际五年级同学给了三年级同学6棵树后，还比三年级同学多植10棵。
问五年级和三年级同学原计划各植树多少棵？例2、甲、乙两车所载乘客人数相等。
如果甲车下来34人，乙车上来52人，则乙车所载乘客人数是甲车所载乘客人数的3倍。
原来甲车载乘客多少人？体验训练2、小熊猫抱着一堆玩具，丢掉的玩具比抱着的玩具多4个，走在路上又丢掉2个玩具，这时丢掉的玩具是抱着玩具的3倍。
这堆玩具原来有多少个？例3、三个小朋友做纸花，小林比小明多做12朵。
小云比小明少做8朵、小林做的纸花朵数是小云做的纸花朵数的3倍。
求三人各做纸花多少朵？体验训练31、小明、小红、小军三人做数学题。
已知小明比小红多做6道数学题，小军做的数学题数是小明做的数学题数的2倍，且小军比小红多做22道数学题。
三人各做多少道数学题？2、甲、乙、丙三根绳子，乙的长度是甲长度的2倍。
丙的长度比乙的长度的3倍还多15米，并且甲的长度比丙的长度少180米。
求甲、乙、丙的长度各是多少米？例4、甲、乙两人卖鸡蛋已知甲的鸡蛋比乙的鸡蛋多85个。
当甲卖出47个鸡蛋，乙卖出64个鸡蛋后，甲剩下的鸡蛋数量是乙剩下的鸡蛋数的4倍。
甲、乙原来各有鸡蛋多少个？体验训练41、甲、乙两桶油，甲桶的油比乙桶的油多34千克，后从甲桶中取走26千克油，从乙桶中取走38千克油，这时甲桶中所剩下的油的质量是乙桶中所剩的油的质量的3倍。
甲、乙两桶原来各有多少千克油?例5 ：被除数比除数大224，商是5，被除数、除数各是多少？体验训练5：被除数比除数大158，商是6，除数、余数各是多少？课后巩固：1、三一班图书馆的图书比三二班图书馆图书多50本，并且三一班图书馆的本数是三二班图书馆本数的3倍。
『第二讲』和倍问题
第二讲和倍问题例1、甲班和乙班共有图书160本，甲班的图书本数是乙班的3倍，甲班和乙班各有图书多少本？[解析]这道题目的关键句是：甲班的图书本数是乙班的3倍，我们划出一倍数，乙班的图书本数是一倍数，那么相对应甲班的图书本数就是3倍数。
那么倍数和：3＋1＝4我们还知道：甲班和乙班共有图书160本。
于是和：160。
所以160÷（3＋1）＝40（本）………乙班40×3＝120（本）………..甲班答：甲班的图书本数是120本，乙班的图书本数是40本。
例2、被除数、除数、商三个数的和是212，已知商是2，被除数和除数各是多少？[解析]我们知道"被除数、除数、商"三者的关系是：被除数÷除数＝商所以，我们把被除数看作大数，除数看作小数，商看作它们的倍数。
那么，这道题的被除数与除数的倍数和：2＋1＝3被除数与除数的和：212－2＝210 （想一想，为什么？）所以，我们解：212－2＝210210÷（1＋2）＝70………除数70×2＝140………被除数答：被除数是70，除数是140。
[练一练]两数相除，商3余4，如果被除数、除数、商及余数相加，和是43。
求被除数和除数？例3、两个数的和是682，其中一个数的个位是0，若把0去掉，则与另一个加数相同。
这两个数各是多少？[解析]已知"一个数的个位是0，若把0去掉，则与另一个加数相同。
"说明"一个数是另一个数的10倍。
"我们把"另一个数"看作1份，"一个数"就是它的10倍数。
这样两个数的和为682，两个数的倍数和10+1=11解：682÷（10＋1）＝6262×10＝620答：一个加数是620，另一个加数是62。
[练一练]1、长方形的周长是6分米，已知长是宽的2倍，长方形的面积是多少平方分米？2、姐姐和妹妹共有人民币264元（两人都是整元的钱），姐姐的钱数的个位是0，如果姐姐把自己钱数的个位上的0去掉，恰好和妹妹的钱数相等。
第二讲： 和倍问题
和倍问题例1、甲班和乙班共有图书240本.甲班的图书本数是乙班的3倍，甲班和乙班各有图书多少本？练习1、学校图书室有故事书和历史书共2332册，历史书是故事书的3倍，故事书和历史书各有多少册？例2、公路旁要种玉兰树、樟树和棕树共1246棵，玉兰树的棵数是棕树的2倍，樟树的棵数是玉兰树的2倍，三种树苗各有多少棵？练习2、张伯伯家果园里种了梨树、桃树、苹果树共960棵，其中梨树的棵数是桃树的2倍，苹果树的棵数是桃树的3倍。
三种果树各多少棵？例3、、杨树和柳树共134棵，杨树比柳树的3倍多14棵，杨树和柳树各有多少棵？练习3、办公室花9840元买了一台打印机和一台复印机。
复印机的价格比打印机价格的2倍少120元。
复印机和打印机各花了多少钱？例4、甲工地有102名工人在绿化草地，乙工地有146名工人在清理土石。
甲工地要调多少人到乙工地，才能使乙工地的工人数是甲工地的3倍？练习4、甲仓库存粮120吨，乙仓库存粮164吨，要是甲仓库的存粮是乙仓库的3倍，那么要从乙仓库运出多少粮食放入甲仓库？例5、已知两个数的和是814，其中一个数的各位数字是0，如果把这个数的个位上的0去掉，则和另一个数相等，求这两个数。
练习5、已知两数之和是946，其中一个数的个位是0.如果把这个数的个位上的0去掉，则和另一个数相等，求这两个数。
例6、水果店新运来苹果，香梨共1502千克，如果苹果减少50千克，香梨增加350千克，那么香梨的质量比苹果的3倍多2千克。
求苹果、香梨各多少千克？练习6、服装城新进男、女衬衣864件，如果男衬衣减少39件，女衬衣增加45件，则女衬衣比男衬衣的2倍多3件。
新进男、女衬衣各多少件？和倍问题作业1、师傅和徒弟共生产零件190个,师傅生产的个数比徒弟的3倍多30个。
师、徒各生产多少个?2、两个粮仓共存粮2200千克,由乙仓运出210千克,甲仓存的粮食是乙仓的2倍多10千克,甲仓库和乙仓库原来各存粮食多少千克？3、三个饲养场共养2700头牛,第二饲养场养牛的头数是第一饲养场的2倍,第三饲养场养的头数是第二饲养场的3倍,三个饲养场各养牛多少头?4、甲桶有油25千克，乙桶有油17千克，从乙桶倒入多少千克给甲桶后，甲桶油是乙桶的5倍？5、果园里有桃树、梨树、苹果树共552棵.桃树比梨树的2倍多12棵，苹果树比梨树少20棵，求桃树、梨树和苹果树各有多少棵？。
三年级_第二讲_盈亏问题
1、一所学校到农村学农，老师给学生安排宿舍，如果每件宿舍住5人，则还有14人没有床位；如果每件宿舍住7人，则多出4个空床位，请回答：宿舍有几间？住宿学生有几人？2、某学校行军拉练，每顶帐篷安排6人住（每人一个铺位计），则有24人没有铺位；如果每顶帐篷住10人，则空出4个铺位，请回答：帐篷有几顶？住宿帐篷的学生有几人？3、把一袋糖分给小朋友，如果每人12颗糖，正好分完；如果每人分18颗糖，有3个小朋友分不到糖，问：这袋糖有多少颗？4、给少先队员分树苗，如果每人分9棵，正好分完；如果每人分12棵，有4人分不到树苗。
问：这批树苗一共有几棵？5、用一根长绳测量井的深度，如果绳子两折时，还多5米，如果绳子三折时，差4米，请问：绳子长几米？6、用一根长绳测量井的深度，如果绳子两折时，还多5米，如果绳子:四折时，差4米，请问：绳子长几米？井深几米？7、一个小队去植树，如果每人栽5棵，还剩10棵；如果每人栽7棵，就少6棵，请问：这个植树小队有几人？一共植树多少棵？8、小科带了钱去买水果，如果买3千克，则多出12元；如果没5千克，则少8元，请问：这种水果每千克多少元？小科带了多少钱？9、用一根长绳测量井的深度，如果三折时，每折多5米；如果5折时，每折差3米，请问：绳子长几米？井深几米？10、工厂给一批工人分配宿舍，如果每间房住8人，则少2间房；如果每间房住10人，则多出2间房。
请问：一共有几间房？这批工人有几人？11、全班同学分组参加校园卫生清洁，如果按每组8人来分，正好分完；如果按每组12人来分，则减少2组。
请问：参加卫生清洁的学生有多少人？12、幼儿园老师给几位小朋友分苹果，如果每个小朋友分3个，就多出4个；如果每人分5个苹果，就少10个，请问：有几个小朋友？有几个苹果？13、有一根绳子绕树3圈，多余2米；如果绕树5圈，则差6米。
请问：树的周长有几米？绳子长有几米？。
第二讲和差问题
第二讲和差问题知识要点及解题基本方法已知两个数的和与他们的差，求这两个数各是多少的应用题叫做和差应用题。
解和差应用题可用以下公式：（和＋差）÷2＝大数和－大数＝小数或（和－差）÷2＝小数小数＋差＝大数基础篇１、两筐苹果共重128千克，第一筐比第二筐多10千克，两筐水果各重多少千克？２、小星星夏令营共有学生91人，其中男生比女生多5人。
小星星夏令营有男女生各多少人？３、买一个笔记本和一支钢笔共用10元，已知笔记本比钢笔便宜6元。
求买钢笔和笔记本各花了多少元？４、两个油桶共盛80千克，如果把第一桶里的油倒出6千克，两个水桶中的油就一样多了。
第一桶原有油多少千克？５、甲、乙两个仓库共存粮9600千克，如果甲仓库给乙仓库800千克，则两仓库的存粮相等，问两仓库各存粮多少千克？６、甲、乙两个生产队计划植树96棵，若甲队的8棵树给乙队植，那两队植树棵数相等。
甲队和乙队划各植多少棵树？７、两个连续的奇数的各是100，则这两个奇数分别是多少？８、两袋面粉共重50千克，若从袋中取出6千克放入乙袋中，这时袋比乙袋多2千克，求两袋原来各有多少千克？９、甲、乙两校共有学生432人，为了照顾学生就近入学，经协商由甲校调入乙校16人，这时甲校比乙校还多24人，原来甲、乙两校各多少人？提高篇1、甲、乙两个钻井队共有83人，甲队有3个工人请假，乙队有4个工人请假，这时队比乙队多2人，甲、乙两个钻井队原来各有多少人？2、小华每天早晨沿长比宽多60米的操场跑步，每天跑6圈，共跑了3000米，问这个操场的长和宽各是多少？3、甲、乙、丙三个班共有学生150人，甲班比乙班多8人，丙班比乙班少2人，求三个班各多少人？]4、甲、乙两个打字员合打一份稿件，按分工，平均每人每小时打14页，3小时即可打完。
当两人打完稿件时，乙发现甲比自己多少打了12页。
甲乙两打字员各打了多少页？作业：1、商店今天卖了大、小两筐苹果，共150千克，第一筐比第二筐多6千克。
第二讲 从整体上看问题
第二讲 从整体上看问题解决数学问题的过程是一个辩证的思维过程，有时需要从局部的、简单的情况入手，以发现整体的规律；有时需要从整体入手，以避免局部细节的干扰。
例1 用0、1、2、3、4五个数字组成四位数，每个四位数中的数字不同，求所有这样的四位数的和。
(“华杯赛”试题)解：千位数字是1的四位数有4×3×2＝24(个)(因为百位数字有4种可能，十位数字有3种可能，个位数字有2种可能)。
同理，千位数字是2、3、4的也各有24个。
百位数字是1的四位数有3×3×2＝18(个)(因为千位数字不能是0，只有3种可能，十位数字可以是0，有3种可能，个位数字有2种可能)。
同理，百位数字是2、3、4的也各有18个。
十位数字、个位数字是1、2、3、4的也各有18个。
因此，所求的总和是1000×(1＋2＋3＋4)×24＋(100＋10＋1)×(1＋2＋3＋4)×18＝259980。
例2 计算：1－)21(12+⨯－)321()21(3++⨯+－)4321()321(4+++⨯++－…－)10321()9321(10++++⨯++++ 。
(小学数学奥林匹克竞赛题) 解：从算式的整体上看，所有分数的分子都等于分母中两个因数的差，于是，原式＝1－(1－31)－(31－61)－…－(451－551)＝1－(1－551)＝551。
例3 用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体ABCD —A 1B 1C 1D 1，大正方体内的对角线AC 1、BD 1、CA 1、DB 1所穿过的小正方体都是红色玻璃小正方体，其他部分都是无色透明玻璃小正方体，小红正方体共用了401个，问：无色透明玻璃小正方体用了多少个？(“华杯赛”试题)解：AC 1、BD 1、CA 1、DB 1四条对角线都穿过位于正方体中心的那个小正方体，此外，任何两条对角线都没有穿过相同的小正方体，所以每条对角线穿过(401－1)÷4＋1＝101(个)小正方体，这表明大正方体的棱是由101个小正方体组成的。
第二讲盈亏问题
第二讲盈亏问题写在前面的话——盈，就是有剩余；亏，则是不足。
顾名思义“盈亏问题”是专门研究这类“一会多一点，一会又不够分”的问题的。
这类问题看上去好像挺复杂，但掌握了解题方法和窍门，就会感到十分方便。
解盈亏问题关键是比较两种方案下的差别，具体步骤如下：１、根据方案求出参与分配者两次分得物品数量之差。
２、根据结果求出两次分配的物品总数之差。
３、根据总差中包含个体差的个数，求出参加分配的数。
解盈亏问题，通常利用比较法求解，一般分为如下三种情况：一盈一亏：（盈＋亏）÷每份数的差＝份数两盈：（大盈－小盈）÷每份数的差＝份数两亏：（大亏－小亏）÷每份数的差＝份数基础篇１、李老师将一批练习本发给班上的学生，如果每人发６本，则少９４本；如果每人发４本，则少２本。
问有多少个学生？有几本练习本？２、王老师给同学们发饼干，每人发５块就多５４块，每人发７块还多６块，王老师一共有多少块饼干？３、幼儿园阿姨给小朋友分梨，每人分3个则多12个；若每人分5个则少6个。
问有多少个小朋友？多少个梨？４、小明从家到学校，他先用每50米的速度走了2钟。
如果这样走下去，他就要迟到8分钟；后来他改用每分钟60米的速度前进，结果早到5分钟。
求小明家到学校的路程？５、某人用一根绳子测量一口井的深度，他把绳子的一端放入井底，井口外绳子长9米，他把这根绳子对折后，将一端放入井底，这时在井口的绳子还有3米，求井深为多少？６、王老师给小朋友分苹果和桔子，苹果数是桔子数的2倍，桔子每人分3个，多4个：苹果每人分7个，少5个，有多少个小朋友？多少个苹果和桔子？７、学校买来一些篮球和排球分各班，已知排球个数是篮球的2倍。
如果篮球每班分2个，则多余4个，如果排球每班5个，则少2个，学校买来篮球和排球各多少个？８、某班学生从图书馆借来的有卡通书是作文书的2倍，平均每人看6本卡通书，则余12本，每人看4本作文书，则差3本，那么这个班学生有几人借书？９、老师将一些钢笔发给班上的学生。
第二讲-消去问题
育才小学体育组第一次买了4个篮球和3个排 球，共用去了141元；第二次买了5个篮球 和4个排球，共用去180元。每个篮球和每 个排球各多少元？
小亚在超市买了4支活动铅笔和3 支圆珠笔，用去了36.9元，小巧 也买同样的3支活动铅笔和5支圆 珠笔，用去了48.3元，请算一算， 每支活动铅笔多少元？
消去问题
在有些应用题里，给出了两个或者 两个以上的未知数量间的关系，要求 出这些未知数的数量。我们在解题时， 可以通过比较条件，分析对应的未知 数量变化的情况，想办法消去其中的 一个未知量，从而把一道数量关系较 复杂的题目变成比较简单的题目解答 出来。这样的解题方法，我们通常把 它叫做“消去法”,也叫“代换法”。
例３.7袋大米和3袋克。求每 袋大米和每袋面粉的重量。
3筐苹果和5筐梨共重138 千克，5筐同样的苹果和 3筐同样的梨共重134千 克。每筐苹果和每筐梨 各重多少千克？
王牌例题：
例4.3头牛和8只羊每天 共吃青草93千克，5头牛 和15只羊每天吃青草165 千克。一头牛和一只羊 每天各吃青草多少千克？
小明带了30元钱去买文具， 买了3本笔记本和5支笔，剩余的 钱，如果再买2支笔还差0.4元， 如果再买2本笔记本则还差2元， 那么每本笔记本多少元？每支笔 多少元?
例题与方法：
在学习例题前，我们先进行一些基本数量关系 的练习，为用消去法解题作好准备。
（1）买1个皮球和1个足 球共用去40元，买同样的 5个皮球和5个足球一共用 去多少元？
练习与思考：
1袋黄豆和1袋绿豆共重50 千克，同样的7袋黄豆和7 袋绿豆共重（ ）千克。
妈妈买了５米花布和３ 米白布，一共用去10２ 元。花布每米１５元， 白布每米多少元？
王牌例题：
第二讲和差问题
第二讲和差问题银星育才三年级奥数【知识导航】和差问题是已知大小两个数的和与两个数的差，求大小两个数各是多少的应用题。
为了解答这种应用题，首先要弄清两个数相差多少的不同叙述方式.有些题目明确给了两个数的差，而有些应用题把两个数的差“暗藏”起来，我们管暗藏的差叫“暗差”。
【经典例题】例1两筐水果共重150千克，第一筐比第二筐多8千克，两筐水果各多少千克？【试一试1】1、果园里有桃树和梨树共150棵，桃树比梨树多20棵，两种果树各有多少棵？2、两筐水果共重150千克，第一筐比第二筐多8千克，两筐水果各多少千克？例2今年小强7岁，爸爸35岁，当两人年龄和是58岁时，两人年龄各多少岁？【试一试2】1、哥哥今年16岁，弟弟今年9岁，当两人的年龄和是45岁时，弟弟是多少岁？2、学校田径运动队中共有学生56名，如果减少6名男同学，则男同学的人数比女同学的人数多2人。
运动队中男同学有多少人？女同学有多少人？例3小明期末考试时语文和数学的平均分数是94分，数学比语文多8分，问语文和数学各得了几分？银星育才三年级奥数【试一试3】1、小敏和他爸爸的平均年龄是29岁，爸爸比他大26岁。
小敏和他爸爸的年龄各是多少岁？2、小兰期末考试时语文和数学的平均分是96分，数学比语文多4分。
小兰语文、数学各得多少分？例4甲、乙两桶油共重30千克，如果把甲桶中6千克油倒入乙桶，那么两桶油重量相等，问甲、乙两桶原有多少油？【试一试4】1、甲、乙两个书架共有书480本，如果从甲书架中取出40本放入乙书架，这时两个书架上书的本数正好相等。
甲、乙两个书架原来各有多少本？2、甲、乙两个仓库共存大米58吨，如果从甲仓调3吨大米到乙仓，两个仓库所存的大米正好相等。
甲、乙两个仓库各存大米多少吨？3、甲乙两校共有学生864人，为了照顾学生就近入学，从甲校调入乙校32名同学，这样甲校学生还比乙校多48人，问甲、乙两校原来各有学生多少人？4、甲、乙两个学校共有学生1245人，如果从甲校调20人去乙校后，甲校比乙校还多5人，两校原有学生各多少人？2银星育才三年级奥数例5电视机厂一、二、三车间共有工人360人，第一车间比第二车间多12人，第三车间比第二车间少18人，三个车间各有工人多少人？【试一试5】1、某工厂将875元奖金分别给创造发明的三名优秀工人。
四下第二讲 周期问题(二)余数的妙用
第二讲周期问题（二）余数的妙用一、知识要点较复杂的周期问题，难点在于从现象或规律中寻找周期，其解题步骤一般如下：1.仔细观察出现的现象，认真分析循环规律，总结出经过几次又开始重新开始，得出一个周期是几。
(一个循环中经过的次数就是一个周期数)2.周期问题的计算方法：总数\一个周期数=几个周期数......还剩下几个。
余数就是不够一个周期，还剩下的个数，如果余数是1，就和周期中的第一个一样，如果余数是2，就和周期中的第二个一样......余数是几，就和周期中的第几个一样。
如果正好整除，没有余数，就和周期中的最后一个一样。
3.有时周期现象并不是从第一个开始的，那就先从总数中减去不成周期的个数，在计算。
二、自我探究【例1】小华数左手的手指，大拇指为1，食指为2，中指为3，无名指为4，小拇指为5.然后换方向再数，小拇指为6，无名指为7，中指为8，食指为9，大拇指为10.再次换方向数，大拇指为11……这样数到55，停在哪个手指上？【例2】在1-2016中能被7整除的数有多少个？能同时被2、3、5整除的数有多少个？【例3】把珠子一个一个地如下图按顺序往返不断投入A、B、C、D、E、F袋中.第1992粒珠子投在_____袋中.【例4】1、2、3、4、5、6、7七盏灯各有一个开关，开始第2、4、6盏灯亮着，一个小朋友从第1到第7，再从第1到第7，拉了2000次，问这时那些灯亮着？三、自我挑战第一关：1.2016年3月21日星期一，2017年的元旦是星期几？2.有一排黑白旗子按下图排列，一共有109面旗子，这排旗子的最后一面是黑色的，那么一共有多少面黑色的旗子？第45面旗子是什么颜色的？前面50面旗子中共有多少个黑色的旗子，多少个白色的旗子？3.小猫咪A、B、C、D、E、F排队依次从猫妈妈手中领鱼干，每只小猫咪每次领一条，领完后再到队尾继续排队领，直到鱼干发完，若猫妈妈有278条鱼干，则最后一个领到鱼干的小猫咪是_________。
工程问题第二讲：中途有人休息的工程问题
工程问题第二讲：中途有人休息的工程问题例1：一件工作，甲独做需40天完成，乙独做需60天完成，现两人合做，中途甲因故休息几天，所以经过27天才完成，甲休息了多少天？ 解： 6033276011=⨯-224016033=÷（天）27-22=5（天） 答：甲休息了5天。
例2：甲、乙两人合作加工一批零件，8天可以完成。
中途甲因事停工3天，因此两人用了10天才完成。
如果由甲单独加工这批零件，需要多少天才能完成？ 解： 1212418124138181)310811=-=÷=-⨯-（ 121211=÷（天） 答：甲需要12天才能完成。
例3：包装一批书本，甲独做8天完成，乙独做12天完成。
现由两人合做这批零件，中途甲因事请假二天。
完成任务时共用多少天？解： 4)12181()21211=+÷⨯-（（天）4+2=6（天）答：完成任务时共用6天。
例4：一项工程，甲独做10天完成；乙独做15天完成；丙独做20天完成。
现在3人合作，甲因病中途休息了几天，这样到第六天才完成全部工程，问甲休息了几天？解： 1036)201151(1=⨯+-3101103=÷（天）6-3=3(天）答：甲休息了3天。
例5：一件工程，甲队单独做10天完成，乙队单独做30天完成.现在两队合作，其间甲队休息了2天，乙队休息了8天（两队不在同一天休息）.问开始到完工共用了多少天时间？ 解： 151323018101=⨯+⨯1311(1)()1151030-÷+=2+8+1= 11（天）答：开始到完工共用了11天。
例6：某项工程，甲单独做需36天完成，乙单独做需45天完成。
如果开工时甲、乙两队合做， 中途甲队退出转做新的工程，那么乙队又做了18天才完成任务。
问：甲队干了多少天？解：将题目的条件倒过来想，变为“乙队先干18天，后面的工作甲、乙两队合干需多少 天？”这样一来，问题就简单多了。
答：甲队干了12天。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
操作：描述了状态之间的关系。 操作：描述了状态之间的关系。它可以是一个行 为步骤，也可以是一个改变过程、规则或操作数。 为步骤，也可以是一个改变过程、规则或操作数。 使状态中的某些分量发生改变， 使状态中的某些分量发生改变，就将使问题由一 个具体状态变化到了另一个具体状态。 个具体状态变化到了另一个具体状态。 问题的状态空间可用一个三元序组来表示： 问题的状态空间可用一个三元序组来表示： 可用一个三元序组来表示 〈 S， F， G〉 S是初始状态集；F是操作的集合；而G为目标状态 初始状态集； 操作的集合； 集。
高级人工智能
问题求解
王浩
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
1/7 7
问题表示及求解 用搜索法对问题求解 有信息的搜索 对抗搜索
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
2/1 12
问题表示及求解
问题表达及其变换 问题的直接求解法 状态空间图搜索算法
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
3/1 12
同构同态变换
原始问题 h 同态问题 易解 难解 原始解答 h-1 同态解答
问题分解法
与图（ 与图（树）描述问题分解。 描述问题分解。 或图（树）描述同构同态变换 。 或图（
合肥工业大学人工智能与数据挖掘研究 室 4/1 12
2011-12-19
状态空间求解法
用状态描述与问题相关的事实和事实间的关系。 用状态描述与问题相关的事实和事实间的关系。
Ee Ep
问题世界的信息环境 合肥工业大学人Байду номын сангаас智能与数据挖掘研究
室
2011-12-19
11/ 11 2
状态空间表示法是人工智能最基本的知识表示方法 状态空间表示法是人工智能最基本的知识表示方法 之一。 之一。 状态：描述某一类事物在不同时刻所处于的信息状况。可 描述某一类事物在不同时刻所处于的信息状况。
问题世界的信息环境
合肥工业大学人工智能与数据挖掘研究 室 2011-12-19 10/ 11 2
En
（3）未知信息环境En 未知信息环境En 对于未知信息环境的问题求解，首先要设法变En En为 对于未知信息环境的问题求解，首先要设法变En为 部分已知信息环境Ep来解决。例如，为了探测海洋、 Ep来解决 部分已知信息环境Ep来解决。例如，为了探测海洋、极 外星球的奥秘， 地、外星球的奥秘，就需要实地探险或发射相应的探测 以便取得必要的信息与知识； 器，以便取得必要的信息与知识；当进入陌生的地带作 战时，需要派出侦察小分队了解地形地物和侦察敌人火 战时， 力部署，或用侦察卫星探测敌情等。 力部署，或用侦察卫星探测敌情等。 En
Ee Ep
问题世界的信息环境
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
9/1 12
（2）部分已知信息环境Ep 当只有部分信息已知，这时其目 部分已知信息环境Ep 当只有部分信息已知， 标和任务是：充分利用已知信息， 标和任务是：充分利用已知信息，把未知的信息不利影响设 法降到最低程度， 法降到最低程度，尽可能按照最佳搜索路径取得理想搜索效 或者设法弥补信息损失，发挥已知信息作用，扬长避短， 果。或者设法弥补信息损失，发挥已知信息作用，扬长避短， 制定策略来克敌制胜。例如，在海陆空战棋或军棋游戏中， 制定策略来克敌制胜。例如，在海陆空战棋或军棋游戏中， 运用知识和经验猜测对方的军事布局， 运用知识和经验猜测对方的军事布局，一方面用手榴弹对付 比我方师长还要厉害的指挥官， 比我方师长还要厉害的指挥官，另一方面要设法用最小代价 摧毁对方强大火力，以便开辟夺取对方军旗的坦途。 摧毁对方强大火力，以便开辟夺取对方军旗的坦途。 Ee Ep
sg 问题求解的状态树表示
合肥工业大学人工智能与数据挖掘研究 室 2011-12-19 17/ 11 2
状态空间图在计算机中有两种存储方式： 状态空间图在计算机中有两种存储方式：一种是 有两种存储方式 图的显式存储，另一种是图的隐式存储 图的隐式存储。 图的显式存储，另一种是图的隐式存储。 图的显式存储: 图的显式存储: 概念：所谓图的显式存储， （1）概念：所谓图的显式存储，即把问题的 全部状态空间图直接都存于计算机中的方式。 全部状态空间图直接都存于计算机中的方式。 诸如一般计算机文件、 诸如一般计算机文件、程序文件和库文件的存 储等，均为图的显式存储方式。 储等，均为图的显式存储方式。 适用条件： （2）适用条件：通常图的显式存储方式需要 占据计算机的大量存储空间和处理时间， 占据计算机的大量存储空间和处理时间，故这 种存储方式仅适用于状态空间十分有限以及较 简单的问题求解。 简单的问题求解。 特点：其优点是直观、明了， （3）特点：其优点是直观、明了，但缺点是 占据存储空间大。 占据存储空间大。
合肥工业大学人工智能与数据挖掘研究 室 2011-12-19
sg
问题求解的状态树表示
18/ 11 2
图的隐式存储: 图的隐式存储: 概念： （1）概念：仅在计算机中存储关于要求解问题的相关各种 知识， 知识，只在必要时再由相关的信息和知识逐步生成状态空间 图的方式称为图的隐式存储。 图的方式称为图的隐式存储。 （2）适用条件：适用于一般问题求解，尤其适宜于状态空 适用条件：适用于一般问题求解， 间庞大的情况。 间庞大的情况。 特点：占据空间小，但不够直观， （3）特点：占据空间小，但不够直观，与图的显式存储刚 好特点互补。 好特点互补。 例如，针对问题的状态空间十分庞大的情况， 例如，针对问题的状态空间十分庞大的情况，人们可采 用图的隐式存储：即只需要存入问题的参数、 用图的隐式存储：即只需要存入问题的参数、参数数值表和 计算公式等，仅在问题求解中，按照推理或搜索过程的需要， 计算公式等，仅在问题求解中，按照推理或搜索过程的需要， 进行参数和参数值的代换与公式计算， 进行参数和参数值的代换与公式计算，再求得状态空间各点 的数值。通过数值的比较与搜索，最后再完成问题的求解。 的数值。通过数值的比较与搜索，最后再完成问题的求解。 19/
已扩展节点、 已扩展节点、未扩展节点的数据结构
OPEN表结构 OPEN表结构 状态结点 父结点 编号 CLOSED表结构 CLOSED表结构 状态结点 父结点
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
15/ 11 2
开 始
状态空间搜索 算法流程： 算法流程：
初始化：S放入OPEN表，CLOES表置空, n=1
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
7/1 12
可把问题世界的全部信息空间划分为三类： 可把问题世界的全部信息空间划分为三类：
（1）全信息环境Ee； 全信息环境Ee； Ee
部分已知信息环境Ep Ep； （2）部分已知信息环境Ep；
（3）未知信息环境En 未知信息环境En En
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
6/1 12
搜索（Search） 即寻找， 搜索（Search），即寻找，设法在庞大状态空间图中找到目 也可以把搜索看作是一种推理， 标。也可以把搜索看作是一种推理，它是人工智能问题求解 的基本方法之一。 的基本方法之一。 主要分为两类性质的搜索： 基本搜索和智能搜索。 主要分为两类性质的搜索：即基本搜索和智能搜索。 基本搜索是一种没有任何经验和知识起作用的 是一种没有任何经验和知识起作用的、 基本搜索是一种没有任何经验和知识起作用的、由某种规则 所确定的非智能性的搜索； 所确定的非智能性的搜索； 启发式搜索（ Search）： ）：其特点在于是一种有准 启发式搜索（Heuristic Search）：其特点在于是一种有准 备的、追求效率而有的放矢的智能搜索， 备的、追求效率而有的放矢的智能搜索，它要求依据某种知 识及信息的指导， 识及信息的指导，通过逐一状态比较而找到符合规定条件的 目标状态解。 目标状态解。
问题演绎法
基本思想：分解原问题成若干个子问题。 基本思想：分解原问题成若干个子问题。
博弈问题求解法
属于对策性课题，表示若干个体开展竞争的过程。 属于对策性课题，表示若干个体开展竞争的过程。
合肥工业大学人工智能与数据挖掘研究 室
2011-12-19
5/1 12
度量问题求解的性能
问题求解算法的输出不是Failure就是解。 问题求解算法的输出不是Failure就是解。 Failure就是解 完备性： 当问题有解时， 完备性 ： 当问题有解时 ， 这个算法能否保证找到 一个解 最优性：算法是否能找到最优解？ 最优性：算法是否能找到最优解？ 时间复杂度：找到一个解需要花费多长时间？ 时间复杂度：找到一个解需要花费多长时间？ 空间复杂度： 在执行算法的过程中需要多少内存？ 空间复杂度 ： 在执行算法的过程中需要多少内存 ？
OPEN为空表NULL ？ N
Y
失败
OPEN表中的第一个结点n移至CLOSE表 n=目标结点D吗 ? N 若n的后继未曾在搜索图G中出现，则将其放入OPEN 表的末端，并提供返回结点n的指针, 置n=n+1 Y 成功
根据后继结点在搜索图G中的出现情况 修改指针方向 依某种准则重新排序OPEN表
合肥工业大学人工智能与数据挖掘研究 室 2011-12-19 16/ 11 2
用一组变量的有序组合来表示为如下形式： 用一组变量的有序组合来表示为如下形式： Sk=[ x0, x1, x2, x3, …]T 其中的每个元素x (i=0,1,2…)称为分量 称为分量， 其中的每个元素xi (i=0,1,2…)称为分量，相应的变量值域 给定每个分量的值，就得到了一个具体的状态。 为[ai,bi]。给定每个分量的值，就得到了一个具体的状态。 状态的维数可以任意，一般为有限值。 状态的维数可以任意，一般为有限值。