随机过程第四章(1)
随机过程习题集-第四章马尔可夫过程
1第四章 马尔可夫过程内容提要1. 马尔可夫过程的概念 （1）马尔可夫过程给定随机过程{}(),X t t T ∈，如果对122,∀≥∀<<<∈n n t t t T ，有11221111{()|(),(),,()}{()|()}n n n n n n n n P X t x X t x X t x X t x P X t x X t x ----<====<=则称{}(),X t t T ∈为马尔可夫过程。
称(){}:,==∈E x X t x t T 为状态空间。
参数集和状态空间都是离散的马尔可夫过程称为离散参数马氏链. 参数连续、状态空间离散的马尔可夫过程称为连续参数马氏链. （2）k 步转移概率设{}(),0,1,2,=X n n 为离散参数马氏链，称()(),(,){|},0,1=+==≥≥i j p n k P X n k j X n i n k为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率，称(),(,)((,)),P =∈i j n k p n k i j E为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率矩阵. 特别地，当1k =时，在时刻n 的一步转移概率和一步转移概率矩阵分别简记为()ij p n 和()n P . （3）初始分布、绝对分布称((0)),,==∈i p P X i i E 为离散参数马氏链{}(),0,1,2,=X n n 的初始分布，记为0P ，称()(){},,==∈j p n P X n j j E 为马尔可夫链{}0n X n ≥的绝对分布，记为P n . （4）离散参数齐次马氏链设{}(),0,1,2,=X n n 是一离散参数马氏链，如果其一步转移概率()ij p n 恒与起始时刻n 无关，记为ij p ，则称{}(),0,1,2,=X n n 为离散参数齐次马氏链。
若{}(),0,1,2,=X n n2是离散参数齐次马氏链，则其k 步转移概率记为(),i j p k ，一步转移概率矩阵和k 转移概率矩阵分别记为P 和().P k(5) 离散参数齐次马氏链的遍历性离散参数齐次马氏链{X (n ) ,n=0,1,2… }，若对一切状态i ，j ，存在与i 无关的极限()()lim 0,ij j n p n i j E →+∞=π>∈则称此马氏链具有遍历性.0,1j j j Ej E ππ∈>∈=∑若且则称{},j j E π∈为离散参数齐次马氏链{X (n ) ,n=0,1,2… }的极限分布，或称为最终分布，记为{},j j E ∏=∈π（6）离散参数齐次马氏链的平稳分布离散参数齐次马氏链{X (n ) ,n=0,1,2… }，若存在{v j , j ∈E } 满足条件：1)0,2)13)j jj Ej i iji Ev j E vv v p ∈∈≥∈==∑∑则称此马氏链是平稳的，称 { v j , j ∈E } 为此马氏链的平稳分布。
随机过程第四章
pii
(n)
1
i
0
证：(1)如i为零常返则i
，由lim n
pii nd
d
i
0
而当n不能被周期d整除时n 0modd ,
必然有pii
(n)
0，故
lim
n
pii
n
0
反之，若lim n
pii
(n)
0,
而i是正常返，
则由lim n
pii (nd )
d
i
0矛盾.
(2) 如i为遍历，即d 1，由上面定理得
即 Tij minn：X m i, X mn j，n 1
而称：
fij (n) P Tij n
P{X mv j，1 v n 1，X mn j / X m i}，n 1 为自状态i出发，经n步首次到达状态j的概率， 简称首达概率。
注：由齐次马氏链性质知，首达概率与出发时刻
p3
① q1 q2
p1
③ q3 ②
p2
求从状态1出发经n步转移首次到达各个状态的概率。
f12
(n)qq11p3 p3源自q m1 1m p1,
q3
,
n 2m, n 2m 1,
m 1 m0
同理：
f13 (n)
p1q2 p1q2
p m1 1
m q1,
p2
,
n 2m, n 2m 1,
m 1 m0
互通关系的状态是同一类型.
定理：如果i j， 则
(1) i与j同为常返或非常返，如为常返，则它们
同为正常返或零常返；
(2) i与j有相同的周期。
1证：因为i j，故存在正整数k与m，使
pij (m) 0, p ji (k ) 0
随机过程-第四章 更新过程
4.1 更新过程定义
上一章我们看到泊松过程的到达时间间隔是服从独立同分布的指数随机变量。现将其 进行推广，考虑到达时间间隔服从独立同分布，但分布函数任意，这样得到的计数过程称为 更新过程。 设 X n , n 1, 2, 是一列服从独立同分布的非负随机变量，分布函数为 F ( x) ，为避 免显而易见的平凡情形， 假设 F (0) P X n 0 1 。 将 X n 解释为第 n 1 个与第 n 个事件 之间相距的时间，记 E ( X n ) 有 0 。令 Tn
这其中利用了 X n , n 1, 2, 的独立同分布性质，这里 [1 F (b)] (0,1) 。又因为
k
Tmk t Tk T0 t , T2k Tk t ,, Tmk T( m1)k t
而且更新区间（相当于时间间隔）服从独立同分布，即
P 1 因 此 存 在 a 0 ， 使 得 P Xn a 0 ， 从 而 由 于 F( 0 ) X n 0 ， P X n a 1 。而 F (a) P X n a P X n a P X n a
为 避 免 因 可 能 的
N (t ) sup n, Tn t
定义 4.1 更新过程：计数过程 N (t ), t 0 称为更新过程。
在更新过程中我们将事件发生一次叫做一次更新， 从而 X n 就是第 n 1 次与第 n 次更新 相距的时间，Tn 表示第 n 次更新发生的时刻， 而 N (t ) 就是 t 时刻或 t 时刻之前发生的总的更 新次数。更新过程一个典型的例子是机器零件的更换。 我们首先要回答是第一个问题是在有限时间内是否会有无限多次更新发生。答案是不 会发生这种情况的概率为 1。由强大数定律可知
第四章 随机过程中的平稳过程
RX ( ) E[ X (t )X (t )] =E[ X (t ) X (t )] RX ( )
R(s, t ) E[ X (s)X (t )] R( )
则称{X(t),t∈T} 为宽（弱、广义）平稳过程，简称宽 平稳过程
2008年12月
陕西师范大学物理学与信息技术学院 ——— 《随机过程》
由于在许多工程技术问题中，常常仅在相关理论(一、二
阶矩)的范围内讨论问题，因此划分出广义平稳随机过程来。
而相关理论之所以重要，是因为在实际中，一、二阶矩能给出 有关平稳随机过程平均功率的几个主要指标，比如，如果随机
过程如果代表噪声电压信号，那么在相关理论范围内就可以给
出直流分量、交流分量，平均功率及功率在频域上的分布(我 们将在后面讨论功率谱密度)等。另外，在电子系统中经常遇
到最多的是正态随机过程，对于正态随机过程而言，它的任意
若令 t 2 ，得
f (t1 , t 2；x1 , x2 ) f (t1 t 2 ,0；x1 , x2 ) f (；x1 , x2 )
其中 同理
t1 t2
二维分布函数也仅与时间差 而与时间起点无关，即
t1 t2
有关，
F (t1 , t 2；x1 , x2 ) F (；x1 , x2 )
j [ l ( t ) k t ] E X X e k l k 1 l 1
bk e jk
k 1
RY ( )
所以， {Y (t ), t }具有平稳性。
2008年12月
陕西师范大学物理学与信息技术学院 ——— 《随机过程》
P
k 0
(解答)《随机过程》第四章习题
第四章 二阶矩过程、平稳过程和随机分析 习题解答1、 设∑=-=Nk k k kn U n X 1)cos(2ασ，其中k σ和k α为正常数，)2,0(~πU U k ，且相互独立，N k ,,2,1 =，试计算},1,0,{ ±=n X n 的均值函数和相关函数，并说明其是否是平稳过程。
解：计算均值函数和相关函数如下0)}{cos(2)cos(2}{)(11=-=⎭⎬⎫⎩⎨⎧-==∑∑==Nk k k k N k k k k n X U n E U n E X E n ασασμ∑∑∑∑∑∑======-=--=--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-⋅⎥⎦⎤⎢⎣⎡-=Ni i i N i i i i i i Ni Nj j j i i j i N j j j j N i i i i X m n U m U n E U m U n E U m U n E m n R 12121111)](cos[)}cos(){cos(2)}cos(){cos(2)cos(2)cos(2),(ασαασαασσασασ因此可知，},1,0,{ ±=n X n 是平稳随机过程。
2、 设有随机过程))(cos()(t t A t X πηω+=，其中0>ω为常数，}0),({≥t t η是泊松过程，A 是与)(t η独立的随机变量，且2/1}1{}1{===-=A P A P 。
（1） 试画出此过程的样本函数，并问样本函数是否连续？ （2） 试求此过程的相关函数，并问该过程是否均方连续？ 解：（1）样本函数不连续。
（2）令：012≥>t t ，下面求相关函数：)(221)(212210)(1212211212121211212212122112221122121121212cos cos )]}(cos[)]({cos[21!)]([)]}(cos[)]({cos[)1(21))]}()(()(cos[))]()(()(2)({cos[21))]}()(()(cos[))]()(()({cos[21))}(cos())({cos(}{))}(cos())(cos({)}()({),(t t t t k t t k kX e t t e t t t t e k t t t t t t t t t t t t t t t E t t t t t t t t E t t t t E A E t t t t A E t X t X E t t R ----∞=--⋅=⋅-++=⋅-⋅-++-=-+-+-+++=-+-++++=++⋅=++==∑λλλωωωωλωωηηπωηηππηωηηπωηηπωπηωπηωπηωπηω因为：t t t R ωξ2cos ),(=因此该过程是均方连续的随机过程。
随机信号4.1
∧
ω0 +∆ω / 2
−ω0 +∆ω / 2
令 ω = ω −ω0 ,ω = ω +ω0 则有
' ''
∧ ∆ω / 2
'
j jω0t j − jω0t j ' jω t ' '' jω''t '' x(t) = − e ∫/A(ω )e dω + 2 e −∆∫/ 2 2 A(ω )e dω = 2 −∆ω 2 ω j jω0t j − jω0t − e a(t) + e a(t) = a(t) sin ω0t 2 2
1
∞
π −∞
∫
x(t −τ )
∧
τ
dτ =
∞
π −∞
∫
x(t +τ )
∧
τ
dτ
x(t)的希尔伯特变换为 的希尔伯特变换为x(t)与1/πt的卷积 的卷积. 的希尔伯特变换为 与 的卷积 因此， 因此，可以把希尔伯特变换看作是信号通过一个冲 激响应为h(t)= 1/πt的线性时不变网络。 的线性时不变网络。 激响应为 的线性时不变网络
一. 希尔伯特变换 ∧ 设有实信号x(t),它的希尔伯特变换记作x(t)或H[x(t)] 设有实信号 它的希尔伯特变换记作 并定义为 ∞
x(t) x(t) = H[x(t)] = ∫ dτ π −∞t −τ 1
∞ ∧
∧
反变换为
1 x(t) ∧ −1 x(t) = H x(t) = − ∫ dτ π −∞t −τ
R∧ ( ) = RXT ( ) τ τ
XT
XT
τ =0
R∧ (0) = RXT (0)
第四章-马尔可夫链-随机过程
计算 n 步转移概率的方法。
切普曼一柯尔莫哥格夫方程：对一切n,m 0，一切 i，j，有(4.2.1)
P nm ij
Pikn Pkmj
k0
证明：
P nm ij
P{ X nm
j|
X0
i}
P{Xn k | X0 i}P{Xnm j | Xn k, X0 i}
顾客数构成一个泊松过程。所以，
Pi, j
e t (t )i1 j dG(t ), j 1,
0
(i 1 j)!
i 1
这是因为若一个来客发现有 i 个人在系统中，那么下一个来客将
发现人数为 i+1 减去已服务完毕的人数，易知有 i+1-j 个人被服
务完毕的概率(对相继来到之间的时间取条件)等于上式的右端。
0
0
0 P43
例 4．1(b) G/M/1 排队系统。假设顾客 依照一个任意的更新过
程来到一个单服务台的服务中心，来到间隔分布为 G。进一步
假设服务分布是指数分布，参数为。若以 Xn 记第 n 个顾客来
到时见到系统中的顾客数，以 Yn 记第 n 个顾客与第(n+1)个顾客
不可被 d 整除的 n 有 Piin 0，且 d 是具有此性质的最大整数(d 是
{n : Piin 0}的最大公约数)。(若对一切 n>0， Piin 0，则定义 i 的周 期是无穷大。)具有周期 1 的状态称为非周期的(aperiodic)。以 d(i)记 i 的周期。
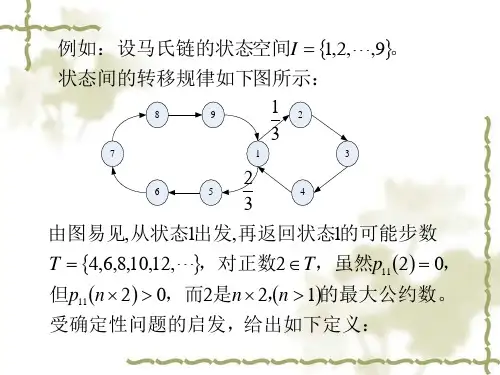
例设马尔可夫链的状态空间I={1,2,,9}， 转移概率如下图
P nm ij
第四章随机过程
设状态空间为 S ，一步转移概率为 P ，初始分布为 p i = P( X 0 = i ), i ∈ S 的齐次
Markov 链 {X n , n ≥ 0}，令 Pij( n ) = P ( X n + m = j X m = i ) = P (X n = j X 0 = i ), n ≥ 2 ，表示
证：
5
Pij( n ) = P( X n = j X 0 = i ) = ∑ P(τ ij = l , X n = j X 0 = i )
l =1 n n
= ∑ P(τ ij = l X 0 = i ) P( X n = j τ ij = l , X 0 = i )
l =1 n
= ∑ P(τ ij = l X 0 = i ) P( X n = j X 0 = i, X 1 ≠ j , L X l −1 ≠ j , X l = j )
4.4 常返与瞬过
在事件 {X 0 = i}上引入一个重要的概率 f ij( n ) ，表示从 i 出发在 n 步转移时首次 到达 j 的概率。用式子表示即是
f ij( 0) = 0, f ij( n ) = P( X n = j , X k ≠ j , k = 1, L n − 1 X 0 = i ) 。
i =1
(m) 定理 4.3.3 的一个直接推论是： 若 Pji > 0 ，存在正整数 N 使得对所有的 ( m + nd ( i )) n > N 恒有 Pji > 0。
定理 4.3.4：设 P 为不可约、非周期、有限状态 Markov 链的一步转移概率矩阵， 则存在正整数 N 使得当 n > N 时， n 步转移概率矩阵 P ( n ) 的所有元素都大于 0。
随机过程 第4章 马尔可夫链
一步转移概率矩阵
p11 P p 21 p12 p 22 p1n p2n
性质： (1) p ij 0 , i , j I
(2)
j I
p ij 1 , i I
（随机矩阵）
n 步转移概率
[定义] 称条件概率
p q q p
0 1
p, i j pij q, i j (i , j 0,1)
二步转移概率矩阵：
P
( 2)
2 2 p q P2 2 pq
2 pq 2 2 p q
[例2] （例4.4）具有吸收壁和反射壁的随机游动
设质点在线段 [1,4] 上作随机游动。假设ห้องสมุดไป่ตู้只能在时刻 nT 发生移动，且只能停留在1,2,3,4点上。当质点转移 到2,3点时，它以1/3的概率向左或向右移动一格，或停 留在原处。当质点移动到点 1 时，它以概率 1 停留在原 处。当质点移动到点4时，它以概率1移动到点3。若以 Xn 表示质点在时刻 n 所处的位置，则{ Xn , n T }是一 个齐次马尔可夫链。
f
(n) 12
( q1 p 3 ) m 1 q1 q 3 , m ( q1 p 3 ) p1 ,
n 2m, m 1 n 2 m 1, m 0
(n) f13
( p1 q 2 ) m 1 p1 p 2 , n 2 m , m 1 m n 2 m 1, m 0 ( p1 q 2 ) q1 ,
pij(n) 不仅与状态 i , j 有关，而且与时刻 n 有关。
当 pij(n) 与时刻 n 无关时，表示马尔可夫链具有平稳 转移概率。
精品文档-随机过程——计算与应用(研究生)(冯海林)-泊松过程1
m!
n!
=P(Ns m)P(Nts Ns =n)
随机过程引论—西安电子科技大学数学与统计学院 冯海林
定理4.2.1 泊松过程的到达时间间隔 相互独立同服从参数为λ指数分布．
n, n 1, 2,
证明： t 0时，F（ 1 t） P{1 t}=P{T1 t}
1 P{T1 t} 1 P{Nt 0} 1 et
随机过程引论—西安电子科技大学数学与统计学院 冯海林
对0 t1 t2，以及充分小的i , (i 1, 2),有 P{t1 1 T1 t1 1, t2 2 T2 t2 2}
P{Nt11 0, Nt11 Nt11 1, Nt2 2 Nt11 0, Nt2 2 Nt2 2 1}
f 2
(t2
)，即
1、
独立.
2
类似可以证 1, 2 n , 独立且同服从参数为的指数分布.
随机过程引论—西安电子科技大学数学与统计学院 冯海林
例1. 两个独立的泊松过程之和仍然是泊松过程.
随机过程引论—西安电子科技大学数学与统计学院 冯海林
例4.1.1 上随机过程的教室A有两入口B和 C.
对时刻t 0,设从B口进入教室的学生人数为NtB , 从C口进入教室的学生人数为NtC ,并假设随机过程
每一种知识都需要努力， 都需要付出，感谢支持！
随机过程引论—西安电子科技大学数学与统计学院 冯海林
知识就是力量，感谢支持！
随机过程引论—西安电子科技大学数学与统计学院 冯海林
一一一一谢谢大家！！
随机过程引论—西安电子科技大学数学与统计学院 冯海林
n
n1
0 P(s - u m1 mi s t u mi Tm u)dP(Tm u)
i 1
随机过程第四章习题解答
第四章习题解答4.1Y1,Y2,···是来自总体Y的随机变量，与X0独立，h(x,y)是实函数.对于n 1，取X n=h(X n−1,Y n).设{X n}的状态空间为I，验证{X n}是马氏链，给出转移概率p ij.解：由题知，Y k与X1,···,X k−1独立,k 1,∀n,i,j,i1,...,i n−1∈I有，P(X n+1=j|X n=i,X n−1=i n−1, (X0)i0)=P(h(i,Y n+1)=j|X n=i,X n−1=i n−1,···,X0=i0)=P(h(i,Y n+1)=j|X n=i)=P(h(i,Y)=j)=P(h(i,Y1)=j|X0=i)=P(X1=j|X0=i).∴X n是马氏链，P ij=P(h(i,Y)=j).4.2设{X i,i 0}是取非负整数值的独立同分布的随机变量序列，V ar(X0)>0.验证以下随机序列是马氏链：(a){X n,n 0};(b){S n,n 0}，其中S n=∑ni=0X i;(c){ξn,n 0}，其中ξn=∑ni=0(1+X i).解：∀n,i,j,i0,···,i n−1∈N+,(a).P(X n+1=j|X n=i,X n−1=i n−1,···,X0=i0)=P(X n+1=j)= P(X n+1=j|X n=i)=P(X1=j)=P(X1=j|X0=i).1第四章离散时间马尔可夫链第四章离散时间马尔可夫链(b).P(S n+1=j|S n=i,S n−1=i n−1,···,X0=i0)=P(X n+1=j−i|X n=i−i n−1,···,X0=i0)=P(X n+1=j−i)=P(X n+1=j−i,S n=i|S n=i)=P(S n+1=j|S n=i)=P(X1=j−i)=P(X1=j−i|X0=i)=P(S1=j|S0=i).(c).P(ξn+1=j|ξn=i,ξn−1=i n−1,···,ξ0=i0)=P(X n+1=ji −1)=P(X n+1=ji−1|ξn=i)=P(ξn+1=j|ξn=i)=P(X1=ji −1)=P(X1=ji−1|X0=i)=P(ξ1=j|ξ0=i).4.3马氏链的状态空间是I=(1,2,3,4,5)，转移概率矩阵P=0.20.80000.50.5000000.50.500.20.3000.500001界定马氏链的状态。
第四章平稳过程课件
第13页共45页
随机过程(西电版） 4.3 平稳过程的各态历经性
第4章 平稳过程
_______
X (t) X (t ) l i m
1
T ______
X (t) X (t )dt
l i m 1
T
a
2
T
cos(t
2T T
) cos(t
)dt
T 2T T
a2 l i m 1
4.1 平稳过程的概念
第4章 平稳过程
（1） mX (t) m （常数）
（2） RX (s,t) RX ( ), t s
则称 {X (t),t T }为宽平稳过程。
显然，一个严平稳过程如果存在二阶矩，则必为宽平稳过 程。以后平稳过程均指宽平稳过程。
例1、设 { X n , n 1,2, }是不相关的随机变量序列，且
1
2
a cos(t )d 0
2 0
RX (t1,t2 ) E[ X (t1) X (t2 )]
E[a cos(t1 )a cos(t2 )]
a2 2
cos
, 其 中
t2
t1.
2024年6月19日星期三
机动 目录 上页 下页 返回 结束
第3页共45页
随机过程(西电版） 4.2 平稳过程相关函数的性质 第4章 平稳过程
2024年6月19日星期三
机动 目录 上页 下页 返回 结束
第14页共45页
随机过程(西电版） 4.3 平稳过程的各态历经性
第4章 平稳过程
lim
T
证明：E[
1 2T
X (t
)
22TT1
2T
] E[l i
C
精品文档-随机过程——计算与应用(研究生)(冯海林)-平稳过程1
平稳过程的定义 定义 5.1.1 设X={Xt,t∈T}是随机过程,如果对任意的
n 1, t1, t2 , , tn T和实数，当t1 ,t2 , , tn T时，
n维随机变量 (Xt1 , Xt2 , , Xtn )和 (Xt1 , Xt2 , , Xtn ) 有相同的联合分布函数,即
则
mX (t)
xdFt (x)
xdF (x)与t无关，为常数
RX (s,t )
x1x
2d
Fs,t (x1, x2 )
x1
x2
dF0,t
s
(
x1,
x2
)，仅与时间间隔有关系
随机过程引论——西安电子科技大学数学与统计学院 冯海林
用定义判断一个过程的严平稳性是困难的. 在理论与应用上多的是宽平稳过程.
Ft1,t2 , ,tn (x1, x2 , , xn ) Ft1 ,t2 , ,tn ( x1, x2 , , xn )
则称X是严平稳过程.
随机过程引论——西安电子科技大学数学与统计学院 冯海林
例5.1.1 设N={Nt,t≥0}是参数为λ 的泊松过程，对任意固定 的常数a>0,令
Xt =Nta Nt ,
例5.1.6 设{An,n=1,2,…N} 和{Bn,n=1,2,…N}是两列实值 随机变量序列.且
E[An ] E[Bn ] 0, E[AnBm ] 0,
E[AnAm ] E[BnBm ] n2mn , 设n >0,定义随机过程：
N
Xt [Ak cos(kt) Bk sin(kt)], t (, ), k 1
2[a 2 min(0, ) min(a, ) min(0, a)]
《随机过程及其在金融领域中的应用》习题四答案
h e e 3 h s3
故原式变为：
f
s1, s2 , s3
lim h0
h e e 3 h s3 h3
e3 s3
其中 0 s1 s2 s3
5、一部 500 页的书总计有 150 个印刷错误，试用泊松过程近似求出连续 4 页无 错误的概率。
（1）解法一：
设X t N1 t N2 t ,t 0,当s t时
PX t X s k PN1 t N2 t N1 s N2 s k
PN1 t N1 s N2 t N2 s k
占用任何时间。
答：
设起始时间为
s
，则速度Va
t
PT t 1 PT t
由于T 为 n 个过程中至少发生一件事情的时刻，故当T t ，即在0,t 时刻内
没有事件发生。
P T t P N1 t 0, , Nn t 0
n P Nk t 0 et n etn k 1
P T t 1 etn t 0
7、假设汽车按强度为 的泊松过程进入一条单向行驶的无限长的高速公路，进 入的第 i 辆车以速度Vi 行驶。假定诸Vi 是独立的正随机变量，有共同分布 F 。试
计算在时刻 t 位于区间 a,b 内的汽车数的均值，假定一辆车超过另一辆车时，不
不妨设 t s 则
E
M 2 T
1 T2
T 0
T 0
E
Nt
Ns
dsdt
1 T2
T 0
T 0
t 2ts dsdt
1
随机过程第4章Markov过程（PDF）
第四章 Markov 过程本章我们先讨论一类特殊的参数离散状态空间离散的随机过程，参数为0{0,1,2,}T N ==L ，状态空间为可列{1,2,}I =L 或有限{1,2,,}I n =L 的情况，即讨论的过程为Markov 链。
Markov 链最初由Markov 于1906年引入，至今它在自然科学、工程技术、生命科学及管理科学等诸多领域中都有广泛的应用。
之后我们将讨论另一类参数连续状态空间离散的随机过程，即纯不连续Markov 过程。
§4.1 Markov 链的定义与性质一、Markov 链的定义定义 4.1设随机序列{;0}n X n ≥的状态空间为I ，如果对0n N ∀∈，及0110011,,,,,{,,,}0n n n n i i i i I P X i X i X i +∈===>L L ，有：11001111{,,,}{}n n n n n n n n P X i X i X i X i P X i X i ++++=======L （4.1.0)则称{;0}n X n ≥为Markov 链。
注1：等式（4.1.0）刻画了Markov 链的特性，称此特性为Markov 性或无后效性，简称为马氏性。
Markov 链也称为马氏链。
定义4.2 设{;0}n X n ≥为马氏链，状态空间为I ，对于,i j I ∀∈，称1{}()ˆn n i j P X j X i p n +===为马氏链{;0}n X n ≥在n 时刻的一步转移概率。
注2：一步转移概率满足：()0,,()1,i j i jj Ip n i j Ipn i I ∈≥∈=∈∑若对于,i j I ∀∈，有1{}()ˆn n i j i j P X j X i p n p +===≡即上面式子的右边与时刻n 无关，则称此马氏链为齐次（或时齐的）马氏链。
设{}0()(0),p i P X i i I ==∈，如果对一切i I ∈都有00()0,()1i Ip i p i ∈≥=∑，称0()p i 为马氏链的初始分布。
西安交通大学汪荣鑫随机过程第二版课后答案
随机过程习题解答第一章习题解答1．设随机变量X 服从几何分布，即：(),0,1,2,kP X k pqk ===。
求X 的特征函数，EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtk k X k f t E ee pq ∞===∑ =()1jt k jtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑（其中 0(1)nnnn n n nx n x x ∞∞∞====+-∑∑∑）令 0()(1)nn S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰同理 2(1)2kkkk k k k k kx k x kx x ∞∞∞∞=====+--∑∑∑∑令2()(1)kk S x k x ∞==+∑ 则211()(1)(1)xkk kk k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰）2、（1） 求参数为(,)p b 的Γ分布的特征函数，其概率密度函数为（2） 其期望和方差；（3）证明对具有相同的参数的b 的Γ分布，关于参数p 具有可加性。
解 （1）设X 服从(,)p b Γ分布，则 （2）'1()(0)Xp E X fjb∴==（4）若(,)i i X p b Γ 1,2i = 则同理可得：()()i i P X b f t b jt∑=∑-3、设ln (),()(kZ F X E Zk =并求是常数）。
X 是一随机变量，()F x 是其分布函数，且是严格单调的，求以下随机变量的特征函数。
（1）(),(0,)Y aF X b a b =+≠是常数； （2）ln (),()(kZ F X E Z k =并求是常数）。
解（1）11{()}{()}[()]P F x y P x F y F F y y --<=<==（01y ≤≤） ∴00()0111y F y yy y <⎧⎪=≤≤⎨⎪>⎩∴()F x 在区间[0，1]上服从均匀分布()F x ∴的特征函数为11001()(1)jtx jtx jt X e f t e dx e jt jt ===-⎰ （2）ln ()()()[]jtz jt F x Z f t E e E e ===1ln 01jt ye dy ⋅⎰=111jty dy jt =+⎰4、设12n X X X ，，相互独立，且有相同的几何分布，试求1nkk X =∑的分布。
随机过程答案
随机过程第三章与第四章习题解答3.1 解：令()N t 表示(0,)t 时间内的体检人数，则()N t 为参数为30的poisson 过程。
以小时为单位。
则((1))30E N =。
4030(30)((1)40)!k k P N e k -=≤=∑。
3.2 解：法一：（1）乘坐1、2路汽车所到来的人数分别为参数为1λ、2λ的poisson 过程，令它们为1()N t 、2()N t 。
1N T 表示1()N t =1N 的发生时刻，2N T 表示2()N t =2N 的发生时刻。
1111111111()exp()(1)!N NN T f t t t N λλ-=-- 2221222222()exp()(1)!N NN T f t t t N λλ-=--1212121221112,12|12211122212(,)(|)()exp()exp()(1)!(1)!N N N N N NNN N T T T T T f t t f t t f t t t t t N N λλλλ--==---- 12212121112211122210012()exp()exp()(1)!(1)!NNt N N N N P T T dt t t t t dt N N λλλλ∞--<=----⎰⎰（2）当1N =2N 、1λ=2λ时，12121()()2N N N N P T T P T T <=>=法二：（1）乘车到来的人数可以看作参数为1λ+2λ的泊松过程。
令1Z 、2Z 分别表示乘坐公共汽车1、2的相邻两乘客间到来的时间间隔。
则1Z 、2Z 分别服从参数为1λ、2λ的指数分布，现在来求当一个乘客乘坐1路汽车后，下一位乘客还是乘坐1路汽车的概率。
212211122210()exp()exp()z p P Z Z dz z z dz λλλλ∞=<=--⎰⎰112λλλ=+。
故当一个乘客乘坐1路汽车后，下一位乘客乘坐2路汽车的概率为1-p 212λλλ=+上面的概率可以理解为：在乘客到来的人数为强度1λ+2λ的泊松过程时，乘客分别以112λλλ+概率乘坐公共汽车1，以212λλλ+的概率乘坐公共汽车2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
j
(2) p j (n) pi (n 1) pij 或 p(n) p(n 1) P
2
1.定义：若过程X (t )在m k时刻处在任一状态 ai 的概率, 只与过程在m时刻的状态有关, 而与
mk
过程在m时刻以前的状态无关,即条件概率满足：
PX m k ai
PX m k ai
mk
/ X m ai , X m1 ai ,, X 1 ai
同理：PX n in / X n1 in1 Pn i n in1
PX 0 i0 , X 1 i1 , X n in PX 0 i0 , X 1 i1 , X n1 in 1
PX n in / X 0 i0 , X 1 i1 , X n 1 in 1
n j i n ji m1 m2 n m1 , m2 2 2 m1 1 m2 (1) j i
20
由于m1 , m2只能取整数，所以n ( j i )必须是 偶数，且在 n 步中哪 m1 步向右，哪m2步向左 是任意的，选取方法为：Cnm
10
ar I
PX
PX m ai
m
PX m k ar / X m ai PX m n a j / X m k ar pir k prj n k
用矩阵形式表示为： Pn Pk Pn k
0 1 n 0 01 1 2 n 0 01
(2) PX 1 ai , X 2 ai ,, X n ai / X 0 ai pi i pi
n 1in
n 1in
总结： 1）齐次马氏链多步转移概率可由一步转移概率确定； P ( n) P n 2) 绝对概率可由初始概率及n步转移概率确定
n
ai I
1
n 1in
证：P{ X 1 ai , X 2 ai ,, X n ai } P U X 0 ai , X 1 ai ,, X n ai
ai I
1
1
2
n
n
PX 0 ai P{ X 1 ai / X 0 ai } P{ X 2 ai /
ai I
1 2
X 0 ai , X 1 ai } P{ X n ai / X 0 ai , X 1 ai X n1 ai }
1 n 1 n 1
pi (0) pii pi i pi
ai I
1 12
n 1in
15
推论： (1) PX 0 ai , X 1 ai ,, X n ai pi (0) pi i pi
第四章 马尔可夫链
1. 2.
3.
4. 5. 6.
马尔可夫链定义 一步转移概率及多步转移概率 Chapman-Kolmogorov方程 初始概率及绝对概率 马尔可夫链状态分类 遍历的马尔可夫链及平稳分布
1
§4.1 马尔可夫链的概念及转移概率 一、马尔可夫链的概念
而X t 在每一时刻t n 0,1,2,, 所处状态记为： X (n) X n，则所能取的状态必为a1 ,a 2 ,之一， 且过程只在0,1,2,, n, 可列个时刻发生状态转移， 即参数空间为：T 0,1,2,, n 假定马尔可夫过程X t 的状态空间为I a1 , a2 ,,
ij
1
即 ai 转 到 态 间 某 从 移 状 空 的 一 即 阵 任 行 素 矩 中 一 元 之 矩 称 随 矩 。 阵 为 机 阵
个 态 必 事 ， 状 是 然 件
和 1， 足 (1)、 )性 的 转移概率中取k n时,即得n步转移概率： pij n pij m, m n PX m n a j / X m ai 对应的n步转移概率矩阵为： p n p n p n p n p n p n P n P(n)也为随机矩阵， 即也满足性质：
p (0), a
j
分布和绝对分布，简记为和p j (0)和p j (n) 。
写成向量形式: p (0) p1 (0), p2 (0),, p j (0), p (n) p1 (n), p2 (n),, p j (n),
12
j
(2) 绝对概率与初始概率的关系
由所有的一步转移概率 pij 构成的矩阵
p11 p12 p1n p p p P 21 22 2n
称为马氏链的一步转移概率矩阵
5
pij 具有性质： (1) (2) pij 0 ai , a j I ai I
p
a jI
ij
整数n 0, ai , a j I， 有：pij n
或 Pn Pk Pn k
简称c k方程。
ar I
p
ir
(k ) prj n k
此乃有名的切普曼 柯尔莫哥洛夫方程，
8
ar
aj
ai
m
m k mn
直观解释对照图
9
证明：利用概率公式及马尔可夫性有： PX m ai , X m n a j PX m ai
17
对任意的n 1， 和整数i0 , i1 , in
P 0 i0 , 1 i1 i0 , n in in 1 P 0 i0 , 1 i1 i0 ,, n 1 in 1 in 2 P n in in 1.
pi ,i 1 p 一步转移概率为： pi ,i 1 q p 0 ii
i I ,0 p 1
j i 1, i 1, j I
下面求它的 n步转移概率 pij (n)
已知每次转移只有两种可能， 向左的概率为q， 向右的概率为p，而n次转移的结果是从i j， 如果n次转移中向右m1次，向左m2次，则
X n , n 0是一随机过程。 向 移 一 1 , 第k次 右 动 格 令 k 向 移 一 1 ， 第k次 左 动 格
则 X n n为 机 动 它 一 随 游 ， 是 个
其状态空间为：
k 0
n
齐 马 链 次 氏 。
19
I ， 2， 1， ，， ， 012
m mk
/ X m ai
m
m 1
1
则称此随机过程X n , n 0为马尔可夫链， 简称马氏链。
3
2、马氏链的转移概率
称条件概率
ai
m
aj
mk
P{X mk a j / X m ai } pij m, m k
为马氏链在m时刻处于ai 状态经k步，在m k时刻 转移到a j 状态的转移概率，记为：pij m, m k
m1 n m1 m2
1
C p q , n j i 为偶数 pij (n) n j i 为奇数 0 C p q , n为偶数 pii (n) 0 n为奇数
p j (n) pi (0) pij (n)
ai I
3)有限维分布可完全由初始概率及一步转移概率确定。
16
例：随机游动，设 0 , 1 , 2 ,是整数值独立随机 变量序列，且 0 , 1 , 2 ,有相同的分布，令X n k
k 0 n
则称X n , n 0为随机游动。
11
5、初始概率与绝对概率
(1) 定义：设X n , n 0为马尔可夫链, 分别称
p j (0) PX 0 a j 和p j (n) PX n a j (a j I ) ， I 和p j (n), a j I 为马氏链的初始
为马氏链的初始概率和绝对概率，并分别称
一步转移概率为： pij PX n j / X n1 i P n j i p j i
18
几种特殊的随机游动 例.无限制的随机游动：质点在直线上作随机游动，
如某一时刻质点位于i，则下一步质点以概率p向 右移动一格到达i 1， 或以概率q 1 p向左移一 格到达i 1， 若以X n 表示时刻n时质点的位置，则
随机游动可以解释为质点在直线上的整数格点上作 运动的质点，初始位置为X 0 0，每隔一个单位时 间质点移动一次，第k次移动的长度为整数 k，于是 X n k 表示在时刻n质点的位置，则X n , n 0是
k 0 n
随机游动，随机游动X n , n 0是时齐马氏链。
11 12 1n 21 22 2n
(1) (2)
pij n 0.
a j I
ai , a j I ai I
7
p n 1.
ij
通常我们还规定：
1 i j p 0 pij m, m ij 0 i j (2)、切普曼—柯尔莫哥洛夫方程 （Chapman-Kolmogorov） 定理：设X n , n 0为齐次马氏链， 则对任意的
i, j , m, k均为正整数, 一般pij m, m k 与i, j , m, k有关， 若pij m, m k 与m无关，则称马氏链为齐次的， 下面我们仅讨论齐次马氏链。
4
3、一步转移概率及矩阵
在上面转移概率中，取k 1即得一步转移概率
pij pij m, m 1 P{X m1 a j / X m ai }
ai I ai I
Pi (n 1) pij