第4章-平面机构力分析习题解答
机构 复习题及答案

第四章平面连杆机构一、填空1. 在铰链四杆机构中,能作整周连续旋转的构件称为_______,只能来回摇摆某一角度的构件称为_______,直接与连架杆相联接,借以传动和动力的构件称为_______。
2. 图1-1为铰链四杆机构,设杆a最短,杆b最长。
试用符号和式子表明它构成曲柄摇杆机条构的件:(1)____________________________ 。
(2)以_______为机架,则_______为曲柄。
3. 设图1-1已构成曲柄摇杆机构。
当摇杆CD为主动件,机构处于BC与从动曲柄AB共线的两个极限位置,称为机构的两个_______位置。
4. 铰链四杆机构的三种基本形式是_______机构,_______机构,_______机构。
5. 平面连杆机急回运动特性可用以缩短_______。
从而提高工作效率。
6. 平面连杆机构的急回特性系数K=______________。
7. 四杆机构中若对杆两两平行且相等,则构成_______机构。
1、槽轮机构能把主动件的______转动转换为从动件周期性的_____运动。
1、连续、间歇;2、机械就是_________和_________的总称。
机器、机构;3、一部完整的机器可归纳成由_________、_________、_________、和控制部分组成。
4、铰链四杆机构由______、______、_______、和运动副组成。
按曲柄的存在情况,分为_____、____和_____三种基本形式。
机架、连架杆、连杆、曲柄摇杆机构、双曲柄机构、双摇杆机构5、凸轮机构是由_________、_________和机架三个基本构件组成。
设计方法称为________。
动力、加工、信息二、选择代号填空1. 平面四杆机构中各构件以___A____相联接。
(a 转动副 b 移动副 c 螺旋副)2. 平面连杆机构当急回特性系数K___A____时,机构就具有急回特性。
(a >1 b =1 c <1)3. 铰链四杆机构中,若最长杆与最短杆之和大与其他两杆之和,则机构有__C_____。
孙桓《机械原理》笔记和课后习题(含考研真题)详解(平面机构的力分析)【圣才出品】

第4章平面机构的力分析4.1 复习笔记一、机构力分析的任务、目的和方法1.作用在机械上的力根据力对机械运动影响的不同,可分为两大类。
(1)驱动力①定义驱动机械运动的力称为驱动力。
②特点驱动力与其作用点的速度方向相同或成锐角,其所作的功为正功,称为驱动功或输入功。
(2)阻抗力①定义阻止机械运动的力称为阻抗力。
②特点阻抗力与其作用点的速度方向相反或成钝角,其所作的功为负功,称为阻抗功。
③分类a.有效阻抗力机械在生产过程中为了改变工作物的外形、位置或状态而受到的阻力,即工作阻力。
克服这类阻力所完成的功称为有效功或输出功。
b.有害阻抗力机械在运转过程中所受到的非生产阻力。
克服这类阻力所作的功称为损失功。
2.机构力分析的任务和目的(1)确定运动副中的反力运动副反力是指运动副两元素接触处彼此作用的正压力和摩擦力的合力。
(2)确定机械上的平衡力或平衡力偶平衡力是指机械在已知外力的作用下,为了使该机构能按给定的运动规律运动,必须加于机械上的未知外力。
3.机构力分析的方法对于不同的研究对象,适用的方法不同。
(1)低速机械惯性力可以忽略不计,只需要对机械作静力分析。
(2)高速及重型机械①惯性力不可以忽略,需对机械作动态静力分析。
②设计新机械时,由于各构件尺寸、材料、质量及转动惯量未知,因此其动态静力分析方法如下:a.对机构作静力分析及静强度计算,初步确定各构件尺寸;b.对机构进行动态静力分析及强度计算,并据此对各构件尺寸作必要修正;c.重复上述分析及计算过程,直到获得可以接受的设计为止。
二、构件惯性力的确定构件惯性力的确定有一般力学法和质量代换法。
1.一般力学方法如图4-1-1(a)所示为曲柄滑块机构,借此说明不同运动形式构件所产生的惯性力。
(1)作平面复合运动的构件惯性力系有两种简化方式。
①简化为一个加在质心S i上的惯性力F I2和一个惯性力偶矩M I2,即F I2=-m2a S2,M I2=-J S2α2②简化为一个大小等于F I2,而作用线偏离质心S2一定距离l h2的总惯性力F I2′,而l h2=M I2/F I2F′I2对质心S2之矩的方向应与α2的方向相反。
西工大教材-机械原理各章习题及答案
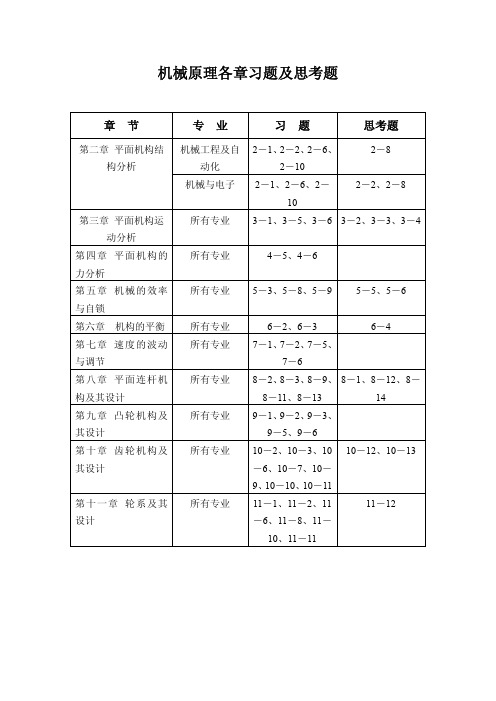
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中,设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下(反行程),此斜面 机构的临界自锁条件和在此条件下正行程(在 F 力作用下)的效率。 解 1)反行程的自锁条件 在外行程(图 a),根据滑块的平衡条件:
解 1 ) 取 比 例 尺 μ 1 = 1mm/mm 绘 制 机 构 运 动 简 图 ( 图 b )
(a)
2 )计算该机构的自由度
n=7
pι=9
ph=2(算齿轮副,因为凸轮与齿轮为一体) p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构;图 b 为凸轮一连杆组合 机构(图中在 D 处为铰连在一起的两个滑块);图 c 为一精压机机构。并问在图 d 所示机构中, 齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同?为什么?
C3 重合点继续求解。
解 1)速度分析(图 b)取重合点 B2 与 B3,有
方向 大小 ?
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B(B1、B2、B3)
ω1
A1 ϕ = 90°
平面机构力分析习题解答

第四章平面机构的力分析解答 典型例题解析例4-1 图4-1所示以锁紧机构,已知各部分尺寸和接触面的摩擦系数f ,转动副的摩擦圆图上虚线圆,在P 力作用下工作面上产生夹紧力Q,试画此时各运动副中的总反力作用线位置和方向(不考虑各构件的质量和转动惯量) 。
图4-1 解[解答] (1) BC 杆是二力杆,由外载荷P 和Q 判断受压,总反力23R F 和43R F 的位置和方向见图。
(2) 楔块4所受高副移动副转动副的三个总反力相平衡,其位置方向及矢量见图。
(3) 杆2也是三力杆,所受的外力P 与A,B 转动副反力相平衡,三个力的位置见图。
例4-2 图示摇块机构,已知,90ABC 曲柄长度,86,200,1002mm l mm l mm l BS AC AB 连杆的质量,22kg m 连杆对其质心轴的转动惯量22.0074.0m kg J S ,曲柄等角速转动s rad /401 , 求连杆的总惯性力及其作用线。
[解答] (1) 速度分析,/41s m l v AB B 其方向垂直于AB 且为顺时针方向 32322C C C B C B C大小: s m /4 0 0 ? 方向: AB BC取mmsm v /2.0 作速度图如(b ),得 02232 B C B C l v(2)加速度分析,/160221s m l a AB B 其方向由B 指向A 。
32323t C2B n C2B 2 C C rC C k C B C大小: 160 0 ? 0 0 ? 方向:A B B C 2BC BCBC取mms m a 2/8 作加速度图如图(C)222/80s m s p a a s 2222/100s m C C a a B C t 222222/76.923160s rad l l l a ABAC B C tB C ,逆时针方向。
(3)计算惯性力,惯性力矩N a m F S I 160222 ,方向如图( )所示。
机械原理习题参考答案

习题参考答案第二章机构的结构分析2-2 图2-38所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图,分析其运动是否确定,并提出修改措施。
4351 2解答:原机构自由度F=3⨯3- 2 ⨯4-1 = 0,结构均可:1为滚子;2为摆杆;3为滑块;4为滑杆;5为齿轮及凸轮;6为连杆;7为齿轮及偏心轮;8为机架;9为压头。
试绘制其机构运动简图,并计算其自由度。
O齿轮及偏心轮ωA齿轮及凸轮BEFDC压头机架连杆滑杆滑块摆杆滚子解答:n=7; P l =9; P h =2,F=3⨯7-2 ⨯9-2 = 12-6 试计算图2-42所示凸轮—连杆组合机构的自由度。
解答:a) n=7; P l =9; P h =2,F=3⨯7-2 ⨯9-2 =1 L 处存在局部自由度,D 处存在虚约束b) n=5; P l =6; P h =2,F=3⨯5-2 ⨯6-2 =1 E 、B 处存在局部自由度,F 、C 处存在虚约束b)a)A EMDFELKJIFBCCDBA2-7 试计算图2-43所示齿轮—连杆组合机构的自由度。
BDCA(a)CDBA(b)解答:a) n=4; P l =5; P h =1,F=3⨯4-2 ⨯5-1=1 A 处存在复合铰链b) n=6; P l =7; P h =3,F=3⨯6-2 ⨯7-3=1 B 、C 、D 处存在复合铰链2-8 试计算图2-44所示刹车机构的自由度。
并就刹车过程说明此机构自由度的变化情况。
解答:① 当未刹车时,F=3⨯6-2 ⨯8=2② 在刹车瞬时,F=3⨯5-2⨯7=1,此时构件EFG 和车轮接触成为一体,位置保持不变,可看作为机架。
③ 完全刹死以后,F=3⨯4-2⨯6=0,此时构件EFG 、HIJ 和车轮接触成为一体,位置保持不变,可看作为机架。
第四章平面机构的力分析

第四章平⾯机构的⼒分析第四章平⾯机构的⼒分析§4-1机构⼒分析的⽬的和⽅法 1、作⽤在机械上的⼒驱动⼒:∠VS 锐⾓(驱动⼒→原动⼒)作功⽣产阻⼒(有效阻⼒)(+、-)阻⼒ : ∠VS 钝⾓有害阻⼒常见的作⽤⼒:原动⼒、摩擦⼒、运动副反⼒、重⼒、“惯性⼒”2、机构⼒分析的⽬的和⽅法影响及其运动的动⼒性能→运转性能、调速、平衡、振动、功率分析⼒(⼒矩)后续机械设计重要参数→尺⼨、机构、强度确定运动副反⼒→强度、摩擦磨损、效率任务(⽬的)确定机构的平衡⼒(或平衡⼒矩)→原动机功率?克服⽣产阻⼒?§4-2构件惯性⼒的确定假设已知构件质量、转动惯量(实际设计中可采⽤类⽐法,初估计,再逐步修正)及运动参数。
1、做平⾯复合运动构件两者可合⼆为⼀:⼒偶等效原理 2、做平⾯移动构件 0=ε 3、绕定轴转动构件§4-3质量代换法1、静代换问题求解解决⽅法图解法(均不考虑构件的弹性变形,属于⼀般刚体运动学、动⼒学问题)解析法惯性⼒ s I a m P -= 惯性⼒矩εs J M -= 绕质⼼轴转动 0=s a 绕⾮质⼼轴转动只需考虑惯性⼒刚体⼏个集中质量使问题简化(有质量、转动惯量)(⼀般是2个)⽤于平衡调速代换代换前后总质量不变代换前后质⼼不变代换前后转动惯量不变静代换动代换任取B 、C 为代换点:解得:代换质量2、动代换问题的求解解得结论:1)静代换简单容易,其代换点B 、C 可随意选取。
2)动代换只能随意选定⼀点,另外⼀点由代换条件确定。
3)使⽤静代换,其惯性⼒偶矩将产⽣误差:()[][][]εεεεm b c k m bc I c b bc c b cb m I c m b m I M C C C B C I --=--=??+++--=?+?--=?22224)m m m C B =+ c m b m c B ?=?c b c m m B += c b b m m c +=m m m k B =+ k m b m k B ?=?c k B I k m b m =+22 (原构件转动惯量)k b k m m B += k b b m m k += B Cm I k =对于⼀般不很精确的机构,静代换使⽤较多两代换点连线必须通过质⼼§4-3⽤图解法作机构的动态静⼒分析(不考虑摩擦⼒)(达朗贝尔原理在机构⼒分析中的应⽤) 1、机构组的静定条件“未知⼒数⽬”= 平衡⽅程数⽬结论:1)求⼀个低副反⼒,需求解两个未知量,⽽⾼副则只需⼀个。
平面机构的运动分析习题和答案Word版
24.在同一构件上.任意两点的绝对加速度间的关系式中不包含哥氏加速度。- - - - ( )
25.当牵连运动为转动.相对运动是移动时.一定会产生哥氏加速度。- - - - - - - - ( )
26.在平面机构中.不与机架直接相连的构件上任一点的绝对速度均不为零。- - - ( )
27.两构件组成一般情况的高副即非纯滚动高副时.其瞬心就在高副接触点处。- - ( )
28.给定导杆机构在图示位置的速度多边形。该瞬时 和 的正确组合应是图。
29.给定图示六杆机构的加速度多边形.可得出
(A)矢量 代表 . 是顺时针方向;
(B)矢量 代表 . 是逆时针方向;
(C)矢量 代表 . 是顺时针方向;
(A)绝对速度等于零的重合点;
(B)绝对速度和相对速度都等于零的重合点;
(C)绝对速度不一定等于零但绝对速度相等或相对速度等于零的重合点。
40.下图是四种机构在某一瞬时的位置图。在图示位置哥氏加速度不为零的机构为。
41.利用相对运动图解法求图示机构中滑块2上 点的速度 的解题过程的恰当步骤和利用的矢量方程为:
9.当两构件组成转动副时.其速度瞬心在处;组成移动副时.其速度瞬心在处;组成兼有相对滚动和滑动的平面高副时.其速度瞬心在上。
10..速度瞬心是两刚体上为零的重合点。
11.铰链四杆机构共有个速度瞬心.其中个是绝对瞬心.个是相对瞬心。
12.速度影像的相似原理只能应用于的各点.而不能应用于机构的的各点。
13.作相对运动的3个构件的3个瞬心必。
14.当两构件组成转动副时.其瞬心就是。
15.在摆动导杆机构中.当导杆和滑块的相对运动为动.牵连运动为动时.两构件的重合点之间将有哥氏加速度。哥氏加速度的大小为;方向与的方向一致。
第4讲 第4章 平面机构的力分析

§ 4-3 运动副中摩擦力的确定
1、移动副中的摩擦
(2)总反力方向的确定
总反力:运动副中的法向反力 (正压力)和 切向反力(摩擦力)的合力称为运动副中的 总反力。
摩擦角:总反力与法向反力之间的夹角 φ 称为摩擦角。即:φ = arctan f 总反力方向的确定方法:
§ 4-3 运动副中摩擦力的确定
3、平面高副中的摩擦
平面高副两元素之间的相对
t
Mf FR21 Ff21
运动通常是滚动兼滑动,故有滚 动摩擦力和滑动摩擦力;因滚动
摩擦力一般较小,机构力分析时
n FN21
12
通常只考虑滑动摩擦力。
总反力方向的确定方法: n
1 2
v12 t
① 总反力与法向反力偏斜一角度 (摩擦角);
d2
M
F
§ 4-3 运动副中摩擦力的确定
4、螺旋副中的摩擦 1)矩形螺纹
拧紧螺母——螺母在力矩 M 和轴向载荷 G 的
d2
M
F ) 联合作用下,逆着 G 等速向上运动 ( 正行程 ) 。 F G tan( M Gd2 tan( ) / 2 F -拧紧螺母时施加在螺纹中径处的圆周力
有效(工作)阻力----机械在生产过程中为了改变工 作物的外形、位置或状态所受到的阻力,克服了阻 力就完成了有效的工作。如车削阻力、起重力等。 有害(工作)阻力----机械运转过程受到的非生产阻 力,克服了这类阻力所作的功纯粹是浪费能量。如 摩擦力、介质阻力等。
§ 4-1 机构力分析的任务、目的与方法
FN21
Ff21 = fv G fv = (1 ~ /2) f
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 平面机构的力分析解答典型例题解析例4-1 图4-1所示以锁紧机构,已知各部分尺寸和接触面的摩擦系数f ,转动副的摩擦圆图上虚线圆,在P 力作用下工作面上产生夹紧力Q,试画此时各运动副中的总反力作用线位置和方向(不考虑各构件的质量和转动惯量) 。
图4-1 解[解答] (1) BC 杆是二力杆,由外载荷P 和Q 判断受压,总反力23R F 和43R F 的位置和方向见图。
(2) 楔块4所受高副移动副转动副的三个总反力相平衡,其位置方向及矢量见图。
(3) 杆2也是三力杆,所受的外力P 与A,B 转动副反力相平衡,三个力的位置见图。
例4-2 图示摇块机构,已知,90=∠ABC 曲柄长度,86,200,1002mm l mm l mm l BS AC AB ===连杆的质量,22kg m =连杆对其质心轴的转动惯量22.0074.0m kg J S =,曲柄等角速转动s rad /401=ω, 求连杆的总惯性力及其作用线。
[解答] (1) 速度分析,/41s m l v AB B ==ω其方向垂直于AB 且为顺时针方向 32322C C C B C B C +=+= 大小: s m /4 0 0 ? 方向: AB ⊥ BC取mmsm v /2.0=μ作速度图如(b ),得 02232===B C B C l v ωω(2)加速度分析,/160221s m l a AB B ==ω其方向由B 指向A 。
32323t C2B n C2B 2 C C rC C k C B C ++=++=大小: 160 0 ? 0 0 ? 方向:A B → B C →2 BC ⊥ BC ⊥BC取mms m a 2/8=μ作加速度图如图(C)222/80s m s p a a s =''=μ 2222/100s m C C a a B C t ='''=μ 222222/76.923160s rad l l l a ABAC B C tBC =-==α,逆时针方向。
(3)计算惯性力,惯性力矩N a m F S I 160222=-=,方向如图( )所示。
m N J M S I .836.6222-=-=α,方向为顺时针方向。
例4-3 在图示的摆动凸轮机构中,已知作用于摆杆3上的外载荷Q,各转动副的轴颈半径r 和当量摩擦系数v f ,C 点的滑动摩擦因素f 以及机构的各部分尺寸。
主动件凸轮2的转向如图,试求图示位置时作用于凸轮2上的驱动力矩M 。
[解答] (1)首先画出,23R F 它与C 点法线成 ϕ角(f arctan =ϕ),偏在法线左侧;23R F 与Q 交于一点,31ω为顺时针,23R F 为顺时针, 13R F 切于摩擦圆(摩擦圆半径ρρv f =)与23R F Q 交于同一点,且对B 点形成力矩与32ω反向,所以13R F 与摩擦圆的切点在B 点左边;画13R F 23R F Q 的力矢量封闭多边形,求出23R F 。
(2) 在C 点处画32R F ,它与23R F 大小相等方向相反, 12R F 切于摩擦圆下方。
(3) 驱动力矩M 等于12R F 与32R F 形成力偶, 32R F 与12R F 距离为l ,则l F M R 21=。
例4-3 在图所示的颚式破碎机中,已知各构件的尺寸重力及其对本身质心轴的转动惯量,以及矿石加于活动颚板2上的压力r F ,设构件1以等角速度1ω转动,方向如图,其重力可忽略不计,求作用在其上点E 沿已知方向xx 的平衡力b F 以及各运动副中的反力。
[解答] (1) 作机构的运动简图速度多边形及加速度多边形用机构比例尺l μ 速度比例尺v μ 加速度比例尺a v 作图如(a)(b)(c) 。
(2)确定各构件的惯性力惯性力偶a G s I I s p gFa m F F μ222222''-=-==' BC a S BC tCBS S I l c n J l a J J M μα''-=-=-=222222 222I I I F Mh =a G s I I s p gFa m F F μ333333''-=-==' CDa S CD t CS S I l c n J l a J J M μα''-=-=-=323333 332I I I F M h =(4) 确定运动副反力及平衡力1) 取杆组2 3作力图如图(d) 2) 列出静力平衡方程式0434*******12=++'++++'++tn I G G r I t n F F? ? ? ? 3) 借助于力矩方程求解,考虑构件3的平衡及考虑构件2的平衡,0=∑C M 0433343=-'-CD t R I G l F h F h F 解出t R F 43的大小 ,0=∑C M 0121222=-'-+BC t R I r r G l F h F h F h F 解出t R F 12的大小4) 取力比例尺F μ作力图, 如(e)图F R R jb F F μ=-=1212 F R R gj F F μ=-=3443 5) 取曲柄1作力图如(f )图04121=++R R b6)取力比例尺F μ作力图, 如(g)图F R R bc F F μ=-=1441 F b ca P μ= 方向如图示第4章 习题解答4-13题[解答]以曲柄滑块机构的第一位置(a )为例分析(属于考虑轴颈摩擦的受力分析)(1)取2构件为研究对象,当角速度1ω为顺时针转动时,观察转动副A 处构件2相对1之间的夹角在逐渐减少,故相对角速度21ω沿顺时针方向,再观察转动副B 处构件2相对于3之间的夹角在逐渐增大,故相对角速度23ω沿顺时针方向;(2)根据外载荷M 和F 的方向,判断二力杆2是受压;(3)根据全反力12R F 衡于摩擦圆相切,而且全反力12R F 对A 点取矩是企图阻止角速度21ω的转动的,故12R F 切于摩擦圆的下方;全反力32R F 对B 点取矩是企图阻止23ω的转动的,故32R F 切于摩擦圆的上方。
由于构件2受12R F 和32R F 作用下任处于平衡,即两力的作用线应共线。
即作用线应同时切于A 处摩擦圆的下方和B 处摩擦圆的上方,画出力图如图(a )示。
其余两位置分析步骤类似(略)。
(同学们只画出力图就行了,分析过程不用写出) 4-14题[解答]4-8题[解答](1)作机构运动简图取尺寸比例尺,/005.0mm m l =μ准确的作出机构运动简图,如图(a)所示。
(2)对机构进行运动分析s rad n /1.15760/1500260/211=⨯==ππω s m s m l v AB B /7.15/1.01.1571=⨯==ωs m s m l a AB B /0.2468/1.0)1.157(221=⨯==ω构件2上B 、C 两点间的运动关系为 CB B C v v v += 大小: ? AB l 1ω ? 方向: AC AB ⊥ BC ⊥取速度比例尺,/)/(1mm s m v =μ作速度如图(b )所示。
s rad l bc l v AB v BC CB /3.3333.01112=⨯===μω τCB nCB a a a a B C ++= 大小: ? AB l 21ω AB l 21ω ? 方向: AC A B → B C → BC ⊥ 2222/9.365/33.0)3.33(s m s m l a BC nCB =⨯==ω取加速度比例尺,/)/(59.362mm s m a =μ作加速度如图(c )所示。
s m s m c p a a C /73.1719/4759.36=⨯=''=μ 其p '方向由c '指向。
根据加速度影响原理求点2s ',于是得 222/63.2085/5759.36s m s m s p a a S =⨯=''=μ 其p '方向由2s '指向。
(3)求构件的惯性力 活塞的惯性力 N a g G a m F C C IC 1.368573.17198.92133=⨯-=-=-= 方向与C a 相反。
连杆的总惯性力N a g G a m F F S S I I 5.532563.20858.925222222=⨯-=-=-==' 连杆的惯性力矩 BCaS BC CB S S I l c b J l a J J M ''⨯-=⨯-=-=ματ22222其方向与2α相反。
总惯性力与质心处的偏矩 222I II F M h =4-19题[解答](1)取构件2为分离体作力图,如图(b )。
(不考虑摩擦),0)(2=∑F M O 0212212=+'--h F h F l F r I CO R221212CO r I R l h F h F F -'=根据构件2的力平衡条件,得032212=+++R r I R F F F F方程中仅有32R F的大小与方向未知,故可用作图法求解。
取合适的力比例尺,作力多边形如图(c )。
da F F R μ=32 其方向由d 指向a 。
(2)取构件1作力图,如图(d ) 根据构件2的力平衡条件,得031121=+'+R I R F F F方程中仅有31R F的大小与方向未知,故可用作图法求解。
取合适的力比例尺,作力多边形如图(e )。
da F F R μ=31 其方向由d 指向a 根据,0)(1=∑F M O 可得321h F M R b = 方向为顺时针(注:可编辑下载,若有不当之处,请指正,谢谢!)。
