(整理)事业单位考试:资料分析之比重与增长率的关系.
事业单位考试:资料分析之比重与增长率的关系word资料5页

事业单位考试:资料分析之比重与增长率的关系在资料分析中,比重是一个很重要的概念,其中有一个重点的知识点是:当部分的增长率大于整体的增长率时,部分的比重上升;当部分的增长率小于整体的增长率时,部分的比重下降。
运用比重与增长率关系的这一知识点,可以让我们在解答某些有关比重的问题时,不必计算而直接通过知识点的运用,推导出结果。
首先我们先来分析一下这个知识点的内容。
【分析】为了更好的让大家理解,我们举一个简单的例子。
比如说一个班里的人总共有1000元钱,其中你有100元钱,这时你的钱数在全班的比重为10%(比重=部分/整体)。
现在全班的钱数增加到2019元,增长率为100%,你的钱增加到150元,增长率为50%。
现在你的钱数占全班钱数的比重为7.5%。
相比之前的10%,现在在整体所占的比重下降了。
同时全班钱数的增长率100%也大于你钱数的增长率50%。
这符合了我们知识点中的——部分的增长率小于整体的增长率时,部分的比重下降;下面我们换一种情况,再来看一下。
最初还是全班有1000元,你有100元,你的钱数占全班钱数的比重为10%,之后全班的钱数增加到1500元,增长率为50%,你的钱数增加到200元,增长率为100%,现在你的钱数占全班钱数的比重就变为13.3%。
相比之前的10%,现在你的钱数在整体所占的比重上升了,同时,全班钱数的增长率50%也小于你钱数的增长率100%。
这也符合了我们知识点中的——当部分的增长率大于整体的增长率时,部分的比重上升。
通过上面简单的例子,让我们比较真切的认识了比重与增长率的关系这一知识点的内容,现在就来具体说一下,怎么样运用这一知识点去解题,以及运用这样的方法去解题的优势和便捷性。
真题回顾全国2019年认定登记的技术合同共计220868项,同比增长7%;总成交金额2226亿元,同比增长22.44%;平均每项技术合同成交金额突破百万元大关,达到100.78万元。
2019年全国共签订技术开发合同73320项,成交金额876亿元,分别比上年增长了13.5%和22.2%;共签订技术转让合同11474项,成交金额420亿元,成交金额同比增长30.8%;技术服务和技术咨询合同成交金额分别为840亿元和90亿元,分别比上年增长了20.9%和5.9%。
资料分析笔记

增长率的四个数据:上期、本期、增长量、增长率增长率 上期=本期-量=率本期+1 本期=上期+量=上期*(1+率) 增长量=本期-上期=上期*率=率率本期*1+ 增长率=上期增长量=1-上本比重: 比重=总量分量分量=总量*比重 总量=比重分量倍数关系:A 指标是B 指标的几倍? A/BA 指标比B 指标增长了几倍,相当于A 是B 的率+1倍 A/B-1=增长率/平均数:平均值=总量/总数 总数=总量/平均值 总量=总数*平均值首先要将上述四种关系吃透,知道它的变化规律,再此基础上学习并掌握几个关系串联的知识点,比重、倍数、平均数综合起来就是这个公式:本期值=BA分母分子所以做题时经常会出现这三种情况:一、已知本期分子/分母, 分子增长率,分母增长率,求上期分子/分母简化后为:子率母率母子++11* 比较上期值时 不一定要全部计算出来,只要看母率和子率的大小了,如果母率>子率,那么这个式子比本期值大,说明上期比本期值大一般问法有:倍数错误!未定义书签。
:已知本期A ,增长率a 。
B ,增长率b ,求上期的A 是B 的几倍。
平均数:已知本期总量A ,增长率a 。
总数B ,增长率b ,求上期平均数 比重:已知本期分量A ,增长率a ,总量B ,增长率b ,求上期比重。
二、根据本期分子/分母,分子增长率,分母增长率,求本期母子与上期母子的增长量简化公式)子率母率(母子++-111*倍数错误!未定义书签。
:已知本期A ,增长率a 。
B ,增长率b ,本期A/B 比上期多多少?。
平均数:已知本期总量A ,增长率a 。
总数B ,增长率b ,求两期平均数的增长量比重:已知本期分量A ,增长率a ,总量B ,增长率b ,求本期比重与上期比重差几个百分点。
三、已知本期分子/分母, 分子增长率,分母增长率,本期母子的值与上期母子的值增长率111-++母率子率倍数错误!未定义书签。
:已知本期指标A ,增长率a 。
(完整版)行测之资料分析以及常用数字

行测之资料分析常用公式以及常用数字● 增长、比重、平均量➢ 增长量=增长率增长率增长后⨯+1 ➢ 增长率=1--增长前增长后增长前增长前增长后= ➢ 年均增长量=年份差年初年末- ➢ 年均增长率=年初(1+x%(增长率))n(年份差)➢ x%(增长率)=1-)(n a b (年初)年末 【注】当x%<5%时, x%=n a b 1- ➢ 隔年增长率=(1+x%)(1+y%)-1➢ 比重=%100⨯整体部分 ➢ 部分=比重×整体➢ 整体=比重部分 ➢ 比重差=%1%%x y x B A +-⨯(整体增长率)(部分增长率)(整体)(部分) 【注】部分增长率>整体增长率 比重↑,部分增长率<整体增长率 比重↓➢ 上年平均量=%1%1x y B A ++⨯(x%为总量增长率,y%分数增长率) ➢ 平均量增长率=%1%%x y x +- (x%为总量增长率,y%分数增长率)常见分数以及平方,根号21=0.5; 31=0.33; 41=0.25; 51=0.2; 61=0.167; 71=0.143; 81=0.125; 91=0.11; 101=0.1; 111=0.09; 43=0.75;83=0.375; 85=0.625; 87=0.87512=1;22=4;32=9;42=16;52=25;62=36;72=49;82=64;92=81;102=100;112=121;122=144;132=169;142=196;152=225;162=256;172=289;182=324;192=361;202=400;6=2.449;7=2.646;8=2.828;9=3;10=3.162;小常识 ✧ 1公顷=15亩 1吨=1000公斤 ✧ 相似比2=面积比✧ V 球=34πr 3✧ V 锥=31sh。
比重增长率题型

比重增长率题型比重增长率题型是在统计学和经济学中常见的一种题型。
它用于计算某个变量在不同时间段或不同组别之间的增长情况。
比重增长率可以帮助我们分析和理解不同变量的变化趋势,并且可以用于比较不同变量之间的增长速度。
比重增长率的计算公式如下:比重增长率=(后一期的比重前一期的比重)/前一期的比重*100其中,比重可以是某个变量在总量中的占比,也可以是某个变量在不同组别中的占比。
比重增长率题型通常有以下几种形式:1.根据给定的数据,计算比重增长率。
例如,某公司在2018年和2019年的销售额分别为100万和120万,求销售额的增长率。
解:首先计算比重增长率的分子和分母,分别是后一期的销售额减去前一期的销售额,再除以前一期的销售额,然后乘以100。
比重增长率=(120100)/100*100=20%2.根据给定的数据,求一个变量在总量中的占比的增长率。
例如,某城市在2010年和2020年的人口分别是100万和150万,求人口的比重增长率。
解:首先计算比重增长率的分子和分母,分别是后一期的人口减去前一期的人口,再除以前一期的人口,然后乘以100。
比重增长率=(150100)/100*100=50%3.根据给定的数据,比较不同组别之间的变化情况。
例如,某商品在2018年和2019年的销售额分别为100万和120万,其中A市场的销售额为50万,B市场的销售额为70万,求A市场和B市场的比重增长率,并比较两个市场的增长速度。
解:首先计算A市场和B市场的比重增长率,分别是后一期的销售额减去前一期的销售额,再除以前一期的销售额,然后乘以100。
A市场的比重增长率=(7050)/50*100=40%B市场的比重增长率=(7050)/50*100=40%可见,A市场和B市场的比重增长率相同,说明两个市场的增长速度相似。
通过上述例子可以看出,比重增长率题型涉及到计算和比较不同变量的增长情况,需要注意计算公式的运用和数据的理解。
VIP快速解决资料分析之比重比较问题
快速解决资料分析之比重比较问题近两年公务员考试行测的资料分析比较复杂的选项会涉及一个考点就是两个基期量之间的除法式子和现期量除法式子之间的比较。
今年现期量分别是A、B,各自的增长率分别是a%,b%,然后问去年两者之间的倍数关系或者几分之几,所占比重等等。
去年比重列式如下:或者。
这类题目大家不要直接去求去年两个量的大小,再去比较,这样计算量明显很大。
遇到这类题目大家记得直接比较增长率的大小关系即可:若A的增长率>B 的增长率,则比重上升。
总结:上期B,增长率b%,现期A,增长率a%,和上期比重比较,B/A*(b%-a%)/(1+b%), 则部分增长率大于整体增长率,比重增加,增加值小于b%-a% 。
下面就以2011年国家公务员考试真题为例,进行方法讲解:一、根据以下资料,回答101~105题。
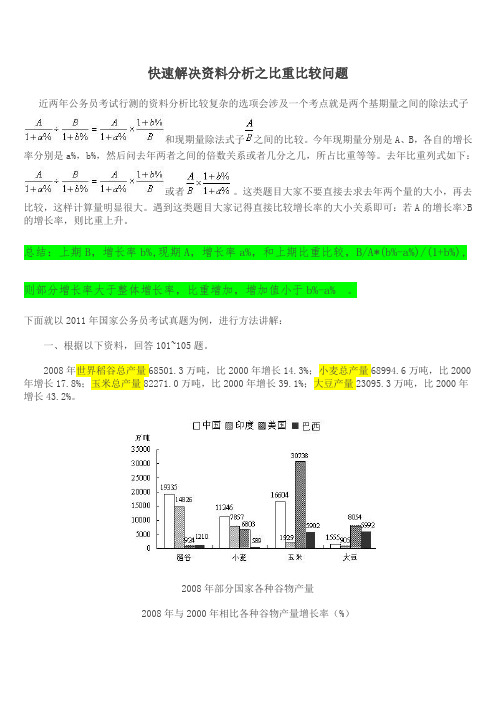
2008年世界稻谷总产量68501.3万吨,比2000年增长14.3%;小麦总产量68994.6万吨,比2000年增长17.8%;玉米总产量82271.0万吨,比2000年增长39.1%;大豆产量23095.3万吨,比2000年增长43.2%。
2008年部分国家各种谷物产量2008年与2000年相比各种谷物产量增长率(%)国家稻谷小麦玉米大豆中国 1.912.956.40.9印度16.3 2.960.271.4美国 6.712.022.07.3巴西9.1254.285.183.0 125、能够从上述资料中推出的是:A、2008年,美国是世界最大的大豆产地;B、2008年,巴西玉米产量占世界总产量的比重比2000年略有下降;C、与2000年相比,2008年中国小麦增产900多亿吨;D、2008年,印度稻谷产量是其小麦产量的2倍以上。
解析:B选项中就是比较2008年比重和2000年比重的大小关系,材料中巴西玉米产量的增长率是85.1%,世界玉米的增长率39.1%,所以比重上升,B错误。
三、根据以下资料,回答111~115题。
2019江西省考行测资料分析:比重难题

2019江西省考行测资料分析:比重难题我们在做题的过程中经常会遇到这样的题目:比重与上年相比上升了或者下降了?例:2017年1~2月,全国完工出口船907万载重吨,同比增长127%;承接出口船订单191万载重吨,同比增长122%。
2月末,手持出口船订单8406万载重吨,同比下降25.9%。
2017年1~2月,重点企业完工出口船886万载重吨,同比增长138%;承接出口船订单171万载重吨,同比增长109%。
2月末,手持出口船订单8129万载重吨,同比下降26.6%。
判断正误:2017年2月末,重点企业手持出口船订单占全国比重低于上年同期。
这就是一道简单的判断比重变化的题目,,这类题目往往只需要简单的观察就能较快的判断出结果。
(通常已知部分A、整体B,以及部分增长率qA、整体增长率qB)求现期比重与去年的比重(基期比重)比较上升了还是下降了,即只需将现期比重与基期比重作差,若结果大于零说明现期比重比基期比重大,比重上升了;相反若结果小于零则代表比重下降了;若作差结果等于零说明比重相等即比重没有变化。
具体的判断过程如下:一般部分/整体和(1+部分增长率)都为正值,因此判断式子结果的正负只需比较部分增长率与整体增长率的关系即可。
判断比重变化部分增长率>整体增长率,结果大于零,现期比重大于基期比重即比重上升;部分增长率<整体增长率,结果小于零,现期比重小于基期比重即比重下降;部分增长率=整体增长率,结果等于零,现期比重等于基期比重即比重不变。
结合上面的例题,部分的增长率即为重点企业手持出口船订单的增长率-26.6%,整体的增长率即为全国企业手持出口船订单的增长率-25.9%。
即部分增长率小于整体增长率,则比重低于上年同期,此题正确。
行测“利润问题”解法四重奏:利润问题早已成国家公务员考试行测中重点题型,一般考生做题常采用方程法、特值法求解,往往不求甚解,分析不透彻,经常将数学题和资料分析进行割裂考虑,不能很好地统一,那么今天中公教育专家给大家带来的这道题有助于大家形成多角度解题这一思维,提高数学的思维能力。
公考资料分析秒杀技之比重增长率公式

公考资料分析秒杀技之比重增长率公式在公考资料分析中,比重增长率是一个非常重要的概念,它的计算方法和公式对于解题有着至关重要的影响。
下面就为大家详细介绍比重增长率的公式及其应用技巧。
一、比重增长率的基本公式比重增长率是指一个量A与另一个量B的比值(即A/B)的增长率。
通常情况下,我们用符号r表示比重增长率,其基本公式可以表示为:r = (A/B) – 1其中,A和B分别表示两个相关的量,r则表示这两个量之间的增长率。
二、比重增长率的实际应用比重增长率在公考资料分析中有着广泛的应用,例如在经济类、科技类、资源类等材料中经常会出现比较类题目,这时候就需要用到比重增长率。
下面我们就通过一个实际的例子来了解其应用。
【例】某地区2016年GDP为200亿元,2017年GDP为220亿元。
根据题目所给数据,我们可以计算出2017年GDP的比重增长率:r = (220/200) – 1 = 10%所以,2017年该地区的GDP相对于2016年的增长率为10%。
三、比重增长率的变形公式通常情况下,比重增长率的公式都是直接计算两个量的比值再减去1。
但在一些特殊情况下,我们可以使用一些变形公式来简化计算。
比如:变形公式1:若r = A/(1+p)B = p*B(p为增长率)此公式适用于两个量都增长的情况,其中A和B的增长率相同。
例如:某市2017年GDP为100亿元,增长率为5%,则2018年GDP为:r = 1+5% = 1.05变形公式2:若r = (A+p)/(B+p) = A/B + A*p/B + p - A/B(p为增长率)此公式适用于其中一个量增长,另一个量不变的情况。
例如:某公司2017年销售额为100万元,增长率为5%,则2018年销售额为:r = 1+5% = 1.05A/B = 1(不变)p = 5% = 0.05(增长率)所以,2018年销售额为:1.05+1×0.05+0.05=1.15(万元)变形公式3:若r = (A q)/(B q) = A/B + A*q/B + q - A/B(q为增长率)此公式适用于两个量都增长的情况,其中A和B的增长率不同。
2024公考行测资料分析重点题型

2024公考行测资料分析重点题型在公务员考试行政能力测验(简称行测)中,资料分析是一个重要的模块,对于考生取得理想成绩起着关键作用。
资料分析主要考查考生对各种形式的数据资料进行综合理解与分析加工的能力。
在这个模块中,有一些重点题型需要我们特别关注和掌握。
首先,增长率相关的题型是必考且重点的。
增长率的计算和比较是常见的考查形式。
增长率的计算,一般会给出现期量和基期量,我们需要通过公式“增长率=(现期量基期量)÷基期量×100%”来得出结果。
而增长率的比较,可能会给出多个数据,让我们判断增长速度的快慢。
这时候需要我们灵活运用计算技巧,比如先观察现期量和基期量的倍数关系,如果倍数关系明显,直接通过倍数大小来判断增长率的大小;如果不明显,再进行具体的计算。
其次,比重问题也是高频考点。
比重的定义是部分在整体中所占的百分比。
在题目中,可能会让我们计算现期比重、基期比重,或者判断比重的变化趋势。
计算现期比重相对简单,直接用部分值除以整体值即可。
基期比重的计算则需要先计算出基期的部分值和整体值,再进行相除。
对于比重的变化趋势,我们可以通过比较部分增长率和整体增长率的大小来判断,如果部分增长率大于整体增长率,比重上升;反之则下降。
再者,平均数的计算和比较也是常考题型。
平均数的计算要明确总数和个数,然后相除得出结果。
平均数的增长率也是一个重要的考点,需要我们掌握其计算公式“平均数增长率=(现期平均数基期平均数)÷基期平均数× 100% =(总量增长率份数增长率)÷(1 +份数增长率)”。
在比较平均数时,同样要注意观察数据特点,选择合适的方法进行比较。
另外,倍数问题也不容忽视。
倍数可以分为现期倍数和基期倍数。
现期倍数直接用两个量相除即可,基期倍数则需要先计算出基期量再进行相除。
在解决资料分析重点题型时,我们还需要掌握一些实用的技巧和方法。
首先是快速阅读材料,抓住关键信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
事业单位考试:资料分析之比重与增长率的关系在资料分析中,比重是一个很重要的概念,其中有一个重点的知识点是:当部分的增长率大于整体的增长率时,部分的比重上升;当部分的增长率小于整体的增长率时,部分的比重下降。
运用比重与增长率关系的这一知识点,可以让我们在解答某些有关比重的问题时,不必计算而直接通过知识点的运用,推导出结果。
首先我们先来分析一下这个知识点的内容。
【分析】为了更好的让大家理解,我们举一个简单的例子。
比如说一个班里的人总共有1000元钱,其中你有100元钱,这时你的钱数在全班的比重为10%(比重=部分/整体)。
现在全班的钱数增加到2000元,增长率为100%,你的钱增加到150元,增长率为50%。
现在你的钱数占全班钱数的比重为7.5%。
相比之前的10%,现在在整体所占的比重下降了。
同时全班钱数的增长率100%也大于你钱数的增长率50%。
这符合了我们知识点中的——部分的增长率小于整体的增长率时,部分的比重下降;
下面我们换一种情况,再来看一下。
最初还是全班有1000元,你有100元,你的钱数占全班钱数的比重为10%,之后全班的钱数增加到1500元,增长率为50%,你的钱数增加到200元,增长率为100%,现在你的钱数占全班钱数的比重就变为13.3%。
相比之前的10%,现在你的钱数在整体所占的比重上升了,同时,全班钱数的增长率50%也小于你钱数的增长率100%。
这也符合了我们知识点中的——当部分的增长率大于整体的增长率时,部分的比重上升。
通过上面简单的例子,让我们比较真切的认识了比重与增长率的关系这一知识点的内容,现在就来具体说一下,怎么样运用这一知识点去解题,以及运用这样的方法去解题的优势和便捷性。
真题回顾
全国2007年认定登记的技术合同共计220868项,同比增长7%;总成交金额2226亿元,同比增长22.44%;平均每项技术合同成交金额突破百万元大关,达到100.78万元。
2007年全国共签订技术开发合同73320项,成交金额876亿元,分别比上年增长了13.5%和22.2%;共签订技术转让合同11474项,成交金额420亿元,成交金额同比增长30.8%;技术服务和技术咨询合同成交金额分别为840亿元和90亿元,分别比上年增长了20.9%和5.9%。
问:下列关于2006年技术开发、技术转让、技术咨询和技术服务四类合同占全国成交金额比重的图形,描述正确的是()
【解析】该题是典型的考察比重的问题,资料中所给的信息都是2007年的,而题干问题所问的却是2006年。
正常的思路应该是,通过资料中的各项数据,分别计算出全国技术合同成交金额2006年的总量以及技术开发、技术咨询、技术转让、技术服务在2006年的实际金额量,最后通过部分/整体的方式算出各个项目的比重,最后根据计算结果去判断选项。
技术咨询的增长率5.9%小于总体的增长率22.44%,则2006年技术咨询的比重一定大于2007年技术咨询的比重(4%),由此直接判断出B为正确选项。
由上述的推导过程,我们可以体会出运用好比重和增长率的关系,可以让我们在解决一些比重的问题时,免于计算的枯燥,而通过合理的推断,就能迅速准确的找出答案。
