2020年中考数学专项总复习——四边形考试测试卷(无答案)
四川省渠县崇德实验学校2020年中考第二轮九年级数学三角形、四边形压轴题专题复习(无答案)

四川省渠县崇德实验学校2020年中考第二轮九年级数学三角形、四边形压轴题专题复习一、选择题1、如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是()A.2B.4C D.2、如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且ACBC=13,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为()A.(2,2) B.(52,52) C.(83,83) D.(3,3)3、如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=12BC,连接GM.有如下结论:①DE=AF;②AN=4AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是()A.①②B.①③C.①②③D.②③④二、填空题4、在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是______5、如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走个小立方块.6、如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①EO⊥AC;②S△AOD=4S△OCF;③AC:BD=:7;④FB2=OF•DF.其中正确的结论有(填写所有正确结论的序号)7、如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC 边上的点D(不与点A,C重合)处,折痕是EF.如图1,当CD=12AC时,tanα1=34;如图2,当CD=13AC时,tanα2=512;如图3,当CD=14AC时,tanα3=724;…依此类推,当CD=1n1+AC(n为正整数)时,tanαn=.8、在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如图所示,依次作正方形OA1B1C1,正方形C1A2B2C2,正方形C2A3B3C3,正方形C3A4B4C4,……,点A1,A2,A3,A4,……在直线l上,点C1,C2,C3,C4,……在x轴正半轴上,则前n个正方形对角线长的和是.三、解答题9、如图1,正方形ABDE和BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M,连接MD,MG,MB.(1)试证明DM⊥MG,并求MBMG的值.(2)如图2,将图1中的正方形变为菱形,设∠EAB=2α(0<α<90°),其它条件不变,问(1)中MBMG的值有变化吗?若有变化,求出该值(用含α的式子表示);若无变化,说明理由.10、【问题探究】(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.①请探究AD与BD之间的位置关系:;②若AC=BC=,DC=CE=,则线段AD的长为;【拓展延伸】(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.11、如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.(1)求证:CE=EF;(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;(3)求△BEF面积的最大值.12、在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=AM.13、如图,四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF的中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.14、已知:如图,在四边形ABCD中,AB∥CD,∠ACB=90°,AB=10cm,BC=8cm,OD 垂直平分A C.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D 出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动,另一个点也停止运动.过点P作PE⊥AB,交BC于点E,过点Q作QF∥AC,分别交AD,OD于点F,G.连接OP,EG.设运动时间为t(s)(0<t<5),解答下列问题:(1)当t为何值时,点E在∠BAC的平分线上?(2)设四边形PEGO的面积为S(cm2),求S与t的函数关系式;(3)在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大?若存在,求出t的值;若不存在,请说明理由;(4)连接OE,OQ,在运动过程中,是否存在某一时刻t,使OE⊥OQ?若存在,求出t的值;若不存在,请说明理由.15、如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD 沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.(1)求线段CE的长;(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.①写出y关于x的函数解析式,并求出y的最小值;②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.16、如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=6,AD=3,求△PDE的面积.17、如图1,菱形AEGH的顶点E、H在菱形ABCD的边上,且∠BAD=60°,请直接写出HD:GC:EB的结果(不必写计算过程)(2)将图1中的菱形AEGH绕点A旋转一定角度,如图2,求HD:GC:EB;(3)把图2中的菱形都换成矩形,如图3,且AD:AB=AH:AE=1:2,此时HD:GC:EB 的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.18、问题提出:如图,图①是一张由三个边长为1的小正方形组成的“L”形纸片,图②是一张a×b的方格纸(a×b的方格纸指边长分别为a,b的矩形,被分成a×b个边长为1的小正方形,其中a≥2,b≥2,且a,b为正整数).把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.探究一:把图①放置在2×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图③,对于2×2的方格纸,要用图①盖住其中的三个小正方形,显然有4种不同的放置方法.探究二:把图①放置在3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图④,在3×2的方格纸中,共可以找到2个位置不同的2 2×方格,依据探究一的结论可知,把图①放置在3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有2×4=8种不同的放置方法.探究三:把图①放置在a×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑤,在a×2的方格纸中,共可以找到个位置不同的2×2方格,依据探究一的结论可知,把图①放置在a×2的方格纸中,使它恰好盖住其中的三个小正方形,共有种不同的放置方法.探究四:把图①放置在a×3的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑥,在a×3的方格纸中,共可以找到个位置不同的2×2方格,依据探究一的结论可知,把图①放置在a×3的方格纸中,使它恰好盖住其中的三个小正方形,共有种不同的放置方法.……问题解决:把图①放置在a×b的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.)问题拓展:如图,图⑦是一个由4个棱长为1的小立方体构成的几何体,图⑧是一个长、宽、高分别为a,b,c(a≥2,b≥2,c≥2,且a,b,c是正整数)的长方体,被分成了a×b×c个棱长为1的小立方体.在图⑧的不同位置共可以找到个图⑦这样的几何体.19、如图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.(1)当MN∥B′D′时,求α的大小.(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.20、如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.(1)如图1,点E在线段AB上时,①求证:AE=CF;②求证:DP垂直平分EF;(2)当AE=1时,求PQ的长.。
四川省内江市第五中学2020年中考九年级数学四边形综合压轴大题备考复习(无答案)

四川省内江市第五中学2020年中考九年级数学四边形综合压轴大题备考复习1、如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.【探究展示】(1)证明:AM=AD+MC;(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.【拓展延伸】(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.2、如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC 于点G.(1)若M为边AD中点,求证△EFG是等腰三角形;(2)若点G与点C重合,求线段MG的长;(3)请用含a的代数式表示△EFG的面积S,并指出S的最小整数值.3、如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.(1)求证:AE⊥BF;(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP到BA的延长线于点Q,求sin∠BQP 的值;(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.4、【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;请运用上述解答中所积累的经验和方法完成下列两题:【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P 为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=2dm,AD=3dm,BD=dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.5、猜想与证明:如图1摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD 上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.拓展与延伸:(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为.(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.6、如图,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O 出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造▱PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在一,四象限,在运动过程中,设▱PCOD的面积为S.①当点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.7、已知,如图1,矩形ABCD中,AD=6,DC=8,矩形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.(1)如图2,当四边形EFGH为正方形时,求CF的长和△FCG的面积;(2)如图1,设AE=x,三角形FCG的面积=y,求与x之间的函数关系式与y的最大值;(3)当△CGF是直角三角形时,求x和y值.8、如图1,点P为四边形ABCD所在平面上的点,如果∠PAD=∠PBC,则称点P为四边形ABCD 关于A、B的等角点,以点C为坐标原点,BC所在直线为x轴建立平面直角坐标系,点B的横坐标为﹣6.9、如图,已知正方形ABCD的边长为4,点E、F分别从C、A两点同时出发,以相同的速度作直线运动.已知点E沿射线CB运动,点F沿边BA的延长线运动,连结DF、DE、EF,EF 与对角线AC所在的直线交于点M,DE交AC于点N.(1)求证:DE⊥DF;(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式,并写出自变量的取值范围;(3)随着点E在射线CB上运动,NA•MC的值是否会发生变化?若不变,请求出NA•MC的值;若变化,请说明理由.10、在△ABC中,已知BA=BC,点P在边AB上,联结CP,以PA、PC为邻边作平行四边形APCD,AC与PD交于点E,∠ABC=∠AEP=α(0°<α<90°).(1)如图(1),求证:∠EAP=∠EPA;(2)如图(2),若点F是BC中点,点M、N分别在PA、FP延长线上,且∠MEN=∠AEP,判断EM和EN之间的数量关系,并说明理由.(3)如图(3),若DC=1,CP=3,在线段CP上任取一点Q,联结DQ,将△DCQ沿直线DQ 翻折,点C落在四边形APCD外的点C′处,设CQ=x,△DC′Q与四边形APCD重合部分的面积为y,写出y与x的函数关系式及定义域.11、将矩形纸片ABCD放在平面直角坐标系中,点A在y轴正半轴上,点B与点O重合(O为原点),点C在x轴正半轴上.若将矩形纸片折叠,使B落在边AD(含端点)上,落点记为E,这时折痕与边BC或者边CD(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF 称为矩形ABCD的“折痕三角形”.(Ⅰ)如图(1),根据“折痕三角形”的定义请你判断矩形ABCD的任意一个“折痕△BEF”的形状(不需要证明);(Ⅱ)如图(2),在矩形ABCD中,AB=2,BC=4,当它的“折痕△BEF”的顶点E位于AD的中点时,画出这个“折痕△BEF”,并求出点F的坐标;(Ⅲ)如图(3),在矩形ABCD中,AB=2,BC=4.该矩形是否存在面积最大的“折痕△BEF”?若存在,说明理由,并求出此时点E的坐标;若不存在,也请你说明理由.12、如图,在直角梯形ABCD中,CD⊥AD,BC∥AD,AD=AB=10cm,BC=4cm.点P自点D 出发以每秒1cm的速度沿DA向点A移动,点Q自点A出发以每秒cm的速度沿AB向点B 移动,点P、Q同时出发,当点P到达点A时,点Q随之停止.设点P、Q运动的时间为t(s)(o≤t≤10).(1)求CD的长;(2)在点P、Q的运动过程中,设△PAQ的面积为y,求y与t的函数关系式;(3)在运动过程中,△PAQ的面积能否是梯形ABCD面积的?若能,求出t的值;若不能,请说明理由;(4)t为何值时,△PAQ是直角三角形.13、四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF﹣BF=EF;(2)如图2,在(1)条件下,AG=BG,求;(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE=(直接写出结果)14、如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO 绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.(1)求证:△CBG≌△CDG;(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.。
2020初中数学中考专题复习——四边形中的线段最值问题专项训练1(附答案详解)

∴BD是∠ABC的平分线,
∴E1在AB上,
由图形对称的性质可知,
BE=BE1= BC= ×4=2,
∵BE=BE1= BC,
∴△BCE1是直角三角形,
∴CE1= = = ,
∴PE+PC的最小值是 ,
故选:B
【点睛】
本题考查菱形的性质、轴对称-最短路线问题,利用了角平分线的性质和直角三角形的判定及勾股定理,掌握确定最短路线的方法是解题的关键.
【详解】
作D点关于AB的对称点D',连接CD'交AB于P,P即为所求,此时PC+PD=PC+PD'=CD',根据两点之间线段最短可知此时PC+PD最小.
作D'E⊥BC于E,则EB=D'A=AD.
∵CD=2AD,
∴DD'=CD,
∴∠DCD'=∠DD'C.
∵∠DAB=∠ABC=90°,
∴四边形ABED'是矩形,
8.如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为 时,求OA的长;
∴DD'∥EC,D'E=AB=3,
∴∠D'CE=∠DD'C,
∴∠D'CE=∠DCD'.
∵∠DCB=60°,
∴∠D'CE=30°,
∴D'C=2D'E=2AB=2×3=6,
2020年中考数学压轴题必考题型四边形问题考点专练(pdf,含解析)

∴∠DCE=45°, ∵∠CDE=90°, ∴△CDE 是等腰直角三角形, ∴CD=DE, ∵E 是 AD 的中点, ∴AD=2CD, ∵AD=BC, ∴BC=2CD. 点睛:本题主要考查了矩形的性质以及平行四边形的判定与性质,要证明两直线平行和两线段 相等、两角相等,可考虑将要证的直线、线段、角、分别置于一个四边形的对边或对角的位置 上,通过证明四边形是平行四边形达到上述目的. 【考点 3】矩形的判定与性质的应用 【例 3】(2019·内蒙古中考真题)如图,在矩形 ABCD 中, AD 8 ,对角线 AC 与 BD 相交 于点 O , AE BD ,垂足为点 E ,且 AE 平分 BAC ,则 AB 的长为_____.
【答案】(1)证明见解析;(2)BC=2CD,理由见解析. 【解析】 分析:(1)利用矩形的性质,即可判定△FAE≌△CDE,即可得到 CD=FA,再根据 CD∥AF, 即可得出四边形 ACDF 是平行四边形; (2)先判定△CDE 是等腰直角三角形,可得 CD=DE,再根据 E 是 AD 的中点,可得 AD=2CD, 依据 AD=BC,即可得到 BC=2CD. 详解:(1)∵四边形 ABCD 是矩形, ∴AB∥CD, ∴∠FAE=∠CDE, ∵E 是 AD 的中点, ∴AE=DE, 又∵∠FEA=∠CED, ∴△FAE≌△CDE, ∴CD=FA, 又∵CD∥AF, ∴四边形 ACDF 是平行四边形; (2)BC=2CD. 证明:∵CF 平分∠BCD,
【答案】 24 5
【解析】
【分析】
根据菱形面积=对角线积的一半可求 AC ,再根据勾股定理求出 BC ,然后由菱形的面积即可得
出结果.
【详解】
∵四边形 ABCD 是菱形,
∴ BO DO 4 , AO CO , AC BD ,
2020年广东省中考数学专题测试卷(五)——四边形

(1)证明:如图 1,∵四边形 ABCD 是矩形, ∴AB=DC,∠A=∠D=90°, ∵E 是 AD 的中点,∴AE=DE, ∴△BAE≌△CDE,∴BE=CE.
(2)①证明:如图 2,由(1)可知,△EBC 是等腰直角三角形, ∴∠EBC=∠ECB=45°, ∵∠ABC=∠BCD=90°,∴∠EBM=∠ECN=45°, ∵∠MEN=∠BEC=90°,∴∠BEM=∠CEN, ∵EB=EC,∴△BEM≌△CEN.
19.如图,在▱ABCD 中,E,F 分别是 AD,BC 上的点, ∠DAF=∠BCE.求证:BF=DE.
证明:∵四边形 ABCD 是平行四边形, ∴∠B=∠D,∠BAD=∠BCD,AB=CD, ∵∠DAF=∠BCE,∴∠BAF=∠DCE,
∠B=∠D
在△ABF 和△CDE 中,AB=CD
,
∠BAF=∠DCE
其中正确的是( C )
A.①③
B.②④
C.①③④ D.②③④
第 10 题图
二、填空题(本大题共 7 小题,每小题 4 分,共 28 分) 11.已知一个多边形的每一个外角都等于 72°,则这个多边形 的边数是 5 . 12.在平面直角坐标系 xOy 中,▱OABC 的三个顶点 O(0,0), A(3,0),B(4,2),则其第四个顶点的坐标是 (1,2) .
(1)证明:∵AB∥CD,∴∠OAB=∠DCA, ∵AC 是∠DAB 的平分线,∴∠OAB=∠DAC, ∴∠DCA=∠DAC,∴CD=AD=AB, ∵AB∥CD,∴四边形 ABCD 是平行四边形, ∵AD=AB,∴▱ABCD 是菱形.
(2)解:∵四边形 ABCD 是菱形,∴OA=OC,BD⊥AC, ∵CE⊥AB,∴OE=OA=OC, ∵BD=2,∴OB=12BD=1, 在 Rt△AOB 中,AB= 5,OB=1, ∴OA= AB2-OB2=2,∴OE=OA=2.
2020年中考数学专题四边形精选试题及答案详解(28页)

2020年中考数学专题四边形精选试题满分:100分时间:100分钟一.选择题(每小题3分,共30分)1.如图,在平行四边形ABCD中,BC=8cm,CD=6cm,∠D=40°,BE平分∠ABC,下列结论错误的是()A.AE=6cm B.ED=2cm C.∠BED=150°D.∠C=140°2.在菱形ABCD中,AC是对角线,CD=CE,连结DE.AC=16,CD=10,则D E的长为()A.B.C.或D.3.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,连结OE.若OE=3,则菱形ABCD的周长是()A.6B.12C.18D.244.在平行四边形ABCD中,下列结论一定成立的是()A.AC⊥BD B.∠A+∠B=180°C.AB=AD D.∠B=∠C 5.已知菱形ABCD的对角线相交于点O,若AC=8,AB=5,则菱形的高为()A.3B.C.4D.6.如图,E是平行四边形内任一点,若S平行四边形ABCD=10,则图中阴影部分的面积是()A.3B.4C.5D.67.如图,菱形ABCD中,∠A=60°,边AB=8,E为边DA的中点,P为边CD上的一点,连接PE、PB,当PE=EB时,线段PE的长为()A.4B.8C.4D.48.如图,已知直角△ABC中,∠B=90°,AB=8,BC=6,把斜边AC分成n 段,以每段为对角线作小长方形,则所有这些小长方形的周长的和是()A.14B.28C.D.9.如图,在菱形ABCD中,DE⊥AB,AD=5,BD=4,则DE的值是()A.3B.C.4D.10.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△;④∠AHB=∠EHD.其中正确的是()CHDA.①③B.①②③④C.①②③D.①③④二.填空题(每小题3分,共30分)11.如图,矩形OABC的顶点A、C分别在坐标轴上,B(8,7),D(5,0),点P是边AB上的一点,连接OP,DP,当△ODP为等腰三角形时,点BP 的长度为.12.如图,四边形ABCD中,∠B+∠ADC=150°,∠1,∠2分别是∠BCD和∠BAD的邻补角,则∠1+∠2=.13.如图,在正方形ABCD中,AB=6,点E、F分别在CD、AD上,CE=DF,BE,CF相交于G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为.14.一个正多边形的某个外角度数是30°,那么这个正多边形有条边,每个内角度数为.15.如图,正方形ABCD的边长为2,E为射线CD上一动点(不与C重合),以CE为边向正方形ABCD外作正方形CEFG,连接DG,直线BE、DG相交于点P,连接AP,则线段AP长度的取值范围是.16.如图,用灰白两色正方形瓷砖铺设地面,第1个图案用了4块灰色的瓷砖,第2个图案用了6块灰色的瓷砖,第3个图案用了8块灰色的瓷砖,…,第n个图案中灰色瓷砖块数为.17.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,AB=2,点E为BC上任意一点(不与点B,点C重合),连接EA,以EA,EC为邻边作平行四边形EADC,连接DE,则DE的最小值为.18.如图,正方形ABCD的面积为256,点E在AD上,点F在AB的延长线上,EC⊥FC,△CEF的面积为200,则BF的长为.19.如图,正方形ABCD中,E、F分别在AB、AD上(AE<BE),DE⊥CF于G,M在CG上,且MG=DG,连BM,N是BM的中点,连结CN,若CN =8,EG=13,则CF=.20.如图,在菱形ABCD中,AB=2,∠DAB=60°,对角线AC,BD相交于点O,过点C作CE∥BD交AB的延长线于点E,连接OE,则OE长为.三.解答题(每题8分,共40分)21.如图,在平行四边形ABCD中,点E在边AD上,点F在边CB的延长线上,联结CE、EF,CE2=DE•CF.(1)求证:∠D=∠CEF;(2)联结AC,交EF于点G,如果AC平分∠ECF,求证:AC•AE=CB•CG.22.如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=2,BC=5,DC=3,点E在边BC上,tan∠AEC=3,点M是射线DC上一个动点(不与点D、C 重合),联结BM交射线AE于点N,设DM=x,AN=y.(1)求BE的长;(2)当动点M在线段DC上时,试求y与x之间的函数解析式,并写出函数的定义域;(3)当动点M运动时,直线BM与直线AE的夹角等于45°,请直接写出这时线段DM的长.23.在△ABC中,AB=AC,AM是△ABC的外角∠CAE的平分线.(1)如图1,求证:AM∥BC;(2)如图2,若D是BC中点,DN平分∠ADC交AM于点N,DQ平分∠ADB 交AM的反向延长线于Q,判断△QDN的形状并说明理由.(3)如图3,在(2)的条件下,若∠BAC=90°将∠QDN绕点D旋转一定角度,DN交边AC于F,DQ交边AB于H,当S△ABC=14时,则四边形AHDF 的面积为.24.如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.(1)求证:GD=EG.(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD 的面积.(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.25.如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F 在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.(1)试求点E的坐标(用含m,n的式子表示);(2)求证:AM=AN;(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.参考答案一.选择题1.解:∵四边形ABCD是平行四边形,∠D=50°,∴AD∥BC,AD=BC=8cm,AB=CD=6cm,∠ABC=∠D=40°,∴∠C=180°﹣∠D=140°,故D正确;∵BE平分∠ABC,∴∠ABE=∠EBC=∠ABC=20°,∴∠AEB=∠EBC=20°,∴∠BED=180°﹣∠AEB=160°,故C错误;∴∠AEB=∠ABE,∴AE=AB=6cm,故A正确;A D=BC=8cm,∴ED=AD﹣AE=2cm,故B正确.故选:C.2.解:连接BD交AC于K.∵四边形ABCD是菱形,∴AC⊥BD,AK=CK=8,在Rt△AKD中,DK===6,∵CD=CE,∴EK=CE﹣CK=10﹣8=2,在Rt△DKE中,DE==2.故选:A.3.解:∵四边形ABCD为菱形,∴AC⊥BD,AB=BC=CD=DA,∴△AOD为直角三角形.∵OE=3,且点E为线段AD的中点,∴AD=2OE=6.C菱形ABCD=4AD=4×6=24.故选:D.4.解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠A=∠C,∠B=∠D,AB∥CD,AD∥BC,AC与BD 互相平分,∴∠A+∠B=180°,故选:B.5.解:∵四边形ABCD是菱形,AC=8,AB=5,∴AC⊥BD,OA=AC=4,OB===3,∴BD=2OB=6,∵S菱形ABCD=AC•BD=BC•AE,∴×6×8=5×AE,∴AE=.故选:B.6.解:设两个阴影部分三角形的底为AD,CB,高分别为h1,h2,则h1+h2为平行四边形的高,∴S△EAD+S△ECB=AD•h1+CB•h2=AD(h1+h2)=S四边形ABCD=5.故选:C.7.解:∵四边形ABCD是菱形,∴AB=AD=8,且∠A=60°,∴△ABD是等边三角形,且点E是AD的中点,∴BE⊥AD,且∠A=60°,∴AE=4,BE=AE=4,∴PE=BE=4,故选:D.8.解:∵∠B=90°,AB=8,BC=6,且斜边AC平均分成n段,∴小矩形的长为=,宽为=,∴一个小矩形的周长为:2(+)=,∴这些小矩形的面积和是n•=28.故选:B.9.解:设AE=x,则BE=AB﹣BE=5﹣x,∵DE⊥AB,∴AD2﹣AE2=DB2﹣BE2,即:52﹣x2=42﹣(5﹣x)2,解得:x=,∴DE==,故选:B.10.解:∵四边形ABCD是正方形,E是AD边上的中点,∴AE=DE,AB=CD,∠BAD=∠CDA=90°,∴△BAE≌△CDE(SAS),∴∠ABE=∠DCE,故①正确;∵四边形ABCD是正方形,∴AD=DC,∠ADB=∠CDB=45°,DH=DH,∴△ADH≌△CDH(SAS),∴∠HAD=∠HCD,∵∠ABE=∠DCE∴∠ABE=∠HAD,∵∠BAD=∠BAH+∠DAH=90°,∴∠ABE+∠BAH=90°,∴∠AGB=180°﹣90°=90°,∴AG⊥BE,故②正确;∵AD∥BC,∴S△BDE=S△CDE,∴S△BDE﹣S△DEH=S△CDE﹣S△DEH,即;S△BHE=S△CHD,故③正确;∵△ADH≌△CDH,∴∠AHD=∠CHD,∴∠AHB=∠CHB,∵∠BHC=∠DHE,∴∠AHB=∠EHD,故④正确;故选:B.二.填空题(共10小题)11.解:∵四边形OABC是矩形,B(8,7),∴OA=BC=8,OC=AB=7,∵D(5,0),∴OD=5,∵点P是边AB的一点,∴OD=DP=5,∵AD=3,∴P A==4,∴PB=3故答案为:3.12.解:∵∠B+∠ADC+∠DAB+∠DCB=360°∠DAB+∠DCB+∠1+∠2=360°∴∠1+∠2=∠B+∠ADC=150°故答案为150°13.解:∵四边形ABCD是正方形,∴∠BCE=∠D=90°,BC=CD,∵阴影部分的面积与正方形ABCD的面积之比为2:3,正方形ABCD的面积=62=36,∴阴影部分的面积为×36=24,∴空白部分的面积为36﹣24=12,在△BCE和△CDF中,∴△BCE≌△CDF(SAS),∴∠CBE=∠DCF,△BCG的面积与四边形DEGF的面积相等,均为×12=6,∵∠DCF+∠BCG=90°,∴∠CBG+∠BCG=90°,即∠BGC=90°,设BG=a,CG=b,则ab=6,又∵a2+b2=62,∴a2+2ab+b2=36+24=60,即(a+b)2=60,∴a+b=2,即BG+CG=2,∴△BCG的周长=6+2,故答案为:6+2.14.解:这个正多边形的边数:360°÷30°=12,每个内角度数为:180°﹣30°=150°.故答案为:12;150°15.解:∵四边形ABCD和四边形CEFG为正方形,∴CB=CD,CE=CG,∠BCD=∠ECG=90°,在△BCE和△DCG中,∴△BCE≌△DCG(SAS),∴∠CBE=∠CDG,而∠BEC=∠DEP,∴∠DPE=∠BCE=90°,连接BD,如图,点P在以BD为直径的圆上,即点P在正方形ABCD的外接圆上,∴AP为此外接圆的弦,∵BD=AB=2,∴0<AP<2,故答案为:0<AP<2.16.解:n=1时,黑瓷砖的块数为:4;n=2时,黑瓷砖的块数为:6;n=3时,黑瓷砖的块数为:8;…;当n=n时,黑瓷砖的块数为:2n+2.故答案为2n+2.17.解:∵∠BAC=90°,∠B=60°,∴∠ACB=30°,∴BC=2AB=4,AC=AB=2,∵四边形EADC是平行四边形,∴EO=DO,CO=AO=,∵DE最短也就是EO最短,∴过O作BC的垂线OF,∵∠ACB=∠FCO,∠CFO=∠CAB=90°,∴△CAB∽△CFO,∴=,即=,∴FO=,∴则DE的最小值为2FO=,故答案为:.18.解:∵∠ECF=90°,∠DCB=90°,∴∠BCF=∠DCE,∵在△CDE与△CBF中,∴△CDE≌△CBF,∴CE=CF.因为Rt△CEF的面积是200,即•CE•CF=200,故CF=20.正方形ABCD的面积=BC2=256,得BC=16.根据勾股定理得:BF==12.故答案为:12.19.解:如图,过点B作BH∥FC,连接GN并延长交BH于点H,连接CH,∵BH∥FC,∴∠BHN=∠MGN,∠HBC=∠GCB,∵N是BM的中点,∴BN=MN,∵∠BHN=∠MGN,BN=MN,∠BNH=∠GNM,∴△BH N≌△MGN(AAS)∴BH=GM,HN=GN,∵DG=GM,∴BH=GD,∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,∴∠DCG+∠BCG=90°,∵DE⊥CF,∴∠DCG+∠CDG=90°,∴∠BCG=∠CDG=∠HBC,且BC=CD,DG=BH,∴△DGC≌△BHC(SAS)∴CH=CG,∠BCH=∠DCG,∴∠BCH+∠BCG=∠DCG+∠BCG=90°,∴∠GCH=90°,且C G=CH,HN=NG,∴CN=NH=NG=8,CN⊥HF,∴CG===16,∵∠A=∠FGD=90°,∴∠AED+∠ADE=90°,∠ADE+∠DFG=90°,∴∠DFG=∠AED,且AD=CD,∠A=∠ADC=90°,∴△ADE≌△DCF(AAS)∴CF=DE,∠ADE=∠DCF,∵∠ADE=∠DCF,∠DGF=∠DGC,∴△DGF∽△CGD,∴∴DG2=FG•GC∴(DE﹣EG)2=(FC﹣EG)2=(16+FG﹣13)2=16•FG ∴FG=9(不合题意舍去),FG=1,∴FC=FG+GC=17,故答案为:17.20.解:∵四边形ABCD是菱形,∠DAB=60°,∴∠OAB=30°,∠AOB=90°.OB=OD,AO=CO,∵AB=2,∴OB=1,AO=OC=,∴DB=2,∵CE∥DB,∴四边形DBEC是平行四边形.∴CE=DB=2,∠ACE=90°,∴OE===,故答案为:.三.解答题(共5小题)21.(1)证明:∵CE2=DE•CF,即=∵四边形ABCD为平行四边形,∴AD∥BC,∴∠DEC=∠ECF,∴△CDE∽△CEF,∴∠D=∠CEF.(2)如图所示:∵AC平分∠ECF,∴∠ECA=∠BCA,∵∠D=∠CEF,∠D=∠B,∴∠CEF=∠B,∴△CGE∽△CAB,∴=,∵AD∥BC,∴∠DAC=∠BCA,∵∠ECA=∠DAC,∴AE=CE,∴=,即AC•AE=CB•CG.22.解:(1)如图1中,作AH⊥BC于H,∵AD∥BC,∠C=90°,∴∠AHC=∠C=∠D=90°,∴四边形AHCD是矩形,∴AD=CH=2,AH=CD=3,∵tan∠AEC=3,∴=3,∴EH=1,CE=1+2=3,∴BE=BC﹣CE=5﹣3=2.(2)延长AD交BM的延长线于G.∵AG∥BC,∴=,∴=,∴DG=,AG=2+=,∵=,∴=,∴y=(0<x<3).(3)①如图3﹣1中,当点M在线段DC上时,∠BNE=∠ABC=45°,∵△EBN∽△EAB,∴EB2=EN•AE,∴,解得x=.②如图3﹣2中,当点M在线段DC的延长线上时,∠ANB=∠ABE=45°,∵△BNA∽△EBA,∴AB2=AE•AN,∴(3)2=•[+解得x=13,综上所述DM的长为或13.23.解:(1)∵AB=AC,∴∠B=∠C,∵AM平分∠EAC,∴∠EAM=∠MAC=∠EAC,∵∠EAC=∠B+∠C,∴∠B=∠EAC,∴∠EAM=∠B,∴AM∥BC;(2)△ADN是等腰直角三角形,理由:∵D是BC的中点,AB=AC,∴AD⊥BC,∴∠ADB=∠ADC=90°,∵DN平分∠ADC,DQ平分∠ADB,∴∠ADN=∠NDC=45°,∠ADQ=∠BDQ=45°,∴∠QDN=90°,∵AM∥BC,∴∠AND=∠NDC=45°,∠AQD=∠BQD=45°,∴∠AND=∠AQD,∴DQ=DN,∴△ADN是等腰直角三角形;(3)由(2)知,∠QDN=90°,∵∠BAC=90°,∴∠QDN+∠BAC=180°,∴∠AHD+∠AFD=180°,∵∠AHD+∠BHD=180°,∴∠BHD=∠AFD,由(2)知,∠ADB=∠QDN=90°,∴∠BDH=∠ADF,在Rt△ABC中,AB=AC,∠ADC=90°,∴BD=CD=AD,∴△BDH≌△ADF(AAS),∴S△BDH=S△ADF,∴S四边形AHDF=S△ADF+S△ADH=S△BDH+S△ADH=S△ABD=S△ABC=7,故答案为:7.24.证明:(1)如图1,延长EG交DC的延长线于点H,∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,AB=CD,AB∥CD,∵AB∥CD,∴∠H=GEB,且BG=CG,∠BGE=∠CGH,∴△CGH≌△BGE(AAS)∴GE=GH,∵DE⊥AB,DC∥AB,∴DC⊥DE,且GE=GH,∴DG=EG=GH;(2)如图1:∵DB⊥EG,∴∠DOE=∠DEB=90°,且∠EDB=∠EDO,∴△DEO∽△DBO,∴∴DE×DE=4×(2+4)=24,∴DE=2,∴EO===2,∵AB∥CD,∴,∴HO=2EO=4,∴EH=6,且EG=GH,∴EG=3,GO=EG﹣EO=,∴GB===,∴BC=2=AD,∴AD=DE,∴点E与点A重合,如图2:∵S四边形ABCD=2S△ABD,∴S四边形ABCD=2××BD×AO=6×2=12;(3)如图3,过点O作OF⊥BC,∵旋转△GDO,得到△G′D'O,∴OG=OG',且OF⊥BC,∴GF=G'F,∵OF∥AB,∴==,∴GF=BG=,∴GG'=2GF=,∴BG'=BG﹣GG'=,∵AB2=AO2+BO2=12,∵EG'=AG'==,=.25.解:(1)过E作EG⊥AO于G.∵∠EGA=∠EAB=∠AOB=90°,∴∠EAG+∠AEG=90°,∠EAG+∠BAO=90°,∴∠BAO=∠AEG,∵AE=AB,∴△EGA≌△AOB(AAS),∴EG=OA=m,AG=OB=n∴E(m,m+n).(2)∵OB=OF,∠BOF=90°,∴∠OFB=∠OBF=45°,∵△EGA≌△AOB,∴AG=OB=OF,∴OA=FG=EG,∴∠GFE=45°,∴∠EFB=90°,∴∠NAE=∠NFB=90°,∵∠ANE=∠FNB,∴∠AEN=∠ABM,∵∠EAN=∠BAM=90°,EA=BA,∴△EAN≌△BAM(ASA),∴AN=AM.(3)如图,∵△ABP与△PCQ全等,∠ABP=∠PCQ=90°∴有两种情形:①当AB=CD,PB=CP时,t==5(s),∴v=(cm/s),②当AB=PC,CQ=PB时,PB=20﹣12=8,∴t==4(s),∴v===2(cm/s).。
2020年中考数学总复习专题演练《四边形综合》(含解析)

中考数学复习专题训练:《四边形综合》1.问题发现:(1)如图①,在△ABC中,∠ACB=90°,AC=b,BC=a,点E是AC的中点,点F在BC边上,将△ECF沿着EF折叠后得到△EPF,连接BP并使得BP最小,请画出符合题意的点P;问题探究:(2)如图②,已知在△ABC和△EBD中,∠ACB=∠BDE=90°,AC=BC=4,BD =DE=2,连接CE,点F是CE的中点,连接AF,求AF的最大值.问题解决:(3)西安大明宫遗址公园是世界文化遗产,全国重点文物保护单位,为了丰富同学们的课外学习生活,培养同学们的探究实践能力,周末光明中学的张老师在家委会的协助下,带领全班同学去大明宫开展研学活动.在公园开设的一处沙地考古模拟场地上,同学们参加了一次模拟考古游戏.张老师为同学们现场设计了一个四边形ABCD的活动区域,如图③所示,其中BD为一条工作人员通道,同学们的入口设在点A处,AD⊥BD,AD∥BC,∠DCB=60°,AB=2米.在上述条件下,小明想把宝物藏在距入口A尽可能远的C 处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出AC的最大值及此时△BCD区域的面积,如果不能,请说明理由.2.已知:如图,在菱形ABCD中,AC=2,∠B=60°.点E为边BC上的一个动点(与点B、C不重合),∠EAF=60°,AF与边CD相交于点F,联结EF交对角线AC于点G.设CE=x,EG=y.(1)求证:△AEF是等边三角形;(2)求y关于x的函数解析式,并写出x的取值范围;(3)点O是线段AC的中点,联结EO,当EG=EO时,求x的值.3.已知在正方形ABCD和正方形CEFG中,直线BG,DE交于点H.(1)如图1,当B,C,E共线时,求证:BH⊥DE.(2)如图2,把正方形CEFG绕C点顺时针旋转α度(0<α<90),M,N分别为BG,DE的中点,探究HM,HN,CM之间的数量关系,并证明你的结论.(3)如图3,∠PDG=45°,DH⊥PG于H,PH=2,HG=4.直接写出DH的长.4.[问题引入](1)如图1,在正方形ABCD中,E、F分别是BC、CD两边上的点,且AE⊥BF,垂足为点P.求证:AE=BF;[类比探究](2)如图2,把(1)中正方形ABCD改为矩形ABCD,且AD=2AB,其余条件不变,请你推断AE、BF满足怎样的数量关系,并说明你的理由;[实践应用](3)如图3,Rt△ABC中,∠BAC=30°,把△ABC沿斜边AC对折得到Rt△ADC,E、F分别为CD、AD边上的点,连接AE、BF,恰好使得AE⊥BF,垂足为点P.请求出的值.5.如图,已知正方形ABCD中,BC=4,AC、BD相交于点O,过点A作射线AM⊥AC,点E是射线AM上一点,联结OE交AB边于点F.以OE为一边,作正方形OEGH,且点A在正方形OEGH的内部,联结DH.(1)求证:△HDO≌△EAO;(2)设BF=x,正方形OEGH的边长为y,求y关于x的函数关系式,并写出定义域;(3)联结AG,当△AEG是等腰三角形时,求BF的长.6.阅读材料:等腰三角形具有性质“等边对等角”.事实上,不等边三角形也具有类似性质“大边对大角”,如图1,在△ABC中,如果AB>AC,那么∠ACB>∠ABC.证明如下:将AB沿△ABC的角平分线AD翻折(如图2),因为AB>AC,所以点B落在AC的延长线上的点B′处.于是,由∠ACB>∠B′,∠ABC=∠B′,可得∠ACB>∠ABC.(1)灵活运用:从上面的证法可以看出,折纸常常能为证明一个命题提供思路和方法.由此小明想到可用类似方法证明“大角对大边”,如图3,在△ABC中,如果∠ACB>∠ABC,那么AB>AC.小明的思路是:沿BC的垂直平分线翻折……请你帮助小明完成后面的证明过程.(2)拓展延伸:请运用上述方法或结论解决如下问题:如图4,已知M为正方形ABCD的边CD上一点(不含端点),连接AM并延长,交BC 的延长线于点N.求证:AM+AN>2BD.7.探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系;②如图2,若∠B、∠D都不是直角,但满足∠B+∠D=180°,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2.点D、E均在边BC 边上,且∠DAE=45°,若BD=1,求DE的长.8.如图1,在矩形ABCD中,AB=4,AD=3,沿对角线AC剪开,再把△ADC沿AB方向平移,得到图2,其中A'D交AC于E,A'C'交BC于F.(1)在图2中,除△ABC与△C'DA'外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;(2)设AA'=x.①当x为何值时,四边形A'ECF是菱形?②设四边形A'ECF的面积为y,求y的最大值.9.在正方形ABCD中,BD为对角线,点E在BD上,过点E作EF⊥CE,交AB于点F,连接CF.(1)如图①,求证:∠ECF=45°;(2)如图②,作FG⊥AB,交BD于点G,求证:DE=GE;(3)在(2)的条件下,如图③,延长FG交CE于点K,延长CE交AD于点M,连接MG、BK,若MG=2EK,GK=2,求线段BK的长.10.如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN =45°.(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM 的延长线交于点P,交AN于Q,直接写出AQ、AP的长.11.如图,菱形ABCD中,AB=10,连接BD,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.(1)求证:AE=CE;(2)若sin∠ABD=,当点P在线段BC上时,若BP=4,求△PEC的面积;(3)若∠ABC=45°,当点P在线段BC的延长线上时,请直接写出△PEC是等腰三角形时BP的长.12.如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE.连接DE并延长交射线AP于点F,连接BF.(1)若∠BAP=α,直接写出∠ADF的大小(用含α的式子表示);(2)求证:BF⊥DF;(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.13.已知正方形OABC在平面直角坐标系中,点A,C分别在x轴,y轴的正半轴上,等腰直角三角形OEF的直角顶点O在原点,E,F分别在OA,OC上,且OA=4,OE=2.将△OEF绕点O逆时针旋转,得△OE1F1,点E,F旋转后的对应点为E1,F1.(Ⅰ)①如图①,求E1F1的长;②如图②,连接CF1,AE1,求证△OAE1≌△OCF1;(Ⅱ)将△OEF绕点O逆时针旋转一周,当OE1∥CF1时,求点E1的坐标(直接写出结果即可).14.菱形ABCD中,E,F为边AB,AD上的点,CF,DE相交于点G.(1)如图1,若∠A=90°,DE=CF,求证:DE⊥CF;(2)如图2,若∠EGC+∠B=180°.求证:DE=CF;(3)如图3,在(1)的条件下,平移线段DE到MN,使G为CF的中点,连接BD交MN于点H,若∠FCD=15°,BN=,请直接写出FG的长度.15.我们定义:对角线互相垂直的四边形叫做垂美四边形.(1)如图1,垂美四边形ABCD的对角线AC,BD交于O.求证:AB2+CD2=AD2+BC2;(2)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BE,CG,GE.①求证:四边形BCGE是垂美四边形;②若AC=4,AB=5,求GE的长.16.(1)观察猜想如图①,点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则△ADB和△EAC是否全等?(填是或否),线段AB、AC、BD、CE之间的数量关系为.(2)问题解决如图②,在Rt△ABC中,∠ABC=90°,AC=6,AB=6,以AC为直角边向外作等腰Rt△DAC,连接BD,求BD的长.(3)拓展延伸如图③,在四边形ABCD中,∠ABC=∠ADC=90°,AB=5,AD=,DC=DA,CG⊥BD于点G,求CG的长,17.已知,在▱ABCD中,AB⊥BD,AB=BD,E为射线BC上一点,连接AE交BD于点F.(1)如图1,若点E与点C重合,且AF=2,求AD的长;(2)如图2,当点E在BC边上时,过点D作DG⊥AE于G,延长DG交BC于H,连接FH.求证:AF=DH+FH;(3)如图3,当点E在射线BC上运动时,过点D作DG⊥AE于G,M为AG的中点,点N在BC边上且BN=1,已知AB=4,请直接写出MN的最小值.18.如图,在矩形ABCD中,E是AB边上的一个动点,把△BCE沿CE折叠,使点B落在点F处,过点F作GH∥CE,分别交AB、CD于点G、H.(1)求证:△EFG是等腰三角形;(2)如图①,若F是GH中点,求∠FGE的度数;(3)如图②,若点G与点A重合,AB=30,BC=20,求FH的长.19.在平面直角坐标系中,已知A(﹣4,0),B(4,0),点C,D在x轴上方,且四边形ABCD的面积为32,(1)若四边形ABCD是菱形,求点D的坐标.(2)若四边形ABCD是平行四边形,如图1,点E,F分别为CD,BC的中点,且AE⊥EF,求AE+2EF的值.(3)若四边形ABCD是矩形,如图2,点M为对角线AC上的动点,N为边AB上的动点,求BM+MN的最小值.20.在平面直角坐标系中,点O为坐标原点,正方形OABC与长方形DEFG的位置如图所示,点A在x轴的正半轴上,点C在y轴的正半轴上,点B的横坐标为a,点D,E在x 轴的负半轴上(点E在点D的右侧),点G的坐标为(b,﹣b),DE=OA,实数a,b 的值满足.(1)求点F的坐标;(2)长方形DEFG以每秒1个单位长度的速度向右平移t(t>0)秒得到矩形D'E'F'G',点D',E',F',G'分别为点D,E,F,G平移后的对应点,设矩形D'E'F'G'与正方形OABC 重合部分的面积为S,用含t的式子表示S,并直接写出相应的t的范围;(3)在(2)的条件下,在长方形DEFG出发运动的同时,点P从点O出发,沿正方形的边以每秒2个单位长度的速度顺时针方向运动(即O→C→B→A→O→C),连接PD',PG',当三角形PD'G'的面积为15时,求S>0时相应的t值,并直接写出此时刻S值及点P的坐标.参考答案1.解:(1)如图①中,点P即为所求.当E,P,B共线时,BP的值最小.(2)如图②中,取BC的中点P,连接PA,PF.∵∠BDE=90°,BD=DE=2,∴BE=BD=4,∴CF=EF,CP=PB=2,∴PF=BE=2,∵∠ACP=90°,AC=4,CP=2,∴PA===2,∵AF≤PA+PF,∴AF≤2+2,∴AF的最大值为2+2.(3)如图③中,作△ABD的外接圆⊙O交CD于E,连接OE,EB,AC.∵∠DBC=90°,∠DCB=60°,∴∠CDB=30°,∴∠EOB=60°,∵EO=EB,∴△EOB是等边三角形,BE=OB=,∵∠ECB=60°,∴点C的运动轨迹是圆弧,不妨设圆心为P,连接PC,PE,PB,则∠EPB=2∠ECB=120°,作PT⊥BE于T,在Rt△PET中,∠PET=30°,ET=BT=BE=,∴PE=PB=PC==,∵∠EBO=60°,∠EBP=30°,∴∠ABP=90°,在Rt△ABP中,AP===13,∵AC≤PA+PC,∴AC≤13+,∴AC的最大值为13+,此时A,P,C共线,如图③﹣1中,作CW⊥AB于W.∵PB∥CW,∴==,∴==,∴CW=+1,BW=2,∴BC===,=•BC•BD=•BC•BC=×(26+2)=13+.∴S△BCD2.(1)证明:∵四边形ABCD为菱形,∴AB=BC,∵∠B=60°,∴△ABC为等边三角形,∴∠BAC=60°,AC=AB,∴∠BAE+∠EAC=60°,∵AB∥CD,∴∠BAC=∠ACF=60°,∵∠EAF=60°,即∠EAC+∠CAF=60°,∴∠BAE=∠CAF,在△AEB和△AFC中,,∴△AEB≌△AFC(ASA),∴AE=AF,∴△AEF为等边三角形;(2)解:过点A作AH⊥BC于点H,∵△AEF为等边三角形,∴AE=EF=,∠AEF=60°,∵∠ABH=60°,∴,BH=HC=1,∴EH=|x﹣HC|=|x﹣1|,∴EF==,∵∠AEF=∠B=60°,∴∠CEG+∠AEB=∠AEB+∠BAE=120°,∴∠CEG=∠BAE,∵∠B=∠ACE=60°,∴△BAE∽△CEG,∴,∴,∴y=EG=(0<x<2),(3)解:∵AB=2,△ABC是等边三角形,∴AC=2,∴OA=OC=1,∵EG=EO,∴∠EOG=∠EGO,∵∠EGO=∠ECG+∠CEG=60°+∠CEG,∠CEA=∠CEG+∠AEF=60°+∠CEG,∴∠EGO=∠CEA,∴∠EOG=∠CEA,∵∠ECA=∠OCE,∴△COE∽△CEA,∴,∴CE2=CO•CA,∴x2=1×2,∴x=(x=﹣舍去),即x=.3.(1)证明:∵在正方形ABCD和正方形CEFG中,BC=CD,CG=CE,∠BCG=∠DCE =90°,∴△BCG≌△DCE(SAS),∴∠CBG=∠CDE,∵∠CDE+∠DEC=90°,∴∠HBE+∠BEH=90°,∴∠BHE=90°,∴BH⊥DE;(2)解:MH2+HN2=2CM2,理由:∵在正方形ABCD和正方形CEFG中,BC=CD,CG=CE,∠BCD=∠GCE=90°,∴∠BCG=∠DCE,∴△BCG≌△DCE(SAS),∴∠CBG=∠CDE,BG=DE,∵∠DPH=∠CPM,∴∠DHP=∠BCP=90°,∴∠MHN=90°,∵M,N分别为BG,DE的中点,∴BM=BG,DN=DE,∴BM=DN,∵BC=CD,∴△BCM≌△DCN(SAS),∴CM=CN,∠BCM=∠DCN,∴∠MCN=∠BCP=90°,∴MH2+HN2=CM2+CN2=2CM2;(3)解:∵DH⊥PG,∴∠DHP=∠DHG=90°,把△PDH沿着PD翻折得到△APD,把△GDH沿着DG翻折得到△DGC,∴AD=DH=CD,∠A=∠C=∠DHP=90°,∠ADP=∠HDP,∠GDH=∠GDC,AP=PH=2,CG=HG=4,∵∠PDG=45°,∴∠ADC=90°,延长AP,CG交于B,则四边形ABCD是正方形,∴∠B=90°,设DH=AD=AB=BC=x,∴PB=x﹣2,BG=x﹣4,∵PG2=PB2+BG2,∴62=(x﹣2)2+(x﹣4)2,解得:x=3+(负值舍去),∴DH=3+.4.证明:[问题引入](1)∵正方形ABCD,∴∠ABC=∠C,AB=BC,∵AE⊥BF,∴∠APB=∠BAP+∠ABP=90°,∵∠ABP+∠CBF=90°,∴∠BAP=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴AE=BF;(2)BF=2AE,理由如下:∵矩形ABCD,∴∠ABC=∠C,AD=BC=2AB,∵AE⊥BF,∴∠APB=∠BAP+∠ABP=90°,∵∠ABP+∠CBF=90°,∴∠BAP=∠CBF,且∠ABE=∠BCF=90°,∴△ABE∽△BCF,∴=2,∴BF=2AE;(3)如图3,过点B作BH⊥AD于H,连接BD,∵把△ABC沿斜边AC对折得到Rt△ADC,∴AD=AB,∠ABC=∠ADC=90°,∠DAC=∠BAC=30°,∴∠DAB=60°,∴△ABD是等边三角形,且BH⊥AD,∴AD=AB=2AH,BH=AH,∴,∵∠ADC+∠EPF+∠DEA+∠DFB=360°,∴∠DEA+∠DFB=180°,且∠DFB+∠BFA=180°,∴∠DEA=∠BFH,∵∠BHF=∠ADE=90°,∴△ADE∽△BHF,∴==5.解:(1)∵在正方形ABCD中,AC⊥BD,∴∠AOD=90°,AO=OD,∵四边形OEGH是正方形,∴∠EOH=90°,OE=OH,∴∠AOE=∠DOH,∴△HDO≌△EAO(SAS);(2)如图1,过O作ON⊥AB于N,则AN=BN=ON=AB=2,∵BF=x,∴AF=4﹣x,∴FN=2﹣x,∴OF===,∴EF=y﹣,∵AM⊥AC,∴AE∥OB,∴,∴=,∴;(3)①当AE=EG时,△AEG是等腰三角形,则AE=OE,∵∠EAO=90°,∴这种情况不存在;②当AE=AG时,△AEG是等腰三角形,如图2,过A作AP⊥EG于P,则AP∥OE,∴∠PAE=∠AEO,∴△APE∽△EAO,∴=,∵AE=AG,∴PE=y=,AE==,∴=,解得:x=2,②当GE=AG时,△AEG是等腰三角形,如图3,过G作GQ⊥AE于Q,∴∠GQE=∠EAO=90°,∴∠GEQ+∠EGQ=∠GEQ+∠AEO=90°,∴∠EGQ=∠AEO,∵GE=OE,∴△EGQ≌△OEA(AAS),∴EQ=AO=2,∴AE=2EQ=4=,∴x=,∴BF=2或.6.解:(1)将∠B沿BC的中垂线DE翻折(如图3),使点B落在点C处.∵∠ACB>∠ABC,∴CD在△ABC的内部,D落在AB上.连接DC,∵DE为BC的中垂线,∴DB=DC,在△ADC中,AD+DC>AC,∴AD+DB>AC,即AB>AC;(2)如图4,延长DC到点E,使得CE=CN,连接AE交BC于点F,连接AC,∵四边形ABCD是正方形,∴∠ACD=∠ACB=45°,∴∠ACE=∠ACN=135°,∵AC=AC,∴△ACE≌△ACN(SAS),∴AE=AN,过点C作PQ⊥AC,分别交AN、AE于点P、Q,由∠ACP=∠ACQ=90°可知AP>AC、AQ>AC,∴AP+AQ>2AC,∵∠ACD>∠E,∠ACD=45°,∠QCE=45°,∴∠QCE>∠E,∴QE>CQ,同理可得PC>PM,由全等或对称性可得PC=CQ,∴QE>PM.∴AM+AN=AM+AE=AM+AQ+QE>AM+AQ+PM=AP+AQ,又∵AP+AQ>2AC,∴AM+AN>2AC,∵正方形ABCD中,AC=BD.∴AM+AN>2BD.7.解:(1)①如图1,∵把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,∴AE=AG,∠BAE=∠DAG,BE=DG,∠B=∠ADG=90°,∵∠ADC=90°,∴∠ADC+∠ADG=90°∴F、D、G共线,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠DAG+∠DAF=45°,即∠EAF=∠GAF=45°,在△EAF和△GAF中,∵,∴△EAF≌△GAF(SAS),∴EF=GF,∵BE=DG,∴EF=GF=DF+DG=BE+DF,故答案为:EF=BE+DF;②成立,理由:如图2,把△ABE绕A点旋转到△ADG,使AB和AD重合,则AE=AG,∠B=∠ADG,∠BAE=∠DAG,∵∠B+∠ADC=180°,∴∠ADC+∠ADG=180°,∴C、D、G在一条直线上,与①同理得,∠EAF=∠GAF=45°,在△EAF和△GAF中,∵,∴△EAF≌△GAF(SAS),∴EF=GF,∵BE=DG,∴EF=GF=BE+DF;(2)解:∵△ABC中,AB=AC=2,∠BAC=90°,∴∠ABC=∠C=45°,由勾股定理得:BC==4,如图3,把△AEC绕A点旋转到△AFB,使AB和AC重合,连接DF.则AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,∵∠DAE=45°,∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC﹣∠DAE=90°﹣45°=45°,∴∠FAD=∠DAE=45°,在△FAD和△EAD中,∴△FAD≌△EAD(SAS),∴DF=DE,设DE=x,则DF=x,∵BC=4,∴BF=CE=4﹣1﹣x=3﹣x,∵∠FBA=45°,∠ABC=45°,∴∠FBD=90°,由勾股定理得:DF2=BF2+BD2,x2=(3﹣x)2+12,解得:x=,即DE=.8.解:(1)△AA′E≌△C′CF,△A′BF≌△CDE,由题意得,四边形A′DCB是矩形,∴A′B=DC,∴AA′=CC′,∵AB∥CD,∴∠BA′F=∠C′,由题意得,∠BA′F=∠A,∴∠A=∠C′,在△AA′E和△C′CF中,,∴△AA′E≌△C′CF(ASA);(2)①设A′E=a,A′F=b,∵A′F∥AC,∴=,即=,解得,b=,同理=,解得,a=x,当A′E=A′F时,四边形A′ECF是菱形,∴=x,解得,x=,∴当x=时,四边形A′ECF是菱形;②由①得,四边形A′ECF的面积为y=3×(4﹣x)﹣×(3﹣x)×(4﹣x)×2=﹣x2+3x=﹣(x﹣2)2+3,∴当x=2时,y的最大值为3.9.解:(1)如图①,连接AE,∵四边形ABCD是正方形,∴AB=BC=AD=CD,∠ABD=∠CBD=45°,且BE=BE,∴△ABE≌△CBE(SAS)∴AE=CE,∠BAE=∠BCE,∵∠ABC+∠FEC+∠BCE+∠EFB=360°,∴∠BCE+∠BFE=180°,∠BFE+∠AFE=180°,∴∠AFE=∠BCE,∴∠BAE=∠AFE,∴EF=AE=EC,且∠FEC=90°,∴△EFC是等腰直角三角形,∴∠ECF=45°;(2)如图②,延长FG交CD于H,∵GF⊥AB,∠ABC=∠BCD=90°,∴四边形BCHF是矩形,∴FH=BC=CD,∠FHC=90°,∵∠AFE=∠BCE,∴∠EFH=∠ECH,且EF=EC,FH=CD,∴△EFH≌△ECD(SAS)∴∠FHE=∠CDE=45°,且∠FHD=90°,∴∠FHE=∠CDE=∠DGH=∠DHE=45°,∴EG=EH,EH=DE,∴EG=DE;(3)如图③,延长FK交CD于H,连接FM,过点M作MP⊥FH于P,∵AD∥BC∥FH,∴∠MDE=∠KGE,且DE=EG,∠MED=∠GEK,∴△MED≌△KEG(ASA)∴ME=EK=MK,MD=GK=2,∵MG=2EK,∴MK=MG,且MP⊥FH,∴GP=PK=1,∵∠ADH=∠DHF=∠MPH=90°,∴四边形MDHP是矩形,∴MD=PH=2,∴GH=3,∴FH=BC=AB=AD=3+FG,∴AM=1+FG,∵FG⊥AB,∠ABD=45°,∴△BFG是等腰直角三角形,∴BF=FG,∴AF=3,∵ME=EK,EF⊥MK,∴FM=FK=FG+2,∵FM2=AM2+AF2,∴(FG+2)2=(FG+1)2+9,∴FG=3,∴BK==.10.解:(1)BM+DN=MN,理由如下:如图1,在MB的延长线上,截取BE=DN,连接AE,∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠ABC=∠D=90°,∴∠ABE=90°=∠D,在△ABE和△ADN中,,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD,∴∠EAN=∠BAD=90°,∵∠MAN=45°,∴∠EAM=45°=∠NAM,在△AEM和△ANM中,,∴△AEM≌△ANM(SAS),∴ME=MN,又∵ME=BE+BM=BM+DN,∴BM+DN=MN;故答案为:BM+DN=MN;(2)(1)中的结论不成立,DN﹣BM=MN.理由如下:如图2,在DC上截取DF=BM,连接AF,则∠ABM=90°=∠D,在△ABM和△ADF中,,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=∠BAD=90°,即∠MAF=∠BAD=90°,∵∠MAN=45°,∴∠MAN=∠FAN=45°,在△MAN和△FAN中,,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.(3)∵四边形ABCD是正方形,∴AB=BC=AD=CD=6,AD∥BC,AB∥CD,∠ABC=∠ADC=∠BCD=90°,∴∠ABM=∠MCN=90°,∵CN=CD=6,∴DN=12,∴AN===6,∵AB∥CD,∴△ABQ∽△NDQ,∴====,∴=,∴AQ=AN=2;由(2)得:DN﹣BM=MN.设BM=x,则MN=12﹣x,CM=6+x,在Rt△CMN中,由勾股定理得:62+(6+x)2=(12﹣x)2,解得:x=2,∴BM=2,∴AM===2,∵BC∥AD,∴△PBM∽△PDA,∴===,∴PM=AM=,∴AP=AM+PM=3.11.(1)证明:∵四边形ABCD是菱形,∴∠ABE =∠CBE ,AB =BC ,在△ABE 和△CBE 中,,∴△ABE ≌△CBE (SAS ),∴AE =CE ;(2)解:连接AC ,交BD 于O ,如图1所示:∵四边形ABCD 是菱形,∴AD ∥BC ,AD =AB =4,∠AOB =90°,OB =OD ,OA =OC ,∴△BEP ∽△DEA , ∴==, ∴=()2=,∵sin ∠ABD ===, ∴OA =2, OB ===4, ∴BD =2OB =8, ∴=,解得:DE =,∴BE =BD ﹣DE =8﹣=, ∴S △DEA =OA •DE =×2×=, S △ABE =OA •BE =×2×==S △BEC , ∴S △BEP =S △DEA =×=, ∴S △PEC =S △BEC ﹣S △BEP =﹣=; (3)解:①由(1)得:△ABE ≌△CBE ,∴∠BAE =∠BCE ,当∠BAE =90°时,则∠BCE =90°,∴∠ECP=90°,∵∠ABC=45°,∴∠EBC=22.5°,∠CPE=45°,∴△PEC是等腰直角三角形,∴CE=CP,∠BEC=90°﹣22.5°=67.5°,过点E作∠FEC=45°交BC于F,如图2所示:则CE=CP=CF,EF=CF,∠BEF=∠BEC﹣∠FEC=67.5°﹣45°=22.5°,∴∠BEF=∠EBC,∴EF=BF,∴CF+CF=BC=10,∴CF==10(﹣1),∴BP=BC+CP=BC+CF=10+10(﹣1)=10;②由(1)得:△ABE≌△CBE,∴∠AEB=∠CEB,当∠BAE=105°时,∠AEB=180°﹣105°﹣22.5°=52.5°,∴∠AEC=2∠AEB=105°,∴∠CEP=75°,∵∠APB=180°﹣105°﹣45°=30°,∴∠ECP=180°﹣75°﹣30°=75°,∴∠ECP=∠CEP,∴△PEC是等腰三角形,过点A作AN⊥BP于N,如图3所示:则△ABN是等腰直角三角形,∴AN=BN=AB=5,∵∠APB=30°,∴tan30°=,即=,∴PN=5,∴BP=BN+PN=5+5,综上所述,△PEC是等腰三角形时BP的长为10或5+5.12.(1)解:由轴对称的性质得:∠EAP=∠BAP=α,AE=AB,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠DAE=90°﹣2α,AD=AE,∴∠ADF=∠AED=(180°﹣∠DAE)=(90°+2α)=45°+α;(2)证明:∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵点E与点B关于直线AP对称,∴∠AEF=∠ABF,AE=AB.∴AE=AD.∴∠ADE=∠AED.∵∠AED+∠AEF=180°,∴在四边形ABFD中,∠ADE+∠ABF=180°,∴∠BFD+∠BAD=180°,∴∠BFD=90°∴BF⊥DF;(3)解:线段AF,BF,CF之间的数量关系为AF=BF+CF,理由如下:过点B作BM⊥BF交AF于点M,如图所示:∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∴∠ABM=∠CBF,∵点E与点B关于直线AP对称,∠BFD=90°,∴∠MFB=∠MFE=45°,∴△BMF是等腰直角三角形,∴BM=BF,FM=BF,在△AMB和△CFB中,,∴△AMB≌△CFB(SAS),∴AM=CF,∵AF=FM+AM,∴AF=BF+CF.13.(Ⅰ)①解:∵等腰直角三角形OEF的直角顶点O在原点,OE=2,∴∠EOF=90°,OF=OE=2,∴EF===2,∵将△OEF绕点O逆时针旋转,得△OE1F1,∴E1F1=EF=2;②证明:∵四边形OABC为正方形,∴OC=OA.∵将△OEF绕点O逆时针旋转,得△OE1F1,∴∠AOE1=∠COF1,∵△OEF是等腰直角三角形,∴△OE1F1是等腰直角三角形,∴OE1=OF1.在△OAE1和△OCF1中,∴△OAE1≌△OCF1(SAS);(Ⅱ)解:∵OE⊥OF,∴过点F与OE平行的直线有且只有一条,并与OF垂直,当三角板OEF绕O点逆时针旋转一周时,则点F在以O为圆心,以OF为半径的圆上.∴过点F与OF垂直的直线必是圆O的切线,又点C是圆O外一点,过点C与圆O相切的直线有且只有2条,不妨设为CF1和CF2,此时,E点分别在E1点和E2点,满足CF1∥OE1,CF2∥OE2.当切点F1在第二象限时,点E1在第一象限.在直角三角形CF1O中,OC=4,OF1=2,cos∠COF1===,∴∠COF1=60°,∴∠AOE1=60°.∴点E1的横坐标=2cos60°=1,点E1的纵坐标=2sin60°=,∴点E1的坐标为(1,);当切点F2在第一象限时,点E2在第四象限.同理可求:点E2的坐标为(1,﹣).综上所述,当OE1∥CF1时,点E1的坐标为(1,)或(1,﹣).14.解:(1)证明:∵菱形ABCD中,∠A=90°∴菱形ABCD是正方形∴AD=DC,∠A=∠CDF=90°在Rt△ADE与Rt△DCF中∴Rt△ADE≌Rt△DCF(HL)∴∠ADE=∠DCF∴∠DCF+∠CDE=∠ADE+∠CDE=∠ADC=90°∴∠CGD=90°∴DE⊥CF(2)证明:∵四边形ABCD是菱形∴AD=CD,∠B=∠ADC,AD∥BC∴∠A+∠B=180°∵∠EGC+∠B=180°,∠EGC+∠CGD=180°∴∠A=∠EGC=∠DGF,∠CGD=∠B=∠ADC ∵∠A=∠DGF,∠ADE=∠GDF∴△ADE∽△GDF∴∴∵∠CGD=∠CDF,∠DCG=∠FCD∴△DCG∽△FCD∴∴∵AD=DC∴DE=CF(3)如图,过点N作NP⊥CD于点P,连接FM∴∠CPN=∠MPN=90°∵四边形ABCD是正方形∴∠ABC=∠BCD=∠ADC=90°,BC=CD∴四边形BCPN是矩形∴NP=BC=CD,PC=BN=在Rt△NPM与Rt△CDF中∴Rt△NPM≌Rt△CDF(HL)∴PM=DF设PM=DF=x,则CM=PC+PM=+x∵由(1)得MN⊥CF,G为CF中点∴MN垂直平分CF∴MF=MC∴∠MFC=∠FCD=15°∴∠DMF=∠MFC+∠FCD=30°∴Rt△DMF中,MF=2DF=2x,DM=DF=x ∴2x=+x∴x=∴DF=,CM=2,CD=CM+DM=2+∵∠GCM=∠MCF,∠CGM=∠CDF=90°∴△CGM∽△CDF∴=∴2CG2=CD•CM=(2+)=8+4∴CG2=4+2=12+2+()2=(1+)2∴FG=CG=1+15.(1)证明:∵垂美四边形ABCD的对角线AC,BD交于O,∴AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得:AD2+BC2=AO2+DO2+BO2+CO2,AB2+CD2=AO2+BO2+CO2+DO2,∴AD2+BC2=AB2+CD2;(2)①证明:连接BG、CE相交于点N,CE交AB于点M,如图2所示:∵正方形ACFG和正方形ABDE,∴AG=AC,AB=AE,∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,∵∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,∴∠ABG+∠BMN=90°,即CE⊥BG,∴四边形BCGE是垂美四边形;②解:∵四边形BCGE是垂美四边形,∴由(1)得:CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC===3,∵正方形ACFG和正方形ABDE,∴CG=AC=4,BE=AB=5,∴GE2=CG2+BE2﹣CB2=(4)2+(5)2﹣32=73,∴GE=.16.解:(1)观察猜想结论:AB+AC=BD+CE,理由如下:如图①,∵DB⊥BC,EC⊥BC,∴∠B=∠C=90°,∠DAE=90°,∴∠D+∠DAB=∠DAB+∠EAC=90°,∴∠D=∠EAC,在△ADB和△EAC中,,∴△ADB≌△EAC(AAS),∴BD=AC,EC=AB,∴BC=AB+AC=BD+CE,故答案为:是,AB+AC=BD+CE;(2)问题解决如图②,过D作DE⊥AB,交BA的延长线于E,由(1)得:△ABC≌△DEA(AAS),∴DE=AB=6,AE=BC===12,Rt△BDE中,BE=AB+AE=18,由勾股定理得:BD===6;(3)拓展延伸如图③,过D作DE⊥BC于E,作DF⊥AB于F,则四边形DEBF是矩形,同(1)得:△CED≌△AFD(AAS),∴CE=AF,DE=DF,∴四边形DEBF是正方形,设AF=x,则BF=DE=DF=x+5,在Rt△ADF中,由勾股定理得:x2+(x+5)2=()2,解得:x=,或x=﹣(舍去),∴AF=,DF=,∴BD=DF=,四边形ABCD的面积=正方形DEBF的面积=()2=,△ABD的面积=AB×DF=×5×=,∴△BCD的面积=四边形ABCD的面积﹣△ABD的面积=BD×CG=﹣=51,∴CG==6.17.(1)解:如图1中,∵AB=BD,∠BAD=45°,∴∠BDA=∠BAD=45°,∴∠ABD=90°,∵四边形ABCD是平行四边形,∴E、C重合时BF=BD=AB,在Rt△ABF中,∵AF2=AB2+BF2,∴(2)2=(2BF)2+BF2,∴BF=2,AB=4,在Rt△ABD中,AD==4;(2)证明:如图2中,在AF上截取AK=HD,连接BK,∵∠AFD=∠ABF+∠2=∠FGD+∠3,∠ABF=∠FGD=90°,∴∠2=∠3,在ABK和△DBH中,,∴△ABK≌△DBH,∴BK=BH,∠6=∠1,AK=DH,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠4=∠1=∠6=45°,∴∠5=∠ABD﹣∠6=45°,∴∠5=∠1,在△FBK和△FBH中,,∴△FBK≌△FBH,∴KF=FH,∵AF=AK+KF,∴AF=DH+FH;(3)解:连接AN并延长到Q,使NQ=AN,连接GQ,取AD的中点O,连接OG,∵∠AGD=90°,∴点G的轨迹是以O为圆心,以OG为半径的弧,且OG=4,当O,G,Q在同一条直线上时,QG的值最小,∴OQ=10,OG=4,∴GQ最小值为6,∵MN是△AGQ的中位线,∴MN的最小值为3.18.解:(1)∵把△BCE沿CE折叠,使点B落在点F处,∴∠BEC=∠FEC,∵GH∥CE,∴∠FGE=∠CEB,∠GFE=∠FEC,∴∠EGF=∠EFG,∴EG=EF,∴△EFG是等腰三角形;(2)如图①,取CE的中点M,连接FM,∵把△BCE沿CE折叠,使点B落在点F处,∴∠EFC=∠B=90°,∴EM=FM,∵AB∥CD,GH∥CE,∴四边形GECH是平行四边形,∴GH=CE,∵F是GH中点,∴FG=EM,∴四边形GEMF是平行四边形,∴GE=FM,由(1)知,GE=EF,∴EG=GF=EF,∴△EFG是等边三角形,∴∠FGE=60°;(3)由(2)知,BE=EF,AE=EF,∴AE=BE=AB=15,∴CH=AE=15,∴DH=30﹣15=15,∴AH===25,如图②,过E作EN⊥AF于N,∴∠ANE=∠B=90°,∵CE∥AH,∴∠EAN=∠BEC,∴△AEN∽△ECB,∴=,∴=,∴AN=9,∴AF=18,∴FH=25﹣18=7.19.解:(1)如图1,过D作DH⊥AB于H,∵A(﹣4,0),B(4,0),∴OA=OB=4,∴AB=8,∵四边形ABCD的面积为32∴8DH=32,∴DH=4,∵四边形ABCD是菱形,∴AD=AB=8,∴AH===4,∴OH=AH﹣OA=4﹣4,∴D(4﹣4,4);(2)如图1,延长EF交x轴于G,∵四边形ABCD是平行四边形,∴CD∥AB,∴∠C=∠FBG,∠CEF=∠FGB,∵CF=BF,∴△CEF≌△BGF(AAS),∴EF=FG,CE=BG,∴EG=2EF,过E作EP⊥x轴于P,∴EP=DH=4,∵CD=AB=8,∴设D(a,4)则C(8+a,4),∵点E为CD的中点,∴E(4+a,4),∴AP=8+a,PG=4﹣a,∴PE2=AP•PG,∴(8+a)•(4﹣a)=16,∴a=2﹣2(负值舍去),∴AP=6+2,PG=6﹣2,∴AE==4,EG==4,∴AE+2EF=AE+EG=4+8;(3)∵四边形ABCD是矩形,∴AB=CD=8,AD=BC=4,∴AC==4,作B关于AC的对称点M′,连接BM′交AC于E,则BM′=2BE=2×=2×=,过M′作M′N⊥AB于N交AC于M,则此时,BM+MN的值最小,且BM+MN的最小值=M′N,∵∠M′EM=∠CEB=90°,BE=,BC=4,∴CE=,∴CM=2CE=,∴AM=,∴AM2﹣AN2=BM2﹣BN2,∴()2﹣AN2=42﹣(8﹣AN)2,∴AN=,∴MN==,∴M′N=,∴BM+MN的最小值为.20.解:(1)∵,∴a﹣4=0,b+6=0,∴a=4,b=﹣6,∵四边形OABC是正方形,点B的横坐标为a,∴OA=4,∵四边形DEFG为长方形,点G的坐标为(b,﹣b),∴F的纵坐标为:﹣b=6,OD=6,∵DE=OA,∴OE=OD﹣DE=OD﹣OA=6﹣4=2,∴F(﹣2,6)(2)∵OE=2,AD=2OA+OE=2×4+2=10,AE=OA+OE=4+2=6,长方形DEFG以每秒1个单位长度的速度向右平移,∴当0<t≤2,t≥10时,S=0;当2<t≤6时,点E'在OA上,如图1所示:S=OC•OE′=4(t﹣2)=4t﹣8;当6<t<10时,点D'在OA上,如图2所示:S=AB•AD'=4(10﹣t)=40﹣4t;∴S=;(3)∵D′G′=DG=6,当三角形PD'G'的面积为15时,∴点P到D′G′的距离为5,∵长方形DEFG以每秒1个单位长度的速度向右平移,点P从点O出发,沿正方形的边以每秒2个单位长度的速度顺时针方向运动(即O→C→B→A→O→C),∵当点P再次运动到AO、OC时,△PD'G'的面积<15,∴分两种情况:①当t=3s时,点P在BC的中点处,如图3所示:即PC=2,DG向右平移了3个单位长度,OD′=OD﹣3=6﹣3=3,此时,PC+OD′=2+3=5,即点P到D′G′的距离为5,P的坐标为:(2,4),OE′=D′E′﹣OD′=4﹣3=1,∴S=OC•OE′=4×1=4;②当t=5s时,点P在AB的中点处,如图4所示:即AP=2,DG向右平移了5个单位长度,OD′=OD﹣5=6﹣5=1,此时,OA+OD′=4+1=5,即点P到D′G′的距离为5,P的坐标为:(4,2),OE′=D′E′﹣OD′=4﹣1=3,∴S=OC•OE′=4×3=12.。
2020中考数学一轮专项复习——四边形中考真题(压轴题)综合提升卷(含详细解答)
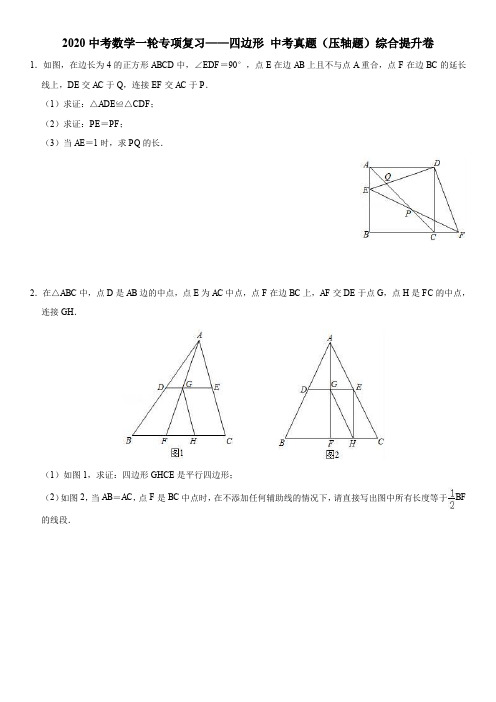
2020中考数学一轮专项复习——四边形中考真题(压轴题)综合提升卷1.如图,在边长为4的正方形ABCD中,∠EDF=90°,点E在边AB上且不与点A重合,点F在边BC的延长线上,DE交AC于Q,连接EF交AC于P.(1)求证:△ADE≌△CDF;(2)求证:PE=PF;(3)当AE=1时,求PQ的长.2.在△ABC中,点D是AB边的中点,点E为AC中点,点F在边BC上,AF交DE于点G,点H是FC的中点,连接GH.(1)如图1,求证:四边形GHCE是平行四边形;(2)如图2,当AB=AC,点F是BC中点时,在不添加任何辅助线的情况下,请直接写出图中所有长度等于BF 的线段.3.一个六边形的花坛被分割成7个部分,其中四边形PRBA,RQDC,QPFE为正方形.记正方形PRBA,RQDC,QPFE的面积分别为S1,S2,S3,RH⊥PQ,垂足为H.(友情提示:正方形的四个内角都等于90度,四边都相等)(1)若PR⊥QR,S1=16,S2=9,则S3=,RH=;(2)若四边形PRBA,RQDC,QPFE的面积分别为25m2、13m2、36m2①求△PRQ的面积;②请判断△PRQ和△DEQ的面积的数量关系,并证明你的结论;③六边形花坛ABCDEF的面积是m2.参考答案1.如图,在边长为4的正方形ABCD中,∠EDF=90°,点E在边AB上且不与点A重合,点F在边BC的延长线上,DE交AC于Q,连接EF交AC于P.(1)求证:△ADE≌△CDF;(2)求证:PE=PF;(3)当AE=1时,求PQ的长.证明:(1)∵四边形ABCD是正方形,∴DA=DC,∠DAE=∠BCD=∠DCF=∠ADC=90°,∴∠ADE+∠EDC=90°∵∠EDF=90°∴∠EDC+∠CDF=90°∴∠ADE=∠CDF在△ADE和△CDF中,∵∴△ADE≌△CDF(ASA).(2)由(1)知:△ADE≌△CDF,∴AE=CF,作FH∥AB交AC的延长线于H.∵四边形ABCD是正方形,∴∠ACB=∠FCH=45°,∵AB∥FH,∴∠HFC=∠ABC=90°,∴∠FCH=∠H=45°,∴CF=FH=AE,在△AEP和△HFP中,∵,∴△APE≌△HPF(AAS),∴PE=PF;(3)如图中,∵AE∥CD,∴,∵AE=1,CD=4,∴,∵四边形ABCD是正方形,∴AB=BC=4,∠B=90°,∴AC=4,∴AQ=AC=,∵AE=FH=CF=1,∴CH=,∴AH=AC+CH=4+=5,由(2)可知:△APE≌△HPF,∴AP=PH,∴AP=AH=,∴PQ=AP﹣AQ=﹣=.2.在△ABC中,点D是AB边的中点,点E为AC中点,点F在边BC上,AF交DE于点G,点H是FC的中点,连接GH.(1)如图1,求证:四边形GHCE是平行四边形;(2)如图2,当AB=AC,点F是BC中点时,在不添加任何辅助线的情况下,请直接写出图中所有长度等于BF 的线段.证明:(1)∵点D是AB边的中点,点E为AC中点,∴DE∥BC,∴=1,∴点G是AF的中点,∵点H是FC的中点,∴FG∥CE,∵GE∥CH,∴四边形GHCE是平行四边形;(2)解:由(1)知,点G是AF的中点,∵点D是AB边的中点,点E为AC中点,∴DG=BF,EG=CF,∵点F是BC中点,∴BF=CF,∴DG=EG=BF,∵四边形GHCE是平行四边形;∴EG=CH,∵点H是FC的中点,∴CH=FH=EG,∴DG=EG=FH=CH=BF,即图中所有长度等于BF的线段为DG,EG,FH,CH.3.一个六边形的花坛被分割成7个部分,其中四边形PRBA,RQDC,QPFE为正方形.记正方形PRBA,RQDC,QPFE的面积分别为S1,S2,S3,RH⊥PQ,垂足为H.(友情提示:正方形的四个内角都等于90度,四边都相等)(1)若PR⊥QR,S1=16,S2=9,则S3=25,RH= 2.4;(2)若四边形PRBA,RQDC,QPFE的面积分别为25m2、13m2、36m2①求△PRQ的面积;②请判断△PRQ和△DEQ的面积的数量关系,并证明你的结论;③六边形花坛ABCDEF的面积是110m2.解:(1)∵PR⊥QR,∴∠PRQ=90°,∴PR2+RQ2=PQ2,∵S1=16,S2=9,∴S 3=16+9=25,∴PR =4,RQ =3,PQ =5,∵RH ⊥PQ ,∴PR •RQ =PQ •RH ,∴RH ==,故答案为:25,2.4;(2)①设PH =a ,则QH =6﹣a ,∵RH 2=PR 2﹣PH 2=RQ 2﹣HQ 2,∴25﹣a 2=13﹣(6﹣a )2,解得:a =4,∴RH 2=PR 2﹣PH 2=25﹣16=9,∴RH =3,∴S △PQR =×6×3=9;②S △PRQ =S △DQE ,证明:延长RQ 到点M ,使QM =RQ ,连结PM ,∵QD =QM ,∠DQE =∠MQP ,QE =QP∴△DQE ≌△MQP (SAS ),∴S △DQE =S △MQP ,∵RQ =QM ,∴S △PRQ =S △MQP ,∴S △PRQ =S △DQE ;③六边形花坛ABCDEF 的面积=25+13+36+4×9=74+36=110m 2.故答案为:110.4.如图.在平行四边形ABCD中(BC>AB),过A作AF⊥BC,垂足为F,过C作CH⊥AB,垂足为H,交AF于G,点E为FC上一点,且GE⊥ED.(1)若FC=2BF=4,AB=2,求平行四边形ABCD的面积;(2)若AF=FC,F为BE中点,求证:ED=(AD+AG).(1)解:∵FC=2BF=4,∴BF=2,∴BC=BF+FC=2+4=6,∵AF⊥BC,∴AF===4,∴平行四边形ABCD的面积=BC×AF=6×4=24;(2)证明:∵AF⊥BC,CH⊥AB,∴∠AFB=∠CFG=∠AHG=90°,∠BAF+∠ABF=∠GCF+∠ABF=90°,∴∠BAF=∠GCF,在△ABF和△CGF中,,∴△ABF≌△CGF(ASA),∴AB=CG,BF=GF,∵F为BE中点,∴BF=EF=GF,∵AF=CF,∴AG=CE,连接AC,如图所示:∵GE⊥ED,∴∠GCD=90°,∵∠AGC=∠AHG+∠BAF=90°+∠BAF,∠ECD=∠GCD+∠GCF=90°+∠GCF,∴∠AGC=∠ECD,∵四边形ABCD是平行四边形,∴AD=BC,AB=DC,∴CG=DC,在△AGC和△ECD中,,∴△AGC≌△ECD(SAS),∴AC=ED,∵AF⊥BC,AF=CF,∴△ACF是等腰直角三角形,∴ED=AC=CF,∵AD+AG=BC+CE=CF+BF+CE=CF+EF+CE=2CF,∴CF=(AD+AG),∴ED=CF=(AD+AG).5.已知,如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.(1)求证:①△BCG≌△DCE.②BH⊥DE.(2)当BH平分DE时,求GC的长.(1)证明:∵正方形ABCD,∴∠BCD=90°,BC=CD,同理:CG=CE,∠GCE=90°,∴∠BCD=∠GCE=90°,,∴△BCG≌△DCE(SAS),∴∠GBC=∠CDE,在Rt△DCE中∠CDE+∠CED=90°,∴∠GBC+∠BEH=90°,∴∠BHE=180°﹣(∠GBC+∠BHE)=90°,∴BH⊥DE;(2)若BH垂直平分DE,连接BD,∴BD=BE,∵BD=,∴CG=CE=BE﹣BC=﹣1.6.如图,过矩形ABCD的对角线AC的中点O做EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.(1)求证:四边形AECF是菱形;(2)若AB=,∠DCF=30°,求EF的长.解:(1)证明:∵O是AC的中点,且EF⊥AC,∴AF=CF,AE=CE,OA=OC,∵四边形ABCD是矩形,∴AD∥BC,∴∠AFO=∠CEO,在△AOF和△COE中,,∴△AOF≌△COE(AAS),∴AF=CE,∴AF=CF=CE=AE,∴四边形AECF是菱形;(2)∵四边形ABCD是矩形,∴CD=AB=,在Rt△CDF中,cos∠DCF=,∠DCF=30°,∴CF==2,∵四边形AECF是菱形,∴CE=CF=2.7.如图,在四边形ABCD中,AD∥BC,AB=8,AD=16,BC=22,∠ABC=90°,点P从点A出发,以每秒1单位的速度向点D运动,点Q从点C同时出发,以每秒v单位的速度向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为t秒.(1)当v=3时,若以点P,Q和点A,B,C,D中的两个点为顶点的四边形为平行四边形,且线段PQ为平行四边形的一边,求t的值;(2)若以点P,Q和点A,B,C,D中的两个点为顶点的四边形为菱形,且线段PQ为菱形的一条对角线,请直接写出t的值.解:(1)∵当P、Q两点与A、B两点构成的四边形是平行四边形时,∵AP∥BQ,∴当AP=BQ时,四边形APQB为平行四边形.此时,t=22﹣3t,t=.当P、Q两点与C、D两点构成的四边形是平行四边形时,∵PD∥QC,∴当PD=QC时,四边形PQCD为平行四边形.此时,16﹣t=3t,t=4,∵线段PQ为平行四边形的一边,故当t=或4时,线段PQ为平行四边形的一边.(2)当PD=BQ=BP时,四边形PBQD能成为菱形.由PD=BQ,得16﹣t=22﹣3t,解得t=3,当t=3时,PD=BQ=13,AP=AD﹣PD=16﹣13=3.在Rt△ABP中,AB=8,根据勾股定理得,BP═≠13∴四边形PBQD不能成为菱形;如果Q点的速度改变为vcm/s时,能够使四边形PBQD在时刻ts为菱形,由题意得,,解得,.故点Q的速度为2cm/s时,能够使四边形PBQD在t=6时为菱形.8.如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.计算:(1)当点E与点D重合时,△BDF的面积为18;当点E为CD的中点时,△BDF的面积为18.证明:(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF 与S正方形ABCD之间的关系,并证明你的猜想;运用:(3)如图2,设BF与CD相交于点H,若△DFH的面积为,求正方形CEFG的边长.解:计算:(1)∵当点E与点D重合时,∴CE=CD=6,∵四边形ABCD,四边形CEFG是正方形,∴DF=CE=AD=AB=6,∴S△BDF=×DF×AB=18,如图,连接CF,∵四边形ABCD和四边形CEFG 均为正方形;∴∠CBD =∠GCF =45°,∴BD ∥CF ,∴S △BDF =S △BDC =S 正方形ABCD =×36=18,故答案为:18,18;证明:(2)S △BDF =S 正方形ABCD ,理由:连接CF .∵四边形ABCD 和四边形CEFG 均为正方形,∴∠CBD =∠GCF =45°,∴BD ∥CF ,∴S △BDF =S △BDC =S 正方形ABCD ;运用:(3)如图2,∵S △BDF =S 正方形ABCD =×36=18,且S △BDF =S △BDH +S △DFH ,∴S △BDH =18﹣=,∴×DH ×6=,∴DH =,∴S △BDH =××EF =,∴EF =4 ∴正方形CEFG 的边长为4.9.已知如图,点C 、D 在线段AF 上,AD =CD =CF ,∠ABC =∠DEF =90°,AB ∥EF .(1)若BC =2,AB =2,求BD 的长;(2)求证:四边形BCED 是平行四边形.(1)解:∵∠ABC=90°,∴AC===2,∵AD=CD,∴BD=AC=;(2)证明:∵AD=CD=CF,∴DF=AC=2,∵∠DEF=90°,∴CE=DF=,∴BD=CE,∵AB∥EF,∴∠A=∠F,在△ABC和△FED中,,∴△ABC≌△FED(AAS),∴BC=ED,∵BD=CE,∴四边形BCED是平行四边形.10.如图,在矩形ABCD中,M是BC上一点,EF垂直平分AM,分别交BC,AM,AD于点E,O,F,连接AE,MF.(1)求证:四边形AEMF是菱形;(2)若AB=6,H为AB的中点,连接OH交AE于点P,OH+OA=9,求△OPE的周长.(1)证明:∵EF垂直平分AM,∴AE=EM,OA=OM.∵四边形ABCD是矩形,∴AD∥BC.∴∠AFO=∠MEO,在△OF和△MOE中,,∴△AOF≌△MOE(AAS).∴OF=OE.∴四边形AEMF是平行四边形.∵AE=EM.∴四边形AEMF是菱形;(2)解:∵O、H分别为AM、AB的中点,∴BM=2OH,AM=2OA,∴AM+BM=2OA+2OH=18.设BM=x,则AM=18﹣x,在Rt△ABM中,由勾股定理得:62+x2=(18﹣x)2,解得:x=8,∴BM=8,AM=10.∴OA=AM=5,设EM=m,则BE=8﹣m,AE=EM=m,在Rt△ABE中,由勾股定理得:62+(8﹣m)2=m2,解得:m=,∴AE=EM=在Rt△AOE中,EO===.∵OP∥EM,∴==1,∴AP=PE,∴OP=EM=,∵PE=AE=,∴△OPE的周长=EO+PE+OP=++=10.11.如图,在平行四边形ABCD中,点E在边AD上,点F在边CB的延长线上,联结CE、EF,CE2=DE•CF.(1)求证:∠D=∠CEF;(2)联结AC,交EF于点G,如果AC平分∠ECF,求证:AC•AE=CB•CG.(1)证明:∵CE2=DE•CF,即=∵四边形ABCD为平行四边形,∴AD∥BC,∴∠DEC=∠ECF,∴△CDE∽△CEF,∴∠D=∠CEF.(2)如图所示:∵AC平分∠ECF,∴∠ECA=∠BCA,∵∠D=∠CEF,∠D=∠B,∴∠CEF=∠B,∴△CGE∽△CAB,∴=,∵AD∥BC,∴∠DAC=∠BCA,∵∠ECA=∠DAC,∴AE=CE,∴=,即AC•AE=CB•CG.12.【猜想】如图1,在平行四边形ABCD中,点O是对角线AC的中点,过点O的直线分别交AD.BC于点E.F.若平行四边形ABCD的面积是8,则四边形CDEF的面积是4.【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD =10,求四边形ABFE 的面积.【应用】如图3,在Rt △ABC 中,∠BAC =90°,延长BC 到点D ,使DC =BC ,连结AD ,若AC =3,AD =2,则△ABD 的面积是 6 .解:猜想:∵四边形ABCD 是平行四边形,∴AD ∥BC ,OA =OC .∴∠EAO =∠FCO ,∠AEO =∠CFO ,在△AOE 和△COF 中,,∴△AEO ≌△CFO (AAS ),∴四边形CDEF 的面积=S △ACD =▱ABCD 的面积=4;故答案为:4;探究:∵四边形ABCD 是菱形,∴AD ∥BC ,AO =CO AC =2.5,BO =BD =5,∠AOD =90°,∴AB =AC =,∠OAE =∠OCF ,∠OEA =∠OFC , 在△AOE 于△COF 中,,∴△AOE ≌△COF (AAS ),∵AC ⊥BD ,∴S 四边形ABFE =S △ABC =AC •BO =××5=.应用:延长AC 到E 使CE =AC =3,在△ABC 与△CDE 中,,∴△ABC ≌△CDE (SAS ),∴∠E =∠BAC =90°,∴DE =,∴S △ABD =S △ADE =AE •DE =×6×2=6.故答案为:613.已知,如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE.(1)DE的长为5.(2)动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,求当t为何值时,△ABP和△DCE全等?(3)若动点P从点B出发,以每秒1个单位的速度仅沿着BE向终点E运动,连接DP.设点P运动的时间为t 秒,是否存在t,使△PDE为等腰三角形?若存在,请直接写出t的值;否则,说明理由.解:(1)∵四边形ABCD是矩形∴AB=CD=4,AD=BC=6,CD⊥BC在Rt△DCE中,DE===5故答案为5.(2)若△ABP与△DCE全等∴BP=CE或AP=CE当BP=CE=3时,则t==3秒当AP=CE=3时,则t==13秒∴求当t为3秒或13秒时,△ABP和△DCE全等.(3)若△PDE为等腰三角形则PD=DE或PE=DE或PD=PE当PD=DE时,∵PD=DE,DC⊥BE∴PC=CE=3∵BP=BC﹣CP=3∴t==3当PE=DE=5时,∵BP=BE﹣PE∴BP=9﹣5=4∴t==4当PD=PE时,∴PE=PC+CE=3+PC∴PD=3+PC在Rt△PDC中,DP2=CD2+PC2.∴(3+PC)2=16+PC2∴PC=∵BP=BC﹣PC∴BP=∴t==综上所述:当t=3秒或4秒或秒时,△PDE为等腰三角形.14.如图1,在正方形ABCD中,点E为边AB上的点,BE:AE=n,连结DE、BD,过点A作AG⊥DE,垂足为点F,与BC、BD分别交于点G、H,连结EH.(1)①求证:AE=BG;②求证:DH:BH=n+1;(2)如图2,当EH∥AD时,求n的值.证明:(1)①∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠ABC=90°,∴∠DAG+∠BAG=90°,∵AG⊥DE,∴∠DAG+∠ADF=90°,∴∠BAG=∠ADF,且AD=AB,∠DAB=∠ABG,∴△ADE≌△BAG(ASA),∴AE=BG.②∵△ADE≌△BAG,∴BG=AE,∵四边形ABCD是正方形∴AD∥BC∴△ADH∽△GBH∴,∵BE:AE=n,BG=AE,AD=AB,∴==.(2)解:设BG=AE=k,则B E=nk,∵EH∥AD∴∠BEH=∠BAD=90°,∠EHB=∠ADB=45°,且∠ABD=45°∴∠EHB=∠ABD∴BE=EH=nk,∵EH∥AD∴△AEH∽△ABG,∴,∴,∵n>0,∴n=.15.如图,在平行四边形ABCD中,∠ACB=45°,点E在对角线AC上,BE的延长线交CD于点F,交AD的延长线于点G.(1)若BE=,EC=,求△BCE的面积;(2)若∠ABE=2∠EBC,且AB=BE,求证:EC=DG.解:(1)如图(1),过E作EN⊥BC于N,∵∠ACB=45°,∴△ENC是等腰直角三角形,∵CE=,∴EN=NC=1,∵BE=,∴BN===3,∴BC=3+1=4,∴△BCE的面积=×4×1=2;(2)如图(2),设∠EBC=x,则∠ABE=2x,∠AEB=∠EBC+∠ACB=45+x,∵AB=BE,∴∠BAE=∠AEB=45+x,∴2x+2(45+x)=180,x=22.5°,∴∠ABE=45°,∠BAE=∠BEA=67.5°,∴∠BEC=180°﹣67.5°=112.5°,过E作EN⊥AB于N,过C作CH⊥AB于H,交BE于M,则∠AHC=90°,∵AB∥CD,∴∠BFC=∠ABE=45°,∠FCM+∠AHC=180°,∴∠FCM=90°,∴△FCM是等腰直角三角形,∴FC=CM,∠EMC=45°,Rt△BCH中,∠HBC=67.5°,∴∠BCH=22.5°,∴∠MBC=∠BCH,∴BM=CM=CF,∵AB=BE=CD,∴BE﹣BM=CD﹣CF,即EM=DF,∵∠DFG=∠EMC=45°,∠MEC=∠FDG=180°﹣67.5°=112.5°,∴△MEC≌△FDG(ASA),∴EC=DG.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年中考数学专项总复习——四边形测试卷
说明:本试卷共6大题,计21小题,满分120分,考试时间100分钟。
中考对接点
平行四边形、矩形、菱形、正方形的性质及判定,多边形的相关概念,多边形的内角和与外角和公式,命题平行线间的距离、中位线定理
单元疑难点
平行四边形及特殊的平行四边形的性质,结合图形变换等相关的计算与证明问题
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A 、B 、C 、D 四个选项,其中只有一个是正确的,请将正确答案的代号填入题后括号内.
1.下列说法正确的是
A.对角线互相垂直的四边形是菱形
B.矩形的对角线互相垂直
C.一组对边平行的四边形是平行四边形
D.对角线相等的菱形是正方形
2.如图,在Rt △ABC 中,∠ACB=90°,CD 为斜边AB 上的中线,点E ,F 分别为BC ,BD 的中点,若AB=8,则EF 的长度为
A.1
B.2
C.3
D.3
3.如图,在菱形ABCD 中,E ,F 分别是AB ,AC 的中点,若EF=2,AC=6,则菱形ABCD 的面积为
A.510
B.15
C.12
D.76
4.如图,正方形ABCO 的顶点C ,A 分别在x 轴,y 轴上,BC 是菱形BDCE 的对角线.若BC=6,BD=5,则点D 的坐标是
A.(10,3)
B.(9,3)
C.(10,2)
D.(9,2)
5.如图,已知∠1=40°,∠A+∠B=140°,则∠C+∠D 的度数为
A.40°
B.60°
C.80°
D.100°
6.如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,这个条件可以是
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
7.如图,在矩形ABCD中,AB=8,AD=6,过点D作直线m//AC,点E,F是直线m上的两个动点,在运动过程中EF=AC,则四边形ACFE的面积是
A.48
B.40
C.24
D.30
8.如图,在□ABCD中,E为边BC上一点,以AE为边作矩形AEFG.若∠BAE=40°,∠CEF=15°,则∠D的大小为
A.25°
B.55°
C.65°
D.75
9.如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐
标为(2,0),点B的坐标为(0,1),点C在第一象限,对角
线BD与x轴平行,直线y=x+4与x轴,y轴分别交于点E,F,
将菱形ABCD沿x轴向左平移个单位长度,当点C落在△EOF
的内部(不包括三角形的边)时,k的值可能是
A.2
B.3
C.4
D.5
10.如图,在□ABCD中,直线l上BD,将直线l沿BD从点B匀速
平移至点D,在运动过程中,直线与口ABCD两边的交点分别记
为点E,F.设线段EF的长为y,平移时间为t,则下列图象中,能
表示y与t的函数关系的大致图象的是
二、填空题(本大题共4小题,每小题5分,满分20分)
11.四边形具有不稳定性,如图,将矩形ABCD按箭头方向变形成平行四边形AB'C'D,使得点B在线段AB的中垂线上,则∠BAB=_________.
12.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD,CB为边作平行四边形CDEB,当AD=时,平行四边形CDEB为菱形.
13.如图,在正方形ABCD中,有一直角三角形PEF,点P与点A重合,
点E在边BC上,PE
=2,EF=1,当点P沿着AB从点A开始运动,点E沿着直线BC运动,
△PEF也随之运动,且当点P运动到点B时运动停止,则在整个运动
过程中点F与点B距离的最大值是_________.
2,若P是□ABCD边上异14.在□ABCD中,∠B=60°,AB=BC=4,点E在边BC上,CE=3
于点E的另一个点,且CE=CP,则AP2的值为.
三、(本大题共2小题,每小题8分,满分16分)
15.如果一个多边形的内角和与外角和之比是13:2,求这个多边形的边数.
16.如图,在菱形ABCD中,O是对角线AC上一点,连接OB,OD.求证:OB=OD.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在正方形ABCD中,G是CD边上任意一点,连接BG,作AE⊥BG于点E,CF⊥BG 于点F.求证:BE=CF.
18.如图,将 ABCD的边DC延长至点E,使CE=CD,连接AE,BE,AC,AE交BC于点O,且∠AOC=2∠ABC,求证:四边形ABEC是矩形.
五、(本大题共2小题,每小题9分,满分18分)
19.如图,在Rt△ABC中,∠ACB=90°,E为CA延长线上一点,D为AB上一点,F为△ABC 外一点,且AC=AE=AF=AD=1,EF∥AB,连接DF,BF.
(1)当∠CAB的度数是多少时,四边形ADFE为菱形?请说明理由.
(2)若四边形ACBF为正方形,求线段AB的长度.
20.如图,四边形ABCD是矩形,∠ECD=∠DBA,∠CED=90°,AF⊥BD于点F.
(1)求证:四边形BCEF是平行四边形.
(2)若AB=4,AD=3,求EC的长.
六、(本题满分10分)
21.如图,四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形、
(2)当线段DE与正方形ABCD的某条边的夹角是35°时,求∠EFC的度数。
