离散数学答案1-)()
《离散数学》题库及标准答案

《离散数学》题库及标准答案《离散数学》题库及答案————————————————————————————————作者:————————————————————————————————日期:《离散数学》题库与答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?( )(1)?Q=>Q→P (2)?Q=>P→Q (3)P=>P→Q (4)?P∧(P∨Q)=>?P答:在第三章里面有公式(1)是附加律,(4)可以由第二章的蕴含等值式求出(注意与吸收律区别)2、下列公式中哪些是永真式?( )(1)(┐P∧Q)→(Q→?R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答:(2),(3),(4)可用蕴含等值式证明3、设有下列公式,请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ?(P→Q)=>P (6) ?P∧(P∨Q)=>?P答:(2)是第三章的化简律,(3)类似附加律,(4)是假言推理,(3),(5),(6)都可以用蕴含等值式来证明出是永真蕴含式4、公式?x((A(x)→B(y,x))∧?z C(y,z))→D(x)中,自由变元是( ),约束变元是( )。
答:x,y, x,z(考察定义在公式?x A和?x A中,称x为指导变元,A为量词的辖域。
在?x A和?x A的辖域中,x的所有出现都称为约束出现,即称x为约束变元,A中不是约束出现的其他变项则称为自由变元。
于是A(x)、B(y,x)和?z C(y,z)中y为自由变元,x和z为约束变元,在D(x)中x为自由变元)5、判断下列语句是不是命题。
若是,给出命题的真值。
( )(1)北京是中华人民共和国的首都。
(2) 陕西师大是一座工厂。
(3) 你喜欢唱歌吗? (4) 若7+8>18,则三角形有4条边。
离散数学习题及答案01

CIS 607: Mathematical Basis for ComputingSOLUTIONS OF HOMEWORK 1Homework 1 -- Propositional Logic, Predicate Logic and ProofsDue Date: February 14, 2017In this homework, you will answer the following questions. Prepare a pdf file for your solutions and upload that pdf file into the blackboard system.Q1)Let p and q be the propositionsp : I bought a lottery ticket this week.q : I won the million dollar jackpot.Express each of these propositions as an English sentence.∙p →qo If I bought a lottery ticket this week, then I won the million dollar jackpot on Friday.∙¬p ∨(p ∧q)o Either I did not buy a lottery ticket this week, or else I did buy one and won the million dollar jackpot on Friday.∙¬p →¬qo If I did not buy a lottery ticket this week, then I did not win the million dollar jackpot on Friday.Q2)Let p and q be the propositionsp : It is below freezing.q : It is snowing.Write these propositions using p and q and logical connectives (including negations).∙It is not below freezing and it is not snowing.o(¬p ∧¬q)∙If it is below freezing, it is also snowing.o p →q∙Either it is below freezing or it is snowing, but it is not snowing if it is below freezing.o(p ∨ q) ∧ ( p →¬q)Q3)Construct a truth table for each of these compound propositions.∙p →(¬q ∨r)∙(p →q) ∧(¬p →r)∙(¬p ↔¬q) ↔(q ↔r)∙Show that ¬(p ↔q) and p ↔¬q are logically equivalent.o p q ¬(p ↔q) p ↔¬qo T T F Fo T F T To F T T To F F F F∙Show that (p →q) →r and p →(q →r) are not logically equivalent.o p q r (p →q) →r p →(q →r)o F F F F TQ5)Determine the truth value of each of these statements if the domain consists of all integers.∙∀n(n + 1 > n)o T∙∃n(2n = 3n)o T (when n=0)∙∃n(n = −n)o T (when n=0)∙∀n(3n ≤4n)o F (when n is a negative integer)Q6)Suppose that the domain of the propositional function P(x) consists of the integers 1, 2, and 3. Write out each of these propositions using disjunctions, conjunctions, and negations.∙∃xP(x)o P(1) ∨P(2) ∨P(3)∙∀xP(x)o P(1) ∧P(2) ∧P(3)∙¬∃xP(x)o¬ (P(1) ∨P(2) ∨P(3))∙¬∀xP(x)o¬ (P(1) ∧P(2) ∧P(3))Express the negations of each of these statements so that all negation symbols immediately precede predicates.∙∀x∃y∀zT (x, y, z)o∃x∀y∃z¬T (x, y, z)∙∀x∃yP(x, y) ∨∀x∃yQ(x, y)o∃x∀y¬P(x, y) ∧∃x∀y¬Q(x, y)∙∀x∃y(P(x, y) ∧∃zR(x, y, z))o∃x∀y(¬P(x, y) ∨∀z¬R(x, y, z))∙∀x∃y(P(x, y) →Q(x, y))o∃x∀y(P(x, y) ∧¬Q(x, y))Q8)∙Determine whether ∀x(P(x) →Q(x)) and ∀xP(x) →∀xQ(x) are logically equivalent. Justify your answer.o NOTo P: is even number, Q: is odd numbero∀x P(x) →∀xQ(x) is true since ∀xP(x) is false and ∀xQ(x) is falseo But ∀x(P(x) →Q(x)) is false∙Determine whether ∀x(P(x) ↔Q(x)) and ∀x P(x) ↔∀xQ(x) are logically equivalent. Justify your answer.o NOTo P: is even number, Q: is odd numbero∀x P(x) ↔∀xQ(x) is true since ∀xP(x) is false and ∀xQ(x) is falseo But ∀x(P(x) ↔Q(x)) is false∙Show that ∃x(P(x) ∨Q(x)) and ∃xP(x) ∨∃xQ(x) are logically equivalent.o if ∃x(P(x) ∨Q(x)) is trueo P(a) ∨Q(a) is true for a constant ‘a’ (∃-inst)o If P(a) is true →∃xP(x)is true →∃xP(x) ∨∃xQ(x) is trueo If Q(a) is true →∃xQ(x)is true →∃xP(x) ∨∃xQ(x) is trueoo if ∃x(P(x) ∨Q(x)) is falseo→ there is no constant such that P(a) ∨Q(a) is trueo→ there is no constant such that P(a) is true or there is no constant such that Q(a) is trueo→∃xP(x) is false and ∃xQ(x) is falseo→∃xP(x) ∨∃xQ(x) is falseQ9)∙Use rules of inference to show that if ∀x(P(x) →(Q(x) ∧S(x))) and ∀x(P(x) ∧R(x)) are true, then ∀x(R(x) ∧S(x)) is true.Step Reason1.∀x(P(x) → (Q(x) ∧ S(x))) Premise2.∀x(P(x) ∧ R(x)) Premise3.P(a) ∧ R(a) for arbitrary a UI from 24.P(a) for arbitrary a Simplification from 35.R(a) for arbitrary a Simplification from 36.P(a) → (Q(a) ∧ S(a))) for arbitrary a UI from 17.(Q(a) ∧ S(a)) for arbitrary a MP from 4 and 68.S(a) for arbitrary a Simplification from 79.R(a) ∧ S(a) for arbitrary a Conjunction from 5 and 810.∀x(R(x) ∧ S(x)) UG from 9∙Use rules of inference to show that if ∀x(P(x) ∨Q(x)), ∀x(¬Q(x) ∨S(x)), ∀x(R(x)→¬S(x)), and ∃x¬P(x) are true, then ∃x¬R(x) is true.Step Reason1.∀x(P(x) ∨ Q(x)) Premise2.∀x(¬Q(x) ∨ S(x)) Premise3.∀x(R(x) →¬S(x)) Premise4.∃x¬P(x) Premise5.¬P(a) for some a EI from 46.P(a) ∨ Q(a) UI from 17.Q(a) for some a Disjunctive Syllogism from 5 and 68.¬Q(a) ∨ S(a) UI from 29.S(a) for some a Disjunctive Syllogism from 7 and 810.R(a) →¬S(a) UI from 311.¬R(a) for some a Modes Tollens from 9 and 1012.∃x¬R(x) Existential Generalization (EG) from 11Q10)∙Use a direct proof to show that every odd integer is the difference of two squares.Direct Proofo Let n be an odd integer such that n=2k+1 where k is an integer (definition of odd integers) o Let squares of two integers k and (k+1) such as k2 and (k+1)2= k2+2k+1o(k+1)2 - k2 = 2k+1o So, n is the difference of two squares.o QED∙Show that if n is an integer and n3+ 5 is odd, then n is even using a proof by contraposition.Proof by Contrapositiono Assume n is an odd integer (negation of even is odd)o So, n=2k+1 where k is an integer (definition of odd integers)o n3 + 5 = (2k+1)3 + 5 = 8k3+12k2 +6k+1+5 = 2(4k3+6k2 +3k+3)o So, n3 + 5 = 2m where m is an integer such that m = (4k3+6k2 +3k+3)o Thus, n3 + 5 is an even integer (negation of “n3 + 5 is odd”)o Then, n is even (not odd)o QED.∙Prove that if n is an integer and 3n + 2 is even, then n is even using a proof by contradiction.Proof by Contradictiono Assume that n is an odd integer (negation of even is odd)o So, n=2k+1 where k is an integer (definition of odd integers)o3n+2 = 3(2k+1)+2 = 6k+5 = 2(3k+2)+1o So, 3n+2 = 2m+1 where m is an integer such that m=3k+2o Thus, 3n+2 is odd (contradiction with our assumption “3n + 2 is even”)o So, n is eveno QED.。
离散数学练习题2 答案
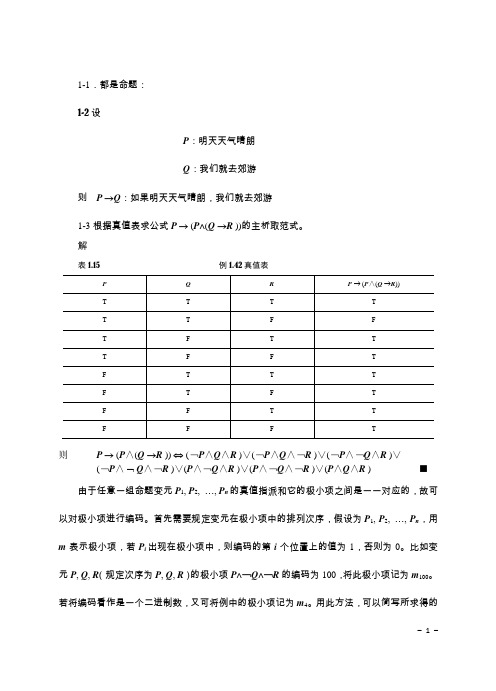
1-1.都是命题:1-2设P:明天天气晴朗Q:我们就去郊游则P →Q:如果明天天气晴朗,我们就去郊游1-3根据真值表求公式P → (P∧(Q →R ))的主析取范式。
解表1.15 例1.42真值表则P → (P∧(Q →R )) ⇔ (﹁P∧Q∧R )∨(﹁P∧Q∧﹁R )∨(﹁P∧﹁Q∧R )∨⌝(﹁P∧Q∧﹁R )∨(P∧﹁Q∧R )∨(P∧﹁Q∧﹁R )∨(P∧Q∧R ) ■由于任意一组命题变元P1, P2, …, P n的真值指派和它的极小项之间是一一对应的,故可以对极小项进行编码。
首先需要规定变元在极小项中的排列次序,假设为P1, P2, …, P n,用m表示极小项,若P i出现在极小项中,则编码的第i个位置上的值为1,否则为0。
比如变元P, Q, R(规定次序为P, Q, R)的极小项P∧﹁Q∧﹁R的编码为100,将此极小项记为m100。
若将编码看作是一个二进制数,又可将例中的极小项记为m4。
用此方法,可以简写所求得的给定公式的主析取范式。
P → (P∧(Q →R )) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7(规定P, Q, R的次序为P, Q, R)公式P → (P∧(Q →R ))的主析取范式。
解P → (P∧(Q →R ))⇔﹁P∨(P∧(﹁Q∨R ))⇔ (﹁P∨P)∧(﹁P∨﹁Q∨R)⇔ (﹁P∨﹁Q∨R )⇔ (﹁P∨﹁Q∨R )1-4试证明(﹁P →Q )∧(P →R )∧(﹁Q∨S ) ⇒S∨R。
证明(1)﹁P →Q P(2)﹁Q∨S P(3)Q →S T, (2), E16(4)﹁P →S T, (1), (3), I13(5)﹁S →P T, (4), E18(6)P →R P(7)﹁S →R T, (5),(6), I13(8)﹁﹁S∨R T, (7),E16(9)S∨R T, (8), E11-5如果迈克有电冰箱,则或者他卖了洗衣机,或者他向别人借了钱。
离散数学答案

2015春课件作业第一部分集合论第一章集合的基本概念和运算1-1 设集合 A ={{2,3,4},5,1},下面命题为真是 A (选择题) [ A ] A.1 ∈A; B.2 ∈ A; C.3 ∈A; D.{3,2,1} ⊆ A。
1-2 A,B,C 为任意集合,则他们的共同子集是 D (选择题) [ D ] A.C; B.A; C.B; D.Ø。
1-3 设 S = {N,Z,Q,R},判断下列命题是否正确(是非题)(1) N ⊆ Q,Q ∈S,则 N ⊆ S,否[错](2)-1 ∈Z,Z ∈S,则 -1 ∈S 。
否[错]1-4 设集合 B = {4,3} ∩Ø, C = {4,3} ∩{ Ø },D ={ 3,4,Ø },E = {x│x ∈R 并且 x2 - 7x + 12 = 0},F = { 4,Ø,3,3},试问:集合 B 与那个集合之间可用等号表示 A (选择题) [A ]A. C;B. D;C. E;D. F.1-5 用列元法表示下列集合:A = { x│x ∈N 且 3-x 〈 3 }(选择题) [D ]A. N;B. Z;C. Q;D. Z+1-6 为何说集合的确定具有任意性 ? (简答题)按照所研究的问题来确定集合的元素。
而我们所要研究的问题当然是随意的。
所以,集合的定义(就是集合成分的确定)就带有任意性。
第二章二元关系2-1 给定 X =(3, 2,1),R 是 X 上的二元关系,其表达式如下:R = {〈x,y〉x,y ∈X 且 x > y } (综合题)求:(1)domR =?; (2)ranR =?; (3)R 的性质。
所谓谓词表达法,即是将集合中所有元素的共同性质用一个谓词概括起来,如本题几例所示。
有的书上称其为抽象原则。
反过来,列元法则是遵照元素的性质和要求,逐一将他们列出来,以备下用,结果如下:R = {<1,1>,<2,2>,<3,3>};(1)DomR={R中所有有序对的x}={3,2,1};(2)RanR={R中所有有序对的y}={3,2,1};(3)R 的性质:自反,对称,传递性质.2-2 设 R 是正整数集合上的关系,由方程 x + 3y = 12 决定,即R = {〈x,y〉│x,y ∈Z+ 且 x + 3y = 12},试给出 dom(R 。
离散数学(第二版)最全课后习题答案详解

27.设 A、B 都是含命题变量项 p1,p2,…,pn的公式,证明: 重言式.
是重言式当且仅当 A 和 B 都是
解:
A
B
0
0
0
1
1
0
1
1
由真值表可得,当且仅当 A 和 B 都是重言式时,
0 0 0 1 是重言式。
28. 设 A、B 都是含命题变量项 p1,p2,…,pn的公式,已知
,该式为重言式,所以论述为真。
18.在什么情况下,下面一段论述是真的:“说小王不会唱歌或小李不会跳舞是正确的,而说如 果小王会唱歌,小李就会跳舞是不正确的.” 解:p:小王会唱歌。q:小李会跳舞。
真值为 1.
真值为 0.可得,p 真值为 1,q 真值为 0.
所以,小王会唱歌,小李不会跳舞。
19.用真值表判断下列公式的类型:
(2)p: 是无理数.
(7)p:刘红与魏新是同学. (10)p:圆的面积等于半径的平方乘以 π. (13)p:2008 年元旦下大雪.
3.写出下列各命题的否定式,并将原命题及其否定式都符号化,最后指出各否定式的真值.
(1)5 是有理数.
答:否定式:5 是无理数. p:5 是有理数.q:5 是无理数.其否定式 q 的真值
5.将下列命题符号化,并指出真值. (1)2 或 3 是偶数. (2)2 或 4 是偶数. (3)3 或 5 是偶数. (4)3 不是偶数或 4 不是偶数. (5)3 不是素数或 4 不是偶数.
答: p:2 是偶数,q:3 是偶数,r:3 是素数,s:4 是偶数, t:5 是偶数 (1)符号化: p q∨ ,其真值为 1. (2)符号化:p r∨ ,其真值为 1. (3)符号化:r t∨ ,其真值为 0. (4)符号化:¬ ∨¬q s,其真值为 1. (5)符号化:¬ ∨¬r s,其真值为 0.
离散数学课后答案

离散数学课后答案习题一6.将下列命题符号化。
(1)小丽只能从框里那一个苹果或一个梨.(2)这学期,刘晓月只能选学英语或日语中的一门外语课.答:(1)(p Λ¬q )ν(¬pΛq)其中p:小丽拿一个苹果,q:小丽拿一个梨(2)(p Λ¬q )ν(¬pΛq)其中p:刘晓月选学英语,q:刘晓月选学日语14.将下列命题符号化.(1) 刘晓月跑得快, 跳得高.(2)老王是山东人或河北人.(3)因为天气冷, 所以我穿了羽绒服.(4)王欢与李乐组成一个小组.(5)李辛与李末是兄弟.(6)王强与刘威都学过法语.(7)他一面吃饭, 一面听音乐.(8)如果天下大雨, 他就乘班车上班.(9)只有天下大雨, 他才乘班车上班.(10)除非天下大雨, 他才乘班车上班.(11)下雪路滑, 他迟到了.(12)2与4都是素数, 这是不对的.(13)“2或4是素数, 这是不对的”是不对的.答:(1)p∧q, 其中, p: 刘晓月跑得快, q: 刘晓月跳得高.(2)p∨q, 其中, p: 老王是山东人, q: 老王是河北人.(3)p→q, 其中, p: 天气冷, q: 我穿了羽绒服.(4)p, 其中, p: 王欢与李乐组成一个小组, 是简单命题.(5)p, 其中, p: 李辛与李末是兄弟.(6)p∧q, 其中, p: 王强学过法语, q: 刘威学过法语.(7)p∧q, 其中, p: 他吃饭, q: 他听音乐.(8)p→q, 其中, p: 天下大雨, q: 他乘班车上班.(9)p→q, 其中, p: 他乘班车上班, q: 天下大雨.(10)p→q, 其中, p: 他乘班车上班, q: 天下大雨.(11)p→q, 其中, p: 下雪路滑, q: 他迟到了.(12) ¬ (p∧q)或¬p∨¬q, 其中, p: 2是素数, q: 4是素数.(13) ¬ ¬ (p∨q)或p∨q, 其中, p: 2是素数, q: 4是素数.16.19.用真值表判断下列公式的类型:(1)p→ (p∨q∨r) (2)(p→¬q) →¬q(3) ¬ (q→r) ∧r(4)(p→q) →(¬q→¬p)(5)(p∧r) ↔( ¬p∧¬q)(6)((p→q) ∧ (q→r)) → (p→r)(7)(p→q) ↔ (r↔s)答:(1), (4), (6)为重言式.(3)为矛盾式.(2), (5), (7)为可满足式习题二9.用真值表求下面公式的主析取范式.(1) (pνq)ν(¬pΛr)(2) (p→q) →(¬p↔q)答:(1)(2)p q (p → q) →(¬p ↔ q)0 0 1 0 0 10 1 1 1 1 01 0 0 1 1 11 1 1 0 0 0从真值表可见成真赋值为01, 10.于是(p → q) →(¬p ↔ q) ⇔ m1 ∨ m211.用真值表求下面公式的主析取范式和主合取范式;(1) (pνq)Λr(2) p→(pνqνr)(3) ¬(q→¬p)Λ¬p15.用主析取范式判断下列公式是否等值:(1) (p→q) →r与q→ (p→r)(2) ¬(pΛq)与(¬pνq)答:(1)(p→q) →r ⇔¬(¬p∨q) ∨ r ⇔¬(¬p∨q) ∨ r ⇔ p¬∧q ∨ r ⇔p¬∧q∧(r¬∨r) ∨(p¬∨p) ∧(q¬∨q)∧r ⇔p¬∧q∧r ∨p¬∧q∧¬r ∨ p ∧q∧r ∨ p∧¬q∧r ∨¬p∧q∧r ∨¬p∧¬q∧r = m101 ∨ m100 ∨ m111 ∨m101 ∨ m011 ∨ m001 ⇔m1 ∨ m3 ∨ m4 ∨ m5 ∨ m7 = ∑(1, 3, 4, 5, 7).而 q→(p→r) ⇔¬q ∨(¬p∨r) ⇔¬q ∨¬p ∨r ⇔(¬p∨p)¬∧q∧(¬r∨r) ∨¬p∧(¬q∨q)∧(¬r∨r) ∨(¬p∨p)∧(¬q∨q)∧r ⇔(¬p¬∧q∧¬r)∨(¬p¬∧q∧r)∨(p¬∧q∧¬r)∨(p¬∧q∧r) ∨(¬p∧¬q∧¬r)∨(¬p∧¬q∧r)∨(¬p ∧q∧¬r)∨(¬p∧q∧r) ∨(¬p∧¬q∧r)∨(¬p∧q∧r)∨(p∧¬q∧r)∨(p∧q∧r) = m0 ∨ m1 ∨ m4 ∨ m5 ∨ m0 ∨ m1 ∨ m2 ∨ m3 ∨ m1 ∨ m3 ∨ m5 ∨m7 ⇔ m0 ∨ m1 ∨ m2 ∨ m3 ∨ m4 ∨ m5 ∨ m7 ⇔∑(0, 1, 2, 3, 4, 5, 7). 两个公式的主吸取范式不同, 所以(p→q) →rk q→ (p→r).16. 用主析取范式判断下列公式是否等值:(1)(p→q) →r与q→ (p→r)(2) ¬ (p∧q)与¬ (p∨q)答:(1)(p→q) →r) ⇔m1∨m3∨m4∨m5∨m7q→ (p→r) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7所以(p→q) →r) k q→ (p→r)(2)¬ (p∧q) ⇔m0∨m1∨m2¬ (p∨q) ⇔m0所以¬ (p∧q) k ¬ (p∨q)习题三15.在自然推理系统P中用附加前提法证明下面各推理:(1)前提: p→ (q→r), s→p, q 结论: s→r(2)前提: (p∨q) → (r∧s), (s∨t) →u 结论: p→u答:(1)证明: ① s 附加前提引入② s→p 前提引入③ p ①②假言推理④ p→(q→r) 前提引入⑤ q→r ③④假言推理⑥ q 前提引入⑦ r ⑤⑥假言推理(2)证明: ① P 附加前提引入② p∨q ①附加③ (p∨q) → (r∧s) 前提引入④ r∧s ②③假言推理⑤④化简⑥ s∨t ⑤附加⑦ (s∨t) →u 前提引入⑧ u ⑥⑦假言推理16.在自然推理系统P中用归谬法证明下面推理:(1)前提: p→¬q, ¬r∨q, r∧¬s 结论: ¬p(2)前提: p∨q, p→r, q→s 结论: r∨s答:(1)证明: ① P 结论否定引入② p→¬q 前提引入③¬q ①②假言推理④¬r∨q 前提引入⑤¬r ③④析取三段论⑥ r∧¬s 前提引入⑦ r ⑥化简⑧¬r∧r ⑤⑦合取⑧ 为矛盾式, 由归谬法可知, 推理正确.(2)证明: ①¬ (r∨s) 结论否定引入② p∨q 前提引入③ p→r 前提引入④ q→s 前提引入⑤ r∨s ②③④构造性二难⑥¬ (r∨s) ∧ (r∨s) ①⑤合取⑥为矛盾式, 所以推理正确.18.在自然推理系统P中构造下面推理的证明.(1)如果今天是星期六, 我们就要到颐和园或圆明园去玩. 如果颐和园游人太多, 我们就不去颐和园玩. 今天是星期六. 颐和园游人太多. 所以我们去圆明园玩.(2)如果小王是理科学生, 他的数学成绩一定很好. 如果小王不是文科生, 他必是理科生. 小王的数学成绩不好. 所以小王是文科学生.(1)令 p: 今天是星期六;q: 我们要到颐和园玩;r: 我们要到圆明园玩;s:颐和园游人太多.前提: p→ (q∨r), s →¬q, p, s. 结论: r.证明① p 前提引入② p→q∨r前提引入③q∨r①②假言推理④s前提引入⑤ s →¬q前提引入⑥¬q ④⑤假言推理⑦ r ③⑥析取三段论r ¬q s →¬q sq∨r p→q∨r p(2)令p: 小王是理科生,q: 小王是文科生,r: 小王的数学成绩很好.前提: p→r, ¬q→p, ¬r 结论: q证明:① p→r 前提引入②¬r 前提引入③¬p ①②拒取式④¬q→p 前提引入⑤ q ③④拒取式习题四在一阶逻辑中将下列命题符号化:(1)没有不能表示成分数的有理数.(2)在北京卖菜的人不全是外地人.(3)乌鸦都是黑色的.(4)有的人天天锻炼身体. 没指定个体域, 因而使用全总个体域.答:(1) ¬∃x(F(x) ∧¬G(x))或∀x(F(x) →G(x)), 其中, F(x): x为有理数, G(x): x能表示成分数.(2) ¬∀x(F(x) →G(x))或∃x(F(x) ∧¬G(x)), 其中, F(x): x在北京卖菜,G(x): x是外地人.(3) ∀x(F(x) →G(x)), 其中, F(x): x是乌鸦, G(x): x是黑色的.(4) ∃x(F(x) ∧G(x)), 其中, F(x): x是人, G(x): x天天锻炼身体.5. 在一阶逻辑中将下列命题符号化:(1)火车都比轮船快.(2)有的火车比有的汽车快.(3)不存在比所有火车都快的汽车.(4)“凡是汽车就比火车慢”是不对的.答:因为没指明个体域, 因而使用全总个体域(1) ∀x∀y(F(x) ∧G(y) →H(x,y)), 其中, F(x): x是火车, G(y): y是轮船, H(x,y):x比y快.(2) ∃x∃y(F(x) ∧G(y) ∧H(x,y)), 其中, F(x): x是火车, G(y): y是汽车, H(x,y):x比y快.(3) ¬∃x(F(x) ∧∀y(G(y) →H(x,y))) 或∀x(F(x) →∃y(G(y) ∧¬H(x,y))), 其中, F(x): x是汽车, G(y): y是火车, H(x,y):x比y快.(4) ¬∀x∀y(F(x) ∧G(y) →H(x,y)) 或∃x∃y(F(x) ∧G(y) ∧¬H(x,y) ), 其中, F(x): x是汽车, G(y): y是火车, H(x,y):x比y慢.9.给定解释I如下:(a)个体域DI为实数集合\.(b)DI中特定元素⎯a =0.(c)特定函数⎯f (x,y)=x−y, x,y∈DI.(d)特定谓词⎯F(x,y): x=y,⎯G(x,y): x<y, x,y∈DI.说明下列公式在I下的含义, 并指出各公式的真值:(1) ∀x∀y(G(x,y) →¬F(x,y))(2) ∀x∀y(F(f(x,y),a) →G(x,y))(3) ∀x∀y(G(x,y) →¬F(f(x,y),a))(4) ∀x∀y(G(f(x,y),a) →F(x,y))答:(1) ∀x∀y(x<y→x≠y), 真值为1.(2) ∀x∀y((x−y=0) →x<y), 真值为0.(3) ∀x∀y((x<y) → (x−y≠0)), 真值为1.(4) ∀x∀y((x−y<0) → (x=y)), 真值为0.习题五5.给定解释I如下:(a) 个体域D={3,4}.(b)⎯f (x)为⎯f (3)=4,⎯f (4)=3.(c)⎯F(x,y)为⎯F(3,3)=⎯F(4,4)=0,⎯F(3,4)=⎯F(4,3)=1.试求下列公式在I下的真值:(1) ∀x∃yF(x,y)(2) ∃x∀yF(x,y)(3) ∀x∀y(F(x,y) →F(f(x),f(y)))答:(1) ∀x∃yF(x,y)⇔(F(3,3)∨F(3,4))∧(F(4,3)∨F(4,4))⇔(0∨1)∧(1∨0) ⇔1(2)∃x∀yF(x,y)⇔(F(3,3)∧F(3,4))∨(F(4,3)∧F(4,4))⇔(0∧1)∨(1∧0)⇔0(3)∀x∀y(F(x,y)→F(f(x),f(y)))⇔(F(3,3)→F(f(3),f(3)))∧(F(4,3)→F(f(4),f(3)))∧(F(3,4)→F(f(3),f(4)))∧(F(4,4)→F(f(4),f(4))) ⇔ (0→0)∧(1→1)∧(1→1)∧(0→0)⇔112.求下列各式的前束范式.(1) ∀xF(x) →∀yG(x, y);(3) ∀xF(x, y) ↔∃xG(x, y);答:前束范式不是唯一的.(1) ∀xF(x) →∀yG(x, y) ⇔∃x(F(x) →∀yG(x, y))⇔∃x∀y(F(x) → G(x, y)).(3) ∀xF(x, y) ↔∃xG(x, y) ⇔ (∀xF(x, y) →∃xG(x, y)) ∧ (∃xG(x, y) →∀xF(x, y)) ⇔ (∀x1F(x1, y) →∃x2G(x2, y)) ∧ (∃x3G(x3, y) →∀x4F(x4, y)) ⇔∃x1∃x2(F(x1, y) → G(x2, y)) ∧∀x3∀x4(G(x3, y) → F(x4, y)) ⇔∃x1∃x2∀x3∀x4((F(x1, y) → G(x2, y)) ∧ (G(x3, y) → F(x4, y))).13.将下列命题符号化, 要求符号化的公式全为前束范式:(1) 有的汽车比有的火车跑得快.(2) 有的火车比所有的汽车跑得快.(3) 说所有的火车比所有的汽车跑得快是不对的.(4) 说有的飞机比有的汽车慢是不对的.答:(1)令F(x):x是汽车,G(y):y是火车,H(x,y):x比y跑得快.∃x(F(x)∧∃y(G(y)∧H(x,y))⇔∃x∃y(F(x)∧G(y)∧H(x, y)).(2)令F(x):x是火车, G( y): y 是汽车,H(x,y):x比y跑得快.∃x(F(x)∧∀y(G(y)→ H(x,y)))⇔∃x∀y(F(x)∧(G y)→H(x,y))).;错误的答案:∃x∀y(F(x)∧G(y)→H(x,y)).(3)令F(x):x是火车,G(y):y是汽车,H(x,y):x比y跑得快.¬∀x(F(x)→∀y(G(y)→H(x,y)))⇔¬∀x∀y(F(x)→(G(y)→H(x,y)))⇔¬∀x∀y(F(x)∧G(y)→H(x,y))(不是前束范式)⇔∃x∃y(F(x)∧G(y)∧H(x,y)).(4)令F(x):x是飞机,G(y):y是汽车,H(x,y):x比y跑得慢.¬∃x(F(x)∧∃y(G(y)∧H(x,y)))⇔¬∃x∃y(F(x)∧G(y)∧H(x,y))(不是前束范式)⇔∀x∀y¬(F(x)∧G(y)∧H(x,y))⇔∀x∀y(F(x)∧G(y)→¬H(x,y)).21.24.在自然推理系统F中, 构造下面推理的证明:每个喜欢步行的人都不喜欢骑自行车. 每个人或者喜欢骑自行车或者喜欢乘汽车. 有的人不喜欢乘汽车, 所以有的人不喜欢步行. (个体域为人类集合) 答:令 F(x): x 喜欢步行, G( x): x喜欢骑自行车, H(x): x 喜欢乘汽车.前提:∀x(F(x)→¬G(x)), ∀x(G(x)∨H(y)),∃x¬H(x).结论:∃x¬F(x).② ∀x(G(x) ∨ H(y)) 前提引入② G(c) ∨ H(c) ①UI③∃x¬H(x) 前提引入④¬H(c) ③UI⑤ G(c) ②④析取三段⑥∀x(F(x) →¬G(x)) 前提引入⑦ F(c) →¬G(c) ⑥UI⑧¬F(c) ⑤⑦拒取⑨∃x¬F(x) ⑧EG习题七12.设A={0, 1, 2, 3}, R是A上的关系, 且R={〈0, 0〉, 〈0, 3〉, 〈2, 0〉, 〈2,1〉, 〈2, 3〉, 〈3, 2〉} 给出R的关系矩阵和关系图.16.设A={a,b,c,d}, R1,R2为A上的关系, 其中R1={〈a,a〉,〈a,b〉,〈b,d〉}R2={〈a,d〉,〈b,c〉,〈b,d〉,〈c,b〉} 求R1·R2, R2·R1,R1²,R2³. R1·R2={〈a,a〉,〈a,c〉,〈a,d〉},R2·R1={〈c,d〉}, R1²={〈a,a〉,〈a,b〉,〈a,d〉},R2³={〈b,c〉,〈b,d〉,〈c,b〉}20.设R1和R2为A上的关系,证明: (1)(R1∪R2) −1=R1−1∪R2−1(2)(R1∩R2) −1=R1−1∩R2−1答:(1)(R1∪R2)−1=R1−1∪R2−1任取〈x,y〉〈x,y〉(∈R1∪R2)−1⇔〈y,x〉(∈R1∪R2)⇔〈y,x〉∈R1∨ (y,x)∈R2)⇔〈x,y〉∈R1−1∨〈x,y〉∈R2−1⇔〈x,y〉∈R1−1∨R2−1所以(R1∪R2) −1=R1−1∪R2−1(2)(R1∩R2) −1=R1−1∩R2−1 任取〈x,y〉〈x,y〉(∈R1∩R2) −1⇔〈y,x〉(∈R1∩R2)⇔〈y,x〉∈R1∧ (y,x)∈R2)⇔〈x,y〉∈R1−1∧〈x,y〉∈R2−1⇔〈x,y〉∈R1−1∧R2−1所以(R1∪R2) −1=R1−1∩R2−126.33.43.16.47.。
离散数学参考答案

离散数学参考答案答题: A. B. C. D. 答题: A. B. C. D. 答题: A. B. C. D. 答题: A. B. C. D. 答题: A. B. C. D. 答题: A. B. C. D.答题: A. B. C. D. 答题: A. B. C. D. 答题: A. B. C. D. 答题: A. B. C. D.答题: A. B. C. D.12.(单选题) 设:p:派⼩王去开会。
q:派⼩李去开会。
则命题:“派⼩王或⼩李中的⼀⼈去开会” 可符号化为:()答题: A. B. C. D. (已提交)参考答案:B问题解析:答题: A. B. C. D.答题: A. B. C. D.答题: A. B. C. D.答题: A. B. C. D.答题: A. B. C. D.答题: A. B. C. D.答题: A. B. C. D.问题解析:20.(单选题) 下⾯“”的等价说法中,不正确的为A.p是q的充分条件B.q是p的必要条件C.q仅当p D.只有q才p答题: A. B. C. D. (已提交)参考答案:C问题解析:答题: A. B. C. D.22.(单选题) 下列式⼦是合式公式的是( )A.(P ú ? Q)B.?(P ù(Q ú R))C.(P ? Q)D.ù Q ? ù R答题: A. B. C. D. (已提交)参考答案:B问题解析:23.(单选题) 公式?((p?q)ù(q ? p))与的共同成真赋值为( ) A.01,10 B.10,01 C.11,00 D.01,11答题: A. B. C. D. (已提交)参考答案:A问题解析:24.(单选题) p,q都是命题,则p?q的真值为假当且仅当( ) A.p为假,q为真B.p为假,q也为假C.p为真,q也为真D.p为真,q为假答题: A. B. C. D. (已提交)参考答案:D问题解析:25.(单选题) n个命题变元组成的命题公式,有( )种真值情况A.n B.C. D.2n答题: A. B. C. D. (已提交)参考答案:C问题解析:26.(单选题) 设A , B 代表任意的命题公式,则德?摩根律为(A ù B)?( )A.?A ù ?B B.?A ú ?BC.A ù ?B D.AúB答题: A. B. C. D. (已提交)参考答案:B问题解析:27.(单选题) 设P , Q 是命题公式,德?摩根律为:(P ú Q)?( )A.?P ù ?Q B.?P ú ?QC.P ù ?Q D.PúQ答题: A. B. C. D. (已提交)问题解析:28.(单选题) 命题公式A与B是等值的,是指()。
《离散数学》课后习题答案

1-1,1-2(1)解:a)是命题,真值为T。
b)不是命题。
c)是命题,真值要根据具体情况确定。
d)不是命题。
e)是命题,真值为T。
f)是命题,真值为T。
g)是命题,真值为F。
h)不是命题。
i)不是命题。
(2)解:原子命题:我爱北京天安门。
复合命题:如果不是练健美操,我就出外旅游拉。
(3)解:a)(┓P ∧R)→Qb)Q→Rc)┓Pd)P→┓Q(4)解:a)设Q:我将去参加舞会。
R:我有时间。
P:天下雨。
Q (R∧┓P):我将去参加舞会当且仅当我有时间和天不下雨。
b)设R:我在看电视。
Q:我在吃苹果。
R∧Q:我在看电视边吃苹果。
c) 设Q:一个数是奇数。
R:一个数不能被2除。
(Q→R)∧(R→Q):一个数是奇数,则它不能被2整除并且一个数不能被2整除,则它是奇数。
(5) 解:a)设P:王强身体很好。
Q:王强成绩很好。
P∧Qb)设P:小李看书。
Q:小李听音乐。
P∧Qc)设P:气候很好。
Q:气候很热。
P∨Qd)设P: a和b是偶数。
Q:a+b是偶数。
P→Qe)设P:四边形ABCD是平行四边形。
Q :四边形ABCD的对边平行。
P Qf)设P:语法错误。
Q:程序错误。
R:停机。
(P∨ Q)→ R(6) 解:a)P:天气炎热。
Q:正在下雨。
P∧Qb)P:天气炎热。
R:湿度较低。
P∧Rc)R:天正在下雨。
S:湿度很高。
R∨Sd)A:刘英上山。
B:李进上山。
A∧Be)M:老王是革新者。
N:小李是革新者。
M∨Nf)L:你看电影。
M:我看电影。
┓L→┓Mg)P:我不看电视。
Q:我不外出。
R:我在睡觉。
P∧Q∧Rh)P:控制台打字机作输入设备。
Q:控制台打字机作输出设备。
P∧Q1-3(1)解:a)不是合式公式,没有规定运算符次序(若规定运算符次序后亦可作为合式公式)b)是合式公式c)不是合式公式(括弧不配对)d)不是合式公式(R和S之间缺少联结词)e)是合式公式。
(2)解:a)A是合式公式,(A∨B)是合式公式,(A→(A∨B))是合式公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
06任务_000 1试卷总分:100? ? ? ?测试时间:0单项选择题?一、单项选择题(共?10?道试题,共?100?分。
)1.??命题公式的析取范式是( ).A.B.C.D.2.??设个体域为整数集,则公式"x$y(x+y=0)的解释可为(??? ).A. 存在一整数x有整数y满足x+y=0B. 任一整数x对任意整数y满足x+y=0C. 对任一整数x存在整数y满足x+y=0D.存在一整数x对任意整数y满足x+y=03. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QC. Q→P⇒ PD. ⌝P∧(P∨Q)⇒Q4. 下列公式中( )为永真式.A. ⌝A∧⌝B ↔⌝A∨⌝BB. ⌝A∧⌝B ↔⌝(A∨B)C. ⌝A∧⌝B ↔A∨BD. ⌝A∧⌝B ↔⌝(A∧B)5. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.6. 命题公式(P∨Q)→R的析取范式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R7. 命题公式(P∨Q)的合取范式是( ).A. (P∧Q)B. (P∧Q)∨(P∨Q)C. (P∨Q)D. ⌝(⌝P∧⌝Q)8. 设命题公式G:,则使公式G取真值为1的P,Q,R赋值分别是( ).A. 0, 0, 0B. 0, 0, 1C. 0, 1, 0D. 1, 0, 09. 命题公式P→Q的主合取范式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q10. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q06任务_0002试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 命题公式(P∨Q)→Q为( )A. 矛盾式B. 可满足式C. 重言式D. 合取范式2. 设个体域为整数集,则公式"x$y(x+y=0)的解释可为( ).A. 存在一整数x有整数y满足x+y=0B. 任一整数x对任意整数y满足x+y=0C. 对任一整数x存在整数y满足x+y=0D.存在一整数x对任意整数y满足x+y=03. 命题公式的析取范式是( ).A.B.C.D.4. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q5. 设命题公式G:,则使公式G取真值为1的P,Q,R赋值分别是( ).A. 0, 0, 0B. 0, 0, 1C. 0, 1, 0D. 1, 0, 06. 在谓词公式(∀x)(A(x)→B(x)∨C(x,y))中,().A. x,y都是约束变元B. x,y都是自由变元C. x是约束变元,y都是自由变元D. x是自由变元,y都是约束变元7. 命题公式P→Q的主合取范式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q8. 设A(x):x是人,B(x):x是教师,则命题“有人是教师”可符号化为().A. ⌝(x)(A(x)∧⌝B(x))B. (∀x)(A(x)∧B(x))C. ⌝(∀x)(A(x)→B(x))D. (x)(A(x)∧B(x))9. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.10. 命题公式(P∨Q)→R的析取范式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R06任务_0003试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.2. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QC. Q→P⇒ PD. ⌝P∧(P∨Q)⇒Q3. 下列公式( )为重言式.A. ⌝P∧⌝Q↔P∨QB. (Q→(P∨Q)) ↔(⌝Q∧(P∨Q))C. (P→(⌝Q→P))↔(⌝P→(P→Q))D. (⌝P∨(P∧Q)) ↔Q4. 命题公式(P∨Q)→R的析取范式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R5. 命题公式P→Q的主合取范式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q6. 在谓词公式(∀x)(A(x)→B(x)∨C(x,y))中,().A. x,y都是约束变元B. x,y都是自由变元C. x是约束变元,y都是自由变元D. x是自由变元,y都是约束变元7. 下列公式中( )为永真式.A. ⌝A∧⌝B ↔⌝A∨⌝BB. ⌝A∧⌝B ↔⌝(A∨B)C. ⌝A∧⌝B ↔A∨BD. ⌝A∧⌝B ↔⌝(A∧B)8. 设A(x):x是书,B(x):x是数学书,则命题“不是所有书都是数学书”可符号化为().A. ┐(∀x)(A(x)→B(x))B. ⌝(x)(A(x)∧B(x))C. (∀x)(A(x)∍B(x))D. ⌝(x)(A(x)∧⌝B(x))9. 设个体域D={a, b, c},那么谓词公式消去量词后的等值式为.A. (A(a)∨A(b)∨A(c))∨(B(a)∧B(b)∧B(b))B. (A(a)∧A(b)∧A(c))∨(B(a)∨B(b)∨B(b))C. (A(a)∨A(b)∨A(c))∨(B(a)∨B(b)∨B(b))D. (A(a)∧A(b)∧A(c))∨(B(a)∧B(b)∧B(b))10. 前提条件的有效结论是( ).A. PB. ⌝PC. QD. ⌝Q06任务_0004试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QC. Q→P⇒ PD. ⌝P∧(P∨Q)⇒Q2. 命题公式(P∨Q)→R的析取范式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R3. 设A(x):x是人,B(x):x是教师,则命题“有人是教师”可符号化为().A. ⌝(x)(A(x)∧⌝B(x))B. (∀x)(A(x)∧B(x))C. ⌝(∀x)(A(x)→B(x))D. (x)(A(x)∧B(x))4. 下列公式( )为重言式.A. ⌝P∧⌝Q↔P∨QB. (Q→(P∨Q)) ↔(⌝Q∧(P∨Q))C. (P→(⌝Q→P))↔(⌝P→(P→Q))D. (⌝P∨(P∧Q)) ↔Q5. 表达式中的辖域是( ).A. P(x, y)B. P(x, y)∨Q(z)C. R(x, y)D. P(x, y)∧R(x, y)6. 命题公式(P∨Q)的合取范式是( ).A. (P∧Q)B. (P∧Q)∨(P∨Q)C. (P∨Q)D. ⌝(⌝P∧⌝Q)7. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q8. 在谓词公式(∀x)(A(x)→B(x)∨C(x,y))中,().A. x,y都是约束变元B. x,y都是自由变元C. x是约束变元,y都是自由变元D. x是自由变元,y都是约束变元9. 命题公式(P∨Q)→Q为( )A. 矛盾式B. 可满足式C. 重言式D. 合取范式10. 设个体域D={a, b, c},那么谓词公式消去量词后的等值式为.A. (A(a)∨A(b)∨A(c))∨(B(a)∧B(b)∧B(b))B. (A(a)∧A(b)∧A(c))∨(B(a)∨B(b)∨B(b))C. (A(a)∨A(b)∨A(c))∨(B(a)∨B(b)∨B(b))D. (A(a)∧A(b)∧A(c))∨(B(a)∧B(b)∧B(b))06任务_0005试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 命题公式P→Q的主合取范式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q2. 设个体域D是整数集合,则命题"x$y (x×y = y)的真值是().A. TB. FC. 不确定D. 以上说法都不是3. 命题公式的析取范式是( ).A.B.C.D.4. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.5. 设个体域为整数集,则公式"x$y(x+y=0)的解释可为( ).A. 存在一整数x有整数y满足x+y=0B. 任一整数x对任意整数y满足x+y=0C. 对任一整数x存在整数y满足x+y=0D.存在一整数x对任意整数y满足x+y=06. 命题公式(P∨Q)→R的析取范式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R7. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QC. Q→P⇒ PD. ⌝P∧(P∨Q)⇒Q8. 设个体域D={a, b, c},那么谓词公式消去量词后的等值式为.A. (A(a)∨A(b)∨A(c))∨(B(a)∧B(b)∧B(b))B. (A(a)∧A(b)∧A(c))∨(B(a)∨B(b)∨B(b))C. (A(a)∨A(b)∨A(c))∨(B(a)∨B(b)∨B(b))D. (A(a)∧A(b)∧A(c))∨(B(a)∧B(b)∧B(b))9. 下列公式中( )为永真式.A. ⌝A∧⌝B ↔⌝A∨⌝BB. ⌝A∧⌝B ↔⌝(A∨B)C. ⌝A∧⌝B ↔A∨BD. ⌝A∧⌝B ↔⌝(A∧B)10. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q。
