2016-2017学年高中北师大版数学必修2(45分钟课时作业):第1章6.2 垂直关系的性质 Word版含解析
2018年高一北师大版数学必修2(45分钟课时作业与单元测试卷):第1章章末检测 Word版含解析
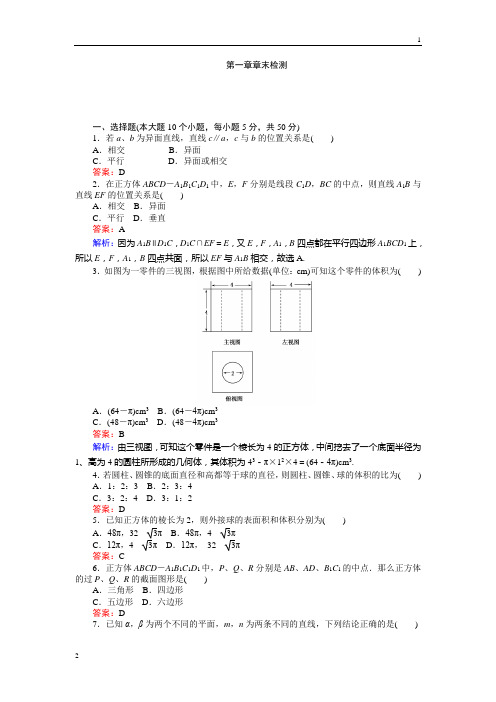
第一章章末检测一、选择题(本大题10个小题,每小题5分,共50分)1.若a、b为异面直线,直线c∥a,c与b的位置关系是()A.相交B.异面C.平行D.异面或相交答案:D2.在正方体ABCD-A1B1C1D1中,E,F分别是线段C1D,BC的中点,则直线A1B与直线EF的位置关系是()A.相交B.异面C.平行D.垂直答案:A解析:因为A1B∥D1C,D1C∩EF=E,又E,F,A1,B四点都在平行四边形A1BCD1上,所以E,F,A1,B四点共面,所以EF与A1B相交,故选A.3.如图为一零件的三视图,根据图中所给数据(单位:cm)可知这个零件的体积为() A.(64-π)cm3B.(64-4π)cm3C.(48-π)cm3D.(48-4π)cm3答案:B解析:由三视图,可知这个零件是一个棱长为4的正方体,中间挖去了一个底面半径为1、高为4的圆柱所形成的几何体,其体积为43-π×12×4=(64-4π)cm3.4.若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积的比为() A.1:2:3 B.2:3:4C.3:2:4 D.3:1:2答案:D5.已知正方体的棱长为2,则外接球的表面积和体积分别为()A.48π,32 3πB.48π,4 3πC.12π,4 3πD.12π,32 3π答案:C6.正方体ABCD-A1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点.那么正方体的过P、Q、R的截面图形是()A.三角形B.四边形C.五边形D.六边形答案:D7.已知α,β为两个不同的平面,m,n为两条不同的直线,下列结论正确的是()A .若m ⊥α,m ⊥n ,则n ∥αB .若m ∥α,n ∥α,则m ∥nC .若m β,且α⊥β,则m ⊥αD .若m ⊥β,且α∥β,则m ⊥α 答案:D解析:A 中可能n α;B 中m ,n 还可能相交或异面;C 中m ,α还可能平行或斜交;一条直线垂直于两平行平面中的一个,也垂直于另一个,所以D 正确.8.四面体S -ABC 中,各个面都是边长为2的正三角形,E ,F 分别是SC 和AB 的中点,则异面直线EF 与SA 所成角等于( )A .90°B .60°C .45°D .30° 答案:C9.设m 、n 是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题: ①若m ⊥α,n ∥α,则m ⊥n②若α∥β,β∥γ,m ⊥α,则m ⊥γ ③若m ∥α,n ∥α,则m ∥n ④若α⊥γ,β⊥γ,则α∥β 其中正确命题的序号是( ) A .①和② B .②和③ C .③和④ D .①和④ 答案:A10.直线m ⊥平面α,垂足是O ,正四面体ABCD 的棱长为4,点C 在平面α上运动,点B 在直线m 上运动,则点O 到直线AD 的距离的取值范围是( )A .[4 2-52,4 2+52]B .[2 2-2,2 2+2]C .[3-2 22,3+2 22]D .[3 2-2,3 2+2] 答案:B 解析:由题意,直线BC 与动点O 的空间关系: 点O 是以BC 为直径的球面上的点,所以O 到AD 的距离为四面体上以BC 为直径的球面上的点到AD 的距离, 最大距离为AD 到球心的距离(即BC 与AD 的公垂线)+半径=2 2+2. 最小距离为AD 到球心的距离(即BC 与AD 的公垂线)-半径=2 2-2.∴点O 到直线AD 的距离的取值范围是:[2 2-2,2 2+2]. 二、填空题(本大题5个小题,每小题5分,共25分)11.已知圆锥的表面积为6π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为________.答案: 212.在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是棱AB ,BC 中点,则三棱锥B -B 1EF 的体积为________.答案:1313.在正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为BB 1和CD 的中点,则直线AM 和D 1N 所成的角为________.答案:90° 14.如图,梯形A ′B ′C ′D ′是水平放置的四边形ABCD 的用斜二测画法画出的直观图.若A ′D ′∥y ′轴,A ′B ′∥C ′D ′,A ′B ′=23C ′D ′=2,A ′D ′=O ′D ′=1,则四边形ABCD 的面积为________.答案:5 解析:如图,建立直角坐标系xOy ,在x 轴上截取OD =O ′D ′=1,OC =O ′C ′=2.过点D 作y 轴的平行线,并在平行线上截取DA =2D ′A ′=2.过点A 作x 轴的平行线,并在平行线上截取AB =A ′B ′=2.连接BC ,即得到了四边形ABCD .可知四边形ABCD 是直角梯形,上、下底边分别为AB =2,CD =3,高AD =2,所以四边形ABCD 的面积S =2+32×2=5.15.如图,在正方体ABCD -A 1B 1C 1D 1中,给出以下四个结论:①直线D 1C ∥平面A 1ABB 1; ②直线A 1D 1与平面BCD 1相交; ③直线AD ⊥平面D 1DB ; ④平面BCD 1⊥平面A 1ABB 1.其中正确结论的序号为________. 答案:①④解析:因为平面A 1ABB 1∥平面D 1DCC 1,D 1C平面D 1DCC 1,所以D 1C ∥平面A 1ABB 1,①正确;直线A 1D 1在平面BCD 1内,②不正确;显然AD 不垂直于BD ,所以AD 不垂直于平面D 1DB ,③不正确;因为BC ⊥平面A 1ABB 1,BC 平面BCD 1,所以平面BCD 1⊥平面A 1ABB 1,④正确.三、解答证明题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.)16.(12分)圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm 2,母线与轴的夹角是45°,求这个圆台的高、母线长和两底面半径.解:x cm,3x cm. 延长AA 1交OO 1的延长线于S , 在Rt △SOA 中,∠ASO =45°,则∠SAO =45°, ∴SO =AO =3x ,∴OO 1=2x ,又S 轴截面=12(6x +2x )·2x =392,∴x =7.故圆台的高OO 1=14 cm ,母线长l = 2O 1O =14 2 cm ,两底面半径分别为7 cm,21 cm.17.(12分)如图,在圆锥SO 中,AB ,CD 为底面圆的两条直径,AB ∩CD =O ,SO =OB =2,P 为SB 的中点.(1)求证:SA ∥平面PCD ; (2)求圆锥SO 的表面积. 解:(1)连接PO ,∵P ,O 分别为SB ,AB 的中点,∴PO ∥SA .又PO 平面PCD ,SA 平面PCD ,∴SA ∥平面PCD .(2)设母线长为l ,底面圆半径为r ,则r =2,l =SB =22, ∴S 底=πr 2=4π,S 侧=πrl =42π, ∴S 表=S 底+S 侧=4(2+1)π.18.(12分)如图,在三棱锥P -ABC 中,P A ⊥底面ABC ,AB ⊥BC ,DE 垂直平分PC ,且分别交AC ,PC 于D ,E 两点,PB =BC ,P A =AB .(1)求证:PC ⊥平面BDE ;(2)试确定线段P A 上点Q 的位置,使得PC ∥平面BDQ . 解:(1)∵PB =BC ,E 为PC 的中点,∴PC ⊥BE . ∵DE 垂直平分PC ,∴PC ⊥DE .又BE 平面BDE ,DE 平面BDE ,且BE ∩DE =E ,∴PC ⊥平面BDE .(2)不妨令P A =AB =1,则有PB =BC =2,计算得AD =33=13AC . ∴点Q 在线段P A 上靠近点A 的三等分点处,即AQ =13AP 时,PC ∥QD ,从而PC ∥平面BDQ .19.(13分)如图,在直三棱柱ADF -BCE 中,AB =AD =DF =a ,AD ⊥DF ,M ,G 分别是AB ,DF 的中点.(1)求该直三棱柱的体积与表面积;(2)在棱AD 上确定一点P ,使得GP ∥平面FMC ,并给出证明.解:(1)由题意,可知该直三棱柱的体积为12×a ×a ×a =12a 3,表面积为12a 2×2+2a 2+a 2+a 2=(3+2)a 2.(2)当点P 与点A 重合时,GP ∥平面FMC . 取FC 的中点H ,连接GH ,GA ,MH .∵G 是DF 的中点,∴GH 綊12CD .又M 是AB 的中点,AB 綊CD ,∴AM 綊12CD .∴GH ∥AM 且GH =AM ,∴四边形GHMA 是平行四边形, ∴GA ∥MH .∵MH 平面FMC ,GA 平面FMC , ∴GA ∥平面FMC ,即当点P 与点A 重合时,GP ∥平面FMC .20.(13分)如图①,有一个等腰直角三角板ABC 垂直于平面α,BC α,AB =BC =5,有一条长为7的细线,其两端分别位于B ,C 处,现用铅笔拉紧细线,在平面α上移动.(1)图②中的PC (PC <PB )的长为多少时,CP ⊥平面ABP ?并说明理由. (2)在(1)的情形下,求三棱锥B -APC 的高. 解:(1)当CP =3时,CP ⊥平面ABP .证明如下:若CP =3,则BP =4,而BC =5, 所以三角形BPC 为直角三角形,且CP ⊥PB . 又平面ABC ⊥平面α,AB ⊥BC ,所以AB ⊥平面α,于是CP ⊥AB .又PB 平面ABP ,AB 平面ABP ,PB ∩AB =B , 所以CP ⊥平面ABP .(2)解法一:如图,过点B 作BD ⊥AP 于点D ,由(1),知CP ⊥平面ABP ,则CP ⊥BD .又AP 平面APC ,CP 平面APC ,AP ∩CP =P , 所以BD ⊥平面APC ,即BD 为三棱锥B -APC 的高. 由于PB =4,AB =5,AB ⊥平面α,所以AP =AB 2+PB 2=25+16=41,由AP ·BD =AB ·PB ,得BD =4×541=204141.即三棱锥B -APC 的高为204141.解法二:由(1),知CP ⊥平面ABP ,所以CP ⊥AP . 又CP =3,BP =4,AB =5,AB ⊥BP , 所以AP =AB 2+PB 2=25+16=41,所以S △APC =12·CP ·AP =3412.设三棱锥B -APC 的高为h ,则V B -APC =13·S △APC ·h =412h .又V A -PBC =13·S △PBC ·AB =13×12×CP ×BP ×AB =10,而V B -APC =V A -PBC ,得412h =10,所以h =204141.即三棱锥B -APC 的高为204141.21.(13分)已知正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直,M 为AC 上一点,N 为BF 上一点,且AM =FN =x ,设AB =a(1)求证:MN ∥平面CBE ; (2)求证: MN ⊥AB ;(3)当x 为何值时,MN 取最小值?并求出这个最小值.证明:(1)在平面ABC 中,作MG ∥AB ,在平面BFE 中,作NH ∥EF ,连接GH ,∵AM =FN ,∴MC =NB ,∵MG AB =MC NC =NBEF∴MG ∥NH ,∴MNHG 为平行四边形,∴MN ∥GH又∵GH ⊆面BEC ,MN 面BEC ,∴MN ∥面BEC (2)∵AB ⊥BC ,AB ⊥BE ,∴AB ⊥面BEC ,∵GH ⊆面GEC ,∴AB ⊥GH ,∵MN ∥GH ,∴MN ⊥AB (3)∵面ABCD ⊥面ABEF ,∴BE ⊥面ABCD ,∴BE ⊥BC∵BG =x2,BH =2a -x 2∴MN =GH =BG 2+BH 2=x 2+x 2-22ax +2a 22=x 2-2ax +a 2(0<a <2a )=⎝⎛⎭⎫x -22a 2+a 22≤22a当且仅当x =22a 时,等号成立;∴当x =22a 时,MN 取最小值22a .。
2016-2017学年高中数学 第一章立体几何初步 1.1.2 简单多面体课件 北师大版必修2

探究一
探究二
探究三
探究四
思想方法
解:(1)错误.棱锥的侧面一定是三角形,可以是等腰三角形,也可以 是正三角形,例如棱长均相等的正三棱锥的各个面都是正三角形.
(2)正确.在三棱锥中,共有4个面,每一个面均可作为底面,每一个 顶点均可作为棱锥的顶点.
(3)错误.只有当棱锥被与其底面平行的平面所截时,才能截得一 个棱锥和一个棱台.
4.棱台 (1)棱台的定义:用一个平行于棱锥底面的平面去截棱锥,底面与截 面之间的部分叫作棱台.原棱锥的底面和截面叫作棱台的下底面和 上底面,其他各面叫作棱台的侧面,相邻侧面的公共边叫作棱台的 侧棱.如图所示.
(2)表示:用表示底面各顶点的字母表示棱台.如上图中的棱台可记 作:四棱台ABCD-A'B'C'D'. (3)分类:按底面多边形的边数分为三棱台、四棱台、五棱台…… (4)特殊的棱台:用正棱锥截得的棱台叫作正棱台.正棱台的侧面是 全等的等腰梯形.
锥的顶点,于是棱台的侧棱所在的直线均相交于同一点,故命题④
为真命题.故选A. 答案:A
探究一
探究二
探究三
探究四
思想方法
探究一
探究二
探究三
探究四
思想方法
变式训练1 下列说法中正确的是
.
①在正方体上任意选择4个不共面的顶点,它们可能是正四面体的4
个顶点;
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
其中假命题的个数是( )
A.0 B.1 C.2 D.3
探究一
探究二
探究三
探究四
思想方法
解析:解答本题可先根据棱柱、棱锥、棱台的结构特征进行详细
分析,再结合已知的各个命题具体条件进行具体分析.显然命题① ②③均是真命题.对于命题④,棱台的侧棱所在的直线就是截得原
2016-2017学年高中政治必修1(45分钟课时作业与单元测试卷):1.2信用卡、支票和外汇含解析

第二课时信用卡、支票和外汇时间:45分钟满分:70分一、选择题(在每小题列出的四个选项中,只有一项是最符合题目要求的,每小题3分,共42分)知识点一信用卡与支票1.2016年初,有不良信用记录的陈先生多次向不同银行申请办信用卡,均被拒绝。
这是因为()A.办理银行信用卡需要资信状况良好B.办理的银行信用卡可以在指定营业机构存取现金C.银行信用卡因使用方便而限量发行D.办理的银行信用卡需在指定场所消费答案:A解析:陈先生申请办信用卡被拒绝的原因在于其有不良信用记录,银行信用卡是商业银行对资信状况良好的客户发行的一种信用凭证,故A符合题意。
银行信用卡并不都是限量发行的,故C错误。
B、D与题意无关。
2.杨女士最近在网上相中了一副某品牌的运动眼镜,她确认购买后,即从其信用卡中支付所需款项给商家。
这种结算方式()①属于现金结算②属于转账结算③方便购物消费④绝对安全便利A.②④B.③④C.①③D.②③答案:D解析:材料中的结算方式属于转账结算,方便购物消费,②③符合题意,①排除。
信用卡支付也存在被盗刷的危险,并非绝对安全,④说法错误。
3.大学生王某从网上成功预订了一张火车票,确认购买后,即从其提供的银行卡上扣除车票费用。
这种结算方式()A.增加了运输部门利润B.提高了消费者的地位C.降低了该商品的价值D.减少现金使用、方便消费答案:D解析:转账结算能够减少现金使用,故D符合题意。
网络购物只是改变了商品交换的方式,并没有增加运输部门的利润,也没有提高消费者的地位,与商品的价值也没有关系,故A、B、C排除。
4.信用卡与转账支票的共同点是()A.购买商品或取得服务可直接使用的信用凭证B.都属于电子货币C.在转账结算中使用的信用工具D.都由银行等金融机构受理答案:C解析:A、B两项都是信用卡的相关职能,而不是与支票的共同点;D项也是片面的,因为以上信用工具不一定只有金融机构才能受理。
5.支票是人们在经济生活往来中经常使用的信用工具。
高中北师大版数学必修2(45分钟课时作业与单元测试卷)第1章单元测试三 Word版含解析

单元测试三本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分分,考试时间分钟.第Ⅰ卷(选择题共分)一、选择题:本大题共小题,每小题分,共分.在下列各题的四个选项中,只有一个选项是符合题目要求的..过两直线:-+=和:++=的交点和原点的直线的方程为( ).-=.+=.-=.+=答案:解析:解方程组(\\(-+=,++=,))得(\\(=-(),=().))∴=-.又过原点,∴直线方程为+=..已知点(+),(-),直线的倾斜角是直线倾斜角的一半,则直线的斜率为( )..不存在答案:解析:=,∴直线的倾斜角为°.∴的倾斜角为°,=°=..已知点()(>)到直线:-+=的距离为,则=( ).--+答案:解析:由=得=-,=--(舍去)..三条直线:-=,:+-=,:--=构成一个三角形,则的范围是( ).∈.∈且≠±,≠.∈且≠±,≠-.∈且≠±,≠答案:.若点()和点(,)关于直线--=对称,则( ).=,=-.=,=-.=,=.=,=答案:解析:由题意,知(\\((--)=-,(+)-(+)-=)),解得(\\(==)),故选..和直线-+=关于轴对称的直线方程是( ).+-=.++=.-+-=.--=答案:解析:设对称直线上任一点坐标为(,)它关于轴对称的点的坐标为(,-).(,-)在直线-+=上∴有-(-)+=即++=即所求直线方程为++=..直线过原点(),且不过第三象限,那么的倾斜角α的取值范围是( ).[°,°] .[°,°].[°,°)或α=°.[°,°]答案:解析:画图知的倾斜角应是钝角或坐标轴上的角,中含锐角不正确,中°不在其倾斜角的范围内应被排除,中含的角不全面..设直线与轴的交点为,且倾斜角为α,若将其绕点按逆时针方向旋转°,得到直线的倾斜角为α+°,则( ).°≤α<°.°≤α<°.°<α≤°.°<α<°答案:解析:解答本题应紧扣直线的倾斜角的取值范围,还要注意到与轴相交的直线的倾斜角不为°.从而有(\\(°<α<°,°≤α+°<°)),所以°<α<°,故选..直线过点(),且与点(-)的距离最远,则的方程为( ).--=.-+=.++=.+-=答案:解析:当⊥时符合要求,∵==,∴的斜率为-.∴的方程为-=-(-),即+-=..一条直线被两条直线++=和--=截得的线段的中点恰好是坐标原点,则这条直线的方程是( ).+=.-=.+=.-=答案:解析:设与++=交于(,--),与直线--=,交于点(,),由()为的中点,故可得(-,),由,两点确定.第Ⅱ卷(非选择题共分)二、填空题:本大题共小题,每小题分,共分.把答案填在题中横线上..已知直线:(+)+--=(∈)在轴上的截距是在轴上的截距的倍,则的值为.答案:-或解析:当直线:(+)+--=(∈)过原点,即--=时,解得=-,此时该直线在两坐标轴上的截距都为,所以在轴上的截距是在轴上的截距的倍,即=-符合题意;当直线:(+)+--=(∈)不过原点,即--≠,即≠-时,易知≠-,该直线在轴上的截距是+,在轴上的截距是,所以由直线在轴上的截距是在轴上的截距的倍,得×=+,解得=.综上所述,的值为-或..直线经过(),(,)(∈)两点,则直线的倾斜角的取值范围为.答案:[°,°]∪(°,°)解析:直线的斜率==-≤.若直线的倾斜角为α,则α≠°,且α≤.又°=,且°≤α<°,∴°≤α≤°或°<α<°..已知直线:(+)+(-)=与:(-)+(+)+=互相垂直,则的值为.答案:-或解析:①若的斜率不存在,此时=,的方程为=,的方程为=-,显然⊥,符合条件;若的斜率不存在,此时=-,易知与不垂直.②当,的斜率都存在时,直线的斜率=-,直线的斜率=-,∵⊥,∴·=-,即·=-,所以=-.综上可知=-或=..已知,,为某一直角三角形的三边长,为斜边,若点(,)在直线++=上,则+的最小值为.答案:解析:求+的最小值就是在直线++=上求一点,使这点到原点的距离的平方最小,因而其最小值为原点到直线++=的距离.由题意得到+≥===,∴+的最小值为..已知直线过点(),且与轴、轴的正半轴分别交于、两点,为坐标原点,则三角形面积的最小值为.答案:。
高中北师大版数学必修2(45分钟课时作业与单元测试卷):第1章7.3 球的表面积和体积 Word版含解析

7.3 球的表面积和体积时间:45分钟 满分:80分班级________ 姓名________ 分数________一、选择题(每小题5分,共5×6=30分)1.已知一个正方体的体积是8,则这个正方体的内切球的表面积是( ) A .8π B .6π C .4π D .π 答案:C解析:设该正方体的棱长为a ,内切球的半径为r ,则a 3=8,∴a =2,∴正方体的内切球直径为2,r =1,∴内切球的表面积S =4πr 2=4π.2.已知两个球的半径之比为,那么这两个球的表面积之比为( ) A ....答案:A解析:设两球的半径分别为r 1,r 2,表面积分别为S 1,S 2,∵r 1∶r 2=1∶3,∴S 1∶S 2=4πr 21∶4πr 22=r 21∶r 22=1∶9.故选A.3.已知正方体、球、底面直径与母线相等的圆柱,它们的表面积相等,则它们的体积的大小关系是( )A .V 正方体=V 圆柱=V 球B .V 正方体<V 圆柱<V 球C .V 正方体>V 圆柱>V 球D .V 圆柱>V 正方体>V 球 答案:B解析:设正方体的棱长、球的半径、圆柱底面圆的半径分别为a ,R ,r ,则S 正方体=6a 2,S 球=4πR 2,S 圆柱=6πr 2,由题意,知S 正方体=S 球=S 圆柱,所以a =πr ,R =32r ,所以V 正方体=a 3=ππr 3,V 球=43πR 3=6πr 3,V 圆柱=2πr 3,显然可知V 正方体<V 圆柱<V 球.4.已知一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在一个球面上,则该球的表面积为( )A.499πB.73πC.283πD.289π答案:C解析:由三视图,知该几何体是一个正三棱柱,其底面是边长为2的正三角形,侧棱长是2,三棱柱的两个底面中心连线的中点与三棱柱的顶点的连线就是其外接球的半径,设其外接球的半径为r ,则r =⎝⎛⎭⎫23×32+12=73,所以该球的表面积为4πr 2=283π. 5.设球内切于圆柱,则此圆柱的全面积与球的表面积之比为( ) A .1:1 B .2:1 C .3:2 D .4:3 答案:C解析:如图为球的轴截面,由题意,设球的半径为r ,则圆柱的底面圆半径为r ,圆柱的高为2r ,于是圆柱的全面积为S 1=2πr 2+2πr ·2r =6πr 2,球的表面积为S 2=4πr 2.∵S 1S 2=6πr 24πr 2=32. 6.球O 的截面把垂直于截面的直径分成两部分,若截面圆半径为3,则球O 的体积为( )A .16π B.16π3C.32π3 D .4 3π 答案:C解析:设直径被分成的两部分分别为r 、3r ,易知(3)2=r ·3r ,得r =1,则球O 的半径R =2,故V =43π·R 3=323π.二、填空题(每小题5分,共5×3=15分)7.已知球的某截面圆的面积为16π,球心到该截面的距离为3,则球的表面积为________.答案:100π解析:因为截面圆的面积为16π,所以截面圆的半径为4.又球心到截面的距离为3,所以球的半径为5,所以球的表面积为100π.8.把直径分别为6 cm,8 cm,10 cm 的三个铁球熔成一个大铁球,则这个大铁球的半径为________cm.答案:6解析:设大铁球的半径为R cm ,由43πR 3=43π×⎝⎛⎭⎫623+43π×⎝⎛⎭⎫823+43π×⎝⎛⎭⎫1023,得R 3=216,得R =6.9.长方体的共顶点的三个侧面面积分别为3、5、15,则它的外接球的表面积为__________.答案:9π解析:设长方体的有公共顶点的三条棱的长分别为x 、y 、z ,则由已知得⎩⎨⎧xy =3,yz =5,zx =15,解得⎩⎨⎧x =3,y =1,z =5所以球的半径R =12x 2+y 2+z 2=32.所以S 球=4πR 2=9π.三、解答题(共35分,11+12+12) 10.如图所示,扇形所含中心角为90°,弦AB 将扇形分成两部分,这两部分各以AO 为轴旋转一周,求这两部分旋转所得旋转体的体积V 1和V 2之比.解:△ABO 旋转成圆锥,扇形ABO 旋转成半球,设OB =R .V半球=23πR 3,V 锥=π3·R ·R 2=π3R 3, ∴(V 半球-V 锥V 锥= 11.某甜品店制作一种蛋筒冰淇淋,其上半部分呈半球形,下半部分呈圆锥形(如图).现把半径为10 cm 的圆形蛋皮等分成5个扇形,用一个扇形蛋皮围成圆锥的侧面(蛋皮厚度忽略不计),求该蛋筒冰淇淋的表面积和体积.解:设圆锥的底面半径为r ,高为h .∵2πr =25π·10,∴r =2.h =102-22=4 6.∴该蛋筒冰淇淋的表面积S =π·1025+2π·22=28π(cm 2).体积V =1 3π·22×4 6+23π·23=163(6+1)π(cm 3).12.如果一个几何体的主视图与左视图是全等的长方形,边长分别是4,2,如图所示,俯视图是一个边长为4的正方形.(1)求该几何体的表面积;(2)求该几何体的外接球的体积.解:(1)由题意可知,该几何体是长方体,其底面是边长为4的正方形,高为2, 因此该几何体的表面积是2×4×4+4×4×2=64.(2)由长方体与球的性质,可得长方体的体对角线是其外接球的直径,则外接球的半径r =1242+42+22=3,因此外接球的体积V =43πr 3=43×27π=36π,所以该几何体的外接球的体积是36π.给高中生的建议初中学生学数学,靠的是一个字:练!高中学生学数学靠的也是一个字:悟!学好数学的核心就是悟,悟就是理解,为了理解就要看做想。
2019-2020学年高中北师版数学a版高一必修1(45分钟课时作业与单元测试卷):第一章_章末检测_word版含解析

第一章章末检测班级__________ 姓名__________ 考号__________ 分数__________本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.下列表示①{0}=∅,②{3}∈{3,4,5},③∅{0},④0∈{0}中,正确的个数为( )A .1B .2C .3D .4答案:B解析:③④正确.2.设全集U =R ,M ={x |x ≥1},N ={x |0≤x <5},则(∁U M )∪(∁U N )为( )A .{x |x ≥0)B .{x |x <1或x ≥5}C .{x |x ≤1或x ≥5}D .{x |x <0或x ≥5}答案:B解析:借助数轴直观选择.3.已知集合A ={0,1,2,3,4,5},B ={1,3,6,9},C ={3,7,8},则(A ∩B )∪C 等于( )A .{0,1,2,6}B .{3,7,8}C .{1,3,7,8}D .{1,3,6,7,8}答案:C解析:直接进行交并运算.4.若集合M ={a ,b ,c }中的元素是△ABC 的三边长,则△ABC 一定不是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形答案:D解析:由集合中元素的互异性可知.5.设集合A ={0,1},集合B ={1,2,3},定义A *B ={z |z =xy +1,x ∈A ,y ∈B },则A *B 集合中真子集的个数是( )A .14B .15C .16D .17答案:B解析:A *B ={1,2,3,4},故集合中有4个元素,则真子集有24-1=15个.6.设集合A ={(x ,y )|x -y =1},B ={(x ,y )|2x +y =8},则A ∩B =( )A .{(3,2)}B .{3,2}C .{(2,3)}D .{2,3}答案:A解析:解⎩⎪⎨⎪⎧ x -y =12x +y =8得⎩⎪⎨⎪⎧x =3y =2. 7.已知集合A ={x ∈R |x <5-2},B ={1,2,3,4},则(∁R A )∩B 等于( )A .{1,2,3,4}B .{2,3,4}C .{3,4}D .{4}答案:D解析:借助数轴直观判断.8.设集合P ={1,2,3,4,5,6},Q ={x ∈R |2≤x ≤6},那么下列结论正确的是( )A .P ∩Q =PB .P ∩Q ÙQC .P ∪Q =QD .P ∩Q ØP答案:D解析:对照答案逐一验证.9.全集U =R ,集合M ={x |x 2-4≤0}则∁U M =( )A .{x |-2<x <2}∴a=4.(2)若P∪Q=Q,即P⊆Q.用数轴表示如下:∴a≤2.。
2018年高一北师大版数学必修2(45分钟课时作业与单元测试卷):第2章单元测试五 圆与圆的方程 Word版

单元测试五 圆与圆的方程班级____ 姓名____ 考号____ 分数____本试卷满分100分,考试时间90分钟.一、选择题:本大题共10小题,每小题4分,共40分.在下列各题的四个选项中,只有一个选项是符合题目要求的.1.过点A (1,2),且与两坐标轴相切的圆的方程是( )A .(x -1)2+(y -1)2=1或(x -5)2+(y -5)2=25B .(x -1)2+(y -3)2=2C .(x -5)2+(y -5)2=25D .(x -1)2+(y -1)2=1答案:A解析:由图形易知满足此条件的圆有两个.2.两圆x 2+y 2=9和x 2+y 2-8x +6y +9=0的位置关系是( )A .相离B .相交C .内切D .外切答案:B解析:4-3<5<4+3.3.过圆x 2+y 2=25上一点P (-4,-3)的圆的切线方程为( )A .4x -3y -25=0B .4x +3y +25=0C .3x +4y -25=0D .3x -4y -25=0答案:B解析:k ==,则切线的斜率为-,且经过(-4,-3)这一点,直线方程为-3-0-4-034434x +3y +25=0.4.若圆x 2+y 2+2x -4y +1=0关于直线2ax -by +1=0对称,则a +b 等于( )A .1B .-1 C. D .-1212答案:C解析:∵圆心(-1,2),∴-2a -2b +1=0,∴a +b =.125.以A (-1,2),B (5,-6)为直径两端点的圆的标准方程是( )A .(x -2)2+(y +2)2=25B .(x +2)2+(y +2)2=25C .(x -2)2+(y -2)2=25D .(x +2)2+(y -2)2=25答案:A解析:A (-1,2),B (5,-6)两点连线的中点为圆心,其圆心坐标为(2,-2),可知选A.6.若直线ax +by -1=0与圆x 2+y 2=1相切,则点P (a ,b )的位置是( )A .在圆上B .在圆外C .在圆内D .以上皆有可能答案:A解析:∵直线与圆相切,∴=1,1a 2+b 2P (a ,b )到圆心的距离d ==1,a 2+b 2∴点P 在圆上.7.圆心为A (1,-2)且与直线x -3y +3=0相切的圆的方程为( )A .(x -1)2+(y +2)2=10B .(x -1)2+(y +2)2=10C .(x +1)2+(y -2)2=10D .(x +1)2+(y -2)2=10答案:B解析:圆半径r ==,故圆的标准方程为(x -1)2+(y +2)2=10.|1+6+3||1+9|108.直线x =2被圆(x -a )2+y 2=4所截得的弦长等于2 ,则a 的值等于( )3A .1或3 B.或- 22C. D .-1或33答案:A解析:由题意|a -2|2+()2=22,解得a =1或3.39.若直线-2ax -by +2=0(a >0,b >0)始终平分圆x 2+y 2-2x -4y +1=0的周长,则+的最小值是( )1a 1b A .4 B .2 C. D.1412答案:A解析:由题意可知,直线过圆心得a +b =1.∴+=+=2++≥2+2 =4.1a 1b a +b a a +b b b a a b ba ×ab 10.直线y =-x +b 与曲线y =有且只有两个公共点,则b 的取值范围是( )4-x 2A .2<b <2 B .2≤b <222C .2≤b ≤2D .2<b ≤222答案:B解析:由图可知,2≤b <2.2二、填空题:本大题共3小题,每小题4分,共12分.把答案填在题中横线上.11.以点C (-3,4)为圆心,2 为半径的圆的方程是________.3答案:(x +3)2+(y -4)2=12.12.点P 在圆x 2+y 2-8x -4y +11=0上,点Q 在圆x 2+y 2+4x +2y =4上,则|PQ |的最小值是________.答案:3 -65解析:P 在圆x 2+y 2-8x -4y +11=0上,即(x -4)2+(y -2)2=9,圆心O 1(4,2),半径为3.Q 在圆x 2+y 2+4x +2y =4上,即(x +2)2+(y +1)2=9,圆心O 2(-2,-1),半径为3,∴|O 1O 2|=[4-(-2)]2+[2-(-1)]2==3 .36+95∴|PQ |min =|O 1O 2|-R 1-R 2=3 -6.513.直线mx +ny =1与圆x 2+y 2=4的交点为整点(横纵坐标均为整数的点),这样的直线的条数是________条.答案:8解析:圆上的点为整点的有四个(±2,0),(0,±2),显然直线mx +ny =1不能过原点.若直线与圆有两个交点,则这样的直线有4条;若直线与圆相切,则这样的直线也有4条,故8条直线.三、解答题:本大题共5小题,共48分,其中第14小题8分,第15~18小题各10分.解答应写出文字说明、证明过程或演算步骤.14.求过点A (1,6)和B (5,6)且与直线2x -3y +16=0相切的圆的方程.解:显然圆心在线段AB 的垂直平分线x =3上设圆心为(3,b ),半径为r ,则(x -3)2+(y -b )2=r 2,得(1-3)2+(6-b )2=r 2,而r =,|6-3b +16|13∴b =3,r =,13∴(x -3)4+(y -3)4=13.15.已知圆C 1:x 2+y 2-10x -10y =0,圆C 2:x 2+y 2+6x -2y -40=0.(1)求圆C 1与圆C 2的公共弦所在的直线的方程;(2)求它们的公共弦长.解:(1)x 2+y 2-10x -10y =0,①;x 2+y 2+6x -2y -40=0,②;②-①得:2x +y -5=0为公共弦所在直线的方程;(2)弦长的一半为=,公共弦长为2.50-20303016.求以两圆C 1:x 2+y 2+2x -3=0,C 2:x 2+y 2-4x -5=0的交点为直径的圆的方程.解:设过C 1、C 2交点的圆的方程为:x 2+y 2+2x -3+λ(x 2+y 2-4x -5)=0,整理即得圆心为(-,0).1-2λ1+λ又∵两圆公共弦为3x +1=0,圆心在公共弦上,∴-3×+1=0,∴λ=.1-2λ1+λ27∴所求圆的方程为9x 2+9y 2+6x -31=0.即x 2+y 2+x -=0.2331917.已知曲线C :x =与直线y =k (x -1)+3只有一个交点,求实数k 的取值范4-y 2围.解:曲线C 的方程可化为x 2+y 2=4,x ≥0,∴曲线C 表示以(0,0)为圆心,2为半径的圆的右半部分,直线过定点M (1,3).如图所示.由图可得k AM =1,k BM =5,∴1≤k <5.又=2,化简得3k 2+6k -5=0,|-k +3|1+k 2解得k =-1±(舍去正根).2 63综上,实数k 的取值范围是1≤k <5或k =-1-.2 6318.已知圆C :x 2+y 2+2x -4y +3=0.(1)若圆C 的切线在x 轴、y 轴上的截距相等,求切线的方程;(2)从圆C 外一点P (x 1,y 1)向圆引一条切线,切点为M ,O 为坐标原点,且有|PM |=|PO |,求使|PM |最小的点P 的坐标.解:(1)由方程x 2+y 2+2x -4y +3=0知,圆心为(-1,2),半径为.2当切线过原点时,设切线方程为y =kx ,则=.|k +2|k 2+12所以k =2±,即切线方程为y =(2±)x .66当切线不过原点时,设切线方程为x +y =a ,则=.所以a =-1或a =3,|-1+2-a |22即切线方程为x +y +1=0或x +y -3=0.所以切线方程为y =(2+)x 或y =(2-)x 或x +y +1=0或x +y -3=0.66(2)设P (x 1,y 1).∵|PO |2+r 2=|PC |2,∴x +y +2=(x 1+1)2+(y 1-2)2,2121即2x 1-4y 1+3=0.要使|PM |最小,只要|PO |最小即可.当直线PO 垂直于直线2x -4y +3=0时,即直线PO 的方程为2x +y =0时,|PM |最小,此时P 点即为两直线的交点,得P 点坐标(-,).31035。
高中北师大版数学必修2(45分钟课时作业与单元测试卷):第1章2 直观图 Word版含解析

2直观图时间:45分钟满分:80分班级________姓名________分数________一、选择题(每小题5分,共5×6=30分)1.水平放置的梯形的直观图是()A.梯形B.矩形C.三角形D.任意四边形答案:A解析:斜二测画法的规则中平行性保持不变,故选A.2.利用斜二测画法可以得到:①水平放置的三角形的直观图是三角形;②水平放置的平行四边形的直观图是平行四边形;③水平放置的正方形的直观图是正方形;④水平放置的菱形的直观图是菱形.以上结论正确的是()A.①②B.①C.③④D.①②③④答案:A解析:因为斜二测画法是一种特殊的平行投影画法,所以①②正确;对于③④,只有平行于x轴的线段长度不变,所以不正确.3.用斜二测画法得到的一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()答案:A解析:直观图中的多边形为正方形,对角线的长为2,所以原图形为平行四边形,位于y轴上的对角线的长为2 2.4.已知一条边在x轴上的正方形的直观图是一个平行四边形,此平行四边形中有一边长为4,则原正方形的面积是()A.16 B.64C.16或64 D.以上都不对答案:C解析:根据直观图的画法,平行于x轴的线段长度不变,平行于y轴的线段变为原来的一半,于是直观图中长为4的边如果平行于x ′轴,则正方形的边长为4,面积为16;长为4的边如果平行于y ′轴,则正方形的边长为8,面积是64.5.若用斜二测画法把一个高为10 cm 的圆柱的底面画在x ′O ′y ′平面上,则该圆柱的高应画成( )A .平行于z ′轴且长度为10 cmB .平行于z ′轴且长度为5 cmC .与z ′轴成45°且长度为10 cmD .与z ′轴成45°且长度为5 cm 答案:A解析:平行于z 轴的线段,在直观图中平行性和长度都不变,故选A.6.若一个水平放置的图形的直观图是一个底角为45°且腰和上底均为1的等腰梯形如图所示,则原平面图形的面积是( )A.2+22B.1+22C .2+ 2D .1+ 2 答案:C解析:由题意,知直观图中等腰梯形的下底为2+1,根据斜二测画法规则,可知原平面图形为直角梯形,上底为1,下底为2+1,高为2,所以其面积为2+ 2.二、填空题(每小题5分,共5×3=15分)7.一条边在x 轴上的正方形的面积是4,按斜二测画法所得的直观图是一个平行四边形,则这个平行四边形的面积是________.答案: 2解析:正方形的面积为4,则边长为2,由斜二测画法的规则,知平行四边形的底为2,高为22,故面积为 2.8.一个水平放置的平面图形的直观图是直角梯形ABCD ,如图所示,∠ABC =45°,AB =AD =1,DC ⊥BC ,则这个平面图形的面积为________.答案:4+22解析:由直观图,可知原图形为直角梯形,且上底为1,下底为22+1,高为2,故面积为12×⎝⎛⎭⎫1+22+1×2=2+22.9.给出下列各命题:(1)利用斜二测画法得到的三角形的直观图还是三角形;(2)利用斜二测画法得到的平行四边形的直观图还是平行四边形; (3)利用斜二测画法得到的正方形的直观图还是正方形; (4)利用斜二测画法得到的菱形的直观图还是菱形;(5)在画直观图时,由于选轴的不同所画的直观图可能不同; (6)水平放置的矩形的直观图可能是梯形. 其中正确的命题序号为____________.答案:(1)(2)(5)三、解答题(共35分,11+12+12)10.将图中所给水平放置的直观图绘出原形.解:11.用斜二测画法画出图中水平放置的△OAB 的直观图.解:(1)在已知图中,以O 为坐标原点,以OB 所在的直线及垂直于OB 的直线分别为x 轴与y 轴建立平面直角坐标系,过点A 作AM 垂直x 轴于点M ,如图1.另选一平面画直观图,任取一点O ′,画出相应的x ′轴、y ′轴,使∠x ′O ′y ′=45°.(2)在x ′轴上取点B ′,M ′,使O ′B ′=OB ,O ′M ′=OM ,过点M ′作M ′A ′∥y ′轴,取M ′A ′=12MA .连接O ′A ′,B ′A ′,如图2.(3)擦去辅助线,则△O ′A ′B ′为水平放置的△OAB 的直观图. 12.画正六棱柱的直观图. 解:画法如下:(1)画轴:画x ′轴、y ′轴、z ′轴,使∠x ′O ′y ′=45°,∠x ′O ′z ′=90°; (2)画底面:画正六边形的直观图ABCDEF (O ′为正六边形的中心);(3)画侧棱:过A ,B ,C ,D ,E ,F 各点分别作z ′轴的平行线,在这些平行线上分别截取AA ′,BB ′,CC ′,DD ′,EE ′,FF ′,使AA ′=BB ′=CC ′=DD ′=EE ′=FF ′;(4)连线成图:连接A ′B ′,B ′C ′,C ′D ′,D ′E ′,E ′F ′,F ′A ′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到正六棱柱ABCDEF -A ′B ′C ′D ′E ′F ′,如图所示.给高中生的建议初中学生学数学,靠的是一个字:练!高中学生学数学靠的也是一个字:悟!学好数学的核心就是悟,悟就是理解,为了理解就要看做想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.2 垂直关系的性质
时间:45分钟 满分:80分
班级________ 姓名________ 分数________
一、选择题(每小题5分,共5×6=30分)
1.已知△ABC 和两条不同的直线l ,m ,l ⊥AB ,l ⊥AC ,m ⊥AC ,m ⊥BC ,则直线l ,m 的位置关系是( )
A .平行
B .异面
C .相交
D .垂直
答案:A
解析:因为直线l ⊥AB ,l ⊥AC ,所以直线l ⊥平面ABC ,同理直线m ⊥平面ABC ,根据线面垂直的性质定理得l ∥m .
2.PO ⊥平面ABC ,O 为垂足,∠ACB =90°,∠BAC =30°,BC =5,P A =PB =PC =10,则PO 的长等于( )
A .5
B .5 2
C .5 3
D .20
答案:C
解析:∵P A =PB =PC ,
∴P 在面ABC 上的射影O 为△ABC 的外心.
又△ABC 为直角三角形,
∴O 为斜边BA 的中点.
在△ABC 中,BC =5,∠ACB =90°,∠BAC =30°,
∴PO =
PC 2-(AB 2
)2=5 3. 3.已知平面α⊥β,直线l α,直线m β,若l ⊥m ,则l 与β的位置关系是( )
A .l ⊥β
B .l ∥β
C .l β
D .以上都有可能
答案:D 解析:若l 垂直于两平面的交线,则l ⊥β;若l 平行两平面的交线,m 垂直两平面的交线,则l ∥β;若l 就是两平面的交线,m 垂直两平面的交线,则l β.故这三种情况都有可能.
4.如图,BC 是Rt △BAC 的斜边,P A ⊥平面ABC ,PD ⊥BC 于点D ,则图中直角三角形的个数是( )
A.3 B.5
C.6 D.8
答案:D
解析:由P A⊥平面ABC,知△P AC,△P AD,△P AB均为直角三角形,又PD⊥BC,P A⊥BC,P A∩PD=D,∴BC⊥平面P AD.∴AD⊥BC,易知△ADC,△ADB,△PDC,△PDB均为直角三角形.又△BAC为直角三角形,所以共有8个直角三角形,故选D.
5.下列命题中错误的是()
A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
答案:D
解析:对于命题A,在平面α内存在直线l平行于平面α与平面β的交线,则l平行于平面β,故命题A正确.对于命题B,若平面α内存在直线垂直于平面β,则平面α与平面β垂直,故命题B正确.对于命题C,设α∩γ=m,β∩γ=n,在平面γ内取一点P不在m,n上,过P作直线a,b,使a⊥m,b⊥n.∵γ⊥α,a⊥m,则a⊥α,∴a⊥l,同理有b⊥l.又a∩b=P,aγ,bγ,∴l⊥γ.故命
题C正确.对于命题D,设α∩β=l,则lα,lβ.故在α内存在直线不垂直于平面β,即命题D错误.故选D.
6.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在()
A.直线AB上
B.直线BC上
C.直线AC上
D.△ABC内部
答案:A
解析:连接AC1,∵BA⊥AC,BC1⊥AC,BA∩BC1=B,∴AC⊥平面ABC1.∵AC平面ABC,∴平面ABC⊥平面ABC1,且交线是AB.故平面ABC1上的点C1在底面ABC上的射影H必在交线AB上.
二、填空题(每小题5分,共5×3=15分)
7.已知P A垂直于平行四边形ABCD所在的平面,若PC⊥BD,则平行四边形ABCD 一定是__________.
答案:菱形
解析:因为P A⊥平面ABCD,所以P A⊥BD,又因为PC⊥BD,所以BD⊥平面P AC,又AC ⊂平面P AC,所以AC⊥BD.
8.如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱P A=a,PB=PD =2a,则它的五个面中,互相垂直的平面有________对.
答案:5
解析:由勾股定理逆定理得P A⊥AD,P A⊥AB,∴P A⊥面ABCD,P A⊥CD,P A⊥CB.由直线与平面垂直的判定定理及平面与平面垂直的判定定理易得结论.平面P AB⊥平面P AD,平面P AB⊥平面ABCD,平面P AB⊥平面PBC,平面P AD⊥平面ABCD,平面P AD⊥平面PCD.
9.如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;
②不论D折至何位置,都有MN⊥AE;
③不论D折至何位置(不在平面ABC内),都有MN∥AB;
④在折起过程中,一定存在某个位置,使EC⊥AD.
答案:①②④
解析:分别取CE,DE的中点Q,P,连接MP,PQ,NQ,可证MNQP是矩形,所以①②正确;因为MN∥PQ,AB∥CE,若MN∥AB,则PQ∥CE,又PQ与CE相交,所以③错误;当平面ADE⊥平面ABCD时,有EC⊥AD,④正确.故填①②④.
三、解答题(共35分,11+12+12)
10.在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=60°,P A⊥平面ABCD,E 为PD的中点,P A=2AB.若F为PC的中点,求证:PC⊥平面AEF.
证明:∵P A=2AB,∠ABC=90°,∠BAC=60°,
∴P A=CA.
又F为PC的中点,∴AF⊥PC.
∵P A⊥平面ABCD,∴P A⊥CD.
∵AC⊥CD,P A∩AC=A,∴CD⊥平面P AC,∴CD⊥PC.
∵E为PD的中点,F为PC的中点,∴EF∥CD,∴EF⊥PC.
又AF⊥PC,AF∩EF=F,
∴PC⊥平面AEF.
11.如图,△ABC是边长为2的正三角形,AE⊥平面ABC,平面BCD⊥平面ABC,BD =CD,BD⊥CD,且AE=1.
(1)求证:AE∥平面BCD;
(2)求证:平面BDE⊥平面CDE.
证明:
(1)取BC的中点M,连接DM,AM,
因为BD=CD,且BD⊥CD,BC=2,
所以DM=1,DM⊥BC.
又平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,
所以DM⊥平面ABC,所以AE∥DM,
又DM平面BCD,AE平面BCD,
所以AE∥平面BCD.
(2)由(1)知AE∥DM,又AE=1,DM=1,
所以四边形DMAE是平行四边形,所以DE∥AM.
因为△ABC为正三角形,所以AM⊥BC.
又平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,
所以AM⊥平面BCD,所以DE⊥平面BCD.
又CD平面BCD,所以DE⊥CD.
因为BD⊥CD,BD∩DE=D,
所以CD⊥平面BDE.
因为CD平面CDE,所以平面BDE⊥平面CDE.
12.如图所示,已知在△BCD中,∠=CD=1,AB⊥平面BCD,∠ADB
=60°,E,F分别是AC,AD上的动点,且AE
AC=AF
AD=λ,(0<λ<1).求证:不论λ为何值,总有平面BEF⊥平面ABC.
证明:∵AB⊥平面BCD,∴AB⊥CD.
∵CD⊥BC且AB∩BC=B,∴CD⊥平面ABC.
又∵AE
AC=AF
AD=λ(0<λ<1),∴不论λ为何值,恒有EF∥CD,
∴EF⊥平面ABC.又EF⊂平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC.。
