偏振光数据以及图表
11-6光的偏振

§11-6 光的偏振P2P 2P21P 2P 1P 2P根据马吕斯定律I = I 0 cos α2I10 2 0 I1 = cos 30 2两束单色自然光 之比为2 0I 20 2 0 I2 = cos 60 2P 1 P 2I10I1I10 cos 60 = 2 0 I 20 cos 30 I P 1 20 1 = 3P 2I2例4 ☆两平行放置的偏振片, 偏振化方向成300角,自然光垂直 入射后, 透射光与入射光的强度之比为多少? (分别讨论 无吸收和10%的吸收的情况)解: 无吸收时根据马吕斯定律I02P 1I1P 2I21 2 0 I 2 = I1 cos α = I 0 cos 30 23 I2 1 2 0 ∴ = cos 30 = 8 I0 2 I0 10%吸收时 Q I = (1 − 10%) 1 2 2 ∴ I 2 = I1 cos α (1−10%) I0 2 2 = cos α (1 − 10%) 2 I2 1 2 0 2 ∴ = cos 30 (1 − 10%) ≈ 0.3 I0 2四、 反射光和折射光的偏振 1、反射和折射时光的偏振自然光在两各向同性 介质分界面上反射和折射 时,反射光和折射光均成 为部分偏振光i iγ特点:反射光是垂直于入射面的振动较强的部分偏振 光,折射光是平行于入射面的振动较强的部分偏振 光。
二.布儒斯特定律1815年布儒斯特发现,当 入射角为某特定值时,反射光 为振动方向垂直于入射面的线 偏振光 此时有布儒斯特角i0 i0γi0 + r =πn1 n2n1 sin i0 = n2 sin r ∴n1 sini0 = n2 sin(π / 2 − i0 ) = n2 cosi0 n2 ∴ tani0 = ----布儒斯特定律 n1由折射定律2•玻璃n2=1.5 , •水n2=1.33 , 注意:布儒斯特角i0 = 56.3° i0 = 53.1°1)当入射角为布儒斯特角时,反射光为振动方向垂 直入射面的线偏振光,而折射光仍为振动方向平行 于入射面的成分占优势的部分偏振光,这是因为反 射光线很弱,光强达不到自然光的一半。
偏振光

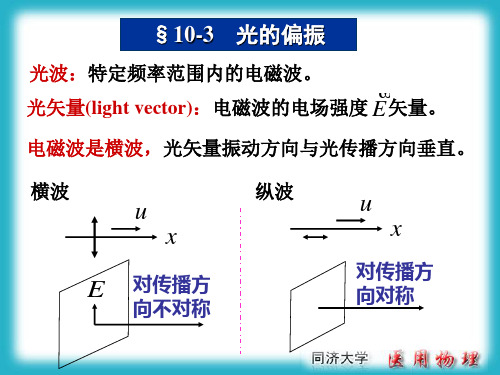
一、几种典型的偏振光自然光:具有一切可能的振动方向的许多光波的总和,各方向振动同时存在或迅速无规则的相互替代。
偏振的数学表示将x,y方向两分量振动中的时间项消去,得到含有振幅和相位差的表达式如下:二、偏振的获得利用透射最大光强值I M和最小光强值I m定义偏振度:偏振度可以描述光的偏振态,但不能完全区分光的偏振状态,比如,自然光与圆偏振光、椭圆偏振与部分偏振光等。
自然光各方向光强相等,p=0;线偏振光最小光强为0,p=1。
A.反射和折射产生偏振当入射角为布儒斯特角时,反射光成为线偏振光。
布儒斯特角是使p光反射率为0的入射角,其计算公式为:tan i B=n2 n1用玻片组可以提高透射光的偏振度。
B.二向色性各向异性的晶体对不同方向的偏振光有不同吸收系数的性质。
天然的偏振片:电气石。
C.散射产生偏振D.晶体的双折射三、马吕斯定律当一束线偏振光通过一张偏振片,若光的电场方向与偏振片透振方向夹角为α,则透射光强为:消光比:两偏振器件透光轴互相垂直时的最小透射光强与透光轴互相平行时的最大透射光强之比。
消光比可以用来衡量偏振器件的质量,消光比越小,产生的偏振度越高。
10-3数量级。
四、晶体简介如果按照光学性质,可以将晶体分为三类:单轴晶体:三角晶系、四角晶系、六角晶系。
如方解石、红宝石、石英、冰等。
双轴晶体:包括正交晶系、单斜晶系和三斜晶系。
如蓝宝石、云母、正方铅矿、硬石膏等。
立方晶系:有三个相互正交的等效的结晶学方向,这就是结晶学上的。
光学性质是各向相同的,与非晶体相同。
五、双折射1、基本概念当一束单色光在晶体的界面折射时,可以产生两束折射光线,这种现象叫双折射。
o光和e光:自然光入射于晶体表面,折射后的两束光都是平面偏振光,其中一束光的折射与在各向同性介质中相同,遵循折射定律,因而称为寻常光(ordinary ray,o光);而另一束光则不遵循折射定律,称为非常光(extraordinary ray,e光)光轴(optical axis of crystal):在双折射晶体中有一个特殊的方向,光沿此方向入射时不发生双折射,这个方向就被称作晶体的光轴,是o光和e光传播速度相同的方向。
偏振光

A
A2 A cosq A1 cos2 q B1 sin 2q 2 1 A sin q A sin 2q B sin 2 q B2 1 2 1
11
1 可知: g11 cos2 q , g12 sin 2q 2 1 g 21 sin 2q , g 22 sin 2 q 2
17
自然光通过光轴夹角为45度的线偏振 器后,又通过了1/4、1/2和1/8波片, 波片快轴沿Y轴方向,试用琼斯矩阵计 算透射光的偏振态。
18
解:自然光通过起偏器,成为线偏振光,其琼斯 矢量为:
A1 1 1 B 2 1 1
l/4波片,l/2 , l/8波片的琼斯矩阵分别为
10
求透光轴(Transmission axis)与x轴成q 角的线偏振器的琼斯矩阵
解:光线的偏振状态为:
~ A1 ~ A2 设入射光 E1= , 出射光E2= B1 B2 沿透光轴方向的分量: q B sin q A=A1 cos 1
B1 B2 q A1 A2
线偏光
***** ? 通过一个1/4波片
通过一快(慢)轴与椭 圆的长(短)轴一致的 ? 1/4波片
圆偏光
*****
先通过一个1/4波片变为 线偏光,再通过一快( ? 慢)轴与线偏光成45度 的1/4波片
椭圆偏光
*****
24
(用实验方法来鉴别光的偏振性质) 2、偏振光的检验
复习:光的偏振性质
y轴
1 itg 2 cos 2q ,itg 2 sin 2q A1 =cos exp(i ) 2 2 B1 itg cos 2q ,1 itg cos 2q 2 2
偏振的图画,动画讲解
n1 n2
i0
i0 90
n2 tan i0 n1
布儒斯特角(polarizting angle ):
玻璃堆
布儒斯特角
i0
线偏振光
应用举例: 激光器谐振腔
圆偏振光 (circularly polarized light)) 光矢量端点在垂直于 光传播方向的截面内描绘 出圆形轨迹。检偏器旋转 一周,光强无变化。
点击图片放大
2. 波片
x y 2 xy 2 cos( ) sin ( 2 1 ) 2 1 2 2 A1 A2 A1 A2
x y 2 xy 2 2 cos( 2 1 ) sin ( 2 1 ) 2 A1 A2 A1 A2
2
2
o e
光轴
光轴
o e
问题:自然光垂直入射双折射晶体表面,投射后 为何不能产生椭圆偏振光?
自 然 光
偏 振 光 A o
Ae
x ye Ae cos (t ) ve
检偏
偏振光
(1) 自然光强 I0 线偏振光强 :
I0 I 2
光强不变无消光
(2) 线偏振光强 I0 线偏振光强 有两次消光现象
(3)部分偏振光(混合) 线偏振光 有两次极大极小
马吕斯定律(Malus law)
A0
A2
I0
A1
I
光强为I0的线偏振光,透过偏振片后,透射强度为:
I I 0 cos
白云石 1.6811
正晶体:石英、冰 负晶体:方解石、电气石、白云石、硝酸钠 正晶体 负晶体
1-2自然光、线偏振光、部分偏振光

1
下表面折射:
As 2 2 As 2 sin i'2 As1 sin 2i10 As1
2
2
2
1
As 2 Ap 2
经过n块玻璃透射:
2
2
即透射光是部分偏振光
n , P 1
透振方向与拉伸方向垂直
2、起偏:
由自然光得到线偏振光
3、马吕斯定律:
入射光分解称两个垂直振 动,一个沿透振方向,一 个垂直于透振方向。
A
θ 入射线 偏振光
第二块偏振片 的透振方向
透射光的振动方向:透振方向
振幅:
光强:
A cos
I A cos I cos
2 2 2
4、检偏:
检验光的偏振态
n2 sin i10 n2 cos i10 2
n2 tan i10 n1
从空气到玻璃:
布儒斯特定律
n1 1 ,n2 1.5 n1 1.5,n2 1
i10 57 i10 33
从玻璃到空气:
由于折射角与入射角之和也是90度,这表明反向入射时, 也满足布儒斯特定律
I I ' 0.15 I s 0.15 2
312例5-2
四、透射光的偏振态
由能量守恒可知,折射光中p分量应大于s分量,是部分偏振光。 讨论自然光以布儒斯特角入射时,从一个玻璃片出射的透射光的 偏振态:
p分量:
Ap 2
2 sin i2 cos i10 tan i2 Ap1 sin( i10 i2 )1)垂直入射或掠入射
i1 0 或 i1 90
A' p1 A's1
A' p1 Ap1
偏振光

• 射面和下面的平行时,则可从上面玻璃见到反射光。但如 上下玻璃的入射面互相垂直,由于垂直第一块入射面的偏 振成为平行第二块入射面的偏振,不能被反射,观察者虽 随第二块转90°角,亦看不到反射光,得黑视场。这里下 面一块称起偏镜,上面一块称检偏镜。只要能产生偏振光 的一对器件,都可以达到起偏与检偏作用。这偏光镜虽简 单,但入射光与出射光不在一条直线上,使用不便。如利 用一堆玻璃片,使入射角也是iP。由于经多片玻璃反射,透 射光接近偏振光,而且与入射光在同一个方向上,很方便。 所用的玻璃堆片每片的质量要好,表面平,光洁度好,以 减少杂散光。
椭圆偏振光
• 在光的传播过程中,空间每个点的电矢量均以光 线为轴作旋转运动,且电矢量端点描出一个椭圆 轨迹,这种光称为椭圆偏振光。迎着光线方向看, 凡电矢量顺时针旋转的称右旋椭圆偏振光,凡逆 时针旋转的称左旋椭圆偏振光。椭圆偏振光中的 旋转电矢量是由两个频率相同、振动方向互相垂 直、有固定相位差的电矢量振动合成的结果
• ②索累补偿器 • 是由两个光轴平行的石英楔板和一个光轴垂直于 两楔板光轴的石英平行平面板组成的复合棱镜。 上楔板可由微动螺旋使其本身作平行的移动。当 上楔板这样移动时,两楔板的总厚度可连续改变。 当两楔板的总厚度等于下面石英平行平面板的厚 度时,穿过补偿器的o光和e光之间位相差为零。 由改变两楔板总厚度与石英平行平面板厚度之差 即可得到较宽截面上有相同位相差的光束。
分类
• 线偏振光
• 部分偏振光 • 椭圆偏振光 • 圆偏振光
线偏振光 • 在光的传播过程中,只包含一种振动,其 振动方向始终保持在光的偏振同一平面内, 这种光称为线偏振光(或平面偏振光)。
• 得到方式:在透明媒质界面上的折射和反射 • 让自然光以偏化角入射在二种不同透明媒质的界 面时,可得完全偏振的反射光与部分偏振的透射 光。以空气与玻璃为例,根据菲涅耳公式(见光 在分界面上的折射和反射),此偏化角(布儒斯特 角)为iP=arctgn。如n=1.5,iP=57°。最简单产生 与检查偏振光的偏振镜是用安置两块玻璃。最好 用黑色玻璃,或用一般玻璃,反面磨毛涂黑,以 吸收透射光及阻挡从玻璃后面射来的光。自然光 先以iP角射向下面一块玻璃,产生偏振垂直入射 面的反射光射向第二块玻璃。当上面的玻璃的入
光的偏振

4、部分偏振光
偏振度
Io— 总 光强
IP — 偏振光的光强 In—自然光的光强
IP IP P Io In I P
IP = 0 P = 0 —— 自然光
In = 0 P = 1 —— 偏振光
13.2 起偏与检偏
一、偏振片的起偏与检偏
2I 0
I0
I I0
P 1// P2
旋光物质
前 表 面 固体旋 光本领 溶液旋 光本领
l
后 表 面
l
单位 o mm
cl
c 溶液的浓度
三、磁致旋光
铅玻璃、二硫化碳、汽油等在磁场中呈旋光性
B
P 迎着光看:
沿B——振动面右旋; 逆B——振动面左旋。
=45o 可制成光隔离器!
13.7 人工双折射
一、 克尔效应(1875年)
注意:光在两块方解石
中都是垂直光轴传播。
折射角小于入射角
Z
前 一 半
Z
e光 o光
n
n
后 一 半
o光 e光
折射角大于入射角
3、二向色性晶体
对o 光和e 光的吸收有很大差异。
Z 电气石
1mm厚的电气石可将 o 光吸收净, e 光 却 有 剩 余 —— 可 制 成偏振片。
例题 一束线偏振光垂直射入一块方解石,入射前光矢量 方向与晶体的主截面成30o角,求:在方解石中o光、e 光的光强之比。
e光的主平面、主截面三者重合。
三、主速度、主折射率
Z
沿光轴方向e、 o光速度相同
Z
正 晶 ve 体
v0
ve
vo
负 晶 体
光的偏振状态解读

• 不加电场 → 液体各向同性 → P2 无透射光
• 加电场→液体呈单轴双折射晶体性质,其光轴平行
于外电场 E P2有透射光
返回
退出
e、o光的光程差为
l ( ne no ) klE 0
2
两相干光的相位差为
2π
π
当 =/2 时,克尔盒相当于一个半波片, P2透光最强 。 • 克尔盒的应用:高速电光开关,电光调制器。 • 克尔盒的缺点:所用液体常有剧毒,易爆炸。
返回
退出
晶体内的子波波阵面(正晶体) vo
vo 光轴
o光的波阵面 球面
ve 光轴
e光的波阵面 旋转椭球面
定义:主折射率
c no vo
c ne ve
返回
退出
no ne
vo ve
no ne
vo ve
正晶体(如石英)
负晶体(如方解石)
返回
退出
四、惠更斯原理在双折射现象中的应用 负晶体为例 (1) (2)
I 2 I1
0
I
π 2
π
3π 2
2π
消光
消光
1 I 2 I 1 cos I 0 cos 2 2
4.部分偏振光通过偏振片后光强的变化规律取决于 其中自然光与线偏振光的比例
返回
退出
§12-14 反射和折射时光的偏振 实验表明, 自然光在两种介质分界面上反射和 折射时,反射光和折射光一般都是部分偏振光(正 入射除外)。 当自然光以布儒斯特角 iB 入射时,其反射光为 线偏振光,光振动垂直于入射面, 折射光仍为部分 偏振光。
H——磁场强度; C——常量。
