2012届高三(理科)模拟试卷
福州市2012届第一学期高三期末质量检查数学(理科)试卷

福州市2012届第一学期期末高三数学(理科)模拟试卷注意事项:1.本科考试分试题卷和答题卷,考生须在答题卷上作答,答题前,请在答题卷的密封线内填写学校、班级、准考证号、姓名;2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟. 参考公式:样本数据12,,,n x x x 的标准差s =x 为样本平均数.第Ⅰ卷 (选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题所给的四个答案中有且只有一个答案是正确的.把正确选项涂在答题卡的相应位置上.)1.已知集合{|3}A x x =>,{}24B x x =<<,那么集合()R A B ð等于 A .{|3}x x ≤B .{|23}x x <≤C .{|34}x x <<D .{|4}x x <2.复数21i i +(i 为虚数单位)等于A .1122i +B .1122i -C .1122i --D .1122i -+ 3.“3c o s 5α=”是 “7cos 225α=-”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 4.执行如图所示的程序框图,若输入x =0.1,则输出m 的值是A .0B .0.1C .1D .1-5.将函数()x x f 2sin =(x ∈R )的图象向右平移4π个单位,则所得到的图象对应的函数在下列区间中单调递增的是A .(,0)4π-B .(0,)2πC .3(,)24ππD .3(,)4ππ 6.已知||1a = ,||2b = ,a 与b 的夹角为120︒,0a c b ++= ,则a 与c 的夹角为A .150︒B .90︒C .60︒D . 30︒7.已知()g x 为三次函数32()3a f x x ax cx =++的导函数,则它们的图象可能是 第4题图图甲图乙A .B.C.D.8.在三次独立重复试验中,事件A 在每次试验中发生的概率相同,若事件A 至少发生一次的概率为6364,则事件A 恰好发生一次的概率为 A .14B .34C .964D .27649.直线y =与椭圆2222:1x y C a b+=(0a b >>)交于A B 、两点,以线段AB 为直径的圆恰好经过椭圆的右焦点,则椭圆C 的离心率为ABC1 D.4-10.设Q 为有理数集,函数1(),R Q Q x f x x ∈⎧=⎨∈⎩,,-1,ð()11x xe g x e -=+,则函数 ()()()h xf xg x =⋅A .是奇函数但不是偶函数B .是偶函数但不是奇函数C .既是奇函数也是偶函数D .既不是偶函数也不是奇函数第Ⅱ卷 (非选择题 共100分)二、填空题(本大题共5小题,每小题4分,共20分,把答案填在答题卡的相应位置上.) 11.计算1213x dx -⎰的值等于 ★★★ .12.在24(1(1-+的展开式中,x 的系数等于★★★ .(用数字作答)13.在圆224x y +=所围成的区域内随机取一个点(,)P x y ,则2x y +≤的概率为 ★★★ .14.“无字证明”(proofs without words), 就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图甲、图乙中阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式: ★★★ .15.如图的倒三角形数阵满足:⑴ 第1行的n 个数,分别是1,3,5,…,21n -;⑵ 从第二行起,各行中的每一个数都等于它肩上的两数之和;⑶ 数阵共有n 行.问:当2012n =时,第32行的第17个数是 ★★★ .三、解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算过程)第14题图第15题图16.(本小题满分13分)在数列{}n a 中,12a =,1n n a a cn +=+(*Νn ∈,常数0c ≠),且1a ,2a ,3a 成等比数列. (Ⅰ)求c 的值;(Ⅱ)求数列{}n a 的通项公式.17.(本小题满分13分)某学院为了调查本校学生2011年9月“健康上网”( 健康上网是指每天上网不超过两小时)的天数情况,随机抽取了40名本校学生作为样本,统计他们在该月30天内健康上网的天数,并将所得数据分成以下六组:[](](]0,5,5,10,,25,30⋅⋅⋅,由此画出样本的频率分布直方图,如图所示.(Ⅰ)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;(Ⅱ)现从这40名的学生中任取2名,设Y 为健康上网天数超过20天的人数,求Y 的分布列及其数学期望E (Y ).18.(本小题满分13分) 如图,在△ABC 中,已知3B π=,34=AC ,D 为BC 边上一点.(Ⅰ)若2AD =,DAC S ∆=,求DC 的长;(Ⅱ)若AB AD =,试求ADC ∆的周长的最大值.19.(本小题满分13分)某种商品原来每件售价为25元,年销售8万件. (Ⅰ)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?(Ⅱ)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到.x 元.公司拟投入21(600)6x -万元作为技改费用,投入50万元作为固定宣传费用,投入15x 万元作为浮动宣传费用.试问:当该商品明年的销售量a 至少应达到多少万件时,才可能使明年的销售收入不低于原收入...与总投入...之和?并求出此时商品的每件定价.20.(本小题满分14分)在平面直角坐标系xOy 中,已知点A ()1,1-,P 是动点,且三角形POA的三边所在直线的斜率满足OP OA PA k k k +=.(Ⅰ)求点P 的轨迹C 的方程;第18题图第17题图(Ⅱ)若Q 是轨迹C 上异于点P 的一个点,且PQ OA λ=,直线OP 与QA 交于点M ,问:是否存在点P 使得PQA ∆和PAM ∆的面积满足2PQA PAM S S ∆∆=?若存在,求出点P 的坐标;若不存在,说明理由.21.(本小题满分14分) 已知函数()ln f x x =,()xg x e =.(Ⅰ)若函数()1()1x x f x x ϕ+=--,求函数()x ϕ的单调区间; (Ⅱ)设直线l 为函数()f x 的图象上一点00(,())A x f x 处的切线.证明:在区间1,+∞()上存在唯一的0x ,使得直线l 与曲线()y g x =相切.福州市2012届第一学期期末高三数学(理科)模拟试卷参考答案一、选择题(本大题共10小题,每小题5分,共50分. 在每小题所给的四个答案中有且只有一个答案是正确的.)1.B 2.D 3.A 4.A 5.B 6.B 7.D 8.C 9.C 10.A 二、填空题(本大题共5小题,每小题4分,共20分.)11.2 12.3- 13.2π14.sin()sin cos cos sin αβαβαβ+=+ 15.372 三、解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算过程.)16.(本小题满分13分)解:(Ⅰ)由题知,12a =,22a c =+,323a c =+, ………2分 因为1a ,2a ,3a 成等比数列,所以2(2)2(23)c c +=+, ………4分 解得0c =或2c =,又0c ≠,故2c =. ………6分 (Ⅱ)当2n ≥时,由1n n a a cn +=+得21a a c -=, 322a a c -=,…1(1)n n a a n c --=-,以上各式相加,得1(1)[12...(1)]2n n n a a n c c --=+++-=, ………9分 又12a =,2c =,故22(2)n a n n n =-+≥, ………11分 当1n =时,上式也成立, ………12分 所以数列{}n a 的通项公式为22n a n n =-+(*Νn ∈). ………13分17.(本小题满分13分)解:(Ⅰ)由图可知,健康上网天数未超过20天的频率为(0.010.020.030.09)50.1550.75+++⨯=⨯=, ………2分∴ 健康上网天数超过20天的学生人数是第20题图40(10.75)400.2510⨯-=⨯=.………4分(Ⅱ)随机变量Y的所有可能取值为0,1,2.………5分P(Y=0)=2302402952CC=, P(Y=1)=111030240513C CC=, P(Y=2)=210240352CC=.……8分所以Y的分布列为11分∴E(Y)=0×2952+1×513+2×352=12.………………………………13分18.(本小题满分13分)解:(Ⅰ)DACS∆=1sin2AD AC DAC∴⋅⋅⋅∠=,∴1sin2DAC∠=.………2分∵233DAC BACπππ∠<∠<-=,∴6DACπ∠=.………3分在△ADC中,由余弦定理,得6cos2222πACADACADDC⋅-+=, ……4分24482228DC∴=+-⨯⨯=,DC∴=………6分(Ⅱ)∵AB AD=,3Bπ=,∴ABD∆为正三角形,在ADC∆中,根据正弦定理,可得,⎪⎭⎫⎝⎛-==CDCCAD3sin32sin34sinππ, ………7分8sinAD C∴=,8sin3DC Cπ⎛⎫=-⎪⎝⎭, ………8分∴ADC∆的周长为8sin8sin3AD DC AC C Cπ⎛⎫++=+-+⎪⎝⎭34cos 23sin 21834sin 21cos 23sin 8+⎪⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛-+=C C C C C …9分 343sin 8+⎪⎭⎫ ⎝⎛+=πC , …………………………………10分22033333ADC C C πππππ∠=∴<<∴<+<,,, ………11分 () 3.326C C f A πππ∴+=当,即=时,有最大值16+8 ADC∆的周长最大值为348+. ……13分 19.(本小题满分13分) 解:(Ⅰ)设每件定价为x 元, 依题意,有25(80.2)2581x x --⨯≥⨯, ………3分 整理得26510000x x -+≤,解得2540x ≤≤. ………5分 ∴ 要使销售的总收入不低于原收入,每件定价最多为40元. ………6分 (Ⅱ)依题意,25>x 时,不等式21125850(600)65ax x x ≥⨯++-+有解, ………8分 等价于25>x 时,1501165a x x ≥++有解, ………9分()150110306x x x +≥==当且仅当时,等号成立 , ………11分 10.2a ∴≥. ………12分. ∴当该商品明年的销售量a 至少应达到10.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元. ………13分20.(本小题满分14分)解:(Ⅰ)设点(,)P x y 为所求轨迹上的任意一点,则由OP OA PA k k k +=得,1111y y x x -+=-+, 整理得轨迹C 的方程为2y x =(0x ≠且1x ≠-). ………4分 (Ⅱ)方法一、设22112200(,),(,),(,)P x x Q x x M x y , 由PQ OA λ=可知直线//PQ OA ,则PQ OA k k =,故2221211010x x x x --=---,即211x x +=-, ………6分 由O M P 、、三点共线可知, 00(,)OM x y = 与211(,)OP x x =共线, ∴ 201100x x x y -=,由(Ⅰ)知10x ≠,故001y x x =, ………8分同理,由00(1,1)AM x y =+- 与222(1,1)AQ x x =+- 共线,∴ 20220(1)(1)(1)(1)0x x x y +--+-=,即2020(1)[(1)(1)(1)]0x x x y ++---=,由(Ⅰ)知21x ≠-,故020(1)(1)(1)0x x y +---=, ………10分 将001y x x =,211x x =--代入上式得0101(1)(2)(1)0x x x x +----=, 整理得0112(1)1x x x -+=+,由11x ≠-得012x =-, ………12分由2PQA PAM S S ∆∆=,得到2QA AM =,因为//PQ OA ,所以2OP OM =,由2PO OM =,得11x =,∴P 的坐标为(1,1). ………14分方法二、设221122(,),(,),P x x Q x x由PQ OA λ=可知直线//PQ OA ,则PQ OA k k =,故2221211010x x x x --=---,即211x x =--, ………6分 ∴直线OP 方程为:1y x x = ①; …………8分直线QA 的斜率为:2111(1)1211x x x ---=----+,∴直线QA 方程为:11(2)(1)y x x -=--+,即11(2)1y x x x =-+--, ② …10分 联立①②,得12x =-,∴点M 的横坐标为定值12-. ……………12分 由2PQA PAM S S ∆∆=,得到2QA AM =,因为//PQ OA ,所以2OP OM =,由2PO OM =,得11x =,∴P 的坐标为(1,1). ………14分21.(本小题满分14分) 解:(Ⅰ) ()1()1x x f x x ϕ+=--11ln -+-=x x x , ()()()22211121-⋅+=-+='x x x x x x ϕ.……………………2分∵0x >且1x ≠, ∴()0x ϕ'>,∴函数()x ϕ的单调递增区间为()()∞+,和11,0. ……………………4分(Ⅱ)∵1()f x x'=,∴001()f x x '=,∴ 切线l 的方程为0001ln ()y x x x x -=-, 即001ln 1y x x x =+-, ① ……………………6分设直线l 与曲线()y g x =相切于点11(,)xx e ,∵()x g x e '=,∴101xe x =,∴10ln x x =-. ……………………8分∴直线l 的方程为()00011ln y x x x x -=+, 即0000ln 11x y x x x x =++, ② ……………………9分由①②得 0000ln 1ln 1x x x x -=+, ∴0001ln 1x x x +=-. …………………11分 下证:在区间1,+∞()上0x 存在且唯一: 由(Ⅰ)可知,()x ϕ11ln -+-=x x x 在在区间1,+∞()上递增. 又12()ln 011e e e e e ϕ+-=-=<--,22222213()ln 011e e e e e e ϕ+-=-=>--, ……………13分 结合零点存在性定理,说明方程()0x ϕ=必在区间2(,)e e 上有唯一的根,这个根就是所求的唯一0x .故结论成立.………………14分。
2012年高考理科综合模拟试卷(化学部分)
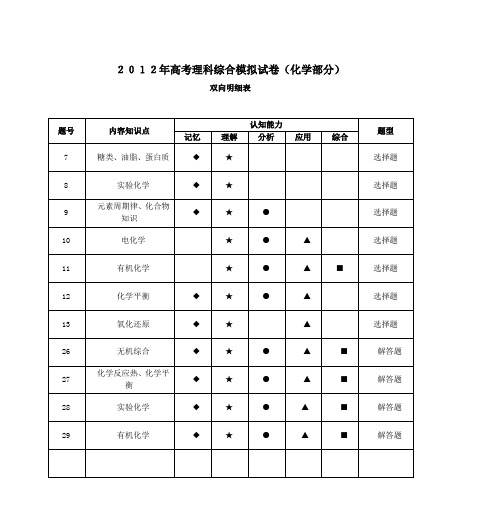
2012年高考理科综合模拟试卷(化学部分)
双向明细表
2012年高考理科综合模拟试卷(化学部分)
理科综合考试时间150分钟满分300分化学部分100分
第Ⅰ卷
相对原子质量:H-1 C-12 O-16 N-14 S-32 Mg-24 Fe-23 Mn—55
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
7、下列说法正确的是()
A.真丝、人造丝灼烧时都有烧焦羽毛的气味。
B.淀粉、纤维素、油脂都是高分子化合物。
C.氨基酸分子中既有氨基,又有羧基,它是两性化合物。
D.许多蛋白质在水中有一定的溶解性,溶于水形成胶体。
加入浓的硫酸钠溶液,有沉淀析出,这种作用称为变性。
【原创】
8、下列说法正确的是()
A、制备硫酸亚铁铵的实验中最后制得的晶体过滤后用蒸馏水洗涤。
B、AgI 沉淀中滴入稀KCl溶液,有白色沉淀出现,说明AgCl比AgI更难溶。
C、倾析法是将不溶物充分沉淀后,先转移沉淀后转移液体。
D、配制好的氢氧化钠溶液用邻苯二甲酸氢钾滴定浓度时,采用酚酞为指示剂。
【原创】
9、X、Y、Z、W为四种短周期元素。
X原子最外层电子数是核外电子层数的3倍;Y最高价与最低价的代数和为6;
Z在地壳中的含量仅次于氧;Y、Z、W同周期,W的常见化合价为+2。
下列说法不正确
...的是()A.存放W单质的仓库失火不能用CO2灭火
B.Z的氧化物通常形成分子晶体。
2012届高三二模考试数学试卷(理)及答案

2012届高三模拟考试数学试题数学试题(理科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生要务必填写答题卷上密封线内的有关项目.2.选择题每小题选出答案后,用铅笔把答案代号填在答题卷对应的空格内.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.请考生保持答题卷的整洁.考试结束后,将答题卷和答题卡交回. 参考公式:锥体的体积公式13V Sh =,其中S 为锥体的底面面积,h 为锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数(1)i ai ⋅+是纯虚数,则实数a 的值是( )A. 1B. 1-C.0D. 0或1-2.已知集合{||2,A x x x =≤∈R },{2,B x x =≤∈Z },则A B = ( )A. (0,2)B. [0,2]C. {0, 2}D. {0,1,2}3.设25025..12,25,()2.a b c ===,则,,a b c 的大小关系是(C )A.a c b >>B. c a b >>C. a b c >>D.b a c >>4.一空间几何体的三视图如图所示,则该几何体的体积为. A. 1 B. 3 C 6 D. 25.设向量(1,0)a = ,11(,)22b = ,则下列结论正确的是 ( )A.a b =B.2a b ⋅= C. a ∥b D. a b - 与b 垂直6.执行如图1所示的程序框图后,输出的值为5,则P 的取值范围( )A.715816P <≤ B. 1516P > C. 715816P ≤< D.3748P <≤ 7. 下列四个判断:①某校高三一班和高三二班的人数分别是,m n ,某次测试数学平均分分别是,a b ,则这两个班的数学平均分为2a b+; ②10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ,则有b a c >>; ③从总体中抽取的样本12221111(,),(,),,(,),,n nn n i i i i x y x y x y x x y y n n ====∑∑ 若记,则回归直线y =bx a +必过点(,x y )④已知ξ服从正态分布(0N ,2)σ,且(20)0.4P ξ-≤≤=,则(2)0.2P ξ>= 其中正确的个数有: ( )A .0个B . 1 个C .2 个D .3个8. 定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩,设111sgn()1sgn()122()()22x x f x f x -+-+=⋅+2()f x ⋅,[0,1]x ∈,其中1()f x =12x +, 2()f x ⋅=2(1)x -, 若1[()][0,)2f f a ∈,则实数a 的取值范围是( )A. 1(0,]4B. 11(,)42C. 11(,]42D. 3[0,]8二、填空题:本大共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题)9.. 已知A 是单位圆上的点,且点A 在第二象限,点B 是此圆与x 轴正半轴的交点,记AOB α∠=, 若点A的纵坐标为35.则s i n α=_____________;tan(2)πα-=_______________.10.以抛物线24y x =的焦点为圆心,且被y 轴截得的弦长等于2的圆的方程为__________________.11.从如图所示的长方形区域内任取一个点()y x M ,,则点M 取自阴影部分的概率为____________.12.已知,x y 满足约束条件5000x y x y y ++⎧⎪-⎨⎪⎩≥≤≤,则24z x y =+的最小值是_________.13.设()11f x x x =-++,若不等式121()a a f x a+--≥对任意实数0a ≠恒成立,则x 取值集合是_______________________.(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图,AB 是圆O 的直径,DE AD =,6,8==BD AB ,则ADAC= ;15.(坐标系与参数方程选做题) 已知直线l 方程是11x ty t =+⎧⎨=-⎩(t 为参数),,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为1ρ=,则圆C 上的点到直线l 的距离最小值是 三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)已知等比数列{}n a 的前n 项和为n S , 11a =,且1S ,22S ,33S 成等差数列. (1)求数列{}n a 通项公式;(2)设n n b a n =+,求数列{}n b 前n 项和n T .17.(本小题满分14分) 有一个3×4×5的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成60个1×1×1的小正方体,从这些小正方体中随机地任取1个,设小正方体涂上颜色的面数为ξ. (1)求0ξ=的概率; (2)求ξ的分布列和数学期望.18.(本小题满分14分)如图5(1)中矩形ABCD 中,已知2AB =,AD =MN 分别为AD 和BC 的中点,对角线BD 与MN 交于O 点,沿MN 把矩形ABNM 折起,使平面ABNM 与平面MNCD 所成角为60 ,如图5(2).(1) 求证:BO DO ⊥;(2) 求AO 与平面BOD 所成角的正弦值.OABDC MNABDCMNO图6B A19.(本小题满分12分)在ABC ∆中,三个内角A ,B ,C 的对边分别为a ,b ,c ,其中2c =,且cos cos 1A bB a == (1)求证:ABC ∆是直角三角形;(2)如图6,设圆O 过,,A B C 三点,点P 位于劣弧AC ︿上,求PAC ∆面积最大值.20.(本小题满分14分)在直角坐标系xOy 中,动点P 与定点(1,0)F 的距离和它到定直线2x =的距离之比是2,设动点P 的轨迹为1C ,Q 是动圆2222:C x y r +=(12)r <<上一点. (1)求动点P 的轨迹1C 的方程; (2)设曲线1C上的三点1122(,),(,)A x y B C x y 与点F 的距离成等差数列,若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k ;(3)若直线PQ 与1C 和动圆2C 均只有一个公共点,求P 、Q 两点的距离PQ 的最大值.21.(本小题满分14分)已知函数()ln(1)f x x mx =++,当0x =时,函数()f x 取得极大值. (1)求实数m 的值;(2)已知结论:若函数()ln(1)f x x mx =++在区间(,)a b 内导数都存在,且1a >-,则存在0(,)x a b ∈,使得0()()()f b f a f x b a-'=-.试用这个结论证明:若121x x -<<,函数121112()()()()()f x f x g x x x f x x x -=-+-,则对任意12(,)x x x ∈,都有()()f x g x >;(3)已知正数12,,,n λλλL ,满足121n λλλ+++=L ,求证:当2n ≥,n N ∈时,对任意大于1-,且互不相等的实数12,,,nx x x L ,都有1122()n n f x x x λλλ+++>L 1122()()()n n f x f x f x λλλ+++L .2012届高考模拟测试数学试题(理科)参考答案和评分标准一.选择题:CACBD ABB二填空题:9.35(2分)247(3分) 10. 22(1)2x y -+= 11. 13 12. 15- 13. 33(,][,)22-∞-+∞ 14. 4315.1三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16.(本题满分14分)解:(1)设数列{}n a 的公比为q ,……………1分若1q =,则111S a ==,21244S a ==,31399S a ==,故13231022S S S +=≠⨯,与已知矛盾,故1q ≠,………………………………………………2分从而得1(1)111n nn a q q S q q--==--,………………………………………………4分由1S ,22S ,33S 成等差数列,得132322S S S +=⨯,即321113411q q q q--+⨯=⨯--, 解得13q =……………………………………………5分 所以11113n n n a a q--⎛⎫=⋅= ⎪⎝⎭.………………………………………………6分(2)由(1)得,11()3n n n b a n n -=+=+,………………………………7分 所以12(1)(2)()n n T a a a n =++++++1(1)(1)(12)12n n b q n nS n q -+=++++=+- ………………………………10分2111()(1)333.12213n n n n n n --+++-=+=-……………………………12分 17.(本题满分12分)(1)60个1×1×1的小正方体中,没有涂上颜色的有6个,61(0)6010P ξ=== … (3分) (2)由(1)可知1(0)10P ξ==;11(1)30P ξ==;2(2)5P ξ==;2(3)15P ξ== … (7分)… (10分)E ξ=0×110+1×1130+2×25+3×215=4730 …(12分)18(本题满分14分)解:(1)由题设,M ,N 是矩形的边AD 和BC 的中点,所以AM ⊥MN, BC ⊥MN, 折叠垂直关系不变,所以∠AMD 是平面ABNM 与平面MNCD 的平面角,依题意,所以∠AMD=60o , ………………………………………………………………………………………………………2分 由AM=DM ,可知△MAD 是正三角形,所以AD=2,在矩形ABCD 中,AB=2,AD=所以,,由题可知,由勾股定理可知三角形BOD 是直角三角形,所以BO ⊥DO ……………………………………………………………………………………… 5分解(2)设E ,F 是BD ,CD 的中点,则EF ⊥CD, OF ⊥CD, 所以,CD ⊥面OEF, OE CD⊥ 又BO=OD ,所以OE ⊥BD, OE⊥面ABCD, OE ⊂面BOD , 平面BOD ⊥平面ABCD过A 作AH ⊥BD ,由面面垂直的性质定理,可得AH ⊥平面BOD ,连结OH ,…………………… 8分 所以OH 是AO 在平面BOD 的投影,所以∠AOH 为所求的角,即AO 与平面BOD 所成角。
2012届高三理综第二次模拟检测考试题

吉林市普通中学2011-2012学年度高中毕业班下学期期中教学质量检测理科综合能力测试注意:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满其中A 、B 代表某些元素,X 、Y 、Z 、P 代表单体,Ⅰ、Ⅱ、Ⅲ、Ⅳ代表由单体形成的多聚体,相关叙述错误的是A .A 和B 所代表的元素中存在相同的种类,如N 元素B .P 在生物体内有20种,可以用双缩脲试剂鉴定C .I 可以代表糖类,也可以代表脂肪D .Y 物质中的单糖是脱氧核糖,Ⅳ的多样性由Ⅱ决定4.下图中甲、乙模型分别代表人体体液中物质交换、人体细胞间的信息传递,分析以下说法,正确的是A .甲图中D 表示细胞内液, A 表示血浆B .如果乙图中B 表示胰岛细胞,则A 可以表示下丘脑细胞C .人体过敏反应时,甲图中的A 增加导致组织水肿D .乙图中激素的传递都需要细胞膜上载体的协助5. 某研究性学习小组的同学对某地区人类(10000人)的遗传病进行调查。
在调查中发现甲种遗传病(简称甲病)发病率较高,往往是代代相传,乙种遗传病(简称乙病)的发病率较低。
下表是甲病和乙病在该地区万人中表现情况统计表(甲、乙病均由核基因控制)。
下列分析不正确的是A. 要了解甲病和乙病的发病率,应对患甲病的家庭进行调查并进行系谱分析B. 根据统计表,甲病最可能是常染色体的显性遗传病C. 控制乙病的基因最可能位于X染色体上。
因为调查显示乙病中男患者多于女患D. 若要快速检测正常人群中的个体是否携带乙病致病基因,可根据碱基互补配对原则,利用DNA分子杂交技术实现6. 种群密度是种群的最基本特征,下列有关研究和调查正确的是A. 种群的年龄组成和性别比例直接决定种群密度B. 研究种群“S”型增长曲线在鱼牧养殖生产上的应用时,人们发现种群数量保持在K值左右可获得最大的经济效益C. 标志重捕法可用于调查蚯蚓的种群密度D. 蚜虫、跳蝻的种群密度可用样方法进行调查7. 下列叙述中,正确的是A. 20℃时,1molSO2的体积一定大于22.4LB. 1mol/LNaCl溶液表示1L水中含有NaCl58.5gC. 常温下,1molCO2与1molH2O所含有的分子总数和原子总数均相等D. 1molO2与足量金属钠反应,得到了4mole—8. 分子式为C3H6ClBr的同分异构体共有(不考虑立体异构)A.4种B.5种C.6种D.7种9. 下列反应中,与乙醛生成乙酸属于同一种反应类型的是A. CH 3CH 2OH → CH 3CHOB.CH 2=CHCl →C.D.CH 3COOH →CH 3COOCH 2CH 310. 下列离子方程式正确的是 A.NaHCO 3溶液中滴入NaOH 溶液:HCO 3—+ OH —= CO 2↑+H 2OB.SiO 2溶于NaOH 溶液:SiO 2+ 2OH —=SiO 32— +H 2OC.向氨水中滴入少量的AlCl 3溶液:Al 3++4OH —=AlO 2—+2H 2OD.NaClO 溶液中加入过量的浓盐酸:3ClO —+ Cl —+4H +=2Cl 2↑+O 2↑+ H 2O11. 下列实验中,不能达到目的的是12.室温下,下列说法正确的是A .将pH=1的H 2SO 4和pH=3的HCl 等体积混合,所得溶液pH=2B .HF 比HCN 易电离,则NaF 溶液的pH 比同浓度NaCN 溶液的pH 大A .实验室用大B .制取SO 2并C .分离淀粉胶D .比较氯碳硅C.向0.1 mol/LCH3COOH溶液中加入少量CH3COONa固体,溶液中增大D.将1 mL pH=3的HX溶液稀释到10 mL,若溶液的pH <4,则HX为弱酸13. 右图中的四条直线分别表示Na、Mg、Al、Fe和足量的Cl2(g)反应,消耗金属的质量(m)与反应掉相同条件下Cl2(g)的体积(V)之间的关系。
河北省2012届高三模拟统考数学理考试卷

省2012届高三模拟统考数学理试卷第1卷一、选择题:本大题共12小题,每一小题5分,在每一小题给出的四个选项中,只有一项为哪一项符合题目要求的. 〔1〕复数313ii+=- 〔A 〕i 〔B 〕i - 〔C 〕2i 〔D 〕2i -〔2〕()f x 是定义在R 上的奇函数,且当0x >时,()23xf x =-,如此(2)f -=〔A 〕1 〔B 〕1- 〔C 〕14 〔D 〕114- 〔3〕数列{}n a 为等差数列,假如23a =,1612a a +=,如此789a a a ++=〔A 〕27 〔B 〕36 〔C 〕45 〔D 〕63 〔4〕抛物线24x y =上一点A 的纵坐标为4,如此点A 到抛物线焦点的距离为〔A 〕10 〔B 〕4 〔C 〕15 〔D 〕5 〔5〕给出如下四个命题:①,sin cos 1R ααα∀∈+>-②3,sin cos 2R ααα∃∈+=③1,sin cos 2R ααα∀∈≤④3,sin cos 4R ααα∃∈=其中正确命题的序号是①②③④〔A 〕①② 〔B 〕①③ 〔C 〕③④ 〔D 〕②④〔6〕如图是一个容量为200的样本频率分布直方图,如此样本数据落在围[13,17)的频数为〔A 〕81 〔B 〕36 〔C 〕24 〔D 〕12〔7〕椭圆221:12x y C m n +=+与双曲线222:1x y C m n-=共焦点,如此椭圆1C 的离心率e 的取值围为〔A 〕2(,1)2 〔B 〕2(0,)2〔C 〕(0,1) 〔D 〕1(0,)2〔8〕O 为坐标原点,A ,B 两点的坐标均满足不等式组3103010x y x y x -+≤⎧⎪+-≤⎨⎪-≥⎩,如此tan AOB ∠的最大值等于 〔A 〕12 〔B 〕34 〔C 〕47 〔D 〕94〔9〕设函数()3cos(2)sin(2)(||)2f x x x πϕϕϕ=+++<,且其图象关于直线0x =对称,如此〔A 〕()y f x =的最小正周期为π,且在(0,)2π上为增函数 〔B 〕()y f x =的最小正周期为π,且在(0,)2π上为减函数〔C 〕()y f x =的最小正周期为2π,且在(0,)4π上为增函数〔D 〕()y f x =的最小正周期为2π,且在(0,)4π上为减函数〔10〕某几何体的三视图入图所示,如此此几何体对应直观图中△PAB 的面积是〔A 〕7 〔B 〕2 〔C 〕3 〔D 〕5〔11〕根据如下列图程序框图,假如输入2146m =,1813n =,如此输出m 的值为〔A 〕1 〔B 〕37 〔C 〕148 〔D 〕333〔12〕函数|21|,2()3,21x x f x x x ⎧-<⎪=⎨≥⎪-⎩,假如方程()0f x a -=有三个不同的实数根,如此实数a 的取值围为〔A 〕(1,3) 〔B 〕(0,3) 〔C 〕(0,2) 〔D 〕(0,1)第2卷本卷包括必考题和选考题两局部。
(003)2012届高三数学(理)模拟试卷

2012届高三数学(理)模拟试卷(003)一.选择题(本大题共10小题,每小题5分,共50分。
每小题只有一个正确选项)1.已知全集U R =,2{log 0}A x x =<,11B xx ⎧⎫=≤⎨⎬⎩⎭,则=B A C U )(( ) A .(1,)+∞ B .[1,)+∞ C .(,0)(1,)-∞+∞ D .(,0)[1,)-∞+∞2.设复数z 的共轭复数为z ,若1z i =-(i 为虚数单位),则2zz z+的值为( ) A .i - B .i 2-C .i 3-D . i3. 已知二次函数2()f x ax bx =+,则“(2)0f ≥”是“函数()f x 在()1,+∞单调递增”的( ) A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件4.执行如图所示的程序框图,若输出x 的值为23,则输入的x 值为(A .0B .1C .2D .11 5. 下列命题中是假命题的是( ) A .m R ∃∈,使243()(1)m m f x m x -+=-⋅是幂函数 B .0a ∀>,函数2()ln ln f x x x a =+-有零点 C .,R αβ∃∈,使cos()cos cos αβαβ+=+D .R ϕ∀∈,函数()sin()f x x ϕ=+都不是偶函数6.已知数列{}n a 满足115,2nn n a a a +==,则73aa =( )A .2B . 4C .5D .527.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:则y 对x 的线性回归方程为( ) A .1-=x y B .1+=x y C .8821+=x y D .176=y 8.将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有1个小球,且每个盒子中的小 球个数都不同,则共有( )种不同放法 A .15 B .18 C .19 D .219. 已知G 是ABC ∆的重心,且0aGA bGB +=,其中c b a ,,分别为角A,B,C 的对边,则cos C =( ) 533310.已知定义域为(0,)+∞的函数()f x 满足:(1)对(0,)x ∀∈+∞,恒有1()()22xf x f =成立; (2)当[1,2]x ∈时,3()482f x x =--.给出如下结论:①对于任意n N ∈,有121(32)()2n n f --⋅=;②对任意的[1,8]x ∈,不等式()6xf x ≤恒成立;③存在n N ∈,使得1(21)()2n n f +=;④“函数()f x 在区间(,)(1)a b a >上单调递减”的充要条件是存在n N ∈,使得11(,)(32,2)n n a b -+⊆⋅.其中所有正确结论的序号是( )A .①②③B .②③④C .①②④D .①②③④二.填空题(本大题共4小题,每小题5分,共20分) 11. 若0sin a xdx π=⎰,则二项式6(展开式中 含x 的项的系数是_______.12.已知一个几何体的三视图及其长度如图所示,则该几何体的体积为 .13.已知抛物线22(0)y px p =>与双曲线22221x y a b-=(0,0)a b >>有相同的焦点F ,点A 是两曲线的交点,且AF x ⊥轴,则双曲线的离心率为 .14.点(,)M x y是不等式组03x y x ⎧≤≤⎪≤⎨⎪≤⎩表示的平面区域Ω内的一动点,使2y x -取得最小值的点为00(,)A x y ,则AM OM ∙(O 为坐标原点)的取值范围是 .三.选作题(请在下列两个小题中任选一题作答,若两题都做,则按所做的第一题计分,共5分) 15.(1)在极坐标系中,定点A (2,π),动点B 在直线sin()4πρθ+=2上运动,则线段AB 的最短长度为 .(2)不等式a a x x 3132-≤--+对任意实数x 恒成立,则实数a 的取值范围为 . 四.解答题(本大题共6小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤.)俯视图侧视图第12题(Ⅰ)求cos A 及sin C 的值; (Ⅱ)若2b =,求ABC ∆的面积.17.(本小题满分12分)某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为45,第二、第三种产品受欢迎的概率分别为p ,q (p >q ),且不同种产品是否受欢迎相互独立.记ξ为公司向市场投放三种新型产品受欢迎的数量,其分布列为(1) (2)求p ,q 的值;(3)求数学期望E ξ.18.(本小题满分12分)已知斜三棱柱111ABC A B C -的底面是直角三角形,90ACB ∠= ,侧棱与底面所成角为θ,点1B 在底面上射影D 落在BC 上. (Ⅰ)求证:AC ⊥平面11BB C C ;(Ⅱ)若点D 恰为BC 中点,且11AB BC ⊥,求θ的大小; (III )若1cos 3θ=,且当1AC BC AA a ===时,求二面角1C AB C --的大小.19.(本小题满分12分)已知数列{}n a 满足:*1()n n S a n N =-∈,其中n S 为数列{}n a 的前n 项1C1B 1ADCBA(2)设11111n n n c a a +=++-,数列{}n c 的前n 项和为nP ,求证:122n P n >-.20.(本小题满分13分)已知椭圆)0(1:2222>>=+b a by a x C 经过点)22,1(P ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.(1)求椭圆的方程;(2)过点1(0,)3M -的动直线l 交椭圆C 于A 、B 两点,试问在坐标平面上是否存在一个定点T ,使得以AB 为直径的圆恒过点T ?若存在,求出点T 的坐标;若不存在,请说明理由.21.(本小题满分14分)已知函数)1(ln ln )(>+=x x x a x x x f 的图象经过)22,(222ee e +(其中e 为自然对数的底数,71.2≈e ). (Ⅰ)求实数a 的值; (Ⅱ)求)(xf 的单调区间;(Ⅲ)证明:对于任意的*N n ∈,都有n n n ee e n n e e e e e )1()()22)(1(22+≥+⨯⋅⋅⋅⨯++成立.2012届高三模拟题数学(理科)答题卷一.选择题(本大题共10小题,每小题5分,共50分)二.填空题(本大题共4小题,每小题5分,共20分)11.12.13.14.三.选作题(共5分)15.(1) ;(2) .四.解答题(本大题共6小题,共75分)16.(12分)17.(12分)18.(12分)19.(12分)1C1B1ADCB A2012届高三数学(理)模拟试卷参考答案一.选择题(本大题共10小题,每小题5分,共50分)二.填空题(本大题共5小题,每小题5分,共25分)11. 240 12.2113.12+ 14.[1,6]- 三.选作题(共5分)15.(1)2; (2) (,1][4,)-∞-+∞ . 四.解答题(本大题共6小题,共75分) 16.(12分)解:(Ⅰ)因为2A B =,所以2cos cos212sin A B B ==-. …………………………1分因为sin B =,所以31sin 21cos 2=-=B A . …………………………………2分由题意可知,)2,0(π∈B所以cos B =……………………4分因为sin sin 22sin cos 3A B B B ===. ………………………………………5分 所以sin sin[()]sin()C A B A B π=-+=+sin cos cos sin A B A B =+=.…7分 (Ⅱ)因为sin sin b aB A=,2b =, ……………………………………………9分=.所以a =. ………………………………………10分所以117.(12分)解:设事件i A 表示“该公司第i 种产品受欢迎”,i =1,2,3由题意知14()5P A =,2()P A p =,3()P A q = …………………………1分 (1)由于事件“该公司至少有一种产品受欢迎”与事件“0ξ=”是对立的,所以该公司至少有一种产品受欢迎的概率是2431(0)14545P ξ-==-=……………………………3分 (2)由题意知12312(0)()(1)(1)545P P A A A p q ξ===--=,123(3)()P P A A A ξ==48545pq ==,整理得29pq =且1p q +=,由p q >,可得21,33p q ==.…………7分 (3)由题意知123123123(1)()()()a P P A A A P A A A P A A A ξ===++41113(1)(1)(1)(1)55545p q p q p q =--+-+-=……………………9分22(2)1(0)(1)(3)45b P P P P ξξξξ===-=-=-==…………………………………10分因此270(0)1(1)2(2)3(3)15E P P P P ξξξξξ=⨯=+⨯=+⨯=+⨯==……………12分18.(12分) 解:(I )∵B 1D ⊥平面ABC ,AC ⊂平面ABC ,∴1B D AC ⊥又∵BC AC ⊥,1B D BC D = ,∴AC ⊥平面11BB C C …………………4分(II )1111111111AB BC BC AB C AC BC BC B C B C AB C AB AC ⊥⎫⊥⎫⎪⊥⇒⇒⊥⎬⎬⊂⎭⎪⎭平面平面与相交∴四边形11BB C C 为菱形, 又∵D 为BC 的中点,⊥D B 1平面ABC∴1B BC ∠为侧棱和底面所成的角θ ∴11cos 2B BC ∠=∴160B BC ∠= ,即侧棱与底面所成角60 . ………………………………8分(III )以C 为原点,CA 为x 轴,CB 为y 轴,过C 点且垂直于平面ABC 的直线为Z 轴,建立空间直角坐标系,则A (a ,0,0),B (0,a ,0),10,,33a C ⎛⎫-⎪ ⎪⎝⎭,平面ABC 的法向量1(0,0,1)=n ,设平面ABC 1的法向量为2(,,)x y z =n ,由2210AB BC ⎧⋅=⎪⎨⋅=⎪⎩n n,得2=n12cos ,<>=n n 12,45<>=n n19.(12分)解:(1)∵1n n S a =- ① ∴111n n S a ++=- ②②-①得11n n n a a a ++=-+,∴*11()2n n a a n N +=∈ ……………………………4分 又当1n =时,111a a =-,∴112a = ∴1*111()()()222n n n a n N -=⋅=∈…………6分 (2)证明:∵11111111111()1()22n n n n n c a a ++=+=++-+-11222121n n n n ++=++- 1121n =-+1++111112()212121n n n ++=---+- …………………………………8分 又1111121(21)2121(21)(21)n n n n n n +++--+-=+-+-=2121222221221n n n n n n ++-<+-+-111112212n n n ++=<+- ……………………11分∴ 1122n n C +>-∴23111111112()22222222n n n P n n n ++>-+++=-+>- ……………12分 20.(13分)解:(1)由题意知,c b = 其中22b a c -= ∴ b a 2=……① ………………2分又点)22,1(P 在椭圆12222=+by a x 上 ∴ 121122=+b a ……② ………………4分 联立①②,解得1,2==b a …………………………………………………………5分 故所求椭圆的方程为1222=+y x …………………………………………………………6分 (2)当直线l 的斜率不存在时,以AB 为直径的圆的方程为221x y +=当直线l 的斜率为0时,以AB 为直径的圆的方程为22116()39x y ++= ∵ 该两圆交点为(0,1),故假设存在符合题意的定点,则该点即为(0,1)T …………8分 方法1:设),(,),(2211y x B y x A则以AB 为直径的圆的方程为0))(())((2121=--+--y y y y x x x x即0)()(2121212122=+++-+-+y y x x y y y x x x y x ……………………………10分∵ ⎪⎪⎩⎪⎪⎨⎧+-=+-=+⎪⎪⎩⎪⎪⎨⎧+-=+-=+)2(918)2(32)2(916)2(3422222122221222212221n m m n y y n m n y y n m n x x n m mn x x 且 ∴ 圆的方程为:0)2(91815)(32)2(3422222222222=+--++++++n m m n y n m n x n m mny x将(0,1)代入显然成立,故存在)1,0(T 符合题意.………………………………13分 方法2:设),(,),(2211y x B y x A ,直线l 斜率为k ,则31:-=kx y l 由091634)21(12312222=--+⇒⎪⎪⎩⎪⎪⎨⎧=+-=kx x k y x kx y ∴ )21(916,)21(34221221k x x k k x x +-=+=+……………………………………10分 ∵ )1,()1,(2211-=-=y x TB y x TA∴ 916)(34)1()34)(34(212122121++-+=--+=∙x x k x x k kx kx x x 0916)21(9)21(16916)21(3434)21(9)1(1622222=+++-=++⨯-++-=k k k k k k k ∴ TB TA ⊥ 故存在符合题意的定点)1,0(T ,使得以AB 为直径的圆恒过该点.……13分21.(14分)解:(Ⅰ)由)(x f y =的图象过点)22,(222e e e +得:1ln ln 22222222=⇒+=+a ee a e e e e .………2分 (Ⅱ)2222)(ln )ln )(ln )(1(ln ln 1)(ln 1ln )(x x x x x x x x x x x x f -+-=-+-=' ………………………4分 由1>x 知0)(ln ln 22>+x x x x ,令x x x g ln )(-=01)(>-='⇒x x x g ,故)(x g 在),1(+∞上为增函数 ∴当1>x 时,0)1(ln )(>>-=g x x x g令0)(='x f 得e x =,令0)(>'x f 得,e x >,令0)(<'x f 得e x <<1故)(x f 的增区间为),(+∞e ,减区间为),1(e . ………8分 (Ⅲ)由(2)知,)(x f 在区间),1(+∞上的最小值为ee ef 1)(+= ………10分 即当1>x 时,ee xf 1)(+≥恒成立 当*N n ∈时,令1>≥=e e x n ,则有ee ef n 1)(+≥ 即01>+≥+ee e n n e n n ………12分 故n n n e e e n n e ee e e )1()()22)(1(22+≥+⨯⋅⋅⋅⨯++成立. ………14分。
2012届高三理综模拟试卷(008)

2012届高三理综模拟试卷(008)本试卷分第Ⅰ卷(选择题,126分)和第Ⅱ卷(非选择题,174分)两部分,全卷共300分,考试时间150分钟. 请按答题卷要求将答案做在“答题卷”上.第Ⅰ卷(选择题,共126分)试题可能用到的相对原子质量:相对原子质量:Na:23 O:16 H:1 Ca :40 Cl :35.5 一、选择题(本题包括1 3小题,每小题只有一个选项符合题意,每小题6分) 1.在棉花叶肉细胞的线粒体基质、细胞质基质、叶绿体基质中可以产生的代谢产物分别是( )A .二氧化碳、丙酮酸、葡萄糖B .丙酮酸、葡萄糖、二氧化碳C .丙酮酸、二氧化碳、葡萄糖D .葡萄糖、丙酮酸、二氧化碳 2.下面甲图是某一高等动物体内细胞分裂的示意图,乙两曲线图分别表示该动物细胞中一条染色体上DNA 的含量变化及一个细胞中染色体组的变化。
下列有关叙述正确的是 ( )A .bc 段和hj 段可能对应于同一细胞分裂图B .甲图相应的是乙图中的hj 段C .如果不考虑基因突变,则等位基因分离可发生在乙图中的hj 段乙D .甲图中染色体、染色单体、核DNA 之比为1∶2∶2,是观察染色体形态和数目最好的时期3.下列有关细胞凋亡的描述中不正确的是:( )A .受到基因调控B .还可称为细胞程序性死亡C .可清除被病原体感染的细胞D .细胞膜快速破裂4.关于探究酶特性的实验叙述中,正确的是 ( )A .若探究温度对酶活性的影响,可选择过氧化氢溶液为底物B .若探究过氧化氢酶的高效性,可选择无机催化剂作为对照C .若探究温度对淀粉酶活性的影响,可选择斐林试剂对实验结果进行检测D .若用淀粉、蔗糖和淀粉酶来探究酶的专一性,可用碘液对实验结果进行检测 5.使用染色剂染色是生物学实验常用的方法,某同学对有关实验做了如下归纳: 上述实验结果的归纳,正确的有 (A.四项B.三项C.二项D.一项6.如图实验装置,玻璃槽中是蒸馏水,半透膜允许单糖分子透过,倒置的长颈漏斗中先装入蔗糖溶液,一定时间后再加入蔗糖酶,最可能的实验结果是 ( )A .在玻璃槽中会检测到蔗糖和蔗糖酶B .在玻璃槽中只能检测到葡糖糖C .漏斗中液面开始先下降,加酶后上升一段时间又下降实验 观察对象染色剂 实验结果① 花生子叶细胞的脂肪颗粒 苏丹Ⅲ 脂肪颗粒被染成橘黄色 ② 人口腔上皮细胞中的DNA 和RNA 分布毗罗红甲基绿 细胞内染成绿色的面积显著大于染成红色的面积 ③ 人口腔上皮细胞中的线粒体 健那绿 线粒体呈现蓝绿色④洋葱根尖分生组织细胞的有丝分裂龙胆紫间期细胞不着色,分裂期细胞染色体着色D.漏斗中液面开始时先上升,加酶后再上升一段时间后又下降7. 化学与环境、科学、技术密切相关。
辽宁省大连24中2012届高三模拟考试理科综合试题

大连24中2012届高三模拟考试理综试题本试卷分第Ⅰ卷(选择题)和第II卷(非选择题)两部分,其中第II卷第33-40题为选考题,其它题为必考题.考生作答时,将答案答在答题一}上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交同。
注意事项:1、答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2、选择题答案使用2B铅笔填涂,如需改动,用橡皮擦擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3、请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.4、保持卡面清洁,不折叠,不破损。
5、做选考题时,考生按照题曰要求作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑。
可能用到的相对原子质量H:1 C: 12 N:14 O:16 Na:23一、选择题:本题共13小题,每小题6分,在每小题给出的4个选项中,只有一项是符合题目要求的。
l。
下列实验中不能够使用哺乳动物成熟的红细胞作为实验材料的是A.探讨细胞的吸水和失水B.研究细胞无氧呼吸的途径C.制备较纯净的细胞膜D.观察细胞的有丝分裂2.与右图所示关系不相符的是A.横坐标是饮水量,则纵坐标可表示抗利尿激素的分泌量B.横坐标是时间,则纵坐标可表示发生质壁分离过程中细胞的质量C.横坐标是环境温度,则纵坐标可表示家兔体内酶的活性D.横坐标是白交代数,则纵坐标可表示一对等位基因的杂合子白交后代中杂合子的比例3.某研究小组发现染色体上抑癌基因邻近的基因能指导合成反义RNA,反义RNA可以与抑癌基因转录形成的mRNA形成杂交分子,从而阻断抑癌基因的表达,使细胞易于癌变。
据图分析,下列叙述中不正确的是A.过程I在细胞核中进行B.若抑癌基因中A占20%,则经过过程l得到的mRNA中C占30%C.参与过程Ⅱ的RNA不只一种D.细胞中若出现了杂交分子,则抑癌基因沉默,此时过程Il 被抑制4.下列有关现代生物进化理论的说法正确的是A.自然选择作用于个体的表现型,使得个体成为进化的基本单位B.基因重组能够产生多种基因,为进化提供大量的原材料C.基因突变可引起种群基因频率的改变,但生物不一定发生进化D.物种的形成必须经过种群之间的隔离5.下列关于生命活动调节的叙述,错误的是A.有些气体分子有调节生命活动的作用B.在胰岛素的分泌调节中存在反馈调节C.脱落酸和细胞分裂素对细胞分裂有拮抗作用D.效应T细胞、浆细胞均能特异性识别抗原6.下列实验中,所用材料和试剂与实验目的匹配正确的是7.下列说法中正确的是①钠在空气中燃烧产生黄色火焰,生成淡黄色的Na2O2②常温下铝制容器可储运浓硫酸或浓硝酸③盐酸既有氧化性又有还原性④Fe (OH)3、FeCI2、H2SiO3都不能直接用化合反应制备⑤SO2能使酸性高锰酸钾溶液褪色,所以它具有漂白性⑥工业上用澄清的石灰水与氯气反应制取漂粉精⑦乙醇与重铬酸钾(K2Cr2O7)溶液混合,橙色溶液变为(蓝)绿色A.②③⑥⑦B.①②③⑦C.①②③④⑥D.①②③⑤8.下列说法不正确的是A.分子式为C5H12的化合物,其一氯代物种类(不考虑立体异构;)不可能是2种B.棉花、羊毛、蚕丝均属于天然纤维C.乙二酸二乙酯、乙二酸乙二酯、二乙酸乙二酯它们互为同分异构体D.石油裂化、油脂皂化和煤的干馏都是化学变化,而石油的分馏和蛋白质的盐析都是物理变化9.X、Y、Z、W均为短周期元素,它们在周期表中的位置如下图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012届高三(理科)模拟试卷(时间120分钟,满分150分)一、选择题:本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={1,2,a -1},B ={0,3,a 2+1},若{2}A B = ,则实数a 的值为 ( ) A .±1 B .1 C .-1 D .02.设l m n 、、表示不同的直线,αβγ、、表示不同的平面,给出下列4个命题: ①若//m l ,且m α⊥,则l α⊥; ②若//m l ,且m ∥α,则//l α; ③若,,l m n αββγγα=== ,则////l m n ;④若,,m l n αββγαγ=== ,且//n β,则//m l .其中正确命题的个数是 ( ) A .1 B .2 C .3 D .43.若关于x 的方程|1|2x a a -=(0,1)a a >≠有两个不等实根,则a 的取值范围是 ( ) A.(0,1)(1,)+∞ B .(0,1) C .(1,)+∞ D .1(0,)24.在平面直角坐标系中,i ,j 分别是与x 轴、y 轴正方向同向的单位向量,O 为坐标原点,设向量OA =2i +j ,OB=3i +k j ,若A ,O ,B 三点不共线,且△AOB 有一个内角为直角,则实数k 的所有可能取值的个数是 ( ) A .1 B .2 C .3 D .4 5.在极坐标系中,圆C :22cos sin 0k k ρρθρθ++-=关于直线l :()4R πθρ=∈对称的充要条件是 ( ) A .k =1 B .k =-1 C .k =±1 D .k =0 6.如图,正六边形ABCDEF 的两个顶点A 、D 为椭圆的两个焦点,其余4个顶点在椭圆上,则该椭圆的离心率是( )117.设等差数列{}n a 的前n 项和为n S ,已知12010a =-,20092007220092007S S -=,则2010S =( ) A .-2008 B .2008 C .-2010 D .2010 8.定义{}()max ,()a ab a b b a b ≥⎧=⎨<⎩,已知实数x ,y 满足|x |≤2,|y |≤2,设{}max 4,3z x y x y =+- 则z 的取值范围是 ( )A .[-7,10]B .[-6,10]C .[-6,8]D .[-7,8]A BCP C B M 二、填空题:本大题共6个小题,每小题5分,共30分,把答案填写在题中的横线上. 9.设复数(1)(2)z ai i =+-,若复数z 在复平面上对应的点在第一象限,则实数a 的取值范围是 .10.不等式33|21log (1)||21||log (1)|x x x x ---<-+-的解集是 . 11.如图,在△ABC 中,AB =3,BC =5,∠ ABC =120°,将△ABC 绕 直线AB 旋转一周,则所形成的旋转体的表面积是 .12.已知点C 在圆O 的直径BE 的延长线上,CA 与圆O 相切于点A ,∠ACB 的平分线分别交AB ,AE 于点D ,F ,则∠ADF = .13.已知函数74sin(2)(066y x x ππ=+≤≤的图象与一条平行于x 轴的直线有三个交点,其横坐标分别为123123,,()x x x x x x <<,则1232x x x ++= .14.已知()⎪⎩⎪⎨⎧--=12211x x x f 121210≤<≤≤x x ,()()()()⋯==-4,3,211n x f f x f n n 则 f 2(x)=0的解集为 ; 53()()f x f x =的解集为 。
三、解答题:本大题共6个小题,共80分,解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分12分)设△ABC 的三内角A 、B 、C 的对边长分别为a 、b 、c ,已知a 、b 、c 成等比数列,且3sin sin 4A C =. (Ⅰ)求角B 的大小;(Ⅱ)若[0,)x π∈,求函数()sin()sin f x x B x =-+的值域.16.(本小题满分13分)某同学利用寒暑假旅游了H 、I 、J 、K 和L 等5个景点,并收藏有H 纪念门票3张,I 纪念门票2张,J 、K 、L 纪念门票各1张,现从中随机抽取5张. (Ⅰ)求抽取的5张门票中恰有3个或恰有4个景点的概率;(Ⅱ)若抽取的5张门票中5个景点都有记10分,恰有4个景点记8分,恰有3个景点记6分,依此类推.设ξ表示所得的分数,求ξ的分布列和数学期望.17.(本小题满分13分)如图,PC ⊥平面ABC ,PM ∥CB ,∠ACB =120°, PM =AC =1,BC =2,异面直线AM 与直线PC 所成的角为60°.(Ⅰ)求二面角M -AC -B 大小的正切值;(Ⅱ)求三棱锥P -MAC 的体积.C18.(本小题满分14分)某县为了贯彻落实党中央国务院关于农村医疗保险(简称“医保”)政策,制定了如下实施方案:2009年底通过农民个人投保和政府财政投入,共集资1000万元作为全县农村医保基金,从2010年起,每年报销农民的医保费都为上一年底医保基金余额的10%,并且每年底县财政再向医保基金注资m 万元(m 为正常数).(Ⅰ)以2009年为第一年,求第n 年底该县农村医保基金有多少万元?(Ⅱ)根据该县农村人口数量和财政状况,县政府决定每年年底的医保基金要逐年增加,同时不超过1500万元,求每年新增医保基金m (单位:万元)应控制在什么范围内.19.(本小题满分14分)过圆22:(6)(4)8C x y -+-=上一点A (4,6)作圆的一条动弦AB ,点P 为弦AB 的中点. (Ⅰ)求点P 的轨迹方程;(Ⅱ)设点P 关于点D (9,0)的对称点为E ,O 为坐标原点,将线段OP 绕原点O 依逆时针方向旋转90°后,所得线段为OF ,求|EF |的取值范围. 20.(本小题满分14分)给出定义在(0,+∞)上的三个函数:()ln f x x =,2()()g x x af x =-,()h x x =-)(x g 在x =1处取极值.(Ⅰ)确定函数h (x )的单调性; (Ⅱ)求证:当21e x <<时,恒有2()2()f x x f x +<-成立;(Ⅲ)把函数h (x )的图象向上平移6个单位得到函数h 1(x )的图象,试确定函数y =g (x )-h 1(x )的零点个数,并说明理由.参考答案一、选择题:本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.【解析】因为{2}A B = ,则a 2+1=2,即a =±1. 但当a =1时,A ={1,2,0}, 此时{0,2}A B = ,不合题意,舍去,所以a =-1,故选C.2.【解析】易知命题①正确;在命题②的条件下,直线l 可能在平面α内,故命题为假;在命题③的条件下,三条直线可以交于一点,故命题为假;在命题④中,由n αγ= 知,α⊂n 且γ⊂n ,由α⊂n 及n ∥β,m αβ= ,得n ∥m ,同理n ∥l ,故m ∥l ,命题④正确,选B.3.【解析】据题意,函数|1|(0,1)x y a a a =->≠的图象与直线2y a =有两个不同的交点.由图知,021a <<,所以1(0,)2a ∈,故选D.4.【解析】由题设,OA =(2,1),OB =(3,k ),则(1,1)AB k =-.当OA ⊥OB 时,OA OB 06k ⋅=⇒=- ;当OA ⊥AB 时,OA AB 01k ⋅=⇒=-;当OB ⊥AB 时,2OB AB 030k k ⋅=⇒-+= (无解).所以k 的所有可能取值有2个,故选B.5.【解析】圆C 的直角坐标方程是2220x y k x y k +++-=,直线l 的直角坐标方程是y =x.若圆C 关于直线l 对称,则圆心21(,)22k C --在直线y =x 上,所以2122k -=-,即k =±1.又k 4+4k +1>0,所以k =1,故选A.6.【解析】连结AE ,则AE ⊥DE .设AD =2c ,则DE =c ,AE.椭圆定义,得2a =AE +ED+c,所以1c e a ===,故选D. 7.【解析】设等差数列{}n a 的公差为d ,则1(1)2n n n S na d -=+,即112n S n a d n -=+. 所以20092007112009120071()()2009200722S S a d a d d ---=+-+=,由已知2d =. 又12010a =-,则201012010120101201021201022S a d --=+=-+⨯=-,所以20102010S =-,故选C.8. 【解析】由题设,{}14()2max 4,313()2x y y x z x y x y x y y x ⎧+≥-⎪⎪=+-=⎨⎪-<-⎪⎩,且|x |≤2,|y |≤2.作可行域,由图知,目标函数4z x y =+在点(2,2)处取最大值10,在点(-2,1)处取最小值-7.目标函数3z x y =-点(2,-2)处取最大值8,在点(-2,1)处 取最小值-7.所以z 的取值范围是[-7,10],故选A .二、填空题:本大题共6个小题,每小题5分,共30分,把答案填写在题中的横线上.9.1(,2)2-.【解析】因为(1)(2)2(21)z ai i a a i =++=-++,由已知20122102a a a ->⎧⇒-<<⎨+>⎩.10. (2,+∞) .【解析】原不等式等价于3(21)log (1)0xx -->,即3210log (1)0x x ⎧->⎨->⎩或3210log (1)0x x ⎧-<⎨-<⎩(无解),由3210log (1)0x x ⎧->⎨->⎩,解得x >2.11..【解析】在△ABC 中,由余弦定理,得AC =7. 过点C 作CO ⊥AB ,垂足为O ,则OC =BCsin60°. 由图知,所形成的旋转体的表面积S 为圆锥AO 和圆锥BO 的表面积之和. 所以S =π×OC ×(BC +AC )=. 12. 45º .【解析】因为AC 为圆O 的切线,则∠B =∠EAC. 又CD 平分∠ACB ,则∠ACD =∠BCD. 所以∠B +∠BCD =∠EAC +∠ACD. 因为BE 是圆O 的直径,则∠BAE =90º, 所以∠B +∠BCD =∠EAC +∠ACD =45º 故∠ADF =∠B +∠BCD =45º. 13.53π. 【解析】取特殊直线y =2,令4sin(2)26x π+=,则1s i n (2)62x π+=.又123706x x x π≤<<≤,则1230,,3x x x ππ===,所以1232x x x ++=53π. 14. )43,0( ⎭⎬⎫⎩⎨⎧=≤≤1x 16150或x x三、解答题:本大题共6个小题,共80分,解答应写出文字说明,证明过程或演算步骤.15.(本小题满分12分)【解】(Ⅰ)因为a 、b 、c 成等比数列,则2b ac =.由正弦定理得2sin sin sin B A C =. (2分)又3sin sin 4A C =,所以23sin 4B =.因为sinB >0,则sin B =. (4分)因为B ∈(0,π),所以B =3π或23π. (5分)C又2b ac =,则a b ≤或b c ≤,即b 不是△ABC 的最大边,故3B =π. (6分)(Ⅱ)因为3B =π,则()s i n ()s i ns i n c o s c o s s i ns i n333f x x x x x x πππ=-+=-+3sin )26x x x π==-. (9分)[0,)x π∈,则5666x πππ-≤-<,所以1sin()[,1]62x π-∈-. (11分)故函数()f x的值域是[. (12分)16.(本小题满分13分) 【解】(Ⅰ)记抽取的5张门票中“恰有3个景点”为事件A ,“恰有4个景点”为事件B. 若抽取的5张门票中恰有3个景点,则至少要抽取2张张家界门票,所以3112221323332358()9()28C C C C C C C P A C ⋅⋅++⋅⋅==. (2分)若抽取的5张门票中恰有4个景点,则至多只能抽取2张张家界门票,所以21231222332333232358()31()56C C C C C C C C C P B C ⋅⋅++⋅⋅+⋅==. (5分)因为事件A ,B 互斥,所以931497()()()2856568P A B P A P B +=+=+==. 故抽取的5张门票中恰有3个或恰有4个景点的概率是78. (6分)(Ⅱ)因为5张门票中至少含有2个景点,则ξ的可能取值为10,8,6,4. (7分)其中113323583(10)28C C C P C ξ⋅⋅===,31(8)()56P P B ξ===, 9(6)()28P P A ξ===,3232581(4)56C C P C ξ⋅===. (10分) 所以ξ的分布列为 . (11分)10 8 6 4P ξ 328 3156 928 15633191420151086428562856562E ξ=⨯+⨯+⨯+⨯==. (13分)17.(本小题满分13分) 【解】方法一:(Ⅰ)取BC 的中点N ,连结MN.由已知,PM //CN ,则MN //PC ,所以MN ⊥平面ABC. (1分)过点N 作NH ⊥AC ,交AC 的延长线于H ,连结MH , 由三垂线定理知,AC ⊥MH.所以∠MHN 为二面角M -AC -B 的平面角. (3分)连结AN ,在△ACN中,由余弦定理,得AN 由已知∠AMN =60°,在Rt △ANM 中,1tan 60ANMN ==. (6分)在Rt △CHN中,sin 60NH CN =⋅=.(7分)在Rt △MNH 中,tan MN MHN NH ∠=== 故二面角M -AC -B 的正切值是332. (8分)(Ⅱ)因为四边形PCNM 为正方形,MN ⊥平面ABC ,则011sin1203212P MAC A PCM A MNC M ACN V V V V AC CN MN ----====⨯⋅⋅⋅= (13分)方法二:(Ⅰ)在平面ABC 内,过点C 作CB 的垂线,按如图所示建立空间直角坐标系C xyz -. 分)设点00(0,0,)(0)P z z >,由已知可得,点1,0)2A -,0(0,1,)M z ,则003(,),(0,0,)2AM z CP z == . 因为直线AM 与直线PC 所成的角为60°,则0||||cos60AM CP AM CP ⋅=⋅ ,即200z z =.解得z 0=1,从而1(0,1,1),,0)2CM CA ==- . (3分)设平面MAC 的一个法向量为n 111(,,)x y z =,则00n CM n CA ⎧⋅=⎪⎨⋅=⎪⎩ ,即11110102y z x y +=⎧-=. P CBNMHA取11x =,则n (1=. (5分)又m =(0,0,1)为平面ABC 的一个法向量,设向量m 与n 的夹角为θ,则cos ||||m n m n θ⋅==. 从而72sin =θ,tan θ= (7分)显然,二面角M -AC -B 的平面角为锐角,故二面角M -AC -B 的正切值是332. (8分)(Ⅱ)因为a =(1,0,0)为平面PCM的一个法向量,1(,0)22CA =- ,则点A 到平面PCM的距离||CA a h a ⋅== . (10分)又PC =PM =1,则11111326212P MAC A PCM V V PC PM h --===⨯⋅⋅⋅=⨯⨯⨯=. (13分)18.(本小题满分14分) 【解】(Ⅰ)设第n 年底该县农村医保基金为a n 万元,则11000a =,1(110%)(2)n n a a m n -=-+≥,即19(2)10n n a a m n -=+≥. (3分)于是1910(10)(2)10n n a m a m n --=-≥. 所以11910(10)()10n n a m a m --=-, 即1910(100010)()10n n a m m -=+-. (6分)故第n 年底该县农村医保基金有1910(100010)()10n m m -+-万元. (7分)(Ⅱ)若每年年底的医保基金逐年增加,则数列{}n a 单调递增. 因为19()10n y -=是减函数,则1000-10m <0时,即m >100. (10分)又1910(100010)()150010n n a m m -=+-≤恒成立,则lim 1500n n a →∞≤.即10m ≤1500,所以m ≤150. (12分)故每年新增医保基金m 的控制范围是(100,150]. (14分)19.(本小题满分14分)【解】(Ⅰ)连结PC ,由垂径分弦定理知,PC ⊥AB ,所以点P 的轨迹是以线段AC 为直径的圆(除去点A ). (2分)因为点A (4,6),C (6,4),则其中点坐标为(5,5),又圆半径2ACr ==故点P 的轨迹方程是22(5)(5)2x y -+-=(x ≠4,y ≠6). (6分)(Ⅱ)因为点P 、E 关于点D (9,0)对称,设点(,)P x y ,则点(18,)E x y --. (7分)设点11(,)F x y ,因为线段OF 由OP 绕原点逆时针旋转则OF ⊥OP ,且|OF |=|OP |,即111y y x x ⋅=-,且222211x y x y +=+. 由111y y x x ⋅=-,得11x yx y =-.令11,(0)y tx x ty t =-=>则222221111()(0)t x y x y t +=+>,所以t =1.因此点F 的坐标为(,)y x -. 所以EF ==设点M (9,-9),则|EF PM =. (11分)因为点P 为圆22(5)(5)2x y -+-=上的点,设圆心为N (5,5),则minPMMN ==max PM MN == (13分)故|EF |的取值范围是2,2].(14分)20.(本小题满分14分)【解】(Ⅰ)由题设,2()ln g x x a x =-,则()2ag x x x'=-. (1分)由已知,(1)0g '=,即202a a -=⇒=. (2分)于是()h x x =-,则'()1h x =(3分) 由'()101h x x =>⇒>,所以h (x )在(1,+∞)上是增函数,在(0,1)上是减函数.(4分)(Ⅱ)当21x e <<时,0ln 2x <<,即0()2f x <<. (5分)欲证2()2()f x x f x +<-,只需证[2()]2()x f x f x -<+,即证2(1)()1x f x x ->+. (6分)设2(1)2(1)()()ln 11x x x f x x x x ϕ--=-=-++,则22212(1)2(1)(1)()(1)(1)x x x x x x x x ϕ+---'=-=++. 当21e x <<时,()0x ϕ'>,所以()x ϕ在区间(1,e 2)上为增函数. (7分)从而当21e x <<时,()(1)0x ϕϕ>=,即2(1)ln 1x x x ->+,故2()2()f x x f x +<-. (9分)(Ⅲ)由题设,1()6h x x =-.令1()()0g x h x -=,则22ln (6)0x x x ---=,即6ln 222++-=-x x x x .(10分)设2()2ln h x x =,23()6(0)h x x x x =-++>,则22()h x x'==20>,得x >4. 所以2()h x 在(4,+∞)上是增函数,在(0,4)上是减函数11分)又3()h x 在(0,12)上是增函数,在(12,+∞)上是减函数因为当x →0时,2()h x →+∞,3()6h x →.又2(1)2h =,3(1)6h =,2(4)42ln 40h =->,3(4)6h =-,则函数)(2x h 与)(3x h 的大致图象如下: (13分)由图可知,当x >0时,两个函数图象有2个交点,故函数y =g (x )-h 1(x )有2个零点.(14分)。
