1.三角形的特性
三角形预习1

三角形预习1三角形是高中数学中重要的几何概念之一,它有着丰富的性质和应用。
在三角形的学习中,了解其基本定义、分类、特性以及解题方法都是非常必要的。
本文将从这些方面展开,帮助你准备三角形的学习。
1. 三角形的定义与分类三角形是由三条线段组成的平面图形,其中每两条线段的交点称为顶点,而三条线段称为边。
根据边的长短关系,三角形可分为等边三角形、等腰三角形和普通三角形。
等边三角形的三边长度相等,等腰三角形的两边长度相等,普通三角形的三边长度都不相等。
2. 三角形的角度特性除了边的长短关系外,三角形还有许多角度的特性。
三角形的内角和为180度,这是三角形的基本性质之一。
同时,三角形中的角也有分类,根据角的大小关系,三角形可分为锐角三角形、钝角三角形和直角三角形。
其中,直角三角形的一个角为90度,而锐角三角形的所有角都小于90度,钝角三角形的一个角大于90度。
3. 三角形的解法解决三角形相关问题时,可以根据已知条件使用不同的解法。
其中一种常用的方法是余弦定理。
余弦定理可用于求解任意三角形的边长关系,它表达为 c^2 = a^2 + b^2 - 2abcosC,其中c为三角形的一边,a和b为另外两条边,C为夹角C的对边。
此外,正弦定理和正切定理也是常用的解法,它们可以帮助我们求解三角形的其他未知量。
4. 三角形的应用三角形不仅仅是数学中的一个概念,它在现实生活中也有许多应用。
例如,在建筑设计中,三角形的稳定性和角度特性对于建筑物的结构设计至关重要。
在地理学中,三角形的测量可用于测量地球的形状和大小。
此外,在导航、天文学、地质学等领域中,三角形的应用也非常广泛。
5. 三角形的常见误区在学习三角形过程中,我们常常会遇到一些常见的误区。
一个常见的误区是忽视边长与角度之间的关系,导致问题无法得到正确的解答。
此外,忽视角度特性也是容易犯的错误之一,角度的大小与三角形的其他特性密切相关,忽略角度对于问题的影响会使解题过程出现错误。
《三角形的特性》优秀教学设计(通用8篇)

《三角形的特性》优秀教学设计《三角形的特性》优秀教学设计(通用8篇)作为一名教职工,通常需要准备好一份教学设计,教学设计是连接基础理论与实践的桥梁,对于教学理论与实践的紧密结合具有沟通作用。
写教学设计需要注意哪些格式呢?以下是小编帮大家整理的《三角形的特性》优秀教学设计,仅供参考,大家一起来看看吧。
《三角形的特性》优秀教学设计篇1教学内容:人教版四年级数学下册第五单元三角形P80、81页例1、例2,练习十四1、2、3题。
教材分析:《三角形的特性》是人教版义务教育课程标准实验教科书四年级数学下册第80--81页的内容。
学生通过第一学段以及四年级上册对空间与图形的学习,对三角形已经有了直观的认识,能够从平面图形中分辨出三角形。
本节内容的设计是在上述的基础上进行的,教材的编写注意从学生已有的经验出发,创设丰富多彩的与现实生活联系紧密的情境和动手实验活动,以帮助学生理解三角形概念,构建数学知识。
学生分析:学生在日常生活中经常接触到三角形,对三角形有一定的感性认识,但几何初步知识无论是线、面、体的特征还是图形的特征、特性,对于小学生来说,都比较抽象。
要解决数学的抽象性与小学生思维特点之间的矛盾,就要充分运用其直观性进行教学。
设计理念:学生对几何图形的认识是通过操作、实践而获得的。
因此本节课从学生已有的生活经验出发,创设教学情境,让学生动手操作,自主探究、合作交流掌握三角形概念以及特性。
教学目标:1、通过动手操作和观察比较,使学生认识三角形,知道三角形的特征及三角形高和底的含义,会在三角形内画高。
2、通过实验,使学生知道三角形的稳定性及其在生活中的应用。
3、培养学生观察、操作的能力和应用数学知识解决实际问题的能力。
4、体会数学与生活的联系,培养学生学习数学的兴趣。
教学重点、难点:重点:理解三角形的含义,掌握三角形的特征、特性。
难点:三角形高的确定及画法。
教具、学具准备:教师准备:多媒体课件,硬纸条制作的长方形和三角形,三角板,作业纸等。
人教版四年级数学下第七讲 三角形(一)精讲精练 提升版

人教版四年级数学下第7讲三角形(一)提高篇知识点一:三角形的特性1、三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连或重合),叫三角形。
2、从三角形的一个顶点到它的对边做一条垂线,顶点和垂足间的线段叫做三角形的高,这条对边叫做三角形的底。
三角形只有3条高。
重点:三角形高的画法:一落二移三画四标3、三角形具有稳定性。
如:自行车的三角架,电线杆上的三角架。
4、三角形三边的关系:三角形任意两边之和大于第三边。
三角形任意两边之差小于第三边。
两边之差〈第三边〈两边之和。
判断三条线段能不能组成三角形,只要看最短的两条边的和是不是大于第三条边。
5、为了表达方便,用字母A、B、C分别表示三角形的三个顶点,三角形可表示成三角形ABC。
知识点二:三角形的分类1、按照角大小来分:锐角三角形,直角三角形,钝角三角形。
2、按照边长短来分:三边不等的△,三边相等的△,等腰△(等边三角形或正三角形是特殊的等腰△)。
3、等边△的三边相等,每个角是60度。
(顶角、底角、腰、底的概念)4、三个角都是锐角的三角形叫做锐角三角形。
5、有一个角是直角的三角形叫做直角三角形。
6、有一个角是钝角的三角形叫做钝角三角形。
7、每个三角形都至少有两个锐角;每个三角形都至多有1个直角;每个三角形都至多有1个钝角。
8、两条边相等的三角形叫做等腰三角形。
9、三条边都相等的三角形叫等边三角形,也叫正三角形。
10、等边三角形是特殊的等腰三角形考点1:三角形的特性【典例1】(2020春•桐梓县期末)下面每组中三条线段,不能围成三角形的是()A.5m、7m、9m B.7dm、5dm、ldmC.4cm、8cm、5cm【典例2】(2020春•桐梓县期末)下面形状中具有稳定性的是()A.B.C.【典例3】(2020春•峄城区期末)把一根13厘米的小棒截成3根整厘米的小棒围成一个三角形.最长的一根小棒不能超过()厘米.【典例4】(2020春•浦城县期末)动物王国举行围篱笆比赛,()围的比较牢固.A.小熊B.公鸡C.小狗【典例5】(2020春•鄄城县期末)爷爷要给一块地围上篱笆,()形状的篱笆稳固不易变形.A.B.C.D.【典例6】(2020春•微山县期末)下面三种物品,利用了三角形稳定性的是()A.三角形花坛B.红领巾C.自行车的三角形车架考点2:三角形的分类【典例1】(2020春•邛崃市期末)如图中是锐角三角形.【典例2】(2019春•梁子湖区期末)在图中,一共有个钝角三角形,6个直角三角形,个等腰三角形,个等边三角形.【典例3】(2020春•灌阳县期末)红领巾按角分类属于三角形,按边分类属于三角形..【典例4】(2020春•洪山区期末)三角形如果有两个角是锐角,就一定是锐角三角形..(判断对错)综合练习一.选择题1.(2020秋•宁化县期中)任意一个三角形中,()有两个锐角。
人教版四年级数学下册第5讲 三角形知识梳理及巩固练习
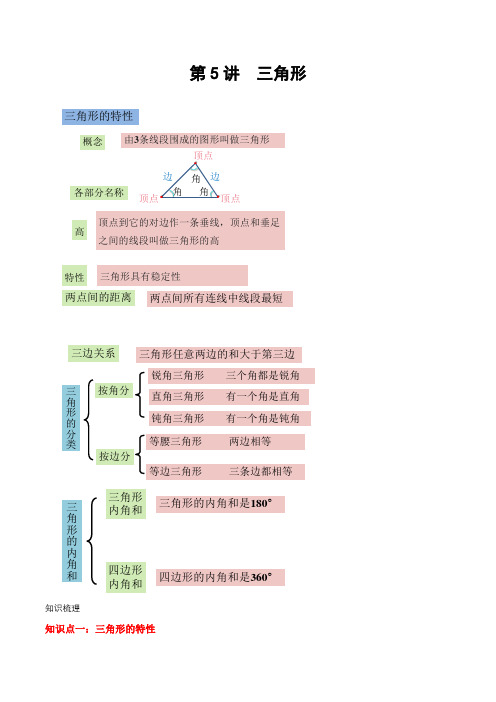
第5讲 三角形三角形的特性概念由3条线段围成的图形叫做三角形各部分名称顶点顶点顶点边边角角角高特性顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高三角形具有稳定性两点间的距离三边关系两点间所有连线中线段最短三角形任意两边的和大于第三边三角形的分类三角形的内角和三角形的内角和是180°三角形内角和四边形内角和四边形的内角和是360°知识梳理知识点一:三角形的特性1. 由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。
这条对边叫做三角形的底。
三角形ABC ,具有稳定性。
2.三角形三边关系三角形任意两边的和大于第三边。
知识点二:三角形的分类 1.按角进行分类1个直角2个锐角1个钝角2个锐角直角三角形钝角三角形锐角三角形3个锐角:2. 按边进行分类三条边相等两条边相等三条边都不等等边三角形(正三角形)等腰三角形知识点三:三角形的内角和考点一:三角形的特性例1.(2019春•沛县月考)一个等腰三角形两条边的长度分别是5厘米和11厘米,这样的三角形有几个?周长是多少厘米?【分析】根据三角形三边的关系:两边之和大于第三条边,一个等腰三角形两条边的长度分别是5厘米和11厘米,只有一种情况:腰为11厘米,底为5厘米时,周长为11+11+5厘米.【解答】解:根据分析,这个等腰三角形的周长为:11+11+5=27(厘米)答:有一个这样的三角形,周长分别为27厘米.【点评】此题关键利用三角形三边的关系,再根据三角形周长的计算方法,列式解答即可.1.(2019春•明光市期末)一个三角形的两边长分别是6厘米和9厘米,第三条边的长度一定大于3厘米,同时小于15厘米.【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可.【解答】解:9﹣6<第三边<9+6,即3<第三边<15.故答案为:3;15.【点评】解答此题的关键是根据三角形的特性进行分析、解答即可.2.(2018春•厦门期末)王老师给同学们准备了一些小棒,数量如图.选用其中的部分小棒搭成一个长方体.(1)长方体一共有12条棱,每组相对的棱有4条,因此,不可能选用8cm的小棒.(2)这个长方体相交于一个顶点的三条棱的长度分别是5cm、4cm和4cm.(3)计算这个长方体的表面积.【分析】(1)(2)根据长方体的特征即可求解;(3)根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答即可.【解答】解:(1)长方体一共有12条棱,每组相对的棱有4条,因此,不可能选用8cm的小棒.(2)这个长方体相交于一个顶点的三条棱的长度分别是5cm、4cm和4cm.(3)(5×4+5×4+4×4)×2=(20+20+16)×2=56×2=112(平方厘米)答:这个长方体的表面积是112平方厘米.故答案为:12,4,8;5,4,4.【点评】此题主要考查长方体的表面积公式的灵活运用,关键是熟记公式.3.(2018春•射阳县月考)把一根12厘米的吸管剪成3段(每段都是整厘米数),摆成一个三角形,共有几种剪法,你能全部列举出来吗?【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可.【解答】解:三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边,且12=3+4+5=4+4+4=2+5+5,符合题意的三角形各边分别为:①3、4、5;②4、4、4;③2、5、5;所以共有3种剪法,可以是3、4、5;4、4、4;2、5、5.【点评】围成三角形中任意两条边的和大于第三边,即最长边要小于总长度的一半,是判断三条线段能否围成一个三角形的关键.考点二:三角形的分类例2.(2020春•灯塔市期末)在点子图上按要求画图.【分析】根据平行四边形、梯形、直角三角形、等腰三角形的定义以及它们的特征,即可画图,因为没有规定的确切数据,所以此题答案不唯一.【解答】解:【点评】此题主要考查了常见的几种简单图形的定义以及画法.1.(2019春•肇州县校级期末)分一分,将正确答案的序号填在括号内.【分析】根据三角形按照角的大小分类情况,三角形按照角的大小分为锐角三角形、直角三角形、钝角三角形.三个角都是锐角的三角形叫做锐角三角形;有一个角等于90°的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形;据此进行判断即可.【解答】解:锐角三角形:①④⑦直角三角形:②⑧钝角三角形:③⑤⑥故答案为:【点评】此题考查的目的是理解掌握三角形按照角的大小分类的情况及应用,要熟悉各类三角形的判定条件.2.(2018秋•醴陵市期末)(探究题)两个椭圆圈重合的部分应是什么三角形?【分析】有两个角相等的直角三角形是等腰直角三角形,据此解答.【解答】解:有两个角相等的直角三角形是等腰直角三角形;所以两个椭圆圈重合的部分应是等腰直角三角形.答:两个椭圆圈重合的部分应是等腰直角三角形.【点评】掌握等腰直角三角形的特点是解题的关键.3.(2016春•岑溪市期中)下面3个三角形被盖住了一个或两个角,你能知道各是什么三角形吗?【分析】根据三角形按角分类的特征可知,三个角都是锐角,这个三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;有一个角是直角的三角形是直角三角形,解答即可.【解答】解:观图可知:第一个三角形有一个角是直角,所以是直角三角形,第二个三角形有一个角是钝角,所以是钝角三角形第三个三角形有2个角是锐角,所以有可能是锐角三角形,也可能是钝角三角形和直角三角形;故答案为:.【点评】正确理解锐角三角形、直角三角形和钝角三角形的定义是解决此题的关键.考点三:三角形的内角和例3.(2020春•铁西区期末)写出下面∠C的度数.【分析】根据三角形内角和为180°,用内角和减去其余两个角的度数即可求出∠C的度数。
直角三角形的特性

直角三角形的特性直角三角形是一种特殊的三角形,它具有一些独特的特性和性质。
在本文中,我们将探讨直角三角形的特性,包括定义、性质和定理。
一、定义直角三角形是指其中一个角度为90度的三角形。
通常我们用一个小方框来表示直角的位置,把直角三角形的两条边相互垂直。
在一个直角三角形中,直角所对应的边称为斜边,而与直角相邻的两条边称为直角边。
二、性质1. 直角三角形的斜边最长。
由勾股定理可得,在一个直角三角形中,斜边的长度总是大于或等于任何一个直角边的长度。
2. 直角三角形的两个直角边的长度满足勾股定理。
勾股定理表明,在一个直角三角形中,直角边的平方和等于斜边的平方。
这可以表示为a² + b² = c²,其中a和b分别为直角边的长度,c为斜边的长度。
3. 直角三角形的两个直角边的长度可以互换。
根据勾股定理,直角三角形中的两个直角边的长度可以任意交换,而不影响三角形的形状。
4. 直角三角形的两个直角边的长度有一定的关系。
根据勾股定理,如果两个直角边的长度分别为a和b,那么它们的比值可以表示为a/b,也可以表示为b/a。
这意味着,直角三角形中的两个直角边的长度具有一定的比例关系。
三、定理直角三角形具有很多重要的定理,其中最著名的是勾股定理。
勾股定理可以用于解决与直角三角形相关的计算问题。
勾股定理:在一个直角三角形中,直角边的平方和等于斜边的平方。
即a² + b² = c²,其中a和b分别为直角边的长度,c为斜边的长度。
除了勾股定理,直角三角形还有其他一些重要的定理,例如正弦定理和余弦定理,它们可以用于计算直角三角形中其他角度或边长的值。
总结:直角三角形是一种具有特殊性质的三角形,其中一个角度为90度。
它的主要特性包括斜边最长、直角边满足勾股定理、直角边的长度可以互换、直角边的长度有一定的比例关系等。
此外,直角三角形还有一些重要的定理,如勾股定理、正弦定理和余弦定理,可以用于解决与直角三角形相关的计算问题。
5三角形:三角形的特性

三角形第1节三角形的特征【知识梳理】1.认识三角形(1)画三角形在平面上任意画三个点(这三个点不在同一直线上),用线段把每两个点连起来,所组成的图形就是三角形。
如下图:三角形ABC:(2)三角形各部分的名称观察所画的三角形你会发现,三角形由三条线段围成,这三条线段叫做三角形的三条边,每两条边所夹的角就是三角形的内角,三角形有3个内角,3个内角的顶点就是三角形的顶点,三角形共有三个顶点。
(3)认识三角形的底和高从一个三角形顶点到它的对边做一条垂线,顶点和垂足之间的线段叫做三角形的高。
这条对边叫做三角形的底。
因为三角形有三个顶点,过每个顶点都可以向对边做高,所以任意一个三角形都可以做三条高。
画高时必须由定点向它的对边画垂线,它们是相对的,当边长不够长时,可画虚线延长。
所画的高用虚线表示并且标上垂直符号。
三角形的三条高总是相交于一点的,这个交点或在三角形内部,或在三角形外部,或在三角形边上,在这里,三角形的内部和外部指的是三角形的三条边所围成的范围的内部或外部。
下一节中我们将学习三角形的分类,我们会发现三角形按角分可分为锐角三角形、直角三角形、钝角三角形,这三种类型的三角形的高的情况也各不相同,如下图所示:1锐角三角形的三条高(三条虚线)直角三角形的三条高(一条虚线加两条直角边)钝角三角形的三条高(三条虚线)为了表达方便我们用字母A、B、C分别表示三角形的三个顶点,这个三角形就表示成三角形ABC。
2.三角形的特性(1)三角形具有稳定性只要三角形的三条边的长度确定,这个三角形的形状和大小就会完全确定,不会改变,因此三角形具有稳定性,它能够起到固定物体的作用,使物体不容易变形。
3.三角形的三边关系(1)三角形的三边关系三角形的任意两边之和大于第三边(2)判断三条线段是否围成三角形,只要把最短的两条边相加与最长的比较即可,如果最短的两条边之和大于第三边,也就证明两边之和大于第三边。
【诊断自测】一、选择题21、下面三组线段中,不可能围成三角形的一组是()。
直角三角形的特征与运用

直角三角形的特征与运用直角三角形是几何学中最基本的三角形之一。
本文将介绍直角三角形的特征、性质以及其在实际运用中的一些场景。
一、直角三角形的特征与性质直角三角形的定义是指其中一个角为90度。
根据直角三角形的性质,我们可以得出以下几个重要结论:1. 边长关系:在直角三角形中,直角边的长度称为直角边,另外两条边分别称为腿和斜边。
根据勾股定理,直角三角形的直角边平方和等于斜边平方,即a² + b² = c²,其中a和b为直角边的长度,c为斜边的长度。
2. 角度关系:直角三角形中,除了直角外,还有两个角,分别称为锐角和钝角。
由于直角为90度,所以锐角的度数总是小于90度,而钝角的度数总是大于90度。
3. 特殊比例关系:在直角三角形中,有几组特殊的边比例关系。
例如,在一个45度的直角三角形中,腿和斜边的长度相等,即a = b = c/√2。
二、直角三角形的运用直角三角形在实际生活中有广泛的应用。
下面列举了几个常见的运用场景:1. 测量与导航:直角三角形被广泛应用于测量和导航领域。
例如,在地理测量中,我们常常使用直角三角形的性质来确定两点之间的距离。
通过测量两点之间的直线距离和形成的夹角,可以利用三角函数计算出实际距离。
2. 建筑与工程:直角三角形在建筑和工程领域也得到了广泛的运用。
例如,在设计斜坡、楼梯和屋顶时,需要考虑直角三角形的性质来确保结构的稳定和安全。
3. 物理学与工业:直角三角形的特性在物理学和工业领域也有重要的应用。
例如,在机械设计中,直角三角形的比例关系被用来计算力的分解和合成,从而实现机械系统的优化和效率提升。
4. 角度测量:直角三角形的角度测量是另一个应用领域。
例如,在地理测量中,我们可以使用直角三角形的性质来测量地平线上的夹角,进而得到地球的曲率和高度差。
5. 三角函数的运用:直角三角形与三角函数之间有密切的关系。
三角函数包括正弦、余弦和正切等,它们可以利用直角三角形的边长关系来定义和计算。
小学奥数模块教程三角形

一、 三角形的定义:(一)、三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连或重合),叫三角形。
(二)、从三角形的一个顶点到它的对边做一条垂线,顶点和垂足间的线段叫做三角形的高,这条对边叫做三角形的底。
三角形只有3条高。
重点:三角形高的画法。
底二、 三角形的特性:(一)、物理特性:稳定性。
如:自行车的三角架,电线杆上的三角架。
(二)、边的特性:任意两边之和大于第三边。
为了表达方便,用字母A 、B 、C 分别表示三角形的三个顶点,三角形可表示成三角形ABC 。
A+B ﹥C三、 三角形的分类:(一)、按照角大小来分:锐角三角形,直角三角形,钝角三角形。
(二)、按照边长短来分:等边三角形(正三角形)、等腰三角形、三条边都不相等的三角形 ※三角形的内角和等于180°;四边形的内角和是360°;五边形的内角和是540°四、 图形的拼组:(一)、用任意2个完全一样的三角形一定能拼成一个平行四边形。
(二)、用2个相同的直角三角形可以拼成一个长方形、一个平行四边形、一个大等腰三角形。
(三)、用2个相同的等腰直角的三角形可以拼成一个正方形、一个平行四边形、一个大的等腰的直角的三角形。
五、 密铺:可以进行密铺的图形有长方形、正方形、三角形以及正六边形等。
顶点 边高知识框架三角形A BC哪种方法更牢固,为什么?【例 1】 是三角形的打“√”,不是三角形的画“○”。
( ) ( ) ( ) ( ) ( )【巩固】 一个三角形有( )个顶点,( )个角和( )条边。
【例 2】 一个三角形有( )条高。
A 、1B 、3C 、无数【巩固】 直角三角形、钝角三角形只有一条高。
( )【巩固】 锐角三角形都有三条高。
( )【例 3】 根据下面每个图形标出的底,画出图形的高。
【例 4】底底底例题精讲【巩固】自行车的三角架运用了三角形的()的特征。
A、稳定性B、有三条边的特征C、易变形【例 5】在能拼成三角形的小棒下面画“☆”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
填一填 从三角形的一个顶点到它的对边 做一条( 垂线 ), ( 顶点 )和( 垂足 ) 之间的线段叫做三角形的( 高 )。
填一填 三角形具有( 稳定 )性。也可以 说:三角形有( 不变形 )的特性。
说一说哪些部分是三角形的? 为什么要用三角形呢?
说一说
第二种,因为三角形具 有稳定性。
画出三角形的高
高 底
底
指一指,上面各图中 哪里有三角形?它们 有什么作用?
让我们来做一个小实验 吧。请你拉一下手中的 三角形,你有什么感觉? 你发现了什么?
三角形具 有 ( 稳定 ) 性 。 也可以说:三角 形有( 不变形 ) 的特性。
用实验来检验一下吧。
你发现了什么?摆不 成的是第几组线条?
三角形任意 两边的和大于第 三边。
单击页面即可演示
我们学过三角形。你能 说出哪些物体上有三角 形吗?
三角形有(三 ) 条边,( 三)个顶 点,有( 三 )个角, 三 ( )条高。
是三角形吗?为什么?邻 两条线段的端点相 连)叫做三角形。
说出下面图形的底和高。
底 底
高
高
底 高 底
高
底
做一做
√
√
√
做一做 用长分别是4厘米、6厘米 和10厘米的三根小棒,能摆出 一个三角形吗? 因为4+6=10(厘米),等 于第三条边10厘米的长度,所 以不能摆成一个三角形。
