黑龙江省牡丹江一中2016届高三上学期9月月考数学(理)试卷
黑龙江省牡丹江市第一高级中学2016届高三上学期期中考
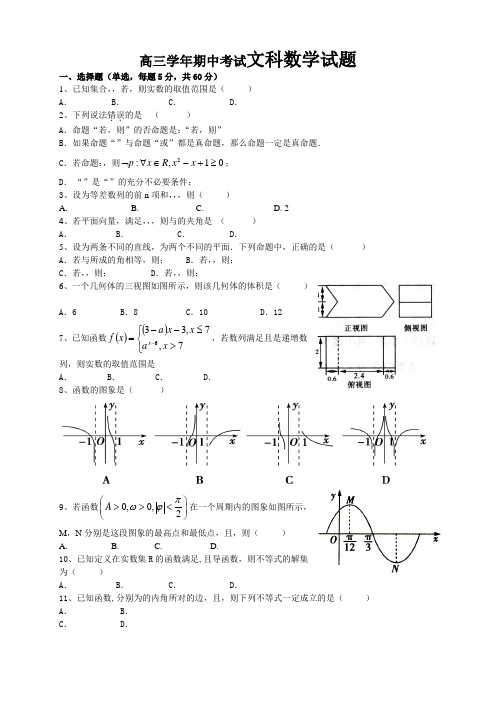
高三学年期中考试文科数学试题一、选择题(单选,每题5分,共60分) 1、已知集合,,若,则实数的取值范围是( ) A . B . C . D . 2、下列说法错误..的是 ( ) A .命题“若,则”的否命题是:“若,则”B .如果命题“”与命题“或”都是真命题,那么命题一定是真命题.C .若命题:,则2:,10p x R x x ⌝∀∈-+≥;D . “”是“”的充分不必要条件; 3、设为等差数列的前n 项和,,,则( )A. B. C. D. 2 4、若平面向量,满足,,,则与的夹角是 ( ) A . B . C . D .5、设为两条不同的直线,为两个不同的平面.下列命题中,正确的是( ) A .若与所成的角相等,则; B .若,,则; C .若,,则; D .若,,则;6、一个几何体的三视图如图所示,则该几何体的体积是( )A .6B .8C .10D .127、已知函数()()⎩⎨⎧>≤--=-7,7,336x a x x a x f x ,若数列满足且是递增数列,则实数的取值范围是A .B .C .D . 8、函数的图象是( )9、若函数0,0,2A πωϕ⎛⎫>><⎪⎝⎭在一个周期内的图象如图所示,M ,N 分别是这段图象的最高点和最低点,且,则( ) A. B. C. D.10、已知定义在实数集R 的函数满足,且导函数,则不等式的解集为( )A .B .C .D .11、已知函数,分别为的内角所对的边,且,则下列不等式一定成立的是( ) A . B . C . D .12、已知函数()224log ,021512,22x x f x x x x ⎧<<⎪=⎨-+≥⎪⎩,若存在实数,,,,满足,其中,则的取值范围是 .A .B .C .D . 二、填空题(每题5分,共20分) 13、已知,则14、数列满足:,,表示前n 项之积,则15、给出下列命题: ①函数()4cos 23f x x π⎛⎫=+⎪⎝⎭的一个对称中心为; ②若为第一象限角,且,则; ③若,则存在实数,使得;④在中,内角所对的边分别为,若︒===25,20,40B b a ,则必有两解. ⑤函数的图象向左平移个单位长度,得到的图象.其中正确命题的序号是 (把你认为正确的序号都填上). 16、如图,在中,,,点D 在线段AC 上,且,,则 . 三、解答题(17题---21题每题各12分,选做题10分)17、若是公差不为0的等差数列的前n 项和,且成等比数列,. (1)求数列的通项公式;(2)设,是数列的前n 项和,求使得对所有都成立的最小正整数.18、等差数列中,,(),是数列的前n 项和.(1)求;(2)设数列满足1212112n n n b b b a a a +++=-(),求的前项和.19、已知函数()22cos 3sin cos 2f x x x x x =--+.(1)当时,求的值域;(2)若△ABC的内角A ,B ,C 的对边分别为,且满足,()()sin 222cos sin A C A C A+=++,求的值. 20、如图,四棱锥中,,四边形是边长为的正方形,若分别是线段的中点. (1)求证:∥底面;(2)若点为线段的中点,求三角形的面积. 21、已知. (1)求函数的单调区间;(2)若关于的方程有实数解,求实数的取值范围; (3)当时,求证:111()2231nf n n <++++-. 四、选做题:请考生在第22、23题两题中任选一题做答,如果多答,则按所做的第一题记分,答时用2B 铅笔在答题卡上把所选题目的题号涂黑。
黑龙江省牡丹江一中2016届高三上学期9月月考数学(理)试卷

牡一中2016届高三九月月考理科数学试卷第Ⅰ卷(选择题)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项符合题意的)1、下列函数中,值域为的是()A:B:C:D:2、在下列结论中,正确的结论为()①“且”为真是“或”为真的充分不必要条件;②“且”为假是“或”为假的充分不必要条件;③“或”为真是“”为假的必要不充分条件;④“”为真是“且”为假的必要不充分条件;A:①②B:①③C:②④D:③④3、对于中的任意,不等式恒成立,则的取值范围是()A:B:C:D:或4、设,若且,则的取值范围是()A:B:C:D:5、若是上的减函数,且的图像过点,,则不等式的解集为,的值是()A:B:C:D:6、当时,不等式恒成立,则实数的取值范围是()A:B:C:D:7、已知是的充要条件,是的充要条件,是的必要条件,是的必要条件,则是的()A:充分不必要条件B:必要不充分条件C:充分条件D:既不充分也不必要条件8、设是偶函数,是奇函数,那么的值为()A:B:C:D:9、已知函数在定义域上是增函数,且,则的单调情况一定是()A:在上递增B:在上递减C:在上递减D:在上递增10、已知二次函数,若在区间内至少存在一个实数,使,则实数的取值范围是()A:B:C:D:11、若,定义,例如,,则函数的奇偶性是()A:是偶函数不是奇函数B:是奇函数不是偶函数C:既是奇函数又是偶函数D:既不是奇函数也不是偶函数12、定义域和值域均为的函数和的图像如图所示,下列命题的是()A:方程有且仅有三个根B:方程有且仅有三个根C:方程有且仅有两个根D:方程有且仅有两个根第Ⅱ卷(非选择题共90分)二、填空题:解答应写出文字说明、证明过程或演算步骤,解答过程书写答题卡的对应位置,写错不给分.17、(本小题满分10分)13、若方程有两个不相等的正实根,则实数的取值范围是;14、若函数满足:对于任意,都有,且成立。
黑龙江省牡丹江一中高二9月月考数学(理)试题

牡一中2016—2017学年度9月月考考试高二数学(理科)试卷一、选择题(每小题5分,共60分) 1、 抛物线x y42-=的准线方程是( )A 1=x B 1-=x C 161=x D 161-=x 2、 双曲线112422=-y x 的渐近线方程是( ) Ax y 3±= B x y 3±= Cx y 31±= D x y 33±= 3、 以点()3,0为焦点的曲线是( )A14522=+x y B 131222=+y x C y x 122-= D 13622=-x y 4、 直线l 与椭圆13422=+y x 相切于点P ,与直线4=x 交于点Q ,以PQ 为直径的圆过定点M ,则M 必在直线( )上..A0=x B 0=y C 1=y D 5=x5、 已知点P 是椭圆15922=+y x 上任意一点,F 是其右焦点,O 是坐标原点, 则PFPO 的最大值为( )A4 B 3 C23D 5 6、已知点P 在椭圆19422=+y x 内部,且21,F F 是其焦点,则下列式子正确的是( ) A 421<+PF PF B 421>+PF PF C621<+PF PF D 621>+PF PF7、 直线044:=-+y x l ,下列曲线:y x -=2,11622=-x y ,12322=+y x ,其中与直线l 只有一个公共点的个数为( )A 0 B 1 C 2 D 38、 直线1+=kx y 与双曲线1422=-y x 交于B A ,两点,且28=AB ,则实数k 的值为( )A7 B 3 C 2 D 19、 已知双曲线()0,012222>>=-b a by a x 的左右焦点分别为21,F F ,过左焦点且倾斜角为30直线与右支交于点A ,则双曲线离心率取值范围是( )A ⎪⎪⎭⎫ ⎝⎛332,1B ()2,1C ⎪⎪⎭⎫ ⎝⎛+∞,332 D ()+∞,210、 在圆422=+y x上任取一点P ,过点P 作x 轴的垂线段PD ,D 为垂足,线段PD 中点为M ,当点P 在圆上运动时,点M 到直线01:=+-y x l 距离最大值为( )A 2210+ B 2210- C 223 D 2211、已知21,F F 是双曲线()0118222>=-a y a x 的左右焦点,过1F 的直线l 与双曲线的左支交于点B ,与右支交于点A ,若2ABF ∆为等边三角形,则21F BF ∆的面积为( ) A36 B 38 C 318 D 2812、已知抛物线x y 22=上两点B A ,满足A 在x 轴上方,B 在x 轴下方,O 是坐标原点且3=⋅,则线段AB 中点M 的坐标满足方程( ) A 1222-=x y B 422+=x y C 12+=x y D 32-=x y二、填空题(每小题5分,共20分) 13、若抛物线x y82=上一点A 到直线2-=x 的距离等于它到点()0,4B 的距离,则AB 的值为14、若点()n m P ,是椭圆1422=+y x 上任意一点,则抛物线my x =2焦点的纵坐标的取值范围是15、已知椭圆()012222>>=+b a by a x 的左顶点为A ,上下两个顶点分别为C B ,,若左焦点是ABC ∆的垂心,则椭圆的离心率为16、若双曲线22221(0,0)x y a b a b-=>>的离心率为2,,A F 分别是它的左顶点和右焦点,点B 的坐标为()0,b ,则ABF ∠cos 的值为 三、解答题(17题10分,18至22题每题12分,共70分) 17、写出椭圆16422=+y x 的长轴长、短轴长、离心率、焦点坐标、顶点坐标..18、已知曲线()2,012:22≠≠=-+m m my m x C ,说明曲线C 的形状,若是椭圆或双曲线,请说明焦点在哪个坐标轴上.19、在直角坐标系xOy 中,1+的线段的两端点D C ,分别在x 轴、y 轴上滑动,2CP PD =.记点P 的轨迹为曲线E .(I )求曲线E 的方程;(2)直线l 与曲线E 交于B A ,两点,线段AB 的中点为⎪⎭⎫⎝⎛1,21M ,求直线l 方程.20、已知抛物线C 顶点在坐标原点,准线垂直于x 轴,且过点()2,2M ,B A ,是抛物线C 上两点,满足MB MA ⊥,(1)求抛物线C 方程;(2)证明直线AB 过定点.21、已知椭圆)0(1:2222>>=+b a by a x C 的右焦点为F ,离心率22=e ,过点F 且斜率为1的直线与椭圆交于D C ,(D 在x 轴上方)两点,(1)证明DFCD是定值;(2)若()0,1F,设斜率为k 的直线l 交椭圆C 于B A ,两点,且以AB 为直径的圆恒过原点O ,求OAB ∆面积最大值。
【精品】2016-2017年黑龙江省牡丹江一中高三上学期数学期末试卷(理科)及答案

2016-2017学年黑龙江省牡丹江一中高三(上)期末数学试卷(理科)一、选择题(每题5分,共60分)1.(5分)设U=R,M={y|y=2x+1,﹣≤x≤},N={x|y=lg(x2+3x)},则(∁U M)∩N=()A.(﹣∞,﹣3]∪(2,+∞)B.(﹣∞,﹣3)∪(0,+∞)C.(﹣∞,﹣3)∪(2,+∞)D.(﹣∞,0)∪(2,+∞)2.(5分)抛物线x2=﹣8y的准线方程是()A.x=B.y=2C.y=D.y=﹣23.(5分)已知动点P,定点M(1,0)和N(3,0),若|PM|﹣|PN|=2,则点P的轨迹是()A.双曲线B.双曲线的一支C.两条射线D.一条射线4.(5分)等差数列{a n}中,a1+a4+a7=39,a3+a6+a9=27,则数列{a n}前9项的和S9等于()A.99B.66C.144D.2975.(5分)已知α,β都是锐角,sinα=,cosβ=,则sin(β﹣α)=()A.﹣B.C.﹣D.6.(5分)设a,b是两条不同的直线,α,β是两个不同的平面,a⊂α,b⊥β,则α∥β是a⊥b的()A.充分不必要条件B.必要不充分条件C.充要条件D.即非充分又非必要条件7.(5分)在△ABC中,若|+|=|﹣|,AB=2,AC=1,E,F为BC边的三等分点,则•=()A.B.C.D.8.(5分)已知点A、B、C、D均在球O上,AB=BC=,AC=3,若三棱锥D﹣ABC体积的最大值为,则球O的表面积为()A.36πB.16πC.12πD.π9.(5分)一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.10.(5分)设m,n∈R,若直线(m+1)x+(n+1)y﹣2=0与圆(x﹣1)2+(y ﹣1)2=1相切,则m+n的取值范围是()A.[1﹣,1+]B.(﹣∞,1﹣]∪[1+,+∞)C.[2﹣2,2+2]D.(﹣∞,2﹣2]∪[2+2,+∞)11.(5分)已知函数f(x)=asinx﹣bcosx(a,b常数,a≠0,x∈R)在x=处取得最小值,则函数y=f(﹣x)是()A.偶函数且它的图象关于点(π,0)对称B.偶函数且它的图象关于点(,0)对称C.奇函数且它的图象关于点(,0)对称D.奇函数且它的图象关于点(π,0)对称12.(5分)已知f(x)为偶函数,且f(x)=f(x﹣4),在区间[0,2]上,f(x)=,g(x)=()|x|+a,若F(x)=f(x)﹣g(x)恰好有4个零点,则a的取值范围是()A.(2,)B.(2,3)C.(2,]D.(2,3]二、填空题(每题5分,共20分)13.(5分)已知等比数列{a n}前n项和为S n,a1+a2=,a4+a5=6,则S6=.14.(5分)椭圆C的中点在原点,焦点在x轴上,若椭圆C的离心率等于,且它的一个顶点恰好是抛物线x2=8y的焦点,则椭圆C的标准方程为.15.(5分)设直线x﹣3y+m=0(m≠0)与双曲线=1(a>0,b>0)的两条渐近线分别交于点A,B.若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是.16.(5分)下列命题中:(1)a=4,A=30°,若△ABC唯一确定,则0<b≤4.(2)若点(1,1)在圆x2+y2+mx﹣y+4=0外,则m的取值范围是(﹣5,+∞);(3)若曲线+=1表示双曲线,则k的取值范围是(1,+∞]∪(﹣∞,﹣4];(4)将函数y=cos(2x﹣)(x∈R)的图象向左平移个单位,得到函数y=cos2x 的图象.(5)已知双曲线方程为x2﹣=1,则过点P(1,1)可以作一条直线l与双曲线交于A,B两点,使点P是线段AB的中点.正确的是(填序号)三、解答题(本大题共有6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(10分)已知函数f(x)=|2x﹣a|+|x+1|.(Ⅰ)当a=1时,解不等式f(x)<3;(Ⅱ)若f(x)的最小值为1,求a的值.18.(12分)已知函数f(x)=2cos2x+sin(2x﹣)(1)求函数f(x)的单调增区间;最大值,以及取得最大值时x的取值集合;(2)已知△ABC中,角A、B、C的对边分别为a,b,c,若f(A)=,b+c=2,求实数a的取值范围.19.(12分)已知数列{a n}中,a1=1,其前n项和为S n,且满足a n=,(n ≥2)(1)求证:数列{}是等差数列;(2)求:前n项和公式S n;(3)证明:当n≥2时,S1+S2+S3+…+S n<.20.(12分)如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,PD=PA,已知AB=2DC=10,BD=AD=8.(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;(2)当三角形PAD为正三角形时,点M在线段PC(不含线段端点)上的什么位置时,二面角P﹣AD﹣M的大小为.21.(12分)已知F1,F2是椭圆=1的两焦点,P是椭圆在第一象限弧上一点,且满足=1过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A,B两点,(1)求点P坐标;(2)求证:直线AB的斜率为定值;(3)求△PAB面积的最大值.22.(12分)已知函数f(x)=(1)当a≥1时,求f(x)在[0,e](e为自然对数的底数)上的最大值;(2)对任意的正实数a,问:曲线y=f(x)上是否存在两点P,Q,使得△POQ (O为坐标原点)是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上?2016-2017学年黑龙江省牡丹江一中高三(上)期末数学试卷(理科)参考答案与试题解析一、选择题(每题5分,共60分)1.(5分)设U=R,M={y|y=2x+1,﹣≤x≤},N={x|y=lg(x2+3x)},则(∁U M)∩N=()A.(﹣∞,﹣3]∪(2,+∞)B.(﹣∞,﹣3)∪(0,+∞)C.(﹣∞,﹣3)∪(2,+∞)D.(﹣∞,0)∪(2,+∞)【解答】解:∵全集U=R,M={y|y=2x+1,﹣≤x≤}=[0,2],∴C U M=(﹣∞,0)∪(2,+∞),∵x2+3x>0,解得x>0或x<﹣3∴集合N=(﹣∞,﹣3)∪(0,+∞)∴N∩(∁U M)=(﹣∞,﹣3)∪(2,+∞)故选:C.2.(5分)抛物线x2=﹣8y的准线方程是()A.x=B.y=2C.y=D.y=﹣2【解答】解:由抛物线x2=﹣8y可得:2p=8,∴=2,其准线方程是y=2.故选:B.3.(5分)已知动点P,定点M(1,0)和N(3,0),若|PM|﹣|PN|=2,则点P的轨迹是()A.双曲线B.双曲线的一支C.两条射线D.一条射线【解答】解:由题意,|MN|=3﹣1=2∵|PM|﹣|PN|=2∴|PM|﹣|PN|=|MN|∴点P的轨迹是射线NP故选:D.4.(5分)等差数列{a n}中,a1+a4+a7=39,a3+a6+a9=27,则数列{a n}前9项的和S9等于()A.99B.66C.144D.297【解答】解:由等差数列的性质可得a1+a7=2a4,a3+a9=2a6,又∵a1+a4+a7=39,a3+a6+a9=27,∴a1+a4+a7=3a4=39,a3+a6+a9=3a6=27,∴a4=13,a6=9,∴a4+a6=22,∴数列{a n}前9项的和S9====99故选:A.5.(5分)已知α,β都是锐角,sinα=,cosβ=,则sin(β﹣α)=()A.﹣B.C.﹣D.【解答】解:∵α,β都是锐角,sinα=,cosβ=,∴cosα==,sin=,∴sin(β﹣α)=sinβcosα﹣cosβsinα=﹣=.故选:B.6.(5分)设a,b是两条不同的直线,α,β是两个不同的平面,a⊂α,b⊥β,则α∥β是a⊥b的()A.充分不必要条件B.必要不充分条件C.充要条件D.即非充分又非必要条件【解答】解:若a⊥b,∵b⊥β,∴a∥β或a⊂β,此时α∥β或α与β相交,即必要性不成立,若α∥β,∵b⊥β,∴b⊥α,∵a⊂α,∴a⊥b,即充分性成立,故α∥β是a⊥b的充分不必要条件,故选:A.7.(5分)在△ABC中,若|+|=|﹣|,AB=2,AC=1,E,F为BC边的三等分点,则•=()A.B.C.D.【解答】解:若|+|=|﹣|,则=,即有=0,E,F为BC边的三等分点,则=(+)•(+)=()•()=(+)•(+)=++=×(1+4)+0=.故选:B.8.(5分)已知点A、B、C、D均在球O上,AB=BC=,AC=3,若三棱锥D﹣ABC体积的最大值为,则球O的表面积为()A.36πB.16πC.12πD.π【解答】解:设△ABC的外接圆的半径为r,则=,∵AB=BC=,AC=3,∴∠ABC=120°,S△ABC∴2r==2∵三棱锥D﹣ABC的体积的最大值为,∴D到平面ABC的最大距离为3,设球的半径为R,则R2=3+(3﹣R)2,∴R=2,∴球O的表面积为4πR2=16π.故选:B.9.(5分)一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【解答】解:该几何体可视为正方体截去两个三棱锥,如图所示,所以其体积为.故选:D.10.(5分)设m,n∈R,若直线(m+1)x+(n+1)y﹣2=0与圆(x﹣1)2+(y ﹣1)2=1相切,则m+n的取值范围是()A.[1﹣,1+]B.(﹣∞,1﹣]∪[1+,+∞)C.[2﹣2,2+2]D.(﹣∞,2﹣2]∪[2+2,+∞)【解答】解:由圆的方程(x﹣1)2+(y﹣1)2=1,得到圆心坐标为(1,1),半径r=1,∵直线(m+1)x+(n+1)y﹣2=0与圆相切,∴圆心到直线的距离d==1,整理得:m+n+1=mn≤,设m+n=x,则有x+1≤,即x2﹣4x﹣4≥0,∵x2﹣4x﹣4=0的解为:x1=2+2,x2=2﹣2,∴不等式变形得:(x﹣2﹣2)(x﹣2+2)≥0,解得:x≥2+2或x≤2﹣2,则m+n的取值范围为(﹣∞,2﹣2]∪[2+2,+∞).故选:D.11.(5分)已知函数f(x)=asinx﹣bcosx(a,b常数,a≠0,x∈R)在x=处取得最小值,则函数y=f(﹣x)是()A.偶函数且它的图象关于点(π,0)对称B.偶函数且它的图象关于点(,0)对称C.奇函数且它的图象关于点(,0)对称D.奇函数且它的图象关于点(π,0)对称【解答】解:由于函数f(x)=asinx﹣bcosx=sin(x+θ)(a,b常数,a≠0,x∈R),根据函数f(x)在x=处取得最小值,则f()=a+b=﹣,∴a=b,∴f(x)=asinx﹣acosx=asin(x﹣),∴f(﹣x)=asin(﹣x﹣)=﹣asinx,故函数f(x)为奇函数且它的图象关于点(π,0)对称,故选:D.12.(5分)已知f(x)为偶函数,且f(x)=f(x﹣4),在区间[0,2]上,f(x)=,g(x)=()|x|+a,若F(x)=f(x)﹣g(x)恰好有4个零点,则a的取值范围是()A.(2,)B.(2,3)C.(2,]D.(2,3]【解答】解:由函数f(x)为偶函数且f(x)=f(x﹣4),则f(x)=f(﹣x),函数的周期为4,则在区间[﹣2,0]上,有f(x)=,分别作出函数y=f(x)在[﹣2,2]的图象,并左右平移4个单位,8个单位,可得y=f(x)的图象,再作y=g(x)的图象,注意上下平移.当经过A(1,)时,a==2,经过B(3,)时,a=2,5﹣=.则平移可得2<a<时,图象共有4个交点,即f(x)﹣g(x)恰好有4个零点,故选:A.二、填空题(每题5分,共20分)13.(5分)已知等比数列{a n}前n项和为S n,a1+a2=,a4+a5=6,则S6=.【解答】解:设等比数列{a n}的公比为q,由于,即a1+a1q=,a1q3+a1q4=6,两式相除,可得,q=2,a1=.则S6==.故答案为:14.(5分)椭圆C的中点在原点,焦点在x轴上,若椭圆C的离心率等于,且它的一个顶点恰好是抛物线x2=8y的焦点,则椭圆C的标准方程为.【解答】解:由题意设椭圆C的标准方程为,a>b>0,∵抛物线x2=8y的焦点为F(0,2),∴由已知得,解得a=4,b=2,∴椭圆C的标准方程为.故答案为:.15.(5分)设直线x﹣3y+m=0(m≠0)与双曲线=1(a>0,b>0)的两条渐近线分别交于点A,B.若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是.【解答】解:双曲线(a>0,b>0)的两条渐近线方程为y=±x,则与直线x﹣3y+m=0联立,可得A(,),B(﹣,),∴AB中点坐标为(,),∵点P(m,0)满足|PA|=|PB|,∴=﹣3,∴a=2b,∴=b,∴e==.故答案为:.16.(5分)下列命题中:(1)a=4,A=30°,若△ABC唯一确定,则0<b≤4.(2)若点(1,1)在圆x2+y2+mx﹣y+4=0外,则m的取值范围是(﹣5,+∞);(3)若曲线+=1表示双曲线,则k的取值范围是(1,+∞]∪(﹣∞,﹣4];(4)将函数y=cos(2x﹣)(x∈R)的图象向左平移个单位,得到函数y=cos2x的图象.(5)已知双曲线方程为x2﹣=1,则过点P(1,1)可以作一条直线l与双曲线交于A,B两点,使点P是线段AB的中点.正确的是(2),(5)(填序号)【解答】解:对于(1),由,得sinB=.当b=8时,sinB=1,B=90°,C=60°,△ABC唯一确定,故(1)错误;对于(2),点(1,1)在圆x2+y2+mx﹣y+4=0外,则12+12+m﹣1+4>0,即m>﹣5,故(2)正确;对于(3),若曲线+=1表示双曲线,则(4+k)(1﹣k)<0,解得k>1或k<﹣4,即k的取值范围是(1,+∞)∪(﹣∞,﹣4),故(3)错误;对于(4),将函数y=cos(2x﹣)(x∈R)的图象向左平移个单位,得到函数图象的解析式为y=cos[2(x+)]=cos(2x+),故(4)错误;对于(5),设A(x1,y1),B(x2,y2),则,,两式作差得:,∴,∴k AB=2,此时直线方程为y﹣1=2(x﹣2),即y=2x﹣3,联立,得2x2﹣12x+11=0,△=144﹣88=56>0,故(5)正确.∴正确命题的序号是(2),(5).故答案为:(2),(5).三、解答题(本大题共有6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(10分)已知函数f(x)=|2x﹣a|+|x+1|.(Ⅰ)当a=1时,解不等式f(x)<3;(Ⅱ)若f(x)的最小值为1,求a的值.【解答】解:(Ⅰ)因为f(x)=|2x﹣1|+|x+1|=;且f(1)=f(﹣1)=3,所以,f(x)<3的解集为{x|﹣1<x<1};…(4分)(Ⅱ)|2x﹣a|+|x+1|=|x﹣|+|x+1|+|x﹣|≥|1+|+0=|1+|当且仅当(x+1)(x﹣)≤0且x﹣=0时,取等号.所以|1+|=1,解得a=﹣4或0.…(10分)18.(12分)已知函数f(x)=2cos2x+sin(2x﹣)(1)求函数f(x)的单调增区间;最大值,以及取得最大值时x的取值集合;(2)已知△ABC中,角A、B、C的对边分别为a,b,c,若f(A)=,b+c=2,求实数a的取值范围.【解答】解:(1)f(x)=2cos2x+sin(2x﹣)=cos2x+sin2x+1=sin(2x+)+1,2kπ﹣≤2x+≤2kπ+,可得函数f(x)的单调增区间[kπ﹣,kπ+](k∈Z),函数f(x)的最大值为2.当且仅当sin(2x+)=1,即2x+=2kπ+,即x=kπ+(k∈Z)时取到.所以函数最大值为2时x的取值集合为{x|x=kπ+,k∈Z}.…(6分)(2)由题意,f(A)=sin(2A+)+1=,化简得sin(2A+)=.∵A∈(0,π),∴2A+=,∴A=.在△ABC中,根据余弦定理,得a2=b2+c2﹣bc=(b+c)2﹣3bc.由b+c=2,知bc≤1,即a2≥1.∴当b=c=1时,取等号.又由b+c>a得a<2.所以a的取值范围是[1,2 ).…(12分)19.(12分)已知数列{a n}中,a1=1,其前n项和为S n,且满足a n=,(n ≥2)(1)求证:数列{}是等差数列;(2)求:前n项和公式S n;(3)证明:当n≥2时,S1+S2+S3+…+S n<.【解答】证明:(1)∵数列{a n}中,a1=1,其前n项和为S n,且满足a n=,(n≥2)﹣S n=2S n S n﹣1,∴当n≥2时,,S n﹣1∴当n≥2时,,∴数列{}是以1为首项,2为公差的等差数列.解:(2)由(1)得=1+(n﹣1)×2=2n﹣1,∴S n=.证明:(3)由(2)知:当n≥2时,==,∴S1+S2+S3+…+S n<1+(1﹣)<﹣<.∴S1+S2+S3+…+S n<.20.(12分)如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,PD=PA,已知AB=2DC=10,BD=AD=8.(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;(2)当三角形PAD为正三角形时,点M在线段PC(不含线段端点)上的什么位置时,二面角P﹣AD﹣M的大小为.【解答】(本小题满分12分)解:(1)证明:因为BD=AD=8,得BD=8,AD=6,又AB=10,所以有AD2+BD2=AB2,即AD⊥BD,又因为平面PAD⊥平面ABCD,且交线为AD,所以PD⊥平面PAD,BD⊂平面BDM,故平面MBD⊥平面PAD.(2)由条件可知,三角形PAD为正三角形,所以取AD的中点O,连PO,则PO 垂直于AD,由于平面PAD⊥平面ABCD,所以PO垂直于平面ABCD,过O点作BD的平行线,交AB于点E,则有OE⊥AD,所以分别以OA、OE、OP为x,y,z轴,建空间直角坐标系所以点O(0,0,0),A(3,0,0),D(﹣3,0,0),B(﹣3,8,0),P(0,0,3),由于AB∥DC且AB=2DC,得到C(﹣6,4,0),设(0<λ<1),则有,因为由(1)的证明可知BD⊥平面PAD,所以平面PAD的法向量可取:,设平面MAD的法向量为,则有,即有由由二面角P﹣AD﹣M的大小为.==,解得故当M满足:PM=PC时符合条件.21.(12分)已知F1,F2是椭圆=1的两焦点,P是椭圆在第一象限弧上一点,且满足=1过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A,B两点,(1)求点P坐标;(2)求证:直线AB的斜率为定值;(3)求△PAB面积的最大值.【解答】(1)解:F1,F2是椭圆=1的两焦点,则c==,即有F1(0,),F2(0,﹣),设P(x,y),(x>0,y>0),则由=1,得x2+y2=3,又=1,解得,x=1,y=.则有点P的坐标为;(2)证明:由题意知,两直线PA、PB的斜率必存在,设直线PB的斜率为k,则直线PB的方程为,由于过点P作倾斜角互补的两条直线PA、PB,则直线PA:y﹣=﹣k(x﹣1).由,消去y,得,设A(x A,y A),B(x B,y B),由韦达定理,得1+x B=,即有,y B=同理可得,y A=,所以为定值.(3)解:由(2)可设直线AB的方程为,联立方程,得,消去y,得,由判别式8m2﹣16(m2﹣4)>0,得,x1+x2=﹣m,x1x2=,|AB|==易知点P到直线AB的距离为,所以,当且仅当m=±2时取等号,满足,所以△PAB面积的最大值为.22.(12分)已知函数f(x)=(1)当a≥1时,求f(x)在[0,e](e为自然对数的底数)上的最大值;(2)对任意的正实数a,问:曲线y=f(x)上是否存在两点P,Q,使得△POQ (O为坐标原点)是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上?【解答】解:(1)∵f(x)=,当0≤x<1时,f′(x)=﹣3x2+2x=﹣3x(x﹣),令f'(x)>0,解得:0≤x<,令f′(x)<0,解得:<x<1,故f(x)在[0,)递增,在(,1)递减,而f()=,∴f(x)在区间[0,1)上的最大值为,1≤x<e时,f(x)=alnx,f′(x)=>0,f(x)在[1,e]递增,f(x)max=f(e)=a≥1,综上f(x)在[0,e]的最大值是a;(2)曲线y=f(x)上存在两点P、Q满足题设要求,则点P,Q只能在y轴的两侧,不妨设P(t,f(t))(t>0),则Q(﹣t,t3+t2),显然t≠1,∵△POQ是以O为直角顶点的直角三角形,∴•=0,即﹣t2+f(t)(t3+t2)=0.(1)是否存在两点P、Q等价于方程(1)是否有解.若0<t<1,则f(t)=﹣t3+t2,代入(1)式得,﹣t2+(﹣t3+t2)(t3+t2)=0,即t4﹣t2+1=0,而此方程无实数解,因此t>1.∴f(t)=alnt,代入(1)式得,﹣t2+(alnt)(t3+t2)=0,即=(t +1)lnt . (*),考察函数在h (x )=(x +1)lnx (x ≥1), 则h′(x )=lnx ++1>0,∴h (x )在[1,+∞)上单调递增,∵t >1,∴h (t )>h (1)=0, 当t→+∞时,h (t )→+∞,∴h (t )的取值范围是(0,+∞). ∴对于a >0,方程(*)总有解,即方程(1)总有解.因此对任意给定的正实数a ,曲线y=f (x )上总存在两点P 、Q ,使得△POQ 是以O 为直角顶点的直角三角形,且此三角形斜边中点在y 轴上.赠送—高中数学知识点【2.1.1】指数与指数幂的运算 (1)根式的概念①如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n n a n 是偶数时,正数a 的正的n n a 表示,负的n 次方根用符号n a -0的n 次方根是0;负数a 没有n 次方根.n a n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:()n n a a =;当n 为奇数时,nn a a =;当n 为偶数时,(0)|| (0)nn a a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:(0,,,m nm na a a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 11()()(0,,,m m m n n n aa m n N a a-+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈【2.1.2】指数函数及其性质 (4)指数函数 函数名称指数函数定义函数(0x y a a =>且1)a ≠叫做指数函数图象1a >01a <<定义域R值域 (0,)+∞过定点 图象过定点(0,1),即当0x =时,1y =.奇偶性 非奇非偶单调性在R 上是增函数在R 上是减函数函数值的 变化情况1(0)1(0)1(0)x x x a x a x a x >>==<< 1(0)1(0)1(0)x x x a x a x a x <>==>< a 变化对 图象的影响 在第一象限内,a 越大图象越高;在第二象限内,a 越大图象越低.xa y =xy(0,1)O1y =xa y =xy (0,1)O 1y =〖2.2〗对数函数 【2.2.1】对数与对数运算(1)对数的定义①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a a MM N N-= ③数乘:log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质函数 名称 对数函数定义函数log (0a y x a =>且1)a ≠叫做对数函数图象1a > 01a <<定义域(0,)+∞x yO(1,0)1x =log a y x=xyO (1,0)1x =log a y x=值域 R过定点 图象过定点(1,0),即当1x =时,0y =.奇偶性 非奇非偶单调性在(0,)+∞上是增函数在(0,)+∞上是减函数函数值的 变化情况log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<a 变化对图象的影响 在第一象限内,a 越大图象越靠低;在第四象限内,a 越大图象越靠高.。
(全优试卷)黑龙江省牡丹江市高三9月月考数学(理)试题 Word版含答案

2017届高三9月份月考数学(理)试题第Ⅰ卷(选择题)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项符合题意的) 1、余弦函数cos()4y x π=+在下列哪个区间为减函数( )A .]4,43[ππ-B .]0,[π-C .]43,4[ππ-D .]2,2[ππ-2、已知34tan =x ,且x 在第三象限,则=x cos ( )A.54 B.54-C.53 D.53-()()12log 321-=x xx f 、若,则()f x 的定义域为( )A.)1,21(B.),21(+∞C.),1()1,21(+∞⋃ D.)2,21( 4、下列函数中是偶函数且值域为(0,)+∞的函数是( )A .|tan |y x =B .1lg 1x y x +=- C .13y x = D .2y x -=5、函数34)(-+=x e x f x的零点所在的区间( )A.)0,41(-B.)410(,C.)21,41(D.)43,21( 6、已知集合}02|{2<--=x x x A ,}11lg |{xx y x B +-==,在区间)3,3(-上任取一实数x ,则B A x ⋂∈的概率为( )A.81B.41C.31D.1217、已知函数2()(1)x f x e x =-+(e 为自然对数的底),则()f x 的大致图象是( )8、已知函数⎪⎩⎪⎨⎧>+≤+=0,40,2)(x x x x a x f x 有最小值,则实数a 的取值范围是( ) A .),4(+∞ B .),4[+∞ C .]4,(-∞ D .)4,(-∞9、已知一元二次方程01)1(2=+++++b a x a x 的两个实根为21,x x ,且1,1021><<x x ,则ab的取值范围是( )A .)21,2(-- B.]21,2(-- C.)21,1(-- D.]21,1(--10、已知0,0>>y x ,且082=-+xy y x ,则y x +的最小值是( ) A.16 B.20 C.18 D.2411、已知函数()⎪⎩⎪⎨⎧≤≤⎪⎭⎫ ⎝⎛<<=153,6sin 30,log 3x x x x x f π,若存在实数4321,,,x x x x ,满足4321x x x x <<<,且()()()()4321x f x f x f x f ===,则2143x x x x +的值等于( ) A.π18 B.18 C.π9 D.912、设函数()y g x =在(,)-∞+∞内有定义,对于给定的正数k ,定义函数:(),(())(),(())k g x g x k g x k g x k ≤⎧=⎨>⎩,取函数()2xg x ex e -=--,若对任意(,)x ∈-∞+∞,恒有()()k g x g x =,则( )A .k 的最大值为12e e --B .k 的最小值为12e e-- C .k 的最大值为2 D .k 的最小值为2第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13、若函数()()3222f x a x ax x =+-+为奇函数,则曲线()y f x =在点()()1,1f --处的切线方程为 .14、已知函数()212log y x ax a =-+在区间[)+∞,2上是减函数,则实数a 的取值范围是 .15、函数)(x f 的定义域为实数集R ,⎪⎩⎪⎨⎧<≤+<≤--=30),1(log 01,1)21()(2x x x x f x对于任意的R x ∈都有)2()2(-=+x f x f .若在区间]3,5[-上函数m mx x f x g +-=)()(恰有三个不同的零点,则实数m 的取值范围是_______________________16、对定义在区间D 上的函数)(x f 和)(x g ,如果对任意D x ∈,都有1)()(≤-x g x f 成立,那么称函数)(x f 在区间D 上可被)(x g 替代,D 称为“替代区间”.给出以下命题:①1)(2+=x x f 在区间),(+∞-∞上可被21)(2+=x x g 替代; ②x x f =)(可被x x g 411)(-=替代的一个“替代区间”为]23,41[;③x x f ln )(=在区间],1[e 可被b x x g -=)(替代,则22≤≤-b e ;④)(sin )(),)(lg()(212D x x x g D x x ax x f ∈=∈+=,则存在实数)0(≠a a ,使得)(x f 在区间21D D ⋂ 上被)(x g 替代;其中真命题的有___________________-三、解答题:本大题共6小题,共70分。
2016年黑龙江省牡丹江一中高三理科上学期人教A版数学9月月考试卷

2016年黑龙江省牡丹江一中高三理科上学期人教A 版数学9月月考试卷一、选择题(共12小题;共60分)1. 函数 y = sin x 的一个单调增区间是 A. −π4,π4B. π4,3π4C. π,3π2 D. 3π2,2π2. 已知 tan x =43,且 x 在第三象限,则 cos x = A. 45 B. −45C. 35D. −353. 若 f x =xlog 122x−1,则 f x 的定义域为 A. 12,1B. 12,+∞C. 12,1 ∪ 1,+∞D. 12,24. 下列函数中是偶函数且值域为 0,+∞ 的函数是 A. y = tan xB. y =lg x +1x−1 C. y =x 13D. y =x −25. 在下列区间中,函数 f x =e x +4x −3 的零点所在的区间为 A. −14,0B. 0,14C. 14,12D. 12,346. 已知集合 A = x x 2−x −2<0 ,B = x y =lg 1−x1+x ,在区间 −3,3 上任取一实数 x ,则x ∈A ∩B 的概率为 A. 18B. 14C. 13D. 1127. 已知函数 f x =e x − x +1 2(e 为自然对数的底数),则 f x 的大致图象是 A. B.C. D.8. 已知函数 f x = 2x +a ,x ≤0x +4x ,x >0有最小值,则实数 a 的取值范围是 A. 4,+∞B. 4,+∞C. −∞,4D. −∞,49. 已知实系数一元二次方程x2+1+a x+a+b+1=0的两个实根为x1,x2,且0<x1<1,x2>1,则ba的取值范围是 A. −1,−12B. −1,−12C. −2,−12D. −2,−1210. 已知x>0,y>0,且2x+8y−xy=0,则x+y的最小值是 A. 16B. 20C. 18D. 2411. 已知函数f x=log3x,0<x<3sinπ6x ,3≤x≤15,若存在实数x1,x2,x3,x4,满足x1<x2<x3<x4,且f x1=f x2=f x3=f x4,则x3+x4x1x2的值等于 A. 18πB. 18C. 9πD. 912. 设函数y=g x在−∞,+∞内有定义,对于给定的整数k,定义函数:g k x=g x,g x≤kk,g x>k,取函数g x=2−e x−e−x,若对任意x∈−∞,+∞恒有gkx=g x,则 A. k的最大值为2−e−1e B. k的最小值为2−e−1eC. k的最大值为2D. k的最小值为2二、填空题(共4小题;共20分)13. 若函数f x=a+2x3−ax2+2x为奇函数,则曲线y=f x在点 −1,f−1处的切线方程为.14. 已知函数y=log1x2−ax+a在区间2,+∞上是减函数,则实数a的取值范围是.15. 函数f x的定义域为实数集R,f x=12x−1,−1≤x<0log2x+1,0≤x<3,对于任意x∈R都有f x+2=f x−2,若在区间−5,3内函数g x=f x−mx+m恰有三个不同的零点,则实数m的取值范围是.16. 对定义在区间D上的函数f x和g x,如果对任意x∈D,都有f x−g x ≤1成立,那么称函数f x在区间D上可被g x替代,D称为“替代区间”.给出以下命题:①f x=x2+1在区间−∞,+∞上可被g x=x2+12替代;②f x=x可被g x=1−14x 替代的一个“替代区间”为14,32;③f x=ln x在区间1,e可被g x=1x −b替代,则0≤b≤1e;④f x=ln ax2+x x∈D1,g x=sin x x∈D2,则存在实数a a≠0,使得f x在区间D1∩D2上被g x替代.其中真命题的有.三、解答题(共6小题;共78分)17. 已知函数f x=log2x+1+x−2−m.(1)当m=7时,求函数f x的定义域;(2)若关于x的不等式f x≥2的解集是R,求m的取值范围.18. (1)设不等式x−a x+a−2<0的解集为N,M= m−14≤m<2,若x∈N是x∈M的必要条件,求a的取值范围.(2)已知命题:“∃x∈x−1<x<1,使等式x2−x−m=0成立”是真命题,求实数m 的取值范围.19. 已知函数f x=ax+b1+x 是定义在−1,1上的奇函数,且f12=25.(1)求函数f x的解析式;(2)用单调性的定义证明f x在−1,1上是增函数;(3)解不等式f t2−1+f t<0.20. 已知函数f x=2cos2x+23sin x cos x+a,且当x∈0,π6时,f x的最小值为2.(1)求a的值,并求f x的单调增区间;(2)将函数y=f x的图象上各点的纵坐标保持不变,横坐标缩短到原来的12,再把所得图象向右平移π12个单位,得到函数y=g x,求方程g x=2在区间0,π2上的所有根之和.21. 如图,在半径为3、圆心角为60∘的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y.(1)按下列要求写出函数的关系式:①设PN=x,将y表示成x的函数关系式;②设∠POB=θ,将y表示成θ的函数关系式;(2)请你选用(1)中的一个函数关系式,求出y的最大值.22. 设函数f x=m ln x+m−1x.(1)若f x存在最大值M,且M>0,求m的取值范围;(2)当m=1时,试问方程xf x−xe =−2e是否有实数根?若有,求出所有实数根;若没有,请说明理由.答案第一部分1. C2. D3. C4. D5. C【解析】因为g x=e x在−∞,+∞上是增函数, x=4x−3在−∞,+∞上是增函数,所以f x=e x+4x−3在−∞,+∞上是增函数.又f −14=e−14−4<0,f0=e0+4×0−3=−2<0,f14=e14−2<0,f12=e12−1>0,所以f14⋅f12<0.6. C7. C8. B9. D 10. C11. B 【解析】当3≤x≤15时,f x=sinπ6x,当0<x<3时,f x=log3x,则函数的图象如图,则0<x1<1<x2<3<x3<x4,且x3,x4,关于x=9对称,因为f x1=f x2,所以−log3x1=log3x2,所以log3x1x2=0,所以x1x2=1,因为f x3=f x4,所以x3+x4=18,所以x3+x4x1x2=18.12. D 【解析】因为对任意x∈−∞,+∞恒有g k x=g x,所以g x≤k在−∞,+∞上恒成立,因为g x=2−e x−e−x,gʹx=−e+e−x,所以当x∈−∞,−1时,gʹx>0,g x为增函数;当x∈−1,+∞时,gʹx<0,g x为减函数;故g x max=g−1=2+e−e=2,故k≥2.第二部分13. y=8x+414. a≤415. −12,−1616. ①②③【解析】①因为f x−g x=12<1;f x可被g x替代;所以该命题为真命题;②f x−g x=x+14x−1;设 x=x+14x −1, ʹx=4x2−14x;所以x∈14,12时, ʹx<0,x∈12,32时, ʹx>0,所以 12=0是 x的最小值,又 14=14, 32=23,所以f x−g x<1,所以f x可被g x替代的一个替代区间为14,32,所以该命题是真命题;③由题意知:f x−g x=ln x−1x+b≤1在x∈1,e上恒成立,设 x=ln x−1x+b,则 x在1,e上为增函数,1=b−1, e=1−1e+b,则b−1≤ x≤1−1e+b,又−1≤ x≤1,所以b−1≥−1, 1−1e+b≤1,即b≥0, b≤1e;所以0≤b≤1e,所以该命题为真命题;④若a>0,解ax2+x>0得,x<−1a或x>0,可取D1=0,+∞,D2=R,所以D1∩D2=0,+∞,可取x=100,则对任意a,f x−g x>1,所以不存在实数a a>0,使得f x在区间D1∩D2上被g x替代,若a<0,解ax2+x>0得,0<x<−1a,所以D1=0,−1a,D2=R,所以D1∩D2=0,−1a,0<ax2+x≤−14a,所以f x≤ln −14a,−1≤g x≤1,所以不存在a,使得f x−g x ≤1,所以不存在实数a a<0,使得f x在区间D1∩D2上被g x替代,综上得,不存在实数a a≠0,使得f x在区间D1∩D2上被g x替代,所以该命题为假命题.所以真命题的有:①②③.第三部分17. (1)当m=7函数f x的定义域即为不等式 x+1+ x−2−7>0的解集,由于x≤−1,−x+1−x−2−7>0,或−1<x<2,x+1−x−2−7>0,或x≥2,x+1+x−2−7>0,所以x<−3,无解,或x>4综上,函数f x的定义域为−∞,−3∪4,+∞(2)若使f x≥2的解集是R,只需m≤ x+1+ x−2−4min恒成立.由于 x+1+ x−2−4≥x+1−x−2−4=−1,所以m的取值范围是−∞,−118. (1)因为x∈N是x∈M的必要条件,所以M⊆N,当a=1时,解集N为空集、不满足题意;当a<1时,N=x a<x<2−a,则a<−14,2−a≥2,即a<−14;当a>1时,a>2−a,此时集合N=x2−a<x<a,则2−a<−14,a≥2,所以a>94;综上所述,a的取值范围为 −∞,−14∪94,+∞ .(2)由题意得,方程x2−x−m=0在−1,1上有解,所以m的取值集合就是函数y=x2−x= x−122−14在−1,1上的值域,值域为 −14,2.所以实数m的取值范围 −14,2.19. (1)因为函数f x=ax+b1+x2是定义在−1,1上的奇函数,所以由f0=0,得b=0.又因为f12=25,所以12a1+14=25,解得a=1;因此函数f x的解析式为:f x=x1+x.(2)设−1<x1<x2<1,则f x1−f x2=x11+x12−x21+x22=x1−x21−x1x21+x121+x22,因为−1<x1<x2<1,所以x1−x2<0,1−x1x2>0,1+x12>0,1+x22>0,从而f x1−f x2<0,即f x1<f x2,所以f x在−1,1上是增函数.(3)因为f x是奇函数,所以f t2−1+f t<0即为f t2−1<−f t=f−t,又因为f x在−1,1上是增函数,所以f t2−1<f−t即为t2−1<−t,解得:−1+52<t<−1+52, ⋯⋯①又因为−1<t2−1<1,−1<t<1,解得−1<t<1且t≠0, ⋯⋯②对照①②,可得t的范围是:−1,0∪0,−1+52.所以,原不等式的解集为−1,0∪0,−1+52.20. (1)f x=2cos2x+23sin x cos x+a=cos2x+1+3sin2x+a=2sin2x+π6+a+1,因为x∈0,π6,所以2x+π6∈π6,π2,所以f x min=a+2=2,故a=0,所以f x=2sin2x+π6+1,由2kπ−π2≤2x+π6≤2kπ+π2k∈Z,解得:kπ−π3≤x≤kπ+π6k∈Z,故f x的单调增区间是 kπ−π3,kπ+π6k∈Z.(2)g x=2sin4 x−π12+π6+1=2sin4x−π6+1,由g x=2得sin4x−π6=12,则4x−π6=2kπ+π6或2kπ+5π6k∈Z,解得x=kπ2+π12或kπ2+π4k∈Z;因为x∈0,π2,所以x=π12或π4,故方程所有根之和为π12+π4=π3.21. (1)①因为ON=3−x2,OM=33x,所以MN=3−x2−33x,所以y=x3−x2−33x x∈0,32.②因为PN=3sinθ,ON=3cosθ,OM=33×3sinθ=sinθ,所以MN=ON−OM=θ−sinθ,所以y=3sinθ 3cosθ−sinθ ,即y=3sinθcosθ−3sin2θ,θ∈0,π3.(2)选择y=3sinθcosθ−3sin2θ=3sin2θ+π6−32,因为θ∈0,π3,所以2θ+π6∈π6,5π6.所以y max=32.22. (1)f x=m ln x+m−1x的定义域为0,+∞,fʹx=mx +m−1=m−1x+mx.当m≤0或m≥1时,f x在区间0,+∞上单调,此时函数f x无最大值.当0<m<1时,f x在区间0,m1−m 内单调递增,在区间m1−m,+∞ 内单调递减,所以当0<m<1时,函数f x有最大值,最大值M=f m1−m =m ln m1−m−m.因为M>0,所以有m ln m1−m −m>0,解之得m>e1+e.所以m的取值范围是e1+e,1.(2)没有实数根.理由如下:当m=1时,方程可化为x ln x−xe x =−2e,即x ln x=xe x−2e,设 x=x ln x,则 ʹx=1+ln x,所以x∈0,1e 时, ʹx<0,所以 x在0,1e上是减函数,当x∈1e ,+∞ 时, ʹx>0,所以 x在1e,+∞ 上是增函数,所以 x min= 1e =−1e.设g x=xe x −2e,则gʹx=1−xe x.所以当x∈0,1时,gʹx>0,即g x在0,1上单调递增;当x∈1,+∞时,gʹx<0,即g x在1,+∞上单调递减.所以g x max=g1=−1e.因为1e≠1,所以数形结合可得 x>g x在区间0,+∞上恒成立,所以方程xf x−xe x =−2e没有实数根.。
【数学】黑龙江省牡丹江市第一高级中学2016届高三上学期期中考试(理)

牡丹江市第一高级中学2016届高三上学期期中考试数学试卷(理)第Ⅰ卷(选择题)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项是符合题意的) 1、设集合,则( ) A .B .C .D .2、下列四个函数中,在区间[]1,1-上是增函数的是( ) A .2xy =B .2y x =C .2log y x =D .sin 2y x =3、已知点()3,5A 、()4,7B 、()1,C x -三点共线,则实数x 的值是( ) A .1-B .1C .3-D .34、下列命题是假命题的是 ( )A .1,20x x R -∀∈>B .*2,(1)0x N x ∀∈->C .R ln 0x x ∃∈<,D .,tan 2x R x ∃∈= 5、设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( ) A .若αβ⊥,m α⊂,n β⊂,则m n ⊥ B .若//αβ,m α⊂,n β⊂,则//m n C .若m n ⊥,m α⊂,n β⊂,则 αβ⊥ D .若m α⊥,//m n ,//n β,则αβ⊥ 6、已知()tan 2πα-=-,则21cos 2cos αα=+( ) A .3- B .25C .3D .52-7、各项均为正数的等差数列{}n a 中,4936a a =,则前12项和12S 的最小值为( )21{|},{|1}A x x x B x x=≤=≥A B =(,1]-∞[0,1](0,1](,0)(0,1]-∞A .78B .48C .60D .728、,AD BE 分别是ABC ∆的中线,若1AD BE ==,且AD 与BE 的夹角为120,则AB AC ⋅=( )A .13B .23C .49D .899、已知R 上的可导函数()f x 的图象如图所示,则不等式()()2230x x f x '-->的解集为( ) A .()(),21,-∞-+∞B .()(),21,2-∞-C .()()(),11,02,-∞--+∞D .()()(),11,13,-∞--+∞10、已知()(),f x g x 都是定义在R 上的函数,()0g x ≠,()()()()f x g x f x g x ''>,且()()x f x a g x =(0a >且1a ≠),()()()()115112f f g g -+=-,若数列()()f n g n ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前n 项和大于62,则n 的最小值为( )A .6B .7C .8D .911、已知函数()f x 的导函数()2sin f x x '=+,且(0)1f =-,数列{}n a 是以4π为公差的等差数列,若234()()()3f a f a f a π++=,则20142a a =( ) A .2016B .2015C .2014D .201312、已知函数2ln 0()41,0x x f x x x x ⎧>⎪=⎨++≤⎪⎩,若关于x 的方程 2()()0f x bf x c -+=(,b c R ∈)有8个不同的实数根,则由点(),b c 确定的平面区域的面积为( )A .16B .13C .12D .23第Ⅱ卷(非选择题 共90分)二、填空题(每小题5分,共20分)13、一个几何体的三视图如图,该几何体的各个顶点都在球O 的球面上,球O 的体积为 ;14、如图,AB 是圆O 的直径,,C D 是圆O 上的点,60CBA ∠=,45ABD ∠=,CD xOA yBC =+,则x y +的值为 ;15、数列{}n a 满足12a =,1111n n n a a a ++-=+,其前n 项积为n T ,则2015T = ;16、已知函数()y f x =是定义在R 上的偶函数,对于任意x R ∈都有()()()63f x f x f +=+成立,当[]12,0,3x x ∈,且12x x ≠时,都有()()12120f x f x x x ->-,给出下列四个命题:①()30f =;②直线6x =-是函数()y f x =的一条对称轴;③函数()y f x =在区间[]9,6--上为增函数;④函数()y f x =在区间[]0,2014上有335个零点。
黑龙江省牡丹江市第一高级中学2016-2017学年高一9月月考数学试题(解析版)

牡一中2016级高一学年9月月考数学试题一、选择题(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1、设集合{}{}4,2,6*=≤∈=B x N x A ,则=B C A ( )A. {}4,2B.{}5,3,1,0C.{}6,5,3,1D.{}6*≤∈x N x 考点:集合的运算 答案:C 试题解析:故答案为:C2、以下六个写法中:①{0}∈{0,1,2}; ②⊆∅{1,2}; ③{0}∅∈ ④{0,1,2}={2,0,1}; ⑤∅∈0; ⑥A A =∅⋂,正确的个数有( ) A. 1个 B. 2个 C. 3个 D. 4个 考点:集合的概念 答案:B试题解析:①错,应{0}{0,1,2};②对,空集是任何集合的子集; ③错,应;④对;⑤错,中没有任何元素,故错; ⑥错,故答案为:B3、 已知函数()()2,2+==x x g x x f ,则()()=3g f ( )A. 25B. 11C. 45D. 27 考点:函数及其表示 答案:A 试题解析:所以故答案为:A4、已知函数()x f 的定义域为()∞+,0,则函数()()x x f x F -++=31的定义域为( ) A. []3,2 B. (]3,1 C. (]3,0 D. (]3,1- 考点:函数的定义域与值域 答案:D试题解析:要使函数有意义,需满足:解得:所以函数的定义域为:。
故答案为:D5、下列各组函数中,是相等函数的是( ) A.55x y =与2x y = B.12)(2--=x x x f 与12)(2--=t t t g (z t ∈)C.24)(2--=x x x f 与2)(+=x x g D.0x y =与01)(x x g =考点:函数及其表示 答案:D试题解析:两个函数要相等,则要求定义域和对应关系相同。
对A :故两个函数不相等;对B :的定义域为R ,()的定义域为Z,故两个函数不相等;对C :的定义域为的定义域为R ,故两个函数不相等;对D :与的定义域为对应关系为:故两个函数相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
牡一中2016届高三九月月考理科数学试卷第Ⅰ卷(选择题)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项符合题意的)1、下列函数中,值域为),0(∞+的是( ) A :xy -=215B :xy -=1)31(C :1)21(-=x yD :x y 21-=2、在下列结论中,正确的结论为( )①“p 且q ”为真是“p 或q ”为真的充分不必要条件; ②“p 且q ”为假是“p 或q ”为假的充分不必要条件; ③“p 或q ” 为真是“p ⌝”为假的必要不充分条件; ④“p ⌝” 为真是“p 且q ”为假的必要不充分条件; A :①② B :①③ C :②④ D :③④3、对于40≤≤m 中的任意m ,不等式342-+>+m x mx x 恒成立,则x 的取值范围是( )A :31≤≤-xB :1-≤xC :3≥xD :1-<x 或3>x4、设|2|)(2x x f -=,若b a <<0且)()(b f a f =,则b a +的取值范围是( )A :)4,0(B :)22,2(C :)4,2(D : )22,0(5、若)(x f 是R 上的减函数,且)(x f 的图像过点)3,0(A ,)1,3(-B ,则不等式2|1)(|<-+t x f 的解集为)2,1(-,t 的值是( )A :1-B :0C :1D :26、当)1,0(∈x 时,不等式)1(log 2+<x x a 恒成立,则实数a 的取值范围是( ) A :),2(∞+ B :),2[∞+ C :)2,1( D :]2,1(7、已知p 是q 的充要条件,r 是s 的充要条件,q 是s 的必要条件,r 是q 的必要条件,则r 是p 的( )A :充分不必要条件B :必要不充分条件C :充分条件D :既不充分也不必要条件8、设ax x f x++=)110lg()(是偶函数,xx bx g 24)(-=是奇函数,那么b a +的值为( ) A :1 B :1- C :21-D :21 9、已知函数)(x f 在定义域R 上是增函数,且0)(<x f ,则)()(2x f x x g =的单调情况一定是( )A :在)0,(-∞上递增B :在)0,(-∞上递减C :在R 上递减D :在R 上递增 10、已知二次函数a a x a x x f ----=222)2(2)(,若在区间]1,0[内至少存在一个实数b ,使0)(>b f ,则实数a 的取值范围是( )A :)1,2(-B :)2,21(-C :)21,2(--D :)1,21(-11、若N n R x ∈∈,,定义)1)....(2)(1(-+++=n x x x x M n x ,例如,24)2)(3)(4(34-=---=-M ,则函数x M x f x sin )(115⋅=-的奇偶性是( )A :是偶函数不是奇函数B :是奇函数不是偶函数C :既是奇函数又是偶函数D :既不是奇函数也不是偶函数12、定义域和值域均为]4,4[-的函数)(x f y =和)(x g y =的图像如图所示,下列命题的是( )A :方程0)]([=x g f 有且仅有三个根B :方程0)]([=x f g 有且仅有三个根C :方程0)]([=x f f 有且仅有两个根D :方程0)]([=x g g 有且仅有两个根第Ⅱ卷 (非选择题 共90分)二、填空题:解答应写出文字说明、证明过程或演算步骤,解答过程书写答题卡的对应位置,写错不给分.17、(本小题满分10分)13、若方程022=+-m mx x 有两个不相等的正实根,则实数的取值范围是 ; 14、若函数)(x f 满足:对于任意0,21>x x ,都有0)(,0)(21>>x f x f ,且)()()(2121x x f x f x f +<+成立。
则称函数)(x f 具有性质M 。
给出下列四个函数:①3x y =②)1(log 2+=x y ③12-=x y ④x y sin = 其中具有性质M 的函数是 ;(满足条件的序号都写出)15、若函数()6,2,3log ,2,a x x f x x x -+≤⎧=⎨+>⎩ (0a > 且1a ≠ )的值域是[)4,+∞ ,则实数a的取值范围是 .16、已知函数)(|2|)(2R x b ax x x f ∈+-=,给出下列命题:①)(x f 必是偶函数②)2()0(f f =时,)(x f 的图像必关于直线1=x 对称 ③若02≤-b a ,则)(x f 在区间),[∞+a 上是增函数④)(x f 有最大值||2b a - 其中正确命题的序号是 ;三、解答题:本大题共小题,共分,解答应写出必要的文字说明、证明过程及演算步骤。
17、(本小题满分12分) 若关于x 的不等式:062≤--a ax x 有解,且对解集中的任意21,x x ,总有满足5||21≤-x x ,求实数a 的取值范围. 18、(本小题满分12分)已知函数)1(log )(2+=x x f ,当点),(y x 在的)(x f y =图象上运动时,点)2,3(yx 是)(x g y =图象上的点。
⑴ 求)(x g y =的表达式;⑵ 当)()(x f x g ≥时,求x 的取值范围。
19、(本小题满分12分)设函数63231)(223+-+-=x a ax x x f )10(<<a (1)函数)(x f 的单调区间、极值。
⑵若当]2,1[++∈a a x 时,恒有a x f <'|)(|,试确定a 的取值范围。
20、(本小题满分12分)设11log )(21--=x axx f 为奇函数,a 为常数。
⑴ 求a 的值;⑵证明)(x f 在区间),1(∞+内单调递增;⑶ 若对于区间]4,3[上的每一个x 值,不等式m x f x+>)21()(恒成立,求实数m 的取值范围。
21、(本小题满分12分)函数)(x f 的定义域为D :}0|{≠x x 且满足对于任意D x x ∈21,,有:)()()(2121x f x f x x f +=⋅⑴ 求)1(f 的值;⑵ 判断)(x f 的奇偶性并证明;⑶ 如果3)62()13(,1)4(≤-++=x f x f f ,且)(x f 在),0(∞+上是增函数,求x 的取值范围。
22、(本小题满分10分)已知0>c ,设p :函数x c y =在R 上的单调递减,q :不等式1|2|>-+c x x 的解集为R ,如果p 和q 有且只有一个正确,求c 的取值范围.牡一中2016年高三数学理科9月月考答案17.解:因为062<--a ax x 有解,所以a ax x y 62--=和x 轴有两个交点 所以0>∆,即0242>+a a ,得240-<>a a 或. 由韦达定理得ax x a x x 6,2121-==+,所以a a x x x x x x 244)()(221221221+=-+=-,因为521≤-x x 所以≤-221)(x x 25即25242≤+a a 得125≤≤-a .综上a 的取值范围是10,2425≤<-<≤-a a 18.解:(1)令,2,3Y yX x ==所以,2,3Y y X x == 因为点),(y x 是函数)(x f y =的图像上,所以)13(2log 2+=X Y ,即)13(2log 21+=X Y 所以)31(log 21)()13(2->=+x x g x ; (2)由),()(x f x g ≥得,log log 21)1(2)13(2++≥x x 所以⎪⎩⎪⎨⎧+≥+>+>+2)1(1301013x x x x 解得10≤≤x .19. 解:(1).34)(22'a ax x x f -+-=令034)(22'=-+-=a ax x x f ,得a x a x 3==或 由表:)当),(a x -∞∈时,0)('<x f ,函数)(x f 为减函数; 当),3(+∞∈a x 时,0)('<x f ,函数)(x f 也为减函数; 当)3,(a a x ∈时,0)('>x f ,函数)(x f 为增函数; 当a x =时,)(x f 取得极小值,极小值为634)(3+-=a a f ;当a x 3=时,)(x f 取得极大值,极大值为6)3(=a f 。
(2)由a x f <)(,得.342a a ax x a <-+-<- 因为,10<<a 所以a a 21>+,22'34)(a ax x x f -+-=在[]2,1++a a 上为减函数.[][].44)2()(,12)1()('min ''max'-=+=-=+=a a f x f a a f x f于是问题转化成求不等式组⎩⎨⎧->-<-aa a a 4412的解,解得.154<<a20.(1)解 ∵f (x )是奇函数,∴f (-x )=-f (x ),∴log 12(1+ax -x -1)=-log 12(1-axx -1)⇔1+ax -x -1=x -11-ax >0⇒1-a 2x 2=1-x 2⇒a =±1.检验a =1(舍),∴a =-1.(2)证明 任取x 1>x 2>1,∴x 1-1>x 2-1>0, ∴0<2x 1-1<2x 2-1⇒0<1+2x 1-1<1+2x 2-1⇒0<x 1+1x 1-1<x 2+1x 2-1⇒log 12(x 1+1x 1-1)>log 12(x 2+1x 2-1),即f (x 1)>f (x 2),∴f (x )在(1,+∞)内单调递增. (3)解 f (x )-(12)x >m 恒成立.令g (x )=f (x )-(12)x ,只需g (x )min >m ,用定义可以证明g (x )在[3,4]上是增函数, ∴g (x )min =g (3)=-98,∴m <-98时原式恒成立即m 的取值范围为(-∞,-98).21解 (1)令x 1=x 2=1,有f (1×1)=f (1)+f (1),解得f (1)=0 (2)f (x )为偶函数,证明如下:令x 1=x 2=-1,有f [(-1)×(-1)]=f (-1)+f (-1),解得f (-1)=0令x 1=-1,x 2=x ,有f (-x )=f (-1)+f (x ),∴f (-x )=f (x ),∴f (x )为偶函数(3)f (4×4)=f (4)+f (4)=2,f (16×4)=f (16)+f (4)=3. 由f (3x +1)+f (2x -6)≤3, 变形为f [(3x +1)(2x -6)]≤f (64). ∵f (x )为偶函数,∴f (-x )=f (x )=f (|x |). ∴不等式①等价于f [|(3x +1)(2x -6)|]≤f (64). 又∵f (x )在(0,+∞)上是增函数,∴|(3x +1)(2x -6)|≤64,且(3x +1)(2x -6)≠0. 解得-73≤x <-13或-13<x <3或3<x ≤5.∴x 的取值范围是{x |-73≤x <-13或-13<x <3或3<x ≤5}.22.解析:函数xc y =在R 上单调递减.10<<⇔c不等式.1|2|1|2|上恒大于在函数的解集为R c x x y R c x x -+=⇔>-+∵⎩⎨⎧<≥-=-+,2,2,2,22|2|c x c c x c x c x x).,1[]21,0(.1,,.210,,.21121|2|.2|2|+∞⋃≥≤<>⇔>⇔>-+∴-+=∴的取值范围为所以则正确且不正确如果则不正确且正确如果的解集为不等式上的最小值为在函数c c Q P c Q P c c R c x x c R c x x y。
