7.6锐角三角函数的简单应用(4)
7.6锐角三角函数的简单应用(2)(058)

响水县双语学校九(8)班数学导学案(058)课题:7.6锐角三角函数的简单应用第2课学生姓名教学目标:进一步掌握解直角三角形的方法,比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题,培养学生把实际问题转化为数学问题的能力。
教学过程:一、自主探究1.给出仰角、俯角的定义如右图,从下往上看,视线与水平线的夹角叫仰角,从上往下看,视线与水平线的夹角叫做俯角。
右图中的∠1就是仰角,∠2就是俯角。
二、自主合作1.为了测量停留在空中的气球的高度,小明先站在地面上某点观测气球,测得仰角为27°,然后他向气球方向前进了50m,此时观测气球,测得仰角为40°。
若小明的眼睛离地面1.6m ,小明如何计算气球的高度呢?三、自主展示3.大海中某小岛的周围10km 范围内有暗礁。
一艘海轮在该岛的南偏西55°方向的某处,由西向东行驶了20km 后到达该岛的南偏西25°方向的另一处。
如果该海轮继续向东行驶,会有触礁的危险吗?四、自主拓展1. 如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高BC 为 米(精确到0.1).(参考数据:414.12≈ 732.13≈)2.如图,A 、B 是两幢地平高度相等、隔岸相望的建筑物,B 楼不能到达,由于建筑物密集,在A 楼的周围没有开阔地带,为测量B 楼的高度,只能充分利A 楼的空间,A 楼的各层都可到达且能看见B 楼,现仅有测量工具为皮尺和测角器(皮尺可用于测量长度,测角器可以测量仰角、俯角或两视线的夹角)。
(1)你设计一个测量B 楼高度的方法,要求写出测量步骤和必需的测量数据 (用字母表示),并画出测量图形。
(2)用你测量的数据(用字母表示)写出计算B 楼高度的表达式。
中考专题复习-锐角三角函数的应用

第8题解图
答: 旗杆AB的高度约为18米.
感谢聆听!
答:A.B间的距离约为115.5海里.
3. (2019内江)如图,两座建筑物DA与CB,其中CB的高为120米,从DA的顶点A测得
CB顶部B的仰角为30°,测得其底部C的俯角为45°,求这两座建筑物的地面距离DC
为多少米? (结果保留根号)
Rt△ABE
Rt△ACE
120
30° 45°
列方程
第3题图
解: 如解图,作FG⊥AB于点G,AG=AB-GB=AB-FD=AB-1.8,
由题意知,△ABE和△FDE均为等腰直角三角形,
∴AB=BE,DE=FD=1.8米,
∴FG=DB=DE+BE=AB+1.8.
在Rt△AFG中,
即
A B -1.8 A B +1.8
∴AB≈18.2≈18.
AG=tan∠AFG=tan39.3°, FG
模型一 解一个直角三角形
基本图形及所作辅 助线
总结
作BE⊥AC,构造Rt△ABE和矩形BDCE,根据已知条件求解
针对训练
1. (2019吉林)墙壁及淋浴花洒截面如图所示.已知花洒底座A与地面的距离AB为170 cm,花洒AC的长为30 cm,与墙壁的夹角∠CAD为43°.求花洒顶端C到地面的距离 CE(结果精确到1 cm).(参考数据: sin43°=0.68,cos43°=0.73,tan43°=0.93)
tanα
3.方向角
锐角三 角函数 的实际 应用
1.方向角:如图4, A点位于O点的北偏东30°方向, B点位于O点的南偏东60° 方向, C点位于O点的北偏西45°方向(或西北方向)
图4
图5
7.5锐角三角函数的简单应用-文档资料

线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,
并求此时P点的坐标.
y
A
OB x
C
i=1: ,背3 水坡AD的坡角β为45°,坝顶宽DC=3米,坝高 4米.
求:(1)迎水坡BC的坡角α;
(2)坝底宽AB的长.
EF
练习1:
如图,某拦河坝截面的原设计方案为
AH∥BC,坡角∠ABC=60°,坝顶到坝脚的距离
AB=6m.为了提高拦河坝的安全性,现将坡
角改为45°,由此,点A需向右平移至点D请你
C .80sin20m
D .80cos20m
2.如图是一个拦水大坝的横断面图,AD∥BC,
(1)斜坡AB=10m,大坝高为8m, 则斜坡AB的坡度
iAB=
;
(2)如果坡度iAB=1 : 3,则坡角∠B=
;
(3)如果坡度iAB=1:2,AB=8cm ,则大坝高度
为.
A
D
BE
C
例1:如图,水坝的横截面是梯形ABCD,迎水坡BC的坡度
7.5锐角三角函数的简单应用(2)
如图,AB是一斜坡,
B
我们把斜坡与水平面的
夹角称为坡角α.
斜坡的垂直高度BC与斜坡 A
C
的水平宽度AC的比称为坡度i .
Байду номын сангаасi tan BC
AC
1.小明沿着坡角为20°的斜坡向上前进80m, 则他上升的高度是( ).
A. 80 m cos 20
B. 80 m sin 20
试求旗杆BC的高度. B
C
DE
A
补充作业
如图, 已知抛物线 y 1 x2与xb轴x交c于A (-4,0) 2
76锐角三角函数应用.docx

学习目标:1. 经历探索实际问题的求解过程,进一步体会三角函数在解决问题过程屮的应用。
2. 能把实际问题转化为数学问题,能进行有关三角函数的计算并能对结果的实际意义进行说明。
3. 正确理解“旋转角、仰角、俯角、视线、方位角”从而正确理解实际问题,解决实际问题。
重点: 灵活应川“锐角三角函数、勾股定理”解直角三角形 难点: 发现、构造可解的直角三角形和盂解的直介三用形 重要概念:畀垂线视线 —水平线I视线解题要领:构造肓角三角形,解决实际问题。
问题引入:长为90 CM 的单摆AB 旋转30°后,最低点B 升高了多少?典型例题 例1・ 国庆长假,小明和同学一•起到游乐场游玩,游乐场人型摩犬轮的半径为20米,旋转-周需要12分钟。
小明乘坐最底部的车厢(离地而约0.5米)开始一周的观光。
(1) 2分钟后,小明离地面的高度是多少(精确到0.1米)?(2) 摩天轮启动多长时间后,小明和地面的高度将首次达到9m ?(提示cos55° =0.575)(3) 小明将有多长时间连续保持在离地面9 m 以上的高度?Z1是俯角,Z2仰角把实际问题抽象为儿何问题,画岀儿何图形, 明确己知量和未知量, 通过添加适为辅助线, 旋转角:ZAOB北例2・升国旗时,某同学站在离旗杆底部20m 处行注目礼,当国旗升至旗杆端时,该同学 视线的仰角恰为40。
,若双眼离地IS 1.5m,则旗杆高度为多少m? (sin40° =0.64, tan40° =0.84)例3・某商场为缓解我市“停车难"问题,拟建造地下停车库,图6是该地下停车库坡道入口 的设计示意图,其中,丄BD, ZBAD = 18°, C 在BD 上,BC=0.5m.根据规定,地下停 车库坡道入口上方耍张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD 的长就是所限制的高度,而小壳认为丿应该以CE 的长作为限制的高度•小明和小亮谁说的对? 请你判断并计算出正确的结果・(结果精确至U 0.1m )参考数据:sinl8° =0.31, cos 18° =0.95,3. 水平地面上的甲、乙两楼的距离为30米,从「卩楼顶部测得乙楼顶部的仰角为30。
九年级(下)数学教案:锐角三角函数的简单应用(全3课时)
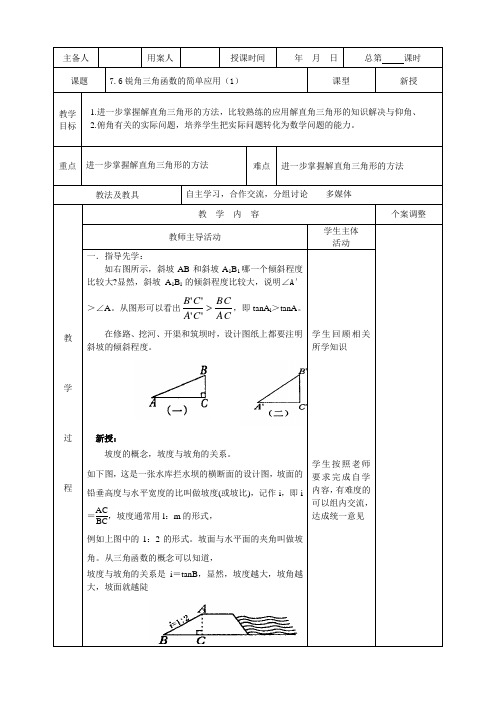
主备人用案人授课时间年月日总第课时课题7.6锐角三角函数的简单应用(1)课型新授教学目标1.进一步掌握解直角三角形的方法,比较熟练的应用解直角三角形的知识解决与仰角、2.俯角有关的实际问题,培养学生把实际问题转化为数学问题的能力。
重点进一步掌握解直角三角形的方法难点进一步掌握解直角三角形的方法教法及教具自主学习,合作交流,分组讨论多媒体教学过程教学内容个案调整教师主导活动学生主体活动一.指导先学:如右图所示,斜坡AB和斜坡A1B1哪一个倾斜程度比较大?显然,斜坡A1B l的倾斜程度比较大,说明∠A′>∠A。
从图形可以看出ACBCCACB'''',即tanA l>tanA。
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度。
新授:坡度的概念,坡度与坡角的关系。
如下图,这是一张水库拦水坝的横断面的设计图,坡面的铅垂高度与水平宽度的比叫做坡度(或坡比),记作i,即i=ACBC,坡度通常用l:m的形式,例如上图中的1:2的形式。
坡面与水平面的夹角叫做坡角。
从三角函数的概念可以知道,坡度与坡角的关系是i=tanB,显然,坡度越大,坡角越大,坡面就越陡学生回顾相关所学知识学生按照老师要求完成自学内容,有难度的可以组内交流,达成统一意见教学过程教学内容个案调整教师主导活动学生主体活动四.检测巩固:如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角。
和坝底宽AD。
(i=CE:ED,单位米,结果保留根号)2.如图,单摆的摆长AB为90cm,当它摆动到∠BAB'的位置时,∠BAB'=30°。
问这时摆球B'较最低点B升高了多少?五.小结反思:通过本节课的学习,你有何收获?你还存在什么疑惑?学生独立完成,有难度的可以组内交流,教师巡视,指导学生分组讨论交流,总结归纳,教师补充板书设计7.6锐角三角函数的简单应用(1)坡度的概念,坡度与坡角的关系。
坡面的铅垂高度与水平宽度的比叫做坡度(或坡比),记作i,即i=ACBC,坡度通常用l:m的形式,坡度与坡角的关系是i=tanB,显然,坡度越大,坡角越大,坡面就越陡布置作业补充习题教学札记教学过程教学内容个案调整教师主导活动学生主体活动1、摩天轮启动多长时间后,小明离地面的高度将首次到达10m?2、小明将有多长时间连续保持在离地面20m以上的空中?三.释疑拓展:如图,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离(精确到l米)。
7.6锐角三角函数的简单应用第1课(沭阳县怀文中学)

初 三 数 学( 7.6锐角三角函数的简单应用第1课)教学目标:通过具体的一些实例,能将实际问题中的数量关系,归结为直角三角形中元素之间的关系。
教学过程:一、自主探究1.在△ABC 中,∠C=90°,∠A=45°,则BC :AC :AB = .2.在△ABC 中,∠C=90°(1)已知∠A=30°,BC=8cm ,求AB 与AC 的长;(2)已知∠A=60°,AC=3cm ,求AB 与BC 的长.二、自主合作解:拓展1.摩天轮启动多长时间后,小明离地面的高度将首次到达10m ?2.小明将有多长时间连续保持在离地面20m 以上的空中? 三、自主展示1.如图,单摆的摆长为90cm,当它摆动到AC 的位置时,∠CAB =15°,问这时摆球C 较最低点B 升高了多少?2.已知跷跷板长4m,当跷跷板的一端碰到的地面时,另一端离地面2m,求此时跷跷板与地面的夹角?3.如图,东西两炮台A 、B 相距2000米,同时发现入侵敌舰C ,炮台A 测得敌舰C 在它的南偏东30°的方向,炮台B 测得敌舰C 在它的正南方,试求敌舰与两炮台的距离(结果保留根号).四、自主拓展3.4.九年级三班小亮同学学习了“测量物体高度”一节课后,他为了测得右图所放风筝的高度,进行了如下操作:(1)在放风筝的点A 处安置测倾器,测得风筝C 的仰角60CBD =︒∠;(2)根据手中剩余线的长度求出风筝线BC 的长度为70米; (3)量出测倾器的高度 1.5AB =米. 根据测量数据,计算出风筝的高度CE 约为 米.(精确到0.11.73)5.如图,某河道要建造一座公路桥,要求桥面离地面高度AC 为3米,引桥的坡角ABC ∠为30°,则引桥的水平距离BC 的长是_________米(结果保留根号) 6.A DB EC 60° 第4题图A B C 第5题图第六题图。
锐角三角函数的简单运用

锐角三角函数的计算方法包括直接计算、利用三角恒等式化简、利用同角关系式化简等。 掌握这些计算方法是解决三角函数问题的基本技能。
对未来学习锐角三角函数的建议
01
深入理解概念
在学习锐角三角函数的过程中,要深入理解其概念,掌握其性质和定理,
这样才能更好地运用它们解决实际问题。
02 03
利用三角函数求长度
在直角三角形中,已知角度和一边长度,可以利用正弦、余弦、正切等三角函数 求出另一边的长度。
利用三角函Байду номын сангаас求距离
在平面几何问题中,可以利用三角函数求两点之间的距离,或者点到直线的距离 。
判断三角形形状问题
利用三角函数判断三角形形状
通过比较三角形的三个内角的三角函数值,可以判断三角形是锐角三角形、直角三角形还是钝角三角 形。
正弦函数的性质
01
02
03
定义域
正弦函数在第一象限和第 二象限有定义,即角度范 围在0到180度之间。
值域
正弦函数的值域为[-1,1], 表示角度的正弦值永远不 会超过1或小于-1。
单调性
正弦函数在第一象限和第 二象限内是单调递增的, 随着角度的增加,正弦值 也会增加。
余弦函数的性质
定义域
余弦函数在第一象限和第 四象限有定义,即角度范 围在0到180度之间。
锐角三角函数的 简单运用
目录
• 引言 • 锐角三角函数的性质 • 锐角三角函数的计算方法 • 锐角三角函数在几何问题中的应
用 • 锐角三角函数在实际问题中的应
用 • 总结与展望
01
引言
锐角三角函数的定义
锐角三角函数是三角函数中的一种, 主要研究锐角的角度与其边长之间的 关系。常见的锐角三角函数有正弦、 余弦和正切。
7.6锐角三角函数的简单应用(2)

7.6 锐角三角函数的简单应用⑵
进一步掌握解直角三角形的方法,比较熟练的应用解直角三角形的知识解决 与仰角、 俯角有关的实际问题, 培养学生把实际问题转化为数学问题的能力. 重点:进一步用解直角三角形的知识解决与方位角有关的实际问题. 难点:灵活运用三角函数解决实际问题. 教学过程 个案
2.如图,飞机在距地面 9km 高空上飞行,先在 A 处测得正前方某小岛 C 的俯角 为 30°,飞行一段距离后, 在 B 处测得该小岛的俯角为 60°.求飞机的飞行距离。
【数学活动室】 教学书中问题 2 怎样测量停留在空中的气球高度呢?明明设计了这样一个方案: 先站在地面上某点处观测气球 , 测得仰角为 27 ° , 然后他向气球方向前进了 50m,此时观测气球,测得仰角为 40°.若明明的眼睛离地面 1.6m, 如何 计算气 球的高度呢?
【知识要点】 认清俯角与仰角
1、当从低处观测高处的目标时,视线与水平线 所成的锐角称为仰角. 2、当从高处观测低处的目标时,视线与水平线 所成的锐角称为俯角. 【典型例题】 如图,AB 和 CD 是同一地面上的两座相距 36 米的楼房,在楼 AB 的楼顶 A 点 测得楼 CD 的楼顶 C 的仰角为 45°,楼底 D 的俯角为 30°.求楼 CD 的高。 若已知楼 CD 高为 30 米,其他条件不变,你能求出两楼之间的距离 BD 吗?
教学反思
C
A B
D
【基础演练】 1、 为改善楼梯的安全性能,准备将楼梯的倾斜角由 60°调整为 45 °.已知调整 后的楼梯比原来多占地 4 米,求楼梯的高度.
D
A
B
C
2、升国旗时,某同学站在离旗杆底部 24m 处行注目礼,当国旗升至旗杆顶端时, 该同学视线的仰角恰为 30°,若双眼离地面 1.5m,求旗杆的高度.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【基础演练】 1. 如图是沿水库拦河坝的背水坡,将坡顶加宽 2 米,坡度由原来的 1:2 改为 1:2.5,已知坝高 6 米.求加宽部分横断面 AFEB 的面积;
F
A
D
E
B
C
2.如图,斜坡 AC 的坡度(坡比)为 1: 3 AC=10 米.坡顶有一旗杆 BC, 旗杆顶端 B 点与 A 点有一条彩带 AB 相连, AB=14 米. 试求旗杆 BC 的高度.
【典型例题】 1.如图,水坝的横截面是梯形 ABCD,迎水坡 BC 的坡角 的坡度 i 为 1:1.2, 坝顶宽 DC=2.5 米,坝高 4.5 米. 求:(1)背水坡 AD 的坡角 (精确到 0.1°); (2)坝底宽 AB 的长(精确到 0.1 米).
为 30°,背水坡 AD
2. 思考:在上题中,为了提高堤坝的 防洪能力,市防汛指挥部决定加固堤坝,要求 坝顶 CD 加宽 0.5 米,背水坡 AD 的坡度改为 1:1.4,已知堤坝的总长度为 5 ㎞,求 完成该项工程所需的土方(精确到 0.1 米 3) 若把此堤坝加高 0.5 米,需要多少土方?
B C A
D
如图,有一段斜坡 BC 长为 10 米,坡角 ∠CBD=30°,为方便残疾人的轮椅车通行,现准备把坡角降为 5°。求斜坡新 起点 A 与原起点 B 的距离 (结果精确到 0.1 米)
教学反思
【知识要点】 1.斜坡坡度 i =
斜坡的垂直高度 斜坡的水平距离
2 .通常我们将坡度 i 写成 1:m 的形式,坡度 i 与坡角 之间的关系为 i tan 。 【热身练习】 1.小明沿着坡角为 20° 的斜坡向上前进 80m, 则他上升的高度是( ).
A.
80 m cos 20
B.
C.80sin 20m
课题 学习目标 重点,难点源自7.6 锐角三角函数的简单应用(4)
1.使学生知道测量中坡度、坡角的概念,掌握坡度与坡角的关系; 2.能利用解直角三角形的知识,解决与坡度有关的实际问题,进一步培养学 生把实际问题转化为数学问题的能力. 重点:坡度、坡角的概念,掌握坡度与坡角的关系. 难点:能利用解直角三角形的知识,解决与坡度有关的实际问题. 教学过程 个案 i=1:m α
80 m sin 20 D.80cos 20m
2.如图是一个拦水大坝的横断面图,AD∥BC, .斜坡 AB=10m,大坝高为 8m, (1)则斜坡 AB 的坡度 iAB ____ . (2)如果坡度 i 1: 3 ,则坡角 B ____ . AB (3)如果坡度 iAB 1: 2, AB 8m ,则大坝高度为___.
