盱眙县第二中学11—12年度第二学期七年级数
盱眙县第二中学11—12年度第二学期七年级数

图4盱眙县第二中学11—12年度第 二学期七年级数学月考试卷(一) 命题人:庄亿农 时间:120分钟 总分:150分 一、快乐A 、B 、C (下列各题给出的四个选项中,只有一个是正确的。
请把你认为正确选项的对应字母填在下列相应的表格中,每小题3分,共30分) 1.如图1,下列说法中正确的是( ▲ ) (A )∠1和∠2是内错角 (B )∠2和∠3是同位角 (C )∠3和∠4是同旁内角 (D )∠1和∠32.下列条件中,不能判定两直线平行的是(▲ ) (A )同旁内角相等 (B )内错角相等 (C )同位角相等 (D )同旁内角互补 3.计算(-2)3的结果是( ▲ ) (A )-6 (B )8 (C )-8 (4.x 3·x 2的运算结果是 ( ▲ ) (A )x (B )x 3 (C )x 5 (D )x 5.用科学记数方法表示0.0000907,得( ▲ ) (A )9.07×10-4 (B )9.07×10-5 (C )9.07×10-6(D )9.07×10-7 6.下列线段能构成三角形的是 (▲ ) (A )1,2,3 (B ) 8,6,4 (C ) 12,5,6 (D ) 2,3,6 7.计算2m 2-m(2m-5n)-n(5m-n)的结果是( ▲ ) (A)-n 2 (B)n 2 (C)-10mn+n 2 (D)10mn+n 2 8.若一个多边形的内角和等于720º,则这个多边形的边数是(▲ ) (A)5 (B)6 (C)7 (D)8 9.如图2,在△ABC 中,D 是BC 延长线上一点, = 120°,则∠A 等于( ▲ ) (A )60° (B )70° (C )80° (D )90° 10.若x 2-6xy+N 是一个完全平方式,那么N 是( ▲ ) (A)9y 2 (B)y 2 (C)3y 2 (D) 6y 2 二、填填补补 (每小题3分,共24分,把答案写在题中横线上) 11.-22+1)31(-= . 12.352)(a a ⋅-= . 13.( )·533186b a ab =.14.(2x-y)( )=4x 2-y 2. 15.如图3,将300的直角三角板ABC 平移后到BDE 位置(C 、B 、E 在同一条直线上),则∠ADE= 0.16.式子20122011531()85(⨯-= . 17.若一个三角形三个内角度数的比为2︰3︰4 则这个三角形是 三角形.18.如图4,把矩形ABCD 沿EF 对折后使两部分重合,若∠1=50º,则∠AEF= º.三、小小神算手(共44分)19.(2×8=16分)计算密 封 线 内 不 准 答 题 ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------F E D C B A 图6(1)(x 2y)·(xy 3) 3; (2)201222)21(⨯-+-.20.( 8分)计算:(1)-x(x 2+xy-1) ; (2) 4(x-y)2-(2x+y)(-y+2x).21.(10分)先化简,再求值:(1)-21a 2bc ·4ab 2c 3,其中a=-1,b=1,c =-21; (2)(a+2b)(a-2b)-(2a-b)(-2a-b),其中a=8,b=-8.22.(10分)已知(m+n)2=7,(m-n)2=3,求下列各式的值:(1)mn ; (2)m 2+n 2.四、试试你的说理能力(共52分)23.(10分)如图5,已知CD ∥AB ,º,求∠BOF 的度数.24.(10分)如图6,将边长都为2个单位的△ABC 沿边BC 向右平移1个单位得到△DEF ,试求四边形ABFD 的周长.25.(10分)一副三角板(即△ABC 和△7叠放在一起,求图中∠α的度数.26.(10分)如图8,点E 在直线DF 上,点B 在直线AC 上,若∠AGB=∠EHF ,∠C=∠D ,试判断∠A 与∠F 之间的关系,并说明理由.27.(12分)小明与小芳共同计算一道题:(2x+a) (3x+b).由于粗心,小明抄错了第一个多项式中a 前面的符号,得结果6x 2+11x -10;小芳漏抄了第二个多项式中x 的系数,得结果为2x 2-9x+10.(1)你能否知道式子中a ,b 的值各是多少?(2)请你算出这道题的正确结果.。
河北省石家庄市新华区2023-2024学年七年级下学期期末数学试题(含答案)

2023—2024学年第二学期期末学业质量监测七年级数学(冀教版)注意事项:1.本试卷共6页,满分100分,考试时长90分钟。
2.答卷前将密封线左侧的项目填写清楚。
3.答案须用黑色字迹的签字笔书写。
一、精心选择(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项只有一项是正确的)1.如图,CF,CE,CD分别是△ABC的中线、角平分线、高,下列线段中,长度最短的是()A.CF B.CE C.CD D.CB2.2−3可以表示为()A.2×2×2B.(−2)×(−2)×(−2)C.2÷2÷2D.12×2×23.如图.∠1与∠2是()A.同位角B.内错角C.同旁内角D.对顶角4.我国陆地上风能储量约为253,000兆瓦,将253,000用科学记数法表示为2.53×10n,则n的值为()A.4B.5C.6D.−55.一款晾衣架的示意图如图所示,支架OP=OQ=30cm(连接处的长度忽略计),则点P,Q之间的距离可以是()A.50cm B.65cm C.70cm D.80cm6.下列运算中,结果正确的是()A.a4⋅a3=a12B.(a3)2=a6C.a6÷a2=a3D.(−3x)2=−9x27.数轴上表示数m,n的点的位置如图所示,则下列结论不正确的是()A.m−n<0B.m+1<n−1C.−3m<−3n D.m2<n28.如图,将长方形纸片按如图方式折叠,已知∠DQP=50∘,则∠CPM=()A.40∘B.50∘C.60∘D.80∘9.等式“☐a2−b2=−(2a−b)(2a+b)”中的“□”表示的数是()A.4B.−4C.16D.−1610.如图,已知直线m平移后得到直线n,∠1=108∘,∠2=35∘.则∠3的度数为()A.98∘B.103∘C.107∘D.143∘11.【问题】已知关于x,y的方程组{3x+5y=4k−2x−3y=2的解满足2x+y=3.求k的值.嘉嘉同学有如下两种解题思路和部分步骤:Ⅰ.将方程组中的两个方程相加并整理,可得到2x+y=2k,再求k的值;Ⅱ.解方程组{2x+y=3,x−3y=2,得到{x=117,y=−17.再代入3x+5y=4k−2中,可求k的值.下列判断正确的是()A.Ⅰ的解题思路不正确B.Ⅱ的解题思路不正确C.Ⅱ的解题思路正确,求解不正确D.Ⅰ与Ⅱ的解题思路与求解都正确12.阅读下面的数学问题:如图,在△ABC中,AE⊥BC于点E,CD⊥AB于点D,AE,CD交于点P,AQ平分∠CAE,CQ平分∠ACD.甲、乙两人经过研究,分别得到如下结论:甲:∠APC+∠ABC=180∘;乙:∠AQC+12∠ABC=180∘.其中判断正确的是()A.甲、乙两人的结论都正确B.甲、乙两人的结论都错误C.甲的结论错误,乙的结论正确D.甲的结论正确,乙的结论错误二、准确填空(本大题共4个小题,每小题3分,共12分.其中16小题第一个空2分,第二个空1分)13.写出一个满足不等式x−6>0的x的整数值为 .14.整式a2−a和(a−1)2的公因式为 .15.命题“若△ABC中的∠A:∠B:∠C=1:2:3,则△ABC是直角三角形”是 .(填“真命题”或“假命题”)16.几何验证:如图1,可验证公式(a+b)2=a2+2ab+b2.(1)公式应用:若m+n=5,mn=6,则m2+n2的值为;,则S1+S2的(2)拓展延伸:如图2,四边形ACDE和四边形BCFG是两个正方形,若DF=6,S△ACF=92值为 .图2三、细心解答(本大题共8个小题,共52分.解答应写出文字说明、说理过程或演算步骤)17.(本小题满分5分)小明在解方程组{x−3y=3,①2x−5y=4②的过程如下:解:由①×2,得2x−6y=6③,…………第一步②−③,得−y=−2,…………第二步得y=2.…………第三步把y=2代入①,得x=9,…………第四步所以原方程组的解为{x=9,y=2.(1)小明的解题过程从第步开始出现错误;(2)请你写出正确的解方程组的过程.18.(本小题满分5分)已知不等式组{2(x−1)≥−3,①4x−2<1+3x.②(1)解该不等式组,并把解集在下面的数轴上表示出来;(2)写出该不等式组的所有正整数解.19.(本小题满分6分)如图,△ABC的顶点都在正方形网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC向左平移7个单位长度得到△A′B′C′.(1)在网格中画出△A′B′C′及A′B′边上的中线C′H和高线C′G;(2)直接写出线段BC所扫过的面积.20.(本小题满分6分)已知A=(a+2b)(a−b)−a5÷a3−(2b)2.(1)先化简A,再求当a=1,b=−3时,A的值;(2)若a=6b,求A的值.21.(本小题满分6分)如图,△ABC中,∠A=70∘,∠ABC=75∘,点D为线段AC上的点(不与点A,C重合),点E在AB的延长线上,连接DE,∠E=40∘,DF平分∠ADE.(1)求∠C的度数;(2)说明BC//DF的理由.22.(本小题满分7分)有三个连续奇数,最小的奇数为2n−1(n为正整数).(1)用含n的代数式表示另外两个奇数;(2)判断这三个奇数的平方和是否是12的倍数.若是,请说明理由;若不是,请写出被12除的余数是多少.23.(本小题满分8分)某校欲租用租赁公司的甲、乙两种型号的大巴车共8辆(两种车型都要租用),将部分师生送去植物园游玩,相关的租车信息如下:信息一:若租用3辆甲型大巴、5辆乙型大巴,共可载客435人;若租用6辆甲型大巴、2辆乙型大巴,共可载客390人。
江苏省淮安市盱眙县2016-2017学年七年级(下)期末数学试卷(解析版)

.
A、由①可得出 x+y=6,A 正确; C、由①﹣②可得出 x•y=8,C 正确; D、由②可得出 x﹣y=2,D 正确. 故选 B.
二、填空题(本大题共 10 小题,每小题 3 分,共 30 分) 9.计算:x5÷x3= x2 . 【考点】48:同底数幂的除法. 【分析】利用同底数的幂的除法法则:底数不变,指数相减即可求解. 【解答】解:x5÷x3=x5﹣3=x2.
25.画图并填空:如图,方格纸中每个小正方形的边长都为 1.在方格纸内将△
ABC 经过一次平移后得到△A′B′C′,图中标出了点 B 的对应点 B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
利用网格点和三角板画图或计算:
(2)画出 AB 边上的中线 CD;
(3)画出 BC 边上的高线 AE;
6.若一个正多边形的每一个内角都等于 120°,则它是( ) A.正六边形 B.正五边形 C.正方形 D.正八边形 【考点】L3:多边形内角与外角. 【分析】首先设这个正多边形的边数为 n,根据多边形内角和公式:180°(n﹣2), 列出方程进行计算即可. 【解答】解:设这个正多边形的边数为 n,由题意得: (n﹣2)×180=120n 解得:n=6. 故选 A.
【解答】解:根据该班一男生请假后,男生人数恰为女生人数的一半,得 x﹣1=
y,即 y=2(x﹣1);根据某班共有学生 49 人,得 x+y=49.
列方程组为
.
故选:D.
8.用四个完全一样的长方形(长、宽分别设为 x、y)拼成如图所示的大正方形, 已知大正方形的面积为 36,中间空缺的小正方形的面积为 4,则下列关系式中不 正确的是( )
【考点】92:二元一次方程的解. 【分析】根据方程的解满足方程,把方程的解代入方程,可得关于 m 的一元一 次方程,根据解方程,可得答案.
专题1.8 数轴贯穿有理数的经典考法【九大题型】(举一反三)(人教版)(原卷版)2

专题1.8 数轴贯穿有理数的经典考法【九大题型】【人教版】【题型1 数轴上点的平移】 (1)【题型2 数轴上点表示的数】 (3)【题型3 判断数轴上点的符号或原点位置】 (4)【题型4 数轴上两点距离的和差倍分问题】 (5)【题型6 数轴与方程思想的运算】 (12)【题型7 数轴上的动点定值问题】 (13)【题型8 数轴上的折叠问题】 (16)【题型9 数轴上点的规律问题】 (19)【题型1 数轴上点的平移】【例1】(2022•惠安县校级月考)在数轴上有三个点A、B、C,如图所示.(1)将点B向左平移4个单位,此时该点表示的数是;(2)将点C向左平移3个单位得到数m,再向右平移2个单位得到数n,则m,n分别是多少?(3)怎样移动A、B、C中的两点,使三个点表示的数相同?你有几种方法?【变式1-1】(2022•沂水县一模)在数轴上,点A,B在原点O的两侧,分别表示数a,1,将点A向右平移2个单位长度,得到点C(点C不与点B重合),若CO=BO,则a的值为()A.1B.﹣1C.﹣2D.﹣3【变式1-2】(2022•乳山市期中)已知点A,B在数轴上表示的数分别是﹣2,3,解决下列问题:(1)将点A在数轴上向左平移1个单位长度后记为A1,A1表示的数是,将点B在数轴上向右平移31个单位长度后记为B1,B1表示的数是;(2)在(1)的条件下,将点B1向移动个单位长度后记为B2,则B2表示的数与A1表示的数互为相反数;(3)在(2)的条件下,将原点在数轴上移动5个单位长度,则点B2表示的数是多少?【变式1-3】(2022•工业园区期末)【理解概念】对数轴上的点P按照如下方式进行操作:先把点P表示的数乘以2,再把表示得到的这个数的点沿数轴向右平移3个单位长度,得到点P′.这样的操作称为点P的“倍移”,数轴上的点A、B、C、D、E、F经过“倍移”后,得到的点分别为A′、B′、C′、D′、E′、F′.【巩固新知】(1)若点A表示的数为﹣1,则点A′表示的数为.(2)若点B′表示的数为9,则点B表示的数为.【应用拓展】(3)若点C表示的数为5,且CD′=3CD,求点D表示的数;(4)已知点E在点F的左侧,将点E′、F′再次进行“倍移”后,得到的点分别为E″、F″,若E″F″=2020,求EF的长.【题型2 数轴上点表示的数】【例2】(2022秋•三元区期中)如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr,本题中π的取值为3.14)(1)把圆片沿数轴向右滚动1周,点Q到达数轴上点A的位置,点A表示的数是;(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,﹣5,+4,+3,﹣2①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?【变式2-1】(2022秋•德惠市校级月考)东方红中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向西走100米到聪聪家,再向东走150米到青青家,再向西走200米到刚刚家,请问:(1)如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出聪聪家与青青家的大概位置(数轴上一格表示50米).(2)聪聪家与刚刚家相距多远?(3)聪聪家向西20米所表示的数是多少?(4)你认为可用什么办法求数轴上两点之间的距离?【变式2-2】(2022春•海淀区校级月考)直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达O'点,点O'对应的数是()A.3B.3.1C.πD.3.2【变式2-3】(2022•南安市模拟)如图,数轴上点D对应的数为d,则数轴上与数﹣3d对应的点可能是()A.点A B.点B C.点D D.点E【题型3 判断数轴上点的符号或原点位置】【例3】(2022秋•岳池县期中)有理数a、b、c在数轴上所对应的点的位置如图所示,有下列四个结论:①(a+b)(b+c)(c+a)>0;②b<b2<1;③|a|<1﹣bc;④|a﹣b|﹣|c﹣a|+|b﹣c|﹣|a|=a.其中正确的b结论有()个.A.4B.3C.2D.1【变式3-1】(2022秋•新郑市期中)已知小红、小刚,小明、小颖四人自南向北依次站在同一直线上,如果把直线看作数轴,四人所在的位置如图所示,则下列描述错误的是()A.数轴是以小明所在的位置为原点B.数轴采用向北为正方向C.小刚所在的位置对应的数有可能是−53D.小刚在小颖的南边【变式3-2】(2022秋•海淀区校级期末)如图,数轴上点A,M,B分别表示数a,a+b,b,那么原点的位置可能是()A.线段AM上,且靠近点A B.线段AB上,且靠近点BC.线段BM上,且靠近点B D.线段BM上,且靠近点M【变式3-3】(2022秋•海陵区校级期中)如图,数轴上的点M,N表示的数分别是m,n,点M在表示0,1的两点(不包括这两点)之间移动,点N在表示﹣1,﹣2的两点(不包括这两点)之间移动,则下列判断正确的是()A.m2﹣2n的值一定小于0B.|3m+n|的值一定小于2C.1m−n的值可能比2000大D.1m +1n的值不可能比2000大【题型4 数轴上两点距离的和差倍分问题】【例4】(2022秋•盱眙县期中)已知数轴上两点A、B,其中A表示的数为﹣2,B表示的数为2,若在数轴上存在一点C,使得AC+BC=n,则称点C叫做点A、B的“n节点”,例如图1所示,若点C表示的数为0,有AC+BC=2+2=4,则称点C为点A、B的“4节点”.请根据上述规定回答下列问题:(1)若点C为点A、B的“n节点”,且点C在数轴上表示的数为﹣3,则n=.(2)若点D是数轴上点A、B的“5节点”,请你直接写出点D表示的数为;(3)若点E在数轴上(不与A、B重合),满足B、E之间的距离是A、E之间距离的一半,且此时点E 为点A、B的“n节点”,求出n的值.【变式4-1】(2022秋•江夏区校级月考)在数轴上,点A代表的数是﹣12,点B代表的数是2,AB代表点A与点B之间的距离.(1)①AB=;②若点P为数轴上点A与B之间的一个点,且AP=6,则BP=;③若点P为数轴上一点,且BP=2,则AP=.(2)若C点为数轴上一点,且点C到点A点的距离与点C到点B的距离的和是35,求C点表示的数.(3)若P从点A出发,Q从原点出发,M从点B出发,且P、Q、M同时向数轴负方向运动,P点的运动速度是每秒6个单位长度,Q点的运动速度是每秒8个单位长度,M点的运动速度是每秒2个单位长度,当P、Q、M同时向数轴负方向运动过程中,当其中一个点与另外两个点的距离相等时,求这时三个点表示的数各是多少?【变式4-2】(2022•长汀县期中)点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C 到B的距离3倍,那么我们就称点C是{A,B}的奇点.例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.(1)数所表示的点是{M,N}的奇点;数所表示的点是{N,M}的奇点;(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,到达点A停止.P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?【变式4-3】(2022•湖里区校级期中)已知数轴上两点A.B对应的数分别为﹣2和7,点M为数轴上一动点.(1)请画出数轴,并在数轴上标出点A、点B;(2)若点M到A的距离是点M到B的距离的两倍,我们就称点M是【A,B】的好点.①若点M运动到原点O时,此时点M【A,B】的好点(填是或者不是)②若点M以每秒1个单位的速度从原点O开始运动,当M是【B,A】的好点时,求点M的运动方向和运动时间(3)试探究线段BM和AM的差即BM﹣AM的值是否一定发生变化?若变化,请说明理由:若不变,请求其值.【题型5 数轴上的行程问题】【例5】(2022秋•东阿县期末)如图,三点A、B、P在数轴上,点A、B在数轴上表示的数分别是﹣4,12(AB两点间的距离用AB表示)(1)C在AB之间且AC=BC,C对应的数为;(2)C在数轴上,且AC+BC=20,求C对应的数;(3)P从A点出发以1个单位/秒的速度在数轴向右运动,Q从B点同时出发,以2个单位/秒在数轴上向左运动.求:①P、Q相遇时求P对应的数②P、Q运动的同时M以3个单位长度/秒的速度从O点向左运动.当遇到P时,点M立即以同样的速度(3个单位/秒)向右运动,并不停地往返于点P与点Q之间,求当点P与点Q相遇时,点M所经过的总路程是多少?【变式5-1】(2022秋•市中区校级期中)如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.(1)请写出与A、B两点距离相等的点M所对应的数;(2)现有一只电子蚂蚁P从B点出发,以6个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?(3)若当电子蚂蚁P从B点出发时,以6个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A 点出发,以4个单位/秒的速度也向左运动,请问:当它们运动多少时间时,两只蚂蚁间的距离为20个单位长度?【变式5-2】(2022•越秀区二模)甲、乙两个昆虫分别在数轴原点和+8的A处,分别以1单位长度/s,1.5单位长度/s速度同时相向而行.(1)第一次相遇在数轴上何处;(2)若同时沿数轴的负方向而行,乙昆虫在数轴上何处追上甲昆虫?(3)在(1)的条件下,两个昆虫分别到达点A和O处后迅速返回第二次相遇于数轴何处?【变式5-3】(2022春•南关区校级月考)一次数学课上,小明同学给小刚同学出了一道数形结合的综合题,他是这样出的:如图,数轴上两个动点M,N开始时所表示的数分别为﹣10,5,M,N两点各自以一定的速度在数轴上运动,且M点的运动速度为2个单位长度/s.(1)M,N两点同时出发相向而行,在原点处相遇,求N点的运动速度.(2)M,N两点按上面的各自速度同时出发,向数轴正方向运动,几秒时两点相距6个单位长度?(3)M,N两点按上面的各自速度同时出发,向数轴负方向运动,与此同时,C点从原点出发沿同方向运动,且在运动过程中,始终有CN:CM=1:2.若干秒后,C点在﹣12处,求此时N点在数轴上的位置.【题型6 数轴与方程思想的运算】【例6】(2022秋•越秀区校级期中)在数轴上有若干个点,每相邻两个点之间的距离是1个单位长度,有理数a,b,c,d表示的点是这些点中的4个,且在数轴上的位置如图所示.已知3a=4b﹣3,则代数式c﹣5d的值是()A.﹣20B.﹣16C.﹣12D.﹣8【变式6-1】(2022秋•余姚市期末)数轴上有6个点.每相邻两个点之间的距离是1个单位长,有理数a,b,c,d所对应的点是这些点中的4个,位置如图所示:(1)完成填空:c﹣a=,d﹣c=,d﹣a=;(2)比较a+d和b+c的大小;(3)如果4c=a+2b,求a+b﹣c+d的值.【变式6-2】(2022秋•武昌区校级月考)如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别是a、b、c、d,且b﹣2a=9,请在图中标出原点O,并求出3c+d﹣2a的值.【变式6-3】(2022•洛川县校级期末)如图所示,数轴(不完整)上标有若干个点,每相邻两点相距一个单位长度,点A,B,C,D对应的数分别是a,b,c,d,且有一个点表示的是原点.若d+2a+5=0,则表示原点的应是点.【题型7 数轴上的动点定值问题】【例7】(2022秋•普宁市期末)已知如图,在数轴上有A,B两点,所表示的数分别为﹣10,﹣4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题:(1)运动前线段AB的长为;运动1秒后线段AB的长为;(2)运动t秒后,点A,点B运动的距离分别为和;(3)求t为何值时,点A与点B恰好重合;(4)在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由.【变式7-1】(2022秋•绥宁县期中)阅读下面的材料:如图1,在数轴上A点所示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB=b﹣a.请用上面的知识解答下面的问题:如图2,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B点,然后向右移动7cm到达C点,用1个单位长度表示1cm.(1)请你在数轴上表示出A.B.C三点的位置:(2)点C到点A的距离CA=cm;若数轴上有一点D,且AD=4,则点D表示的数为;(3)若将点A向右移动xcm,则移动后的点表示的数为;(用代数式表示)(4)若点B以每秒2cm的速度向左移动,同时A.C点分别以每秒1cm、4cm的速度向右移动.设移动时间为t秒,试探索:CA﹣AB的值是否会随着t的变化而改变?请说明理由.【变式7-2】(2022秋•黄陂区期末)数轴上A,B,C三点对应的数a,b,c满足(a+40)2+|b+10|=0,B为线段AC的中点.(1)直接写出A,B,C对应的数a,b,c的值.(2)如图1,点D表示的数为10,点P,Q分别从A,D同时出发匀速相向运动,点P的速度为6个单位/秒,点Q的速度为1个单位/秒.当点P运动到C后迅速以原速返回到A又折返向C点运动;点Q运动至B点后停止运动,同时P点也停止运动.求在此运动过程中P,Q两点相遇点在数轴上对应的数.(3)如图2,M,N为A,C之间两点(点M在N左边,且它们不与A,C重合),E,F分别为AN,CM的中点,求AC−MN的值.EF【变式7-3】(2022•荔湾区期末)数轴上有两点A,B,点C,D分别从原点O与点B出发,沿BA方向同时向左运动.(1)如图,若点N为线段OB上一点,AB=16,ON=2,当点C,D分别运动到AO,BN的中点时,求CD的长;(2)若点C在线段OA上运动,点D在线段OB上运动,速度分别为每秒1cm,4cm,在点C,D运动的值.的过程中,满足OD=4AC,若点M为直线AB上一点,且AM﹣BM=OM,求ABOM【题型8 数轴上的折叠问题】【例8】(2022秋•丰台区校级期中)平移和翻折是初中数学两种重要的图形变化(1)平移运动①把笔尖放在数轴的原点处,先向负方向移动3个单位长度,再向正方向移动2个单位长度,这时笔尖的位置表示什么数?用算式表示以上过程及结果是A.(+3)+(+2)=+5 B.(+3)+(﹣2)=+1 C.(﹣3)﹣(+2)=﹣5 D.(﹣3)+(+2)=﹣1②一机器人从原点O开始,第1次向左跳1个单位,紧接着第2次向右跳2个单位,第3次向左跳3个单位,第4次向右跳4个单位,…,依次规律跳,当它跳2017次时,落在数轴上的点表示的数是.(2)翻折变换①若折叠纸条,表示﹣1的点与表示3的点重合,则表示2017的点与表示的点重合;②若数轴上A、B两点之间的距离为2018(A在B的左侧,且折痕与①折痕相同),且A、B两点经折叠后重合,则A点表示B点表示.③若数轴上折叠重合的两点的数分别为a,b,折叠中间点表示的数为.(用含有a,b的式子表示)【变式8-1】(2022秋•苏州期末)一条数轴上有点A、B、C,其中点A、B表示的数分别是﹣16、9,现以点C为折点,将数轴向右对折,若点A对应的点A′落在点B的右边,并且A′B=3,则C点表示的数是.【变式8-2】(2022秋•丰城市期中)操作探究:小聪在一张长条形的纸面上画了一条数轴(如图所示),操作一:(1)折叠纸面,使1表示的点与﹣1表示的点重合,则﹣3表示的点与表示的点重合;操作二:(2)折叠纸面,使﹣2表示的点与6表示的点重合,请你回答以下问题:①﹣5表示的点与数表示的点重合;②若数轴上A、B两点之间距离为20,其中A在B的左侧,且A、B两点经折叠后重合,求A、B两点表示的数各是多少③已知在数轴上点M表示的数是m,点M到第②题中的A、B两点的距离之和为30,求m的值.【变式8-3】(2022秋•邗江区校级月考)已知在纸面上有一数轴,折叠纸面.(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与数表示的点重合(2)若﹣2表示的点与4表示的点重合,回答以下问题:①数7对应的点与数对应的点重合;②若数轴上A、B两点之间的距离为2019(点A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?(3)点C在数轴上,将它向右移动4个单位,再向左2个单位后,若新位置与原位置到原点的距离相等,则C原来表示的数是多少?请列式计算,说明理由.【题型9 数轴上点的规律问题】【例9】(2022秋•茅箭区校级月考)已知数轴上有A,B,C三点,它们分别表示数a,b,c,且|a+6|+(b+3)2=0,又b,c互为相反数.(1)求a,b,c的值.(2)若有两只电子蚂蚁甲、乙分别从A,C两点同时出发相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒,当两只蚂蚁在数轴上点m处相遇时,求点m表示的数.(3)若电子蚂蚁从B点开始连续移动,第1次向右移动1个单位长度;第2次向右移动2个单位长度;第3次向左移动3个单位长度;第4次向左移动4个单位长度;第5次向右移动5个单位长度;第6次向右移动6个单位长度;第7次向左移动7个单位长度;第8次向左移动8个单位长度…依次操作第2019次移动后到达点P,求P点表示的数.,我们称点P′是【变式9-1】(2022秋•成都期末)在数轴上,点P表示的数是a,点P′表示的数是11−a 点P的“相关点”,已知数轴上A1的相关点为A2,点A2的相关点为A3,点A3的相关点为A4…,这样,则点A2016在数轴上表示的数是.依次得到点A1、A2、A3、A4,…,A n.若点A1在数轴表示的数是12【变式9-2】(2022秋•翁牛特旗期中)已知A、B在数轴上对应的数分别用+2、﹣6表示,P是数轴上的一个动点.(1)数轴上A、B两点的距离为8.(2)当P点满足PB=2P A时,求P点表示的数.(3)将一枚棋子放在数轴上k0点,第一步从k点向右跳2个单位到k1,第二步从k1点向左跳4个单位到k2,第三步从k2点向右跳6个单位到k3,第四步从k3点向左跳8个单位到k4.①如此跳6步,棋子落在数轴的k6点,若k6表示的数是12,则k o的值是多少?②若如此跳了1002步,棋子落在数轴上的点k1002,如果k1002所表示的数是1998,那么k0所表示的数是__(请直接写答案).【变式9-3】(2022秋•海淀区校级期中)如图,数轴上有三个点A、B、C,表示的数分别是﹣4、﹣2、3,请回答:(1)若将点B向左移动3个单位后,三个点所表示的数中,最小的数是;(2)若使点B所表示的数最大,则需将点C至少向移动个单位;(3)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动个单位;(4)若移动A、B、C三点中的两个点,使三个点表示的数相同,移动方法有种,其中移动所走的距离和最少的是个单位;(5)若在原点处有一只小青蛙,一步跳1个单位长.小青蛙第1次先向左跳1步,第2次再向右跳3步,然后第3次再向左跳5步,第4次再向右跳7步,…,按此规律继续跳下去,那么跳第101次时,应跳________-步,落脚点表示的数是;跳了第n次(n是正整数)时,落脚点表示的数是.。
淮安市盱眙县2022-2023学年第二学期初二数学期中考试试卷及答案

18
a
围棋类
14
0.28
喜剧类
8
0.16
国画类
b
0.20
根据以上信息完成下列问题: (1)直接写出频数分布表中 a 的值; (2)补全频数分布条形图; (3)若全校共有学生 1500 名,估计该校最喜爱围棋的学生大约有多少人?
21.已知,如图,在 ABCD 中, E, F 是对角线 BD 上的两点,且 BF DE .求证: AE CF .
22.如图,▱ABCD 中,点 E、F 分别在 AB、CD 上,且 BE=DF,EF 与 AC 相交于点 P,求证:PA=PC.
23.如图,菱形 ABCD 中,AE⊥BC 于点 E,∠BAE=30°,AD=4cm. (1)求菱形 ABCD 的各角的度数; (2)求 AE 的长.
24.如图,BN、CM 分别是△ABC 的两条高,点 D、点 E 分别是 BC、MN 的中点.
(3)试估算口袋中黑、白两种颜色的球各有多少只?
20.某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型
(分为书法、围棋、戏剧、国画共 4 类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
项目类型
频数
频率
书法类
任意摸出 1 个球,摸出白球可能性______摸出黄球可能性.(填“等于”或“小于”或“大于”).
12.在 ABCD 中, A C 220 ,则 B =____°.
13.在菱形 ABCD 中, AC 6 , BD 8 ,则菱形 ABCD 的周长是_______.
14.如图,已知矩形 ABCD,P、R 分别是 BC 和 DC 上的点,E、F 分别是 PA,PR 的中点.如果 DR=3, AD=4,则 EF 的长为______.
2021-2022学年江苏省淮安市盱眙县七年级下学期期中数学试题

2021-2022学年江苏省淮安市盱眙县七年级下学期期中数学试题1. 2022北京冬奥会吉祥物“冰墩墩”以熊猫为原型进行设计创作.如图,通过平移吉祥物“冰墩墩”可以得到的图形是()A.B.C.D.2.新型冠状病毒的直径约为0.00000097米,0.00000097用科学记数法表示为()A.9.7×10 ﹣10B.9.7×10 ﹣11C.9.7×10 ﹣8D.9.7×10 ﹣73.如果三角形的两边分别为3和7,那么这个三角形的第三边可能是()A.2 B.3 C.5 D.104.下列运算结果中正确的是()A.a2• a3=a6B.(a3)3=a6C.(﹣2 a)3=﹣2 a3D.a2 + a2=2 a25.下列多边形内角和为720°的是()A.B.C.D.6.下列多项式能直接用完全平方公式进行因式分解的是()A.B.C.D.7.如图,已知直线AB∥CD,当点E在直线AB与CD之间时,下列关系式成立的是()A.∠BED=∠ABE+∠CDE B.∠BED=∠ABE-∠CDEC.∠BED=∠CDE-∠ABE D.∠BED=2∠CDE-∠ABE8.如图,点C是线段BG上的一点,以BC,CG为边向两边作正方形,面积分别是和,两正方形的面积和,已知BG=6,则图中阴影部分面积为()A.4 B.6 C.7 D.89.分解因式:﹣4x2+16=_____.10.计算(﹣a2b)3=__.11.如图,直线a、b被c所截,,当______°时,12.是的中线,,,和的周长的差是______.13.若,则x的值等于_________.14.如图,在△ABC中,BF,CF是角平分线,∠A=70°,则∠BFC=______°.15.如图,小明从A点出发,前进4m到点B处后向右转20°,再前进4m到点C处后又向右转20°,…,这样一直走下去,他第一次回到出发点A时,一共走了____m.16.将一副三角板如图1所示摆放,直线,现将三角板ABC绕点A以每秒1°的速度顺时针旋转,同时三角板DEF绕点D以每秒2°的速度顺时针旋转,如图2,设时间为t 秒,当时,若边BC与三角板的一条直角边(边DE,DF)平行,则所有满足条件的t的值为 _____.17.计算(1)a3.a3-2a6(2)18.把下列各式分解因式(1)x2+2xy+y2(2)5x3﹣20x19.先化简,再求值:(2m+3)·(2m﹣3)﹣(m﹣1)2+(2m)3÷(﹣8m),其中m满足m2+m-3=0.20.如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A'B'C',图中标出了点B的对应点B'.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题保留画图痕迹:(1)画出△A'B'C';(2)连接AA'、CC',那么AA'与CC'的关系是_____,线段AC扫过的图形的面积为____;21.如图所示,已知AD,AE分别是△ABC的高和中线,AB=3cm,AC=4 cm,BC=5 cm,∠CAB=90°.(1)求AD的长.(2)求△ABE的面积.22.如图,已知点D、F、E、G都在△ABC的边上EF AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请任下面的空格处填写理由或数学式)解:∵EF AD.(已知)∴∠2=∠3(_____)∵∠1=∠2.(已知)∴∠1=∠3(_____)∴DG AB,(____)∴∠AGD+∠BAC=180°,(两直线平行,同旁内角互补)∵∠BAC=70°,(已知)∴∠AGD+70°=180°(等量代换)∴∠AGD=______.23.如图,AE平分∠BAC,∠CAE=∠CEA.(1)AB与CD有怎样的位置关系?为什么?(2)若∠C=50°,求∠CEA的度数.24.将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上.(1)请求出∠ABO度数(2)请求出∠BOE的度数25.(1)计算判断:,(填“>”“<”或“=”);(2)猜想发现:___(a≠0,b≠0,m是正整数,填“>”“<”或“=”);(3)拓展应用:计算26.对于一个图形,通过不同的方法计算图形的面积,就可以得到一个数学等式.(1)模拟练习:如图,写出一个我们熟悉的数学公式:_____;(2)解决问题:如果a+b=5,ab=3;求a2+b2的值;(3)类比探究:如果一个长方形的长和宽分别为(8﹣x)和(x﹣2),且(8﹣x)2+(x﹣2)2=20,求这个长方形的面积.27.直线AB、CD为平面内两条直线,点M、点N分别在直线AB、CD上,点P(P不在直线AB、CD上)为平面内一动点.(1)如图1,若AB、CD相交于点O,∠MON=40°;①当点P在△OMN内部时,求证:∠MPN-∠OMP-∠ONP=40°;②小芳发现,当点P在∠MON内部运动时,∠MPN、∠OMP、∠ONP还存在其它数量关系,这种数量关系是;③探究,当点P在∠MON外部时,∠MPN、∠OMP、∠ONP之间的数量关系共有种;(2)如图2,若AB//CD,请直接写出∠MPN与∠AMP、∠CNP之间存在的所有数量关系是.。
2024-2025学年江苏省淮安市苏教版七年级数学上册期中测试 题

2024-2025学年江苏省淮安市苏教版七年级数学上册期中测试题1.三车魏景元四年(公元263年),由我国古典数学理论的奠基人之一刘徽完成了《九章算术注》十卷,《重差》为第一卷,它是我国学者编撰的最早的一部测量数学著作,亦为地图学提供了数学基础,该卷中的第一个问题是求海岛上的山峰的高度,这本书的名称是()A.《海岛算经》B.《孙子算经》C.《九章算术》D.《五经算术》2.据统计,2013年河南省旅游业总收入达到约3875.5亿元,若将3875.5亿用科学记数法表示为3.8755×10n,则n等于()A.10B.11C.12D.133.小丽在纸上画了一条数轴后,折叠纸面,使数轴上表示2的点与表示-4的点重合;若数轴上A、B两点之间的距离为10(A在B的左侧),且A、B两点经上述折叠后重合,则A点表示的数是()A.-5B.-6C.-10D.-44.下列说法中:①﹣a一定是负数;②|﹣a|一定是正数;③有理数不是整数就是分数;④绝对值等于它本身的数是1;正确的说法有()个A.1B.2C.3D.45.如图,数轴上的A、B两点分别表示有理数a、b,下列式子中不正确的是()A.a+b<0B.a﹣b<0C.﹣a+b>0D.|b|>|a|6.大润发超市有三种袋装大米质量分别为10±0.1kg,10±0.2kg,10±0.3kg各十袋,从中抽取两袋,则它们质量相差最大为()A.0.3kg B.0.4kg C.0.5kg D.0.6kg7.将化成小数,则小数点后第个数字为()A.B.C.D.8.,b,c在数轴上的位置如图,化简:|c﹣b|+|a﹣b|﹣|a+c|=()A.0B.-2b C.2b-2a D.2a9.若与互为相反数,则的值为()A.3B.C.1D.10.计算:=__________.11.到原点的距离等于3的数是______.12.在中,底数是_____,其计算结果为_____.13.已知,,且,则的值等于__________.14.已知|x|=4,y2=25,xy<0,则x﹣y=__.15.多项式x|m|﹣(m﹣3)x+6是关于x的三次三项式,则m的值是_____.16.若,,则的值是___________.17.计算:(1)1÷(﹣3)×(2)(3)18.把下列各数填入相应的括号内.,0.212112111…(1)正数集合:{…};(2)负数集合:{…};(3)整数集合:{…};(4)分数集合:{…}.19.化简与求值先化简,再求值:其中20.形如的式子叫做二阶行列式,它的运算法则用公式表示为=ad﹣bc,依此法则计算:.21.如图,已知a、b、c在数轴上的位置.(1)c﹣b0,a+b0,a﹣c0.(填“>”或“<”)(2)化简:﹣|c﹣b|﹣|a+b|+|a﹣c|.22.巡道员每天沿着一条东西向的铁路进行巡视维护.他早晨从住地出发,先向东走了7km,休息半小时之后又向东走了3km,然后折返向西走了12km.(1)此时他在住地的方,与住地的距离是km;(2)若巡道员最终返回住地,问这一天他巡视维护共走了多少路程?23.已知a、b满足(a﹣b+1)2+|a+b﹣2|=0,求代数式的值.24.一天上午,某出租车被安排以地为出发地,只在东西方向的道路上营运,规定:向东行驶为正,向西行驶为负,行车里程(单位:)依先后次序记录如下:,.假设该出租车每次乘客下车后,都停车等待下一位乘客,直到下一位乘客上车再出发.(1)将最后一位乘客送到目的地后,出租车在地哪个方向,距离多远?(2)若出租车按每千米3元的价格收费,则该出租车司机当天上午的营业额是多少元?25.小王家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.(1)木地板和地砖分别需要多少平方米?(2)如果地砖的价格为每平方米元,木地板的价格为每平方米元,那么小王一共需要花多少钱?26.材料1:一般地,个相同因数相乘:记为.如,此时,3叫做以2为底的8的对数,记为(即)(1)计算__________,__________.材料2:新规定一种运算法则:自然数1到的连乘积用表示,例如:,,,,…在这种规定下(2)求出满足该等式的:(3)当为何值时,27.我国著名数学家华罗庚说过“数缺形时少直观,形少数时难人微”,数形结合是解决数学问题的重要思想方法.请阅读下列材料:材料(一):代数式|x﹣2|的几何意义是数轴上表示有理数x所对应的点与表示有理数2所对应的点之间的距离;因为|x+1|=|x﹣(﹣1)|,所以|x+1|的几何意义就是数轴上表示有理数x所对应的点与表示有理数﹣1所对应的点之间的距离.材料(二):如图,点A、B、P分别表示有理数数﹣1、2、x,AB=3,∵|x+1|+|x﹣2|的几何意义是线段PA与PB的长度之和,∴当点P在线段AB上时,PA +PB=3,当点P在点A的左侧或点B的右侧时,PA+PB>3,∴|x+1|+|x﹣2|的最小值是3;解决问题:(1)在数轴上,若点M表示的数为﹣2,点Q表示的数为1,点N表示的数为6,请画出一条数轴,标出点M、Q、N的位置,①线段NQ=;②若数轴上点C表示的有理数为x,求|x+2|+|x﹣6|的最小值.(2)若代数式|x+a|+|x﹣3|的最小值是2,求a的值.。
食堂检查
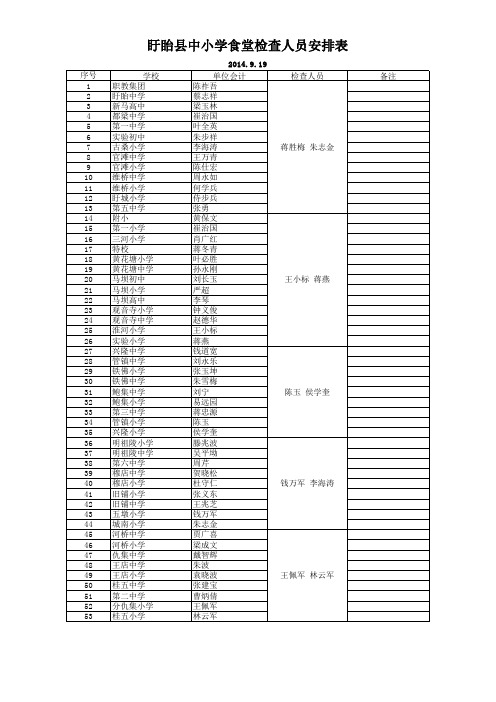
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 学校 职教集团 盱眙中学 新马高中 都梁中学 第一中学 实验初中 古桑小学 官滩中学 官滩小学 维桥中学 维桥小学 盱城小学 第五中学 附小 第一小学 三河小学 特校 黄花塘小学 黄花塘中学 马坝初中 马坝小学 马坝高中 观音寺小学 观音寺中学 淮河小学 实验小学 兴隆中学 管镇中学 铁佛小学 铁佛中学 鲍集中学 鲍集小学 第三中学 管镇小学 兴隆小学 明祖陵小学 明祖陵中学 第六中学 穆店中学 穆店小学 旧铺小学 旧铺中学 五墩小学 城南小学 河桥中学 河桥小学 仇集中学 王店中学 王店小学 桂五中学 第二中学 分仇集小学 桂五小学 2014.9.19 单位会计 陈祚吾 蔡志祥 梁玉林 崔治国 叶全英 朱步祥 李海涛 王万青 陈仕宏 周永如 何学兵 侍步兵 张勇 黄保文 崔治国 肖广红 蒋冬青 叶必胜 孙永刚 刘长玉 严超 李琴 钟义俊 赵德华 王小标 蒋燕 钱道宽 刘永乐 张玉坤 朱雪梅 刘宁 易远园 蒋忠源 陈玉 侯学奎 滕兆波 吴平坳 周芹 贺晓松 杜守仁 张义东 王兆芝 钱万军 朱志金 贾广喜 梁成文 戴智辉 朱波 袁晓波 张建宝 曹炳倩 王佩军 林云军 检查人员 备注
蒋胜梅 朱志金
王小标 蒋燕
陈玉云军
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图4 盱眙县第二中学11—12年度第
二学期七年级数学月考试卷(一)
命题人:庄亿农 时间:120分钟 总分:150分
一、快乐A 、B 、C (下列各题给出的四个选项中,只有一个是正确的。
请把你认为正确选项的对应字母填在下列相应的表格中,每
小题3分,共30分)
1.如图1,下列说法中正确的是( ▲ ) (A )∠1和∠2是内错角 (B )∠2和∠3是同位角
(C )∠3和∠4是同旁内角 (D )∠1和∠3是同旁
内角
2(A )同旁内角相等 (C )同位角相等 3.计算(-2)3的结果是((A )-6 (B )8 4.x 3·x 2的运算结果是 ( ▲ )
(A )x (B )x 3 (C )x 5 (D )x 6
5.用科学记数方法表示0.0000907,得( ▲ )
(A )9.07×10-4 (B )9.07×10-5 (C )9.07×10-6(D )9.07×10-7
6.下列线段能构成三角形的是 (▲ )
(A )1,2,3 (B ) 8,6,4 (C ) 12,5,6 (D ) 2,3,6
7.计算2m 2-m(2m-5n)-n(5m-n)的结果是( ▲ )
(A)-n 2 (B)n 2 (C)-10mn+n 2 (D)10mn+n 2
8.若一个多边形的内角和等于720º,则这个多边形的边数是(▲ )
(A)5 (B)6 (C)7 (D)8
9.如图2,在△ABC 中,D 是BC 延长线上一点, = 120°,则∠A 等于( ▲ )
(A )60° (B )70° (C )80° (D )90°
10.若x 2-6xy+N 是一个完全平方式,那么N 是( ▲ )
(A)9y 2 (B)y 2 (C)3y 2 (D) 6y 2
二、填填补补 (每小题3分,共24分,把答案写在题中横线上)
11.-22+13
1
(-= . 12.352)(a a ⋅-= .
13.( )·533186b a ab =.
14.(2x-y)( )=4x 2-y 2. 15.如图3,将300的直角三角板ABC 平移后到BDE 位置(C 、B 、E 在同一条直线上),则∠ADE= 0.
16.式子20122011)5
31()85
(⨯-= . 17.若一个三角形三个内角度数的比为2︰3︰4 则这个三角形是 三角形.
18.如图4,把矩形ABCD 沿EF 对折后使两部分重合,若∠1=50º,则∠AEF= º.
三、小小神算手(共44分)
19.(2×8=16分)计算
(1)(x 2y)·(xy 3) 3; (2)2012222
1
(⨯-+-.
F
E D C B A 图6
20.( 8分)计算:
(1)-x(x 2+xy-1) ; (2) 4(x-y)2
-(2x+y)(-y+2x).
21.(10分)先化简,再求值:
(1)-21a 2bc ·4ab 2c 3,其中a=-1,b=1,c =-2
1; (2)(a+2b)(a-2b)-(2a-b)(-2a-b),其中a=8,b=-8.
22.(10分)已知(m+n)2=7,(m-n)2=3,求下列各式的值:
(1)mn ; (2)m 2+n 2.
四、试试你的说理能力(共52分)
23.(10分)如图5,已知CD ∥AB ,º,求∠BOF 的度数.
24.(10分)如图6,将边长都为2个单位的△ABC 沿边BC 向右平移1个单位得到△DEF ,试求四边形ABFD 的周长.
25.(10分)一副三角板(即△ABC 和△7叠放在一起,求图中∠α的度数.
26.(10分)如图8,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,试判断∠A与∠F之间的关系,并说明理由.
27.(12分)小明与小芳共同计算一道题:(2x+a) (3x+b).由于粗心,小明抄错了第一个多项式中a前面的符号,得结果6x2+11x -10;小芳漏抄了第二个多项式中x的系数,得结果为2x2-9x+10.
(1)你能否知道式子中a,b的值各是多少?
(2)请你算出这道题的正确结果.。
