第四章 3-3 平面的投影
合集下载
3-平面的投影

Z PV PW PV X X Z Z PW
X
O
YW
O PH
YW
O PH
YW
YH 水平面
YH 侧平面
YH 正平面
投影面平行面—总结 投影面平行面 总结
积聚性
a′ ′ b′ ′ c′ a″ c″ ′ ″ ″ b″ ″积聚性Βιβλιοθήκη a实形性b
c
水平面
投影特性: 投影特性: 在它所平行的投影面上的投影反映实形。 在它所平行的投影面上的投影反映实形。 另两个投影面上的投影分别积聚成与相应 的投影轴平行的直线。 的投影轴平行的直线。
侧垂面的迹线表示法 侧垂面的迹线表示法
Z
Z PV X PH
V
S
Sw
β PW α
O YH Z
YW
W
X O
β
Y X YH O
Sw α
YW
投影面垂直面—总结 投影面垂直面 总结
为什么? 为什么 类似形 ? 是什么位置 的平面? ′ 的平面? a′ b′ ′ c′ c″ ′ ″
β
b″ ″ a″ ″
类似形
Z b' B c' a' X a b C c c" A O b" a" b' a' c' a b Y c a"
b"
c"
投影特性: 投影特性: 积聚为一条线,具有积聚性 1) abc 、 a′b′c′ 积聚为一条线,具有积聚性 侧面投影∆ 反映∆ 2) 侧面投影∆ a″b″c″ 反映∆ ABC实形
用迹线表示的 迹线表示的 投影面平行面的投影
(c) 作正垂面
f
e
(d) 作一般位置平面 (有无穷多个) 有无穷多个)
X
O
YW
O PH
YW
O PH
YW
YH 水平面
YH 侧平面
YH 正平面
投影面平行面—总结 投影面平行面 总结
积聚性
a′ ′ b′ ′ c′ a″ c″ ′ ″ ″ b″ ″积聚性Βιβλιοθήκη a实形性b
c
水平面
投影特性: 投影特性: 在它所平行的投影面上的投影反映实形。 在它所平行的投影面上的投影反映实形。 另两个投影面上的投影分别积聚成与相应 的投影轴平行的直线。 的投影轴平行的直线。
侧垂面的迹线表示法 侧垂面的迹线表示法
Z
Z PV X PH
V
S
Sw
β PW α
O YH Z
YW
W
X O
β
Y X YH O
Sw α
YW
投影面垂直面—总结 投影面垂直面 总结
为什么? 为什么 类似形 ? 是什么位置 的平面? ′ 的平面? a′ b′ ′ c′ c″ ′ ″
β
b″ ″ a″ ″
类似形
Z b' B c' a' X a b C c c" A O b" a" b' a' c' a b Y c a"
b"
c"
投影特性: 投影特性: 积聚为一条线,具有积聚性 1) abc 、 a′b′c′ 积聚为一条线,具有积聚性 侧面投影∆ 反映∆ 2) 侧面投影∆ a″b″c″ 反映∆ ABC实形
用迹线表示的 迹线表示的 投影面平行面的投影
(c) 作正垂面
f
e
(d) 作一般位置平面 (有无穷多个) 有无穷多个)
建筑制图与阴影透视 第3版 第4章 点、直线、平面的投影

投影重合为一点 投影反映线段实长
积聚性
ab=AB
a ● b
●
● a ● b
a●
b●
●B
A●
●b a●
直线倾斜于投影面 投影比空间线段短
ab=AB.cos
⒉ 直线在三个投影面中的投影特性
其投影特性取决于直线与三个投影面间的相对位置
正平线(平行于V面)
平行于某一投影面而 与其余两投影面倾斜
投影面平行线 侧平线(平行于W面)
使aaz=aax
ax
a●
解法二:
用圆规直接量
取aaz=aax
a● ax
a●
az
a
●
三、两点的相对位置
两点的相对位置指两点 在空间的上下、前后、左 右位置关系。
判断方法:
上
上
a●
Z ●a
左
右后 前
X
b 下●
o
下 ● b Y
后
左 a● 右
●
b
Y
前
B点在A点之前、 之右、之下。
重影点:
空间两点在某一 投影面上的投影重合 为一点时,则称此两 点为该投影面的重影 点。
① 在其平行的投影面上的投影反映实形,并反映直线与另两投影面倾角的实大。 ② 另两个投影面上的投影平行于相应的投影轴,其到相应投影轴距离反映直线 与它所平行的投影面之间的距离。
读图: 一直线如果有一个投影平行于投影轴,而另有一个投影倾斜时,
它就是一条投影面平行线,平行于该倾斜投影所在的投影面。
投影面平行线的投影特性:
“一斜两直线”, 定是平行线; 斜线在哪面, 平行哪个面(投影面)。
(2)投影面垂直线的投影特性
b’
机械制图 第四章平面的投影

(3)相交两直线;
(4)平行两直线;
(5)任意平面图形。
不 在 同 一 直 线 上 的 三 点
b’
a’ ’
c’ x c a b b’ a’ ’
平 行 两 直 线
一 直 线 和 直 线 外 的 一 个 点
b’
b’
a’ ’
c’ x a b b’ a’ ’ c
相 交 两 直 线
a’ ’
c’ x a b c
面,再将投影面垂直面变为投影面平行面。
例 求△ABC的实形。
分 析 1.先将△ABC变换 为H1面的垂直面; 2.再将△ABC变换 为V2面的平行面。
bH1
bV1
b’
d’
aH1 d H1 dV1 cH1 aV1 cV1
反映△ABC的实形
c’
a’
XV H
c
d
图 4-23
a b
1’
2’
分析: 如ⅠⅡ在P面内 则ⅠⅡ与AB, AC或者 相交; 或者与其中一 条相交而与另一条平
X
a’
3’
b’ a 1 3
c’ 4’
行。
2
b
c
4
图 4-12
直线ⅠⅡ 不在 P面内。
三、平面内的投影面平行线
b’
投影特性
1.符合投影面平行线的 投影特性;
X a a’
e’ d’
c’
2.满足直线在平面内的
第四章 平面的投影
§4-1 平面的表示法
§4-2 各种位置平面的投影
§4-3 平面内的线和点 §4-4 平面图形的实形
(编制 李小平)
§4-1 平面的表示法
一、几何元素表示法
二、迹线表示法
一、几何元素表示法
(4)平行两直线;
(5)任意平面图形。
不 在 同 一 直 线 上 的 三 点
b’
a’ ’
c’ x c a b b’ a’ ’
平 行 两 直 线
一 直 线 和 直 线 外 的 一 个 点
b’
b’
a’ ’
c’ x a b b’ a’ ’ c
相 交 两 直 线
a’ ’
c’ x a b c
面,再将投影面垂直面变为投影面平行面。
例 求△ABC的实形。
分 析 1.先将△ABC变换 为H1面的垂直面; 2.再将△ABC变换 为V2面的平行面。
bH1
bV1
b’
d’
aH1 d H1 dV1 cH1 aV1 cV1
反映△ABC的实形
c’
a’
XV H
c
d
图 4-23
a b
1’
2’
分析: 如ⅠⅡ在P面内 则ⅠⅡ与AB, AC或者 相交; 或者与其中一 条相交而与另一条平
X
a’
3’
b’ a 1 3
c’ 4’
行。
2
b
c
4
图 4-12
直线ⅠⅡ 不在 P面内。
三、平面内的投影面平行线
b’
投影特性
1.符合投影面平行线的 投影特性;
X a a’
e’ d’
c’
2.满足直线在平面内的
第四章 平面的投影
§4-1 平面的表示法
§4-2 各种位置平面的投影
§4-3 平面内的线和点 §4-4 平面图形的实形
(编制 李小平)
§4-1 平面的表示法
一、几何元素表示法
二、迹线表示法
一、几何元素表示法
机械制图习题集答案1-5
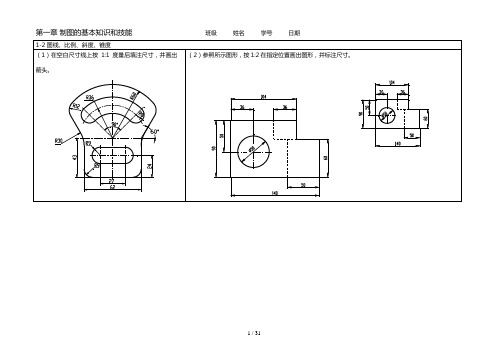
第一章制图的基本知识和技能班级姓名学号日期
第一章制图的基本知识和技能班级姓名学号日期
第一章制图的基本知识和技能班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第四章变换投影面法班级姓名学号日期
第四章变换投影面法班级姓名学号日期
第四章变换投影面法班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
31 / 31。
平面的投影

new
new
r′
r〃
r
例如:在该平面立体中Q 例如:在该平面立体中Q为水平面 ,P为侧垂面,AB为侧平线,CD为 为侧垂面,AB为侧平线,CD ,P为侧垂面,AB为侧平线,CD为 侧垂线. 侧垂线.
new
投影面平行面的投影特性
new
在所平行的投影面上的 投影反映实形, 另外两投影 投影反映实形 , 积聚为直线且平行于相应投 影轴. 影轴.
二,平面内对投影面的最大斜度线. 平面内对投影面的最大斜度线.
平面内垂直于该投影面内任 意一条投影面平行线的直线, 意一条投影面平行线的直线,称 为平面内对相应投影面的最大斜 度线. 度线.
new
平面内对投影面的最大斜度线有三种
1.垂直于平面内水平线的直线,是平面 垂直于平面内水平线的直线, 内对水平面的最大斜度线. 对水平面的最大斜度线. 内对正平面的最大斜度线. 对正平面的最大斜度线. 3.垂直于平面内侧平线的直线,是平面 垂直于平面内侧平线的直线, 对侧平面的最大斜度线. 内对侧平面的最大斜度线.
new
例4-1:已知平面 的两投影,求第三投影. 的两投影,求第三投影.
已知平面的两投影,求第三投影. 例4-1:已知平面的两投影,求第三投影.
new
new
例4-2:找出图中 所标各面的第三投影, 所标各面的第三投影, 并判断它们的空间位置. 并判断它们的空间位置.
1"
new
2"
3" 水平面
例4-9:求三角形ABC对H面的倾角 求三角形ABC对 ABC
new
最大斜度 线实长
最大斜度线 水平投影
ABC对 例4-10:求三角形ABC对V面的倾角 β :求三角形ABC
3平面的投影

●
YH
习题答案
c′ b′ f′
—— P4(3)
p′ m′ s′ Z m″ p″ s″
n′ q′ a′ X b
●
t′
d′
e′ O f e
X mq pn
O
q″
n″ t″ YW
t
s YH
cd a
AB、CD是 相交 线;
PQ、MN是 相交 线;
AB、EF是 平行 线;
CD、EF是 交叉 线;
PQ、ST是 平行 线;
三、用有积聚性的迹线表示特殊位置平面
Z V
(书P25)
PV
Z
PV
X
P
PH
H
PW
W
PW
YW
X PH
Y
O YH
迹线是平面与投影面的交线
铅垂面
Z Z
V
PV
PV PW
P
X PW
X PH
Y
o o
YW
PH
YH
正垂面
Z V RW RV X RH Y YH oo YW Z RW RV X RH
R
水平面
Z Z QV QW
a″
X
O
YW
a
YH
Z
V
b´
B
n´ a´ A
b
b"
W N
a" C n"
c"
a H
n c
若直线在平面上,则该直线必通过平面上的两个已知点或 通过平面上的一个点且平行于平面上某一直线。
Y
例 1: 判定点K是否在平面ΔABC上?
b'
K点不在Δ ABC上
e' a'
第四章点线面的投影 (1)

b′
Δy
ΔΖ
β
Δy α 实长
例2 已知直线AB的H投影及a′,其α为30°,求AB的 V投影。
b'
△Z
△Z
α
例3 已知ab,b′,β=30°,求a′b′。 a′
b′
a′b′
b
60°
a
例4 已知AB实长40㎜,点A距V面30㎜,求ab, 问有几解?
例5 已知AB=40㎜,α=30°,β=45°,求AB的两投影。
用定比关系,如图中的(2)。
三、交叉两直线—既不平行又不相交的两条 直线
( 1)
( 2)
( 3)
投影特性:交叉两直线的投影可能表现为相互平
行,但不可能所有同面投影均平行,如上图中 (1);交叉两直线的投影也可能表现为相交,但 同面投影的交点不是真正交点的投影,不满足投影 规律,如上图示(2)、(3)。
例3
求AB、CD的公垂线(或距离)。 a' n' b' n a(b)
距离
c' m'
d'
c
m d
作业:
P21-28。
§4-6 平面的投影
平面的表示方法 平面的分类及其投影特性
一、平面的表示方法
b' a' b a c c' a' b b' c'
a
不在一条直线 上的三个点
c
直线及直线 外一点
a′ b′
a〞 b〞
a b
若zA > zB ,表示A在B之上。
右图中,A在B的左后上方。
重影点及其可见性判定:
如果空间两点恰好位于某一投影面的一条垂 线上,该两点在该投影面上的投影重合为一点, 则称这两点为对该投影面的重影点。
Δy
ΔΖ
β
Δy α 实长
例2 已知直线AB的H投影及a′,其α为30°,求AB的 V投影。
b'
△Z
△Z
α
例3 已知ab,b′,β=30°,求a′b′。 a′
b′
a′b′
b
60°
a
例4 已知AB实长40㎜,点A距V面30㎜,求ab, 问有几解?
例5 已知AB=40㎜,α=30°,β=45°,求AB的两投影。
用定比关系,如图中的(2)。
三、交叉两直线—既不平行又不相交的两条 直线
( 1)
( 2)
( 3)
投影特性:交叉两直线的投影可能表现为相互平
行,但不可能所有同面投影均平行,如上图中 (1);交叉两直线的投影也可能表现为相交,但 同面投影的交点不是真正交点的投影,不满足投影 规律,如上图示(2)、(3)。
例3
求AB、CD的公垂线(或距离)。 a' n' b' n a(b)
距离
c' m'
d'
c
m d
作业:
P21-28。
§4-6 平面的投影
平面的表示方法 平面的分类及其投影特性
一、平面的表示方法
b' a' b a c c' a' b b' c'
a
不在一条直线 上的三个点
c
直线及直线 外一点
a′ b′
a〞 b〞
a b
若zA > zB ,表示A在B之上。
右图中,A在B的左后上方。
重影点及其可见性判定:
如果空间两点恰好位于某一投影面的一条垂 线上,该两点在该投影面上的投影重合为一点, 则称这两点为对该投影面的重影点。
《机械制图》习题3
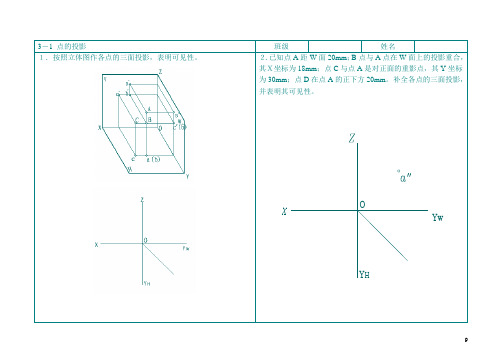
3-2直线的投影
班级
姓名
1.根据下列直线的两面投影,判断直线对投影面的相对位置(填空),作出直线的第三投影,并在直观图中标出对应直线的题号(填空)和符求一点C,使AC:CB=5:2,作出点C的投影。
3.过点A做正平线AB,使倾角α=30°,AB=30mm,有几解?作出其中一解。
班级
姓名
1.根据平面图形的两个投影,求作它的第三投影,并判断平面的空间位置。
(1) (2) (3)
2.已知正垂面P与H面倾角为30°,作出V、W面投影。
3.包含直线AB作一个正方形,使它垂直于H面。
3-3平面的投影
班级
姓名
4.注全平面P、Q和直线AB、CD的三面投影,并根据它们对投影面的相对位置填空。
3-1点的投影
班级
姓名
1.按照立体图作各点的三面投影,表明可见性。
2.已知点A距W面20mm;B点与A点在W面上的投影重合,其X坐标为18mm;点C与点A是对正面的重影点,其Y坐标为30mm;点D在点A的正下方20mm。补全各点的三面投影,并表明其可见性。
3-1点的投影
班级
姓名
3.已知A、B、C各点对投影面的距离,作各点的三面投影。
4.已知点的坐标,作点的三面投影。
⑴A(25,10,20)﹑B(10,20,20)
⑵C(20,15,25)﹑B(20,10,15)
3-1点的投影
班级
姓名
5.已知点的三面投影,判断它们的相对位置(上下、左右、前后),并填空。
点A在点B之()、()、()
6.已知立体上三点ABC的两个投影,求第三投影,并比较它们坐标大小。
4.已知水平线AB在H面上方20mm,求作它的其余两面投影,并在该直线上取一点K,使AK=20mm。
班级
姓名
1.根据下列直线的两面投影,判断直线对投影面的相对位置(填空),作出直线的第三投影,并在直观图中标出对应直线的题号(填空)和符求一点C,使AC:CB=5:2,作出点C的投影。
3.过点A做正平线AB,使倾角α=30°,AB=30mm,有几解?作出其中一解。
班级
姓名
1.根据平面图形的两个投影,求作它的第三投影,并判断平面的空间位置。
(1) (2) (3)
2.已知正垂面P与H面倾角为30°,作出V、W面投影。
3.包含直线AB作一个正方形,使它垂直于H面。
3-3平面的投影
班级
姓名
4.注全平面P、Q和直线AB、CD的三面投影,并根据它们对投影面的相对位置填空。
3-1点的投影
班级
姓名
1.按照立体图作各点的三面投影,表明可见性。
2.已知点A距W面20mm;B点与A点在W面上的投影重合,其X坐标为18mm;点C与点A是对正面的重影点,其Y坐标为30mm;点D在点A的正下方20mm。补全各点的三面投影,并表明其可见性。
3-1点的投影
班级
姓名
3.已知A、B、C各点对投影面的距离,作各点的三面投影。
4.已知点的坐标,作点的三面投影。
⑴A(25,10,20)﹑B(10,20,20)
⑵C(20,15,25)﹑B(20,10,15)
3-1点的投影
班级
姓名
5.已知点的三面投影,判断它们的相对位置(上下、左右、前后),并填空。
点A在点B之()、()、()
6.已知立体上三点ABC的两个投影,求第三投影,并比较它们坐标大小。
4.已知水平线AB在H面上方20mm,求作它的其余两面投影,并在该直线上取一点K,使AK=20mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b'
a'
B
b"
A
a"
C
b c a
c"
(2) 物体上平面的投影分析
s' s"
a' a s
c' a" (c") c
为侧垂面 为一般位置平面 为一般位置平面 为水平面
2. 投影面垂直面的投影特性
(1) 投影面垂直面的投影特性
(2) 物体上垂直面的投影分析
(1) 投影面垂直面的投影特性
γ α YW β γ YH YH
b'1 b'1 α B1 b1 b1 α
(a)
(b)
[例题7] 平面的旋转
(三)不指明轴旋转法
1. 问题的提出
2. 不指明轴旋转法
[例题8]
[例题9]
3. 总可定出旋转轴
[例题10]
[例题8] 平面的旋转b'
n'
1
n'1 c'1
两个图形 十分靠近或 重叠,影响 图形的清晰 度。
n
b1 n1 c1
§4.5 平面的投影
一、平面的表示法 二、平面的投影
三、各种位置平面的投影特性
四、例题
一、平面的表示方法
a' c' c'
a' c' b' b' c a b (b) b (c)
a'
b'
a'
d' c' b'
b'
c a b (a) c
a'
c' a a c b
c a d
(d)
(e)
二、平面的投影
E
F M
H
β
α
YW
(2) 物体上垂直面的投影分析
3. 投影面平行面的投影特性
(1) 投影面平行面的投影特性
(2) 物体上垂直面的投影分析
(1) 投影面平行面的投影特性
(2) 物体上平行面的投影分析
投影面平行面的投影特性: 在平面所平行的投影面上,其投影反映实形;其余两个投影积聚成直线且分别平行于 相应的投影轴。
§4.7 平面上的直线和点
一、平面上的直线
二、平面上的点
三、投影面垂直面上的点和直线
一、平面上的直线
1. 平面上的直线
2. 在平面上作正平线和水平线
1. 平面上的直线
D B
C M
A
N
2. 在平面上作正平线和水平线
e'
d'
e d
二、平面上的点
1. 平面上的点
2. 例题
1. 平面上的点
D B
a'1 c'1 b'1
c1
b1
θ θ
a1
θ
(二)几何元素在轴所垂直的投影面上的投影,旋转 前后的形状和大小不变。
当线段和平面图形绕垂直于某一投影面的轴旋转时, 它们对该投影面的夹角不变。因此,它们在该投影面上投 影的形状和大小不变。
[例题6] [例题7] 旋转轴通过端点A 平面的旋转
[例题6] 旋转轴通过端点A
R
R
m'1
θ
l' R
θ
l'
m'1
θ
L
M1
m1 l l (a) (b)
m1
[例题3] 点绕铅垂轴旋转
l' m'1 L θ M1 l' m'1
R
R R θ l m1
θ
l
m1
(a)
(b)
三、直线和平面的旋转
(一)旋转必须遵循“三同”原则
(二)几何元素在轴所垂直的投影面上的投影,旋转前后 的形状和大小不变。 (三)不指明轴旋转法
b' n' a' a'1 b'1 n'1 c'1
c'
a1
b n
a
b1 n1 c1
c
[例题15] 一般位置平面旋转为水平面
b'1 n' a'1 c'1 n'1 b'2 a'2 c'2
a1
a2
n
b1 n1 c1
b2 c2
[例题16] 求两平面之间的夹角
b'1 b'2
c'1
c'2 d'1 a'1 a'2 c1 c2 d'2
(一)旋转必须遵循“三同”原则
线段和平面图形都是由若干个相距一定位置的点所组 成,为了保证它们之间的相对位置旋转时保持不被改变, 必须遵循:绕同一根轴,向同一方向和旋转同一角度的“ 三同”原则。
[例题4] [例题5] 线段的旋转 平面的旋转
[例题4] 线段的旋转
a'1
b'1
θ
a1 b1 θ
[例题5] 平面的旋转
a"
y
a y
§4-8
旋转法——绕投影面垂直轴旋转
一、旋转法的基本概念
二、点旋转时的投影变换规律
三、直线和平面的旋转 四、四个基本问题
一、旋转法的基本概念
旋转法就是投影面保持不动,使空间几何元素绕某一 轴旋转,旋转到有利于解题的位置。
[例题1] 平面旋转为正平面
[例题1 ]
△ABC旋转为正平面
c'1
a1
b1 a2b2 d2
d1
[例题17] 旋转点D至平面ABC上
e' d'1 L
f'
E D1
F e d1 f
本章结束
C1
c1
二、点旋转时的投影变换规律
当点绕垂直于某一投影面的轴旋转时,点在该投影面 上的投影,作以轴的投影为圆心和以旋转半径为半径的圆 周运动;而在另一投影面上的投影,则作直线运动,且该 直线必垂直于轴在该投影面上的投影。
[例题2] [例题3] 点绕正垂轴旋转 点绕铅垂轴旋转
[例题2] 点绕正垂面旋转
d a b
c d(a) e m f c(b) a
d b
c
(a)
(b)
(c)
三、 各性
2. 投影面垂直面的投影特性
3. 投影面平行面的投影特性
1. 一般位置平面的投影特性
(1) 一般位置平面的投影特性
(2) 物体上平面的投影分析
(1) 一般位置平面的投影特性
例题15
[例题16] [例题17] 求两平面之间的夹角 旋转点D至平面ABC上
[例题11] 直线绕铅垂轴旋转
l'
l'
L
b'1 α α b1 l
b'1
α
B1
b1
l
[例题12] 直线绕正垂轴旋转
b'1 l'
b1 l
[例题13] 一般位置线段旋转为铅垂线
a'1 l'
b'1
l'1
b1
a1
l
l1
[例题14] 把一般位置平面变为投影面垂直面
F
[例题15] 设在四棱台前侧面BCED上有一点A。已知它的水平 投影a,求正面投影a'。
b'
a' f' a'
f'
a f
f
a
三、投影面垂直面上的点和直线
1. 投影面垂直面上的点和直线
2. 例题
1. 投影面垂直面上的点和直线
QH PH
PH
PH
[例题16] 给出两坡顶屋面上一点A的V投影a',求a和a"。
[例题9] 不指明轴旋转法
b'1 a'1 n'1 c'1
a1
n b1 n1 c1
[例题10] 总可定出旋转轴
l'
l
四、四个基本问题
(一) 把一般位置直线旋转为投影面平行线 例题11 例题12
(二) 把一般位置直线旋转为投影面垂直线
例题13 (三)把一般位置平面旋转为投影面垂直面 例题14 (四)把一般位置平面旋转为投影面平行面
a'
B
b"
A
a"
C
b c a
c"
(2) 物体上平面的投影分析
s' s"
a' a s
c' a" (c") c
为侧垂面 为一般位置平面 为一般位置平面 为水平面
2. 投影面垂直面的投影特性
(1) 投影面垂直面的投影特性
(2) 物体上垂直面的投影分析
(1) 投影面垂直面的投影特性
γ α YW β γ YH YH
b'1 b'1 α B1 b1 b1 α
(a)
(b)
[例题7] 平面的旋转
(三)不指明轴旋转法
1. 问题的提出
2. 不指明轴旋转法
[例题8]
[例题9]
3. 总可定出旋转轴
[例题10]
[例题8] 平面的旋转b'
n'
1
n'1 c'1
两个图形 十分靠近或 重叠,影响 图形的清晰 度。
n
b1 n1 c1
§4.5 平面的投影
一、平面的表示法 二、平面的投影
三、各种位置平面的投影特性
四、例题
一、平面的表示方法
a' c' c'
a' c' b' b' c a b (b) b (c)
a'
b'
a'
d' c' b'
b'
c a b (a) c
a'
c' a a c b
c a d
(d)
(e)
二、平面的投影
E
F M
H
β
α
YW
(2) 物体上垂直面的投影分析
3. 投影面平行面的投影特性
(1) 投影面平行面的投影特性
(2) 物体上垂直面的投影分析
(1) 投影面平行面的投影特性
(2) 物体上平行面的投影分析
投影面平行面的投影特性: 在平面所平行的投影面上,其投影反映实形;其余两个投影积聚成直线且分别平行于 相应的投影轴。
§4.7 平面上的直线和点
一、平面上的直线
二、平面上的点
三、投影面垂直面上的点和直线
一、平面上的直线
1. 平面上的直线
2. 在平面上作正平线和水平线
1. 平面上的直线
D B
C M
A
N
2. 在平面上作正平线和水平线
e'
d'
e d
二、平面上的点
1. 平面上的点
2. 例题
1. 平面上的点
D B
a'1 c'1 b'1
c1
b1
θ θ
a1
θ
(二)几何元素在轴所垂直的投影面上的投影,旋转 前后的形状和大小不变。
当线段和平面图形绕垂直于某一投影面的轴旋转时, 它们对该投影面的夹角不变。因此,它们在该投影面上投 影的形状和大小不变。
[例题6] [例题7] 旋转轴通过端点A 平面的旋转
[例题6] 旋转轴通过端点A
R
R
m'1
θ
l' R
θ
l'
m'1
θ
L
M1
m1 l l (a) (b)
m1
[例题3] 点绕铅垂轴旋转
l' m'1 L θ M1 l' m'1
R
R R θ l m1
θ
l
m1
(a)
(b)
三、直线和平面的旋转
(一)旋转必须遵循“三同”原则
(二)几何元素在轴所垂直的投影面上的投影,旋转前后 的形状和大小不变。 (三)不指明轴旋转法
b' n' a' a'1 b'1 n'1 c'1
c'
a1
b n
a
b1 n1 c1
c
[例题15] 一般位置平面旋转为水平面
b'1 n' a'1 c'1 n'1 b'2 a'2 c'2
a1
a2
n
b1 n1 c1
b2 c2
[例题16] 求两平面之间的夹角
b'1 b'2
c'1
c'2 d'1 a'1 a'2 c1 c2 d'2
(一)旋转必须遵循“三同”原则
线段和平面图形都是由若干个相距一定位置的点所组 成,为了保证它们之间的相对位置旋转时保持不被改变, 必须遵循:绕同一根轴,向同一方向和旋转同一角度的“ 三同”原则。
[例题4] [例题5] 线段的旋转 平面的旋转
[例题4] 线段的旋转
a'1
b'1
θ
a1 b1 θ
[例题5] 平面的旋转
a"
y
a y
§4-8
旋转法——绕投影面垂直轴旋转
一、旋转法的基本概念
二、点旋转时的投影变换规律
三、直线和平面的旋转 四、四个基本问题
一、旋转法的基本概念
旋转法就是投影面保持不动,使空间几何元素绕某一 轴旋转,旋转到有利于解题的位置。
[例题1] 平面旋转为正平面
[例题1 ]
△ABC旋转为正平面
c'1
a1
b1 a2b2 d2
d1
[例题17] 旋转点D至平面ABC上
e' d'1 L
f'
E D1
F e d1 f
本章结束
C1
c1
二、点旋转时的投影变换规律
当点绕垂直于某一投影面的轴旋转时,点在该投影面 上的投影,作以轴的投影为圆心和以旋转半径为半径的圆 周运动;而在另一投影面上的投影,则作直线运动,且该 直线必垂直于轴在该投影面上的投影。
[例题2] [例题3] 点绕正垂轴旋转 点绕铅垂轴旋转
[例题2] 点绕正垂面旋转
d a b
c d(a) e m f c(b) a
d b
c
(a)
(b)
(c)
三、 各性
2. 投影面垂直面的投影特性
3. 投影面平行面的投影特性
1. 一般位置平面的投影特性
(1) 一般位置平面的投影特性
(2) 物体上平面的投影分析
(1) 一般位置平面的投影特性
例题15
[例题16] [例题17] 求两平面之间的夹角 旋转点D至平面ABC上
[例题11] 直线绕铅垂轴旋转
l'
l'
L
b'1 α α b1 l
b'1
α
B1
b1
l
[例题12] 直线绕正垂轴旋转
b'1 l'
b1 l
[例题13] 一般位置线段旋转为铅垂线
a'1 l'
b'1
l'1
b1
a1
l
l1
[例题14] 把一般位置平面变为投影面垂直面
F
[例题15] 设在四棱台前侧面BCED上有一点A。已知它的水平 投影a,求正面投影a'。
b'
a' f' a'
f'
a f
f
a
三、投影面垂直面上的点和直线
1. 投影面垂直面上的点和直线
2. 例题
1. 投影面垂直面上的点和直线
QH PH
PH
PH
[例题16] 给出两坡顶屋面上一点A的V投影a',求a和a"。
[例题9] 不指明轴旋转法
b'1 a'1 n'1 c'1
a1
n b1 n1 c1
[例题10] 总可定出旋转轴
l'
l
四、四个基本问题
(一) 把一般位置直线旋转为投影面平行线 例题11 例题12
(二) 把一般位置直线旋转为投影面垂直线
例题13 (三)把一般位置平面旋转为投影面垂直面 例题14 (四)把一般位置平面旋转为投影面平行面
