4第四章-平面的投影PPT课件
合集下载
机械制图课件-4平面的投影
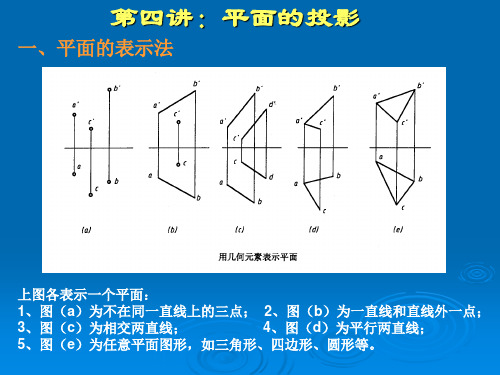
四、平面上的直线和点
点和直线在平面上的几何条件是: (1)点在平面上,则该点必定在这个平面的一条直线上。 (2)直线在平面上,则该直线经过这个平面上的两个点;或者
通过这个平面上的一个点,且平行于这个平面上的另一直线。
如图所示,相交两直线AB、AC确定一平面P,点K取自 直线AB,所以点K必在平面P上。
(2)水平面
平行于H面,对V,W面垂直。
水平面的投影特性: 1、在平面所平行的H投影面上的投影反映平面图形的实形。 2、另外V、W面两投影都积聚成直线;并平行于相应的投影轴。
(3)侧平面
平行于W面,对H,V面垂直。
侧平面的投影特性: 1、在平面所平行的W投影面上的投影反映平面图形的实形。 2、另外H、V面两投影都积聚成直线;并平行于相应的投影轴。
垂直于V面,与H、W面倾斜。
投影特性: 1、平面在所垂直的投影面V面上的投影积聚为一斜直线,该投影与 投影轴的夹角分别反映平面与H、W面的真实倾角α、γ; 2、平面的H、W面投影均为类似形。
⑵铅垂面 垂直于H面,与V、W面倾斜
投影特性: 1、平面在所垂直的投影面H面上的投影积聚为一斜直线,该投影 与投影轴的夹角分别反映平面与H、W的真实倾角β、γ。 2、平面的V、W面投影均为类似形。
a ●
b● X
k●
d ● c
●
O
b●
c
k●
●●
a●
d
例4 已知三棱锥SAB面上一点K的V投影k′,试求 其H投影k
过k′作s′m′;求出sm(直线SM称辅助线,用细实线绘制); 在sm上求出k 。 或者过k′作k′m′∥s′a′;由m′求出m; 过m作直线平行于sa;在该直线上求出k。
例5 补全平面图形PQRST的两面投影
平面的投影PPT课件

(一)平面上的点和直线 (二)平面上的特殊直线 (三)例 题
V
b´
B
n´
a´
N
XA
b
an
H
Z
b"
W
n" a" C c"
c
Y
第15页/共31页
(一)平面上的点和直线的几何条件
1、点在平面上的几何条件: 若点在平面上,则该点必定位于平面上的某一直线上。反之,若一点位于平面上
的某一直线上,则该点必定位于平面上。
V
Z SV
Z SV
β SW
X
SW
X
S OW
α
O
YW
H
SH
Y
SH
YH
第11页/共31页
投影面平行面——水平面
V
z
a′
A
b′ c′
b″
B
a″
cW″
x
C
O
a
b
z a ′ b ′ c ′ b a ″ c ″
″
X
o
YW
b
a
c
H
Y
c YH
水平面的投影特性:
1、a′b′c′、a″b″c″积聚为一条线,具有积聚性。
c d
2、平面上对投影面的最大倾斜线
平面内与某一投影面成最大倾角的直线,称为 平面上对该投影面的最大倾斜线。在平面内有无 数条最大倾斜线,是一组互相平行的直线。
最大倾斜线的投影特性:
E
1.对投影面倾角最大的直线;
A
2.最大倾斜线垂直于平面内的
P
F
投影面平行线;
θ
3.平面对投影面的夹角等于平
画法几何课件第四章平面的投影及投影变换应用

§4-3 平面内的直线和点
一、直线在平面内的几何条件 二、平面内的一般位置直线
三、平面内的投影面平行线
四、平面内对投影面的最大斜度线 五、平面内的点
§4-1 平面的表示法
一、直线在平面内的几何条件
通过一平面上的两个点;
通过平面上一点同时又平行该平面上另一直线。
M N
平行
§4-1 平面的表示法
Z
V
Z
X
O
PW
YW
P
X o
PW
Y
PH
YH
PH
§4-1 平面的表示法
二、投影面平行面
3.侧平面 投影特点: W 投影反映实形;
H 投影和 V 投影积聚为直线; 积聚投影垂直于OX 轴。
V
Z
实形
Z
X
o Y
X
O
YW
YH
§4-1 平面的表示法
二、投影面平R RV
X
Z
RV
O
X
o
a‟ c‟
迹线表示平面
a‟ 30° x o
b‟ x
d‟
30°
RV
o
d b a c
§4-1 平面的表示法
RH
a
一、投影面垂直面
例2 包含AB(ab,a‟b‟ )作铅垂面。
b‟
a‟
X
c‟ b c O
a
§4-1 平面的表示法
一、投影面垂直面
例3 完成侧垂面的水平投影。
1„ 2„ Z 1“ 2“ 3„ 6„ 1 2 4 3
投影分析:
侧垂面 注意:
4„
X 5„
4“ 3“
5“ 6“ YW
V、H 投影的
机械制图-平面的投影 ppt课件

ppt课件
19
平面上取点的方法:首先面上取线
例:已知K点在平面ABC上,求K点的水平投影。
b d
●
k
c
a'
b
d
a
●k
c
通过在面内作辅助线(细实线)求解
ppt课件
20
例:已知ABC给定一平面,试判断点D是否属
于该平面。
b
b
e d c
d e
c
a
a
c a
ed
b
点D不属于平面ApBptC课件
c a de
d' a'
BC为水平线 b'c'//OX
1'
b'
a 1
b
c' d
c
ppt课件
26
例:已知ABC 给定一平面,试过点C 作属于该平面的 正平线,过点A作属于该平面的水平线。
m a
b
k n
c
正平线上的点Y坐 标相同,水平线上 的点Z坐标相同, 交点K是既满足Y坐 标又满足Z坐标的 点。
b
m
k
n
c
ppt课件
四、平面上的直线和点 1、平面上取任意直线
在平面内取 直线的方法
定理一
若一直线过平面上的 两点,则此直线必在 该平面内。
定理二
若一直线过平面上的一点, 且平行于该平面上的另一 直线,则此直线在该平面 内。
ppt课件
16
例:已知平面由直线AB、AC所确定,试在平面 内任作一条直线。
解法一
m a
根据定理一
28
立 体 图
正垂面
铅垂面
侧垂面
γ
《平面的投影》课件

平面的投影
这份PPT课件将帮助您全面了解平面的投影,包括它的定义、分类、特点、 投影方法、应用场景和错误类型等内容。
什么是投影?
投影的定义
投影是指由于光线或任何其他射线在遇到物体 后向另一个表面传导所形成的图形。
常见的投影方式
包括平面投影、立体投影、透视投影、等角投 影等。这里我们重点介绍平面投影。
投影中的错误
1
投影中常见的错误
包括形状、尺寸、位置、比例和方向等方面,容易导致误解或产生错误的结果。
2
如何避免投影中的错误
遵循标准规范,加强沟通和理解,注重细节,确保投影结果准确无误。
结语
总结
本课程介绍了平面投影的定义、分类、特点、投影 方法、应用场景和错误类型。了解平面投影对提高 工作效率和准确性十分必要。
学习平面投影重要性
针对工程制图、建筑设计和工业生产等行业,掌握 平面投影技术可以提高工作效率和准确性,具有十 分重要的价值。
3 正交投影的应用举例
建筑设计、机械加工图、工程制图等领域广泛应用。
斜投影
斜投影的特点 斜投影的投影方法
斜投影的应用举例
图形投影后有较强的视觉效果,与投影方向有关。
平移图形使其重心处于投影平面上,之后向该平 面引垂线,再由垂线顶点进行投影,得到图形的 斜投影。 室内设计、漫画插画、动画制作等领域中常见。
平面的投影
பைடு நூலகம்
平面投影的定义
当一个平面被光源所照射,它在投影平面上所成的 图形称为该平面的平面投影。
平面投影的分类
包括正交投影和斜投影两种。
正交投影
1 正交投影的特点
图形投影后呈现平行四边形或矩形,与投影方向无关。
2 正交投影的投影方法
这份PPT课件将帮助您全面了解平面的投影,包括它的定义、分类、特点、 投影方法、应用场景和错误类型等内容。
什么是投影?
投影的定义
投影是指由于光线或任何其他射线在遇到物体 后向另一个表面传导所形成的图形。
常见的投影方式
包括平面投影、立体投影、透视投影、等角投 影等。这里我们重点介绍平面投影。
投影中的错误
1
投影中常见的错误
包括形状、尺寸、位置、比例和方向等方面,容易导致误解或产生错误的结果。
2
如何避免投影中的错误
遵循标准规范,加强沟通和理解,注重细节,确保投影结果准确无误。
结语
总结
本课程介绍了平面投影的定义、分类、特点、投影 方法、应用场景和错误类型。了解平面投影对提高 工作效率和准确性十分必要。
学习平面投影重要性
针对工程制图、建筑设计和工业生产等行业,掌握 平面投影技术可以提高工作效率和准确性,具有十 分重要的价值。
3 正交投影的应用举例
建筑设计、机械加工图、工程制图等领域广泛应用。
斜投影
斜投影的特点 斜投影的投影方法
斜投影的应用举例
图形投影后有较强的视觉效果,与投影方向有关。
平移图形使其重心处于投影平面上,之后向该平 面引垂线,再由垂线顶点进行投影,得到图形的 斜投影。 室内设计、漫画插画、动画制作等领域中常见。
平面的投影
பைடு நூலகம்
平面投影的定义
当一个平面被光源所照射,它在投影平面上所成的 图形称为该平面的平面投影。
平面投影的分类
包括正交投影和斜投影两种。
正交投影
1 正交投影的特点
图形投影后呈现平行四边形或矩形,与投影方向无关。
2 正交投影的投影方法
点直线平面的投影课件

直线的投影
根据直线的方向和投影角度,确定 其在平面上的投影线。
点的轨迹
当点在直线上移动时,其在平面上 的投影点的轨迹形成一条直线。
直线与平面的投影问题解析
直线与平面的交点
根据直线的方向和平面的法线, 确定直线与平面的交点。
平面与直线的交线
根据平面的法线和直线的方向, 确定平面与直线的交线。
直线与平面的夹角
平行关系
如果直线与平面平行,则 它们的投影也平行。
点与平面的投影性 质
点与平面的相对位置关系
垂直关系
点与平面的相对位置关系可以通过其 投影在平面上的位置关系来反映。
如果点与平面垂直,则它们的投影也 垂直。
投影的特性
点与平面在空间中的位置关系,可以 通过其投影在平面上的位置关系来反 映。
03
点、直线和平面的投影应用
感谢观看
点在直线上的投影应用
确定点的投影
通过连接直线上的两个点,与投 影面交于一点,即为该点的投影。
判断点的位置
根据投影点和直线之间的关系, 判断点是否在直线上或与直线平行。
直线在平面上的投影应用
确定直线的投影
选择直线上的两个点,与投影面连接,得到直线的投影。
判断直线的位置
根据投影线与平面的交点或平行关系,判断直线是否在平面 上或与平面平行。
01
02
03
点的投影
点在空间中确定后,其投线在空间中确定后,其 投影在平面上也唯一确定。
投影的特性
点与直线在空间中的位置 关系,可以通过其投影在 平面上的位置关系来反映。
直线与平面的投影性质
平面的投影
平面在空间中确定后,其 投影在平面上也唯一确定。
投影的特性
机械制图第四节平面的投影课件
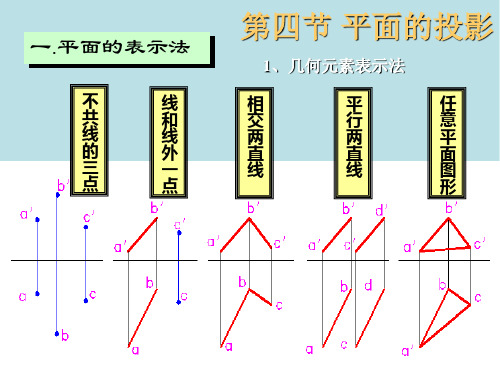
铅垂面
正垂面
侧垂面
2 投影面垂直面
投影特性
α
γ
β
α
2 另外两个投影均为类似形.
3、一般位置平面
1三个投影均为类似形,不反映实形。 2不反映该平面对投影面的倾角。
2.平面表示法--迹线表示法
平面与投影面的交线称为平面的Leabharlann 线OXPV
PH
P
R
水平面
正平面
用迹线表示特殊平面
PH
PV
α
γ
铅垂面
侧平面
实形
平行于OX轴
平行于OY轴
正平面
1 投影面平行面
水平面
正平面
侧平面
实形
平行于OX轴
平行于OZ轴
侧平面
1 投影面平行面
水平面
正平面
侧平面
实形
平行于OY轴
平行于OZ轴
1投影面平行面
水平面
正平面
侧平面
另外两个投影积聚成直线且平行于相应的投影轴.
在所平行的投影面上的投影反映实形;
投影特性
特殊面内取点、取线
只要点或线的投影落在面有积聚性的投影上,则点或线就在面内
利用面的积聚性
例:补全平面多边形的正面投影(cd∥ef)
c'
1
g'
注意利用CD与EF的平行关系
问题实质:在平面DEF内求两点C、G
3、过已知点、线作平面
一般面有无数个
投影面垂直面要限定角度
投影面平行面只有一个
例:在平面内ABC内找一点K,使它距H面25mm,距V面20mm
不共线的三点
线和线外一点
相交两直线
平行两直线
正垂面
侧垂面
2 投影面垂直面
投影特性
α
γ
β
α
2 另外两个投影均为类似形.
3、一般位置平面
1三个投影均为类似形,不反映实形。 2不反映该平面对投影面的倾角。
2.平面表示法--迹线表示法
平面与投影面的交线称为平面的Leabharlann 线OXPV
PH
P
R
水平面
正平面
用迹线表示特殊平面
PH
PV
α
γ
铅垂面
侧平面
实形
平行于OX轴
平行于OY轴
正平面
1 投影面平行面
水平面
正平面
侧平面
实形
平行于OX轴
平行于OZ轴
侧平面
1 投影面平行面
水平面
正平面
侧平面
实形
平行于OY轴
平行于OZ轴
1投影面平行面
水平面
正平面
侧平面
另外两个投影积聚成直线且平行于相应的投影轴.
在所平行的投影面上的投影反映实形;
投影特性
特殊面内取点、取线
只要点或线的投影落在面有积聚性的投影上,则点或线就在面内
利用面的积聚性
例:补全平面多边形的正面投影(cd∥ef)
c'
1
g'
注意利用CD与EF的平行关系
问题实质:在平面DEF内求两点C、G
3、过已知点、线作平面
一般面有无数个
投影面垂直面要限定角度
投影面平行面只有一个
例:在平面内ABC内找一点K,使它距H面25mm,距V面20mm
不共线的三点
线和线外一点
相交两直线
平行两直线
4第四章 平面的投影
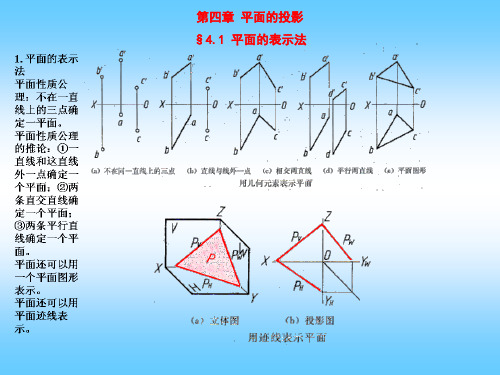
三、将一般位置平面变换成投影面平行面(需经二次变换,先变换成投影面垂直面, 再变换成投影面平行面)
例:已知△ 的两面投影,在△ 平面内取一点 ,使它到 、 两点等距,到 边的距离 。
四、用平面图形上被保留的投影面的平行线作投影面垂直面的实形
用换面法作正垂面的真形
用平面图形上被保留的投影 面平行线作正垂面的真形
Q
C
投影特性:(1) abc 积聚为一条线 (2) abc、 abc为 ABC的类似形 (3) abc与OX、 OZ的夹角反映α、 角的真实大小
b
侧垂面的投影
b' S B SW b" a' c"
b"
β
c'
a"
C A
c"
b
a" c
a
投影特性: (1) abc积聚为一条线 (2) abc、 abc为 ABC的类似形 (3) abc与OZ、 OY的夹角反映α、β角的真实大小
处于投影面平行面位置的迹线平面的投影特性: a.在平行的投影面上无迹线; b.在另外两个投影面上的迹线有积聚性,且平行于相应投影轴。
[例]等边三角形 是侧平面,已知点 的 面和 面投影, 与 面的倾角α °, 的方向为向上、向前,真长 为 ,点 在 的前下方,作出△ 的三面投影。
§4.3 平面上的点和直线 一、平面内的点和直线应满足下列几何条件: ①若点位于平面内的任一直线上,则此点在该平面上;②若一直线通过平面内的 两个点,或一直线通过平面上一已知点且平行于平面内的另一直线,则此直线必 在该平面内。
处于投影面垂直面位置的迹线平面的投影特性: a.在所垂直的投影面上的迹线有积聚性,它与投影轴的夹角分别反映平面对另两个投影 面的真实倾角; b.在另外两个投影面上的迹线,分别垂直于相应的投影轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021
第四章 平面
§4-1 平面的表示法
§4-2 各种位置平面的投影特性
§4-3 属于平面的点和直线
2021
§4-1 平面的客观形态
一、以几何元素呈现的平面
用几何元素表示平面有五种形式:不在同一直线上 的三点;直线及外一点;相交二直线;平行二直线;任 意平面图形本身。
二、以迹线呈现的平面
平面的迹线为空间平面与投影面的交线。特殊位置 平面其具有积聚性的投影与其同面迹线是一致的。
2021
1 取属于垂直面的点和直线(1)
b
2
e k
f
m
g
n
c
3
a
1
a k
e
K属于ABC
b
c
2
3
ⅡⅢ MN不属于ⅠⅡⅢ
几何元素表示平面
1 取属于垂直面的点和直线
b a
PH a b
2021
e f RV
f e
2021
2 过一般位置直线总可作投影面的垂直面
V
a
A
b
BP
正垂面的迹线表示法
V QV W Q
2021
QV γ α
H
3 、侧垂面
V
S B
b
SW
b
W a
2021
b c β c
α a
c
C
a
A
H
b c
a 投影特性:1、 abc积聚为一条线
2 、 abc、 abc为 ABC的类似形 3 、 abc与OZ、 OY的夹角反映α、β角的真实大小
侧垂面的迹线表示法
V S
取属于平面的点和直线
B
F
E
2021
b e
f
d c
a
D
C
c
a
A
d
f
e
b
取属于定平面的直线,要经过属于该平面的已知两点;或经过属 于该平面的一已知点,且平行于属于该平面的一已知直线。
2021
例题 已知 ABC给定一平面,试判断点D是否属于该平面。
b
e d c
a
c a
e
d
b
例题2 已知点D在 ABC上,试求点D的2021水平投影 。
B
b
A
b a
a C c
c
2021
b a
b
b
a
c
c
c a
投影特性:1、abc、abc 、abc 均为 ABC的类似形 2、不反映、、 的真实角度
2021
§4-3 属于平面的点和直线
一、属于一般位置平面的点和直线 二、属于特殊位置平面的点和直线 三、属于平面的投影面平行线 四、属于平面的最大斜度线
一、属于一般位置平面的点和直线 2021
2021
(1) 过正垂线作平面 (迹线表示法)
m(n)
n
m(n)
PV
m (n)
SV
m (n )
QV
RV
n
n
n
m
m
m
m
(2) 过正平线作平面
e
e
f
2021
SH e f
e
f
f
g
g
2、迹线的空间位置特点 平面迹线 既属于平面,又属于投影面。
3、迹线的投影特点 迹线的一个投影 即其本身,其余投影在投影轴上。
4、平面迹线的作图 先作出平面内 任意两直线的迹点,再连接其同名 迹点即平面的同面迹线,注意利用 迹线共点。
特殊位置平面用具有积聚性的 迹线表示。
m2
2021
迹线平面与几何平面的转换
b
e d
c
a
a
c
d e
b
2021
例题 已知点E在 ABC上,试求点E的正面投影 。
b
e
d
c
a
a
c
d
e
b
2021
二、属于特殊位置平面的点和直线
1 取属于垂直面的点和直线 2 过一般位置直线总可作投影面的垂直面 (1) 几何元素表示法 (2) 迹线表示法 3 过特殊位置直线作平面 (1) 过正垂线作平面 (2) 过正平线作平面
ba
投影特性:
1、abc 、 abc 积聚为一条线,具有积聚性 2 、正平面投影abc反映 ABC实形
3 、 侧平面
V
c
B
b
b
b
W
a
a
A
a
c
a
bC
c
a
Hc
b
2021
b a
c
投影特性:
c
1、 abc 、 abc 积聚为一条线,具有积聚性
2 、 侧平面投影abc 反映 ABC实形
三、一般位置平面
b
a
一、用几何元素表示平面
b
b
2021
b
a c
a c
b
a d
b
b ad
a c
a c
b
a c
a c
b
b
a
c
c
c
a
c
b
二、平面的迹线表示法
V
PV
P
H PH
V
QV
Q H QH
2021
PV PH QV
QH
一般位置平面的迹线求法
n1 PV n2
b′ c′
a′ Px
m1 a b c
PH
Px —— 迹线集合点
1、平面迹202线1 的定义 平面的迹线是 平面与投影面的交线。平面P与H投 影面的交线称作平面的水平迹线, 用PH表示;平面P与V投影面的交线 称作平面的正面迹线,用PV表示。 (平面名称的大写字母加右下标注 相应投影面名称)。 PH、 PV是平 面P的两条直线,不是一直线的两投 影。
PV
c a
Px
b
a
c
PH
b
2021
§4-2 各种位置平面的投影特性
一、投影面的垂直面 1 铅垂面 2 正垂面 3 侧垂面 二、投影面的平行面 1 水平面 2 正平面 3 侧平面 三、一般位置平面
1、 铅垂面
V P B
A
2021
c
a
W
b
c a
b
a b
H
C PH c
a
c
投影特性:1、 abc积聚为一条线
SH
W X
H
2021
Z
β
SH
O
α
Y
Y
1、水平面
2021
V
a
A
a
b c
B
b
H
b a W c
C
c
a b c
b a
b a c
c 投影特性:
1、 abc、 abc积聚为一条线积聚为一条线,具有积聚性
2 、 水平投影abc反映 ABC实形
2 、正平面
2021
V
b
a
b
b
B
b
c
W
A a
c
C
c
a
a
c
c H
b
a
c
1 平面上的直线 直线在平面上的几何条件是:
①通过平面上的两点; ②通过平面上的一点且平行于平面上的一条直线。 2 平面上的点
点在平面上的几何条件是:点在平面内的某一直线上。 在平面上取点、直线的作图,实质上就是在平面内作辅助线 的问题。 利用在平面上取点、直线的作图,可以解决三类问题:判别 已知点、线是否属于已知平面;完成已知平面上的点和直线的 投影;完成多边形的投影。
V
a
SV
A
b
B S
a
H
b PH
过一般位置直线AB 作H面的垂直面PH
a
b
H
过一般位置直线AB作V 面的垂直面SH
2021
(1) 过一般位置直线作投影面的垂直面
(几何元素表示法)
e
e (n)
f
f’
m
n
f
f
e (m)
e
(2) 过一般位置直线作投影面的垂20直21 面 (迹线表示法)
SV
QW
b
b
a
a
b PH a
b
2 、 abc、 abc为ABC的类似形
3 、 abc与OX、 OY的夹角反映、角的真实大小
铅垂面迹线表示法
2021
V P W
H PH
PH
2、 正垂面
V
b
QV
a
A
c
C H
2021
b
c
W B
a
α
Q
c
a
b c
a
投影特性:1、 abc 积聚为一条线 b 2 、 abc、abc ABC的类似形 3 、 abc与OX、 OZ的夹角反映α、 角的真实大小
第四章 平面
§4-1 平面的表示法
§4-2 各种位置平面的投影特性
§4-3 属于平面的点和直线
2021
§4-1 平面的客观形态
一、以几何元素呈现的平面
用几何元素表示平面有五种形式:不在同一直线上 的三点;直线及外一点;相交二直线;平行二直线;任 意平面图形本身。
二、以迹线呈现的平面
平面的迹线为空间平面与投影面的交线。特殊位置 平面其具有积聚性的投影与其同面迹线是一致的。
2021
1 取属于垂直面的点和直线(1)
b
2
e k
f
m
g
n
c
3
a
1
a k
e
K属于ABC
b
c
2
3
ⅡⅢ MN不属于ⅠⅡⅢ
几何元素表示平面
1 取属于垂直面的点和直线
b a
PH a b
2021
e f RV
f e
2021
2 过一般位置直线总可作投影面的垂直面
V
a
A
b
BP
正垂面的迹线表示法
V QV W Q
2021
QV γ α
H
3 、侧垂面
V
S B
b
SW
b
W a
2021
b c β c
α a
c
C
a
A
H
b c
a 投影特性:1、 abc积聚为一条线
2 、 abc、 abc为 ABC的类似形 3 、 abc与OZ、 OY的夹角反映α、β角的真实大小
侧垂面的迹线表示法
V S
取属于平面的点和直线
B
F
E
2021
b e
f
d c
a
D
C
c
a
A
d
f
e
b
取属于定平面的直线,要经过属于该平面的已知两点;或经过属 于该平面的一已知点,且平行于属于该平面的一已知直线。
2021
例题 已知 ABC给定一平面,试判断点D是否属于该平面。
b
e d c
a
c a
e
d
b
例题2 已知点D在 ABC上,试求点D的2021水平投影 。
B
b
A
b a
a C c
c
2021
b a
b
b
a
c
c
c a
投影特性:1、abc、abc 、abc 均为 ABC的类似形 2、不反映、、 的真实角度
2021
§4-3 属于平面的点和直线
一、属于一般位置平面的点和直线 二、属于特殊位置平面的点和直线 三、属于平面的投影面平行线 四、属于平面的最大斜度线
一、属于一般位置平面的点和直线 2021
2021
(1) 过正垂线作平面 (迹线表示法)
m(n)
n
m(n)
PV
m (n)
SV
m (n )
QV
RV
n
n
n
m
m
m
m
(2) 过正平线作平面
e
e
f
2021
SH e f
e
f
f
g
g
2、迹线的空间位置特点 平面迹线 既属于平面,又属于投影面。
3、迹线的投影特点 迹线的一个投影 即其本身,其余投影在投影轴上。
4、平面迹线的作图 先作出平面内 任意两直线的迹点,再连接其同名 迹点即平面的同面迹线,注意利用 迹线共点。
特殊位置平面用具有积聚性的 迹线表示。
m2
2021
迹线平面与几何平面的转换
b
e d
c
a
a
c
d e
b
2021
例题 已知点E在 ABC上,试求点E的正面投影 。
b
e
d
c
a
a
c
d
e
b
2021
二、属于特殊位置平面的点和直线
1 取属于垂直面的点和直线 2 过一般位置直线总可作投影面的垂直面 (1) 几何元素表示法 (2) 迹线表示法 3 过特殊位置直线作平面 (1) 过正垂线作平面 (2) 过正平线作平面
ba
投影特性:
1、abc 、 abc 积聚为一条线,具有积聚性 2 、正平面投影abc反映 ABC实形
3 、 侧平面
V
c
B
b
b
b
W
a
a
A
a
c
a
bC
c
a
Hc
b
2021
b a
c
投影特性:
c
1、 abc 、 abc 积聚为一条线,具有积聚性
2 、 侧平面投影abc 反映 ABC实形
三、一般位置平面
b
a
一、用几何元素表示平面
b
b
2021
b
a c
a c
b
a d
b
b ad
a c
a c
b
a c
a c
b
b
a
c
c
c
a
c
b
二、平面的迹线表示法
V
PV
P
H PH
V
QV
Q H QH
2021
PV PH QV
QH
一般位置平面的迹线求法
n1 PV n2
b′ c′
a′ Px
m1 a b c
PH
Px —— 迹线集合点
1、平面迹202线1 的定义 平面的迹线是 平面与投影面的交线。平面P与H投 影面的交线称作平面的水平迹线, 用PH表示;平面P与V投影面的交线 称作平面的正面迹线,用PV表示。 (平面名称的大写字母加右下标注 相应投影面名称)。 PH、 PV是平 面P的两条直线,不是一直线的两投 影。
PV
c a
Px
b
a
c
PH
b
2021
§4-2 各种位置平面的投影特性
一、投影面的垂直面 1 铅垂面 2 正垂面 3 侧垂面 二、投影面的平行面 1 水平面 2 正平面 3 侧平面 三、一般位置平面
1、 铅垂面
V P B
A
2021
c
a
W
b
c a
b
a b
H
C PH c
a
c
投影特性:1、 abc积聚为一条线
SH
W X
H
2021
Z
β
SH
O
α
Y
Y
1、水平面
2021
V
a
A
a
b c
B
b
H
b a W c
C
c
a b c
b a
b a c
c 投影特性:
1、 abc、 abc积聚为一条线积聚为一条线,具有积聚性
2 、 水平投影abc反映 ABC实形
2 、正平面
2021
V
b
a
b
b
B
b
c
W
A a
c
C
c
a
a
c
c H
b
a
c
1 平面上的直线 直线在平面上的几何条件是:
①通过平面上的两点; ②通过平面上的一点且平行于平面上的一条直线。 2 平面上的点
点在平面上的几何条件是:点在平面内的某一直线上。 在平面上取点、直线的作图,实质上就是在平面内作辅助线 的问题。 利用在平面上取点、直线的作图,可以解决三类问题:判别 已知点、线是否属于已知平面;完成已知平面上的点和直线的 投影;完成多边形的投影。
V
a
SV
A
b
B S
a
H
b PH
过一般位置直线AB 作H面的垂直面PH
a
b
H
过一般位置直线AB作V 面的垂直面SH
2021
(1) 过一般位置直线作投影面的垂直面
(几何元素表示法)
e
e (n)
f
f’
m
n
f
f
e (m)
e
(2) 过一般位置直线作投影面的垂20直21 面 (迹线表示法)
SV
QW
b
b
a
a
b PH a
b
2 、 abc、 abc为ABC的类似形
3 、 abc与OX、 OY的夹角反映、角的真实大小
铅垂面迹线表示法
2021
V P W
H PH
PH
2、 正垂面
V
b
QV
a
A
c
C H
2021
b
c
W B
a
α
Q
c
a
b c
a
投影特性:1、 abc 积聚为一条线 b 2 、 abc、abc ABC的类似形 3 、 abc与OX、 OZ的夹角反映α、 角的真实大小
