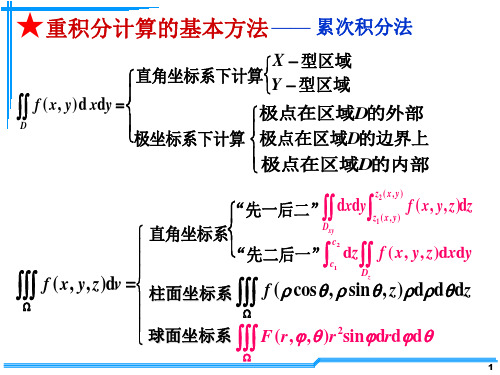
第四节 重积分的应用
高等数学 第九章 重积分 第四节 重积分应用

∫∫∫Ω xd xd y d z ∫∫∫Ω
V zd x d y d z V
∫∫∫Ω yd xd y d z
V
,
( V = ∫∫∫ d x d y d z为Ω的体积 ) Ω
上页 下页 返回 结束
若物体为占有xOy 面上区域 D 的平面薄片 其面密度 的平面薄片, 若物体为占有 则它的质心坐标 质心坐标为 则它的质心坐标为
上页 下页 返回 结束
三、物体的质心
设空间有n个质点 设空间有 个质点, 分别位于 (xk , yk , zk ) , 其质量分别 个质点 为 mk ( k =1, 2, L, n ) ,由力学知 该质点系的质心坐标 由力学知,
∑xk mk
为
n
x=
k =1 n
∑yk mk
, y=
k =1 n
n
∑zk mk
∴ dA = 1 + f x2 + f y2 dσ 曲面S的面积元素 曲面S
∴ A = ∫∫ 1 + f x2 + f y2 dσ ,
D
∂z ∂z A = ∫∫ 1 + (∂x )2 + (∂y )2dxdy 曲面面积公式为: 曲面面积公式为: Dxy
上页
下页
返回
结束
小结 1. 设曲面 S 的方程为:z = f ( x , y ) 的方程为:
设曲面的方程为: 3.设曲面的方程为:y = h( z , x ) 则曲面面积公式为: 则曲面面积公式为: A =
∫∫
Dzx
1+ (
∂y 2 ∂z
) + ( ) dzdx.
∂y 2 ∂x
上页 下页 返回 结束
例 4. 求球面 x 2 + y 2 + z 2 = a 2 含在圆柱体 2 2 x + y = ax 内部的那部分面积 内部的那部分面积.
重积分的应用

3
计算复杂几何形状的表面积
对于复杂的几何形状,可以通过将其分割成小的 部分,然后对每一部分进行重积分,最后求和得 到总表面积。
03
重积分在概率论中的应用
概描述随机变量在各个取值上的概率分布情况,通过重积分计算随机变量
的概率分布。
02
离散型随机变量的概率密度函数
对于离散型随机变量,概率密度函数表示随机变量取各个可能值的概率,
对于离散型随机变量,期望值表示所有可能取值的加权平均,通过重积分计算离散型随 机变量的期望值。
连续型随机变量的期望值
对于连续型随机变量,期望值表示在各个实数区间上的概率密度函数的积分,通过重积 分计算连续型随机变量的期望值。
随机变量的方差
随机变量的方差
表示随机变量取值与其期望值的 偏离程度,通过重积分计算随机 变量的方差。
02
重积分的几何应用
计算面积
计算平面图形的面积
计算参数曲线的长度
通过重积分可以计算平面图形的面积, 例如矩形、圆形、三角形等。
对于参数曲线,重积分可以用来计算 其长度。
计算曲面面积
重积分也可以用来计算曲面在某个平 面上的投影面积,这在工程和物理中 非常有用。
计算体积
计算三维物体的体积
重积分可以用来计算三维物体的体积,例如球体、圆柱体、圆锥体 等。
计算期权价格
期权定价模型
重积分在期权定价模型中有重要应用, 通过重积分可以计算出期权的合理价格 。
VS
隐含波动率
利用重积分,还可以计算出期权的隐含波 动率,为投资者提供更加全面的信息。
05
重积分在工程设计中的应用
优化设计参数
结构优化
重积分被广泛应用于结构优化设计,通过计算不同设计方 案下结构的应力、应变等参数,选择最优的设计方案,降 低结构重量并提高其承载能力。
经典高等数学课件D10-4重积分的应用
x 2 y 2 a 2 .由
z x , x a2 x2 y2
得 1 (
z y , 2 2 2 y a x y
z 2 z 2 a ) ( ) . x y a2 x2 y2
12
A上
D
a a x y a
2 2 2
dxdy D : x 2 y 2 a 2 .
设曲面S的方程为z 如图, 设小区域
z
z f ( x, y )
f ( x, y ),
M
o
曲面S在xoy面上的投影为区 域D,
sS d
d
( x, y)
点(x,y) d, d D, 以 为S上过点M(x,y,z)的切平面, d
的边界为准线, 母线平行于z轴的 截切平面 小柱面, 截曲面S为 dS, 为 dA, 则有 dA dS.
C2 D
7 所求质心是(0, ). 3
o
x
17
推广: 占有空间有界闭区域, 在点( x, y, z )处的密度为 ( x, y, z )
(假定 ( x, y, z )在上连续)的物体的质心坐标(x , y , z )为:
1 x x ( x, y, z )dv , M 1 y y ( x, y, z )dv , M 1 z z ( x, y, z )dv , M
D
D
y
( x, y)
又M ( x , y )d , 则薄片的质心坐标为:
D
o
d
x
m yi x ( x , yxi mi )d i y ( x, y )d M xM i 1 y M M i 1 y ,, y x n D y n x x D . MM M M ( x , m)d m y i i ( x, y )d
重积分应用与计算

重积分应用与计算重积分是微积分中一项重要的概念,它广泛应用于各个科学领域,特别是物理学、工程学和经济学等。
重积分的计算方法包括二重积分和三重积分,通过对多元函数进行积分,可以解决许多实际问题。
本文将介绍重积分的应用,并重点讨论其计算方法。
一、重积分的应用1. 质量和质心重积分可以用于计算物体的质量和质心。
对于一个二维物体,其质量可以通过计算其面积的重积分来得到。
例如,一个有界闭区域D的质量可以表示为:m = ∬D ρ(x,y) dA其中,ρ(x,y)表示单位面积上的密度函数。
质心的坐标可以由下式给出:(x_c, y_c) = (∬D xρ(x,y) dA, ∬D yρ(x,y) dA)类似地,对于一个三维物体,质量和质心的计算也可以通过重积分来实现。
2. 总量和平均值重积分可以用于计算一个区域内某个量的总量和平均值。
例如,在物理学中,可以通过对速度场进行重积分来计算液体或气体的总质量流量。
在经济学中,可以通过对产量或消费量的重积分来计算总产量或总消费量。
对于一个二维区域D,某个量f(x,y)的总量可以表示为:Q = ∬D f(x,y) dA平均值可以表示为:f_avg = (1/area(D)) * ∬D f(x,y) dA其中,area(D)表示D的面积。
3. 概率和期望值在概率论中,重积分可以用于计算概率和期望值。
对于一个二维区域D上的离散随机变量,其概率函数可以表示为p(x,y),概率p(x,y)在区域D上的积分即为该随机变量落在D内的概率。
期望值可以表示为:E[f(x,y)] = ∬D f(x,y) * p(x,y) dA其中,f(x,y)是随机变量的函数。
二、重积分的计算方法1. 二重积分二重积分用于计算平面二维区域上的积分。
常用的计算方法包括直角坐标系下的面积法和极坐标系下的极坐标法。
面积法:设D为平面上的有界闭区域,f(x,y)为定义在D上的连续函数。
则D上f的二重积分可以表示为:∬D f(x,y) dA = ∫[a,b]∫[c,d] f(x,y) dx dy其中,[a,b]和[c,d]分别为D在x轴和y轴上的投影区间。
高等数学-重积分的 计算 及应用

D
例如计算: I x2d
D:
D
I y2d
D
I 1
(x2 y2 )d
a4
2D
4
14
x2 y2 a2
例6
d
D (a2 x2 y2 )3/ 2
其中 D : 0 x a ; 0 y a
y yx
a
解:如图D是关于直线 y x 对称。
D2
D1
r a
cos
原式 2
D1
o 4
D1 D2 D
x
连续, 所以
6
D (x y) d D2 (x y) d D1 (x y) d
4
dy
6
12 y
y2 (x y)d x
2
dy
4
4 y
y2 (x y)d x
2
2
54311 15
9
例2. 计算 x2 y2 4 d , 其中 D : x2 y2 9
F(0) 0
利用洛必达法则与导数定义,得
lim
t0
F
(t ) t4
lim
t 0
4 f (t) 4 t3
t
2
lim
t 0
f (t) t
f
(0)
f (0)
33
f (x, y, z) d v
x
D
z2 (x, y) f (x, y, z)dz dxdy
z1( x, y)
记作 dxdy z2 (x, y) f (x, y, z)dz
D
z1( x, y)
20
y D
dxd y
微元线密度≈
f (x, y, z) dxdy
方法2. 截面法 (“先二后一”)
重积分应用案例

重积分与微分几何、偏微分方程等数学分支有着密切的联系。未来可以 加强这些领域之间的交叉研究,以推动重积分理论的深入发展和应用拓 展。
THANKS
感谢观看
其他物理量如流量、压力等计算
流量计算
在流体力学中,流量是单位时间内通过某一 截面的流体体积。对于连续分布的流体,如 管道中的水流或气流,流量可以通过重积分 来计算。即对每个小微元的流速与其截面面 积的乘积进行积分。
压力计算
在静力学中,压力是垂直作用于单位面积上 的力。对于连续分布的物体,如液体中的压 力分布或固体中的应力分布,可以通过重积 分来计算。即对每个小微元的压力与其作用 面积的乘积进行积分。
02
重积分计算方法
直角坐标系下重积分
投影法
将重积分区域投影到某一坐标平面上 ,通过对投影区域进行单重积分来计 算重积分。
截面法
通过垂直于某一坐标轴的平面将重积 分区域切割成若干个小区域,对每个 小区域进行单重积分后再求和。
极坐标系下重积分
极坐标变换
将直角坐标系下的重积分通过极坐标变换转化为极坐标系下的重积分,简化计算 过程。
流速场描述
利用重积分对流速场进行建模,了解流体在空间中的速度分布情 况。
压力场描述
通过重积分描述压力场,掌握流体内部压力变化规律。
流体动力学分析
结合流速场和压力场信息,对流体动力学问题进行分析,如流体 流动、传热、传质等。
控制系统中系统稳定性和性能评估
系统稳定性分析
利用重积分对控制系统稳定性进 行评估,判断系统是否能在受到 扰动后恢复到平衡状态。
激发学习兴趣和动力
通过介绍有趣的重积分应用案例,激发读者对重积分学习的兴趣和动力,提高 学习效果。
D84重积分的应用-PPT文档资料

A Dyz
x x2 2 1 ( ) ( )d y d z y z
则有 h ( z , x ) , ( z , x ) D , 若光滑曲面方程为 y z x
A Dzx
y y2 2 1 ( ) ( )d z d x z x
上页 下页
上页 下页
8.4.1 重积分在几何上的应用
一、平面图形的面积
d .
D
2 2 所围图形的面积. 例1 求曲线 r 2 a cos 2
解 曲线为一双纽线,图形关于极轴和极点都对称. y 因此曲线所围成图形的面积
A 4 d 4 4d
D
0
0 0
a2 cos 2
2acos 2 r dr 0
M
2
3 3 16 a 4 a 3 4 cos sin d ( 1 cos ) 3 0 3
0
d
0 sin d
上页 下页
2 2 例4. 用三重积分计算由曲面 x y z2 5 及 x2 y2 4z 所围成的立体的体积.
D : 0 r 2 a cos , 0
2 2 V 4 4 a r r d r d D
D
0
2 2 2 4 a x y dxdy
2
o
2a
D
y
x
y 2 ax x2
4
2
d
0
2 a cos
4 a rr d r
2
2
y
32 3 2 3 a ( 1 sin ) d 3 0 323 2 a( ) 3 2 3
4 重积分的应用

| cos( n, z ) | = | cos γ i | =
1 1 + f x2 (ξ i ,η i ) + f y2 (ξ i ,η i )
.
因为 Ai 在 xy 平面上的投影为 σ i , 所以
σ i Ai = = 1 + f x2 (ξ i ,η i ) + f y2 (ξ i ,ηi ) σ i . cos γ i
20
由
∫∫∫ z dxdydz =
V
π
4
abc 2 ,
故得
z=
π
4
abc
2
3c 2π abc = , 3 8
2007年8月 南京航空航天大学 理学院 数学系 2
平面 π i , 并在 π i 上取出一小块 Ai , 使得 Ai 与 S i 在
x y 平面上的投影都是 σ i
z S : z = f ( x, y)
(见图). 见图).
在点 M i 附
近用切平面 Ai 代替小 代替小 曲面片 Si , 从而当 T 充分小时, 充分小时, 有
i =1
Hale Waihona Puke n的面积. 作为 S 的面积. 现在按照上述曲面面积的概念, 现在按照上述曲面面积的概念, 来建立曲面面积的 计算公式. 计算公式. 为此首先计算 Ai 的面积 由于切平面 π i 的法向量就 的面积. 是曲面 是曲面 S 在点 M i (ξ i ,η i , i ) 处的法向量 n, 记它与 z 轴的夹角为 γ i , 则
y = f ( x ), x ∈ [a , b] ( f ( x ) ≥ 0).
求证此曲线绕 x 轴旋转一周得到的旋转面的面积为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【解】 球心为原点, z轴与轴l重合
:x y z a
2 2 2
2
2
I z ( x 2 y 2 ) dv ( r sin2 cos 2 r 2 sin2 sin2 )r 2 sindrdd
r 4 sin3 drdd
D
a
2a
补充
y( x )
A
2 a
0
y( x )dx a(1 cos t )d[a( t sin t )]
0
2
a 2 (1 cos t ) 2 dt 3a 2 .
0
机动 目录 上页 下页 返回 结束
2
由于区域关于直线 x a对称 ,
所以形心在 x a上,
为 m1 , m2 ,, mn.则该质点系的质心的坐标为
My x M
mi xi i 1 mi i 1
n
n
,
Mx y M
m i yi i 1 mi i 1
n
n
.
机动 目录 上页 下页 返回 结束
设有一平面薄片,占有 xoy面上的闭区域 D , 在点( x , y )处的面密度为 ( x , y ),假定 ( x , y ) 在 D 上连续,平面薄片的质心 (二重积分表示)
画出积分域、选择坐标系、确定积分序、
定出积分限、计算要简便
机动 目录 上页 下页 返回 结束
1.设曲面的方程为: z f ( x , y )
设光滑曲面 则面积 A 可看成曲面上各点 M ( x , y , z ) 处小切平面的面积 d A 无限积累而成. 设它在 D 上的投影为 d , 则 d cos d A 1 cos 2 2 1 f x ( x, y) f y ( x, y)
【推广】 空间立体对质点的引力(略)
机动 目录 上页 下页 返回 结束
六、小结
【几何应用】曲面的面积
【物理应用】质心、转动惯量、 对质点的引力
(注意审题,熟悉相关物理知识)
机动 目录 上页 下页 返回 结束
【思考题】
与前例3(2)相同
求位于两圆 a cos , b cos 之间的均匀薄片的重心. (0 a b)
补充
【例 8】已知均匀矩形板(面密度为常数 )的 长和宽分别为 b 和 h ,计算此矩形板对于通过 其形心且分别与一边平行的两轴的转动惯量 .
1 【解】 先求形心 x xdxdy, AD
区域面积 A b h,
建立坐标系如图
h
1 y ydxdy. AD
y
因为矩形板均匀,
【例 10】求面密度为常量、半径为 R 的均匀圆形 薄片: x2 y 2 R2 , z 0 对位于 z 轴上的 点 M 0 (0,0, a) 处的单位质点的引力. ( a 0)
【解】 由积分区域的对称性知 Fx Fy 0,
Fz af
D
z
( x, y)
(x y a )
D
2 2 ( b a ) b ba a 8 2 2 . 2(b a ) 4 (b a )
机动 目录 上页 下页 返回 结束
2.空间物体的质心
(推广)
占有空间有界闭区域 、在点( x , y , z ) 处的面 密度为 ( x , y , z ) (假定 ( x , y , z ) 在 上连续)的 物体的质心坐标是 (三重积分表示)
2 2
点到x轴的距离平方 点到原点的距离平方
I o ( x 2 y 2 z 2 ) ( x , y , z )dv
I xoy z ( x , y , z )dv
2
点到xoy面的距离平方
机动 目录 上页 下页 返回 结束
【例9】 求密度为的均匀球体对于过球心 的一条
n
.
机动 目录 上页 下页 返回 结束
设有一平面薄片,占有 xoy面上的闭区域 D ,在点( x , y )处的面密度为 ( x , y ) ,假定 ( x , y )在 D 上连续,平面薄片对于 x 轴和 y 轴 的转动惯量为
薄片对于x 轴的转动惯量
I x y ( x , y )d ,
机动 目录 上页 下页 返回 结束
例1. 计算双曲抛物面 被柱面 出的面积 A . 解: 曲面在 xoy 面上投影为
所截
D: x y R ,
2 2 2
则
2
A
D
D
1 z x z y d xd y
z
2
1 x y d xd y
2 2
R
z=xy
y
d
由元素法
x ( x, y )d x , ( x, y )d
D D
y ( x, y )d y . ( x , y )d
D D
当薄片是均匀的,重心称为形心.
1 x xd , AD 1 y yd . 其中 A d AD D
即
x a,
1 2a y( x ) 1 y ydxdy dx ydy 0 AD A 0
1 2a a 2 2 0 [ y ( x )] dx 6a 6
所求形心坐标为 ( a, 5 ) . 6
0
2
5 [1 cos t ] dt . 6
3
机动 目录 上页 下页 返回 结束
设 xoy 平面 上有 n 个 质 点, 它们 分别位 于
( x1 , y1 ),( x2 , y2 ),, ( xn , yn )处,质量分别为 m1 , m2 ,, mn .则该质点系对于
轴的转动惯量依次为
x 轴和
2
y
I x m i yi
i 1
n
2
,
I y mi xi
i 1
Fx f
D
( x, y) x
(x y a )
2 2 2
3 2
d , Fy f
D
3 2
( x, y) y
(x y a )
2 2 2
3 2
d ,
Fz af
D
( x, y)
(x y a )
2 2 2
d .
f 为引力常数
机动 目录 上页 下页 返回 结束
o
b
x
b h 由对称性知形心坐标 x , y . 2 2
机动 目录 上页 下页 返回 结束
将坐标系平移如图
对u 轴的转动惯量
h
y
v
o
u
b
I u v dudv
2 D
3 bh 2 . h v dv b du 2 2 12
h 2 b 2
o
x
对v轴的转动惯量
xy
2.若光滑曲面方程为 x g( y, z ) , ( y, z ) Dy z , 则有
A
D
yz
x 2 x 2 1 ( ) ( ) d yd z y z
3.若光滑曲面方程为
y h ( z , x) , ( z , x) Dz x , 则有
A
D
zx
y 2 y 2 1 ( ) ( ) d zd x z x
机动 目录 上页 下页 返回 结束
d sin d r 4dr
3 0 0 0
2
a
a5 3 2 sin d 5 0
2 5 4 2 2 a a M 5 3 5 4 3 其中 M a 为球体的质量. 3
机动 目录 上页 下页 返回 结束
0
2
0
1 r 2 r dr
.
o
3 2 2 2 [ ( 1 R ) 1 ) ] 3
a
x
机动 目录 上页 下页 返回 结束
三、质心 ( x , y )
1.平面薄片的质心
设 xoy平面上有 n个质点,它们分别位于
( x1 , y1 ), ( x2 , y2 ),, ( xn , yn )处,质量分别
机动 目录 上页 下页 返回 结束
x a ( t sin t ) 【例 5】设平面薄板由 ,(0 t 2) y a (1 cos t ) 与 x轴围成,它的面密度 1,求形心坐标.
【解】先求区域 D 的面积 A,
0 t 2 , 0 x 2a
1 x x ( x , y , z )dv M 1 z z ( x , y , z )dv M
M ( x , y , z )dv
1 y y ( x , y , z )dv M
机动 目录 上页 下页 返回 结束
四、转动惯量
1.平面薄片的转动惯量
cos d
D
机动 目录 上页 下页 返回 结束
b 3 h I v u dudv . 12 D
2
机动 目录 上页 下页 返回 结束
2.空间立体的转动惯量
类似地,占有空间有 界闭域,体密度为 x , y , z ( 假定在上连续)的物体对于某轴、点、面的转动 惯量分别为
I x ( y z ) ( x , y , z )dv
d A 1 f x ( x, y) f y ( x, y) d
2 2
在D上偏 导数连续
z
S
n
M
o x
d y
(称为曲面S的面积元素)
机动 目录 上页 下页 返回 结束
2 2 A 1 f f 故有曲面面积公式 x y d , D
