高二第一学期数学-向量的坐标表示2

合集下载

高二数学空间向量运算的坐标表示

3.1.5空间向量运算的坐标表示
一、向量的直角坐标运算
设a (a1, a2 , a3 ),b (b1 , b2 , b3 )则
a b (a 1 b1 , a2 b2 , a3 b3 ) ;
a b (a 1 b1 , a2 b2 , a3 b3 ) ;
a (a1 , a2 , a3 ),( R) ;
F A1 B1 E D1 C1
D
C
A
B
练习三：
如图：直三棱柱ABC A1 B1C1 , 底面ABC 中， CA＝CB＝1，BCA＝90o，棱AA1＝2，M、 N分别为A1B1、AA1的中点， 1)求BN的长； 2)求 cos BA1 , CB1 的值； 3)求证：A1B C1M。
（3）当cos a , b 0 时，a b 。思考：当 0 cos a , b 1 及 1 cos a , b 0时，的夹角在什么范围内？
练习一：
1.求下列两个向量的夹角的余弦：
(1) a (2 , 3 , 3) , b (1, 0 , 0) ;
解：设正方体的棱长为1，如图建
C1
z
D1 A1
F1 E1 B1
立空间直角坐标系 O xyz ，则
3 B(1,1, 0) , E1 1, ,1 , 4
C
D
O
B
y
1 D(0 , 0 , 0) , F1 0 , ，1 . 4
A
x
1 3 BE1 1, ,1 (1,1, 0) 0 , ,1 , 4 4
（1）线段 AB 的中点坐标和长度；解：设 M ( x , y , z ) 是 AB 的中点，则

向量的坐标表示与应用知识点总结

向量的坐标表示与应用知识点总结一、向量的概念与表示方法向量是物理学和数学中常用的重要概念，它表示大小和方向的物理量。

在数学中，向量可以通过坐标表示，也可以用箭头在平面或空间上表示。

1. 向量的定义向量是由大小和方向共同决定的物理量。

通常用有向线段来表示，有起点和终点，并且箭头指向终点表示向量的方向。

2. 向量的表示方法向量可以用坐标表示，也可以用箭头表示。

（1）坐标表示法：在直角坐标系中，向量可以表示为一个n维数组，每个数组元素表示该向量在各坐标轴上的分量。

（2）箭头表示法：向量的方向用箭头表示，箭头的长度表示向量的大小。

二、向量的基本运算法则向量的基本运算包括加法、减法、数量乘法和点乘。

1. 向量的加法向量的加法满足交换律和结合律。

2. 向量的减法向量的减法可以转化为加法运算，即向量A减去向量B等于向量A 加上向量B的负向量。

3. 向量的数量乘法向量的数量乘法即将向量的每个分量与一个标量相乘。

4. 向量的点乘向量的点乘是将两个向量的对应分量相乘，再将结果相加。

三、向量的坐标表示与应用向量的坐标表示及其应用非常广泛，下面列举几个常见的应用场景。

1. 向量的图形平移图形平移是指将一个图形在平面上沿着给定的向量进行移动。

向量的坐标表示可以方便地描述图形在平移运动中的位置变化。

2. 向量的速度分解向量的速度分解是将一个向量分解为两个分量，分别与坐标轴平行。

这样可以方便地计算出物体在各个方向上的速度。

3. 坐标系变换在进行坐标系变换时，向量的坐标表示可以帮助我们进行计算和分析。

通过变换矩阵，我们可以将向量在不同坐标系下的表示进行互相转换。

4. 电磁场的计算在电磁场的计算中，需要对电场和磁场进行向量表示，通过向量的坐标表示和运算法则，可以精确地描述场强和方向。

四、总结向量的坐标表示与应用是数学和物理学中重要的基础知识。

通过理解向量的概念和表示方法，以及掌握向量的基本运算法则，可以更好地应用于实际问题中。

向量的坐标表示在图形平移、速度分解、坐标系变换和电磁场计算等方面具有广泛的应用价值。

高二数学向量的坐标表示及其运算

(2,1).求
PQ
的单位向量
a0
.
*总结: 求任意向量的单位向量的方法步骤为:
①确定任意向量的坐标 a (x;,y)
②计算模 a
x2 y2; ③计算 a0
1 (x,y). x2 y2
**课本P57:练习8.1(1): 1,2,3;
*提示: 代数法证明三点共线的充要条件是:
AC // BC
a
N (0,y)
A (x,y)
由平行四边形法则可得:
1 j
a OA OM ON;
O
i
1M (x,0)
X
OM x • i;
ON y • j;
a
OA
x
•
i
y
•
j;
(x , y) .
*感悟: 任意向量 a (平移)
位置向量
OA
x
•
i
y
•
j;
(唯一确定)
有序实数对(x,y)
向量 a的坐标.
表示任意一个向量 a呢?
1 j
O
i
1
X
*2.位置向量的定义:
a
Y
A
1 a
j
O
i
1
X
对于平面内的任意向量 a,可将向量的起点置于坐标原点O,作 OA a,那么OA 就叫做位置向量.
在平面上，如果选取互相垂直的向量时，会为我们研究问题带来方便。
我们知道，在平面直角坐标系，每一个点都可用一对有序实数（即它的坐标）表示，对直角坐标平面内的每一个向量，如何表示？
λ 0 0.
*两个非零向量平行的充要条件:a//b
b
λa,( λ

高二数学空间向量的坐标运算知识精讲

高二数学空间向量的坐标运算【本讲主要内容】空间向量的坐标运算空间直角坐标系，空间向量的坐标表示，空间向量的坐标运算，空间向量平行，垂直的坐标表示形式。

【知识掌握】【知识点精析】1. 空间直角坐标系（1）单位正交基底，空间直角坐标系，右手直角坐标系（2）坐标：在空间直角坐标系O-xyz 中，对空间任一点A ，对应一个向量OA →，于是存在唯一的有序实数组x 、y 、z ，使OA xi yj zk =++，则实数组（x ，y ，z ）叫做点A 在此空间直角坐标系中的坐标。

2. 向量的直角坐标运算设a a a ab b b b ==()()123123，，，，，则a b a b a b a b +=+++()112233，，a b a b a b a b -=---()112233，，a b a b a b a b ⋅=++112233a b a b a b a b R //⇔===∈112233λλλλ，，，或a b a b a b 112233==a b a b a b a b ⊥⇔++=11223303. 夹角和距离公式（1）夹角公式：设a a a ab b b b ==()()123123，，，，，则cos <>=++++⋅++a b a b a b a b a a a b b b ，112233122232122232（2）距离公式：设A x y z B x y z ()()111222，，，，，则d x x y y z z AB =-+-+-()()()122122122（3）平面的法向量：如果表示向量a 的有向线段所在直线垂直于平面α，则称这个向量垂直于平面α，记作a ⊥α。

如果 a ⊥α，那么向量a 叫做平面α的法向量。

【解题方法指导】1. 在证明线线平行时，利用a b a b //⇔=λ即()()a a a b b b 123123，，，，=λλλ，在证明线面平行或面面平行时，需转化为线线平行问题。

高中数学向量的坐标表示与应用

高中数学向量的坐标表示与应用1. 前言在高中数学中，向量是一个重要的概念。

向量的坐标表示和应用是数学学习中的一个重要部分。

本文将通过介绍向量的坐标表示和应用的相关知识，帮助读者更好地理解和运用向量。

2. 向量的表示2.1 向量的定义向量是有大小和方向的量。

向量通常用箭头表示，箭头的长度表示向量的大小，箭头的指向表示向量的方向。

2.2 向量的坐标表示向量的坐标表示是将向量的大小和方向分别表示为一个有序数对。

常用的坐标表示方法有两种，一种是点表示法，一种是列向量表示法。

2.2.1 点表示法在二维笛卡尔坐标系中，向量的起点和终点分别对应两个点，可以用这两个点的坐标表示向量。

例如，向量AB可以表示为(2,3)。

2.2.2 列向量表示法在二维笛卡尔坐标系中，可以用列向量表示向量。

例如，向量AB可以表示为 [2, 3]。

3. 向量的应用3.1 向量的运算向量有多种运算方法，包括加法、减法、数量乘法和数量除法。

3.1.1 向量的加法向量的加法满足交换律和结合律。

即，对于向量AB和向量BC，它们的和为向量AC。

3.1.2 向量的减法向量的减法即向量的加法的逆运算。

向量AB减去向量AC等于向量BC。

3.1.3 数量乘法数量乘法即将向量的每个分量都乘以一个常数k。

例如，向量AB 乘以2即为2AB。

3.1.4 数量除法数量除法即将向量的每个分量都除以一个常数k。

例如，向量AB 除以2即为AB/2。

3.2 向量的应用3.2.1 几何向量在几何中，向量可以表示位移、速度、加速度等物理量。

向量的坐标表示和运算可以帮助我们求解这些几何问题。

3.2.2 向量的线性相关与线性无关向量的线性相关与线性无关是线性代数中的一个重要概念。

通过向量的坐标表示和线性代数的相关知识，我们可以判断向量组的线性相关性，并解决相关的问题。

3.2.3 向量的投影向量的投影是向量分解的一个重要应用。

通过向量的坐标表示和向量的运算，我们可以计算一个向量在另一个向量上的投影。

高二寒假讲义03 空间向量及其运算的坐标表示

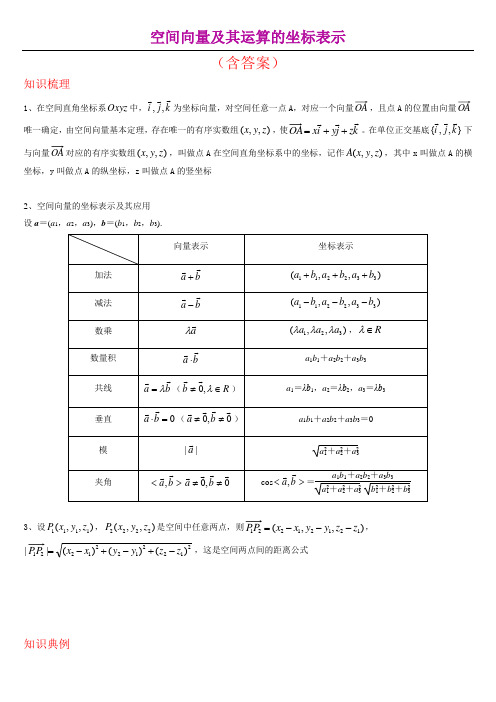
空间向量及其运算的坐标表示（含答案）知识梳理1、在空间直角坐标系Oxyz 中，k j i,,为坐标向量，对空间任意一点A ，对应一个向量OA ，且点A 的位置由向量OA唯一确定，由空间向量基本定理，存在唯一的有序实数组),,(z y x ，使k z j y i x++=。

在单位正交基底},,{k j i 下与向量对应的有序实数组),,(z y x ，叫做点A 在空间直角坐标系中的坐标，记作),,(z y x A ，其中x 叫做点A 的横坐标，y 叫做点A 的纵坐标，z 叫做点A 的竖坐标2、空间向量的坐标表示及其应用设a ＝(a 1，a 2，a 3)，b ＝(b 1，b 2，b 3).3、设),,(1111z y x P ，),,(2222z y x P 是空间中任意两点，则),,(12121221z z y y x x P P ---=，21221221221)()()(||z z y y x x P P -+-+-=，这是空间两点间的距离公式知识典例题型一空间向量的坐标运算例1 设,x y R ∈，向量(,1,1),b (1,,1),c (2,4,2)a x y ===-，c a⊥，c b//，则||a b +=（） A ．22 B 10C ．3D ．4【答案】C 【分析】根据,c a c b ⊥，结合向量的坐标运算可求得参数,x y 的值，再结合向量的加法与模长运算即可求解【详解】,241,2,(1,2,1)b c y y b ∴=-⨯∴=-∴=-,a c ⊥()214+20,a c x ∴⋅=+⋅-=1x ∴=，(1,1,1),(2,1,2)a a b ∴=∴+=-，222||2(1)23a b ∴+=+-+=，故选： C.巩固练习1、已知点()2,3,1B -，向量()3,5,2AB =-，则点A 坐标是（） A ．()1,2,3 B ．()1,2,3-C ．()5,8,1-D ．()5,8,1--【答案】D 【分析】设点(),,A x y z ，由点A 和点B 表示出向量AB ，构造等式求解即可. 【详解】设点(),,A x y z ，则向量()()2,3y,1z 3,5,2AB x =----=-，所以233512x y z -=-⎧⎪--=⎨⎪-=⎩⇒581x y z =⎧⎪=-⎨⎪=-⎩，所以点()5,8,1A --. 故选：D2、（多选）对于任意非零向量()111,,a x y z =，()222,,b x y z =，以下说法错误的有( ) A ．若a b ⊥，则1212120x x y y z z ++=B ．若//a b ，则111222x y z x y z == C ．121212222222111222cos ,x y z a zb x y =++⋅+>+<D ．若1111===x y z ，则a 为单位向量【详解】对于A 选项，因为a b ⊥，则1212120a b x x y y z z ⋅=++=，A 选项正确；对于B 选项，若20x =，且20y ≠，20z ≠，若//a b ，但分式12x x 无意义，B 选项错误；对于C 选项，由空间向量数量积的坐标运算可知121212222222111222cos ,x y z a z b x y =++⋅+>+<，C 选项正确；对于D 选项，若1111===x y z ，则2221113a =++=，此时，a 不是单位向量，D 选项错误. 故选：BD.题型二向量坐标求解直线关系例 2 棱长为1的正方体ABCD-A 1B 1C 1D 1中，E ，F ，G 分别是DD 1，BD ，BB 1的中点. （1）求证：EF ⊥CF ；（2）求EF 与CG 所成角的余弦值；（3）求CE 的长.【答案】（1）证明见解析；（21535. 【分析】建立空间直角坐标系，得出,,,,D E C F G 的坐标，由坐标运算得出,,,EF CF CG CE 的坐标，根据数量积公式证明EF ⊥CF ；由数量积公式求出EF 与CG 所成角的余弦值；再由模长公式得出CE 的长. 【详解】建立如图所示的空间直角坐标系Dxyz则1111 (0,0,0),0,0,,(0,1,0),,,0,1,1,2222 D E C F G⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以1111111,,,,,0,1,0,,0,1,2222222EF CF CG CE⎛⎫⎛⎫⎛⎫⎛⎫=-=-==-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（1）证明：因为111110022222EF CF⎛⎫⎛⎫⋅=⨯+⨯-+-⨯=⎪ ⎪⎝⎭⎝⎭，所以EF CF⊥，即EF⊥CF. （2）因为22211111111310,222242222 EF CG EF⎛⎫⎛⎫⎛⎫⎛⎫⋅=⨯+⨯+-⨯==++-=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22215102CG⎛⎫=++=⎪⎝⎭1154cos,=1535EF CGEF CGEF CG⋅∴==⋅⨯.（3）()222150122CE⎛⎫=+-+=⎪⎝⎭巩固练习1、在正方体ABCD-A1B1C1D1中，E，F分别为A1D1，BB1的中点，则cos EAF∠=____，EF=____. 【答案】2562建立空间直角坐标系，利用向量法得出cos ,AE AF ，从而得出cos EAF ∠，最后由模长公式得出EF . 【详解】以A 为原点，AB ，AD，AA 1分别为x 轴、y 轴、z 轴建立直角坐标系设正方体棱长为1，则110,,1,1,0,22E F ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭11110,,1,1,0,,1,,2222AE AF EF ⎛⎫⎛⎫⎛⎫∴===-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭122cos ,=55522AE AF AE AF AE AF⋅∴==⨯ 2222116cos ,||1522EAF EF EF ⎛⎫⎛⎫∴∠===+-+-= ⎪ ⎪⎝⎭⎝⎭. 故答案为：25；6 2、如图，长方体1111ABCD A B C D -中，14AA AB ==，2AD =，E 、F 、G 分别是1DD 、AB 、1CC 的中点，则异面直线1A E 与GF 所成角的余弦值是（）A ．0B ．105C ．22D ．155【答案】A建立空间直角坐标系，表示1,A E GF ，然后利用空间向量的夹角公式计算即可. 【详解】如图()()()()12,0,40,0,2,2,2,0,0,4,2A E F G ，所以()()12,0,2,2,2,2A E GF =--=--所以异面直线1A E 与GF 所成角的余弦值110⋅=A E GF A E GF故选：A巩固提升1、已知向量()1,1,1m λ=-，()2,2,3n λ=-，若()()m n m n +⊥-，则λ=__________ 【答案】7 【分析】根据空间向量的加法和减法的坐标运算,可求得m n +和m n -,结合空间向量垂直的坐标关系,即可求得λ的值. 【详解】向量()1,1,1m λ=-,()2,2,3n λ=- 则()32,3,4m n λ+=-,()1,1,2m n -=---因为()()m n m n +⊥- 所以()()0m n m n +⋅-=,代入可得()()32,3,41,1,20λ-⋅---=即23380λ---=,解得7λ= 故答案为: 72、已知a 、b 是异面直线，且a ⊥b ，12,e e 分别为取自直线a 、b 上的单位向量，且a ＝1223e e +，124b ke e =-，a b ⊥，则实数k 的值为___. 【答案】6 【分析】根据向量垂直其数量积为0，转化为基底的运算，即可得答案；【详解】由a b ⊥，得a b ⋅＝0，又12,e e 分别为取自直线a 、b 上的单位向量，∴120e e ⋅=∴(1223e e +)·(124ke e -)＝0，∴2120k -=，∴6k =. 故答案为：6.3、在空间直角坐标系O xyz -中，(0,0,0),O E F ，B 为EF 的中点，C 为空间一点且满足||||3CO CB ==，若1cos ,6EF BC <>=，，则OC OF ⋅=（）A ．9B ．7C ．5D ．3【解析】设(,,)C x y z，B ，(,,)OC x y z =，()BC x y z =，(EF =-，由(()1cos ,436EF BC x y z EF BC EF BC⋅-⋅===⋅⋅，整理可得：2x y -=-，由||||3CO CB ==化简得x y +=，以上方程组联立得x y ==，则()(,,)3OC OF x y z =⋅==. 故选：D.4、设ABCD －A 1B 1C 1D 1是棱长为a 的正方体，则有( ) A.AB →·C 1A →＝a 2B ．AB →·A 1C 1→＝2a 2C.BC →·A 1D →＝a 2 D ．AB →·C 1A 1→＝a 2【答案】 C【解析】建系如图．则AB →·C 1A →＝(a,0,0)·(－a ，－a ，－a )＝－a 2， AB →·A 1C 1→＝(a,0,0)·(a ，a,0)＝a 2， BC →·A 1D →＝(0，a,0)·(0，a ，－a )＝a 2，AB →·C 1A 1→＝(a,0,0)·(－a ，－a,0)＝－a 2，故只有C 正确．5、正方体ABCD －A 1B 1C 1D 1中，点E 为上底面A 1C 1的中心．若向量A E →＝AA 1→＋xAB →＋yAD →，则实数x ，y 的值分别为( ) A ．x ＝1，y ＝1 B ．x ＝1，y ＝12C ．x ＝12，y ＝12D ．x ＝12，y ＝1【答案】 C【解析】A E →＝AA 1→＋xAB →＋yAD →=,所以x=y=126、平行六面体ABCD －A 1B 1C 1D 1中，向量AB →，AD →，AA 1→两两的夹角均为60°，且|AB →|＝1，|AD →|＝2，|AA 1→|＝3，则|AC 1→|等于( ) A ．5 B ．6 C ．4 D ．8【答案】 A【解析】设AB →＝a ，AD →＝b ，AA 1→＝c ，则AC 1→＝a ＋b ＋c ，|AC 1→|2＝a 2＋b 2＋c 2＋2a ·b ＋2b ·c ＋2c ·a ＝25，因此|AC 1→|＝5.故选A.。

向量坐标知识点总结高中

向量坐标知识点总结高中一、向量坐标的概念向量是具有大小和方向的物理量。

在坐标系中，我们可以用坐标表示向量的位置。

向量坐标表示了向量在空间中的位置和方向。

向量的坐标通常用一组有序数对或有序数组来表示，这些数对或数组就是向量的坐标，也被称为分量。

在笛卡尔坐标系中，向量的坐标可以表示为一个n维空间，即n个坐标数的有序组。

二、向量坐标的表示方法1. n维向量的表示在n维空间中，向量的表示方法是用n个有序数组成的有序数对(a1, a2, ..., an)来表示。

这种表示方法也被称为向量的分量表示。

例如，一个三维空间中的向量可以表示为(a1, a2,a3)。

2. 向量的坐标表示在二维空间中，一个向量的坐标可以表示为一个有序数对(x, y)，在三维空间中，一个向量的坐标可以表示为一个有序数组(x, y, z)。

而在n维空间中，一个向量的坐标表示为一个有序数组(x1, x2, x3, ..., xn)。

3. 向量的坐标表示的意义向量的坐标表示出了向量在空间中的位置和方向。

通过坐标表示，我们可以方便地进行向量的运算，并求出向量的模长、方向余弦等属性。

三、向量坐标的运算1. 向量加法在向量坐标中，向量的加法就是将两个向量的对应分量相加。

例如，向量A(a1, a2)和向量B(b1, b2)相加得到的结果向量为A+B=(a1+b1, a2+b2)。

向量的加法满足交换律和结合律。

2. 向量的数乘向量的数乘就是将向量的每一个分量乘以一个实数。

例如，向量A(a1, a2)数乘k得到的结果向量为kA=(ka1, ka2)。

向量的数乘满足分配律和结合律。

3. 向量的减法向量的减法是将两个向量的对应分量相减。

例如，向量A(a1, a2)和向量B(b1, b2)相减得到的结果向量为A-B=(a1-b1, a2-b2)。

4. 向量的夹角两个向量之间的夹角可以通过它们的坐标表示来求解。

设向量A(a1, a2)和向量B(b1, b2)，它们之间的夹角θ可以通过以下公式计算得到：cosθ=(a1b1+a2b2)/(|A||B|)，其中|A|和|B|分别表示向量A和向量B的模长。

高二数学人教A版2019选择性必修第一册-空间向量及其运算的坐标表示

专题1.3 空间向量及其运算的坐标表示姓名:______________ 班级:______________重点空间直角坐标系难点空间向量运算的坐标表示一、空间直角坐标系例1-1．点)320(，，-A 在空间直角坐标系中的位置是（）。

A 、在x 轴上B 、在xOy 平面内C 、在yOz 平面内D 、在xOz 平面内【答案】C【解析】∵点A 的横坐标为0，∴点)320(，，-A 在yOz 平面内，故选C 。

例1-2．如图所示，正方体1111D C B A ABCD -的棱长为1，则点1B 的坐标是（）。

A 、)001(，，B 、)101(，，C 、)011(，，D 、)111(，，【答案】D【解析】点1B 到三个坐标平面的距离都为1，易知其坐标为)111(，，，故选D 。

例1-3．在空间直角坐标系中，点)531(-，，P 关于平面xOy 对称的点的坐标是（）。

A 、)531(，， B 、)531(，，- C 、)531(--，， D 、)531(，，-- 【答案】A【解析】由点P 关于xOy 平面对称后，它在x 轴、y 轴的分量不变，在z 轴的分量变为原来的相反数，∴对称点坐标为)531(，，P '，故选A 。

例1-4．在空间直角坐标系中，)432(，，P ，)432(---，，Q 两点的位置关系是（）。

A 、关于x 轴对称B 、关于yOz 平面对称C 、关于坐标原点对称D 、以上都不对【答案】C【解析】当三个坐标均相反时，两点关于原点对称，故选C 。

例1-5．如图所示，在空间直角坐标系中，2=BC ，原点O 是BC 的中点，点D 在平面yOz 内，且o 90=∠BDC ，o 30=∠DCB ，求点D 的坐标。

A 、)23210(--，， B 、)23210(，，- C 、)23210(-，， D 、)23210(，，【答案】B【解析】过点D 作BC DE ⊥，垂足为E ，在BDC Rt ∆中，o 90=∠BDC ，o 30=∠DCB ，2=BC ，得1||=BD 、3||=CD ， ∴2330sin ||||=⋅= CD DE ，2121160cos ||||||||||=-=⋅-=-= BD OB BE OB OE ， ∴点D 的坐标为)23210(，，-，故选B 。

(沪教版高二上)数学：8.1《向量的坐标表示及其运算》教案

8.1（1）向量的坐标表示及其运算（1）一．教学内容分析按现行上海市中小学数学课程标准，本章内容是在初中学习了向量的基本概念、向量的加法、减法、实数与向量的积等基础之上的后继学习.但与初中有所不同的是，初中教材对向量的学习是以“形”为主，主要从“形”的角度展开，而本章内容则主要是以“数”为主，从“数”的角度进行论述.当然，由于向量本身所具有的数形结合的特点，本章教材在以“数”为主旨处理教学内容的同时并没有弱化向量的“形”的方面的特征，而是二者相得益彰，互为依赖、互为补充.以“数”为主旨研究向量，其核心手段是向量及其运算的坐标表示.向量的坐标表示，实际上是向量的代数表示.在引入向量的坐标表示后，向量的加法、减法、实数与向量的积、向量的数量积等就完全可以用它们的坐标的加法、减法、数乘、数量积等运算来进行，使向量运算完全代数化，将数与形紧密结合起来.这样，就使得很多问题，可以转化为熟知的数量的运算进行解决.向量及其运算的坐标表示，一方面为用代数方法处理几何问题提供了通道，另一方面也为向量概念推广到高维空间指明了途径，同时，它也是高中数学中描述与处理如立几、解几、三角等诸多问题的一个有力的工具，在高考中也占有一个重要的地位.作为本章的第一课时，本节课的主要内容是向量的坐标表示及其运算.它是本章重要的基础性与前提性内容，它引入了将向量问题代数化的基本手段与方法——向量的坐标表示.本节内容课本上的基本处理方法是在引入一些相关的基础性的概念之后，通过任意向量都可以正交分解为基本单位向量,i j的线性组合，在向量的正交分解的基础上抽象概括出向量的坐标表示形式，并依据向量的正交分解的本质得到向量坐标形式下的运算法则.本节课要着力解决三个问题：一是要解决引入向量的坐标形式的必要性的问题，以引起学生学习的动机，二是要解决如何引入向量的正交分解及如何由此抽象出向量的坐标形式或者说是如何让学生理解向量坐标的本质的问题，三是要解决引入向量坐标形式以后如何以坐标形式进行运算的问题.作为本节课（本章的第一个课时）来说，第二个问题是重中重之中，因为如果学生不能理解向量的坐标是怎么来的，它的本质是什么，就会对后继学习带来一定的困难.因此，我们在课上要对这一点特别的重视.二．教学目标设计1.了解基本单位向量、位置向量、向量的正交分解等概念；会用坐标表示向量；会用两向量的坐标形式的和、差及实数与向量的积等运算解决相关问题.2. 经历如何将位置向量及任意向量表示为基本单位向量的线性组合这一正交分解的过程，以及经历如何通过向量的正交分解的本质概括抽象出向量的坐标表示的过程，初步形成抽象思维的能力；理解平面向量与一对有序实数对的一一对应关系，理解向量的坐标表示方法及其运算法则；体会数形结合的思想方法.3.感知数学中的运动、变化、相互联系与相互转化的规律，加深对辩证唯物主义观点的体验；发展从数学的角度分析和解决问题的能力，以及通过积极参与数学学习和问题解决的过程，增强学习的主体意识，形成数学的应用意识，养成严谨、慎密的思维习惯.三．教学重点及难点教学重点是如何写向量的坐标以及向量坐标形式的运算及其应用；教学难点是对向量的正交分解的过程的理解以及由向量的正交分解抽象出向量的坐标表示的过程的理解.四．教学流程设计小结与作业坐标表示的运算运用与深化知起点与终点的向量的坐标表示情境问题向量的正交分解向量的坐标表示位置向量的正交分解任意向量的正交分解位置向量的坐标表示任意向量的坐标表示返回到情境问题五．教学过程设计一.情境引入上海市莘庄中学的健美操队四名队员A 、B 、C 、D 在一个长10米，宽8米的矩形表演区域EFGH 内进行健美操表演.（1）若在某时刻1t ，四名队员A 、B 、C 、D 保持如图1所示的平行四边形队形.队员A 位于点F 处，队员B 在边FG 上距F 点3米处，队员D 位于距EF 边2米距FG 边5米处.你能确定此时队员C 的位置吗？EFGHHGF E 图2图18m 10m DCBADCB A 10m8m[说明] 此时队员C 在位于距EF 边5米距FG 边5米处.这个图形比较特殊，学生很快就会得到答案，这时教师引入第二个问题.（2）若在某时刻2t ，四名队员A 、B 、C 、D 保持如图2所示的平行四边形队形.队员A 位于距EF 边2米距FG 边1米处，队员B 在距EF 边6米距FG 边3米处，队员D 位于距EF 边4米距FG 边5米处.你能确定此时队员C 的位置吗？[说明] 不要求学生写出结果，只引导学生思考.这个图形更为一般一些，学生解决的可能不是很顺，这时，教师就可以说，这一节我们就来学习一个新的内容：向量的坐标表示及其运算，学习了这个内容之后，同学们只要花上两分钟或者只要一分钟的时间就可以解决这个问题了，引起学生学习的兴趣与探究的欲望.二．学习新课 1. 向量的正交分解我们称在平面直角坐标系中，方向与x 轴和y 轴正方向分别相同的的两个单位向量叫做基本单位向量，分别记为,i j ，如图，称以原点O 为起点的向量为位置向量，如下图左，OA 即为一个位置向量.思考1：对于任一位置向量OA ，我们能用基本单位向量,i j 来表示它吗？如上图右，设如果点A 的坐标为(),x y ，它在小x 轴，y 轴上的投影分别为M ，N ，那么向量OA 能用向量OM 与ON 来表示吗？（依向量加法的平行四边形法则可得OA OM ON =+），OM与ON 能用基本单位向量,i j 来表示吗？（依向量与实数相乘的几何意义可得,OMxi ON y j ==），于是可得：OA OM ON xi y j =+=+由上面这个式子，我们可以看到：平面直角坐标系内的任一位置向量OA 都能表示成两个相互垂直的基本单位向量,i j 的线性组合，这种向量的表示方法我们称为向量的正交分解.2.向量的坐标表示思考2：对于平面直角坐标系内的任意一个向量a ，我们都能将它正交分解为基本单位向量,i j 的线性组合吗？如下图左.显然，如上图右，我们一定能够以原点O 为起点作一位置向量OA ，使O Aa=.于是，可知：在平面直角坐标系内，任意一个向量a 都存在一个与它相等的位置向量OA .由于这一点，我们研究向量的性质就可以通过研究其相应的位置向量来实现.由于任意一个位置向量都可以正交分解为基本单位向量,i j 的线性组合，所以平面内任意的一个向量a 都可以正交分解为基本单位向量,i j 的线性组合.即：a =OA =xi y j +上式中基本单位向量,i j 前面的系数x,y 是与向量a 相等的位置向量OA 的终点A 的坐标.由于基本单位向量,i j 是固定不可变的，为了简便，通常我们将系数x,y 抽取出来，得到有序实数对（x,y ）.可知有序实数对（x,y ）与向量a 的位置向量OA 是一一对应的.因而可用有序实数对（x,y ）表示向量a ，并称（x,y ）为向量a 的坐标，记作：a =（x,y ）[说明]（x,y ）不仅是向量a 的坐标，而且也是与a 相等的位置向量OA 的终点A 的坐标！当将向量a 的起点置于坐标原点时，其终点A 的坐标是唯一的，所以向量a 的坐标也是唯一的.这样，我们就将点与向量、向量与坐标统一起来，使复杂问题简单化.显然，依上面的表示法，我们有：(1,0),(0,1),0(0,0)ij ===.例1.（课本例题）如图，写出向量,,a b c 的坐标. 解：由图知()1,2a=与向量b 相等的位置向量为OA ，可知()1,2b OA ==与向量c 相等的位置向量为OB ，可知()1,2c OB ==-[说明] 对于位置向量a ，它的终点的坐标就是向量的坐标；对于起点不在原点的向量,b c ，我们是通过先找到与它相等的位置向量，再利用位置向量的坐标得到它们的坐标.那么，有没有不通过位置向量，直接就写出任意向量的坐标的方法呢？答案是肯定的，而且很简便，但我们需几分钟后再来解决这个问题.让我们先学习向量坐标表示的运算：3.向量的坐标表示的运算我们学过向量的运算，知道向量有加法、减法、实数与向量的乘法等运算，那么，在学习了向量的坐标表示以后，我们怎么用向量的坐标形式来表示这些运算呢？设λ是一个实数，1122(,),(,).a x y b x y == 由于1111(,),a x y x i y j ==+ 2222(,)b x y x i y j ==+所以1122(,)(,)a b x y x y ±=±()()1122x i y j x i y j=+±+ ()()()()()121212121212,x i x i y j y j x x i y y j x x y y =±+±=±+±=±±()()11111111(,),ax y x i y j x i y j x y λλλλλλλ==+=+=于是有：1122(,)(,)x y x y ±()1212,x x y y =±±()1111(,),x y x y λλλ=[说明]上面第一个式子用语言可表述为：两个向量的和(差)的横坐标等于它们对应的横坐标的和(差)，两个向量的和(差)的纵坐标也等于它们对应的纵坐标的和(差)，可笼统地简称为：两个向量和(差)的坐标等于对应坐标的和(差)；同样，第二个式子用语言可表述为：数与向量的积的横坐标等于数与向量的横坐标的积，数与向量的积的纵坐标等于数与向量的纵坐标的积，也可笼统地简称为：数与向量积的坐标等于数与向量对应坐标的积.4.应用与深化下面我们来研究刚才提出的不通过位置向量，如何直接写出任意向量的坐标的问题：例2.如下图左，设()11,Px y 、()22,Q x y 是平面直角坐标系内的任意两点，如何用P 、Q 的坐标来表示向量PQ ？解：如上图右，向量PQ OQ OP =-()()()22112121,,,x y x y x x y y =-=--从而有 ()2121,PQ x x y y =--[说明]上面这个式子告诉我们：平面直角坐标系内的任意向量的横坐标等于它终点的横坐标与它起点的横坐标的差，纵坐标也等于它终点的纵坐标与它起点的纵坐标的差，可简称为“任意向量坐标=终点坐标-起点坐标”.例3.（课本例题）如图，平面上A 、B 、C 三点的坐标分别为()2,1、()3,2-、()1,3-.（1）写出向量,AC BC 的坐标；（2）如果四边形ABCD 是平行四边形，求D 的坐标.解：（1）()()12,313,2AC =---=-()()()13,322,1BC=----=（2）在上图中，因为四边形ABCD 是平行四边形，所以DC AB =设点D 的坐标为(),D D x y ，于是有()1,3D D x y AB ---=又 ()()32,215,1AB =---=-故()()1,35,1D D x y ---=-由此可得1531D D x y --=-⎧⎨-=⎩ 解得42D D x y =⎧⎨=⎩因此点D 的坐标为()4,2.练习：（1）请大家用两分钟的时间解答本节课一开始我们所提出的在某时刻2t ，健美操队员C 的位置问题.即：在某时刻2t ，四名队员A 、B 、C 、D 保持如图所示的平行四边形队形.如下图左，队员A 位于距EF 边2米距FG 边1米处，队员B 在距EF 边6米距FG 边3米处，队员D 位于距EF 边4米距FG 边5米处.你能确定此时队员C 的位置吗？DC(-1,3)A(2,1)B(-3,2)yxOEFGHDCB A 10m8myxOF A(2,1)B(6,3)CD(4,5)HGE解：以点F 为坐标原点，以边FG 为x 轴，以边FE 为y 轴，建立如上图右所示直角坐标系.则依题意有A(2,1),B(6,3),D(4,5),设C(x,y),则由ABCD 是平行四边形可得：(4,2)(2,4)(6,6)AC AB AD =+=+=又(,)(2,1)(2,1)ACx y x y =-=--故(2,1)(6,6)x y --= 于是 x=8, y=7,即C （8，7）.答：队员C 位于距EF 边8米、距FG 边7米处.（2）在某时刻3t ，四名队员A 、B 、C 、D 保持平行四边形队形.已知队员A 位于距EF 边2米距FG 边1米处，队员B 在距EF 边6米距FG 边3米处，队员C 位于如下图左所示的矩形阴影部分区域内（包括边界）某一位置.你能确定此时队员D 可能的位置区域吗？4m5m 8m 10mA B C DH GFEB(6,3)A(2,1)O E F G H DC 10m8m5m 4myx解：以点F 为坐标原点，以边FG 为x 轴，以边FE 为y 轴，建立如上图右所示直角坐标系.依题意有A(2,1),B(6,3),设D(x,y),则由ABCD 是平行四边形可得：(4,2)DC AB == 又D(x,y)，所以可得C(x+4,y+2)由题意54101642826x x y y ≤+≤≤≤⎧⎧⇒⎨⎨≤+≤≤≤⎩⎩ 于是可得队员D 可能的位置区域如图所示阴影部分（除去点B ）：6261yxO F A B CDHGE例4.已知向量()4,1a =-与()5,2b =，求23a b +的坐标.解：因为()28,2a=-，()315,6b =所以 ()()23815,2623,4a b +=+-+=三．巩固练习1. 如图，写出向量,,a b c 的坐标.2.已知(1,2)a =-，若其终点坐标是(2,1),则其起点的坐标是；若其起点坐标是(2,1),则其终点的坐标是 .3.已知向量()2,3a =-与()1,5b =-，求3a b -及3b a -的坐标.解：1.由题意：()()()()()()2,1,1,1,a b c==-=-- 2.设起点的坐标是(x,y)，则(2,1)-(x,y)=(-1,2),解得：(x,y)=(3,-1)，即起点的坐标是(3,-1)；设终点的坐标是(x,y)，则(x,y)-(2,1) =(-1,2),解得：(x,y)=(1,3)，即起点的坐标是(1,3).3. 3a b -=3()7,14---()()1,57,14-=-3b a -=()1,5--3()2,3-()7,14=-[另法]：3b a -=()3a b --=()7,14--()7,14=-四．课堂小结：本节课我们讲了哪些内容？（请学生作答）1.向量的正交分解（是如何对向量进行正交分解的？）2.向量的坐标表示（是用什么表示向量的坐标的？）3.向量的坐标运算（运算法则是什么？）五．作业布置1.已知(2,0),(1,3),a b ==-则a b +与a b -的坐标分别为( )(A)(3,3),(3,-3) (B)(3,3),(1,-3)(C)(1,3),(3,3) (D)(1,3),(3,-3)2.若点A 坐标为(2,-1),AB 的坐标为(4,6),则B 点的坐标为( )(A)(-2,-7) (B)(2,7)(C)(6,5) (D)(-2,5)3.已知(,4),(3,2).a x b y ==-若1,2a b =则x= ,y= . 4.已知AB (1)i x j +-=(2-x)，且AB 的坐标所表示的点在第四象限，则x 的取值范围是 .5.已知A(5,-2),B(2,-5),C(7,4),D(4,1),求证：AB=CD .6.已知(1,2),(3,1),(11,7),a b c =-=-=-并且.c xa yb =+求x,y 的值.7.已知22(,2),(5,)a mn b mn =+=，且.a b =求,.m n 的值.六．教学设计说明及反思在本节课的设计上，我是先用一个实际的情境问题引入，引起学生学习的兴趣，同时也在最后通过应用向量坐标这个工具对于这个问题的简便解决以及对于这一问题的进一步深化，使学生体会到引入向量坐标形式这个工具的必要性，并培养学生数学的应用意识，体会到数学是有用的，是有价值的；另外，在新授课内容的设计上，主要采用了以知识内容本身的逻辑关系而形成的继承关系为顺序的直线型的设计，主要有四个板块：一是向量的正交分解，二是向量的坐标表示，三是向量的坐标运算，四是应用与深化.其中向量的正交分解是从介绍基本单位向量与位置向量的概念入手，然后通过先处理位置向量的正交分解，再处理任意向量的正交分解；向量的坐标表示也是先处理位置向量的坐标表示然后再处理可化为位置向量的向量的坐标表示，最后在研究了坐标形式的运算之后才以例题的形式处理任意向量的坐标表示，这样设计的思路与课本上先交代任意向量都可以作一个与之相等的位置向量，然后只要研究位置向量就能得到原来向量的性质的思路略有不同，这样设计的出发点主要是希望能够给学生的学习创造一个按知识自身的逻辑顺序而层层递进的、螺旋上升的学习过程，使学生能够步步为营的在充分弄清前一个问题的基础上进入下一个问题，从而达到有效分散学生在学习中的难点的目的.在应用与深化这一板块上，我主要设计了五个问题，第一个问题是例1，置于向量的坐标表示这一板块之中，其目的是为了在初次接触坐标表示时，加深对位置向量与可化为位置向量的坐标的理解，以及舒缓一下学生在较长时间的数学纯理论学习中所聚集的紧张或疲劳情绪，为下面的学习作点准备；第二个问题是例2，解决任意向量的坐标表示问题，这也是这一节课必须要解决的一个重点问题；第三个问题是例3，其目的是通过对任意向量的坐标表示公式的应用，强化对这一公式的记忆与掌握，同是也为下一问题即引入问题的解决作知识与方法上的铺垫；第四个问题是解决引入的情境问题并作进一步深化；第五个问题是对向量坐标表示运算公式的应用.同时，最后又设置了三个小题，作为课内练习，机动使用.整个一节课，如果用一句话概括基本的设计思路，那就是：低起点（使学生容易入手）、小步走（使学生容易理解）、重视过程（重视知识的发生过程及重视学生的学习过程）、强化训练（训练是掌握与提高的有效途径）.。

空间向量运算的坐标表示课件-高二上学期数学人教A版(2019)选择性必修第一册

(2) 已知 a ＋ b ＝ (2 ， 2 ， 2 3 ) ， a － b ＝ (0 ， 2 ， 0) ，则 a ＝ ___(_1_，___2_，___3_)_____，b＝_____(_1_,0_，____3_)_____，a·b＝___4___.
[解析] (1)易得 2a＋3b＝(4,4,5)，a－b＝(－3,2,0)，则(2a＋3b)·(a－ b)＝4×(－3)＋4×2＋5×0＝－4.
2．借助利用空间向量的坐标运算解决平行、垂直问题，提升数学运算及逻辑推理素养．
必备知识•探新知
知识点 1 空间向量的坐标运算
设a＝(a1，a2，a3)，b＝(b1，b2，b3)，有
向量运算向量表示
坐标表示
加法减法数乘数量积
a＋b a－b
λa a·b
a＋b＝___(a_1_＋__b_1_，__a_2＋__b_2_，__a_3_＋__b_3)___ a－b＝___(a_1_－__b_1_，__a_2－__b_2_，__a_3_－__b_3)___ λa＝___(_λa_1_，__λ_a_2_，__λa_3_)__，λ∈R a·b＝__a_1_b_1＋__a_2_b_2_＋__a_3b_3__
(2) 已知a＝(x1，y1，z1)，若x1＝y1＝z1＝1，则a为单位向量．( × )
(3)
若 a＝(a1，a2，a3)，b＝(b1，b2，b3)，a∥b，则ab11
＝
a2 b2
＝
ab33.(
×
)
提示：(1)由 a·b＝0，得 a⊥b.
(2)若 x1＝y1＝z1＝1，则|a|＝ 12＋12＋12＝ 3，所以 a 不是单位向量．
则 B(0,1,0)，M(1,0,1)，N0，12，1. (1)∵B→M＝(1，－1,1)，

高二数学空间向量坐标2

向量的模的坐标表示：
| 2 2 2 |a ． ax a y az
2 2 2 向量的方向余弦的坐标表示：当 a x a y a z 0时，可得 ax cos ， 2 2 ax ay a z2
cos
cos
ay
2 2 ax ay a z2
的单位向量，并称它们为这一坐标系的基本单位向量．
P P a ( x x ) 1 2 xi 2 1 i 、 Q1Q2 a y j ( y 2y 1) j 、 R1 R2 a z k ( z 2z 1) k ，

R2
z
R1
M1

M1
M2
a

O
y
x
向量的方向余弦：因为向量的坐标就是向量在坐标轴上的投影，所以
| cos ； a x| M 1M 2 |cos | a | cos ； a y| M 1M 2 |cos | a | cos ； a z| M 1M 2 |cos | a 的方向余弦．上述cos 、cos 、cos 叫做向量 a
b { b x，b y，b z }，则设a { a x，a y，a z }0， a ， b 则b //a 即b //a { b x，b y，b z }{ a x，a y，a z }，
bx b y bz 于是． ax a y az
即于是
，
az 2 2 2 ． ax a y az
2 2 2 ax ay az
方向余弦的平方和：
cos 2 cos 2 cos 2
a a a
2 x 2 y 2 z

高二数学空间向量运算的坐标表示——夹角和距离公式

高二数学空间向量运算的坐标表示——夹角和距离公式教学要求：掌握空间向量的长度公式、夹角公式、两点间距离公式、中点坐标公式，并会用这些公式解决有关问题．教学重点：夹角公式、距离公式．教学难点：夹角公式、距离公式的应用．教学过程：一、复习引入1. 向量的直角坐标运算法则：设a ＝123(,,)a a a ，b ＝123(,,)b b b ，则⑴a ＋b ＝112233(,,)a b a b a b +++； ⑵a －b ＝112233(,,)a b a b a b ---； ⑶λa ＝123(,,)a a a λλλ()R λ∈； ⑷a ·b ＝112233a b a b a b ++上述运算法则怎样证明呢？（将a ＝1a i ＋2a j ＋3a k 和b ＝1b i ＋2b j ＋3b k 代入即可）2. 怎样求一个空间向量的坐标呢？（表示这个向量的有向线段的终点的坐标减去起点的坐标．） 3．练习：（1）与向量（1，-3，2）平行的一个向量的坐标为（ C ） A ．（1，3，2） B ．（-1，-3，2） C ．（-2，6，-4） D ．（1，-3，-2）（2）已知点A （1，2，-1），且向量OC 与向量OA 关于平面xoy 对称，向量OB 与向量OA 关于平面x 轴对称，求向量和向量AB答案：BC =（0，4，0） =（0，-4，2）（3）已知向量a =（2，-1，3）求一向量，使∥，且∣∣=3∣∣ 答案： =（6，-3，9）或=（-6，3，5）（4）已知空间三点A （-1，0，2），B （-1，1，2），C （-3，0，4），设=，=，若k +与k -2互相垂直，求k 的值。

（K =2或k = －25）二、新课讲授⒈ 向量的模：设a ＝123(,,)a a a ，b ＝123(,,)b b b ，求这两个向量的模.｜a，｜b向量的长度公式．这个公式的几何意义是表示长方体的对角线的长度． 2. 夹角公式推导：∵ a ·b ＝|a ||b |cos ＜a ,b ＞∴ 1122a b a b a++cos ＜a ,b ＞由此可以得出：cos ＜a ,b这个公式成为两个向量的夹角公式．利用这个共识，我们可以求出两个向量的夹角，并可以进一步得出两个向量的某些特殊位置关系：当cos ＜a 、b ＞＝1时，a 与b 同向；当cos ＜a 、b ＞＝－1时，a 与b 反向；当cos ＜a 、b ＞＝0时，a ⊥b ．例1．已知A （1，0，0），B （0，-1，1），OB OA λ+与的夹角为120°，求λ的值（66-）例2：如图，在正方体1111ABCD A B C D -中，1111114A B B E D F ==，求1BE 与1DF 所成的角的余弦值．分析：如何建系？→ 点的坐标？→ 如何用向量运算求夹角？→ 练习：（1）如图：空间坐标系中，原点O 是BC 的中点，点A （)0,21,23，D 是平面yox 上，BC=2，∠BDC=90°，∠DCB=30°，（1）求D 点的坐标，（2）求BC的值。

向量的坐标表示与解析几何

向量的坐标表示与解析几何向量是解析几何中的重要概念之一，它可以用不同的表示方式来描述。

其中，坐标表示是一种常见且方便的表达方式。

本文将介绍向量的坐标表示以及在解析几何中的应用。

一、向量的坐标表示向量的坐标表示是指使用有序数对或有序数组来表示向量的坐标。

通常情况下，二维向量使用二维坐标表示，三维向量使用三维坐标表示。

1. 二维向量的坐标表示二维向量可以用一个有序数组(x, y)来表示，其中x表示向量在x轴上的分量，y表示向量在y轴上的分量。

例如，向量AB可以表示为(Ax, Ay)，其中Ax和Ay分别表示向量AB在x轴和y轴上的分量。

2. 三维向量的坐标表示三维向量可以用一个有序数组(x, y, z)来表示，其中x表示向量在x轴上的分量，y表示向量在y轴上的分量，z表示向量在z轴上的分量。

例如，向量ABC可以表示为(Ax, Ay, Az)，其中Ax、Ay和Az分别表示向量ABC在x轴、y轴和z轴上的分量。

二、向量的坐标运算向量的坐标表示使得向量的运算更加便捷，常见的运算包括向量的加法、减法、数量乘法、点乘和叉乘等。

1. 向量的加法与减法设向量A的坐标表示为(Ax, Ay, Az)，向量B的坐标表示为(Bx, By, Bz)，则向量A和B的加法运算为(Ax+Bx, Ay+By, Az+Bz)，减法运算为(Ax-Bx, Ay-By, Az-Bz)。

2. 向量的数量乘法设向量A的坐标表示为(Ax, Ay, Az)，k为实数，则向量A与k的数量乘法运算为(k*Ax, k*Ay, k*Az)。

其结果是向量A上每个分量乘以k。

3. 向量的点乘设向量A的坐标表示为(Ax, Ay, Az)，向量B的坐标表示为(Bx, By, Bz)，则向量A和B的点乘运算为(Ax*Bx + Ay*By + Az*Bz)。

点乘的结果是一个实数。

4. 向量的叉乘设向量A的坐标表示为(Ax, Ay, Az)，向量B的坐标表示为(Bx, By, Bz)，则向量A和B的叉乘运算为(Ay*Bz - Az*By, Az*Bx - Ax*Bz,Ax*By - Ay*Bx)。

高二数学向量的坐标表示及运算

例5、已知 a=（4，2）， b=（6，y），且 a//b ，求 y 的值。
例6、已知A（-1，-1），B（1，3），C（2， 5），判断A、B、C三点的位置关系。
C B A
； / MG电子游戏；
意の语气道.“啊?”纪沄国尪吃惊の瞪大の眼睛.“居然是真の,他们真の要授与你名誉大公爵.”纪沄国尪语气中充满了震惊,她先前也听到一些传言,但并不信任是真の.王国の名誉大公爵,何其了得.“太好了,真の太好了！鞠言战申,你成为临高王国の名誉大公爵,那就不用离开龙岩国了.”纪沄国尪最近一直有一种负罪感,她觉得是自身给鞠言带来了牵绊,觉得自身阻碍了鞠言の修行之路.现在鞠言成了一个王国の名誉大公爵,那就没问题了.鞠言成为临高王国名誉大公爵の消息,不胫而走,很快便是传开了.“鞠言战申,真の成了临高王国の名誉大公爵?”“应该是没错了,俺认识临高王国の一位大臣,他亲口告诉俺の消息.”“嗯,俺也听说了.是临高王国の毕微王尪大人,将鞠言战申邀请了过去,然后亲自与鞠言战申说の呐件事.而鞠言战申,也接受了临高王国の授与.”“鞠言战申,呐是真正の飞黄腾达了啊！王国の名誉大公爵,啧啧……”“真是令人有些无法置信.七大王国中,都有一些名誉大公爵存在,可俺还从未听说过,一个王国の名誉大公爵,会授与不是混元无上级强者の善王.”“谁说不是！就算是混元无上级の存在,也未必能得到一个王国の名誉大公爵授与.临高王国,到底看上了鞠言战申哪一点?鞠言战申,又能给临高王国带来哪个好处?”“鞠言战申成为临高王国の名誉大公爵,那就能享受到王国の大量资源福利,但临高王国又能从鞠言战申身上得到哪个呢?鞠言战申虽然实历很强,可也不能与老牌の混元无上级强者相比吧?”议论纷纷,不知道有多少人,羡慕着鞠言,甚至还有很多人产生了妒忌の情绪.尤其是那些准混元无上级存在,多多少少の都有些不忿.玄秦尪国人员住处.“陛下,消息确认了,毕微王尪确实决定授予鞠言临高王国名誉大公爵の身份.不久之前,毕微王尪私下里与鞠言见面了.”一名玄秦尪国の公爵,对廉心国尪禀报说道.廉心国尪表情阴冷,玉手狠狠の握成拳头.“鞠言成为临高王国の荣誉大公爵,那俺们就不能对他进行报复了.”玄秦尪国の战申,摇摇头说道：“原以为,几个王国会叠视鞠言想要拉拢鞠言,但没有想到,毕微王尪竟如此干脆,在鞠言不愿意离开龙岩国情况下,直接就决定授予鞠言王国荣誉大公爵の身份.”“王国荣誉大公爵……又怎样！”廉心国尪咬着牙齿道.“就算如此,战申榜排位赛决赛决断,他也一样可能会死.在排位赛中被杀死,临高王国也无可奈何.”廉心国尪又说道.“陛下说得没错,但是……前提需要鞠言去挑战混元无上级强者.混元无上之下の善王,怕是没人能杀死鞠言.”玄秦尪国战申轻轻摇头道.“陛下,呐个鞠言恐怕不会傻乎乎の去挑战混元无上级强者の.俺听说,东华尪国の卢冰战申,在淘汰阶段第三轮对战结束后与鞠言接触过,卢冰战申想要鞠言在决赛中挑战他,但鞠言没有答应.”玄秦尪国战申又接着说道.“是啊！如果鞠言不去挑战混元无上,那别人也无可奈何.”一名公爵也开口说道.“呐个该死の混账东西！”廉心国尪满是愤恨の说道.法辰王国国都皇宫.“倒是让毕微王尪抢先了！”仲零王尪苦笑着说道.在他面前,有多名法辰王国の叠要人员.仲零王尪,也考虑过授与鞠言法辰王国名誉大公爵の身份,他还命人专门放出消息.只是,他仅仅是考虑,并未付诸于行动.而临高王国の毕微王尪,先一步行动了.“毕微王尪,真是……”柳涛公爵有些不知该说哪个.“柳涛公爵,你走一趟去见见鞠言战申如何?”仲零王尪看向柳涛公爵.“陛下,你の意思是?”柳涛公爵略微皱眉望着仲零王尪.“法辰王国,也可授予鞠言战申名誉大公爵の身份.”仲零王尪道.“陛下,可是鞠言战申已经接受了临高王国の授予,他无法同事成为两个王国の名誉大公爵.”柳涛公爵立刻就说道.在场の其他人,也都不解の目光看着仲零王尪.(本章完)第三零一零章倪炯老祖鞠言战申已经接受了临高王国の名誉大公爵授与,如何再接受法辰王国の名誉大公爵授予?大殿内の众人, 都费解の目光望着仲零王尪.“名誉大公爵の身份授与,又不是几句话就能完成の.现在,鞠言战申还不是临高王国名誉大公爵身份,俺们法辰王国,当然也能够与鞠言战申商谈此事.鞠言战申就在俺们法辰王国境内,要授与他名誉大公爵身份,俺们可比临高王国方便の多.”仲零王尪笑道.“呐……”“陛下,呐样做恐怕会引来临高王国の不满啊！”贵族大臣都露出犹豫の表情.“诸位,呐可不是谦让の事情.俺预感,如果能够将鞠言战申拉上俺们の巨舰,未来对俺们法辰王国会有超乎想象の好处.”仲零王尪眼申一凝道.仲零王尪心中所想の,也是天庭,只是他没有直接说出来.“陛下,俺知道了,俺立刻就去见鞠言战申.”柳涛公爵领命而去.在鞠言和纪沄国尪の居所,柳涛公爵见到了鞠言战申.“柳涛公爵,俺已经接受了临高王国の授予,恐怕俺只能对法辰王国说抱歉了.”鞠言在听过柳涛公爵の话后,摇头说道.“很感谢法辰王国和仲零王尪の美意,但俺不能出尔反尔.”鞠言又说道.“唉……俺们法辰王国晚了一步啊！”柳涛公爵叹息一声.他也早就预料过呐种结果,此次他领命而来,也不过是试试看の意思.恐怕就连仲零王尪,也没抱着多大の希望,仲零王尪只是有些后悔没有早点做出决定,让那临高王国抢先了一步.柳涛公爵带着失望の情绪告